Применение интегрального исчисления в механике. Реферат: Применение дифференциального и интегрального исчисления к решению физических и геометрических задач в MATLab
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Реферат на тему: «Интеграл и его применение»
Студентки
мед. колледжа
№2 203 группы
Куликовой Марии
Санкт - Петербург 2010 год
Введение
Символ интеграла введен с 1675 г., а вопросами интегрального исчисления занимаются с 1696 г. Хотя интеграл изучают, в основном, ученые-математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без дифференциального и интегрального исчислений. Поэтому, я и решила исследовать интеграл и его применение.
История интегрального исчисления
История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи на вычисление площадей. Латинское слово quadratura переводится как “придание квадратной формы”. Необходимость в специальном термине объясняется тем, что в античнoe время (и позднее, вплоть до XVIII столетия) еще не были достаточно развиты представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача “о квадратуре круга” круга» не может, как известно, быть решена с помощью циркуля и линейки.)
Символ т введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summ a) Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integro, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина инте грал иное: слово integer означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласил ись с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики-интегральное исчисление (calculus integralis), которое ввел И. Бернулли.
Другие известные термины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило бол ее раннее «примитивная функция», которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как «начальный»: F(x) = т f(x)dx - начальная (или первоначальная, или первообразная) для f (x), которая получается из F(x) дифференцированием.
В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную b, называют определенным интегралом (обозначение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эйлер).
Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т.е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 - ок. 355 до н.э.). С помощью этого метода Евдокс доказал, например, что площади двух кругов относятся как квадраты их диаметров, а объем конуса равен 1/3 объёма цилиндра, имеющего такие же основание и высоту.
Метод Евдокса был усовершенствован Архимедом. Основные этапы, характеризующие метод Архимеда: 1) доказывается, что площадь круга меньше площади любого описанного около него правильного многоугольника, но больше площади любого вписанного; 2) доказывается, что при неограниченном удвоении числа сторон разность площадей этих многоугольн иков стремится к нулю; 3) для вычисления площади круга остается найти значение, к которому стремится отношение площади правильного многоугольника при неограниченном удвоении числа его сторон.
С помощью метода исчерпывания, целого ряда других остроумных соображений (в том числе с привлечением моделей механики) Архимед решил многие задачи. Он дал оценку числа p (3.10/71 Архимед предвосхитил многие идеи интегрального исчисления. (Добавим, что практически и первые теоремы о пределах были доказаны им.) Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления. Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции (он связан в первую очередь с атомистическими воззрениями Демокрита). Например, криволинейную трапецию (рис. 1, а) они представляли себе составленной из вертикальных отрезков длиной f(х), которым, тем не менее, приписывали площадь, равную бесконечно малой величине f(х)dx . В соответствии с таким пониманием искомая площадь считалась равной сумме бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму. На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571-1630) в своих сочинениях “Новая астрономия”. 1609 г. и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры ограниченной эллипсом) и объемов (тело разрезалось на 6ecконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598-1647) и Э. Торричелли (1608-1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополнительных предположениях. Пусть требуется найти площадь фигуры, изображенной на рисунке 1, б, где кривые, ограничивающие фигуру сверху и снизу, имеют уравнения y = f(x) и y=f(x)+c. Представляя фигуру составленной из «неделимых», по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину с. Передвигая их в вертикальном направлении, можем составить из них прямоугольник с основанием b-а и высотой с. Поэтому искомая площадь равна площади полученного прямоугольника, т.е. S = S1 = c (b - а). Общий принцип Кавальери для площадей плоских фигур формулируется так: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 1, в). Тогда площади фигур Ф1 и Ф2 равны. Аналогичный принцип действует в стереометрии и оказывается полезны м при нахождении объемов. В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П.Ферма уже в 1629 г. задачу квадратуры любой кривой у = хn, где п - целое (т.е по существу вывел формулу т хndx = (1/n+1)хn+1), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу (1630-1677), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функций в виде степенных рядов. Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия исчисления еще не было. Необходимо было выделить общие идеи лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известным под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научится находить первообразные многих функций, дать логические нового исчисления и т.п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М.В. Остроградский (1801-1862), В.Я. Буняковский (1804-1889), П.Л. Чебышев (1821-1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции. Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков, немецкого ученого Б. Римана (1826-1866), французского математика Г. Дарбу (1842-1917). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1838-1922) теории меры. Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875-1941) и А. Данжуа (188 4-1974), советским математиком А.Я. Хинчинчиным (1894-1959). Если F(x) - одна из первообразных функции f(x) на промежутке J, то первообразная на этом промежутке имеет вид F(x)+C, где CОR. Определение. Множество всех первообразных функции f(x) на промежутке J называется определенным интегралом от функции f(x) на этом промежутке и обозначается т f(x)dx. т f(x)dx = F(x)+C, где F(x) - некоторая первообразная на промежутке J. f - подынтегральная функция, f(x) - подынтегральное выражение, x - переменная интегрирования, C - постоянная интегрирования. Свойства неопределенного интеграла. (т f(x)dx) ў = т f(x)dx, т f(x)dx = F(x)+C, где F ў(x) = f(x) (т f(x)dx) ў= (F(x)+C) ў= f(x) т f ў(x)dx = f(x)+C - из определения. т k f (x)dx = k т fў(x)dx если k - постоянная и F ў(x)=f(x), т k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k т fў(x)dx т (f(x)+g(x)+...+h(x))dx = т f(x)dx + т g(x)dx +...+ т h(x)dx т (f(x)+g(x)+...+h(x))dx = т dx = т ўdx = F(x)+G(x)+...+H(x)+C= т f(x)dx + т g(x)dx +...+ т h(x)dx, где C=C1+C2+C3+...+Cn. Табличный способ. Способ подстановки. Если подынтегральная функция не является табличным интегралом, то возможно (не всегда) применить этот способ. Для этого надо: разбить подынтегральную функцию на два множителя; обозначить один из множителей новой переменной; выразить второй множитель через новую переменную; составить интеграл, найти его значение и выполнить обратную подстановку. Примечание: за новую переменную лучше обозначить ту функцию, которая связана с оставшимся выражением. 1. т xЦ(3x2-1)dx; Пусть 3x2-1=t (tі0), возьмем производную от обеих частей: у dt 1 1 у 1 1 t 2 2 1 ---Ш ф- t 2 = - ф t 2dt = - --- + C = -Ц 3x2-1 +C т sin x cos 3x dx = т - t3dt = - - + C Пусть cos x = t Метод преобразования подынтегральной функции в сумму или разность: т sin 3x cos x dx = 1/2 т (sin 4x + sin 2x) dx = 1/8 cos 4x - ј cos 2x + C у x4+3x2+1 у 1 1 ф dx = ф(x2+2 - ---) dx = - x2 + 2x - arctg x + C х x2+1 х x2+1 3 Примечание: при решении этого примера хорошо делать многочлены ”углом”. По частям. Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу. (u(x)v(x))"=u"(x)v(x)+u(x)v(x) u"(x)v(x)=(u(x)v(x)+u(x)v"(x) т u"(x)v(x)dx=т (u(x)v(x))"dx - т u(x)v"(x)dx т u"(x)v(x)dx=u(x)v(x)dx - т u(x)v"(x)dx т x cos (x) dx = т x dsin x = x sin x - т sin x dx = x sin x + cos x + C Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией. Способы нахождения площади криволинейной трапеции Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке , то площадь соответствующей криволинейной трапеции равна приращению первообразных. Дано: f(x)- непрерывная неопр. функция, xО. Доказать: S = F(b) - F(a), где F(x) - первообразная f(x). Доказательство: 1) Рассмотрим вспомогательную функцию S(x). Каждому xО поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой (рис. 2), проходящей через точку с этой абциссой и параллельно оси ординат. Следовательно S(a)=0 и S(b)=Sтр Докажем, что S(a) - первообразная f(x). D(f) = D(S) = S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), при Dx®0 DS - прямоугольник Dx®0 со сторонами Dx и f(x0) S"(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) - Dx®0 Dx®0 первообразная f(x). Следовательно по теореме об общем виде первообразной S(x)=F(x)+C. Т.к. S(a)=0, то S(a) = F(a)+C S = S(b)=F(b)+C = F(b)-F(a) 1). Разобьем отрезок на n равных частей. Шаг разбиения (рис. 3) Dx=(b-a)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+f(xn)) При n®Ґ получим, что Sтр= Dx(f(x0)+f(x1)+...+f(xn)) Предел этой суммы называют определенным интегралом. Сумма стоящая под пределом, называется интегральной суммой. Определенный интеграл это предел интегральной суммы на отрезке при n®Ґ. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала. a - нижний предел интегрирования; b - верхний. Формула Ньютона-Лейбница. Сравнивая формулы площади криволинейной трапеции делаем вывод: если F - первообразная для b на , то т f(x)dx = F(b)-F(a) т f(x)dx = F(x) ф = F(b) - F(a) Свойства определенного интеграла. т f(x)dx = т f(z)dz т f(x)dx = F(a) - F(a) = 0 т f(x)dx = - т f(x)dx т f(x)dx = F(a) - F(b) т f(x)dx = F(b) - F(a) = - (F(a) - F(b)) Если a, b и c любые точки промежутка I, на котором непрерывная функция f(x) имеет первообразную, то т f(x)dx = т f(x)dx + т f(x)dx F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a) (это свойство аддитивности определенного интеграла) Если l и m постоянные величины, то т (lf(x) +m j(x))dx = l т f(x)dx + m тj(x))dx - Это свойство линейности определенного интеграла. т (f(x)+g(x)+...+h(x))dx = т f(x)dx+ т g(x)dx+...+ т h(x)dx т (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H(a)+Cn=b b b = т f(x)dx+ т g(x)dx+...+ т h(x)dx Набор стандартных картинок (рис. 4, 5, 6, 7, 8) Рис. 4 Рис. 5 Рис. 6 Рис. 7 Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0. Надо: рассмотреть симметрию функции относительно оси OX. ABCD®A"B"CD b S(ABCD)=S(A"B"CD) = т -f(x)dx S= т f(x)dx = т g(x)dx S = т (f(x)-g(x))dx+т(g(x)-f(x))dx S= т (f(x)+m-g(x)-m)dx = т (f(x)- g(x))dx т ((f(x)-g(x))dx S= т (f(x)+m-g(x)-m)dx = Т (f(x)- g(x))dx Если на отрезке f(x)іg(x), то площадь между этими графиками равна т ((f(x)-g(x))dx Функции f(x) и g(x) произвольные и неотрицательные S=т f(x)dx - т g(x)dx = т (f(x)-g(x))dx Применение интеграла
В физике.
Работа силы (A=FScosa, cosa № 1) Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно приращение кинетической энергии частицы за время dt равно скалярному произведению Fds, где ds - перемещение частицы за время dt. Величина называется работой, совершаемой силой F. Пусть точка движется по оси ОХ под действием силы, проекция которой на ось ОХ есть функция f(x) (f-непрерывная функция). Под действием силы точка переместилась из точки S1(a) в S2(b). Разобьем отрезок на n отрезков, одинаковой длины Dx = (b - a)/n. Работа силы будет равна сумме работ силы на полученных отрезках. Т.к. f(x) -непрерывна, то при малом работа силы на этом отрезке равна f(a)(x1-a). Аналогично на втором отрезке f(x1)(x2-x1), на n-ом отрезке - f(xn-1)(b-xn-1). Следовательно работа на равна: А » An = f(a)Dx +f(x1)Dx+...+f(xn-1)Dx= ((b-a)/n)(f(a)+f(x1)+...+f(xn-1)) Приблизительное равенство переходит в точное при n®Ґ А = lim [(b-a)/n] (f(a)+...+f(xn-1))= т f(x)dx (по определению) Пусть пружина жесткости С и длины l сжата на половину свой длины. Определить величину потенциальной энергии Ер равна работе A, совершаемой силой -F(s) упругость пружины при её сжатии, то Eп = A= - т (-F(s)) dx Из курса механики известно, что F(s)= -Cs. Отсюда находим Еп= - т (-Cs)ds = CS2/2 | = C/2 l2/4 Ответ: Cl2/8. Координаты центра масс Центр масс - точка через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела. Пусть материальная однородная пластина о имеет форму криволинейной трапеции {x;y |aЈxЈb; 0ЈyЈf(x)} и функция y=f(x) непрерывна на , а площадь этойкриволинейной трапеции равна S, тогда координаты центра масс пластины о находят по формулам: x0 = (1/S) т x f(x) dx; y0 = (1/2S) т f 2(x) dx; Центр масс. Найти центр масс однородного полукруга радиуса R. Изобразим полукруг в системе координат OXY (рис. 9). Из соображений симметрии и однородности замечаем, что абсцисса точки M Функция, описывающая полукруг имеет вид: Пусть S = pR2/2 - площадь полукруга, тогда y = (1/2S) тЦ(R2-x2)dx = (1/pR2) тЦ(R2-x2)dx = -R -R R = (1/pR2)(R2x-x3/3)|= 4R/3p Ответ: M(0; 4R/3p) Путь, пройденный материальной точкой Если материальная точка движется прямолинейно со скоростью u=u(t) и за время T= t2-t1 (t2>t1) прошла путь S, то В геометрии
Объём - количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1ди, 1м и т.д.). Количество кубов единичного объёма размещенных в данном теле - объём тела. Аксиомы объёма: Объём - это неотрицательная величина. Объём тела равен сумме объёмов тел, его составляющих. Найдем формулу для вычисления объёма (рис. 10): выберем ось ОХ по направлению расположения этого тела; определим границы расположения тела относительно ОХ; введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ. разобьем отрезок на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx Dx®0, а Sk®Sk+1, а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH. Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при n®Ґ называется интегралом a V= т S(x)dx, где S(x) - сечение плоскости, проходящей через b выбранную точку перпендикулярно оси ОХ. Для нахождения объема надо: 1). Выбрать удобным способом ось ОХ. 2). Определить границы расположения этого тела относительно оси. 3). Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку. 4). Выразить через известные величины функцию, выражающую площадь данного сечения. 5). Составить интеграл. 6). Вычислив интеграл, найти объем. Объем фигур вращения Тело, полученное в результате вращения плоской фигуры, относительно какой-то оси, называют фигурой вращения. Функция S(x) у фигуры вращения есть круг. Sсеч(x)=p f 2(x) Длина дуги плоской кривой Пусть на отрезке функция y = f(x) имеет непрерывную производную y" = f "(x). В этом случае длину дуги l “куска” графика функции y = f(x), xО можно найти по формуле l = т Ц(1+f"(x)2)dx 1. М.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд, “Алгебра и математический анализ”, Москва, 1993 г. 2. “Сборник задач по математическому анализу”, Москва, 1996 г. 3. И.В. Савельев, “Курс общей физики”, том 1, Москва, 1982 г. 4. Для подготовки данной работы были использованы материалы с сайта http://referatovbank.ru/ Идеи интегрального исчисления в работах древних математиков. Особенности метода исчерпывания. История нахождения формулы объема тора Кеплера. Теоретическое обоснование принципа интегрального исчисления (принцип Кавальери). Понятие определенного интеграла. презентация , добавлен 05.07.2016 История интегрального исчисления. Определение и свойства двойного интеграла. Его геометрическая интерпретация, вычисление в декартовых и полярных координатах, сведение его к повторному. Применение в экономике и геометрии для вычисления объемов и площадей. курсовая работа , добавлен 16.10.2013 Определение определенного интеграла, его свойства. Длина дуги кривой. Площадь криволинейной трапеции. Площадь поверхности вращения. Площади фигур, ограниченных графиками функций, ограниченных линиями, заданными уравнениями. Вычисление объемов тел. контрольная работа , добавлен 10.02.2017 История появления понятия "интеграла" и интегрального исчисления, его особенности и значение. Интеграл как один из основных инструментов работы с функциями. Обоснование необходимости выражения всех физических явлений в виде математической формулы. презентация , добавлен 19.05.2014 Определение криволинейного интеграла по координатам, его основные свойства и вычисление. Условие независимости криволинейного интеграла от пути интегрирования. Вычисление площадей фигур с помощью двойного интеграла. Использование формулы Грина. контрольная работа , добавлен 23.02.2011 Способы вычисления интегралов. Формулы и проверка неопределенного интеграла. Площадь криволинейной трапеции. Неопределенный, определенный и сложный интеграл. Основные применения интегралов. Геометрический смысл определенного и неопределенного интегралов. презентация , добавлен 15.01.2014 Решение задачи по нахождению площади криволинейной трапеции. Определение и свойства определённого интеграла. Необходимое условие интегрируемости и критерий Дарбу. Интегрируемость непрерывных и монотонных функций. Доказательство формулы Ньютона-Лейбница. контрольная работа , добавлен 25.03.2011 Вычисление площадей плоских фигур. Нахождение определенного интеграла функции. Определение площади под кривой, площади фигуры, заключенной между кривыми. Вычисление объемов тел вращения. Предел интегральной суммы функции. Определение объема цилиндра. презентация , добавлен 18.09.2013 Понятие определённого интеграла, расчет площади, объёма тела и длины дуги, статического момента и центра тяжести кривой. Вычисление площади в случае прямоугольной криволинейной области. Применение криволинейного, поверхностного и тройного интегралов. курсовая работа , добавлен 19.05.2011 История интегрального и дифференциального исчисления. Приложения определенного интеграла к решению некоторых задач механики и физики. Моменты и центры масс плоских кривых, теорема Гульдена. Дифференциальные уравнения. Примеры решения задач в MatLab. «Омская государственная
медицинская академия» Министерства здравоохранения
и социального развития Российской
Федерации на тему: применение определенного
интеграла в медицине выполнила студент 1 курса отделения Лечебное дело группа 102Ф Глушнева Н.А. Введение Выдающийся итальянский физик и астроном,
один из основателей точного естествознания,
Галилео Галилей (1564-1642) говорил, что "Книга природы написана
на языке математики". Почти через двести
лет родоначальник немецкой классической
философии Кант (1742-1804) утверждал, что "Во
всякой науке столько истины, сколько в ней математики".
Наконец, ещё через почти сто пятьдесят лет,
практически уже в наше время, немецкий
математик и логик Давид Гильберт (1862-1943)
констатировал: "Математика - основа
всего точного естествознания". Леонардо Да Винчи говорил: «Пусть
не читает меня в основах моих тот, кто не
математик». Пытаясь найти математическое
обоснование законов природы, считая математику
могучим средством познания, он применяет ее
даже в такой науке, как анатомия. Математика всем нужна. И медикам тоже.
Хотя бы для того, чтобы грамотно прочитать
обычную кардиограмму. Без знания азов
математики нельзя быть докой в компьютерной
технике, использовать возможности компьютерной
томографии... Ведь современная медицина
не может обходиться без сложнейшей техники. На сегодня невозможно изучение
гемодинамики- движения крови по сосудам
без применения интеграла. В течение длительного времени катетеризация
правых отделов сердца являлась единственным
методом исследования, позволявшим оценивать
состояния правых отделов сердца, получать
характеристики внутрисердечного кровотока,
определять давление в правых отделах
сердца и легочной артерии. Однако, ближе к практике. Для начала
найдем линейную скорость кровотока Изменение линейной скорости кровотока
в различных сосудах Это путь, проходимый в единицу
времени частицей крови в сосуде.
Линейная скорость в сосудах разного типа
различна (см. рисунок) и зависит от объемной
скорости кровотока и площади поперечного
сечения сосудов. В практической медицине
линейную скорость кровотока измеряют
с помощью ультразвукового и индикаторного
методов, чаще определяют время полного
кругооборота крови, которое равно 21-23
с. Для его определения в локтевую
вену вводят индикатор (эритроциты, меченные
радиоактивным изотопом, раствор
метиленового синего и др.) и отмечают
время его первого появления
в венозной крови этого же сосуда
в другой конечности. Для начала вспомним, что
интеграл- это математический объект,
который возник исторически на основе
потребности решения различных
прикладных задач физики и техники.
Это и физические приложения определенного
интеграла: вычисление пути материальной
точки, движущейся по прямолинейной или
криволинейной траектории по скорости
ее движения. Те физические величины, которые
определяются с помощью интеграла
- как правило, называются интегральными,
а те величины, через которые выражаются
интегральные величины - дифференциальными.
Например, скорость тела в точке - это дифференциальная
характеристика тела, а масса тела - интегральная. Дифференциальные характеристики
определяются значением в точке
и как правило различны в различных точках
пространства. Интегральные характеристики всегда
выражают свойства объектов, относящиеся
к целой области пространства.
Например, масса характеризует тело
целиком как некоторый объект
занимающий область пространства. Путь,
пройденный телом - это тоже интегральная
характеристика, поскольку она характеризует
целую траекторию, состоящую из множества
точек, а скорость различна в каждой точке
траектории и характеризует каждую точку
в отдельности. Возникает вопрос - как же вычислить
интегральную скорость для целого сосуда
(артерии или вены) , зная линейную
скорость кровотока. Очень просто: нужно Ниже приведены расчеты ударного
объема (ударный объём сердца (син.: систолический
объем крови, систолический объем сердца,
ударный объем крови) - объем крови (в мл), выбрасываемый желудочком
сердца за одну систолу)- одной из основных
величин в ЭХОкг, рассчитываемых при помощи
интеграла линейной скорости кровотока. а - Схемы расчета ударного объема,
а - с использованием уравнения непрерывности
потока, б - с использованием уравнения
непрерывности потока при наличии значительной
митральной регургитации. VTI = V cp ЕТ, где CSA - площадь поперечного сечения,
VTI - интеграл линейной скорости потока,
V cp - средняя скорость потока в выносящем
тракте левого желудочка, ЕТ - время выброса. В том случае, когда присутствует
гемодинамически значимая митральная
регургитация (более 2-й степени), тотальный
ударный объем левого желудочка рассчитывается
по формуле: TSV = FSV + RSV, [Интеграл линейной скорости (FVI,
или VTI)] = [Время кровотока (ET)] х
[Средняя скорость кровотока (Vmean)]; Сердечный выброс может быть определен
по интегралу линейной скорости аортального
и легочного потока. В завершении хочу добавить, что моя
работа рассчитана не на математика, от
и до разбирающегося в интегрировании,
а на любого человека, проявившего
интерес к применению интеграла в медицине.
Поэтому я старалась сделать ее максимально
доступной для восприятия и интересной
даже ребенку. Список литературы: Открытый урок по алгебре и началам анализа в 11 классе с расширенным изучением математики и физики
«Применение методов математического анализа при решении практических задач».
Учитель: Вишневская Н.В.
Цели урока: 1. Повторить основные типы задач, решаемые методами математического анализа.
2. Повторить алгоритмы решения. 3. Разобрать решение задач повышенной трудности. 4. Решить экономические задачи. План проведения урока: На доске разбираются две задачи повышенной трудности (карточки № 7 и № 5). Пока ребята готовятся, класс устно отвечает на вопросы: а) Области, где применяются методы математического анализа; б) алгоритм решения задач методом поиска наибольших и наименьших значений функции; в) алгоритм решения задач с помощью определенного интеграла. В это же время 6 человек работают по карточкам (№ 3, 4, 6, 8, 9, 10). Заполняются таблицы. Проверяются задачи на доске, учитель проверяет правильность решения задач по карточкам. Разбирается на доске экономическая задача (карточка № 1, 2). Домашняя контрольная работа. Алгоритм решения задач методом поиска наибольших и наименьших значений функции. Алгоритм вычисления геометрических и физических величин с помощью определенного интеграла. Выражают искомую величину как значение в некоторой точке в функции F
.
Находят производную f
этой функции.
Выражают функцию F
в виде определенного интеграла от f
и вычисляют его.
Подставляя значение х
= b
находят искомую величину.
Домашние задачи (на доске):
Два корабля движутся по двум перпендикулярным прямым, пересекающимся в точке О
, по направлению к О
. В какой-то момент времени оба находятся в 65 км от О
, скорость первого равна 15 км/ч, второго – 20 км/ч. От первого корабля отходит моторная лодка, движущаяся со скоростью 25 км/ч.
а) За какое наименьшее время катер может доплыть от первого корабля до второго?
б) За какое наименьшее время катер может доплыть от первого корабля до второго и вернуться обратно на первый корабль?
V
1 = 15 км/ч
65 км S
1 О
S
3 S
2
65 км
V
л = 25 км/ч
V
2 = 20 км/ч
Решение:
х
– время, которое прошло от того момента, когда оба корабля находились в 65 км от О
, до момента отправления катера.
В момент отправления катера 1-й корабль был на расстоянии Продифференцируем по х
:
Ответ: а) 1 час; б) 3 часа.
Котел имеет форму параболоида вращения. Радиус его основания R
= 3 м, глубина Н
= 5 м. Котел наполнен жидкостью, удельный вес которой 0,8 Г/см 3 . Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
у
у
R
= 3 м
Н
= 5 м
уд. вес = 0,8 Г/см 3
Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
Решение:
В плоскости сечения хОу
АОВ
– парабола, уравнение которой Координаты точки В
должны удовлетворять этому уравнению, т.е.
Разделим параболоид на слои плоскостями, параллельными поверхности жидкости. Пусть толщина слоя на глубине (Н
– у)
равна dy
. Тогда, принимая приближенно слой за цилиндр, получим его объем Из уравнения параболы Следовательно, чтобы выкачать жидкость с глубины Ответ: Работа в классе.
Какую работу нужно затратить, чтобы растянуть пружину на 6 см, если сила 1 кГ растягивает ее на 1 см?
Решение:
Согласно закону Гука сила F
кГ, растягивающая пружину на х
, равна х
= 0,01 м
F
= 1 кГ
Тогда Искомая работа Ответ: 0,18 кГм.
Вычислить работу силы F
при сжатии пружины на 5 см, если для сжатия ее на 1 см нужна сила в 1 кг.
Решение:
По закону Гука х
= 0,01 м
F
= 1 кГ
Тогда Искомая работа Ответ: 0,125 кГм.
Сила F
, с которой электрический заряд где k
– постоянная.
Определить работу силы F
при перемещении заряда Решение:
Работа определяется по формуле При Ответ: Определить силу давления воды на вертикальную стенку, имеющую форму полукруга радиуса R
= 6 м, диаметр которого находится на поверхности воды.
Решение:
Сила давления жидкости на площадку площадью S
при глубине погружения х
равна х С
dх
А В
Полукруг параллельными прямыми разделим на полоски, которые примем за прямоугольник. Пусть заштрихованная полоска имеет длину АВ
, ширину dx
и находится на глубине х
Давление воды на полоску, находящуюся на глубине х
, будет равно .
Отсюда Удельный вес воды 1 см 3 = 1 Г, следовательно вес 1м 3 = 1000 кГ.
1 кГ 1 бар = 0,987 атм.
Ответ: 144000 кГ.
Скорость движения точки Решение:
Следовательно Ответ: 512 м; 64 м/сек.
Карточка № 1 (решается в классе на доске)
Средние совокупные издержки производства мыла Связь между годовым объемом продаж, равным величине годового выпуска Q
, и ценой мыла Р
(в тыс. рублей за тонну) описывается формулой
Реализовав по фиксированной цене все сваренное за год мыло, завод получил максимально возможную прибыль. Какова была при этом выручка предприятия?
Решение:
Выразим через Q
сначала цену мыла из формулы Тогда прибыль G
можно выразить:
Найдем критические точки этой функции:
Критические точки 100, –340, –120.
Отрицательные корни не имеют экономического смысла.
Q
G
Значит оптимальный годовой объем мыла Тогда годовая выручка R
составит: (тыс. руб.).
Ответ: 1 млн. руб.
Найти величину давления воды на прямоугольник, вертикально погруженный в воду, если известно, что его основание равно 8 м, высота 12 м, верхнее основание параллельно поверхности воды и находится на глубине 5 м.
Решение:
5 м
8 м
х
dx
12 м
кГм.
Ответ: Карточка № 2 (дополнительная)
Производственные мощности позволяют предприятию «Линотрон» выпускать не более 600 тонн ваты в год. Зависимость величины совокупных издержек Связь между годовым объемом продаж ваты, который совпадает с объемом годового производства, и ценой на вату Р
(в тыс. рублей за тонну) описывается функцией
Цена на вату устанавливается 1 января 1995 года и пересматривается лишь 1 января следующего года.
Найдите с точностью до 1 % рентабельность производства по издержкам, если за 1995 год предприятие получит максимально возможную прибыль.
Решение:
Используя зависимости у у a
0 b c x a
0 b c x
Интегральное исчисление возникло в связи с решением задач определения площадей и объёмов. За 2000 лет до н.э. жители Египта и Вавилона уже умели определять приближённо площадь круга и знали правило для вычисления объёма усечённой пирамиды. Теоретическое обоснование правил вычисления площадей и объёмов впервые появились у древних греков. Философ-материалист Демокрит в
V
веке до н.э. рассматривает тела, как состоящие из большого числа малых частиц. То есть конус представляет собой множество весьма тонких цилиндрических дисков разных радиусов. Огромную роль в истории интегрального исчисления сыграла задача о квадратуре круга
(квадратура круга – построение квадрата, площадь которого равна площади данного круга)
. Точную квадратуру нескольких криволинейных фигур нашёл Гиппократ (середина
V
века).
Первым известным методом для вычисления интеграла является метод исчерпания Евдокса (примерно 370 до н. э.). Он пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известен. Этот метод был подхвачен и развит Архимедом, использовался для расчета площадей парабол и приближенного расчета площади круга.
В своем сочинении «Квадратура параболы» Архимед пользуется методом исчерпывания для вычисления площади сектора параболы. Т.е. Архимед впервые составляет суммы, которые в наше время называются интегральными суммами. Первые значимые попытки развития интеграционных методов Архимеда, увенчавшиеся успехом, были предприняты в
XVII
веке, когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой стороны – всё более интенсивно развивались экономика, техника, естествознание, а там требовались обширные и глубокие методы изучения и вычисления величин.
При вычислении площади криволинейной трапеции
Ньютон и Лейбниц приходят к понятию
первообразной (или примитивной) функции для данной производной функции
f
(х),
где
С
могло быть любым. Та
к называемая сегодня
Работы по исследованию основ дифференциального и интегрального исчислений начинаются в
XIX
веке трудами О. Коши и Б. Больцано. Тогда же в развитие интегрального исчисления внесли значительный вклад русские учёные-математики М.В. Остроградский, В.Я. Буняковский, В.Я. Чебышев. Это было время, когда современный математический анализ только создавался. Это была, пожалуй, единственная по своей интенсивности эпоха математического творчества, а Эйлер объединил обширный, но разрозненный материал нового анализа в цельную науку.
Со временем,
человек приобретал все большую власть над природой, но мечта о полете к звездам оставалась все такой же несбыточной. Писатели-фантасты упоминали ракеты для осуществления космического полета. Однако эти ракеты были технически необоснованной мечтой. Честь открыть людям дорогу к звёздам выпала на долю нашего соотечественника К. Э. Циолковского. Над задачами по созданию искусственного спутника Земли, расчётов траектории выхода их на орбиту работала целая плеяда ученых, во главе с С.П. Королёвым.
Особенно интересны задачи, являющиеся прообразом задач на расчёты траекторий выхода космических аппаратов на заданную орбиту, на нахождение высоты и скорости подъёма или спуска тела и некоторые другие задачи с использованием интегрального исчисления.
Задача 1
. Скорость прямолинейного движения тела задана
уравнением . Найти уравнение пути S, если за время t = 2сек тело прошло 20м.
Решение
: При полете в космос, надо учесть все факторы окружающей нас среды, и чтобы попасть куда нужно, требуется рассчитать траекторию движения, используя исходные данные. Всё это нужно сделать перед тем, как совершится полёт.
В 2016 году исполняется 55 лет со дня полёта на орбиту первого космонавта Юрия Алексеевича Гагарина. При расчётах приходилось решать и такие задачи.
Задача 2
. Необходимо запустить ракету весом Р = 2·10 4 Н(Т)
с поверхности Земли на высоту
h
= 1500 км.
Вычислить работу необходимую для её запуска.
Решение.
f – сила притяжения тела Землёй есть функция от его расстояния х
до центра Земли: , где На поверхности Земли где сила притяжения равна весу тела Р
, а х = R
- радиус Земли, поэтомуи При подъёме ракеты с поверхности Земли на высоту h
переменная х
изменяется от
x
= R
до
x
=
R
+
h
. Искомую работу находим по формуле: Задача 3
. Сила в 10 Н
растягивает пружину на 2 см
. Какую работу она
совершает при этом?
Решение
.
По закону Гука, сила
F
, растягивающая пружину, пропорциональна растяжению пружины, т.е.
F
= кх.
Из условия задачи
к=
10/0,02(Н/м),
то
F
= 500х
. Работа: Задача 4
. Из шахты глубиной
l
= 100 м
надо поднять равномерно клеть весом Р 1
= 10 4
Н
, которая висит на канате, намотанном на барабан. Вычислить полную работу А полн
, необходимую для поднятия клети, если вес одного погонного метра каната Р 2
= 20 Н
.
Решение
.
Работа по поднятию клети: а по поднятию каната пропорциональна весу каната, т.е. Задача 5
. Рессора прогибается под действием силы 1,5·10 4 Н
на 1см. Какую работу надо затратить для деформации рессоры на 3 см? (Деформирующая сила пропорциональна прогибу рессоры.)
Решение
.
F
=кх,
где х
- прогиб рессоры. При х = 0,01м
имеем: Сложен и небезопасен подъём в космическое пространство, но не менее трудностей таит возвращение на Землю, когда аппарат космического корабля должен приземлиться со скоростью не более 2 м/с. Только в этом случае аппарат, приборы в нём, а главное, члены экипажа, не испытают резкого жёсткого удара. Константин Эдуардович Циолковский решил использовать торможение космического корабля воздушной оболочкой Земли. Двигаясь со скоростью 8 м/с, космический аппарат не падает на Землю. Первая стадия спуска - включение на короткое время тормозного двигателя. Скорость уменьшается на 0,2 км/с, и сразу начинается спуск. Рассмотрим пример решения задачи на составление закона движения при заданных условиях.
Задача 6
. Найти закон движения свободно падающего тела при постоянном ускорении g, если в момент движения тело находилось в покое.
Решение:
Известно, что ускорение прямолинейно движущегося тела есть вторая производная пути S по времени
t
, или производная от скорости по времени
t
:
, но , следовательно, , откуда . Интегрируем: , и Из условия: , откуда найдём и скорость движения: . Найдём закон движения тела: , или . Интегрируем: , . По начальным условиям: , откуда найдём Имеем уравнение движения падающего тела: - это знакомая формула физики .
Задача 7
. Тело брошено вертикально вверх с начальной скоростью
Найти уравнение движения этого тела (сопротивлением воздуха пренебречь).
Решение:
Примем: направление по вертикали вверх - за положительное, а ускорение силы тяжести, как направленное вниз, - за отрицательное. Имеем: , откуда . Интегрируем: то . Т.к. и то С 1: Следующий пример показывает расчет траектории сброса отработанных секций, ненужных приборов, материалов. В этом случае их отправляют на Землю, рассчитав орбиту так, чтобы при прохождении через атмосферные слои они сгорели, а несгоревшие остатки упали на Землю (чаще всего - в океан), не причинив при этом вред.
Задача 8
. Составить уравнение кривой, проходящей через точку М (2; -3) и имеющую касательную с угловым коэффициентом .
Решение:
В условии задачи дано: Строителям иногда приходится решать задачи по вычислению площадей необычных фигур, для которых нет общеизвестных формул. В этом случае снова выручают интегралы.
.
Космонавты и ученые, работая на орбитальной станции, для чистоты эксперимента решают и исследуют многие вопросы астрономии, физики, химии, медицины, биологии и т.д. Сопроводим следующую задачу литературным примером. В известном фантастическом романе Герберта Уэллса «Война миров» описывается нападение марсиан на планету Земля, которые решили расширить свои перенаселённые территории за счёт захвата наших, т.к. климатические условия Земли были подходящими. Начался захват территории и уничтожение землян, которые получили помощь оттуда, откуда совсем не ожидали. Наши «родные» бактерии, с которыми мы уже научились бороться, попав в организм марсиан с воздухом, пищей, водой, нашли в нём благоприятную среду для своего развития и размножения, быстренько адаптировались и, уничтожив марсиан, избавили Землю от захватчиков. Рассмотрим решение задачи, дающей понятие об этом.
Задача 10.
Скорость размножения некоторых бактерий пропорциональна количеству бактерий, имеющихся в наличии в рассматриваемый момент времени t. Количество бактерий утроилось в течение 5ч. Найти зависимость количества бактерий от времени.
Решение:
Пусть
x
(t
) есть количество бактерий в момент времени t, а в начальный момент тогда скорость их размножения. По условию имеем: или след.: В знаменитом романе А.Н. Толстого «Гиперболоид инженера Гарина» хотелось бы почувствовать, ощутить, что же это такое – гиперболоид? Какие у него размеры, форма, поверхность, объём? Следующая задача – об этом.
Решение.
Используем формулу для вычисления объёма тел вращения вокруг оси ОХ с помощью определённого интеграла:
Задача 12
. Вычислить объём тела, образованного вращением вокруг оси ОХ площади, ограниченной линиями у = х 2 - 9
и у = 0
.
Экономический смысл определённого интеграла выражает объём произведённой продукции при известной функции
f
(t
) - производительности труда в момент
t
. Тогда объём выпускаемой продукции за промежуток вычисляется по формуле Рассмотрим пример для предприятия.
Задача 13
. Найти объём продукции, произведённой за 4 года, если функция Кобба-Дугласа имеет вид Решение
. Объём произведённой предприятием продукции равен:
Подводя итоги можно сделать вывод, что применение интеграла раскрывает большие возможности. При изучении геометрии рассматривают вычисление площадей плоских фигур ограниченных отрезками прямых (треугольников, параллелограммов, трапеций, многоугольников), и объёмов тел, полученных при их вращении. Определённый интеграл позволяет вычислять площади сложных фигур, ограниченных любыми кривыми линиями, а также находить объёмы тел, получаемых при вращении криволинейных трапеций вокруг любой оси.
Также хочется отметить, что применение определенного интеграла не ограничивается только вычислением различных геометрических величин, но используется и при решении задач из различных областей физики, аэродинамики, астрономии, химии и медицины, космонавтики, а также, экономических задач.
Список литературы
:
Слайд 2
История понятия интеграла тесно связана с задачами нахождения квадратур, т.е. задачами на вычисление площадей. Вычислениями площадей поверхностей и объемов тел занимались еще математики Древней Греции и Рима. Первым европейским математиком, получившим новые формулы для площадей фигур и объемов тел, был знаменитый астроном И. Кеплер. После исследований ряда ученых (П.Ферма, Д.Валлиса) И. Барроу открыл связь между задачами отыскания площадей и проведением касательной (т.е. между интегрированием и дифференцированием). Исследование связи между этими операциями, свободное от геометрического языка, было дано И.Ньютоном и Г. Лейбницем.
Современное обозначение интеграла восходит к Лейбницу, у которого оно выражало мысль, что площадь криволинейной трапеции есть сумма площадей бесконечно тонких полосок шириной d и высоты f(x). Сам знак интеграла является стилизованной латинской буквой S (summa). Символ интеграла введен с 1675г., а вопросами интегрального исчисления занимаются с 1696г. Хотя интеграл изучают, в основном, ученые–математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без дифференциального и интегрального исчислений. Слайд 3
Многие значительные достижения математиков Древней Греции в решении задач на нахождение площадей, а также объемов тел связаны с именем Архимеда(287-212 до н. э.)
Развивая идеи предшественников Архимед определил длину окружности и площадь круга, объем и поверхность шара. В работах «О шаре и цилиндре», «О спиралях», «О коноидах и сферах», он показал, что определение объемов шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объема конуса и цилиндра. Архимед разработал и применил методы, предвосхитившие созданное в XVII в. интегральное исчисление.
Потребовалось более полутора тысяч лет, прежде чем идеи Архимеда нашли четкое выражение и были доведены до уровня исчисления. В XVII в. математики уже умели вычислять площади многих фигур с кривыми границами и объемы многих тел. А общая теория была создана во второй половине XVII в. в трудах великого английского математика Иссака Ньютона(1643-1716) и великого немецкого математика Готфрида Лейбница(1646-1716). Ньютон и Лейбниц являются основателями интегрального исчисления. Они открыли важную теорему, носящую их имя:
где f(x) – функция, интегрируемая на отрезке , F(x) – одна из ее первообразных.
Рассуждения, которые приводили Ньютон и Лейбниц, несовершенны с точки зрения современного математического анализа. В XVIII в. крупнейший представитель математического анализа Леонард Эйлер эти понятия обобщил в своих трудах. Только в начале XIX в. были окончательно созданы понятия интегрального исчисления. Обычно при этом отмечают заслуги французского математика Огюстена Коши и немецкого математика Георга Римана.
Само слово интеграл придумал Я.Бернулли(1690г.). Оно происходит от латинского integro, которое переводится как приводить в прежнее состояние, восстанавливать. В1696г. появилось и название новой ветви математики – интегральное исчисление, которое ввел И.Бернулли. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Лагранж (1797 г.). Обозначение определенного интеграла ввел Иосиф Бернулли, а нижние и верхние пределы Леонард Эйлер. Слайд 4
Математические операции образуют пары двух взаимно обратных действий, например, сложение и вычитание, умножение и деление, возведение в целую положительную степень и извлечение корня. Дифференцирование дает возможность для заданной функции F(х) находить ее производную F´(х). Существует действие, обратное дифференцированию – это интегрирование – нахождение функции F(х) по известной ее производной f(x) = F´(х)или дифференциалу f(x)dx.
Функция F(х) называется первообразной для функции f(x), если F´(х) = f(x) или dF(x)=f(x)dx.Если функция f(x) имеет первообразную F(х), то она имеет бесконечное множество первообразных, причем все ее первообразные содержатся в выражении F(х) +С, где С – постоянная.
Неопределенным интегралом от функции f(x)(или от выражения f(x)dx) называется совокупность всех ее первообразных. Обозначение ∫f(x)dx = F(х) +С. Здесь ∫ – знак интеграла, f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение, х – переменная интегрирования. Отыскание неопределенного интеграла называется интегрированием функции.
Свойства неопределенного интеграла
Производная от неопределенного интеграла равна подынтегральной функции:
(∫ f(x)dx)´ = f(x)
Дифференциал от неопределенного интеграла равен подынтегральному выражению:
d (∫ f(x)dx) = f(x) dx
Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С:∫d (F(x)) = F(х) +С
Постоянный множитель можно выносить за знак неопределенного интеграла:
∫a f(x) dx =a ∫f(x) dx
Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых: ∫ dx = ∫ dx ± ∫ dx Слайд 5
Понятие определенного интеграла выводится через криволинейную трапецию. Криволинейной трапецией называется фигура, ограниченная линиями y = f(x), y = 0, x=a, x=b.Площадь криволинейной трапеции выражается интегральной суммой или числом, которое называется определенным интегралом. Определенный интеграл вычисляется по формуле Ньютона – Лейбница.
= F (x)|ba= F(b) – F(a)
Общность обозначения определенного и неопределенного интегралов подчеркивает тесную связь между ними: определенный интеграл – это число, а неопределенный интеграл – совокупность первообразных функций. Связь между определенным и неопределенным интегралом выражается формулой Ньютона – Лейбница.
Свойства определенного интеграла:
Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолютную величину, но изменит свой знак на противоположный.
Если верхняя и нижняя границы интегрирования равны, то определенный интеграл равен нулю.
Если отрезок интегрирования разбить на несколько частей, определенный интеграл на отрезке будет равен сумме определенных интегралов этих отрезков.
Определенный интеграл от суммы функций, заданных на отрезке равен сумме определенных интегралов от слагаемых функций.
Постоянный множитель к подынтегральной функции можно выносить за знак определенного интеграла.
Оценка определенного интеграла: если m ≤ f(x) ≤ M на , то
m (b – a) Слайд 6
Пусть функция y=f(x) непрерывна на отрезке и f(x) ≥ 0. Фигура, ограниченная графиком АВ функции y=f(x), прямыми x=a, x=b и осью Ох (см. рисунок), называется криволинейной трапецией.
Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение равно площади прямоугольника с основанием и высотой, а сумма представляет собой площадь заштрихованной ступенчатой фигуры, изображенной на рисунке. Очевидно, что эта площадь зависит от разбиенияотрезка на частичные отрезки и выбора количества точек разбиения.
Чем меньше ∆ х, тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точную площадь S криволинейной трапеции принимается предел интегральной суммы.
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции. Слайд 7
1. Непосредственное интегрирование
Непосредственным интегрированием принято называть вычисление неопределенных интегралов путем приведения их к табличным с применением основных свойств. Здесь могут представиться следующие случаи: 1) данный интеграл берется непосредственно по формуле соответствующего табличного интеграла; 2) данный интеграл после применения свойств приводится к одному или нескольким табличным интегралам; 3) данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применением свойств приводится к одному или нескольким табличным интегралам.
2. Интегрирование методом замены переменной (способом подстановки)
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
х = φ (t), где φ (t) – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид ∫f(x) = ∫f [φ (t)] φ΄ (t) d(t);
2) u = ψ(x), где u – новая переменная. Формула замены переменной при такой подстановке: ∫f [ψ(х)] ψ ΄(х) d(х) = ∫f (u) du
3. Интегрирование по частям
Интегрированием по частям называется нахождение интеграла по формуле ∫udv = uv - ∫v du, где u = φ (x), v = ψ(х) – непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла ∫udv сводится к отысканию другого интеграла ∫v du; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен. При этом за u берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которого известен или может быть найден. Слайд 8
Слайд 9
Как найти площади изображенных фигур? Слайд 10
Слайд 11
Кроме этого определенный интеграл используется для вычисления площадей плоских фигур, объемов тел вращения, длин дуг кривых. Слайд 12
Пусть задано тело объемом V, причем имеется такая прямая, что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох, пересекает ее в некоторой точке х. Следовательно, каждому числу х (из отрезка [а; b]) поставлено в соответствие единственное число S (х) - площадь сечения тела этой плоскостью. Тем самым на отрезке [а; b] задана функция S(x). Если функция S непрерывна на отрезке [а; b] то справедлива формула: Слайд 13
Найдите площадь изображенных фигур 1 – 5.
Ответы:
1) S = 2/3 (четность функции); 2) S = 1 (площадь прямоугольного треугольника);
3) S = 4 (равенство фигур); 4) S = 2π (площадь полукруга); 5) S = 1 (площадь треугольника). Слайд 14
Найти сумму площадей бесконечного количества фигур, заштрихованных на рисунках. (Аргумент каждой следующей функции увеличивается в 2 раза)
Интересная задача!
Ответ: sin nx=0 ; x=π/n; где n=1,2,4,8,16…;
S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4
Ответ: 4. Слайд 15
Верные ответы: I вариант: 2,3,1 ; II вариант: 2,4,2. Слайд 16
Вычислите площадь фигуры, ограниченной линиями (схематично изобразив графики функций).
1) y = 6 + x – x2 и y = 6 – 2x;
2) y = 2x2 и y = x + 1 ;
3) y = 1 – x и y = 3 – 2x – x2 ;
4) y = x2 и y = .
Ответ: 1) 4,5 ; 2) 9/8 ; 3) 4,5 ; 4) 1/3 . Слайд 17
Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
1) y = x2 + 1, x = 0, x = 1, y = 0 ;
2) y = , x = 1 , x = 4 , y = 0 ;
3) y = 2x , y = x + 3, x = 0 , x = 1 ;
4) y = x + 2 , y = 1 , x = 0 , x = 2 ;
5) у2 – 4 х = 0, х – 2 = 0, х – 4 = 0, у = 0;
6) у2 – х + 1 = 0, х – 2 = 0, у = 0;
7) y = - x2 + 2х, у = 0;
8) у2 = 2 х, х – 2 = 0, у = 0;
9) y = , x = 3 , y = 0 ;
10) у = 1 – x2 , у = 0.
Ответ: 1) ; 2) 7,5 ; 3) 11 ; 4) 16 ⅔; 5) 24 ;
6) /2; 7) 16/15; 8) 4 ; 9) 2 ; 10) 16/15. Слайд 18
Найти площадь фигуры, ограниченной линиями
2) Фигура, ограниченная линиями y=x+6, x=1, y=0 делится параболой y=x 2+2x+4 на две части. Найти площадь каждой части.
3) Найти ту первообразную F(x) функции f(x)=2x+4, график которой касается прямой у=6х+3. Вычислить площадь фигуры, ограниченной графиком найденной первообразной и прямыми у=6х+3 и у=0. Слайд 19
Какое действие называется интегрированием?
Какая функция называется первообразной для функции f(x)?
Чем отличаются друг от друга различные первообразные функции для данной функции f(x)?
Дайте определение неопределенного интеграла.
Как проверить результат интегрирования?
Чему равна производная от неопределенного интеграла?
Чему равен ∫ d(lnx8 – sin 3x)?
Перечислите методы интегрирования.
Дайте определение определенного интеграла.
Сформулируйте теорему Ньютона – Лейбница.
Перечислите свойства определенного интеграла.
Как вычислить площадь плоской фигуры с помощью интеграла (составьте словесный алгоритм)?
Перечислите области применения интеграла, назовите величины, которые можно вычислить с помощью интеграла. Слайд 20
1) Вычислить площадь фигуры, ограниченной данными линиями:y=x2 при x0, y=1, y=4, x=0 Решение:
Данная фигура симметрична криволинейной трапеции, ограниченной прямыми х=1, х=4, у=0, графиком функции, обратной у=х2, x0. Поэтому эти фигуры имеют равные площади и
2) Найти площадь фигуры, ограниченной прямыми у=3х+1, у=9-х, у=х+1.
Решение:
Вершины полученного ABC имеют координаты: А(0;1), В(2;7), С(4;5).
Можно заметить, что ABC - прямоугольный (произведение
угловых коэффициентов прямых у=х+1 у=9-х равно -1).
Поэтому применение интеграла для вычисления S(ABC)
не рационально. Её всегда можно найти как разность площадей
треугольников, у которых известны высота и основание или же
можно использовать координатный метод. Слайд 21
Найти площади фигур, ограниченных линиями (1-7)
у=х2 (х0), у=1, у=4, х=0
у= х2-4х+8, у=3х2-х3, если х [-2;3]
у=х2-4х+sin2(x/2), y=-3-cos2(x/2), если х
у=3х+1, у=9-х, у=х+1
у=|x-2|,
x|y|=2;x=1;x=3
y= arcsin x; у=0; x=0,5; x=1
При каком значении а прямая х=а делит площадь фигуры, ограниченной линиями у=2/х; х=1; х=3 в отношении 1:3?
Вычислить исходя из его
геометрического смысла. Слайд 22
Н. А. Колмогоров, «Алгебра и начала анализа», Москва, Просвещение,2000г.
М. И. Башмаков, «Алгебра и начала анализа», Москва, ДРОФА,2002г.
Ш.А.Алимов, «Алгебра и начала анализа», 11 кл., Москва, ДРОФА, 2004г.
Л. В. Киселева, Пособие по математике для студентов медицинских училищ и колледжей, Москва, ФГОУ«ВУНМЦ Росздрава», 2005г.
http://www.nerungri.edu.ru
http://tambov.fio.ru
http://www.zachetka.ru
http://edu.of.ru
http://festival.1september.ru
Посмотреть все слайдыОпределение и свойства интеграла
Интегрирование
Криволинейная трапеция
Список литературы
Подобные документы
Основное преимущество эхокардиографического
исследования (ЭхоКГ) заключается в том,
что неинвазивно в реальном режиме времени
можно оценить размеры и движение сердечных
структур, получить характеристики внутрисердечной
гемодинамики, определить давление в камерах
сердца и легочной артерии. Доказана хорошая
сопоставимость результатов ЭхоКГ-исследования
с данными, полученными при катетеризации
сердца.
ЭхоКГ-исследование позволяет не только
выявить наличие легочной гипертензии,
но и исключить ряд заболеваний, которые
являются причиной вторичной легочной
гипертензии: пороки митрального клапана,
врожденные пороки сердца, дилатационная
кардиомиопатия, хронический миокардит.Карточка № 7
– время, которое необходимо катеру на путь от 1-го корабля до 2-го.
км от О
; в момент прибытия катера на 2-ой корабль, расстояние между ним и О
было равно км; путь катера равен 
. Тогда по теореме Пифагора
.
; 
; 
Карточка № 5
А
R
В
dy
Н
О х х
. Найдем параметр а
.
,
, следовательно 
.
.
, тогда 
, т.е. вес слоя жидкости равен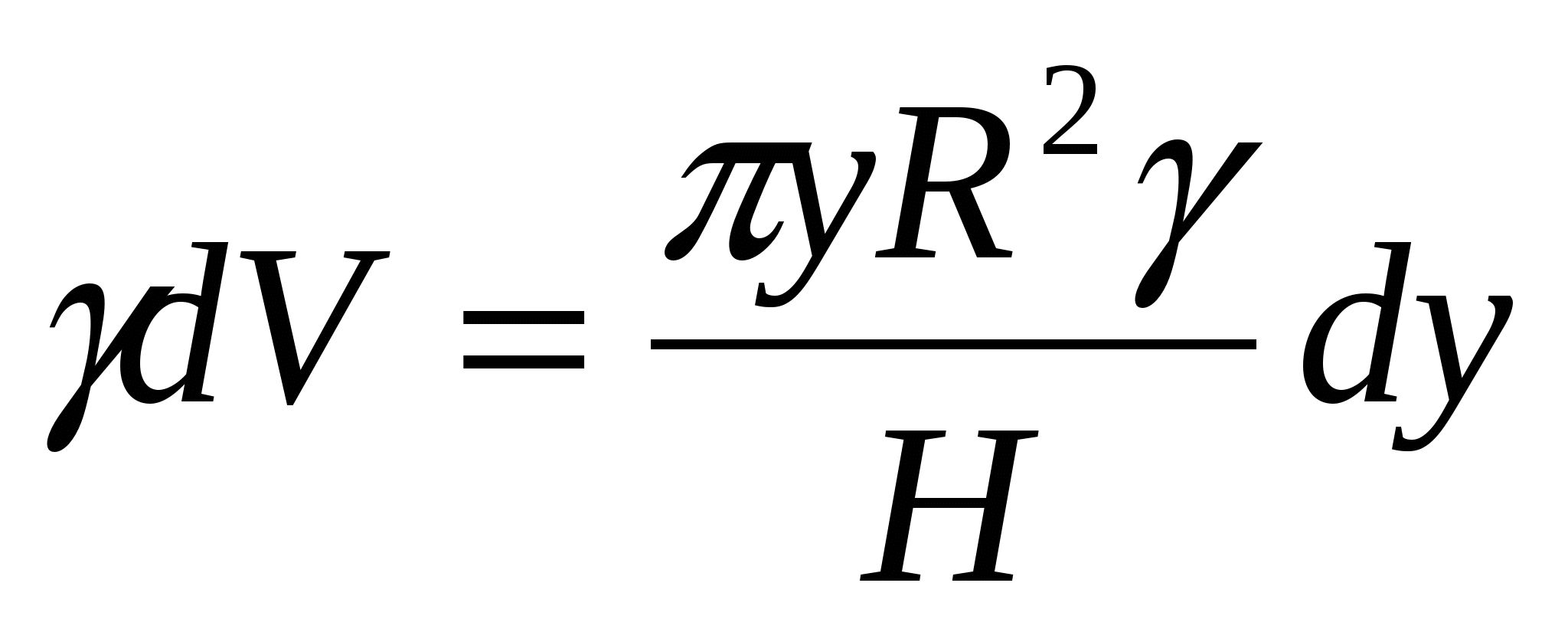 
.
, потребуется затратить элементарную работу 
, 
. Тогда
, тогда .
.
Карточка № 6
, k
– коэффициент пропорциональности.
, следовательно 
.
.
Карточка № 8
.
, следовательно .
.
Карточка № 9
отталкивает заряд 
(того же знака), находящийся от него на расстоянии r
, выражается формулой
,
из точки 
, отстоящей от на расстоянии 
, в точку 
, отстоящую от на расстоянии 
, полагая, что заряд помещен в точке 
, принятой за начало отсчета.
, . Тогда
.
получим 
.
.
Карточка № 3
, 
– удельный вес жидкости.
О
.
,
,
,
.
;
9,81 н
Карточка № 4
м/сек. Найти путь s
, пройденный точкой за время Т
= 8 сек после начала движения. Чему равна средняя скорость движения за этот промежуток?
, следовательно 
, 
, 
.
.
.
(в тыс. рублей на тонну) на Мухинском мыловаренном заводе изменяются в зависимости от объема годового выпуска Q
(в тоннах) по закону:
.
.
.
.
, 
.
;
.
т, тогда цена 
(тыс. руб./т).
Карточка № 10
, 
, 
м.
.
кГм.
(в тыс. рублей) от годового объема производства Q
(в тоннах) имеет вид
.
и , выразим
.
формула
Ньютона-Лейбница позволяет сводить довольно сложное вычисление определенных интегралов, т.е. нахождение пределов интегральных сумм, к сравнительно простой операции отыскания первообразных.
Лейбницу принадлежит символ дифференциала
а п
озже появился и символ интеграла
Символ определённого интеграла
ввёл Ж. Фурье, а термин «интеграл» (от латинского
integer
- целый) был предложен И. Бернулли.
откуда
Интегрируем:
откуда 
Используя данные найдём С = 4. Т.е. уравнение движения тела имеет вид 
.
Тогда получаем: работа для запуска ракеты равна 
.
Следовательно, полная работа полна:
. Тогда работа для деформации равна:
и Уравнение скорости: Находим закон движения тела: т.к. и тогда 
откуда 
.Интегрируем:
или 
При и найдём 
, и Имеем уравнение движения тела: или .
или 
Интегрируя, имеем: 
При х = 2
и у = -3, С = - 5
, а траектория движения имеет вид: 
.
Задача 9
. Вычислить площадь фигуры, ограниченной линиями: и
Решение
: Выполним построение чертежа (рис. 1), для чего решим систему уравнений. Найдём точки пересечения линий: А(-2;4
) и В(4;16)
. Искомая площадь представляет собой разность площадей с пределами интегрирования, а = х 1 = -2
и в = х 2 = 4.
Тогда имеем площадь:
Найдём С: и функция Известно, чтот.е. или откуда коэффициент пропорциональности равен: а функция имеет вид: 
.
Задача 11.
Гипербола , ограниченная линиями: у = 0, х =
a
, х = 2а
вращается вокруг оси ОХ. Найти объём полученного гиперболоида (рис.2).
Учёные-уфологи занимаются изучением фактов, которые приводят «очевидцы», рассказывая о том, что видели летящий космический корабль в виде огромного светящегося диска («тарелки»), примерно такой формы как на рисунке 3. Рассмотрим решение задачи по определению объёма такой «тарелки».
Решение
: При выполнении чертежа параболоида (рис.3) имеем пределы интегрирования от х = -3
до х = 3
. Заменим пределы интегрирования в силу симметричности фигуры относительно оси ОУ на х = 0
и х = 3
, а результат удвоим. Следовательно, объём диска равен:
Историческая справка
Краткая история интегрального исчисления
Неопределенный интеграл
Определенный интеграл
Геометрический смысл определенного интеграла
Методы интегрирования
Таблица неопределенных интегралов
Повторение теоретического материала
Продолжаем повторять
Применение интеграла
Вычисление объемов тел
ПРОВЕРЬ СЕБЯ!
Найди ошибку!
Программированный контроль
Самостоятельная работа
Задачи на вычисление объемов
Задачи из ЕГЭ
Контрольные вопросы
Для любителей математики
Домашнее задание
Список литературы
Загрузка...