Find the equation of a straight line given by the intersection of two planes. Plane intersection

ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under angle between two planes we mean one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . So . Because and , then

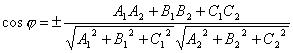Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

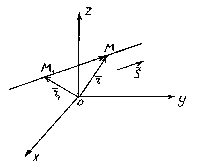
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y and z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

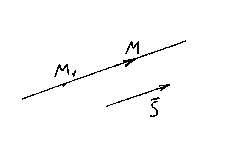
Let be M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, and is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

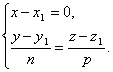
However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox and Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

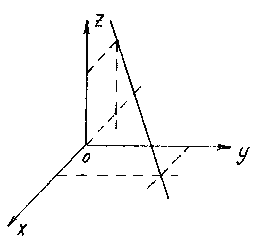
To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors and . Therefore, for the direction vector of the straight line l you can take the cross product of normal vectors:

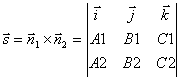Example. Give the general equations of the straight line to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

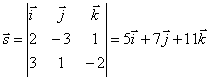. Hence, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get

In general, any two non-parallel planes given by the general equations

determine their line of intersection. These equations are called general equations straight

Ticket 6 Write down an expression for the angle between a straight line and a plane, the condition of parallelism and perpendicularity of a straight line and a plane.

corner between a straight line and a plane we will call the angle formed by the straight line and its projection onto the plane. Let the plane be given by the equations

Consider vectors and . If the angle between them is acute, then it will be , where φ is the angle between the line and the plane. Then .

If the angle between the vectors and is obtuse, then it is equal to . Hence . Therefore, in any case. Remembering the formula for calculating the cosine of the angle between vectors, we get .

The condition of perpendicularity of a line and a plane. A line and a plane are perpendicular if and only if the direction vector of the line and the normal vector of the plane are collinear, i.e. .

Condition of parallelism of a straight line and a plane. A line and a plane are parallel if and only if the vectors and are perpendicular.

Ticket 7. Define an ellipse. Write the equation of the ellipse in canonical form. Vertices, foci, axes and eccentricity of the ellipse.

Definition: An ellipse is the locus of points in a plane, for each of which the sum of the distances to two given points of the same plane, called the foci of the ellipse, is a constant value.

Let be F 1 and F 2 - foci of the ellipse. Start O coordinate systems are located in the middle of the segment F 1 F 2. Axis Ox direct along this segment, the axis Oy- perpendicular to this segment (Fig.).

Definition: The points of intersection of an ellipse with its axes of symmetry are called vertex ellipse a, the center of symmetry is the center of the ellipse, the segment between two vertices containing foci is called major axis of the ellipse, half of its length semi-major axis of an ellipse. The segment between the vertices on the axis of symmetry that does not contain foci is called minor axis of the ellipse, half of its length is the minor semiaxis. The value is called ellipse eccentricity.

If the ellipse is given by canonical equations, then its vertices have coordinates (– a;0), (a;0),(0; –b), (0;b), the semi-major axis is a, the minor semiaxis is equal to b. Value c, which is half the distance between the foci, is determined from the formula c 2 = a 2 – b 2 .

The eccentricity of the ellipse characterizes the degree of elongation of the ellipse. The closer the eccentricity is to zero, the more the ellipse looks like a circle. The closer the eccentricity is to 1, the more the ellipse is stretched. Note that, by definition, for an ellipse 0< <1.

The equation is called the canonical equation of the ellipse.

Ticket 8 Define hyperbole. Write the equation of the hyperbola in canonical form. Vertices, foci, axes, asymptotes and eccentricity of the hyperbola,

Definition: A hyperbola is a locus of points in a plane, for each of which the absolute value of the difference in distances to two fixed points of the same plane, called the foci of the hyperbola, is a constant value.

Just as in the case of an ellipse, to obtain the equation of a hyperbola, we choose an appropriate coordinate system. The origin of coordinates is located in the middle of the segment between the foci, the axis Ox direct along this segment, and the y-axis is perpendicular to it.

The equation is called canonical equation hyperbole.

A hyperbola has two mutually perpendicular axes of symmetry, one of which contains the foci of the hyperbola, and a center of symmetry. If a hyperbola is given by a canonical equation, then its axes of symmetry are the coordinate axes Ox and Oy, and the origin is the center of symmetry of the hyperbola.

Definition: Intersection points of the hyperbola given by the canonical equation with the axis Ox called vertices of the hyperbola, the segment between them is called the real axis of the hyperbola. The segment of the y-axis between the points (0;– b) and (0; b) is called the imaginary axis. Numbers a and b are called the real and imaginary semiaxes of the hyperbola, respectively. The origin of coordinates is called its center. The value is called eccentricity hyperbole.

Comment: From equality b 2 = c 2 – a 2 it follows that c>a, that is, the hyperbola >1. Eccentricity characterizes the angle between the asymptotes, the closer to 1, the smaller this angle.

Ticket 9. Define a parabola. Write the parabola equation in canonical form. Directrix, focus of a parabola

A parabola is the locus of points in a plane that are equidistant from a given point F and a given line d that does not pass through a given point. This geometric definition expresses parabola directory property.

The directorial property of a parabola The point F is called the focus of the parabola, the line d is called the directrix of the parabola, the midpoint O of the perpendicular dropped from the focus to the directrix is the vertex of the parabola, the distance p from the focus to the directrix is the parameter of the parabola, and the distance p2 from the vertex of the parabola to its focus is the focus distance (Fig. a). The straight line perpendicular to the directrix and passing through the focus is called the axis of the parabola (the focal axis of the parabola). The segment FM connecting an arbitrary point M of the parabola with its focus is called the focal radius of the point M. The segment connecting two points of the parabola is called the chord of the parabola.

For an arbitrary point of the parabola, the ratio of the distance to the focus to the distance to the directrix is equal to one. Comparing the directory properties of the ellipse, hyperbola and parabola, we conclude that parabola eccentricity is by definition equal to one

.Geometric definition of a parabola , expressing its directory property, is equivalent to its analytical definition - the line given by the canonical equation of the parabola:

Ticket 10. What is a square, identity, symmetric, orthogonal matrix. Define transposed and inverse matrices.

Definition 1.Matrix is called a rectangular table of numbers containing - rows and - columns. .

Definition 2. Numbers and are called Matrix orders(or say the matrix has size )

Definition 3. The numbers that make up this matrix are called its elements.

1. Definition 4. The matrix is called Square if the number of rows is equal to the number of columns. In the case of a square matrix, the concepts main diagonal(these are numbers - ) and Side diagonal(these are numbers - ).

2.Symmetrical A (symmetric) matrix is a square matrix whose elements are symmetrical with respect to the main diagonal. More formally, a matrix is called symmetric if .

This means that it is equal to its transposed matrix:

3. Identity matrix is called a diagonal matrix in which all diagonal elements are equal to one. For example, the identity matrix of the third order is the matrix

orthogonal matrix

square matrix A, for which A -1 = A T called orthogonal matrix. Basic properties of an orthogonal matrix: The modulus of the determinant of an orthogonal matrix is equal to one. This property follows from the properties of determinants:

The sum of the squares of the elements of any column of an orthogonal matrix is equal to one.

The scalar product of a row and itself is equal to 1, and to any other row is 0. The same is true for columns.

The sum of the products of the elements of any row of an orthogonal matrix by the corresponding elements of another row is equal to zero.

inverse matrix is a matrix that, when multiplied both on the right and on the left by a given matrix, gives the identity matrix. Denote the inverse of the matrix BUT through , then according to the definition we get: where E is the identity matrix.

The inverse matrix does not exist for all matrices. A necessary and sufficient condition for nondegeneracy is

det( A) ≠ 0 or rank( A) = N.

Properties of inverse matrices

· , where denotes the determinant.

· for any two invertible matrices and .

· , where denotes the transposed matrix.

· for any coefficient .

· If it is necessary to solve a system of linear equations , (b is a non-zero vector) where is the desired vector, and if it exists, then . Otherwise, either the dimension of the solution space is greater than zero, or there are none at all.

Transposed matrix- matrix obtained from the original matrix by replacing rows with columns.

Formally, the transpose matrix for the size matrix is the size matrix , defined as .

Ticket 11. What are equivalent matrices. List elementary transformations of matrices. What can be said about the ranks of equivalent matrices.

Definition. The matrices obtained as a result of an elementary transformation are called equivalent.

Elementary transformations over rows of matrices the following string transformations are called:

1. multiplying a string by a non-zero number;

2. permutation of two lines;

3. addition to one row of the matrix of its other row, multiplied by some non-zero number.

4. If a matrix is passed from matrix to matrix with the help of equivalent transformations over rows, then such matrices are called equivalent and denote .

5. Method of elementary transformations

6. The rank of a matrix is equal to the number of non-zero rows in the matrix after it has been reduced to a stepped form using elementary transformations over the matrix rows.

Ticket 12 What is a basis minor. State the basic minor theorem.

Definition. The rank of the matrix A is the maximum order of the non-zero minor (the minor is the determinant of a square matrix). Designated .

Definition. The minor that determines the rank of the matrix is called the Basis Minor. The rows and columns that form the BM are called basic rows and columns.

Definition. Column system is called linearly dependent numbers , not all equal to zero and such that:

Basis minor theorem

The columns of the matrix included in the basis minor form a linearly independent system. Any column of the matrix is linearly expressed in terms of the remaining columns from the basic minor.

In the size matrix, a minor of the -th order is said to be basic if it is nonzero and all -ro order minors are equal to zero or do not exist at all.

Consequence. If all columns of a matrix are linearly expressed in terms of columns that form a linearly independent system, then the rank of the matrix is .

Ticket 13 What is a homogeneous and non-homogeneous system of equations. What is called the solution of a system of equations. Explain the terms: compatible system of equations, incompatible system of equations. What systems of equations are called equivalent?

Definition 1. If all free terms are equal to zero, then the system is called homogeneous, and heterogeneous - otherwise.

Definition 2. The solution of the system is the set of n numbers with 1 , with 2 , …, with n , when substituting into the system, instead of unknowns, m numerical identities.

Definition 3. A system is called compatible (incompatible) if it has at least one solution (has no solutions).

Definition 4. A joint system of linear algebraic equations is called definite (indefinite) if it has a unique solution (set of solutions).

Definition.

Two systems of linear equations are called equivalent (equivalent), if they have the same solutions.

Equivalent systems are obtained, in particular, by elementary transformations of the system, provided that the transformations are performed only on the strings of the system.

Ticket 14 What is the fundamental system of solutions of a homogeneous system of equations. What is called the general solution of a homogeneous system of equations.

Definition. The basis of the solution space of a system of linear homogeneous equations is called its fundamental decision system.

Theorem on the structure of the general solution of a homogeneous system of equations:

Any solution of a homogeneous system of linear equations is defined by the formula

where X 1 , X 2 , … , X n − r- fundamental system of solutions of a homogeneous system of linear equations and C 1 , C 2 , … , C n − r are arbitrary constants.

Properties of the general solution of a homogeneous system of equations:

1. For any values C 1 , C 2 , … , C n − r X, defined by formula (3), is a solution to system (1).

2. Whatever the decision X 0 , there are numbers C 1 0 , … , C n − r 0 such that

Conclusion: To find the fundamental system and the general solution of the homogeneous system, we need to find the basis of the kernel of the corresponding linear operator.

Ticket 16. Give a definition of a linear space and formulate its properties.

A bunch of L called linear or vector space , if for all elements (vectors) of this set the operations of addition and multiplication by a number are defined and it is true:

1. Each pair of elements x and y from L meets element x + y from L , called sumx and y, and:

x + y = y+x− addition is commutative;

x + (y + z) = (x + y) + z− addition is associative;

x +0 = x− there is only one null element 0 (x +0 = x for anyone x from L );

x + (− x)= 0 − for each element x from L there is only one opposite element −x (x + (−x) = 0 for anyone x from L) .

2. Each pair x and α, where α − number, and x element from L , corresponds to the element α x, called workα andx, and:

α·(β · x) = (α·β) · x− multiplication by a number is associative: ;

1· x = x− for any element x from L .

3. The operations of addition and multiplication by a number are related by the relations:

α·( x + y) = α· x + α· y− multiplication by a number is distributive with respect to the addition of elements;

(α + β )· x = α· x + β · x− multiplication by a vector is distributive with respect to the addition of numbers.

Ticket 17. A subspace of a linear space. Its properties. Linear shell.

Definition of a linear subspace

A non-empty subset L of a linear space V is called linear subspace space V if

1) u+v∈L ∀u,v∈L (the subspace is closed with respect to the addition operation);

2) λv∈L ∀v∈L and any number λ (the subspace is closed with respect to the operation of multiplying a vector by a number).

Property 1 Any subspace of a linear space R is a linear space.

Property 2 dim M ≤ dim Rn.

Property 3 (on completion of the basis). If (ep)k is a basis in a subspace M of a linear space Rn, and k< n, то можно так выбрать элементы в Rn ek+1, ek+2, . . . , en, что (ep)n будет базисом в Rn.

Definition.Linear shell is a set of vectors that define a linear subspace. Strictly speaking, a linear span is the set of all linear combinations of given vectors. Let's also highlight the features:

Ticket 18. Define Euclidean space. Explain the vector normalization operation.

Definition Let V be a vector space. We say that V is given an inner product if any two vectors x, y ∈ V are associated with a real number, called the inner product of these vectors and denoted by xy or (x, y), so that the following conditions are satisfied (here x, y, z are arbitrary vectors from V, and

t is an arbitrary real number):

1) xy = yx (scalar product is commutative);

2) (tx)y = t(xy);

3) (x + y)z = xz + yz (scalar product is distributive with respect to addition);

4) xx >=0, and xx = 0 if and only if x = 0.

The vector space in which the scalar product is given is called Euclidean. Properties 1)–4) are called the axioms of the Euclidean space.

Vector call normalized or singular if its length is equal to one. To normalize an arbitrary non-zero vector is to divide it by its length. The result is a unit vector co-directed to the original one.
The scalar product of an arbitrary vector by a unit will give the exact length of the projection of this vector onto the direction of the unit. To get not just the length, but the projection vector itself, we need to multiply this length by our unit vector:

Ticket 19 What is an orthonormal basis. Explain the Gram-Schmidt orthogonalization process using a two-dimensional basis as an example.

Orthonormal system consisting of n vectors n-dimensional Euclidean space, forms the basis of this space. Such a basis is called orthonormal basis.

If a e 1 , e 2 , ..., en -orthonormal basis n-dimensional Euclidean space and

x = x 1 e 1 + x 2 e 2 + ... + x n e n - vector decomposition x over this basis, then the coordinates xi vector x in an orthonormal basis are calculated by the formulas xi =(x, ei ), i= 1, 2, ..., n.

GRAMA-SCHMIDT, Given a linearly independent system of vectors b 1 , b 2 , …, b l , a l+1 , …, a n l ≥ 1(1) the part to which it is orthogonal, we denote b l+1 orthogonal component of the vector and l+1 with respect to the orthogonal system b 1 , b 2 , …, b l Then1. Vector system b 1 , b 2 , …, b l , b l+1 , a l+2 , …, a n(2) is equivalent to (1).

2. The system of vectors (2) is linearly independent, and its part b 1 , b 2 , …, b l , b l+1– orthogonal. Using the concept of an orthogonal component, we describe the process of transformation of a linearly independent system a 1 , a 2 , …, a n into an orthogonal system b 1 , b 2 , …, b n non-zero vectors, which is called system orthogonalization a 1 , a 2 , …, a n.This process consists of n steps, n is the number of vectors in the original system a 1 , a 2 , …, a n.

1 step. We believe b 1 \u003d a 1 and get the system b 1 , a 2 , …, a n

2 step. Let us replace the vector in system (3) a 2 orthogonal component with respect to b 1, and we get the system: b 1 ,b 2 , a 3 ,…, a n (4)

According to the orthogonalization steps, system (4) is linearly independent, and its part b 1, b 2-orthogonal.

Assume that we have already built a linearly independent system b 1 , b 2 , …, b k-1 , a k ,…, a n, (5)

in which b 1 , b 2 , …, b k-1 are orthogonal.

At the kth step k = 3, n, we replace the vector in system (5) a k its orthogonal component with respect to the system b 1 , b 2 , …, b k-1 and get the system b 1 , …,b k , a k+1 , …, a n.

After performing the nth step, we obtain a linearly independent and orthogonal system of vectors b 1 , b 2 , …, b n.

Ticket 20.Define an operator in a linear space. Which operator is called linear.

Operator called the rule according to which each element x X a single element is matched y some non-empty set Y . The operator is said to act from X in Y .

The action of the operator is denoted y = A (x), y- image x, x- prototype y.

If each element y from Y has a single preimage x from X , y= A (x), the operator is called one-to-one mapping X in Y or transformation X , X - scope of operator definition.

Let be X and Y two linear spaces. Operator A acting from X in Y , is called line operator, if for any two elements u and v from X and any number α is valid:

A(u+ v) = A (u) + A (v) , A (α· u) = α· A (u).

Ticket 21. Give an example of a linear operator. What operations on linear operators do you know?

Canonical equations of the straight line

Formulation of the problem. Find the canonical equations of a straight line defined as a line of intersection of two planes (general equations)

Solution plan. Canonical equations of a straight line with a direction vector passing through this point , have the form

. (1)

Therefore, in order to write the canonical equations of a straight line, it is necessary to find its directing vector and some point on the straight line.

1. Since the line belongs to both planes simultaneously, its direction vector is orthogonal to the normal vectors of both planes, i.e. according to the definition of a vector product, we have

. (2)

2. Choose some point on the line. Since the directing vector of the line is not parallel to at least one of the coordinate planes, the line intersects this coordinate plane. Therefore, as a point on a line, the point of its intersection with this coordinate plane can be taken.

3. We substitute the found coordinates of the directing vector and point into the canonical equations of the straight line (1).

Comment. If the vector product (2) is equal to zero, then the planes do not intersect (parallel) and it is not possible to write down the canonical equations of the straight line.

Task 12. Write the canonical equations of the line.

Canonical equations of a straight line:

where are the coordinates of any point on the line, is its direction vector.

Find any point on the line . Let then

Hence, are the coordinates of a point belonging to the line.