Plot a circle using an equation. Circle on the coordinate plane
Build function
We bring to your attention a service for drawing function charts online, all rights to which belong to the company Desmos... Use the left column to enter functions. You can enter it manually or using the virtual keyboard at the bottom of the window. To enlarge the window with the graph, you can hide both the left column and the virtual keyboard.
Benefits of charting online
- Visual display of entered functions
- Building very complex graphs
- Creation of graphs, given implicitly (for example, ellipse x ^ 2/9 + y ^ 2/16 = 1)
- The ability to save charts and receive a link to them, which becomes available to everyone on the Internet
- Scale control, line color
- Possibility of plotting graphs by points, using constants
- Simultaneous construction of several graphs of functions
- Plotting in polar coordinates (use r and θ (\ theta))
It is easy to build charts of varying complexity online with us. Construction is done instantly. The service is in demand for finding intersection points of functions, for displaying graphs for their further movement in a Word document as illustrations when solving problems, for analyzing the behavioral features of function graphs. The optimal browser for working with charts on this page of the site is Google Chrome. Operation is not guaranteed with other browsers.
If you place a unit number circle on a coordinate plane, then coordinates can be found for its points. The numerical circle is positioned so that its center coincides with the point of origin of the plane, that is, the point O (0; 0).
Usually on the unit number circle, points are marked corresponding from the origin on the circle
- quarters - 0 or 2π, π / 2, π, (2π) / 3,
- mid-quarters - π / 4, (3π) / 4, (5π) / 4, (7π) / 4,
- thirds of quarters - π / 6, π / 3, (2π) / 3, (5π) / 6, (7π) / 6, (4π) / 3, (5π) / 3, (11π) / 6.
On the coordinate plane with the above location of the unit circle on it, you can find the coordinates corresponding to these points of the circle.
The coordinates of the ends of the quarters are very easy to find. At point 0 of the circle, the x coordinate is 1, and y is 0. It can be denoted as A (0) = A (1; 0).
The end of the first quarter will be located on the positive y-axis. Therefore, B (π / 2) = B (0; 1).
The end of the second quarter is on the negative semiaxis: C (π) = C (-1; 0).
End of the third quarter: D ((2π) / 3) = D (0; -1).
But how do you find the coordinates of the midpoints of the quarters? To do this, build a right-angled triangle. Its hypotenuse is a segment from the center of the circle (or origin) to the midpoint of the quarter circle. This is the radius of the circle. Since the circle is unit, the hypotenuse is 1. Next, a perpendicular is drawn from the point of the circle to any axis. Let it be towards the x-axis. It turns out a right-angled triangle, the lengths of the legs of which are the x and y coordinates of the point of the circle.
The quarter circle is 90º. And half a quarter is 45 degrees. Since the hypotenuse is drawn to the point of the middle of the quarter, the angle between the hypotenuse and the leg extending from the origin is 45º. But the sum of the angles of any triangle is 180º. Therefore, the angle between the hypotenuse and the other leg is also 45º. It turns out an isosceles right triangle.
From the Pythagorean theorem we obtain the equation x 2 + y 2 = 1 2. Since x = y and 1 2 = 1, the equation is simplified to x 2 + x 2 = 1. Solving it, we get x = √½ = 1 / √2 = √2 / 2.
Thus, the coordinates of the point are M 1 (π / 4) = M 1 (√2 / 2; √2 / 2).
In the coordinates of the points of the midpoints of other quarters, only the signs will change, and the moduli of the values will remain the same, since the right-angled triangle will only be inverted. We get:
M 2 ((3π) / 4) = M 2 (-√2 / 2; √2 / 2)
M 3 ((5π) / 4) = M 3 (-√2 / 2; -√2 / 2)
M 4 ((7π) / 4) = M 4 (√2 / 2; -√2 / 2)
When determining the coordinates of the third parts of the quarters of the circle, a right-angled triangle is also built. If we take the point π / 6 and draw a perpendicular to the x-axis, then the angle between the hypotenuse and the leg lying on the x-axis will be 30º. It is known that a leg lying opposite an angle of 30 degrees is equal to half of the hypotenuse. So, we found the y-coordinate, it is equal to ½.
Knowing the lengths of the hypotenuse and one of the legs, according to the Pythagorean theorem, we find another leg:
x 2 + (½) 2 = 1 2
x 2 = 1 - ¼ = ¾
x = √3 / 2
Thus, T 1 (π / 6) = T 1 (√3 / 2; ½).
For the point of the second third of the first quarter (π / 3), it is better to draw the perpendicular to the axis to the y axis. Then the angle at the origin of coordinates will also be 30º. Here, the x coordinate will be equal to ½, and y, respectively, √3 / 2: T 2 (π / 3) = T 2 (½; √3 / 2).
For other points in the third quarters, the signs and order of the coordinate values will change. All points that are closer to the x-axis will have an x-coordinate modulo √3 / 2. Those points that are closer to the y-axis will have a y-value of √3 / 2 in absolute value.
T 3 ((2π) / 3) = T 3 (-½; √3 / 2)
T 4 ((5π) / 6) = T 4 (-√3 / 2; ½)
T 5 ((7π) / 6) = T 5 (-√3 / 2; -½)
T 6 ((4π) / 3) = T 6 (-½; -√3 / 2)
T 7 ((5π) / 3) = T 7 (½; -√3 / 2)
T 8 ((11π) / 6) = T 8 (√3 / 2; -½)
Analytical geometry provides uniform techniques for solving geometric problems. To do this, all specified and required points and lines are referred to one coordinate system.
In the coordinate system, each point can be characterized by its coordinates, and each line by an equation with two unknowns, the graph of which this line is. Thus, a geometric problem is reduced to an algebraic one, where all calculation techniques are well developed.
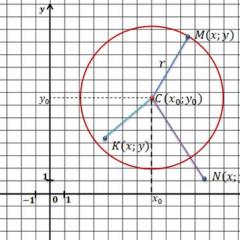
A circle is a locus of points with one specific property (each point of a circle is equidistant from one point, called the center). The equation of the circle must reflect this property, satisfy this condition.
The geometric interpretation of the circle equation is the line of the circle.
If you place a circle in a coordinate system, then all points of the circle satisfy one condition - the distance from them to the center of the circle must be the same and equal to the circle.
Circle centered at point A and radius R put in the coordinate plane.
If the coordinates of the center (a; b) , and the coordinates of any point of the circle (x; y) , then the equation of the circle has the form:
If the square of the radius of the circle is equal to the sum of the squares of the differences of the corresponding coordinates of any point of the circle and its center, then this equation is the equation of the circle in a flat coordinate system.
If the center of the circle coincides with the origin point, then the square of the radius of the circle is equal to the sum of the squares of the coordinates of any point on the circle. In this case, the equation of the circle takes the form:
Consequently, any geometric figure as a locus of points is determined by the equation connecting the coordinates of its points. Conversely, the equation connecting the coordinates NS and at , define a line as a locus of points of the plane, the coordinates of which satisfy the given equation.
Examples of solving problems about the equation of a circle
Task. Equate a given circle
Equate a circle with center O (2; -3) and radius 4.Solution.
Let us turn to the formula for the equation of the circle:
R 2 = (x-a) 2 + (y-b) 2
Let's plug in the values into the formula.
Circle radius R = 4
Circle center coordinates (as required)
a = 2
b = -3
We get:
(x - 2) 2 + (y - (-3)) 2 = 4 2
or
(x - 2) 2 + (y + 3) 2 = 16.
Task. Does a point belong to the equation of a circle
Check if point belongs A (2; 3) circle equation (x - 2) 2 + (y + 3) 2 = 16 .Solution.
If a point belongs to a circle, then its coordinates satisfy the equation of the circle.
To check if the point with the given coordinates belongs to the circle, we substitute the coordinates of the point into the equation of the given circle.
In the equation ( x - 2) 2 + (y + 3) 2 = 16
we substitute, according to the condition, the coordinates of the point A (2; 3), that is
x = 2
y = 3
Let us check the truth of the obtained equality
(x - 2) 2 + (y + 3) 2 = 16
(2
- 2) 2 + (3
+ 3) 2 = 16
0 + 36 = 16 equality is wrong
So the given point not belong the given equation of the circle.
Let the circle have a radius 
, and its center is at the point 
... Point 
lies on the circle if and only if the modulus of the vector 
is equal to 
, that is. The last equality holds if and only if
Equation (1) is the desired equation of the circle.
Equation of a straight line passing through a given point, perpendicular to a given vector
perpendicular to vector 
.
Point 
and 
perpendicular. Vectors 
and 
are perpendicular if and only if their dot product is zero, that is 
... Using the formula for calculating the scalar product of vectors given by their coordinates, we write the equation of the desired straight line in the form
Let's look at an example. Find the equation of the straight line passing through
the middle of the segment AB is perpendicular to this segment if the coordinates of the points are respectively equal to A (1; 6), B (5; 4).
We will argue as follows. To find the equation of a line, we need to know the point through which this line passes, and the vector perpendicular to this line. The vector perpendicular to the given line will be the vector, since, according to the problem statement, the line is perpendicular to the segment AB. Point 
define from the condition that the straight line passes through the middle of AB. We have. Thus 
and the equation takes the form.
Let us clarify the question whether this line passes through the point M (7; 3).
We have, therefore, this line does not pass through the specified point.
Equation of a straight line passing through a given point parallel to a given vector
Let the line pass through the point 
parallel to vector 
.
Point 
lies on the straight line if and only if the vectors 
and 
colinear. Vectors 
and 
colinear if and only if their coordinates are proportional, that is
(3)
The resulting equation is the equation of the desired straight line.
Equation (3) can be represented as
, where 
takes any values 
.
Therefore, we can write
, where 
(4)
The system of equations (4) is called parametric equations of the straight line.
Let's look at an example. Find the equation of the straight line passing through the points. We can construct the equation of a straight line if we know a point and a vector parallel or perpendicular to it. There are two points available. But if two points lie on a straight line, then the vector connecting them will be parallel to this straight line. Therefore, we will use equation (3), taking as a vector 
vector 
... We get
(5)
Equation (5) is called the equation of a straight line passing through two given points.
General equation of the straight line
Definition. The general equation of a first-order line on a plane is an equation of the form 
, where 
.
Theorem. Any straight line on a plane can be given in the form of an equation of a first-order line, and any equation of a first-order line is an equation of some straight line on a plane.
The first part of this theorem is easy to prove. On any straight line, you can specify some point 
vector perpendicular to it 
... Then, according to (2), the equation of such a straight line has the form. We denote 
... Then the equation takes the form 
.
We now turn to the second part of the theorem. Let there be an equation 
, where 
... For definiteness, we assume 
.
Let's rewrite the equation as:
;
Consider on the plane the point 
, where 
... Then the resulting equation has the form, and is the equation of the straight line passing through the point 
perpendicular to vector 
... The theorem is proved.
In the course of proving the theorem, we along the way proved
Statement. If there is a straight line equation of the form 
, then the vector 
perpendicular to this line.
Equation of the form
is called the general equation of a straight line on a plane.
Let there be a straight line 
and point 
... It is required to determine the distance from the specified point to the straight line.
Consider an arbitrary point 
on a straight line. We have 
... Distance 
from point 
to the straight line is equal to the modulus of the vector projection 
per vector 
perpendicular to this line. We have
,
transforming, we get the formula:
Let there be given two straight lines given by the general equations
,
... Then the vectors 
are perpendicular to the first and second straight lines, respectively. Injection 
between straight lines is equal to the angle between vectors 
,
.
Then the formula for determining the angle between the straight lines is:
.
The condition of perpendicularity of straight lines is:
.
Lines are parallel or coincide if and only if the vectors 
colinear. Wherein the condition for the coincidence of straight lines has the form:
,
and the condition for the absence of intersection is written as:
... Prove the last two conditions yourself.
Let us investigate the nature of the behavior of the straight line according to its general equation.
Let the general equation of the line be given 
... If 
, then the straight line passes through the origin.
Consider the case when none of the coefficients is equal to zero 
... We rewrite the equation in the form:
,
,
Where 
... Let's find out the meaning of the parameters 
... Find the intersection points of the straight line with the coordinate axes. At 
we have 
, and at 
we have 
... That is 
are the segments that are cut off by a straight line on the coordinate axes. Therefore the equation
is called the equation of a straight line in segments.
When 
we have 
... When 
we have 
... That is, the straight line will be parallel to the axis 
.
Recall that slope of the straight line
called the tangent of the angle of inclination of this straight line to the axis 
... Let the line cut off on the axis 
section 
and has a slope 
... Let the point 
lies with this
Then 
=
=
... And the equation of the straight line will be written in the form
.
Let the line pass through the point 
and has a slope 
... Let the point 
lies on this straight line.
Then 
=
.
The resulting equation is called the equation of a straight line passing through a given point with a given slope.
Given two lines 
,
... We denote 
- the angle between them. Let be 
,
angles of inclination to the X-axis of the corresponding straight lines
Then 
=
,
.
Then the condition for parallelism of straight lines has the form 
, and the perpendicularity condition
In conclusion, we will consider two problems.
Task ... The vertices of the ABC triangle have coordinates: A (4; 2), B (10; 10), C (20; 14).
Find: a) the equation and the length of the median drawn from the vertex A;
b) the equation and the length of the height drawn from the top A;
c) the equation of the bisector drawn from the vertex A;
Let's define the equation of the median AM.
Point М () is the middle of the segment BC.
Then 
,
... Consequently, the point M has coordinates M (15; 17). The median equation in the language of analytical geometry is the equation of a straight line passing through the point A (4; 2) parallel to the vector = (11; 15). Then the median equation has the form. Median length AM = 
.
The height equation AS is the equation of a straight line passing through the point A (4; 2) perpendicular to the vector = (10; 4). Then the height equation is 10 (x-4) +4 (y-2) = 0.5x + 2y-24 = 0.
Height length is the distance from point A (4; 2) to line BC. This line passes through point B (10; 10) parallel to the vector = (10; 4). Its equation has the form 
, 2x-5y + 30 = 0. Distance AS from point A (4; 2) to line BC, therefore, is equal to AS = 
.
To determine the equation of the bisector, we find a vector parallel to this straight line. To do this, we will use the property of the rhombus diagonal. If from point A we put off the unit vectors equally directed from the vectors, then the vector equal to their sum will be parallel to the bisector. Then we have = +.
={6;8},
,
={16,12},
.
Then = 
The vector = (1; 1), collinear to the given one, can serve as the direction vector of the desired straight line. Then the equation of the required straight line has seen or x-y-2 = 0.
Task. The river flows in a straight line passing through points A (4; 3) and B (20; 11). Little Red Riding Hood lives at point C (4; 8), and her grandmother lives at point D (13; 20). Every morning Little Red Riding Hood takes an empty bucket from home, goes to the river, scoops up water and takes it to grandmother. Find the shortest road for Little Red Riding Hood.
Let's find the point E, symmetrical to the grandmother, relative to the river.
To do this, we first find the equation of the straight line along which the river flows. This equation can be considered as the equation of a straight line passing through the point A (4; 3) parallel to the vector. Then the equation of the line AB has the form.
Next, we find the equation of the straight line DE passing through point D perpendicular to AB. It can be considered as the equation of a straight line passing through point D, perpendicular to the vector 
... We have
Now we find point S - the projection of point D onto line AB, as the intersection of lines AB and DE. We have a system of equations
.
Therefore, the point S has coordinates S (18; 10).
Since S is the midpoint of the segment DE, then.
Likewise.
Consequently, the point E has coordinates E (23; 0).
Let us find the equation of the line CE, knowing the coordinates of two points of this line
We find the point M as the intersection of lines AB and CE.
We have a system of equations
.
Consequently, point M has coordinates 
.
Topic 2. The concept of the equation of a surface in space. Sphere equation. The equation of a plane passing through a given point is perpendicular to a given vector. General equation of the plane and its study Condition of parallelism of two planes. Distance from point to plane. Line equation concept. A straight line in space. Canonical and parametric equations of a straight line in space. Equations of a straight line passing through two given points. Conditions for parallelism and perpendicularity of a straight line and a plane.
First, we give a definition of the concept of an equation of a surface in space.
Let in space 
given some surface 
... The equation 
is called the equation of the surface 
if two conditions are met:
1.for any point 
with coordinates 
lying on the surface is satisfied 
, that is, its coordinates satisfy the surface equation;
2.any point 
whose coordinates satisfy the equation 
, lies on the line.
Loading...