Видове интеграли и методи за тяхното решаване. Решаване на интеграли онлайн
Намирането на неопределения интеграл е много често срещан проблем във висшата математика и други технически клонове на науката. Дори решаването на най-простите физически задачи често не е пълно без изчисляването на няколко прости интеграла. Следователно от училищна възраст ни учат на техники и методи за решаване на интеграли, дават се множество таблици с интеграли от най-простите функции. С течение на времето обаче всичко това се забравя безопасно, или нямаме достатъчно време за изчисления, или трябва да намерете решение на неопределения интегралот много сложна функция. За да разрешите тези проблеми, нашата услуга ще бъде незаменима за вас, което ви позволява да намерите точно неопределения интеграл онлайн.
Решете неопределения интеграл
Включена онлайн услуга сайтви позволява да намерите онлайн интегрално решениебързо, безплатно и високо качество. Можете да замените търсенето в таблиците на необходимия интеграл с нашата услуга, където чрез бързо въвеждане на желаните функции ще получите решението на неопределения интеграл в табличен вариант. Не всички математически сайтове могат да изчисляват неопределени интеграли от функции онлайн бързо и ефективно, особено ако трябва да намерите неопределен интегралот сложна функция или такива функции, които не са включени в общия курс на висшата математика. Сайт сайтще помогне решаване на интеграла онлайн и се справят със задачата. Използвайки онлайн решението на интеграла в сайта на сайта, винаги ще получите точния отговор.
Дори ако искате сами да изчислите интеграла, благодарение на нашата услуга ще ви бъде лесно да проверите отговора си, да намерите грешка или печатна грешка или да се уверите, че задачата е изпълнена безупречно. Ако решавате задача и трябва да изчислите неопределения интеграл като спомагателно действие, тогава защо да губите време за тези действия, които може би вече сте извършвали хиляди пъти? Освен това допълнителните изчисления на интеграла могат да бъдат причина за печатна грешка или малка грешка, която впоследствие доведе до неправилен отговор. Просто използвайте нашите услуги и намерете неопределен интеграл онлайнбез никакви усилия. За практически задачи за намиране интегралнафункции онлайнтози сървър е много полезен. Трябва да въведете дадена функция, да получите онлайн неопределено интегрално решениеи сравнете отговора с вашето решение.
Думата "интеграл" идва от латинското integralis - интеграл. Това име е предложено през 17 век. ученик на великия Лайбниц (а също и на изключителен математик) И. Бернули. Какво е интеграл в съвременния смисъл? По-долу ще се опитаме да дадем изчерпателен отговор на този въпрос.
Исторически предпоставки за възникване на понятието интеграл
В началото на 17 век. водещи учени разглеждат голям брой физически (предимно механични) проблеми, при които е необходимо да се изследва зависимостта на едни величини от други. Най-очевидните и неотложни проблеми бяха определянето на моменталната скорост на неравномерното движение на тялото във всеки един момент от време и обратната задача за намиране на големината на пътя, изминат от тялото за определен период от време по време на такъв движение. Днес вече знаем какъв е интегралът от скоростта на движение – това е изминатият път. Но разбирането как да го изчислим, знаейки скоростта във всеки момент от време, не се появи веднага.
Първо, от разглеждането на такива зависимости на физическите величини, например пътя от скоростта, се формира математическата концепция за функцията y = f(x). Изучаването на свойствата на различни функции доведе до раждането на математическия анализ. Учените активно търсят начини за изследване на свойствата на различни функции.
Как се стигна до изчисляването на интеграли и производни?
След като Декарт създаде основите на аналитичната геометрия и възможността да се изобразят графично функционалните зависимости в осите на декартовата координатна система, изследователите се изправиха пред две големи нови задачи: как да начертаят допирателна към крива линия във всяка точка от нея и как да намерят площта на фигурата, ограничена отгоре от тази крива и прави линии, успоредни на координатните оси. Неочаквано се оказа, че първият от тях е еквивалентен на намиране на моментната скорост, а вторият - на намиране на изминатото разстояние. В крайна сметка, с неравномерно движение, той беше изобразен в декартовите координатни оси "разстояние" и "време" чрез някаква извита линия.
Геният на Лайбниц и Нютон в средата на 17 век. са разработени методи за решаване на двата проблема. Оказа се, че за да се направи допирателна към крива в дадена точка, е необходимо да се намери стойността на така наречената производна на функцията, която описва тази крива в разглежданата точка, и тази стойност се оказва равна на скоростта на промяна на функцията, т.е. по отношение на зависимостта "път от скорост" собствената моментна скорост на тялото.
За да се намери площта, ограничена от крива линия, беше необходимо да се изчисли определен интеграл, който даде точната му стойност. Производната и интеграла са основните понятия на диференциалното и интегралното смятане, които са в основата на съвременния математически анализ – най-важният раздел на висшата математика.
Площ под кривата
И така, как да определим точната стойност? Нека се опитаме да разкрием процеса на неговото изчисляване чрез интеграла подробно, от самото начало.
Нека f е непрекъсната функция на интервала. Помислете за кривата y \u003d f (x), показана на фигурата по-долу. Как да намерим площта на областта, ограничена от кривата), оста x и линиите x = a и x = b? Тоест площта на засенчената фигура на фигурата.

Най-простият случай е, когато f е постоянна функция; т.е. кривата е хоризонтална линия f(X) = k, където k е константа и k ≥ 0, както е показано на фигурата по-долу.

В този случай площта под кривата е просто правоъгълник с височина k и ширина (b - a), така че площта се дефинира като: k · (b - a).
Площите на някои други прости фигури, като триъгълник, трапец и полукръг, са дадени с формули от планиметрията.
Площта под всяка непрекъсната крива y = f(x) се дава от определен интеграл, който се записва по същия начин като обикновен интеграл.
Риманова сума
Преди да се потопим в подробен отговор на въпроса какво е интеграл, нека подчертаем някои основни идеи.
Първо, площта под кривата се разделя на определен брой n вертикални ивици с достатъчно малка ширина Δx. След това всяка вертикална ивица се заменя с вертикален правоъгълник с височина f(x), ширина Δx и площ f(x)dx. Следващата стъпка е да се формира сумата от площите на всички тези правоъгълници, наречена сума на Риман (вижте снимките по-долу).
Начертавайки нашите правоъгълници с ширина Δx, можем да вземем тяхната височина равна на стойността на функцията на левия ръб на всяка лента, т.е. най-левите точки на техните горни къси страни с ширина Δx ще лежат върху кривата. В същото време, в участъка, където функцията расте и нейната крива е изпъкнала, всички правоъгълници са под тази крива, т.е. тяхната сума очевидно ще бъде по-малка от точната стойност на площта под кривата в този участък (виж фигурата По-долу). Този метод на апроксимация се нарича ляв.

По принцип е възможно да се начертаят апроксимиращи правоъгълници по такъв начин, че най-десните точки на техните горни къси страни с ширина Δx да лежат върху кривата. Тогава те ще бъдат над кривата и приближението на площта в тази област ще бъде по-голямо от нейната точна стойност, както е показано на фигурата по-долу. Този метод се нарича дясна ръка.

Но можем да вземем и височината на всеки от апроксимиращите правоъгълници, която е просто равна на някаква стойност на функцията в произволна точка x* i вътре в съответната лента Δx i (виж фигурата по-долу). В същото време може дори да не вземем една и съща ширина на всички ленти.

Нека направим риманова сума:

Преход от римановата сума към определения интеграл
Във висшата математика е доказана теорема, която гласи, че ако с неограничено увеличаване на броя n на апроксимиращите правоъгълници, тяхната най-голяма ширина клони към нула, тогава римановата сума A n клони към определена граница A. Числото A е същото за всеки метод за формиране на апроксимиращи правоъгълници и за произволен избор на точки x* i .
Визуално обяснение на теоремата е дадено от фигурата по-долу.
От него се вижда, че колкото по-тесни са правоъгълниците, толкова по-близо е площта на стъпаловидна фигура до областта под кривата. Когато броят на правоъгълниците е n→∞, тяхната ширина е Δx i →0, а границата A на сумата A n е числено равна на желаната площ. Тази граница е определеният интеграл на функцията f (x):

Интегралният символ, който е модифицирана курсивна буква S, е въведен от Лайбниц. Дж. Б. Фурие предложи да се постави обозначението на интеграла над и под неговите граници. В този случай началните и крайните стойности на x са ясно посочени.
Геометрична и механична интерпретация на определения интеграл
Нека се опитаме да дадем подробен отговор на въпроса какво е интеграл? Нека разгледаме интеграла върху сегмент от функцията f(x) положителен вътре в него и приемем, че горната граница е по-голяма от долната a Ако ординатите на функцията f(x) са отрицателни вътре, тогава абсолютната стойност на интеграла е равна на площта между оста x и графиката y=f(x), докато самият интеграл е отрицателен. В случай на еднократно или многократно пресичане от графиката y = f (x) на оста на абсцисата на сегмента, както е показано на фигурата по-долу, за да изчислите интеграла, трябва да определите разликата, в която ще намалее да бъде равна на общата площ на секциите, разположени над оста на абсцисата, а изваждането - общата площ на земята под нея. Така че, за функцията, показана на фигурата по-горе, определеният интеграл от a до b ще бъде равен на (S1 + S3) - (S2+S4). Механичната интерпретация на определения интеграл е тясно свързана с геометричната. Нека се върнем към секцията "Римановата сума" и си представим, че графиката, показана на фигурите, изразява функцията на скоростта v=f(t) за неравномерно движение на материална точка (оста на абсцисата е оста на времето). Тогава площта на всеки апроксимиращ правоъгълник с ширина Δt, който изградихме при формиране на сумата на Риман, приблизително ще изрази пътя на точката във времето Δt, а именно v(t*)Δt. Общата сума от площите на правоъгълниците на отсечката от t 1 \u003d a до t 2 \u003d b приблизително ще изрази пътя s във времето t 2 - t 1 и неговата граница, т.е. интегралът (дефиниран) от a до b на функцията v \u003d f (t ) над dt ще даде точната стойност на пътя s. Ако се върнем към обозначението му, тогава е напълно възможно да приемем, че a = const, а b е специфична стойност на някаква независима променлива x. Тогава определеният интеграл с горната граница x̃ се превръща от определено число във функция на x̃. Такъв интеграл е равен на площта на фигурата под кривата, обозначена с точките aABb на фигурата по-долу. При фиксирана линия aA и движеща се Bb, тази област става функция на f(x̃), а нарастванията Δx̃ все още се нанасят по оста x, а нарастванията на функцията f(x̃) са нарастванията на площта под крива. Да предположим, че сме дали на променливата x̃ = b малко увеличение Δx̃. Тогава увеличението на площта на фигурата aABb е сумата от площта на правоъгълника (защрихована на фигурата) Bb∙Δx̃ и площта на фигурата BDC под кривата. Площта на правоъгълника е равна на Bb∙Δx̃ = f(x̃)Δx̃, тоест е линейна функция на приращението на независимата променлива. Площта на фигурата BDC очевидно е по-малка от площта на правоъгълника BDCK = Δx̃∙Δy и при Δx̃ → 0 намалява още по-бързо. Следователно, f(x̃)Δx̃ = f(x̃)dx̃ е диференциалът на променливата площ aABb, т.е. диференциалът на определен интеграл От това можем да заключим, че изчисляването на интегралите се състои в намиране на функции чрез дадени изрази за техните диференциали. Интегралното смятане е просто система от начини за търсене на такива функции чрез техните известни диференциали. Той свързва връзката между диференциране и интегриране и показва, че съществува операция, обратна на диференцирането на функция – нейното интегриране. Той също така показва, че ако някоя функция f(x) е непрекъсната, тогава прилагайки тази математическа операция към нея, можете да намерите цял ансамбъл (набор, набор) от функции, които са антипроизводни за нея (или по друг начин, да намерите неопределен интеграл от нея ). Нека функцията F(x) е обозначението за резултата от интегрирането на функцията f(x). Съответствието между тези две функции в резултат на интегрирането на втората от тях се обозначава по следния начин: Както се вижда, няма ограничения за интегриране за интегралния символ. Това означава, че е преобразуван от определен интеграл в неопределен интеграл. Думата "неопределен" означава, че резултатът от операцията за интегриране в този случай не е една, а много функции. В крайна сметка, освен самата функция F(x), всяка функция F(x)+С, където С = const, удовлетворява и последните изрази. Това означава, че постоянният член в ансамбъла от антипроизводни може да се задава произволно. Трябва да се подчертае, че ако дефинираният интеграл на функция е число, то неопределеният е функция, по-точно набор от тях. Терминът "интегриране" се използва за дефиниране на операцията за търсене на двата вида интеграли. То е точно обратното на съответното правило за диференциация. Как се вземат неопределените интеграли? Ще разгледаме примери за тази процедура за конкретни функции. Нека разгледаме обща функция за мощност: След като сме направили това с всеки член в израза на интегрируемата функция (ако има повече от един), добавяме константа в края. Припомнете си, че вземането на производната на константа я унищожава, така че вземането на интеграла от която и да е функция ще ни даде реконструкция на тази константа. Означаваме го C, тъй като константата е неизвестна - може да бъде произволно число! Следователно можем да имаме безкрайно много изрази за неопределения интеграл. Нека разгледаме прости неопределени интеграли, примери за които са показани по-долу. Нека намерим интеграла на функцията: f(x) = 4x 2 + 2x - 3. Да започнем с първия мандат. Разглеждаме степента 2 и я увеличаваме с 1, след което разделяме първия член на получения степен 3. Получаваме: 4(x 3) / 3. След това гледаме следващия член и правим същото. Тъй като има степен 1, полученият показател ще бъде 2. Така че разделяме този член на 2: 2(x 2) / 2 = x 2 . Последният член има x фактор, но ние просто не го виждаме. Можем да мислим за последния член като (-3x 0). Това е еквивалентно на (-3)∙(1). Ако използваме правилото за интегриране, ще добавим 1 към степента, за да я повишим на първа степен, и след това ще разделим последния член на 1. Получаваме 3x. Това правило за интегриране работи за всички стойности на n с изключение на n = - 1 (защото не можем да разделим на 0). Разгледахме най-простия пример за намиране на интеграл. Като цяло решаването на интеграли не е лесна задача, а вече натрупаният опит в математиката е добра помощ в това. В раздела по-горе видяхме, че всяка формула за диференциране дава съответна формула за интегриране. Следователно всичките им възможни варианти отдавна са получени и обобщени в съответните таблици. Таблицата с интеграли по-долу съдържа формули за интегриране на основни алгебрични функции. Тези формули трябва да се знаят наизуст, като се запомнят постепенно, тъй като се консолидират чрез упражнения. Друга таблица на интегралите съдържа основните тригонометрични функции: Оказва се, че е много лесно да направите това, като можете да интегрирате, т.е. да намерите неопределени интеграли. И формулата на основателите на интегро-диференциалното смятане на Нютон и Лайбниц помага за това Според него изчисляването на желания интеграл се състои на първия етап в намирането на неопределения, след това изчисляване на стойността на намерената антипроизводна F(x) при заместване на x, която първо е равна на горната граница, след това на долната , и накрая, при определяне на разликата на тези стойности. В този случай константата C може да бъде пропусната. защото изчезва, когато се извърши изваждането. Помислете за някои интеграли с подробно решение. Намерете площта на графика под една полувълнова синусоида. Изчислете засенчената площ под хиперболата. Разгледайте сега интегралите с подробно решение ,
използвайки свойството адитивност в първия пример и заместването на междинна интегрираща променлива във втория. Нека изчислим определения интеграл на дробно-рационалната функция: y=(1+t)/t3 от t=1 до t=2. Сега показваме как можем да опростим вземането на интеграла чрез въвеждане на междинна променлива. Нека е необходимо да се изчисли интегралът от (x+1) 2 . Говорихме за определен интеграл за краен интервал на функция f(x), непрекъсната върху него. Но редица специфични проблеми водят до необходимостта от разширяване на концепцията за интеграл до случая, когато границите (една или и двете) са равни на безкрайност или когато функцията е прекъсната. Например, при изчисляване на площи под криви, асимптотично приближаващи се до координатните оси. За да се разшири концепцията за интеграла в този случай, в допълнение към преминаването към границата при изчисляване на Риманова сума от апроксимиращите правоъгълници се извършва още един. При такова двойно преминаване до предела се получава неправилен интеграл. За разлика от него всички споменати по-горе интеграли се наричат правилни. определен интеграл
от непрекъсната функция е(х) на крайния интервал [ а, б] (където ) е приращението на някои от неговите антипроизводни на този сегмент. (Като цяло разбирането ще бъде значително по-лесно, ако повторите темата за неопределения интеграл) В този случай нотацията Както може да се види на графиките по-долу (увеличението на антипроизводната функция е обозначено с ), Определеният интеграл може да бъде положителен или отрицателен.(Изчислява се като разлика между стойността на антидеривата в горната граница и стойността му в долната граница, т.е. Ф(б) - Ф(а)). Числа аи бсе наричат съответно долна и горна граница на интегриране и интервалът [ а, б] е сегментът на интеграцията. По този начин, ако Ф(х) е някаква антипроизводна функция за е(х), тогава, според определението, Равенство (38) се нарича Формула на Нютон-Лайбниц
. Разликата Ф(б) – Ф(а) се пише накратко така: Следователно формулата на Нютон-Лайбниц ще бъде написана, както следва: Нека докажем, че определеният интеграл не зависи от това коя антипроизводна на подинтегралната функция е взета при изчисляването му. Позволявам Ф(х) и F( х) са произволни първопроизводни на интегралната функция. Тъй като това са антипроизводни с една и съща функция, те се различават с постоянен член: Ф( х) = Ф(х) + ° С. Така Така се установява, че на отсечката [ а, б] инкременти на всички първопроизводни на функцията е(х) съвпада. По този начин, за да се изчисли определеният интеграл, е необходимо да се намери произволна антипроизводна на интегралната функция, т.е. Първо трябва да намерите неопределения интеграл. Постоянна С
изключени от последващи изчисления. След това се прилага формулата на Нютон-Лайбниц: стойността на горната граница се замества в антипроизводната функция б
, по-нататък - стойността на долната граница а
и изчислете разликата F(b) - F(a)
. Полученото число ще бъде определен интеграл.. В а = бприето по дефиниция Пример 1 Решение. Нека първо намерим неопределения интеграл: Прилагане на формулата на Нютон-Лайбниц към антипроизводната (при С= 0), получаваме Въпреки това, когато се изчислява определен интеграл, е по-добре да не се намира антипроизводната отделно, а веднага да се запише интеграла във формата (39). Пример 2Изчислете определен интеграл Решение. Използване на формулата Теорема 2.Стойността на определения интеграл не зависи от обозначението на променливата за интегриране, т.е. Позволявам Ф(х) е антипроизводно за е(х). За е(т) антипроизводната е същата функция Ф(т), в който независимата променлива е обозначена по различен начин. следователно, Въз основа на формула (39) последното равенство означава равенство на интегралите Теорема 3.Постоянният фактор може да бъде изваден от знака на определен интеграл, т.е. Теорема 4.Определеният интеграл от алгебричния сбор на краен брой функции е равен на алгебричния сбор от определените интеграли на тези функции, т.е. Теорема 5.Ако интегриращият сегмент е разделен на части, тогава определеният интеграл по целия сегмент е равен на сумата от определените интеграли по неговите части, т.е. ако Теорема 6.При пренареждане на границите на интегриране абсолютната стойност на определения интеграл не се променя, а се променя само неговият знак, т.е. Теорема 7(теорема за средната стойност). Определеният интеграл е равен на произведението от дължината на отсечката за интегриране и стойността на интегралната функция в някаква точка вътре в него, т.е. Теорема 8.Ако горната граница на интегриране е по-голяма от долната и интегралната функция е неотрицателна (положителна), то определеният интеграл също е неотрицателен (положителен), т.е. ако Теорема 9.Ако горната граница на интегриране е по-голяма от долната граница и функциите и са непрекъснати, тогава неравенството може да се интегрира термин по термин, т.е. Свойствата на определения интеграл ни позволяват да опростим директното изчисляване на интеграли. Пример 5Изчислете определен интеграл Използвайки теореми 4 и 3, и при намиране на антипроизводни - таблични интеграли (7) и (6), получаваме Позволявам е(х) е непрекъснат на интервала [ а, б] функция и Ф(х) е негов прототип. Помислете за определения интеграл и през тпроменливата за интегриране се обозначава, за да не се бърка с горната граница. Когато се промени хопределеният интеграл (47) също се променя, т.е. тя е функция на горната граница на интегриране х, което означаваме с Ф(х), т.е. Нека докажем, че функцията Ф(х) е антипроизводно за е(х) = е(т). Наистина, диференциране Ф(х), получаваме защото Ф(х) е антипроизводно за е(х), а Ф(а) е постоянна стойност. Функция Ф(х) е един от безкрайния набор от антипроизводни за е(х), а именно този, който х = аотива на нула. Това твърдение се получава, ако в равенство (48) поставим х = аи използвайте теорема 1 от предишния раздел. където, по дефиниция, Ф(х) е антипроизводно за е(х). Ако в интегралната функция направим промяната на променливата тогава, в съответствие с формула (16), можем да запишем В този израз антипроизводна функция за Наистина, неговата производна, според правилото за диференциране на сложна функция, е равно на Нека α и β са стойностите на променливата т, за което функцията приема съответно стойностите аи б, т.е. Но, според формулата на Нютон-Лайбниц, разликата Ф(б) – Ф(а) има Калкулаторът решава интеграли с описание на действията ПОДРОБНО на руски и безплатно! Това е онлайн услуга една стъпка: Това е онлайн услуга една стъпка: Тази услуга ви позволява да проверите вашите изчисленияза коректност Интегрално смятане. примитивна функция. определение:
Извиква се функцията F(x). антидеривна функцияфункции f(x) на сегмента, ако в която и да е точка от този сегмент равенството е вярно: Трябва да се отбележи, че може да има безкрайно много антипроизводни за една и съща функция. Те ще се различават един от друг с някакво постоянно число. F 1 (x) = F 2 (x) + C. Неопределен интеграл. определение:
Неопределен интегралфункции f(x) е набор от антипроизводни функции, които се дефинират от отношението: Записвам: Условието за съществуване на неопределен интеграл на определен отсечка е непрекъснатостта на функцията на този отсечка. Имоти:
1.
2.
3.
4.
пример:
Намирането на стойността на неопределения интеграл е свързано основно с намирането на антипроизводната функция. За някои функции това е доста трудна задача. По-долу ще разгледаме методи за намиране на неопределени интеграли за основните класове функции – рационални, ирационални, тригонометрични, експоненциални и др. За удобство стойностите на неопределените интеграли на повечето елементарни функции се събират в специални таблици на интеграли, които понякога са много обемни. Те включват различни най-често срещани комбинации от функции. Но повечето от формулите, представени в тези таблици, са следствия една от друга, така че по-долу е дадена таблица с основни интеграли, с които можете да получите стойностите на неопределените интеграли от различни функции. Интегрална смисъл Интегрална смисъл lnsinx+ C вътрешен Интеграционни методи. Нека разгледаме три основни метода на интеграция. Директна интеграция. Методът на директно интегриране се основава на допускането за възможната стойност на антипроизводната функция с по-нататъшна проверка на тази стойност чрез диференциране. Като цяло отбелязваме, че диференцирането е мощен инструмент за проверка на резултатите от интеграцията. Помислете за прилагането на този метод на пример: Необходимо е да се намери стойността на интеграла Имайте предвид, че за разлика от диференцирането, където са използвани ясни техники и методи за намиране на производната, правилата за намиране на производната и накрая дефиницията на производната, такива методи не са достъпни за интегриране. Ако при намирането на производната използвахме, така да се каже, конструктивни методи, които въз основа на определени правила доведоха до резултат, то при намирането на антипроизводната трябва да разчитаме основно на познаването на таблиците на производните и антипроизводните. Що се отнася до метода на директно интегриране, той е приложим само за някои много ограничени класове функции. Има много малко функции, за които можете веднага да намерите анти-производната. Поради това в повечето случаи се използват методите, описани по-долу. Метод на заместване (замяна на променливи). теорема:
Ако искате да намерите интеграла Доказателство
:
Нека разграничим предложеното равенство: Съгласно горното свойство № 2 на неопределения интеграл: е(х)
dx
=
е[
(т)]
(т)
dt което, като се вземе предвид въведеното обозначение, е първоначалното предположение. Теоремата е доказана. Пример.Намерете неопределения интеграл Нека направим замяна т
=
sinx,
dt
=
cosxdt. Пример.
Замяна По-долу ще разгледаме други примери за използване на метода на заместване за различни видове функции. Интегриране по части. Методът се основава на добре познатата формула за производното на продукт: (uv) = uv + vu където u и v са някои функции на x. В диференциална форма: d(uv) = udv + vdu След интегриране получаваме: Получихме формула за интегриране по части, която ни позволява да намерим интегралите на много елементарни функции. Пример.
Както можете да видите, последователното прилагане на формулата за интегриране по части ви позволява постепенно да опростите функцията и да доведете интеграла до табличен. Пример.
Вижда се, че в резултат на многократното прилагане на интегриране по части, функцията не може да бъде опростена до табличен вид. Последният получен интеграл обаче не се различава от оригиналния. Следователно, ние го прехвърляме в лявата част на равенството. По този начин интегралът беше намерен без изобщо да се използват таблици с интеграли. Преди да разгледаме подробно методите за интегриране на различни класове функции, даваме още няколко примера за намиране на неопределени интеграли чрез свеждането им до таблични. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Интегриране на елементарни дроби. определение:
Елементарнодроби от следните четири вида се наричат: аз II. m, n са естествени числа (m 2, n 2) и b 2 - 4ac<0. Първите два вида интеграли от елементарни дроби се свеждат съвсем просто до таблични замествания t = ax + b. Помислете за метод за интегриране на елементарни дроби от формата III. Интегралът от дроб от тип III може да бъде представен като: Тук в общи линии е показано редуцирането на интеграла от част от вид III до два таблични интеграла. Помислете за приложението на горната формула с примери. Пример. Най-общо казано, ако тричленът ax 2 + bx + c има израза b 2 - 4ac > 0, тогава дробът по дефиниция не е елементарен, но въпреки това може да се интегрира по горния начин. Пример.
Пример. Нека сега разгледаме методи за интегриране на най-простите дроби от тип IV. Първо, разгледайте специален случай за M = 0, N = 1. Тогава интегралът на формата Вторият интеграл, включен в това равенство, ще бъде взет по части. Означете: За оригиналния интеграл получаваме: Получената формула се нарича повтарящи се.Ако го приложите n-1 пъти, ще получите интеграл от таблицата Нека сега се върнем към интеграла от елементарна дроб от формата IV в общия случай. В полученото равенство, първият интеграл с помощта на заместването т
=
u 2
+
ссе свежда до табличен Въпреки очевидната сложност на интегрирането на елементарна фракция от тип IV, на практика е доста лесно да се приложи за фракции с малка степен н, а универсалността и обобщеността на подхода прави възможно прилагането на този метод много просто на компютър. Пример:
Интегриране на рационални функции. Интегриране на рационални дроби. За да се интегрира рационална дроб, е необходимо тя да се разложи на елементарни дроби. теорема:
Ако където A i , B i , M i , N i , R i , S i са някои постоянни стойности. При интегриране на рационални дроби се прибягва до разлагане на първоначалната дроб на елементарни. За намиране на стойностите A i , B i , M i , N i , R i , S i използвайте т.нар. метод на неопределените коефициенти, чиято същност е, че за да бъдат два полинома идентично равни, е необходимо и достатъчно коефициентите при едни и същи степени на x да са равни. Ще разгледаме приложението на този метод на конкретен пример. Пример. Свеждайки до общ знаменател и приравнявайки съответните числители, получаваме: Пример. Защото Ако дробът не е правилен, първо трябва да изберете цялата част от нея: 6 6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3 9x3 + 8x2 - 76x - 7 9x 3 - 12x 2 - 51x +18 20x2-25x-25 Разлагаме знаменателя на получената дроб на фактори. Вижда се, че при x = 3 знаменателят на дробта става нула. Тогава: 3x 3 – 9x 2 3x 2 + 5x - 2 Така че 3x 3 - 4x 2 - 17x + 6 = (x - 3)(3x 2 + 5x - 2) = (x - 3)(x + 2)(3x - 1). Тогава: За да се избегне при намиране на несигурни коефициенти на отваряне на скоби, групиране и решаване на система от уравнения (която в някои случаи може да се окаже доста голяма), т.нар. метод на произволна стойност. Същността на метода е, че няколко (според броя на несигурните коефициенти) произволни стойности на x се заменят в израза, получен по-горе. За да се опростят изчисленията, е обичайно да се вземат като произволни стойности точките, в които знаменателят на дроба е равен на нула, т.е. в нашия случай - 3, -2, 1/3. Получаваме: Накрая получаваме: Пример. Нека намерим неопределени коефициенти: Тогава стойността на дадения интеграл: Интегриране на някои тригонометрични функции. Може да има безкрайно много интеграли от тригонометрични функции. Повечето от тези интеграли изобщо не могат да бъдат изчислени аналитично, така че нека разгледаме някои от основните типове функции, които винаги могат да бъдат интегрирани. Интеграл на формата Тук R е обозначението на някаква рационална функция на променливите sinx и cosx. Интегралите от този тип се изчисляват с помощта на заместването Тогава По този начин: Описаната по-горе трансформация се нарича универсално тригонометрично заместване. Пример. Несъмненото предимство на това заместване е, че с негова помощ винаги е възможно да се трансформира тригонометрична функция в рационална и да се изчисли съответният интеграл. Недостатъците включват факта, че трансформацията може да доведе до доста сложна рационална функция, чието интегриране ще отнеме много време и усилия. Ако обаче е невъзможно да се приложи по-рационална промяна на променливата, този метод е единственият ефективен. Пример. Интеграл на формата функцияРcosx.
Въпреки възможността за изчисляване на такъв интеграл с помощта на универсалното тригонометрично заместване, по-рационално е да се приложи заместването т
=
sinx. Функция Пример. Най-общо казано, за прилагане на този метод е необходима само нечетността на функцията по отношение на косинуса, а степента на синуса, включена във функцията, може да бъде всяка, както цяло число, така и дробно. Интеграл на формата функцияРе странно по отношение наsinx.
По аналогия с разглеждания по-горе случай, заместването т =
cosx.
Пример. Интеграл на формата функцияРдори относителноsinxиcosx.
За трансформиране на функцията R в рационална се използва заместването t = tgx. Пример. Интеграл от произведението на синусите и косинусите различни аргументи. В зависимост от вида на работата ще се приложи една от трите формули: Пример. Пример. Пример. Пример. Понякога се използват някои нестандартни трикове. Пример. Интегриране на някои ирационални функции. Не всяка ирационална функция може да има интеграл, изразен чрез елементарни функции. За да се намери интеграл на ирационална функция, трябва да се приложи заместване, което ще позволи да се трансформира функцията в рационална, чийто интеграл винаги може да бъде намерен, както е известно. Помислете за някои техники за интегриране на различни видове ирационални функции. Интеграл на формата С помощта на заместване Пример. Ако ирационалната функция включва корени от различни степени, тогава е рационално да вземем корена на степента, равен на най-малкото общо кратно на степените на корените, включени в израза като нова променлива. Нека илюстрираме това с пример. Пример. Интегриране на биномни диференциали.
Диференциал на определен интеграл


Фундаментална връзка на интегралното смятане

Основно правило за интеграция



Таблици на интегралите


Как да изчислим определен интеграл




Върху неправилните интеграли

![]() (38)
(38)![]() (39)
(39)
![]()
![]()
![]()
Свойства на определения интеграл
![]() (40)
(40)![]()
![]() (41)
(41)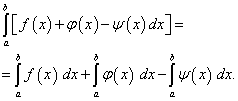 (42)
(42)![]() (43)
(43)![]() (44)
(44)![]() (45)
(45)
![]() (46)
(46)![]()

Определен интеграл с променлива горна граница
![]() (47)
(47)![]() (48)
(48)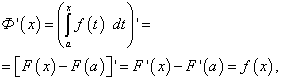
Изчисляване на определени интеграли чрез метода на интегриране по части и метода на промяна на променливата
![]()


Решаване на неопределени интеграли
Решение на определени интеграли
Решаване на двойни интеграли
Решаване на неправилни интеграли
Решение на тройни интеграли
Възможности





























 . Въз основа на добре познатата формула за диференциация
. Въз основа на добре познатата формула за диференциация  можем да заключим, че желаният интеграл е равен на
можем да заключим, че желаният интеграл е равен на  , където C е някакво постоянно число. От друга страна обаче
, където C е някакво постоянно число. От друга страна обаче  . Така накрая можем да заключим:
. Така накрая можем да заключим:
 , но е трудно да се намери антипроизводната, тогава като заменим x = (t) и dx = (t)dt, получаваме:
, но е трудно да се намери антипроизводната, тогава като заменим x = (t) и dx = (t)dt, получаваме: .
.
 Получаваме:
Получаваме: , и в съответствие с горните свойства на неопределения интеграл:
, и в съответствие с горните свойства на неопределения интеграл: или
или  ;
;





 III.
III. 
 IV.
IV. 


 може да бъде представено чрез маркиране на пълния квадрат в знаменателя като
може да бъде представено чрез маркиране на пълния квадрат в знаменателя като  . Нека направим следната трансформация:
. Нека направим следната трансформация:
 .
.
 , а разглежданата по-горе рекурентна формула се прилага към втория интеграл.
, а разглежданата по-горе рекурентна формула се прилага към втория интеграл.
 е правилна рационална дроб, чийто знаменател P(x) е представен като продукт на линейни и квадратни фактори (обърнете внимание, че всеки полином с реални коефициенти може да бъде представен по следния начин: П(х)
= (х -
а)
…(х
-
б)
(х 2
+
px +
q)
…(х 2
+
rx +
с)
), тогава тази фракция може да бъде разложена на елементарни по следната схема:
е правилна рационална дроб, чийто знаменател P(x) е представен като продукт на линейни и квадратни фактори (обърнете внимание, че всеки полином с реални коефициенти може да бъде представен по следния начин: П(х)
= (х -
а)
…(х
-
б)
(х 2
+
px +
q)
…(х 2
+
rx +
с)
), тогава тази фракция може да бъде разложена на елементарни по следната схема:








 x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6
x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6 3x 3 – 4x 2 – 17x + 6x - 3
3x 3 – 4x 2 – 17x + 6x - 3

 =
=





 .
.
 . Това заместване ви позволява да преобразувате тригонометрична функция в рационална.
. Това заместване ви позволява да преобразувате тригонометрична функция в рационална. ,
,




 ако
ако може да съдържа cosx само в четни степени и следователно може да се преобразува в рационална функция по отношение на sinx.
може да съдържа cosx само в четни степени и следователно може да се преобразува в рационална функция по отношение на sinx.
 ако
ако


 Понякога, когато се интегрират тригонометрични функции, е удобно да се използват добре познати тригонометрични формули за намаляване на реда на функциите.
Понякога, когато се интегрират тригонометрични функции, е удобно да се използват добре познати тригонометрични формули за намаляване на реда на функциите.


 къдетон- естествено число.
къдетон- естествено число. функцията е рационализирана.
функцията е рационализирана.


