Mathematical expectation of a continuous random variable. Mathematical expectation is the probability distribution of a random variable Days mathematical expectation week
As already known, the distribution law completely characterizes a random variable. However, the distribution law is often unknown and one has to limit oneself to lesser information. Sometimes it is even more profitable to use numbers that describe a random variable in total; such numbers are called numerical characteristics of a random variable.
Mathematical expectation is one of the important numerical characteristics.
The mathematical expectation is approximately equal to the average value of a random variable.
Mathematical expectation of a discrete random variable is the sum of the products of all its possible values and their probabilities.
If a random variable is characterized by a finite distribution series:
| X | x 1 | x 2 | x 3 | … | x n |
| R | p 1 | p 2 | p 3 | … | r p |
then the mathematical expectation M(X) is determined by the formula:
The mathematical expectation of a continuous random variable is determined by the equality:
where is the probability density of the random variable X.
Example 4.7. Find the mathematical expectation of the number of points that fall out when a dice is thrown.
Solution:
Random value X takes the values 1, 2, 3, 4, 5, 6. Let's make the law of its distribution:
| X | ||||||
| R |
Then the mathematical expectation is:
Properties of mathematical expectation:
1. The mathematical expectation of a constant value is equal to the constant itself:
M(S)=S.
2. The constant factor can be taken out of the expectation sign:
M(CX) = CM(X).
3. The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations:
M(XY) = M(X)M(Y).
Example 4.8. Independent random variables X And Y are given by the following distribution laws:
| X | Y | ||||||
| R | 0,6 | 0,1 | 0,3 | R | 0,8 | 0,2 |
Find the mathematical expectation of a random variable XY.
Solution.
Let's find the mathematical expectations of each of these quantities:
random variables X And Y independent, so the desired mathematical expectation:
M(XY) = M(X)M(Y)=
Consequence. The mathematical expectation of the product of several mutually independent random variables is equal to the product of their mathematical expectations.
4. The mathematical expectation of the sum of two random variables is equal to the sum of the mathematical expectations of the terms:
M(X + Y) = M(X) + M(Y).
Consequence. The mathematical expectation of the sum of several random variables is equal to the sum of the mathematical expectations of the terms.
Example 4.9. 3 shots are fired with probabilities of hitting the target equal to p 1 = 0,4; p2= 0.3 and p 3= 0.6. Find the mathematical expectation of the total number of hits.
Solution.
The number of hits on the first shot is a random variable X 1, which can take only two values: 1 (hit) with probability p 1= 0.4 and 0 (miss) with probability q 1 = 1 – 0,4 = 0,6.
The mathematical expectation of the number of hits in the first shot is equal to the probability of hitting:
Similarly, we find the mathematical expectations of the number of hits in the second and third shots:
M(X 2)= 0.3 and M (X 3) \u003d 0,6.
The total number of hits is also a random variable consisting of the sum of hits in each of the three shots:
X \u003d X 1 + X 2 + X 3.
The desired mathematical expectation X we find by the theorem of mathematical, the expectation of the sum.
Random variables, in addition to distribution laws, can also be described numerical characteristics .
mathematical expectation M (x) of a random variable is called its average value.
The mathematical expectation of a discrete random variable is calculated by the formula
Where – values of a random variable, p i- their probabilities.
Consider the properties of mathematical expectation:
1. The mathematical expectation of a constant is equal to the constant itself
2. If a random variable is multiplied by a certain number k, then the mathematical expectation will be multiplied by the same number
M (kx) = kM (x)
3. The mathematical expectation of the sum of random variables is equal to the sum of their mathematical expectations
M (x 1 + x 2 + ... + x n) \u003d M (x 1) + M (x 2) + ... + M (x n)
4. M (x 1 - x 2) \u003d M (x 1) - M (x 2)
5. For independent random variables x 1 , x 2 , … x n the mathematical expectation of the product is equal to the product of their mathematical expectations
M (x 1, x 2, ... x n) \u003d M (x 1) M (x 2) ... M (x n)
6. M (x - M (x)) \u003d M (x) - M (M (x)) \u003d M (x) - M (x) \u003d 0
Let's calculate the mathematical expectation for the random variable from Example 11.
M(x) == ![]() .
.
Example 12. Let the random variables x 1 , x 2 be given by the distribution laws, respectively:
x 1 Table 2
x 2 Table 3
Calculate M (x 1) and M (x 2)
M (x 1) \u003d (- 0.1) 0.1 + (- 0.01) 0.2 + 0 0.4 + 0.01 0.2 + 0.1 0.1 \u003d 0
M (x 2) \u003d (- 20) 0.3 + (- 10) 0.1 + 0 0.2 + 10 0.1 + 20 0.3 \u003d 0
The mathematical expectations of both random variables are the same - they are equal to zero. However, their distribution is different. If the values of x 1 differ little from their mathematical expectation, then the values of x 2 differ to a large extent from their mathematical expectation, and the probabilities of such deviations are not small. These examples show that it is impossible to determine from the average value what deviations from it take place both up and down. Thus, with the same average annual precipitation in two localities, it cannot be said that these localities are equally favorable for agricultural work. Similarly, by the indicator of average wages, it is not possible to judge the proportion of high- and low-paid workers. Therefore, a numerical characteristic is introduced - dispersion D(x) , which characterizes the degree of deviation of a random variable from its mean value:
D (x) = M (x - M (x)) 2 . (2)
Dispersion is the mathematical expectation of the squared deviation of a random variable from the mathematical expectation. For a discrete random variable, the variance is calculated by the formula:
D(x)= ![]() =
= ![]() (3)
(3)
It follows from the definition of variance that D (x) 0.
Dispersion properties:
1. Dispersion of the constant is zero
2. If a random variable is multiplied by some number k, then the variance is multiplied by the square of this number
D (kx) = k 2 D (x)
3. D (x) \u003d M (x 2) - M 2 (x)
4. For pairwise independent random variables x 1 , x 2 , … x n the variance of the sum is equal to the sum of the variances.
D (x 1 + x 2 + ... + x n) = D (x 1) + D (x 2) + ... + D (x n)
Let's calculate the variance for the random variable from Example 11.
Mathematical expectation M (x) = 1. Therefore, according to the formula (3) we have:
D (x) \u003d (0 - 1) 2 1/4 + (1 - 1) 2 1/2 + (2 - 1) 2 1/4 \u003d 1 1/4 + 1 1/4 \u003d 1/2
Note that it is easier to calculate the variance if we use property 3:
D (x) \u003d M (x 2) - M 2 (x).
Let's calculate the variances for random variables x 1 , x 2 from Example 12 using this formula. The mathematical expectations of both random variables are equal to zero.
D (x 1) \u003d 0.01 0.1 + 0.0001 0.2 + 0.0001 0.2 + 0.01 0.1 \u003d 0.001 + 0.00002 + 0.00002 + 0.001 \u003d 0.00204
D (x 2) \u003d (-20) 2 0.3 + (-10) 2 0.1 + 10 2 0.1 + 20 2 0.3 \u003d 240 +20 \u003d 260
The closer the dispersion value is to zero, the smaller the spread of the random variable relative to the mean value.
The value is called standard deviation. Random fashion x discrete type Md is the value of the random variable, which corresponds to the highest probability.
Random fashion x continuous type Md, is a real number defined as the maximum point of the probability distribution density f(x).
Median of a random variable x continuous type Mn is a real number that satisfies the equation
In the theory of probability and in many of its applications, various numerical characteristics of random variables are of great importance. The main ones are the mathematical expectation and variance.
1. Mathematical expectation of a random variable and its properties.
Consider first the following example. Let the factory receive a batch consisting of N bearings. Wherein:
m 1 x 1,
m2- number of bearings with outer diameter x 2,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
m n- number of bearings with outer diameter x n,
Here m 1 +m 2 +...+m n =N. Find the arithmetic mean x cf outside diameter of the bearing. Obviously,
The outer diameter of a bearing taken out at random can be considered as a random variable taking the values x 1, x 2, ..., x n, with corresponding probabilities p 1 \u003d m 1 / N, p 2 \u003d m 2 /N, ..., p n =m n /N, because the probability pi the appearance of a bearing with an outer diameter x i is equal to m i /N. Thus, the arithmetic mean x cf the outside diameter of a bearing can be determined using the relationship 
Let be a discrete random variable with a given probability distribution law
Values
x 1
x 2
. . .
x n
Probabilities
p1
p2
. . .
p n
mathematical expectation discrete random variable the sum of pairwise products of all possible values of a random variable and their corresponding probabilities is called, i.e. *
It is assumed that the improper integral on the right side of equality (40) exists.
Consider the properties of mathematical expectation. In doing so, we confine ourselves to proving only the first two properties, which we will carry out for discrete random variables.
1°. The mathematical expectation of the constant C is equal to this constant.
Proof. permanent C can be thought of as a random variable that can only take on one value C with probability equal to one. That's why ![]()
2°. The constant factor can be taken out of the expectation sign, i.e. ![]()
Proof. Using relation (39), we have 
3°. The mathematical expectation of the sum of several random variables is equal to the sum of the mathematical expectations of these variables:
There will also be tasks for an independent solution, to which you can see the answers.
Mathematical expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of dispersion. The mathematical expectation is often referred to simply as the mean. random variable. Dispersion of a random variable - a characteristic of dispersion, dispersion of a random variable around its mathematical expectation.
In many problems of practice, a complete, exhaustive description of a random variable - the law of distribution - either cannot be obtained, or is not needed at all. In these cases, they are limited to an approximate description of a random variable using numerical characteristics.
Mathematical expectation of a discrete random variable
Let's come to the concept of mathematical expectation. Let the mass of some substance be distributed between the points of the x-axis x1 , x 2 , ..., x n. Moreover, each material point has a mass corresponding to it with a probability of p1 , p 2 , ..., p n. It is required to choose one point on the x-axis, which characterizes the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, in which the abscissa of each point xi enters with a "weight" equal to the corresponding probability. The mean value of the random variable thus obtained X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:
Example 1 A win-win lottery was organized. There are 1000 winnings, 400 of which are 10 rubles each. 300 - 20 rubles each 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for a person who buys one ticket?
Solution. We will find the average win if the total amount of winnings, which is equal to 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, is divided by 1000 (the total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average gain can also be represented in the following form:
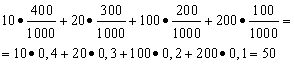
On the other hand, under these conditions, the amount of winnings is a random variable that can take on the values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average payoff is equal to the sum of the products of the size of the payoffs and the probability of receiving them.
Example 2 The publisher decided to publish a new book. He is going to sell the book for 280 rubles, of which 200 will be given to him, 50 to the bookstore, and 30 to the author. The table gives information about the cost of publishing a book and the likelihood of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable "profit" is equal to the difference between the income from the sale and the cost of the costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publishing is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher's profit:
![]() .
.
Example 3 Chance to hit with one shot p= 0.2. Determine the consumption of shells that provide the mathematical expectation of the number of hits equal to 5.
Solution. From the same expectation formula that we have used so far, we express x- consumption of shells:
![]() .
.
Example 4 Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of hitting with each shot p = 0,4 .
Hint: find the probability of the values of a random variable by Bernoulli formula .
Expectation Properties
Consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of the product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of the random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can not be limited only to mathematical expectation
In most cases, only the mathematical expectation cannot adequately characterize a random variable.
Let random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:

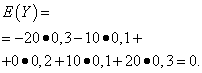
However, their distribution is different. Random value X can only take values that are little different from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average wage does not make it possible to judge the proportion of high- and low-paid workers. In other words, by mathematical expectation one cannot judge what deviations from it, at least on average, are possible. To do this, you need to find the variance of a random variable.
Dispersion of a discrete random variable
dispersion discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:

The standard deviation of a random variable X is the arithmetic value of the square root of its variance:
![]() .
.
Example 5 Calculate variances and standard deviations of random variables X And Y, whose distribution laws are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula for E(X)=E(y)=0 we get:

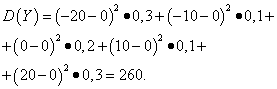
Then the standard deviations of random variables X And Y constitute
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small and random Y- significant. This is a consequence of the difference in their distribution.
Example 6 The investor has 4 alternative investment projects. The table summarizes the data on the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find for each alternative the mathematical expectation, variance and standard deviation.
Solution. Let us show how these quantities are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectation. This means that in the long run everyone has the same income. The standard deviation can be interpreted as a measure of risk - the larger it is, the greater the risk of the investment. An investor who doesn't want much risk will choose project 1 because it has the smallest standard deviation (0). If the investor prefers risk and high returns in a short period, then he will choose the project with the largest standard deviation - project 4.
Dispersion Properties
Let us present the properties of the dispersion.
Property 1. The dispersion of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7 It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Denote by p the probability with which a random variable takes on a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let's derive the equation for mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
The law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of the variance:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then see the solution
Example 8 Discrete random variable X takes only two values. It takes the larger value of 3 with a probability of 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9 An urn contains 6 white and 4 black balls. 3 balls are taken from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random value X can take the values 0, 1, 2, 3. The corresponding probabilities can be calculated from rule of multiplication of probabilities. The law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Mathematical expectation and dispersion of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). In contrast to a discrete random variable, for which the function argument xi changes abruptly, for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its mean value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If a density function of a continuous random variable is given, then it enters directly into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
The arithmetic average of all possible values of a continuous random variable is called its mathematical expectation, denoted by or .
Characteristics of DSW and their properties. Mathematical expectation, variance, standard deviation
The distribution law fully characterizes the random variable. However, when it is impossible to find the distribution law, or this is not required, one can limit oneself to finding values, called numerical characteristics of a random variable. These quantities determine some average value around which the values of a random variable are grouped, and the degree of their dispersion around this average value.
mathematical expectation A discrete random variable is the sum of the products of all possible values of a random variable and their probabilities.
The mathematical expectation exists if the series on the right side of the equality converges absolutely.
From the point of view of probability, we can say that the mathematical expectation is approximately equal to the arithmetic mean of the observed values of the random variable.
Example. The law of distribution of a discrete random variable is known. Find the mathematical expectation.
| X | ||||
| p | 0.2 | 0.3 | 0.1 | 0.4 |
Solution:
9.2 Expectation Properties
1. The mathematical expectation of a constant value is equal to the constant itself.
2. A constant factor can be taken out of the expectation sign. ![]()
3. The mathematical expectation of the product of two independent random variables is equal to the product of their mathematical expectations.
This property is valid for an arbitrary number of random variables.
4. The mathematical expectation of the sum of two random variables is equal to the sum of the mathematical expectations of the terms.
This property is also true for an arbitrary number of random variables.
Let n independent trials be performed, the probability of occurrence of event A in which is equal to p.
Theorem. The mathematical expectation M(X) of the number of occurrences of event A in n independent trials is equal to the product of the number of trials and the probability of occurrence of the event in each trial.
Example. Find the mathematical expectation of a random variable Z if the mathematical expectations of X and Y are known: M(X)=3, M(Y)=2, Z=2X+3Y.
Solution:
9.3 Dispersion of a discrete random variable
However, the mathematical expectation cannot fully characterize a random process. In addition to the mathematical expectation, it is necessary to introduce a value that characterizes the deviation of the values of the random variable from the mathematical expectation.
This deviation is equal to the difference between the random variable and its mathematical expectation. In this case, the mathematical expectation of the deviation is zero. This is explained by the fact that some possible deviations are positive, others are negative, and as a result of their mutual cancellation, zero is obtained.
Dispersion (scattering) Discrete random variable is called the mathematical expectation of the squared deviation of the random variable from its mathematical expectation.
In practice, this method of calculating the variance is inconvenient, because leads to cumbersome calculations for a large number of values of a random variable.
Therefore, another method is used.
Theorem. The variance is equal to the difference between the mathematical expectation of the square of the random variable X and the square of its mathematical expectation.
Proof. Taking into account the fact that the mathematical expectation M (X) and the square of the mathematical expectation M 2 (X) are constant values, we can write:
Example. Find the variance of a discrete random variable given by the distribution law.
| X | ||||
| X 2 | ||||
| R | 0.2 | 0.3 | 0.1 | 0.4 |
Solution: .
9.4 Dispersion properties
1. The dispersion of a constant value is zero. .
2. A constant factor can be taken out of the dispersion sign by squaring it. ![]() .
.
3. The variance of the sum of two independent random variables is equal to the sum of the variances of these variables. .
4. The variance of the difference of two independent random variables is equal to the sum of the variances of these variables. .
Theorem. The variance of the number of occurrences of event A in n independent trials, in each of which the probability p of the occurrence of the event is constant, is equal to the product of the number of trials and the probability of occurrence and non-occurrence of the event in each trial.
9.5 Standard deviation of a discrete random variable
Standard deviation random variable X is called the square root of the variance.
![]()
Theorem. The standard deviation of the sum of a finite number of mutually independent random variables is equal to the square root of the sum of the squared standard deviations of these variables.


