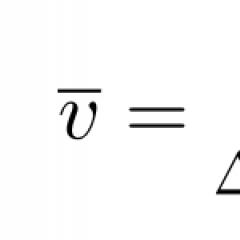Graph of s versus t. Uniformly accelerated motion: formulas, examples

Figure 1. Graphs of uniform motion. Author24 - online exchange of student work

The simplest type of motion is uniform motion. It can be fixed when the acceleration of the body at any moment of time is equal to zero. In other words, uniform motion is represented in the form of a certain ideal position of the body, when its speed will be the same at any given time. When a body passes equal distances in equal periods of time, the movement acquires the characteristics of uniform rectilinear movement. In real life, such characteristics practically never occur.

Definition 1

Path is the length of the trajectory along which a specific body moved over a certain period of time.

Definition 2

Displacement is the distance between the starting and ending points of a body’s trajectory.

Path and displacement are different concepts, since path is a scalar quantity, and displacement is a vector quantity. In this case, the magnitude of the displacement vector is equal to the segment connecting the starting and ending points of the trajectory of the body.

Uniform speed

Definition 3

The speed of uniform motion is called the vector modulus, which is calculated using a certain formula. It states that the vector will be equal to the ratio of the path traveled by the body to the time spent on its passage.

With uniform motion, the direction of the velocity vector coincides with the direction of movement. This rule must be taken into account when constructing a graph of uniform motion. Displacement and path for such a movement will have the same values.

Uniform motion also includes a state of rest. In this case, the body travels equal distances in equal time intervals. At rest, all values will be zero. With uniform movement, the distance traveled consists of the following composite indicators:

initial coordinate;
product of the speed of the body and the time of movement.

Uniform motion graphs

When constructing a graph of uniform motion with a change in speed over time, you will get a straight line that will run parallel to the x-axis line. The area of the resulting rectangle is equal to the length of the path traveled by the body in a specific time. That is, the area of the rectangle will be equal to the product of all its sides.

After plotting the dependence of the distance traveled on time, the speed at which the body moved is calculated. In this case, the graph has a straight line drawn from the origin. The required value of the velocity vector modulus will be the tangent of the angle of inclination of the straight line relative to the abscissa axis. When graphing uniform motion, the x-axis is the time axis. A strong slope of the graph indicates that the body's speed is high.

In physics, the following notations for uniform motion are used:

It shows the invariance of speed, which is expressed as a constant.

Uniform movement passes along:

curvilinear trajectory;
rectilinear trajectory.

Uniform motion is described by the formula:

In this formula, $s$ is the path that the body has traveled from the initial reference point, $t$ is the time the body travels, and $s_0$ is the value of the path at the initial time.

Straight-line movement

Note 1

Movement is called rectilinear if it occurs in a straight line.

The trajectory of rectilinear movement is a straight line. With the speed of uniform motion there is no dependence on time, since at any point of the trajectory it is directed similarly to the movement of the body. In other words, the displacement vector coincides in direction with the velocity vector. The average speed in any period of time is equal to the instantaneous speed.

The speed of uniform rectilinear motion shows the value of the movement of a material point per unit time.

With such movement, the total acceleration is expressed by the formula:

In the international system of measurements, the unit of acceleration is the acceleration at which the speed of a body changes by 1 meter every second.

Equally alternating motion

A special case of uneven motion of a body is uniform rectilinear motion.

Uniformly variable motion is a motion when the speed of a material point changes equally over any equal intervals of time. The acceleration of a body during uniformly alternating motion remains at a constant level in direction and magnitude.

There are two types of uniformly alternating motion: uniformly accelerated and uniformly decelerated.

The motion of a body or material point with positive acceleration is considered uniformly accelerated. With this method of movement, it can accelerate with acceleration at a constant level.

The motion of a body with negative acceleration is called uniformly slow. With this type of movement, the body slows down at a uniform level.

The average speed of alternating motion can be determined by dividing the movement of the body by the time during which this movement occurred. The unit of average speed is m/s.

Instantaneous speed and acceleration

The speed of a body or a material point is called instantaneous if it exists at a specific moment in time or at a given point in the trajectory of motion. This value is called the limit value, since the average speed of a body tends to it as the time period decreases infinitely. It is denoted by $Δt$.

Instantaneous speed is expressed using the following formula:

The quantity that determines changes in the speed of a body is called acceleration. These are the limiting values of the quantity and the change in speed tends to it with an infinite decrease in the time interval $Δt$.

Displacement during uniform linear motion is calculated by the formula:

The value $υx$ is the projection of the velocity onto the X axis.

It follows that the law of uniform rectilinear motion has the following form:

At the initial moment of time $xo = 0$, so the remaining values take the form.

3. Consider Figure 4.6.
a) At what points on the graph is the angle of inclination of the tangent the greatest?

Instant and average speed

least?

2. Average speed

vav = l/t. (1)

5. Find:

c) Sasha’s average speed.

6. Find:

b) Sasha’s average speed.

Analysis of the training test for the 2008/2009 Internet Olympiad in Physics

Grade 11. Kinematics

Question No. 1

Using the graph presented in the figure, determine the speed of the cyclist three seconds after the start of the movement.

Solution.

The figure shows a graph of the path versus time. The graph is a straight line, which means the cyclist moved uniformly. Let us determine from the graph the distance covered by the cyclist in a fixed period of time. For example, in 3 s a cyclist covered 9 m. The cyclist’s speed is V = L / t = 9/3 = 3 m/s.

Question No. 2

The pedestrian and the cyclist began moving towards each other at the same time. Their speeds are equal to V1 = and V2 = , respectively. Determine the time of movement until the meeting if the initial distance between them is L = .

Solution.

Let us determine the speed of the cyclist in the pedestrian reference frame V12 = V1 + V2 = 6 + 30 = 36 km/h = 10 m/s. So, a pedestrian and a cyclist approach each other at a speed of 10 m/s, then their travel time until they meet is t = L / V12 = 700/10 = 70 s.

Question No. 3

The car was moving at a speed of 15 m/s for 5 s. How far did he travel during this time?

Solution.

The car moved uniformly, so the distance traveled is L = Vt = 155 = 75 m.

Question No. 4

A ball thrown vertically upward returns to its original position. The figure shows a graph of its speed versus time. At what point in time did the ball reach its maximum height?

Solution.

At the moment when the ball reaches its maximum height, its speed is zero. According to the graph presented in the figure, we determine that the speed of the ball is zero at time t = 2 s.

Question No. 5

Which of the above quantities are vector quantities?

(Tick all vector quantities)

Solution.

Of these quantities, velocity, acceleration and displacement are vector quantities. Path is a scalar quantity.

Question No. 6

The athlete ran a distance of 400 m along the stadium track and returned to the starting point. Determine the path L traveled by the athlete and the module of his movement S.

Solution.

The distance traveled by the athlete is L = 400 m. The displacement module is S = 0, since the athlete returned to the point from which he started moving.

Question No. 7

The speed of a body moving rectilinearly and uniformly accelerated changed when moving from point 1 to point 2 as shown in the figure. What direction does the acceleration vector have on this section of the path?

Solution.

It can be seen from the figure that the modulus of the body’s velocity decreases as it moves, which means that the acceleration vector is directed towards the movement, that is, to the left.

Question No. 8

Using the graph of the velocity modulus versus time, determine the acceleration of a rectilinearly moving body at the time t = 2 s.

Solution.

Using the graph, we determine the change in the speed of a body at a fixed point in time. For example, in the first two seconds the body speed changed by 6 m/s (from V0 = 3 m/s to Vt = 9 m/s). Acceleration a = (Vt – V0) / t = 6/2 = 3 m/s2.

Question No. 9

When a car moves at uniform acceleration for five seconds, its speed increases from 10 to 15 m/s. What is the acceleration module of the car?

Solution.

Acceleration of the car a = (Vt – V0) / t= (15 – 10)/5 = 5/5 = 1 m/s2.

Question No. 10

The car starts from rest with constant acceleration a = 1 m/s2. How far does the car travel in the first ten seconds of movement?

Solution.

The car moves uniformly accelerated without an initial speed - the distance traveled is L = at2/2 = 1102/2 = 50 m.

Question No. 11

A raft floats uniformly down a river at a speed of 3 km/h. The rafter moves across the raft at a speed of 4 km/h. What is the speed of the rafter in the reference frame associated with the shore?

Solution.

The speed of the rafter in the reference frame associated with the shore

Question No. 12

The helicopter rises vertically at a constant speed. What is the trajectory of a point at the end of a helicopter rotor blade in the reference frame associated with the helicopter body?

Solution.

Imagine that you are in the cockpit of a helicopter, that is, you are motionless relative to the body of the helicopter. In this case, you can see that any point on the helicopter rotor describes a circle.

Question No. 13

The body moves along the X axis according to the law presented in the figure, where x is the coordinate in meters, t is time in seconds. Determine the acceleration modulus of the body.

Solution.

The equation for the dependence of the coordinate on time for rectilinear uniformly accelerated motion in general form has the form X(t) = X0 + V0хt + akht2/2, where X0 is the initial coordinate, and V0х and akh are the projections of the initial velocity and acceleration onto the X axis.

Equating the terms that include t2, we obtain akht2/2 = –4.5t2. Where does the projection of acceleration come from aх = –9 m/s2, and the acceleration module a= 9 m/s2.

Question No. 14

The figure shows graphs of the velocity modulus versus time for four bodies. Which of these bodies (or which bodies) have traveled the furthest?

Solution.

The figure shows graphs of the speed of moving bodies versus time. As is known, the path traveled by a body is the area lying under the velocity graph. It is clear from the figure that the figure of maximum area lies under the graph for body 4. This means that during the period of time from 0 to t0 body 4 has traveled the longest distance.

Question No. 15

The body moves in a straight line. The figure shows a graph of the body's speed versus time. At what time interval(s) is the acceleration projection negative?

Solution.

Let's analyze the graph:

1. over the period of time from 0 to 1 s, the speed of the body is constant, therefore ax = 0;

2. over a period of time from 1s to 2s, the speed of the body decreases, so the projection of acceleration is ah< 0;

3. in the time interval from 2s to 3s the body is at rest, therefore ax = 0;

4. in the time interval from 3s to 4s, the speed of the body increases, so the projection of acceleration ax > 0.

So, the acceleration projection is negative over the time interval from 1s to 2s.

Question No. 16

A car moving with an initial speed of 20 m/s accelerates with a constant acceleration a = 2 m/s2 for 5 s. How far did he travel during this time?

Solution.

To calculate the path, you can use the formula L = V0t + at2/2 = 205 + 252/2 = .

How to find the average speed from a graph

1. Instantaneous speed

In this section we will consider uneven motion. However, in this case we will need what we know about rectilinear uniform motion.

Figure 4.1 shows the positions of an accelerating car on a straight highway with a time interval of 1 s. The arrow points to the rear view mirror, the position of which we will consider further in more detail.

We see that at equal intervals of time the car travels different paths, that is, it moves unevenly.

Let us now reduce successive time intervals by 20 times - to 0.05 s - and monitor the change in the position of the car for half a second (this is not difficult to do, for example, using video recording).

In order not to clutter Figure 4.2, it shows only two positions of the car with a time interval of 0.5 s. Successive vehicle positions at 0.05 s intervals are marked by the position of its rear view mirror (shown in red).

We see that when successive equal time intervals are small enough, then the distances covered by the car during these time intervals are practically the same. This means that the movement of the car over such short periods of time can be considered rectilinear and uniform with good accuracy.

It turns out that any movement (even curvilinear) has this remarkable property: if we consider it over a sufficiently short period of time Δt, it is very similar to rectilinear uniform movement! Moreover, the shorter the period of time, the greater the similarity.

The speed of a body over a sufficiently short period of time is called its speed at a given moment of time t if this moment of time is in the interval Δt. And its more accurate name is instantaneous speed.

How short the time interval Δt must be so that during this interval the movement of the body can be considered rectilinear and uniform, depends on the nature of the body’s movement.

In the case of car acceleration, this is a fraction of a second. And, for example, the movement of the Earth around the Sun can be considered with good accuracy to be rectilinear and uniform even during the day, although the Earth flies more than two and a half million kilometers in space during this time!

1. Using Figure 4.2, determine the instantaneous speed of the car. Take the length of the car to be 5 m.

The value of the instantaneous speed of the car is shown by the speedometer (Fig. 4.3).

How to find instantaneous speed from a graph of coordinates versus time

Figure 4.4 shows a graph of coordinates versus time for a car moving along a straight highway.

We see that it moves unevenly, because the graph of its coordinates versus time is a curve, not a straight line segment.

Let's show how to determine from this graph the instantaneous speed of a car at any point in time - say, at t = 3 s (point on the graph).

To do this, consider the movement of a car over such a short period of time during which its movement can be considered linear and uniform.

Figure 4.5 shows the section of the graph that interests us at a tenfold increase (see, for example, the time scale).

We see that this section of the graph is practically indistinguishable from a straight line segment (red segment). In successive equal time intervals of 0.1 s, the car travels almost identical distances - 1 m each.

2. What is the instantaneous speed of the car at the moment t = 3 s?

Returning to the previous scale of the drawing, we will see that the red straight line, with which a small section of the graph practically coincided, is tangent to the graph of the dependence of the coordinate on time at a given moment in time (Fig. 4.6).

So, the instantaneous speed of a body can be judged by the angular coefficient of the tangent to the graph of the coordinate versus time: the greater the angular coefficient of the tangent, the greater the speed of the body. (The described method of determining instantaneous speed using a tangent to a graph of the dependence of a coordinate on time is associated with the concept of the derivative of a function. You will study this concept in the course “Algebra and the beginnings of aialis.”) And at those points of the graph where the angle of inclination of the tangent is zero, then there is a tangent parallel to the time axis t, the instantaneous speed of the body is zero.

3. Consider Figure 4.6.
b) Find the maximum and minimum instantaneous speed of the car during the first 6 seconds of its movement.

2. Average speed

Many problems use the average speed associated with the distance traveled:

vav = l/t. (1)

The average speed defined in this way is a scalar quantity, since the path is a scalar quantity. (Sometimes, to avoid confusion, it is called average ground speed.)

For example, if a car drove 120 km around the city for three hours (at the same time it could accelerate, brake and stop at intersections), then its average speed is 40 km/h.

4. How much will the average speed of the car just mentioned decrease if the total driving time increases by 1 hour due to traffic stops?

Average speed on two sections of traffic

In many problems, the movement of a body is considered in two areas, in each of which the movement can be considered uniform. In this case, according to the definition of average speed (1), we can write:

vav = (l1 + l2)/(t1 + t2), (2)

where l1 and t1 are the path and time for the first section, and l2 and t2 for the second. Let's look at examples.
Sasha left the village on a bicycle at a speed of 15 km/h and rode for an hour. And then the bike broke down, and Sasha walked for another hour at a speed of 5 km/h.

5. Find:
a) the path traveled by Sasha during the entire movement;
b) the total time of Sasha’s movement;
c) Sasha’s average speed.

In the case considered, the average speed turned out to be equal to the arithmetic mean of the speeds at which Sasha rode and walked. Is this always fair? Consider the following example.
Let Sasha ride a bicycle for an hour at a speed of 15 km/h, and then walk the same distance on foot at a speed of 5 km/h.

6. Find:
a) the path that Sasha walked on foot;
b) the path traveled by Sasha during the entire movement;
c) the total time of Sasha’s movement;
b) Sasha’s average speed.

Looking at this case, you will see that this time the average speed is not equal to the arithmetic average of the driving and walking speeds. And if you look even more closely, you will notice that in the second case the average speed is less than in the first. Why?

7. Compare the periods of time during which Sasha drove and walked in the first and second cases.

Let us summarize the situations discussed above.

Let us first consider the case when the body moved at different speeds for equal periods of time.

Let the body move at speed v1 for the first half of the entire time of movement, and for the second half at speed v2. Is it possible to find the average speed of movement over the entire section if neither the total time of movement nor the distance traveled by the body during the entire movement is known?

You can: to do this, we introduce notations for all the quantities we need, regardless of whether they are known or unknown. This is a common technique for solving many problems.

Let us denote the entire time of movement by t, the entire path by l, and the paths covered during the first and second half of the time of movement by l1 and l2, respectively.

8. Express in terms of v1, v2 and t:
a) l1 and l2; b) l; c) average speed.

Having found the answers to these questions, you will find out whether the statement is true in the general case: if a body moved in two sections with different speeds for equal periods of time, then its average speed along the entire path is equal to the arithmetic mean of the speeds of movement in the two sections.

Let us now consider the case when the body moved at different speeds for the first and second half of the path.

Now let the body move for the first half of the entire path at speed v1, and for the second half at speed v2. Let us again denote the entire time of movement by t, the entire path by l, and the time intervals during which the body moved in the first and second sections will be denoted by t1 and t2, respectively.

9. Express in terms of v1, v2 and l:
a) t1 and t2; b) t; c) average speed.

By answering these questions, you will find out whether the statement is true in the general case: if a body moved over two sections of equal length with different speeds, then its average speed along the entire path is not equal to the arithmetic mean of these speeds.

10. Prove that the average speed of a body that moved in two sections of equal length with different speeds is less than if it moved in two sections with the same speeds for equal periods of time.
Clue. For each of the two cases, express the average speed in terms of the speeds in the first and second sections and compare the resulting expressions.

11. On the first section of the path the body moved with speed v1, and on the second – with speed v2. What is the ratio of the lengths of these sections if the average speed of movement turns out to be equal to the arithmetic mean of v1 and v2?

Additional questions and tasks

12. For one third of the entire time, the train traveled at speed v1, and the remaining time at speed v2.
a) Express the distance traveled by the train in terms of v1, v2 and the entire travel time t.
b) Express the average speed of the train in terms of v1 and v2.
c) Find the numerical value of the average speed at v1 = 60 km/h, v2 = 90 km/h.

13. The car traveled three quarters of the entire distance at speed v1, and the remaining part of the journey at speed v2.
a) Express the entire time of movement of the car in terms of v1, v2 and the entire distance traveled l.
b) Express the average speed of the car in terms of v1 and v2.
c) Find the numerical value of the average speed at v1 = 80 km/h, v2 = 100 km/h.

14. The car drove for 2 hours at a speed of 60 km/h. How long after this must he drive at a speed of 80 km/h so that his average speed over the entire journey becomes equal to 66.7 km/h?

15. Transfer into your notebook (by cells) the graph of the dependence of the car’s coordinates on time, shown in Figure 4.4. Consider that the car is moving along the x-axis.
a) Determine graphically the average speed for 6 s.
b) Using the tangent line, determine at what approximately instants of time the instantaneous speed of the car was equal to its average speed over 6 s.

16. A body moves along the x axis. The dependence of the body coordinates on time is expressed by the formula x = 0.2 * t2.
a) Choose a convenient scale and draw a graph of x(t) for the first 6 s.
b) Using this graph, find the moment in time at which the instantaneous speed of the body was equal to the average speed for the entire time of movement.

§ 12. Graphs of path versus time.

If the trajectory of a point’s movement is known, then the dependence of the path traversed by the point on the elapsed period of time provides a complete description of this movement. We have seen that for uniform motion such a dependence can be given in the form of formula (9.2). The relationship between and for individual points in time can also be specified in the form of a table containing the corresponding values of the time period and the distance traveled. Let us be given that the speed of some uniform motion is 2 m/s. Formula (9.2) in this case has the form . Let's make a table of the path and time of such movement:

The dependence of one quantity on another is often convenient to depict not with formulas or tables, but with graphs, which more clearly show the picture of changes in variable quantities and can facilitate calculations. Let's plot the dependence of the distance traveled on time for the movement in question. To do this, take two mutually perpendicular straight lines - coordinate axes; We will call one of them (the abscissa axis) the time axis, and the other (the ordinate axis) the path axis. Let us choose scales for depicting time intervals and paths and take the point of intersection of the axes as the initial moment and as the starting point on the trajectory. Let us plot on the axes the values of time and distance traveled for the movement under consideration (Fig. 18). To “bind” the values of the distance traveled to moments in time, we draw perpendiculars to the axes from the corresponding points on the axes (for example, points 3 s and 6 m). The point of intersection of the perpendiculars corresponds simultaneously to both quantities: path and moment, and in this way the “binding” is achieved. The same construction can be performed for any other points in time and corresponding paths, obtaining for each such pair of time - path values one point on the graph. In Fig.

Determine from the graph the average speed of the body for periods of time

18 such a construction is made, replacing both rows of the table with one row of points. If such a construction were carried out for all points in time, then instead of individual points, a solid line would be obtained (also shown in the figure). This line is called a path versus time graph or, in short, a path graph.

Rice. 18. Graph of the path of uniform motion at a speed of 2 m/s

Rice. 19. For exercise 12.1

In our case, the path graph turned out to be a straight line. It can be shown that the graph of the path of uniform motion is always a straight line; and vice versa: if the graph of the path versus time is a straight line, then the movement is uniform.

Repeating the construction for a different speed, we find that the graph points for higher speeds lie higher than the corresponding graph points for lower speeds (Fig. 20). Thus, the greater the speed of uniform motion, the steeper the rectilinear path graph, i.e., the greater the angle it makes with the time axis.

Rice. 20. Graphs of the path of uniform movements with speeds of 2 and 3 m/s

Rice. 21. Graph of the same movement as in Fig. 18, drawn on a different scale

The slope of the graph depends, of course, not only on the numerical value of the speed, but also on the choice of time and length scales. For example, the graph shown in Fig. 21 gives the path versus time for the same movement as the graph in Fig. 18, although it has a different slope. From here it is clear that it is possible to compare movements by the slope of graphs only if they are drawn on the same scale.

Using path graphs, you can easily solve various motion problems. For example in Fig. 18 dashed lines show the constructions necessary to solve the following problems for a given movement: a) find the path traveled in 3.5 s; b) find the time it takes to travel 9 m. In the figure, the answers are found graphically (dashed lines): a) 7 m; b) 4.5 s.

On graphs describing uniform rectilinear motion, the coordinate of the moving point can be plotted along the ordinate axis instead of the path. This description opens up great possibilities. In particular, it makes it possible to distinguish the direction of movement relative to the axis. In addition, by taking the origin of time to be zero, it is possible to show the movement of the point at earlier moments of time, which should be considered negative.

Rice. 22. Graphs of movements with the same speed, but at different initial positions of the moving point

Rice. 23. Graphs of several movements with negative speeds

For example, in Fig. 22 straight line I is a graph of motion occurring at a positive speed of 4 m/s (i.e. in the direction of the axis), and at the initial moment the moving point was at a point with coordinate m. For comparison, the same figure shows a graph of the motion that occurs with the same speed, but at which at the initial moment the moving point is at the point with the coordinate (line II). Straight. III corresponds to the case when at the moment the moving point was at a point with coordinate m. Finally, straight line IV describes the movement in the case when the moving point had a coordinate at the moment c.

We see that the slopes of all four graphs are the same: the slope depends only on the speed of the moving point, and not on its initial position. When changing the initial position, the entire graph is simply transferred parallel to itself along the axis up or down at the appropriate distance.

Graphs of movements occurring at negative speeds (i.e. in the direction opposite to the direction of the axis) are shown in Fig. 23. They are straight, inclined downwards. For such movements, the coordinate of the point decreases over time.

12.3. The path graph for a point moving at a speed cuts off a segment on the ordinate axis. How does the distance from the starting point depend on time? Write the formula for this relationship.

12.4. A point moving at a speed is at a distance from the initial point at the moment.

How does distance depend on time?

12.5. The point, moving uniformly along the axis, had coordinates m and m at moments of time s and s, respectively. Find graphically at what moment the point passed through the origin of coordinates and what the coordinate was at the initial moment. Find the projection of the velocity onto the axis.

12.6. Using a path graph, find when and at what distance from point A a car leaving point A will be overtaken by a second car leaving the same point 20 minutes after the first, if the first car is moving at a speed of 40 km/h, and the second is moving at a speed of 40 km/h. at a speed of 60 km/h.

12.7. Using a graph, find where and when cars will meet, leaving simultaneously towards each other at speeds of 40 and 60 km/h from points A and B, located at a distance of 100 km from each other.

Path graphs can also be constructed for cases in which a body moves uniformly for a certain period of time, then moves uniformly but at a different speed for another period of time, then changes speed again, etc. For example, in Fig. 26 shows a motion graph in which the body moved during the first hour at a speed of 20 km/h, during the second hour at a speed of 40 km/h and during the third hour at a speed of 15 km/h.

Exercise:12.8. Construct a graph of the path for movement in which, over successive hourly intervals, the body had speeds of 10, -5, 0, 2, -7 km/h. What is the total displacement of the body?

1. Finding a path using a graph of speed versus time

Let's show how you can find the path traveled by a body using a graph of speed versus time.

Let's start with the simplest case - uniform motion. Figure 6.1 shows a graph of v(t) – speed versus time. It is a segment of a straight line parallel to the base of time, since with uniform motion the speed is constant.

The figure enclosed under this graph is a rectangle (it is shaded in the figure). Its area is numerically equal to the product of speed v and time of movement t. On the other hand, the product vt is equal to the path l traversed by the body. So, with uniform motion

the path is numerically equal to the area of the figure enclosed under the graph of speed versus time.

Let us now show that uneven motion also has this remarkable property.

Let, for example, the graph of speed versus time look like the curve shown in Figure 6.2.

Let us mentally divide the entire time of movement into such small intervals that during each of them the movement of the body can be considered almost uniform (this division is shown by dashed lines in Figure 6.2).

Then the path traveled during each such interval is numerically equal to the area of the figure under the corresponding lump of the graph. Therefore, the entire path is equal to the area of the figures contained under the entire graph. (The technique we used is the basis of integral calculus, the basics of which you will study in the course “Beginnings of Mathematical Analysis.”)

2. Path and displacement during rectilinear uniformly accelerated motion

Let us now apply the method described above for finding the path to rectilinear uniformly accelerated motion.

The initial speed of the body is zero

Let's direct the x axis in the direction of body acceleration. Then ax = a, vx = v. Hence,

Figure 6.3 shows a graph of v(t).

1. Using Figure 6.3, prove that in case of rectilinear uniformly accelerated motion without initial speed, the path l is expressed in terms of the acceleration module a and the time of movement t by the formula

Main conclusion:

in rectilinear uniformly accelerated motion without initial speed, the distance traveled by the body is proportional to the square of the time of movement.

In this way, uniformly accelerated motion differs significantly from uniform motion.

Figure 6.4 shows graphs of the path versus time for two bodies, one of which moves uniformly, and the other uniformly accelerates without an initial speed.

2. Look at Figure 6.4 and answer the questions.
a) What color is the graph for a body moving with uniform acceleration?
b) What is the acceleration of this body?
c) What are the speeds of the bodies at the moment when they have covered the same path?
d) At what point in time are the velocities of the bodies equal?

3. Having set off, the car covered a distance of 20 m in the first 4 s. Consider the car’s motion to be rectilinear and uniformly accelerated. Without calculating the acceleration of the car, determine how far the car will travel:
a) in 8 s? b) in 16 s? c) in 2 s?

Let us now find the dependence of the projection of displacement sx on time. In this case, the projection of acceleration onto the x axis is positive, so sx = l, ax = a. Thus, from formula (2) it follows:

sx = axt2/2. (3)

Formulas (2) and (3) are very similar, which sometimes leads to errors when solving simple problems. The fact is that the displacement projection value can be negative. This will happen if the x axis is directed opposite to the displacement: then sx< 0. А путь отрицательным быть не может!

4. Figure 6.5 shows graphs of travel time and displacement projection for a certain body. What color is the displacement projection graph?

The initial speed of the body is not zero

Let us recall that in this case the dependence of the velocity projection on time is expressed by the formula

vx = v0x + axt, (4)

where v0x is the projection of the initial velocity onto the x axis.

We will further consider the case when v0x > 0, ax > 0. In this case, we can again take advantage of the fact that the path is numerically equal to the area of the figure under the velocity versus time graph. (Consider other combinations of signs for the projection of initial velocity and acceleration yourself: the result will be the same general formula (5).

Figure 6.6 shows a graph of vx(t) for v0x > 0, ax > 0.

5. Using Figure 6.6, prove that in case of rectilinear uniformly accelerated motion with an initial speed, the displacement projection

sx = v0x + axt2/2.

This formula allows you to find the dependence of the x coordinate of the body on time. Let us recall (see formula (6), § 2) that the coordinate x of the body is related to the projection of its displacement sx by the relation

where x0 is the initial coordinate of the body. Hence,

x = x0 + sx, (6)

From formulas (5), (6) we obtain:

x = x0 + v0xt + axt2/2. (7)

6. The dependence of the coordinate on time for a certain body moving along the x axis is expressed in SI units by the formula x = 6 – 5t + t2.
a) What is the initial coordinate of the body?
b) What is the projection of the initial velocity onto the x-axis?
c) What is the projection of acceleration on the x-axis?
d) Draw a graph of the x coordinate versus time.
e) Draw a graph of the projected velocity versus time.
f) At what moment is the speed of the body equal to zero?
g) Will the body return to the starting point? If so, at what point(s) in time?
h) Will the body pass through the origin? If so, at what point(s) in time?
i) Draw a graph of the displacement projection versus time.
j) Draw a graph of the distance versus time.

3. Relationship between path and speed

When solving problems, the relationships between path, acceleration and velocity (initial v0, final v, or both) are often used. Let us derive these relations. Let's start with movement without an initial speed. From formula (1) we obtain for the time of movement:

Let's substitute this expression into formula (2) for the path:

l = at2/2 = a/2(v/a)2 = v2/2a. (9)

Main conclusion:

in rectilinear uniformly accelerated motion without initial speed, the distance traveled by the body is proportional to the square of the final speed.

7. Having set off, the car picked up a speed of 10 m/s over a distance of 40 m. Consider the car’s motion to be linear and uniformly accelerated. Without calculating the acceleration of the car, determine how far from the start of movement the car traveled when its speed was equal to: a) 20 m/s? b) 40 m/s? c) 5 m/s?

Relationship (9) can also be obtained by remembering that the path is numerically equal to the area of the figure enclosed under the graph of speed versus time (Fig. 6.7).

This consideration will help you easily cope with the next task.

8. Using Figure 6.8, prove that when braking with constant acceleration, the body travels the distance lт = v02/2a to a complete stop, where v0 is the initial speed of the body, a is the acceleration modulus.

In the case of braking of a vehicle (car, train), the distance traveled to a complete stop is called the braking distance. Please note: the braking distance at the initial speed v0 and the distance traveled during acceleration from standstill to speed v0 with the same acceleration a are the same.

9. During emergency braking on dry asphalt, the acceleration of the car is equal in absolute value to 5 m/s2. What is the braking distance of a car at initial speed: a) 60 km/h (maximum permitted speed in the city); b) 120 km/h? Find the braking distance at the indicated speeds during icy conditions, when the acceleration module is 2 m/s2. Compare the stopping distance values you found with the length of the classroom.

10. Using Figure 6.9 and the formula expressing the area of a trapezoid through its height and half the sum of the bases, prove that for rectilinear uniformly accelerated motion:
a) l = (v2 – v02)/2a, if the speed of the body increases;
b) l = (v02 – v2)/2a, if the speed of the body decreases.

11. Prove that the projections of displacement, initial and final velocity, as well as acceleration are related by the relation

sx = (vx2 – v0x2)/2ax (10)

12. A car on a path of 200 m accelerated from a speed of 10 m/s to 30 m/s.
a) How fast was the car moving?
b) How long did it take the car to travel the indicated distance?
c) What is the average speed of the car?

Additional questions and tasks

13. The last car is uncoupled from a moving train, after which the train moves uniformly, and the car moves with constant acceleration until it comes to a complete stop.
a) Draw on one drawing graphs of speed versus time for a train and a carriage.
b) How many times is the distance covered by the carriage to the stop less than the distance covered by the train in the same time?

14. Having left the station, the train traveled at a uniform acceleration for some time, then for 1 minute at a uniform speed of 60 km/h, and then again at a uniform acceleration until it stopped at the next station. The acceleration modules during acceleration and braking were different. The train covered the distance between stations in 2 minutes.
a) Draw a schematic graph of the projection of the speed of the train as a function of time.
b) Using this graph, find the distance between the stations.
c) What distance would the train travel if it accelerated on the first section of the route and slowed down on the second? What would be its maximum speed?

15. A body moves uniformly accelerated along the x axis. At the initial moment it was at the origin of coordinates, and the projection of its speed was equal to 8 m/s. After 2 s, the coordinate of the body became 12 m.
a) What is the projection of the acceleration of the body?
b) Plot a graph of vx(t).
c) Write a formula expressing the dependence x(t) in SI units.
d) Will the speed of the body be zero? If yes, at what point in time?
e) Will the body visit the point with coordinate 12 m a second time? If yes, at what point in time?
f) Will the body return to the starting point? If yes, then at what point in time, and what will be the distance traveled?

16. After the push, the ball rolls up an inclined plane, after which it returns to the starting point. The ball was at a distance b from the initial point twice at time intervals t1 and t2 after the push. The ball moved up and down along the inclined plane with the same acceleration.
a) Direct the x-axis upward along the inclined plane, select the origin at the initial position of the ball and write a formula expressing the dependence x(t), which includes the modulus of the initial velocity of the ball v0 and the modulus of the acceleration of the ball a.
b) Using this formula and the fact that the ball was at a distance b from the starting point at times t1 and t2, create a system of two equations with two unknowns v0 and a.
c) Having solved this system of equations, express v0 and a in terms of b, t1 and t2.
d) Express the entire path l traveled by the ball in terms of b, t1 and t2.
e) Find the numerical values of v0, a and l for b = 30 cm, t1 = 1s, t2 = 2s.
f) Plot graphs of vx(t), sx(t), l(t).
g) Using the sx(t) graph, determine the moment when the ball’s modulus of displacement was maximum.

1. Instantaneous speed

In this section we will consider uneven motion. However, in this case we will need what we know about rectilinear uniform motion.

We see that at equal intervals of time the car travels different paths, that is, it moves unevenly.

How short the time interval Δt must be so that during this interval the movement of the body can be considered rectilinear and uniform, depends on the nature of the body’s movement.

1. Using Figure 4.2, determine the instantaneous speed of the car. Take the length of the car to be 5 m.

The value of the instantaneous speed of the car is shown by the speedometer (Fig. 4.3).

How to find instantaneous speed from a graph of coordinates versus time

Figure 4.4 shows a graph of coordinates versus time for a car moving along a straight highway.

We see that it moves unevenly, because the graph of its coordinates versus time is a curve, not a straight line segment.

Let's show how to determine from this graph the instantaneous speed of a car at any point in time - say, at t = 3 s (point on the graph).

To do this, consider the movement of a car over such a short period of time during which its movement can be considered linear and uniform.

Figure 4.5 shows the section of the graph that interests us at a tenfold increase (see, for example, the time scale).

2. What is the instantaneous speed of the car at the moment t = 3 s?

3. Consider Figure 4.6.
a) At what points on the graph is the angle of inclination of the tangent the greatest? least?
b) Find the maximum and minimum instantaneous speed of the car during the first 6 seconds of its movement.

2. Average speed

Many problems use the average speed associated with the distance traveled:

vav = l/t. (1)

The average speed defined in this way is a scalar quantity, since the path is a scalar quantity. (Sometimes, to avoid confusion, it is called average ground speed.)

For example, if a car drove 120 km around the city for three hours (at the same time it could accelerate, brake and stop at intersections), then its average speed is 40 km/h.

4. How much will the average speed of the car just mentioned decrease if the total driving time increases by 1 hour due to traffic stops?

Average speed on two sections of traffic

vav = (l1 + l2)/(t1 + t2), (2)

5. Find:
a) the path traveled by Sasha during the entire movement;
b) the total time of Sasha’s movement;
c) Sasha’s average speed.

6. Find:
a) the path that Sasha walked on foot;
b) the path traveled by Sasha during the entire movement;
c) the total time of Sasha’s movement;
b) Sasha’s average speed.

7. Compare the periods of time during which Sasha drove and walked in the first and second cases.

Let us summarize the situations discussed above.

Let us first consider the case when the body moved at different speeds for equal periods of time.

You can: to do this, we introduce notations for all the quantities we need, regardless of whether they are known or unknown. This is a common technique for solving many problems.

Let us denote the entire time of movement by t, the entire path by l, and the paths covered during the first and second half of the time of movement by l1 and l2, respectively.

8. Express in terms of v1, v2 and t:
a) l1 and l2; b) l; c) average speed.

Let us now consider the case when the body moved at different speeds for the first and second half of the path.

9. Express in terms of v1, v2 and l:
a) t1 and t2; b) t; c) average speed.

Additional questions and tasks

The car traveled three quarters of the entire distance at speed v1, and the remaining part of the journey at speed v2.
a) Express the entire time of movement of the car in terms of v1, v2 and the entire distance traveled l.
b) Express the average speed of the car in terms of v1 and v2.
c) Find the numerical value of the average speed at v1 = 80 km/h, v2 = 100 km/h.

14. The car drove for 2 hours at a speed of 60 km/h. How long after this must he drive at a speed of 80 km/h so that his average speed over the entire journey becomes equal to 66.7 km/h?

Graphical representation of uniform linear motion

Mechanical movement is represented graphically. The dependence of physical quantities is expressed using functions. Designate:

V (t) - change in speed over time

a(t) - change in acceleration over time

Behind acceleration versus time. Since during uniform motion the acceleration is zero, the dependence a(t) is a straight line that lies on the time axis.

Dependence of speed on time. Since the body moves rectilinearly and uniformly (v = const), i.e. the speed does not change over time, then the graph with the dependence of speed on time v(t) is a straight line parallel to the time axis.

The projection of the body's movement is numerically equal to the area of the rectangle AOBC under the graph, since the magnitude of the movement vector is equal to the product of the velocity vector and the time during which the movement was made.

The rule for determining the path using the graph v(t): in case of rectilinear uniform motion, the magnitude of the displacement vector is equal to the area of the rectangle under the velocity graph.

Dependence of displacement on time. Graph s(t) - sloping line :

The graph shows that the projection of the velocity is equal to:

Having considered this formula, we can say that the larger the angle, the faster the body moves and it covers a greater distance in less time.

The rule for determining speed from the graph s(t): The tangent of the angle of inclination of the graph to the time axis is equal to the speed of movement.

Uneven straight motion.

Uniform motion is motion at a constant speed. If the speed of a body changes, it is said to be moving unevenly.

A movement in which a body makes unequal movements at equal intervals of time is called uneven or variable movement.

To characterize uneven motion, the concept of average speed is introduced.

Average driving speed equal to the ratio of the entire path traveled by a material point to the period of time during which this path was traveled.

In physics, the greatest interest is not the average, but instantaneous speed , which is defined as the limit to which the average speed tends over an infinitesimal period of time Δ t:

Instant speedvariable motion is the speed of a body at a given point in time or at a given point on the trajectory.

The instantaneous velocity of a body at any point on a curvilinear trajectory is directed tangentially to the trajectory at that point.

The difference between average and instantaneous speeds is shown in the figure.

The movement of a body in which its speed changes equally over any equal periods of time is called uniformly accelerated or uniformly alternating motion.

Acceleration -this is a vector physical quantity that characterizes the rate of change in speed, numerically equal to the ratio of the change in speed to the period of time during which this change occurred.

If the speed changes equally throughout the entire movement, then the acceleration can be calculated using the formula:

Designations:

V x - Velocity of a body during uniformly accelerated motion in a straight line

V x o - Initial velocity of the body

a x - Body acceleration

t - Time of body movement

Acceleration shows how quickly the speed of a body changes. If the acceleration is positive, then the speed of the body increases, the movement is accelerated. If the acceleration is negative, it means the speed is decreasing and the movement is slow.

The SI unit of acceleration is [m/s2].

Acceleration is measured accelerometer

Speed equation for uniformly accelerated motion:v x = v xo + a x t

Equation of uniformly accelerated rectilinear motion(movement during uniformly accelerated motion):

Designations:

S x - Displacement of a body during uniformly accelerated motion in a straight line

V x o - Initial velocity of the body

V x - Velocity of a body during uniformly accelerated motion in a straight line

a x - Body acceleration

t - Time of body movement

More formulas for finding displacement during uniformly accelerated linear motion, which can be used when solving problems:

If the initial and final speeds and acceleration are known.

If the initial and final speeds of movement and the time of the entire movement are known

Graphical representation of uneven linear motion

Mechanical movement is represented graphically. The dependence of physical quantities is expressed using functions. Designate:

V(t) - change in speed over time

S(t) - change in displacement (path) over time

1) Analytical method.

We consider the highway to be straight. Let's write down the equation of motion of a cyclist. Since the cyclist moved uniformly, his equation of motion is:

(we place the origin of coordinates at the starting point, so the initial coordinate of the cyclist is zero).

The motorcyclist was moving at uniform acceleration. He also started moving from the starting point, so his initial coordinate is zero, the initial speed of the motorcyclist is also zero (the motorcyclist began to move from a state of rest).

Considering that the motorcyclist started moving later, the equation of motion for the motorcyclist is:

In this case, the speed of the motorcyclist changed according to the law:

At the moment when the motorcyclist caught up with the cyclist, their coordinates are equal, i.e. or:

Solving this equation for , we find the meeting time:

This is a quadratic equation. We define the discriminant:

Determining the roots:

Let's substitute numerical values into the formulas and calculate:

We discard the second root as not corresponding to the physical conditions of the problem: the motorcyclist could not catch up with the cyclist 0.37 s after the cyclist started moving, since he himself left the starting point only 2 s after the cyclist started.

Thus, the time when the motorcyclist caught up with the cyclist:

Let's substitute this time value into the formula for the law of change in speed of a motorcyclist and find the value of his speed at this moment:

2) Graphic method.

On the same coordinate plane we build graphs of changes over time in the coordinates of the cyclist and motorcyclist (the graph for the cyclist’s coordinates is in red, for the motorcyclist – in green). It can be seen that the dependence of the coordinate on time for a cyclist is a linear function, and the graph of this function is a straight line (the case of uniform rectilinear motion). The motorcyclist was moving with uniform acceleration, so the dependence of the motorcyclist’s coordinates on time is a quadratic function, the graph of which is a parabola.