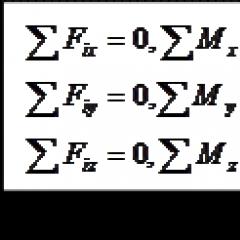Conditions for the equilibrium of a system of forces in space. Theoretical mechanics

Equilibrium condition for a spatial system of converging forces: the algebraic sum of the projections of all forces onto three mutually perpendicular coordinate axes must be equal to zero, i.e.

To find the moment of force relative to the axis z, need to design the force to the plane N perpendicular to the axis z(Fig. 12), then find the moment of projection F n relative to point O, which is the intersection point of the plane N suck z. Moment of projection F n and will be a moment of strength relative to the axis z:

Spatial system of arbitrarily located forces is a system of forces whose lines of action do not lie in the same plane and do not intersect at one point. The resultant of such a system of forces is also equal to the geometric sum of these forces, but is depicted by the diagonal of complex volumetric figures (tetrahedron, octahedron, etc.).

Equilibrium condition for a spatial system of arbitrarily located forces: the algebraic sum of the projections of all forces onto three mutually perpendicular coordinate axes must be equal to zero and the algebraic sum of the moments of all forces relative to the same coordinate axes must be equal to zero, i.e.

Friction

Friction called resistance to body movement. The force with which a body resists movement is called friction force.

The friction force is always directed in the direction opposite to the movement. The friction force depends on the material of the rubbing bodies, the cleanliness of the processing and the presence of lubricant and does not depend on the size of the rubbing surfaces.

Friction happens: dry, semi-liquid, liquid.

Distinguish between friction rest, movement, sliding And rolling. The static friction force is greater than the moving friction force.

The friction force is equal to the product of the normal pressure force and the sliding friction coefficient (Fig. 14):

F tr =R n ƒ,

Where Rn = mg cos a - normal pressure force;

ƒ - sliding friction coefficient.

Sliding friction coefficient The ratio of the friction force to the normal pressure force is called:

Materials that have very little friction are called anti-friction(babbitt, bronze, graphite). Used for the manufacture of bearings, etc.

Materials with high friction are called frictional(special plastics using asbestos and copper). Used for brake pad linings and clutch disc linings.

When the sliding surface is lubricated, the body begins to move with less friction.

Let us decompose the force of gravity G into components G ’ and G " (Fig. 15)

Let's create an equilibrium equation:

Where h- distance from the surface to the line of action of the force;

k- rolling friction coefficient. It is equal to the segment OS (see Fig. 16)

F dv = F tr,

F tr =R p k/h

If h = d,

F tr =R p k/d

if h = g,

F tr =R p k/d

We combine the origin of coordinates with the point of intersection of the lines of action of the forces of the system. We project all forces onto the coordinate axes and sum up the corresponding projections (Fig. 7.4). We obtain the projections of the resultant on the coordinate axes:

The module of the resultant system of converging forces is determined by the formula

The direction of the resultant vector is determined by the angles

Arbitrary spatial system of forces

Bringing an arbitrary spatial system of forces to the center of O.

A spatial system of forces is given (Fig. 7.5, a). Let's bring it to the center O.

Forces must be moved in parallel, and a system of pairs of forces is formed. The moment of each of these pairs is equal to the product of the force modulus and the distance to the center of reduction.

A beam of forces arises at the reduction center, which can be replaced by the total force (main vector) F GL (Fig. 7.5, b).

The moments of pairs of forces can be added, obtaining the total moment of the system M ch (main moment).

Thus, an arbitrary spatial system of forces is reduced to the main vector and the main moment.

The main vector is usually decomposed into three components directed along the coordinate axes (Fig. 7.5, c).

Usually the total moment is decomposed into components: three moments relative to the coordinate axes.

The absolute value of the main vector (Fig. 7.5b) is equal to

The absolute value of the main moment is determined by the formula.

Equilibrium equations for a spatial system of forces

At equilibrium F ch = 0; M ch = 0. We obtain six equilibrium equations:

The six equilibrium equations of the spatial system of forces correspond to six independent possible movements of the body in space: three movements along the coordinate axes and three rotations around these axes.

Examples of problem solving

Example 1. On a cube-shaped body with an edge A= 10 cm three forces act (Fig. 7.6). Determine the moments of forces relative to the coordinate axes coinciding with the edges of the cube.

Solution

1. Moments of forces about the axis Oh:

2. Moments of forces about the axis OU.

Example 2. Two wheels are fixed on a horizontal shaft, g 1 = 0.4 m; g 2 = 0.8 m. Other dimensions are in Fig. 7.7. Force is applied to wheel 1 F 1, to wheel 2 - power F 2= 12 kN, F 3= 4kN.

Define strength F 1 and reactions in the hinges A And IN in a state of balance.

Let us remind you:

1. In equilibrium, six equilibrium equations are satisfied.

Moment equations should be written relative to the supports A and B.

2. Powers F 2 \\O x; F 2\\Oy;F 3\\Oy.

The moments of these forces relative to the corresponding axes are equal to zero.

3. The calculation should be completed by verification using additional equilibrium equations.

Solution

1. Determine strength F\, having composed the equation of moments of forces relative to the Oz axis:

2. Determine reactions in support A. There are two reaction components acting on the support ( Y A ; X A ).

We compose the equation of moments of forces about the axis Oh"(in support IN).

Rotation around an axis Oh" not happening:

The minus sign means that the reaction is directed in the opposite direction.

Rotation around an axis OU" does not happen, we draw up an equation for the moments of forces relative to the axis OU"(in support IN):

3. Determine the reactions in support B. Two components of the reaction act on the support ( X B , Y B ). We compose the equation of moments of forces about the axis Oh(support A):

We compose the equation of moments about the axis OU(support A):

4.Check. We use projection equations:

The calculation was done correctly.

Example 3. Determine the numerical value of the force P 1 , at which the shaft Sun(Fig. 1.21, A) will be in equilibrium. At the found force value P 1 determine support reactions.

Forces acting on gears R And P 1 directed tangentially to the initial circles of the wheels; strength T And T 1 - according to the radii of the wheels; strength A 1 parallel to the shaft axis. T = 0.36P, 7T 1 = P 1; A 1 = 0.12P 1.

Solution

The shaft supports shown in Fig. 1.21, a, should be considered as spatial hinge supports that prevent linear movements in the directions of the axes And And v(the selected coordinate system is shown in Fig. 1.21, b).

We free the shaft from the connections and replace their action with reactions V V, N V, V C, N C (Fig. 1.21, b). We have obtained a spatial system of forces, for which we draw up equilibrium equations using the selected coordinate system (Fig. 1.21.6):

Where A 1*1.25D/2 - moment about the axis And strength A 1, applied to the right gear.

Moments about the axis And strength T 1 And A 1(applied to the middle gear), P 1 (applied to the right gear) and P are equal to zero, since the forces P, T 1, P 1 are parallel to the axis And, and force A 1 crosses the axis And.

where V C = 0.37P;

where V B =0.37P.

hence the reactions V B And V C defined correctly;

Where A 1 * 1.25D/2- moment about the axis v strength A 1, applied to the middle gear.

Moments about the axis v forces T, P 1 (applied to the middle gear), A 1 And T 1(applied to the right gear) are equal to zero, since the forces T, R 1, T 1 parallel to the axis v, force A 1 crosses the axis v.

whence H C = 0.81P;

from where H C = 1.274P

Let's create a verification equation:

hence the reactions N V And N S defined correctly.

In conclusion, we note that the support reactions turned out to have a plus sign. This indicates that the selected directions V B, N B, V C And N S coincide with the actual directions of bond reactions.

Example 4. The pressure force of the steam engine connecting rod P = 25 kN is transmitted to the middle of the crankshaft journal at the point D at an angle α = 30° to the horizontal with the knee cheeks vertical (Fig. 1.22). A belt drive pulley is mounted on the end of the shaft. The tension of the driving branch of the belt is two times greater than that of the driven branch, i.e. S 1 = 2S 2 . Flywheel gravity force G = 10 kN.

Determine the tension of the belt drive branches and the reactions of the bearings A And IN, neglecting the mass of the shaft.

Solution

We consider the equilibrium of a horizontal crankshaft with a pulley. We apply the specified forces in accordance with the problem conditions P, S 1, S 2 And G . We free the shaft from the supporting fasteners and replace their action with reactions V A, N A, V B And N V. We select the coordinate axes as shown in Fig. 1.22. Hinged A And IN no reactions occur along the axis w, since the tension of the belt branches and all other forces act in planes perpendicular to this axis.

Let's create equilibrium equations:

In addition, according to the conditions of the problem, we have another equation

So there are six unknown forces here S 1, S 2, N A, V A, N B And V B and six equations connecting them.

Equation of projections onto an axis w in the example under consideration turns into the identity 0 = 0, since all forces lie in planes perpendicular to the axis w.

Substituting S 1 =2S 2 into the equilibrium equations and solving them, we find:

Reaction value N V It turned out with a minus sign. This means that in reality its direction is opposite to that assumed in Fig. 1.22.

Test questions and assignments

1. Write down the formulas for calculating the main vector of a spatial system of converging forces.

2. Write down the formula for calculating the main vector of a spatial system of arbitrarily located forces.

3. Write down the formula for calculating the main moment of a spatial system of forces.

4. Write down the system of equilibrium equations for the spatial system of forces.

5. Which equilibrium equation should be used to determine the reaction of the rod R 1 (Fig. 7.8)?

6. Determine the main moment of the force system (Fig. 7.9). The reference point is the origin of coordinates. The coordinate axes coincide with the edges of the cube, the edge of the cube is 20 cm; F 1 - 20kN; F 2 - 30kN.

7. Determine the Xb reaction (Fig. 7.10). The vertical axis with the pulley is loaded by two horizontal forces. Powers F 1 And F 2 parallel to the axis Oh. AO = 0.3 m; OB= 0.5 m; F 1 = 2kN; F 2 = 3.5 kN.

Recommendation. Create an equation for moments about the axis OU" at the point A.

8. Answer the test questions.

Vector equilibrium conditions for an arbitrary system of forces: for the equilibrium of a system of forces applied to a rigid body, it is necessary and sufficient that the main vector of the force system is equal to zero and the main moment of the force system relative to any center of reduction is also equal to zero. Otherwise: in order for ~0, the following conditions are necessary and sufficient:

,
or
,
. (19)

Equilibrium conditions for a spatial system of forces in analytical form

For the equilibrium of a spatial system of forces applied to a solid body, it is necessary and sufficient that the three sums of the projections of all forces on the Cartesian coordinate axes are equal to zero and the three sums of the moments of all forces relative to the three coordinate axes are also equal to zero.

. (20)

Equilibrium conditions for a spatial system of converging forces

For the equilibrium of a spatial system of converging forces applied to a solid body, it is necessary and sufficient that the sums of the projections of forces on each of the three rectangular coordinate axes be equal to zero:

;
;
, (21)

In the case of a plane system of converging forces, one of the coordinate axes, usually
, is chosen perpendicular to the forces, and the other two axes are chosen, respectively, in the plane of the forces. D For the equilibrium of a plane system of converging forces acting on a solid body, it is necessary and sufficient that the sums of the projections of these forces onto each of the two rectangular coordinate axes lying in the plane of the forces are equal to zero:

;
, (22)

Equilibrium conditions for a spatial system of parallel forces

Let's direct the axis
parallel to the forces: for the equilibrium of a spatial system of parallel forces applied to a solid body, it is necessary and sufficient that the algebraic sum of these forces be equal to zero and the sum of the moments of forces relative to two coordinate axes perpendicular to the forces are also equal to zero:

Equilibrium conditions for a plane system of forces

Let's position the axes
And
in the plane of action of forces.

Equilibrium conditions for a plane system of forces in the first form: for the equilibrium of a plane system of forces acting on a solid body, it is necessary and sufficient that the sums of the projections of these forces onto each of the two rectangular coordinate axes located in the plane of action of the forces are equal to zero and the sum of the algebraic moments of forces relative to any point located in the plane of action forces was also zero:

(24)

For the equilibrium of a plane system of parallel forces applied to a solid body, it is necessary and sufficient that the algebraic sum of the forces be equal to zero and the sum of the algebraic moments of the forces relative to any point located in the plane of the forces is also equal to zero:

(25)

Three-moment theorem (second form of equilibrium conditions): for the equilibrium of a plane system of forces applied to a rigid body, it is necessary and sufficient that the sums of the algebraic moments of the forces of the system relative to any three points located in the plane of action of the forces and not lying on the same straight line are equal to zero:

Third form of equilibrium conditions: for the equilibrium of a plane system of forces applied to a solid body, it is necessary and sufficient that the sums of the algebraic moments of forces relative to any two points lying in the plane of action of the forces are equal to zero and the algebraic sum of the projections of these forces onto any axis of the plane that is not perpendicular to the straight line , passing through two moment points, was also equal to zero, i.e.

That., for the equilibrium of an arbitrary spatial system of forces, it is necessary and sufficient that the algebraic sum of the projections of all these forces onto each of the three arbitrarily chosen coordinate axes is equal to zero and that the algebraic sum of their moments relative to each of these axes is also equal to zero.

Conditions (1.33) are called equilibrium conditions of an arbitrary spatial system of forces in analytical form.

Equilibrium conditions for a spatial system of parallel forces. If the lines of action of all the forces of a given system of forces are located in different planes and are parallel to each other, then such a system of forces is called spatial system of parallel forces.

Using the equilibrium conditions (1.33) of an arbitrary spatial system of forces, one can find the equilibrium conditions of a spatial system of parallel forces. (The equilibrium conditions we previously derived for plane and spatial systems of converging forces, an arbitrary plane system of forces and a plane system of parallel forces could also be obtained using the equilibrium conditions (1.33) of an arbitrary spatial system of forces).

Let a spatial system of parallel forces act on a solid body (Figure 1.26). Since the choice of coordinate axes is arbitrary, it is possible to choose coordinate axes so that the axis z was parallel to the forces. With this choice of coordinate axes, the projections of each of the forces on the axis X And at and their moments about the axis z will be equal to zero, and, therefore, the equalities , and are satisfied regardless of whether a given system of forces is in equilibrium or not, and therefore cease to be equilibrium conditions. Therefore, system (1.33) will give only three equilibrium conditions:

Hence, for the equilibrium of a spatial system of parallel forces, it is necessary and sufficient that the algebraic sum of the projections of all forces onto the axis parallel to these forces equals zero and that the algebraic sum of their moments relative to each of the two coordinate axes perpendicular to these forces also equals zero.

1. Select a body (or point) whose equilibrium should be considered in this problem.

2. Free the selected body from bonds and depict (arrange) all active forces and reaction forces of discarded bonds acting on this body (and only on this body). A body freed from connections, with a system of active and reaction forces attached to it, should be depicted separately.

3. Write equilibrium equations. To draw up equilibrium equations, you must first select the coordinate axes. This choice can be made arbitrarily, but the resulting equilibrium equations will be solved more easily if one of the axes is directed perpendicular to the line of action of some unknown reaction force. The solution of the resulting equilibrium equations should, as a rule, be carried out to the end in general form (algebraically). Then, for the required quantities, formulas will be obtained that allow one to analyze the results found; numerical values of the found quantities are substituted only into the final formulas. Equilibrium equations are compiled using the analytical method of solving problems on the equilibrium of a system of converging forces. However, if the number of converging forces whose equilibrium is considered is three, then it is convenient to apply the geometric method for solving these problems. The solution in this case comes down to the fact that instead of the equilibrium equations of all acting forces (active and reaction bonds), a force triangle is constructed, which, based on the geometric condition of equilibrium, must be closed (the construction of this triangle should begin with a given force). By solving the force triangle, we find the required quantities.

Dynamics

To understand the dynamics section, you need to know the following information. From mathematics - the scalar product of two vectors, differential equations. From physics – the laws of conservation of energy and momentum. Oscillation theory. It is recommended to review these topics.

As was clarified in § 4.4, the necessary and sufficient conditions for the equilibrium of a spatial system of forces applied to a rigid body can be written in the form of three projection equations (4.16) and three moments (4.17):

, , . (7.14)

If the body is completely fixed, then the forces acting on it are in equilibrium and equations (7.13) and (7.14) serve to determine the support reactions. Of course, there may be cases where these equations are not enough to determine the support reactions; We will not consider such statically indeterminate systems.

For a spatial system of parallel forces, the equilibrium equations take the form (§ 4.4[‡]):

, , . (7.15)

Let us now consider cases when the body is only partially fixed, i.e. the connections that are imposed on the body do not guarantee the balance of the body. Four special cases can be indicated.

1. A solid body has one fixed point. In other words, it is attached to a fixed point using a perfect spherical joint.

Let us place the origin of the fixed coordinate system at this point. Action of connection at a point A Let's replace it with a reaction; since it is unknown in magnitude and direction, we will present it in the form of three unknown components , , , directed respectively along the axes , , .

Equilibrium equations (7.13) and (7.14) in this case will be written in the form:

1) ,

2) ,

3) ,

4) ,

5) ,

The last three equations do not contain reaction components, since the line of action of this force passes through the point A. Consequently, these equations establish the relationships between the active forces necessary for the equilibrium of the body, and the first three equations can be used to determine the components of the reaction.

Thus, the condition for the equilibrium of a rigid body that has one fixed point is the equality to zero of each of the algebraic sums of the moments of all active forces of the system relative to three axes intersecting at a fixed point of the body .

2. The body has two fixed points. This will, for example, be the case if it is attached to two fixed points using hinges.

Let us choose the origin of coordinates at the point A and direct the axis along the line passing through the points A And IN. Let us replace the action of bonds with reactions, directing the components of the reaction along the coordinate axes. Let us denote the distance between points A And IN through A; then the equilibrium equations (7.13) and (7.14) will be written in the following form:

1) ,

2) ,

3) ,

4) ,

5) ,

The last equation does not contain reaction forces and establishes the connection between the active forces necessary for the balance of the body. Hence, the condition for the equilibrium of a rigid body that has two fixed points is the equality to zero of the algebraic sum of the moments of all active forces applied to the body relative to the axis passing through the fixed points . The first five equations are used to determine the unknown components of the reactions , , , , , .

Note that the components and cannot be determined separately. From the third equation, only the sum + is determined and, therefore, the problem with respect to each of these unknowns for a rigid body is statically indeterminate. However, if at the point IN If there is not a spherical, but a cylindrical hinge (i.e., a bearing), which does not interfere with the longitudinal sliding of the body along the axis of rotation, then the problem becomes statically definable.

The body has a fixed axis of rotation along which it can slide without friction. This means that at points A And IN there are cylindrical hinges (bearings), and the components of their reactions along the axis of rotation are equal to zero. Consequently, the equilibrium equations will take the form:

1) ,

2) ,

4) ,

5) ,

Two of the equations (7.18), namely the third and sixth, impose restrictions on the system of active forces, and the remaining equations serve to determine the reactions.

The body rests at three points on a smooth surface, and the support points do not lie on the same straight line. Let us denote these points by A, IN And WITH and compatible with the plane ABC coordinate plane Ahu. Replacing the action of the connections with vertical reactions , and , we write the equilibrium conditions (7.14) in the following form:

3) ,

4) ,

5) ,

The third - fifth equations can serve to determine unknown reactions, and the first, second and sixth equations represent the conditions connecting the active forces and necessary for the equilibrium of the body. Of course, for the body to balance, the following conditions must be met: , , since at the support points only reactions of the direction accepted above can occur.

If the body rests on a horizontal plane at more than three points, then the problem becomes statically indeterminable, since in this case there will be as many reactions as there are points, and there will only be three equations left to determine the reactions.

Problem 7.3. Find the main vector and main moment of the system of forces shown in Fig. The forces are applied to the vertices of the cube and directed along its edges, and , . The length of the edge of the cube is A.