Second order inverse matrix example. Inverse matrix online

Service purpose. With the help of this service online, you can find algebraic complements, transposed matrix AT, adjoint matrix and inverse matrix.

Online calculator. Inverse matrix.

The solution is carried out directly on the website (online) and is free of charge. The calculation results are presented in a Word report and in Excel format (i.e. it is possible to check the solution). see design example.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Algebraic complements.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Then inverse matrix can be written as:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Finding the inverse matrix

The matrix А-1 is called the inverse matrix with respect to the matrix if А * А-1 =, where is the identity matrix of the th order. An inverse matrix can only exist for square matrices.

see also Inverse matrix by the Jordan-Gauss method

Algorithm for finding the inverse matrix

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Finding the transposed matrix AT.
Definition of algebraic complements. Replace each element of the matrix with its algebraic complement.
Composing an inverse matrix from algebraic additions: each element of the resulting matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

The following algorithm for finding the inverse matrix is similar to the previous one, with the exception of some steps: first, the algebraic complements are calculated, and then the union matrix is determined.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Definition of algebraic complements.
Filling the union (reciprocal, adjoint) matrix.
Composing an inverse matrix from algebraic complements: each element of the adjoint matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Example # 1. Let's write the matrix as follows:

An inverse matrix exists if the determinant of the matrix is nonzero. Find the determinant of the matrix:
= -1 (-1 4 - (- 2 5)) - 2 (2 4 - (- 2 (-2))) + 3 (2 5 - (- 1 (-2))) = 10. The determinant is 10 and is not equal to zero. We continue the solution.
Find the transposed matrix:
Algebraic complements.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Then inverse matrix can be written as:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Another algorithm for finding the inverse matrix

Let us give another scheme for finding the inverse matrix.

Find the determinant of the given square matrix.
Find the algebraic complements to all elements of the matrix.
We write the algebraic complements of row elements into columns (transposition).
We divide each element of the resulting matrix by the determinant of the matrix.

As you can see, the transposition operation can be applied both at the beginning, over the original matrix, and at the end, over the obtained algebraic complements.

Special case: The inverse of the identity matrix is the identity matrix.

Example No. 2. Find the inverse of a matrix .
Solution.
1. Find
.
2. We are looking for the algebraic complements of each element of the matrix A:
; ; .
We got the algebraic additions of the elements of the first line.

Find Inverse Matrix Online

Similarly, for the elements of the second and third lines, we get:
; ; .
; ; .
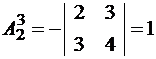Combining points 3 and 4, we get the inverse matrix

.
To check, make sure that A-1A = E.

Instruction. To obtain a solution, it is necessary to set the dimension of the matrix. Next, in a new dialog box, fill in the matrix.

Finding the inverse matrix

The matrix А-1 is called the inverse matrix with respect to the matrix if А * А-1 =, where is the identity matrix of the th order. An inverse matrix can only exist for square matrices.

Service purpose. With the help of this service online, you can find algebraic complements, transposed matrix AT, adjoint matrix and inverse matrix. The solution is carried out directly on the website (online) and is free of charge. The calculation results are presented in a Word report and in Excel format (i.e. it is possible to check the solution). see design example.

Finding the inverse matrix online

see also Inverse matrix by the Jordan-Gauss method

Algorithm for finding the inverse matrix

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Finding the transposed matrix AT.
Definition of algebraic complements. Replace each element of the matrix with its algebraic complement.
Composing an inverse matrix from algebraic additions: each element of the resulting matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Definition of algebraic complements.
Filling the union (reciprocal, adjoint) matrix.
Composing an inverse matrix from algebraic complements: each element of the adjoint matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Example # 1. Let's write the matrix as follows:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Then inverse matrix can be written as:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Another algorithm for finding the inverse matrix

Let us give another scheme for finding the inverse matrix.

Find the determinant of the given square matrix.
Find the algebraic complements to all elements of the matrix.
We write the algebraic complements of row elements into columns (transposition).
We divide each element of the resulting matrix by the determinant of the matrix.

As you can see, the transposition operation can be applied both at the beginning, over the original matrix, and at the end, over the obtained algebraic complements.

To check, make sure that A-1A = E.

Instruction. To obtain a solution, it is necessary to set the dimension of the matrix. Next, in a new dialog box, fill in the matrix.

Finding the inverse matrix is an important part of the linear algebra section. With the help of such matrices, if they exist, you can quickly find a solution to a system of linear equations.

A matrix is called inverse to a matrix if the following equalities hold.

If the determinant of a matrix is nonzero, then the matrix is called not particularly or non-degenerate.

For a matrix to have an inverse, it is necessary and sufficient that it be non-degenerate

Algorithm for finding the inverse matrix

Let we have a square matrix

and you need to find the opposite to it. To do this, follow these steps:

1. Find the determinant of the matrix. If it is not equal to zero, then we perform the following actions. Otherwise, this matrix is degenerate and for it there is no inverse

2. Find the algebraic complements of the elements of the matrix. They are equal to minors multiplied by the power of the sum of the row and column for which we are looking.

3. Construct a matrix from the algebraic complements of the elements of the matrix of the matrix and proto-transpose it. This matrix is called attached or allied and denoted.

4. Divide the attached matrix into determinants. The resulting matrix will be inverse and have the properties that are described at the beginning of the article.

Find the matrix inverse to the matrix (Dubovik V.P., Yurik I.I.

Finding the inverse matrix

"Higher mathematics. Collection of problems")

1) Find the determinant of the matrix

Since the determinant is not zero (), the inverse matrix exists. Find the matrix made up of algebraic complements

The complement matrix will take the form

We transpose it and get the attached

We divide it by a determinant and get the inverse

We see that in the case when the determinant is equal to one, the adjoint and inverse matrices coincide.

2) Calculate the determinant of the matrix

Find the matrix of algebraic complements

The final form of the complement matrix

We transpose it and find the union matrix

Find the inverse matrix

3) Let's calculate the determinant of the matrix. To do this, expand it into the first line. As a result, we obtain two nonzero terms

Find the matrix of algebraic complements. The schedule of the determinant is carried out in rows and columns in which there are more zero elements (marked in black).

The final form of the complement matrix is as follows.

We transpose it and find the associated matrix

Since the determinant of the matrix is equal to one, the inverse matrix coincides with the adjoint one. This example is back.

When calculating the inverse matrix, errors associated with incorrect signs when calculating the determinant and the complement matrix are typical.

Higher mathematics »Matrices and determinants» Inverse matrix »Calculation of the inverse matrix using algebraic additions.

Algorithm for calculating the inverse matrix using algebraic complements: the adjoint (adjoint) matrix method.

The matrix $ A ^ (- 1) $ is called inverse with respect to the square matrix $ A $ if the condition $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ is satisfied, where $ E $ Is the identity matrix, the order of which is equal to the order of the matrix $ A $.

Non-degenerate matrix - a matrix, the determinant of which is not equal to zero. Accordingly, a degenerate matrix is one for which the determinant is equal to zero.

The inverse matrix $ A ^ (- 1) $ exists if and only if the matrix $ A $ is non-degenerate. If the inverse matrix $ A ^ (- 1) $ exists, then it is unique.

There are several ways to find the inverse of a matrix, and we will look at two of them. This page will discuss the adjoint matrix method, which is considered standard in most higher mathematics courses. The second method for finding the inverse matrix (the method of elementary transformations), which involves the use of the Gauss method or the Gauss-Jordan method, is discussed in the second part.

The adjoint (adjoint) matrix method

Let the matrix $ A_ (n \ times n) $ be given. In order to find the inverse of $ A ^ (- 1) $, three steps are required:

Find the determinant of the matrix $ A $ and make sure that $ \ Delta A \ neq 0 $, i.e. that the matrix A is non-degenerate.
Make up the algebraic complements $ A_ (ij) $ of each element of the matrix $ A $ and write the matrix $ A_ (n \ times n) ^ (*) = \ left (A_ (ij) \ right) $ from the found algebraic complements.
Write the inverse matrix taking into account the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

The matrix $ (A ^ (*)) ^ T $ is often referred to as adjoined (reciprocal, adjoint) to the matrix $ A $.

If the solution is done manually, then the first method is good only for matrices of relatively small orders: the second (example No. 2), the third (example No. 3), the fourth (example No. 4). Other methods are used to find the inverse of a higher-order matrix. For example, the Gauss method, which is discussed in the second part.

Example # 1

Find the inverse of $ A = \ left (\ begin (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ end (array) \ right) $.

inverse matrix

Since all the elements of the fourth column are equal to zero, then $ \ Delta A = 0 $ (that is, the matrix $ A $ is degenerate). Since $ \ Delta A = 0 $, the matrix inverse to the matrix $ A $ does not exist.

Example No. 2

Find the inverse of the matrix $ A = \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $.

We use the adjoint matrix method. First, we find the determinant of the given matrix $ A $:

$$ \ Delta A = \ left | \ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Since $ \ Delta A \ neq 0 $, then the inverse matrix exists, therefore we will continue the solution. We find the algebraic complements of each element of a given matrix:

\ begin (aligned) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ end (aligned)

We compose a matrix from algebraic complements: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Transpose the resulting matrix: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (the resulting matrix is often referred to as the adjoint or adjoint matrix to the $ A $ matrix). Using the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, we have:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $$

So the inverse is found: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $ A ^ (- 1) \ cdot A = E $ or $ A \ cdot A ^ (- 1) = E $. Let us check the equality $ A ^ (- 1) \ cdot A = E $. In order to work less with fractions, we will substitute the matrix $ A ^ (- 1) $ not in the form $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, and as $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array ) \ right) $:

Answer: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $.

Example No. 3

Find the inverse of the matrix $ A = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $.

Let's start by calculating the determinant of the matrix $ A $. So, the determinant of the matrix $ A $ is as follows:

$$ \ Delta A = \ left | \ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right | = 18-36 + 56-12 = 26. $$

Since $ \ Delta A \ neq 0 $, then the inverse matrix exists, therefore we will continue the solution. We find the algebraic complements of each element of a given matrix:

We compose a matrix of algebraic complements and transpose it:

$$ A ^ * = \ left (\ begin (array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (array) \ right); \; (A ^ *) ^ T = \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $$

Using the formula $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, we get:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (array) \ right) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ end (array) \ right) $$

So $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \ end (array) \ right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $ A ^ (- 1) \ cdot A = E $ or $ A \ cdot A ^ (- 1) = E $. Let us check the equality $ A \ cdot A ^ (- 1) = E $. In order to work less with fractions, we will substitute the matrix $ A ^ (- 1) $ not in the form $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $, and as $ \ frac (1) (26) \ cdot \ left ( \ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

The check was successful, the inverse $ A ^ (- 1) $ was found correctly.

Answer: $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \ end (array) \ right) $.

Example No. 4

Find the inverse of $ A = \ left (\ begin (array) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ end (array) \ right) $.

For a fourth-order matrix, finding the inverse matrix using algebraic complements is somewhat difficult. However, such examples are found in test papers.

To find the inverse of a matrix, you first need to calculate the determinant of the matrix $ A $. The best way to do this in this situation is to expand the determinant by row (column). We select any row or column and find the algebraic complements of each element of the selected row or column.

For example, for the first line we get:

The determinant of the matrix $ A $ is calculated by the following formula:

$$ \ Delta A = a_ (11) \ cdot A_ (11) + a_ (12) \ cdot A_ (12) + a_ (13) \ cdot A_ (13) + a_ (14) \ cdot A_ (14) = 6 \ cdot 556 + (- 5) \ cdot (-300) +8 \ cdot (-536) +4 \ cdot (-112) = 100. $$

Algebraic Complement Matrix: $ A ^ * = \ left (\ begin (array) (cccc) 556 & -300 & -536 & -112 \\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96 \ end (array) \ right) $.

Joined matrix: $ (A ^ *) ^ T = \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) $

Inverse matrix:

$$ A ^ (- 1) = \ frac (1) (100) \ cdot \ left (\ begin (array) (cccc) 556 & -77 & -93 & 473 \\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463 \\ -112 & 4 & 36 & -96 \ end (array) \ right) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28 / 25 & 1/25 & 9/25 & -24/25 \ end (array) \ right) $$

Examination:

Consequently, the inverse matrix is found correctly.

Answer: $ A ^ (- 1) = \ left (\ begin (array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \ end (array) \ right ) $.

In the second part, a different way of finding the inverse matrix will be considered, which involves the use of transformations of the Gauss method or the Gauss-Jordan method.

Online classes in higher mathematics

Finding the inverse matrix

The matrix А-1 is called the inverse matrix with respect to the matrix if А * А-1 =, where is the identity matrix of the th order. An inverse matrix can only exist for square matrices.

see also Inverse matrix by the Jordan-Gauss method

Algorithm for finding the inverse matrix

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Finding the transposed matrix AT.
Definition of algebraic complements. Replace each element of the matrix with its algebraic complement.
Composing an inverse matrix from algebraic additions: each element of the resulting matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Definition of algebraic complements.
Filling the union (reciprocal, adjoint) matrix.
Composing an inverse matrix from algebraic complements: each element of the adjoint matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Example # 1. Let's write the matrix as follows:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Then inverse matrix can be written as:

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Another algorithm for finding the inverse matrix

Let us give another scheme for finding the inverse matrix.

Find the determinant of the given square matrix.
Find the algebraic complements to all elements of the matrix.
We write the algebraic complements of row elements into columns (transposition).
We divide each element of the resulting matrix by the determinant of the matrix.

As you can see, the transposition operation can be applied both at the beginning, over the original matrix, and at the end, over the obtained algebraic complements.

To check, make sure that A-1A = E.

Instruction. To obtain a solution, it is necessary to set the dimension of the matrix. Next, in a new dialog box, fill in the matrix.

The matrix А -1 is called the inverse matrix with respect to the matrix А if А * А -1 = Е, where Е is the n-th order unit matrix. An inverse matrix can only exist for square matrices.

Service purpose... With the help of this service online, you can find algebraic complements, transposed matrix A T, adjoint matrix and inverse matrix. The solution is carried out directly on the website (online) and is free of charge. The calculation results are presented in a Word report and in Excel format (i.e. it is possible to check the solution). see design example.

Instruction. To obtain a solution, it is necessary to set the dimension of the matrix. Next, in a new dialog box, fill in the matrix A.

See also Inverse matrix using the Jordan-Gauss method

Algorithm for finding the inverse matrix

Finding the transposed matrix A T.
Definition of algebraic complements. Replace each element of the matrix with its algebraic complement.
Composing an inverse matrix from algebraic additions: each element of the resulting matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.

Next inverse matrix algorithm is similar to the previous one, except for some steps: first, the algebraic complements are calculated, and then the adjoint matrix C is determined.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix A. If it is not equal to zero, we continue the solution; otherwise, the inverse matrix does not exist.
Definition of algebraic complements.
Filling the union (reciprocal, adjoint) matrix C.
Composing an inverse matrix from algebraic complements: each element of the adjoint matrix C is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
A check is made: the original and the resulting matrices are multiplied. The result should be the identity matrix.

Example # 1. Let's write the matrix as follows:

Algebraic complements. ∆ 1,2 = - (2 4 - (- 2 (-2))) = -4 ∆ 2,1 = - (2 4-5 3) = 7 ∆ 2,3 = - (- 1 5 - (- 2 2)) = 1 ∆ 3.2 = - (- 1 (-2) -2 3) = 4

A -1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Another algorithm for finding the inverse matrix

Let us give another scheme for finding the inverse matrix.

Find the determinant of the given square matrix A.
Find the algebraic complements to all elements of the matrix A.
We write the algebraic complements of row elements into columns (transposition).
We divide each element of the resulting matrix by the determinant of the matrix A.

As you can see, the transposition operation can be applied both at the beginning, over the original matrix, and at the end, over the obtained algebraic complements.

A special case: The inverse of the identity matrix E is the identity matrix E.

We continue talking about actions with matrices. Namely - in the course of studying this lecture, you will learn how to find the inverse matrix. Learn. Even if math is tight.

What is an inverse matrix? Here you can draw an analogy with reciprocal numbers: consider, for example, the optimistic number 5 and its inverse. The product of these numbers is equal to one:. With matrices, everything is similar! The product of a matrix by its inverse matrix is - identity matrix, which is the matrix analogue of a numeric unit. However, first things first, we will solve an important practical issue, namely, we will learn how to find this very inverse matrix.

What do you need to know and be able to do to find the inverse matrix? You must be able to decide determinants... You must understand what it is matrix and be able to perform some actions with them.

There are two main methods for finding the inverse of a matrix:
by using algebraic complements and using elementary transformations.

Today we will explore the first, easier way.

Let's start with the most terrible and incomprehensible. Consider square matrix. The inverse matrix can be found by the following formula:

Where is the determinant of the matrix, is the transposed matrix of the algebraic complements of the corresponding elements of the matrix.

The concept of an inverse matrix exists only for square matrices, matrices "two by two", "three by three", etc.

Designations: As you probably already noticed, the inverse of the matrix is indicated by a superscript

Let's start with the simplest case - a two-by-two matrix. Most often, of course, "three by three" is required, but, nevertheless, I strongly recommend studying a simpler task in order to master the general principle of the solution.

Example:

Find the inverse of a matrix

We decide. The sequence of actions can be conveniently broken down into points.

1) First, find the determinant of the matrix.

If your understanding of this action is not good enough, read the material How to calculate the determinant?

Important! In the event that the determinant of the matrix is ZERO- inverse matrix DOES NOT EXIST.

In the example under consideration, as it turned out, which means that everything is in order.

2) Find the matrix of minors.

To solve our problem, it is not necessary to know what a minor is, however, it is advisable to read the article How to calculate the determinant.

The matrix of minors has the same dimensions as the matrix, that is, in this case.
The matter is small, it remains to find four numbers and put them instead of asterisks.

Back to our matrix
Let's look at the top-left element first:

How to find it minor?
And this is done like this: THINKINGLY cross out the row and column in which this element is located:

The remaining number is minor of this element, which we write into our matrix of minors:

Consider the following matrix element:

We mentally cross out the row and column in which this element is located:

What is left is the minor of this element, which we write into our matrix:

Similarly, we consider the elements of the second line and find their minors:

Ready.

It's simple. In the matrix of minors, you need CHANGE SIGNS two numbers:

These are the numbers that I have circled!

- a matrix of algebraic complements of the corresponding elements of the matrix.

And it's just ...

4) Find the transposed matrix of algebraic complements.

- transposed matrix of algebraic complements of the corresponding elements of the matrix.

5) Answer.

Remembering our formula
Everything is found!

So the inverse of the matrix is:

The answer is best left as it is. NOT NECESSARY divide each element of the matrix by 2, since you get fractional numbers. This nuance is discussed in more detail in the same article. Matrix operations.

How can I check the solution?

It is necessary to perform matrix multiplication or

Examination:

The already mentioned identity matrix Is a matrix with ones on main diagonal and zeros elsewhere.

Thus, the inverse is correct.

If you carry out an action, then the result will also be the identity matrix. This is one of the few cases where matrix multiplication is permutable, more information can be found in the article Properties of operations on matrices. Matrix expressions... Also note that during the check, the constant (fraction) is brought forward and processed at the very end - after matrix multiplication. This is a standard technique.

Let's move on to a more common case in practice - the "three by three" matrix:

Example:

Find the inverse of a matrix

The algorithm is exactly the same as for the two-by-two case.

We find the inverse matrix by the formula:, where is the transposed matrix of algebraic complements of the corresponding elements of the matrix.

1) Find the determinant of the matrix.

Here the determinant is revealed on the first line.

Also, do not forget that, which means that everything is fine - inverse matrix exists.

2) Find the matrix of minors.

Minors matrix has a dimension "three by three" and we need to find nine numbers.

I'll go into a couple of minor details in detail:

Consider the following matrix element:

THOUGHTLY cross out the row and column in which this element is located:

The remaining four numbers are written into the determinant "two by two"

This qualifier is "two by two" and is the minor of this element... It needs to be calculated:

That's it, the minor is found, we write it into our matrix of minors:

As you may have guessed, there are nine two-by-two determinants to be computed. The process, of course, is dreary, but the case is not the most difficult, it can be worse.

Well, to consolidate - finding another minor in the pictures:

Try to calculate the rest of the minors yourself.

Final Result:
- the matrix of the minors of the corresponding elements of the matrix.

The fact that all the minors turned out to be negative is pure coincidence.

3) Find the matrix of algebraic complements.

In the matrix of minors, it is necessary CHANGE SIGNS strictly for the following elements:

In this case:

We do not consider finding the inverse matrix for the “four by four” matrix, since such a task can only be given by a sadistic teacher (so that the student calculates one determinant “four by four” and 16 determinants “three by three”). In my practice, I met only one such case, and the customer of the test paid for my torment quite dearly =).

In a number of textbooks, manuals, you can find a slightly different approach to finding the inverse matrix, however, I recommend using the above solution algorithm. Why? Because the likelihood of getting confused in calculations and signs is much less.

This topic is one of the most hated among students. Only determinants are probably worse.

The trick is that the very concept of an inverse element (and I'm not just talking about matrices now) refers us to the operation of multiplication. Even in the school curriculum, multiplication is considered a complex operation, and matrix multiplication is generally a separate topic, which I have devoted a whole paragraph and video tutorial to.

We won't go into the details of matrix calculations today. Just remember: how matrices are denoted, how they are multiplied and what follows from this.

Repetition: matrix multiplication

First of all, let's agree on the notation. A matrix $ A $ of size $ \ left [m \ times n \ right] $ is simply a table of numbers, in which there are exactly $ m $ rows and $ n $ columns:

\ = \ underbrace (\ left [\ begin (matrix) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) \\ (( a) _ (21)) & ((a) _ (22)) & ... & ((a) _ (2n)) \\ ... & ... & ... & ... \\ ((a) _ (m1)) & ((a) _ (m2)) & ... & ((a) _ (mn)) \\\ end (matrix) \ right]) _ (n) \]

In order not to accidentally confuse rows and columns in places (believe me, you can mix up a 1 with a 2 in the exam - what can we say about some lines there), just take a look at the picture:

Determination of indices for matrix cells

What's happening? If you place the standard coordinate system $ OXY $ in the upper left corner and direct the axes so that they cover the entire matrix, then each cell of this matrix can be uniquely associated with the coordinates $ \ left (x; y \ right) $ - this will be the row number and column number.

Why is the coordinate system located in the upper left corner? Because it is from there that we begin to read any texts. It's very easy to remember.

Why is the $ x $ axis directed downwards and not to the right? Again, everything is simple: take the standard coordinate system (the $ x $ axis goes to the right, the $ y $ axis goes up) and rotate it so that it encloses the matrix. This is a 90 degree clockwise rotation - we can see its result in the picture.

In general, we figured out how to determine the indices of the matrix elements. Now let's deal with multiplication.

Definition. Matrices $ A = \ left [m \ times n \ right] $ and $ B = \ left [n \ times k \ right] $, when the number of columns in the first is the same as the number of rows in the second, are called consistent.

In that order. You can be confused and say, they say, the matrices $ A $ and $ B $ form an ordered pair $ \ left (A; B \ right) $: if they are consistent in this order, then it is completely unnecessary that $ B $ and $ A $, those. the pair $ \ left (B; A \ right) $ is also matched.

Only matched matrices can be multiplied.

Definition. The product of matched matrices $ A = \ left [m \ times n \ right] $ and $ B = \ left [n \ times k \ right] $ is a new matrix $ C = \ left [m \ times k \ right] $ , whose elements $ ((c) _ (ij)) $ are calculated by the formula:

\ [((c) _ (ij)) = \ sum \ limits_ (k = 1) ^ (n) (((a) _ (ik))) \ cdot ((b) _ (kj)) \]

In other words: to get the element $ ((c) _ (ij)) $ of the matrix $ C = A \ cdot B $, you need to take the $ i $-row of the first matrix, the $ j $ -th column of the second matrix, and then multiply in pairs elements from this row and column. Add up the results.

Yes, that's such a harsh definition. Several facts immediately follow from it:

Matrix multiplication, generally speaking, is non-commutative: $ A \ cdot B \ ne B \ cdot A $;
However, multiplication is associative: $ \ left (A \ cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ right) $;
And even distributively: $ \ left (A + B \ right) \ cdot C = A \ cdot C + B \ cdot C $;
And again distributively: $ A \ cdot \ left (B + C \ right) = A \ cdot B + A \ cdot C $.

The distributivity of multiplication had to be described separately for the left and right multiplier-sum, precisely because of the non-commutativity of the multiplication operation.

If, nevertheless, it turns out that $ A \ cdot B = B \ cdot A $, such matrices are called permutation matrices.

Among all the matrices that are multiplied there by something, there are special ones - those that, when multiplied by any matrix $ A $, again give $ A $:

Definition. Matrix $ E $ is called identity if $ A \ cdot E = A $ or $ E \ cdot A = A $. In the case of a square matrix $ A $ we can write:

The unit matrix is a frequent guest when solving matrix equations. And in general, a frequent visitor to the world of matrices. :)

And also because of this $ E $, someone came up with all the game that will be written next.

What is inverse matrix

Since matrix multiplication is a very time consuming operation (you have to multiply a bunch of rows and columns), the concept of an inverse matrix is also not the most trivial one. And requiring some explanation.

Key definition

Well, it's time to learn the truth.

Definition. The matrix $ B $ is called inverse to the matrix $ A $ if

The inverse matrix is denoted by $ ((A) ^ (- 1)) $ (not to be confused with the degree!), So the definition can be rewritten as follows:

It would seem that everything is extremely simple and clear. But when analyzing such a definition, several questions immediately arise:

Does an inverse matrix always exist? And if not always, then how to determine: when it exists and when it does not?
And who said that there is exactly one such matrix? What if for some initial matrix $ A $ there is a whole crowd of inverse ones?
What do all these reverse look like? And how, in fact, are they to be counted?

As for the calculation algorithms - we will talk about this a little later. But we will answer the rest of the questions right now. Let us form them in the form of separate statements-lemmas.

Basic properties

Let's start with what the matrix $ A $ should look like in order for it to have $ ((A) ^ (- 1)) $. Now we will make sure that both of these matrices must be square, and of the same size: $ \ left [n \ times n \ right] $.

Lemma 1. Given a matrix $ A $ and its inverse $ ((A) ^ (- 1)) $. Then both of these matrices are square, with the same order $ n $.

Proof. It's simple. Let the matrix $ A = \ left [m \ times n \ right] $, $ ((A) ^ (- 1)) = \ left [a \ times b \ right] $. Since the product $ A \ cdot ((A) ^ (- 1)) = E $ exists by definition, the matrices $ A $ and $ ((A) ^ (- 1)) $ are matched in the indicated order:

\ [\ begin (align) & \ left [m \ times n \ right] \ cdot \ left [a \ times b \ right] = \ left [m \ times b \ right] \\ & n = a \ end ( align) \]

This is a direct consequence of the matrix multiplication algorithm: the coefficients $ n $ and $ a $ are "transitory" and must be equal.

At the same time, the inverse multiplication is also defined: $ ((A) ^ (- 1)) \ cdot A = E $, therefore the matrices $ ((A) ^ (- 1)) $ and $ A $ are also matched in the indicated order:

\ [\ begin (align) & \ left [a \ times b \ right] \ cdot \ left [m \ times n \ right] = \ left [a \ times n \ right] \\ & b = m \ end ( align) \]

Thus, without loss of generality, we can assume that $ A = \ left [m \ times n \ right] $, $ ((A) ^ (- 1)) = \ left [n \ times m \ right] $. However, according to the definition, $ A \ cdot ((A) ^ (- 1)) = ((A) ^ (- 1)) \ cdot A $, so the sizes of the matrices are strictly the same:

\ [\ begin (align) & \ left [m \ times n \ right] = \ left [n \ times m \ right] \\ & m = n \ end (align) \]

So it turns out that all three matrices - $ A $, $ ((A) ^ (- 1)) $ and $ E $ - are square sizes $ \ left [n \ times n \ right] $. The lemma is proved.

Well, that's not bad already. We see that only square matrices are invertible. Now let's make sure that the inverse is always the same.

Lemma 2. Given a matrix $ A $ and its inverse $ ((A) ^ (- 1)) $. Then this inverse is the only one.

Proof. Let's go from the contrary: let the matrix $ A $ have at least two copies of its inverse - $ B $ and $ C $. Then, according to the definition, the following equalities are true:

\ [\ begin (align) & A \ cdot B = B \ cdot A = E; \\ & A \ cdot C = C \ cdot A = E. \\ \ end (align) \]

From Lemma 1 we conclude that all four matrices - $ A $, $ B $, $ C $ and $ E $ - are square of the same order: $ \ left [n \ times n \ right] $. Therefore, the product is defined:

Since matrix multiplication is associative (but not commutative!), We can write:

\ [\ begin (align) & B \ cdot A \ cdot C = \ left (B \ cdot A \ right) \ cdot C = E \ cdot C = C; \\ & B \ cdot A \ cdot C = B \ cdot \ left (A \ cdot C \ right) = B \ cdot E = B; \\ & B \ cdot A \ cdot C = C = B \ Rightarrow B = C. \\ \ end (align) \]

We got the only possible option: two copies of the inverse matrix are equal. The lemma is proved.

The above reasoning repeats almost word for word the proof of the uniqueness of the inverse for all real numbers $ b \ ne 0 $. The only essential addition is taking into account the dimension of the matrices.

However, we still do not know anything about whether any square matrix is invertible. Here the determinant comes to our aid - this is a key characteristic for all square matrices.

Lemma 3. You are given a matrix $ A $. If its inverse matrix $ ((A) ^ (- 1)) $ exists, then the determinant of the original matrix is nonzero:

\ [\ left | A \ right | \ ne 0 \]

Proof. We already know that $ A $ and $ ((A) ^ (- 1)) $ are square matrices of size $ \ left [n \ times n \ right] $. Therefore, for each of them, you can calculate the determinant: $ \ left | A \ right | $ and $ \ left | ((A) ^ (- 1)) \ right | $. However, the determinant of the product is equal to the product of the determinants:

\ [\ left | A \ cdot B \ right | = \ left | A \ right | \ cdot \ left | B \ right | \ Rightarrow \ left | A \ cdot ((A) ^ (- 1)) \ right | = \ left | A \ right | \ cdot \ left | ((A) ^ (- 1)) \ right | \]

But according to the definition, $ A \ cdot ((A) ^ (- 1)) = E $, and the determinant of $ E $ is always 1, therefore

\ [\ begin (align) & A \ cdot ((A) ^ (- 1)) = E; \\ & \ left | A \ cdot ((A) ^ (- 1)) \ right | = \ left | E \ right |; \\ & \ left | A \ right | \ cdot \ left | ((A) ^ (- 1)) \ right | = 1. \\ \ end (align) \]

The product of two numbers is equal to one only if each of these numbers is different from zero:

\ [\ left | A \ right | \ ne 0; \ quad \ left | ((A) ^ (- 1)) \ right | \ ne 0. \]

So it turns out that $ \ left | A \ right | \ ne 0 $. The lemma is proved.

In fact, this requirement is quite logical. Now we will analyze the algorithm for finding the inverse matrix - and it will become quite clear why, with a zero determinant, no inverse matrix, in principle, can exist.

But first, let's formulate an "auxiliary" definition:

Definition. A degenerate matrix is a square matrix of size $ \ left [n \ times n \ right] $, whose determinant is zero.

Thus, we can assert that every invertible matrix is non-degenerate.

How to find the inverse of a matrix

Now we will consider a universal algorithm for finding inverse matrices. In general, there are two generally accepted algorithms, and we will also consider the second one today.

The one that will be discussed now is very efficient for matrices of size $ \ left [2 \ times 2 \ right] $ and - partially - of size $ \ left [3 \ times 3 \ right] $. But starting from the size $ \ left [4 \ times 4 \ right] $ it is better not to use it. Why - now you yourself will understand everything.

Algebraic complements

Get ready. There will be pain now. No, do not worry: a beautiful nurse in a skirt, stockings with laces and will not give you an injection in the buttock. Everything is much more prosaic: algebraic additions and Her Majesty "Union Matrix" are coming to you.

Let's start with the main thing. Let there be a square matrix of size $ A = \ left [n \ times n \ right] $, whose elements are named $ ((a) _ (ij)) $. Then, for each such element, an algebraic complement can be defined:

Definition. Algebraic complement $ ((A) _ (ij)) $ to the element $ ((a) _ (ij)) $ located in the $ i $ -th row and $ j $ -th column of the matrix $ A = \ left [n \ times n \ right] $ is a construction of the form

\ [((A) _ (ij)) = ((\ left (-1 \ right)) ^ (i + j)) \ cdot M_ (ij) ^ (*) \]

Where $ M_ (ij) ^ (*) $ is the determinant of the matrix obtained from the original $ A $ by deleting the same $ i $ -th row and $ j $ -th column.

Again. The algebraic complement to the matrix element with coordinates $ \ left (i; j \ right) $ is denoted as $ ((A) _ (ij)) $ and is calculated according to the scheme:

First, delete the $ i $ -line and the $ j $ -th column from the original matrix. We get a new square matrix, and we denote its determinant as $ M_ (ij) ^ (*) $.
Then we multiply this determinant by $ ((\ left (-1 \ right)) ^ (i + j)) $ - at first this expression may seem brain-boring, but in fact we are just finding out the sign in front of $ M_ (ij) ^ (*) $.
We count - we get a specific number. Those. the algebraic complement is exactly a number, not some new matrix, etc.

The matrix $ M_ (ij) ^ (*) $ itself is called the complementary minor to the element $ ((a) _ (ij)) $. And in this sense, the above definition of an algebraic complement is a special case of a more complex definition - what we considered in the lesson about the determinant.

Important note. Generally, in "adult" mathematics, algebraic additions are defined as follows:

We take $ k $ rows and $ k $ columns in a square matrix. At their intersection, we get a matrix of size $ \ left [k \ times k \ right] $ - its determinant is called the minor of order $ k $ and is denoted by $ ((M) _ (k)) $.

Then we delete these "favorites" $ k $ lines and $ k $ columns. Again, we get a square matrix - its determinant is called the complementary minor and is denoted $ M_ (k) ^ (*) $.

Multiply $ M_ (k) ^ (*) $ by $ ((\ left (-1 \ right)) ^ (t)) $, where $ t $ is (now attention!) The sum of the numbers of all selected lines and columns ... This will be the algebraic addition.

Take a look at the third step: there is actually a sum of $ 2k $ terms! Another thing is that for $ k = 1 $ we get only 2 terms - these will be the same $ i + j $ - "coordinates" of the element $ ((a) _ (ij)) $, for which we are looking for an algebraic complement.

Thus, today we use a slightly simplified definition. But as we will see later, it will be more than enough. The next thing is much more important:

Definition. The adjoint matrix $ S $ to the square matrix $ A = \ left [n \ times n \ right] $ is a new matrix of size $ \ left [n \ times n \ right] $, which is obtained from $ A $ by replacing $ (( a) _ (ij)) $ algebraic complements $ ((A) _ (ij)) $:

\\ Rightarrow S = \ left [\ begin (matrix) ((A) _ (11)) & ((A) _ (12)) & ... & ((A) _ (1n)) \\ (( A) _ (21)) & ((A) _ (22)) & ... & ((A) _ (2n)) \\ ... & ... & ... & ... \\ ((A) _ (n1)) & ((A) _ (n2)) & ... & ((A) _ (nn)) \\\ end (matrix) \ right] \]

The first thought that arises at the moment of realizing this definition is "this is how much you have to count!" Relax: you will have to count, but not so much. :)

Well, this is all very nice, but why is it necessary? Here's why.

The main theorem

Let's go back a little. Remember, in Lemma 3 it was stated that an invertible matrix $ A $ is always non-degenerate (that is, its determinant is nonzero: $ \ left | A \ right | \ ne 0 $).

So, the opposite is also true: if the matrix $ A $ is not degenerate, then it is always invertible. And there is even a search scheme $ ((A) ^ (- 1)) $. Check it out:

The inverse matrix theorem. Let a square matrix $ A = \ left [n \ times n \ right] $ be given, and its determinant is nonzero: $ \ left | A \ right | \ ne 0 $. Then the inverse matrix $ ((A) ^ (- 1)) $ exists and is calculated by the formula:

\ [((A) ^ (- 1)) = \ frac (1) (\ left | A \ right |) \ cdot ((S) ^ (T)) \]

And now - everything is the same, but in legible handwriting. To find the inverse of a matrix, you need:

Calculate determinant $ \ left | A \ right | $ and make sure it is nonzero.
Construct the union matrix $ S $, i.e. count 100500 algebraic complements $ ((A) _ (ij)) $ and place them in place of $ ((a) _ (ij)) $.
Transpose this matrix $ S $, and then multiply it by some number $ q = (1) / (\ left | A \ right |) \; $.

And that's it! The inverse matrix $ ((A) ^ (- 1)) $ is found. Let's take a look at examples:

\ [\ left [\ begin (matrix) 3 & 1 \\ 5 & 2 \\\ end (matrix) \ right] \]

Solution. Let's check the reversibility. Let's calculate the determinant:

\ [\ left | A \ right | = \ left | \ begin (matrix) 3 & 1 \\ 5 & 2 \\\ end (matrix) \ right | = 3 \ cdot 2-1 \ cdot 5 = 6-5 = 1 \]

The determinant is nonzero. Hence, the matrix is invertible. Let's compose the union matrix:

Let's count the algebraic additions:

\ [\ begin (align) & ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | 2 \ right | = 2; \\ & ((A) _ (12)) = ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ left | 5 \ right | = -5; \\ & ((A) _ (21)) = ((\ left (-1 \ right)) ^ (2 + 1)) \ cdot \ left | 1 \ right | = -1; \\ & ((A) _ (22)) = ((\ left (-1 \ right)) ^ (2 + 2)) \ cdot \ left | 3 \ right | = 3. \\ \ end (align) \]

Please note: determinants | 2 |, | 5 |, | 1 | and | 3 | - these are the determinants of matrices of size $ \ left [1 \ times 1 \ right] $, not modules. Those. if the determinants contained negative numbers, it is not necessary to remove the "minus".

In total, our union matrix looks like this:

\ [((A) ^ (- 1)) = \ frac (1) (\ left | A \ right |) \ cdot ((S) ^ (T)) = \ frac (1) (1) \ cdot ( (\ left [\ begin (array) (* (35) (r)) 2 & -5 \\ -1 & 3 \\\ end (array) \ right]) ^ (T)) = \ left [\ begin (array) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (array) \ right] \]

So that is all. The problem has been solved.

Answer. $ \ left [\ begin (array) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (array) \ right] $

Task. Find the inverse of the matrix:

\ [\ left [\ begin (array) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (array) \ right] \]

Solution. Again we consider the determinant:

\ [\ begin (align) & \ left | \ begin (array) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (array) \ right | = \ begin (matrix ) \ left (1 \ cdot 2 \ cdot 1+ \ left (-1 \ right) \ cdot \ left (-1 \ right) \ cdot 1 + 2 \ cdot 0 \ cdot 0 \ right) - \\ - \ left (2 \ cdot 2 \ cdot 1+ \ left (-1 \ right) \ cdot 0 \ cdot 1 + 1 \ cdot \ left (-1 \ right) \ cdot 0 \ right) \\\ end (matrix) = \ \ & = \ left (2 + 1 + 0 \ right) - \ left (4 + 0 + 0 \ right) = - 1 \ ne 0. \\ \ end (align) \]

The determinant is nonzero - the matrix is invertible. But now there will be the most tough: you need to count as many as 9 (nine, damn them!) Algebraic additions. And each of them will contain the qualifier $ \ left [2 \ times 2 \ right] $. Flew:

\ [\ begin (matrix) ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (matrix) 2 & -1 \\ 0 & 1 \\\ end (matrix) \ right | = 2; \\ ((A) _ (12)) = ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ left | \ begin (matrix) 0 & -1 \\ 1 & 1 \\\ end (matrix) \ right | = -1; \\ ((A) _ (13)) = ((\ left (-1 \ right)) ^ (1 + 3)) \ cdot \ left | \ begin (matrix) 0 & 2 \\ 1 & 0 \\\ end (matrix) \ right | = -2; \\ ... \\ ((A) _ (33)) = ((\ left (-1 \ right)) ^ (3 + 3)) \ cdot \ left | \ begin (matrix) 1 & -1 \\ 0 & 2 \\\ end (matrix) \ right | = 2; \\ \ end (matrix) \]

In short, the union matrix will look like this:

Therefore, the inverse of the matrix will be like this:

\ [((A) ^ (- 1)) = \ frac (1) (- 1) \ cdot \ left [\ begin (matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\ end (matrix) \ right] = \ left [\ begin (array) (* (35) (r)) - 2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\ end (array) \ right] \]

Well, that's all. Here is the answer.

Answer. $ \ left [\ begin (array) (* (35) (r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\ end (array) \ right ] $

As you can see, at the end of each example, we ran a check. In this regard, an important note:

Don't be lazy to check. Multiply the original matrix by the found inverse - you should get $ E $.

This check is much easier and faster than looking for an error in further calculations, when, for example, you are solving a matrix equation.

Alternative way

As I said, the inverse matrix theorem works great for the sizes $ \ left [2 \ times 2 \ right] $ and $ \ left [3 \ times 3 \ right] $ (in the latter case, it’s not so “great "), But for large matrices, sadness begins.

But do not worry: there is an alternative algorithm, which can be used to calmly find the inverse even for the matrix $ \ left [10 \ times 10 \ right] $. But, as is often the case, to consider this algorithm, we need a little theoretical background.

Elementary transformations

Among the various transformations of the matrix, there are several special ones - they are called elementary. There are exactly three such transformations:

Multiplication. You can take the $ i $ th row (column) and multiply it by any number $ k \ ne 0 $;
Addition. Add to the $ i $ th row (column) any other $ j $ th row (column) multiplied by any number $ k \ ne 0 $ (you can, of course, and $ k = 0 $, but what's the point ? Nothing will change though).
Rearrangement. Take the $ i $ th and $ j $ th rows (columns) and swap them.

Why these transformations are called elementary (for large matrices they do not look so elementary) and why there are only three of them - these questions are beyond the scope of today's lesson. Therefore, we will not go into details.

Another thing is important: we have to perform all these perversions on the attached matrix. Yes, yes: you heard right. Now there will be one more definition - the last one in today's lesson.

Attached matrix

Surely at school you solved systems of equations using the addition method. Well, there, subtract another from one string, multiply some string by a number - that's all.

So: now everything will be the same, but already "in an adult way." Ready?

Definition. Let the matrix $ A = \ left [n \ times n \ right] $ and the identity matrix $ E $ of the same size $ n $ be given. Then the adjoint matrix $ \ left [A \ left | E \ right. \ right] $ is a new $ \ left [n \ times 2n \ right] $ matrix that looks like this:

\ [\ left [A \ left | E \ right. \ right] = \ left [\ begin (array) (rrrr | rrrr) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) & 1 & 0 & ... & 0 \\ ((a) _ (21)) & ((a) _ (22)) & ... & ((a) _ (2n)) & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... \\ ((a) _ (n1)) & ((a) _ (n2)) & ... & ((a) _ (nn)) & 0 & 0 & ... & 1 \\\ end (array) \ right] \]

In short, we take the matrix $ A $, on the right we assign to it the identity matrix $ E $ of the required size, separate them with a vertical bar for beauty - here's the adjoined one. :)

What's the catch? Here's what:

Theorem. Let the matrix $ A $ be invertible. Consider the adjoint matrix $ \ left [A \ left | E \ right. \ right] $. If using elementary string conversions bring it to the form $ \ left [E \ left | B \ right. \ right] $, i.e. by multiplying, subtracting and rearranging the rows to get from $ A $ the matrix $ E $ on the right, then the matrix $ B $ obtained on the left is the inverse of $ A $:

\ [\ left [A \ left | E \ right. \ right] \ to \ left [E \ left | B \ right. \ right] \ Rightarrow B = ((A) ^ (- 1)) \]

It's that simple! In short, the algorithm for finding the inverse matrix looks like this:

Write the appended matrix $ \ left [A \ left | E \ right. \ right] $;
Perform elementary string conversions until $ E $ appears instead of $ A $;
Of course, something will also appear on the left - some matrix $ B $. This will be the opposite;
PROFIT! :)

Of course, this is much easier said than done. So let's look at a couple of examples: for sizes $ \ left [3 \ times 3 \ right] $ and $ \ left [4 \ times 4 \ right] $.

Task. Find the inverse of the matrix:

\ [\ left [\ begin (array) (* (35) (r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\ end (array) \ right] \ ]

Solution. We compose the attached matrix:

\ [\ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\ end (array) \ right] \]

Since the last column of the original matrix is filled with ones, let's subtract the first row from the rest:

\ [\ begin (align) & \ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\ end (array) \ right] \ begin (matrix) \ downarrow \\ -1 \\ -1 \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end (array) \ right] \\ \ end (align) \]

There are no more ones, except for the first line. But we do not touch it, otherwise in the third column the newly removed units will begin to “multiply”.

But we can subtract the second line twice from the last - we get one in the lower left corner:

\ [\ begin (align) & \ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end (array) \ right] \ begin (matrix) \ \\ \ downarrow \\ -2 \\\ end (matrix) \ to \\ & \ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \\ \ end (align) \]

Now we can subtract the last row from the first and twice from the second - this way we "zero" the first column:

\ [\ begin (align) & \ left [\ begin (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \ begin (matrix) -1 \\ -2 \\ \ uparrow \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \\ \ end (align) \]

Multiply the second row by −1, and then subtract it 6 times from the first and add it 1 time to the last:

\ [\ begin (align) & \ left [\ begin (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \ begin (matrix) \ \\ \ left | \ cdot \ left (-1 \ right) \ right. \\ \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \ begin (matrix) -6 \\ \ updownarrow \\ +1 \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrr | rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\ end (array) \ right] \\ \ end (align) \]

All that remains is to swap lines 1 and 3:

\ [\ left [\ begin (array) (rrr | rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\ end (array) \ right] \]

Ready! On the right is the desired inverse matrix.

Answer. $ \ left [\ begin (array) (* (35) (r)) 4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\ end (array) \ right ] $

Task. Find the inverse of the matrix:

\ [\ left [\ begin (matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\ end (matrix) \ right] \]

Solution. Again, we compose the attached:

\ [\ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (array) \ right] \]

Let's get a little sleepy, grieve over how much we have to count now ... and start counting. First, let's zero the first column by subtracting row 1 from rows 2 and 3:

\ [\ begin (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (array) \ right] \ begin (matrix) \ downarrow \\ -1 \\ -1 \\ \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (array) \ right] \\ \ end (align) \]

We see too many "cons" in lines 2-4. Multiply all three rows by −1, and then burn out the third column by subtracting row 3 from the rest:

\ [\ begin (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \ end (array) \ right] \ begin (matrix) \ \\ \ left | \ cdot \ left (-1 \ right) \ right. \\ \ left | \ cdot \ left (-1 \ right) \ right. \\ \ left | \ cdot \ left (-1 \ right) \ right. \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\ end (array) \ right] \ begin (matrix) -2 \\ -1 \\ \ updownarrow \\ -2 \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (array) \ right] \\ \ end (align) \]

Now is the time to "fry" the last column of the original matrix: subtract row 4 from the rest:

\ [\ begin (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (array ) \ right] \ begin (matrix) +1 \\ -3 \\ -2 \\ \ uparrow \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (array) \ right] \\ \ end (align) \]

Final Roll: Burn out the second column by subtracting row 2 from rows 1 and 3:

\ [\ begin (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end ( array) \ right] \ begin (matrix) 6 \\ \ updownarrow \\ -5 \\ \ \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (array) \ right] \\ \ end (align) \]

And again on the left is the identity matrix, which means the inverse is on the right. :)

Answer. $ \ left [\ begin (matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\ end (matrix) \ right] $

So that is all. Check it yourself - scrap it for me. :)

In this article, we will talk about the matrix method for solving a system of linear algebraic equations, find its definition and give examples of the solution.

Definition 1

Inverse matrix method is a method used to solve a SLAE in the event that the number of unknowns is equal to the number of equations.

Example 1

Find a solution to a system of n linear equations with n unknowns:

a 11 x 1 + a 12 x 2 +. ... ... + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 +. ... ... + a n n x n = b n

Matrix type of recording : A × X = B

where A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n is the matrix of the system.

X = x 1 x 2 ⋮ x n - column of unknowns,

B = b 1 b 2 ⋮ b n - column of free coefficients.

From the equation we got, you need to express X. To do this, you need to multiply both sides of the matrix equation on the left by A - 1:

A - 1 × A × X = A - 1 × B.

Since A - 1 × A = E, then E × X = A - 1 × B or X = A - 1 × B.

Comment

The inverse matrix to the matrix A has the right to exist only if the condition d e t A is not equal to zero. Therefore, when solving SLAE by the inverse matrix method, first of all, d e t A.

If d e t A is not equal to zero, the system has only one solution: using the inverse matrix method. If d e t А = 0, then the system cannot be solved by this method.

An example of solving a system of linear equations using the inverse matrix method

Example 2

We solve the SLAE by the inverse matrix method:

2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2

How to solve?

We write the system in the form of a matrix equation A X = B, where

A = 2 - 4 3 1 - 2 4 3 - 1 5, X = x 1 x 2 x 3, B = 1 3 2.

We express from this equation X:

Find the determinant of the matrix A:

det A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25

d e t А is not equal to 0, therefore, the inverse matrix solution method is suitable for this system.

Find the inverse matrix A - 1 using the union matrix. We calculate the algebraic complements A i j to the corresponding elements of the matrix A:

A 11 = (- 1) (1 + 1) - 2 4 - 1 5 = - 10 + 4 = - 6,

A 12 = (- 1) 1 + 2 1 4 3 5 = - (5 - 12) = 7,

A 13 = (- 1) 1 + 3 1 - 2 3 - 1 = - 1 + 6 = 5,

A 21 = (- 1) 2 + 1 - 4 3 - 1 5 = - (- 20 + 3) = 17,

A 22 = (- 1) 2 + 2 2 3 3 5 - 10 - 9 = 1,

A 23 = (- 1) 2 + 3 2 - 4 3 - 1 = - (- 2 + 12) = - 10,

A 31 = (- 1) 3 + 1 - 4 3 - 2 4 = - 16 + 6 = - 10,

A 32 = (- 1) 3 + 2 2 3 1 4 = - (8 - 3) = - 5,

A 33 = (- 1) 3 + 3 2 - 4 1 - 2 = - 4 + 4 = 0.

We write down the union matrix A *, which is composed of the algebraic complements of the matrix A:

A * = - 6 7 5 17 1 - 10 - 10 - 5 0

We write the inverse matrix according to the formula:

A - 1 = 1 d e t A (A *) T: A - 1 = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

We multiply the inverse matrix A - 1 by the column of free terms B and get the solution to the system:

X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1

Answer : x 1 = - 1; x 2 = 0; x 3 = 1

If you notice an error in the text, please select it and press Ctrl + Enter