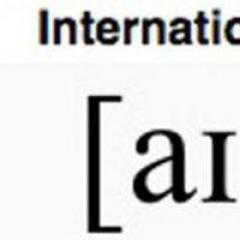The concept of function. Limited features

Since the indicated areas are respectively equal

SΔOAC=0,5∙O.C.∙O.A.∙sin α= 0.5sinα, S sect. OAC = 0,5∙O.C. 2 ∙α=0.5α, SΔOBC=0,5∙O.C.∙BC= 0.5tgα.

Hence,

sin α< α < tg α.

Let us divide all terms of the inequality by sin α > 0: .

But . Therefore, based on Theorem 4 on limits, we conclude that the derived formula is called the first remarkable limit.

Thus, the first remarkable limit serves to reveal uncertainty. Note that the resulting formula should not be confused with the limits Examples.

11.Limit and its associated limits.

THE SECOND REMARKABLE LIMIT

The second remarkable limit serves to reveal the uncertainty of 1 ∞ and looks like this:

Let us pay attention to the fact that in the formula for the second remarkable limit, the exponent must contain an expression inverse to that which is added to the unit at the base (since in this case it is possible to introduce a change of variables and reduce the sought limit to the second remarkable limit)

Examples.

1. Function f(x)=(x-1) 2 is infinitesimal at x→1, since (see figure).

2. Function f(x)= tg x– infinitesimal at x→0.

3. f(x)= log(1+ x) – infinitesimal at x→0.

4. f(x) = 1/x– infinitesimal at x→∞.

Let us establish the following important relationship:

Theorem. If the function y=f(x) representable with x→a as a sum of a constant number b and infinitesimal magnitude α(x): f (x)=b+ α(x) That .

Conversely, if , then f (x)=b+α(x), Where a(x)– infinitesimal at x→a.

Proof.

1. Let us prove the first part of the statement. From equality f(x)=b+α(x) should |f(x) – b|=| α|. But since a(x) is infinitesimal, then for arbitrary ε there is δ – a neighborhood of the point a, in front of everyone x from which, values a(x) satisfy the relation |α(x)|< ε. Then |f(x) – b|< ε. And this means that .

2. If , then for any ε >0 for all X from some δ – neighborhood of a point a will |f(x) – b|< ε. But if we denote f(x) – b= α, That |α(x)|< ε, which means that a– infinitesimal.

Let's consider the basic properties of infinitesimal functions.

Theorem 1. The algebraic sum of two, three, and in general any finite number of infinitesimals is an infinitesimal function.

Proof. Let us give a proof for two terms. Let f(x)=α(x)+β(x), where and . We need to prove that for any arbitrary small ε > 0 found δ> 0, such that for x, satisfying the inequality |x – a|<δ , performed |f(x)|< ε.

So, let’s fix an arbitrary number ε > 0. Since according to the conditions of the theorem α(x) is an infinitesimal function, then there is such δ 1 > 0, which is |x – a|< δ 1 we have |α(x)|< ε / 2. Likewise, since β(x) is infinitesimal, then there is such δ 2 > 0, which is |x – a|< δ 2 we have | β(x)|< ε / 2.

Let's take δ=min(δ 1 , δ2 } .Then in the vicinity of the point a radius δ each of the inequalities will be satisfied |α(x)|< ε / 2 and | β(x)|< ε / 2. Therefore, in this neighborhood there will be

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

those. |f(x)|< ε, which is what needed to be proved.

Theorem 2. Product of an infinitesimal function a(x) for a limited function f(x) at x→a(or when x→∞) is an infinitesimal function.

Proof. Since the function f(x) is limited, then there is a number M such that for all values x from some neighborhood of a point a|f(x)|≤M. Moreover, since a(x) is an infinitesimal function at x→a, then for an arbitrary ε > 0 there is a neighborhood of the point a, in which the inequality will hold |α(x)|< ε /M. Then in the smaller of these neighborhoods we have | αf|< ε /M= ε. And this means that af– infinitesimal. For the occasion x→∞ the proof is carried out similarly.

From the proven theorem it follows:

Corollary 1. If and , then

Corollary 2. If c= const, then .

Theorem 3. Ratio of an infinitesimal function α(x) per function f(x), the limit of which is different from zero, is an infinitesimal function.

Proof. Let . Then 1 /f(x) there is a limited function. Therefore, a fraction is the product of an infinitesimal function and a limited function, i.e. function is infinitesimal.

Examples.

1. It is clear that when x→+∞ function y=x 2 + 1 is infinitely large. But then, according to the theorem formulated above, the function is infinitesimal at x→+∞, i.e. .

The converse theorem can also be proven.

Theorem 2. If the function f(x)- infinitesimal at x→a(or x→∞) and does not vanish, then y= 1/f(x) is an infinitely large function.

Conduct the proof of the theorem yourself.

Examples.

3. , since the functions and are infinitesimal at x→+∞, then, as the sum of infinitesimal functions is an infinitesimal function. A function is the sum of a constant number and an infinitesimal function. Consequently, by Theorem 1 for infinitesimal functions we obtain the required equality.

Thus, the simplest properties of infinitesimal and infinitely large functions can be written using the following conditional relations: A≠ 0

13. Infinitesimal functions of the same order, equivalent infinitesimals.

Infinitesimal functions and are called infinitesimal of the same order of smallness if , denote . And finally, if it does not exist, then infinitesimal functions are incomparable.

EXAMPLE 2. Comparison of infinitesimal functions

Equivalent infinitesimal functions.

If , then infinitesimal functions are called equivalent, denote ~ .

Locally equivalent functions:

When if

Some equivalences(at ):

One-sided limits.

So far we have considered determining the limit of a function when x→a in an arbitrary manner, i.e. the limit of the function did not depend on how it was located x towards a, to the left or right of a. However, it is quite common to find functions that have no limit under this condition, but they do have a limit if x→a, remaining on one side of A, left or right (see figure). Therefore, the concepts of one-sided limits are introduced.

If f(x) tends to the limit b at x tending to a certain number a So x accepts only values ​​less than a, then they write and call blimit of the function f(x) at point a on the left.

So the number b called the limit of the function y=f(x) at x→a on the left, if whatever positive number ε is, there is such a number δ (smaller a

Likewise, if x→a and takes on large values a, then they write and call b limit of the function at the point A on right. Those. number b called limit of the function y=f(x) as x→a on the right, if whatever positive number ε is, there is such a number δ (greater A) that inequality holds for all.

Note that if the limits on the left and right at the point a for function f(x) do not coincide, then the function has no limit (two-sided) at the point A.

Examples.

1. Consider the function y=f(x), defined on the segment as follows

Let's find the limits of the function f(x) at x→ 3. Obviously, and

In other words, for any arbitrarily small number of epsilon, there is a delta number depending on epsilon such that from the fact that for any x satisfying the inequality it follows that the differences in the values ​​of the function at these points will be arbitrarily small.

Criterion for the continuity of a function at a point:

Function will continuous at point A if and only if it is continuous at point A both on the right and on the left, that is, so that at point A there are two one-sided limits, they are equal to each other and equal to the value of the function at point A.

Definition 2: The function is continuous on a set if it is continuous at all points of this set.

Derivative of a function at a point

Let dana be defined in a neighborhood. Let's consider

If this limit exists, then it is called derivative of the function f at the point .

Derivative of a function– the limit of the ratio of the increment of the function to the increment of the argument, when the argument is incremented.

The operation of calculating or finding the derivative at a point is called differentiation .

Rules of differentiation.

Derivative functions f(x) at the point x=x 0 is called the ratio of the increment of a function at this point to the increment of the argument, as the latter tends to zero. Finding the derivative is called differentiation. The derivative of a function is calculated according to the general rule of differentiation: Let us denote f(x) = u, g(x) = v- functions differentiable at a point X. Basic rules of differentiation 1) (the derivative of a sum is equal to the sum of its derivatives) 2) (from here, in particular, it follows that the derivative of the product of a function and a constant is equal to the product of the derivative of this function and the constant) 3) Derivative of a quotient: , if g  0 4) Derivative of a complex function: 5) If the function is specified parametrically: , then

Examples.

1. y = x a is a power function with an arbitrary exponent.

Implicit function

If a function is given by the equation y=ƒ(x), resolved with respect to y, then the function is given in explicit form (explicit function).

Under implicit task functions understand the definition of a function in the form of an equation F(x;y)=0, not resolved with respect to y.

Any explicitly given function y=ƒ (x) can be written as implicitly given by the equation ƒ(x)-y=0, but not vice versa.

It is not always easy, and sometimes impossible, to solve an equation for y (for example, y+2x+cozy-1=0 or 2 y -x+y=0).

If the implicit function is given by the equation F(x; y) = 0, then to find the derivative of y with respect to x there is no need to resolve the equation with respect to y: it is enough to differentiate this equation with respect to x, while considering y as a function of x, and then solve the resulting equation for y."

The derivative of an implicit function is expressed in terms of the argument x and the function y.

Example:

Find the derivative of the function y, given by the equation x 3 + y 3 -3xy = 0.

Solution: The function y is specified implicitly. We differentiate with respect to x the equality x 3 + y 3 -3xy = 0. From the resulting relation

3x 2 +3y 2 y"-3(1 y+x y")=0

it follows that y 2 y"-xy"=y-x 2, i.e. y"=(y-x 2)/(y 2 -x).

Higher order derivatives

It is clear that the derivative

functions y=f(x) there is also a function from x:

y" =f " (x)

If the function f" (x) is differentiable, then its derivative is denoted by the symbol y"" =f "" (x) x twice.
The derivative of the second derivative, i.e. functions y""=f""(x), called third derivative of the function y=f(x) or derivative of the function f(x) of third order and is indicated by the symbols

At all n-i derivative or derivative n th order function y=f(x) indicated by symbols

Phil Leibniz:

Let us assume that the functions and are differentiable together with their derivatives up to the nth order inclusive. Applying the rule for differentiating the product of two functions, we obtain

Let's compare these expressions with the powers of the binomial:

The correspondence rule is striking: in order to obtain a formula for the 1st, 2nd or 3rd order derivative of the product of functions and , you need to replace the powers and in the expression for (where n= 1,2,3) derivatives of the corresponding orders. In addition, zero powers of quantities and should be replaced by derivatives of zero order, meaning by them the functions and:

Generalizing this rule to the case of derivatives of arbitrary order n, we get Leibniz's formula,

where are the binomial coefficients:

Rolle's theorem.

This theorem allows one to find critical points and then, using sufficient conditions, to examine the function for extrema.

Let 1) f(x) be defined and continuous on some closed interval; 2) there is a finite derivative, at least in the open interval (a;b); 3) at the ends of the interval f-i takes equal values ​​f(a) = f(b). Then between points a and b there is a point c such that the derivative at this point will be = 0.

According to the theorem about the property of functions that are continuous on an interval, the function f(x) takes on its max and min values ​​on this interval.

f(x 1) = M – max, f(x 2) = m – min; x 1 ;x 2 О

1) Let M = m, i.e. m £ f(x) £ M

Þ f(x) will take constant values ​​on the interval from a to b, and Þ its derivative will be equal to zero. f’(x)=0

2) Let M>m

Because according to the conditions of the theorem, f(a) = f(b) Þ will take its smallest or greatest value not at the ends of the segment, but Þ will take M or m at the interior point of this segment. Then, by Fermat’s theorem, f’(c)=0.

Lagrange's theorem.

Finite Increment Formula or Lagrange's mean value theorem states that if a function f is continuous on the interval [ a;b] and differentiable in the interval ( a;b), then there is a point such that

Cauchy's theorem.

If the functions f(x) and g(x) are continuous on the interval and differentiable on the interval (a, b) and g¢(x) ¹ 0 on the interval (a, b), then there is at least one point e, a< e < b, такая, что

Those. the ratio of increments of functions on a given segment is equal to the ratio of derivatives at point e. Examples of problem solving course of lectures Calculation of the volume of a body from known areas of its parallel sections Integral calculus

Examples of coursework Electrical engineering

To prove this theorem, at first glance it is very convenient to use Lagrange’s theorem. Write down a finite difference formula for each function and then divide them by each other. However, this idea is erroneous, because point e for each function is generally different. Of course, in some special cases this point of the interval may turn out to be the same for both functions, but this is a very rare coincidence, and not a rule, and therefore cannot be used to prove the theorem.

Proof. Consider the helper function

As x→x 0, the value of c also tends to x 0; Let us go to the limit in the previous equality:

Because , That .

That's why

(the limit of the ratio of two infinitesimals is equal to the limit of the ratio of their derivatives, if the latter exists)

L'Hopital's rule, at ∞/∞.

Please note: all definitions involve a numerical set X, which is part of the domain of the function: X with D(f). In practice, most often there are cases when X is a numerical interval (segment, interval, ray, etc.).

Definition 1.

A function y = f(x) is said to be increasing on a set X with D(f) if for any two points x 1 and x 2 of the set X such that x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).

Definition 2.

A function y = f(x) is said to be decreasing on a set X with D(f) if for any two points x 1 and x 2 of the set X such that x 1< х 2 , функции выполняется неравенство f(x 1) >f(x 2).

In practice, it is more convenient to use the following formulations: a function increases if a larger value of the argument corresponds to a larger value of the function; a function decreases if a larger value of the argument corresponds to a smaller value of the function.

In the 7th and 8th grades we used the following geometric interpretation of the concepts of increasing or decreasing a function: moving along the graph of an increasing function from left to right, we seem to be climbing a hill (Fig. 55); moving along the graph of a decreasing function from left to right, it’s as if we are going down a hill (Fig. 56).
Usually the terms “increasing function”, “decreasing function” are combined under the general name monotonic function, and the study of a function for increasing or decreasing is called the study of a function for monotonicity.

Let us note one more circumstance: if a function increases (or decreases) in its natural domain of definition, then we usually say that the function is increasing (or decreasing) - without indicating the numerical set X.

Example 1.

Examine the function for monotonicity:

A) y = x 3 + 2; b) y = 5 - 2x.

Solution:

a) Take arbitrary values ​​of the argument x 1 and x 2 and let x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

The last inequality means that f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).

So from x 1< х 2 следует f(х 1) >f(x 2), which means that the given function is decreasing (on the entire number line).

Definition 3.

A function y - f(x) is said to be bounded from below on a set X with D(f) if all values ​​of the function on the set X are greater than a certain number (in other words, if there is a number m such that for any value x є X the inequality f( x) >m).

Definition 4.

A function y = f(x) is said to be bounded from above on a set X with D(f) if all values ​​of the function are less than a certain number (in other words, if there is a number M such that for any value x є X the inequality f(x) holds< М).

If the set X is not specified, then it is understood that we are talking about the function being bounded from below or from above in the entire domain of definition.

If a function is bounded both below and above, then it is called bounded.

The boundedness of a function is easily read from its graph: if a function is bounded from below, then its graph is entirely located above a certain horizontal line y = m (Fig. 57); if a function is bounded from above, then its graph is entirely located below some horizontal line y = M (Fig. 58).

Example 2. Examine for boundedness of a function
Solution. On the one hand, the inequality is quite obvious (by the definition of a square root, this means that the function is bounded below. On the other hand, we have and therefore
This means that the function is upper bounded. Now look at the graph of the given function (Fig. 52 from the previous paragraph). The limitation of the function both above and below can be read quite easily from the graph.

Definition 5.

The number m is called the smallest value of the function y = f(x) on the set X C D(f) if:

1) in X there is a point x 0 such that f(x 0) = m;

2) for all x from X the inequality m>f(x 0) holds.

Definition 6.

The number M is called the largest value of the function y = f(x) on the set X C D(f), if:
1) in X there is a point x 0 such that f(x 0) = M;
2) for all x from X the inequality
We denoted the smallest value of a function in both the 7th and 8th grades by the symbol y, and the largest by the symbol y.

If the set X is not specified, then it is assumed that we are talking about finding the smallest or largest value of the function in the entire domain of definition.

The following useful statements are quite obvious:

1) If a function has Y, then it is bounded below.
2) If a function has Y, then it is bounded above.
3) If the function is not bounded below, then Y does not exist.
4) If the function is not bounded above, then Y does not exist.

Example 3.

Find the smallest and largest values ​​of a function
Solution.

It is quite obvious, especially if you use the function graph (Fig. 52), that = 0 (the function reaches this value at points x = -3 and x = 3), a = 3 (the function reaches this value at x = 0.
In 7th and 8th grades we mentioned two more properties of functions. The first was called the convexity property of a function. A function is considered to be convex downward on an interval X if, by connecting any two points of its graph (with abscissas from X) with a straight line segment, we find that the corresponding part of the graph lies below the drawn segment (Fig. 59). continuity A function is convex upward on an interval X if, by connecting any two points of its graph (with abscissas from X) of the function with a straight line segment, we find that the corresponding part of the graph lies above the drawn segment (Fig. 60).

The second property - continuity of a function on the interval X - means that the graph of the function on the interval X is continuous, i.e. has no punctures or jumps.

Comment.

In fact, in mathematics everything is, as they say, “exactly the opposite”: the graph of a function is depicted as a solid line (without punctures or jumps) only when the continuity of the function is proven. But a formal definition of the continuity of a function, which is quite complex and subtle, is not yet within our capabilities. The same can be said about the convexity of a function. When discussing these two properties of functions, we will continue to rely on visual and intuitive concepts.

Now let's review our knowledge. Remembering the functions that we studied in the 7th and 8th grades, let’s clarify what their graphs look like and list the properties of the function, adhering to a certain order, for example this: domain of definition; monotone; limitation; , ; continuity; range; convex.

Subsequently, new properties of functions will appear, and the list of properties will change accordingly.

1. Constant function y = C

The graph of the function y = C is shown in Fig. 61 - straight line, parallel to the x axis. This is such an uninteresting feature that there is no point in listing its properties.

The graph of the function y = kx + m is a straight line (Fig. 62, 63).

Properties of the function y = kx + m:

1)
2) increases if k > 0 (Fig. 62), decreases if k< 0 (рис. 63);

4) there is neither the largest nor the smallest value;
5) the function is continuous;
6)
7) there is no point in talking about convexity.

The graph of the function y = kx 2 is a parabola with a vertex at the origin and with branches directed upward if k > O (Fig. 64), and downward if k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Properties of the function y - kx 2:

For the case k> 0 (Fig. 64):

1) D(f) = (-oo,+oo);


4) = does not exist;
5) continuous;
6) E(f) = the function decreases, and on the interval, decreases on the ray;
7) convex upward.

The graph of the function y = f(x) is plotted point by point; The more points of the form (x; f(x)) we take, the more accurate an idea of ​​the graph we will get. If you take a lot of these points, then you will get a more complete picture of the graph. It is in this case that intuition tells us that the graph should be depicted as a solid line (in this case, in the form of a parabola). And then, reading the graph, we draw conclusions about the continuity of the function, about its convexity downwards or upwards, about the range of values ​​of the function. You must understand that of the listed seven properties, only properties 1), 2), 3), 4) are “legitimate” - “legitimate” in the sense that we are able to justify them by referring to precise definitions. We have only visual and intuitive ideas about the remaining properties. By the way, there is nothing wrong with this. From the history of the development of mathematics it is known that humanity often and for a long time used various properties of certain objects, without knowing the exact definitions. Then, when such definitions could be formulated, everything fell into place.

The graph of the function is a hyperbola, the coordinate axes serve as asymptotes of the hyperbola (Fig. 66, 67).

1) D(f) = (-00,0)1U (0,+oo);
2) if k > 0, then the function decreases on the open ray (-oo, 0) and on the open ray (0, +oo) (Fig. 66); if to< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) is not limited either from below or from above;
4) there is neither the smallest nor the largest value;
5) the function is continuous on the open ray (-oo, 0) and on the open ray (0, +oo);
6) E(f) = (-oo,0) U (0,+oo);
7) if k > 0, then the function is convex upward at x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, i.e. on the open beam (0, +oo) (Fig. 66). If to< 0, то функция выпукла вверх при х >O and convex downward at x< О (рис. 67).
The graph of the function is a branch of a parabola (Fig. 68). Function properties:
1) D(f) = , increases on the ray )