Намерете дължината на страната ab онлайн. Уравнение на права линия с наклон

Числено равен на тангенса на ъгъла (представляващ най-малкото завъртане от оста Ox към оста Oy) между положителната посока на абсцисната ос и дадената права линия.

Тангенсът на ъгъл може да се изчисли като съотношението на срещуположната страна към съседната страна. ке винаги равно на , т.е. производната на уравнението на права линия по отношение на х.

За положителни стойности на наклона ки нулев коефициент на смяна bправата линия ще лежи в първия и третия квадрант (в които хИ гкакто положителни, така и отрицателни). В същото време големи стойности на ъгловия коефициент кпо-стръмната права линия ще съответства, а по-плоската ще съответства на по-малките.

Права и перпендикулярна, ако , и успоредна, ако .

Бележки

Фондация Уикимедия. 2010 г.

• Ифит (цар на Елида)
• Списък на укази на президента на Руската федерация „За награждаване с държавни награди“ за 2001 г

Вижте какво е „Ъглов коефициент на права линия“ в други речници:

наклон (директен)- - Теми: нефтена и газова индустрия EN наклон... Ръководство за технически преводач

Фактор на наклона- (математическо) число k в уравнението на права линия в равнината y = kx+b (вижте Аналитична геометрия), характеризиращо наклона на правата линия спрямо оста x. В правоъгълната координатна система U. k = tan φ, където φ е ъгълът между ... ... Велика съветска енциклопедия

Уравнения на права

АНАЛИТИЧНА ГЕОМЕТРИЯ- раздел от геометрията, който изучава най-простите геометрични обекти с помощта на елементарна алгебра, базирана на метода на координатите. Създаването на аналитичната геометрия обикновено се приписва на Р. Декарт, който очертава нейните основи в последната глава на своя... ... Енциклопедия на Collier

Време за реакция- Измерването на времето за реакция (RT) е може би най-уважаваният предмет в емпиричната психология. Възниква в областта на астрономията през 1823 г. с измерването на индивидуалните разлики в скоростта на възприемане на звезда, пресичаща линия на телескоп. Тези… Психологическа енциклопедия

МАТЕМАТИЧЕСКИ АНАЛИЗ- клон на математиката, който предоставя методи за количествено изследване на различни процеси на промяна; се занимава с изучаването на скоростта на промяна (диференциално смятане) и определянето на дължините на кривите, площите и обемите на фигури, ограничени от извити контури и ... Енциклопедия на Collier

Направо- Този термин има други значения, вижте Директен (значения). Правата линия е едно от основните понятия на геометрията, тоест няма точна универсална дефиниция. В систематичното представяне на геометрията правата линия обикновено се приема като една... ... Wikipedia

Права- Изображение на прави линии в правоъгълна координатна система Правата линия е едно от основните понятия на геометрията. В систематичното представяне на геометрията правата линия обикновено се приема като едно от началните понятия, което е само индиректно дефинирано... ... Wikipedia

Директен- Изображение на прави линии в правоъгълна координатна система Правата линия е едно от основните понятия на геометрията. В систематичното представяне на геометрията правата линия обикновено се приема като едно от началните понятия, което е само индиректно дефинирано... ... Wikipedia

Малък вал- Да не се бърка с термина "Елипса". Елипса и нейните фокуси Елипса (на старогръцки ἔλλειψις недостатък, в смисъл на липса на ексцентричност до 1) геометричното място на точки M от евклидовата равнина, за които сумата от разстоянията от две дадени точки е F1... ... Уикипедия

Нека на равнина, където има правоъгълна декартова координатна система, права линия лминава през точка M 0 успоредно на насочващия вектор А (фиг. 96).

Ако прав лпресича оста О х(в точка N), след това под прав ъгъл лс ос О хще разберем ъгъла α, с който е необходимо да завъртим оста O хоколо точка N в посока, обратна на въртенето по часовниковата стрелка, така че оста O хсъвпадна с права линия л. (Това се отнася за ъгъл, по-малък от 180°.)

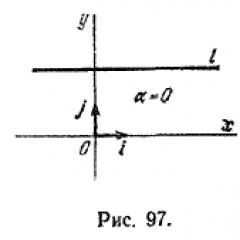
Този ъгъл се нарича ъгъл на наклон прав. Ако прав луспоредна на оста O х, тогава ъгълът на наклон се приема за нула (фиг. 97).

Тангенсът на ъгъла на наклон на права линия се нарича наклон на права линия и обикновено се обозначава с буквата к:

tan α = к. (1)

Ако α = 0, тогава к= 0; това означава, че правата е успоредна на оста O хи наклонът му е нула.

Ако α = 90°, тогава к= tan α няма смисъл: това означава, че права линия, перпендикулярна на оста O х(т.е. успоредно на оста O при), няма наклон.

Наклонът на линия може да се изчисли, ако са известни координатите на всеки две точки от тази линия. Нека са дадени две точки на права: M 1 ( х 1 ; при 1) и M 2 ( х 2 ; при 2) и нека, например, 0< α < 90°, а х 2 > х 1 , при 2 > при 1 (фиг. 98).

Тогава от правоъгълния триъгълник M 1 PM 2 намираме

$$ k=tga = \frac(|M_2 P|)(|M_1 P|) = \frac(y_2 - y_1)(x_2 - x_1) $$

$$ k=\frac(y_2 - y_1)(x_2 - x_1) \;\; (2)$$

По подобен начин е доказано, че формула (2) е вярна и в случай на 90°< α < 180°.

Формула (2) губи смисъл, ако х 2 - х 1 = 0, т.е. ако е права луспоредна на оста O при. За такива прави линии няма коефициент на наклон.

Задача 1.Определете ъгловия коефициент на прим, преминаващ през точките

M 1 (3; -5) и M 2 (5; -7).

Замествайки координатите на точките M 1 и M 2 във формула (2), получаваме

\(k=\frac(-7-(-5))(5-3)\) или к = -1

Задача 2.Определете наклона на правата, минаваща през точките M 1 (3; 5) и M 2 (3; -2).

защото х 2 - х 1 = 0, то равенството (2) губи смисъл. Няма наклон за тази права линия. Правата M 1 M 2 е успоредна на оста O при.

Задача 3.Определете наклона на правата, минаваща през началото и точката M 1 (3; -5)

В този случай точка M 2 съвпада с началото. Прилагайки формула (2), получаваме

$$ k=\frac(y_2 - y_1)(x_2 - x_1)=\frac(0-(-5))(0-3)= -\frac(5)(3); \;\; k= -\frac(5)(3) $$

Нека създадем уравнение на права линия с ъглов коефициент к, минаваща през точката

М 1 ( х 1 ; при 1). Съгласно формула (2) ъгловият коефициент на права линия се намира от координатите на двете й точки. В нашия случай е дадена точка M 1, а като втора точка можем да вземем всяка точка M( Х; при) желаната права линия.

Ако точка M лежи на права линия, която минава през точка M 1 и има ъглов коефициент к, тогава по силата на формула (2) имаме

$$ \frac(y-y_1)(x-x_1)=k \;\; (3) $$

Ако точка M не лежи на права, то равенството (3) не е в сила. Следователно равенството (3) е уравнението на правата линия, минаваща през точката M 1 ( х 1 ; при 1) с наклон к; това уравнение обикновено се записва като

г- г 1 = к(х - х 1). (4)

Ако правата пресича оста О прив някакъв момент (0; b), тогава уравнение (4) приема формата

при - b = к (х- 0),

г = kx + b. (5)

Това уравнение се нарича уравнение на права линия с наклон k и начална ордината b.

Задача 4.Намерете ъгъла на наклона на правата √3 x + 3при - 7 = 0.

Нека намалим това уравнение до формата

$$ y= =\frac(1)(\sqrt3)x + \frac(7)(3) $$

следователно к= tan α = - 1 / √ 3, откъдето α = 150°

Задача 5.Напишете уравнение за права линия, минаваща през точка P(3; -4) с ъглов коефициент к = 2 / 5

Заместване к = 2 / 5 , х 1 = 3, г 1 = - 4 в уравнение (4), получаваме

при - (- 4) = 2 / 5 (х- 3) или 2 х - 5при - 26 = 0.

Задача 6.Напишете уравнение за права линия, минаваща през точка Q (-3; 4) и компонент с положителна посока на оста O хъгъл 30°.

Ако α = 30°, тогава к= тен 30° = √ 3 / 3 . Заместване в уравнение (4) на стойностите х 1 , г 1 и к, получаваме

при -4 = √ 3 / 3 (х+ 3) или √3 х-3г + 12 + 3√3 = 0.

В математиката един от параметрите, който описва позицията на линия в декартовата координатна равнина, е ъгловият коефициент на тази линия. Този параметър характеризира наклона на правата спрямо абсцисната ос. За да разберете как да намерите наклона, първо си припомнете общата форма на уравнението на права линия в координатната система XY.

Като цяло всяка права линия може да бъде представена чрез израза ax+by=c, където a, b и c са произволни реални числа, но a 2 + b 2 ≠ 0.

С помощта на прости трансформации такова уравнение може да се доведе до формата y=kx+d, в която k и d са реални числа. Числото k е наклонът и уравнението на линия от този тип се нарича уравнение с наклон. Оказва се, че за да намерите наклона, просто трябва да намалите първоначалното уравнение до формата, посочен по-горе. За по-пълно разбиране разгледайте конкретен пример:

Задача: Намерете наклона на правата, дадена от уравнението 36x - 18y = 108

Решение: Нека трансформираме първоначалното уравнение.

Отговор: Необходимият наклон на тази линия е 2.

Ако по време на преобразуването на уравнението сме получили израз като x = const и в резултат не можем да представим y като функция на x, тогава имаме работа с права линия, успоредна на оста X. Ъгловият коефициент на такава права линия е равна на безкрайност.

За линии, изразени с уравнение като y = const, наклонът е нула. Това е типично за прави линии, успоредни на абсцисната ос. Например:

Задача: Намерете наклона на правата, дадена от уравнението 24x + 12y - 4(3y + 7) = 4

Решение: Нека приведем първоначалното уравнение в неговия общ вид

24x + 12y - 12y + 28 = 4

Невъзможно е да се изрази y от получения израз, следователно ъгловият коефициент на тази линия е равен на безкрайност, а самата линия ще бъде успоредна на оста Y.

Геометрично значение

За по-добро разбиране, нека разгледаме снимката:

На фигурата виждаме графика на функция като y = kx. За да опростим, нека вземем коефициента c = 0. В триъгълника OAB съотношението на страната BA към AO ще бъде равно на ъгловия коефициент k. В същото време съотношението BA/AO е тангенса на острия ъгъл α в правоъгълния триъгълник OAB. Оказва се, че ъгловият коефициент на правата е равен на тангенса на ъгъла, който тази права сключва с абсцисната ос на координатната мрежа.

Решавайки проблема как да намерим ъгловия коефициент на права линия, намираме тангенса на ъгъла между нея и оста X на координатната мрежа. Граничните случаи, когато въпросната права е успоредна на координатните оси, потвърждават горното. Наистина, за права линия, описана с уравнението y=const, ъгълът между нея и абсцисната ос е нула. Тангенсът на нулевия ъгъл също е нула и наклонът също е нула.

За прави линии, перпендикулярни на оста x и описани с уравнението x=const, ъгълът между тях и оста X е 90 градуса. Тангенсът на прав ъгъл е равен на безкрайност, а ъгловият коефициент на подобни прави също е равен на безкрайност, което потвърждава написаното по-горе.

Наклон на допирателната

Често срещана задача в практиката е намирането на наклона на допирателната към графиката на функция в определена точка. Тангентата е права линия, следователно концепцията за наклон е приложима и към нея.

За да разберем как да намерим наклона на допирателната, ще трябва да си припомним понятието производна. Производната на всяка функция в определена точка е константа, числено равна на тангенса на ъгъла, образуван между допирателната в определена точка към графиката на тази функция и абсцисната ос. Оказва се, че за да определим ъгловия коефициент на тангентата в точката x 0, трябва да изчислим стойността на производната на оригиналната функция в тази точка k = f"(x 0). Нека да разгледаме примера:

Задача: Намерете наклона на правата, допирателна към функцията y = 12x 2 + 2xe x при x = 0,1.

Решение: Намерете производната на оригиналната функция в общ вид

y"(0.1) = 24. 0.1 + 2. 0.1. e 0.1 + 2. e 0.1

Отговор: Необходимият наклон в точка x = 0,1 е 4,831

Фигурата показва ъгъла на наклона на правата линия и показва стойността на ъгловия коефициент за различни опции за местоположението на правата линия спрямо правоъгълната координатна система.

Намирането на наклона на права линия с известен ъгъл на наклон към оста Ox не представлява никакви затруднения. За да направите това, достатъчно е да си припомните дефиницията на ъгловия коефициент и да изчислите тангенса на ъгъла на наклон.

Пример.

Намерете наклона на правата, ако нейният ъгъл на наклон спрямо абсцисната ос е равен на .

Решение.

По условие. След това, по дефиниция на наклона на права линия, изчисляваме .

Отговор:

Задачата за намиране на ъгъла на наклона на права линия към оста x с известен наклон е малко по-сложна. Тук е необходимо да се вземе предвид знакът на наклона. Когато ъгълът на наклона на правата е остър и се намира като . Когато ъгълът на наклона на правата е тъп и може да се определи по формулата .

Пример.

Определете ъгъла на наклона на правата спрямо абсцисната ос, ако нейният наклон е равен на 3.

Решение.

Тъй като по условие ъгловият коефициент е положителен, ъгълът на наклона на правата спрямо оста Ox е остър. Изчисляваме го по формулата.

Отговор:

Пример.

Наклонът на правата е . Определете ъгъла на наклона на правата спрямо оста Ox.

Решение.

Нека обозначим k е ъгловият коефициент на правата линия, - ъгълът на наклона на тази права линия спрямо положителната посока на оста Ox. защото , тогава използваме формулата, за да намерим ъгъла на наклона на линията със следната форма . В него заместваме данните от условието: .

Отговор:

Уравнение на права с ъглов коефициент.

Уравнение на права линия с наклонима формата , където k е наклонът на правата, b е някакво реално число. Използвайки уравнението на права линия с ъглов коефициент, можете да посочите всяка права линия, която не е успоредна на оста Oy (за права линия, успоредна на ординатната ос, ъгловият коефициент не е дефиниран).

Нека разберем значението на фразата: „права линия в равнина във фиксирана координатна система се дава от уравнение с ъглов коефициент от вида „.“ Това означава, че уравнението е изпълнено от координатите на която и да е точка от правата и не е удовлетворено от координатите на други точки от равнината. Така, ако при заместване на координатите на точка се получи правилното равенство, тогава правата минава през тази точка. В противен случай точката не лежи на правата.

Пример.

Правата линия е дадена от уравнение с наклон. Точките също ли принадлежат на тази права?

Решение.

Нека заместим координатите на точката в първоначалното уравнение на правата с наклона: . Получихме правилното равенство, следователно точка M 1 лежи на правата.

При заместване на координатите на точка получаваме неправилно равенство: . Следователно точка M 2 не лежи на правата.

Отговор:

Точка M 1 принадлежи на линията, M 2 не принадлежи.

Трябва да се отбележи, че през точката минава права линия, определена от уравнението на права линия с ъглов коефициент, тъй като когато заместим нейните координати в уравнението, получаваме правилното равенство: .

По този начин уравнението на права линия с ъглов коефициент определя на равнината права линия, минаваща през точка и образуваща ъгъл с положителната посока на оста x, и .

Като пример, нека изобразим права линия, определена от уравнението на права линия с ъглов коефициент от формата . Тази линия минава през точка и има наклон радиани (60 градуса) спрямо положителната посока на оста Ox. Неговият наклон е равен на .

Уравнение на права с наклон, минаваща през дадена точка.

Сега ще решим един много важен проблем: ще получим уравнението на права линия с даден наклон k и минаваща през точката .

Тъй като правата минава през точката, равенството е вярно . Не знаем числото b. За да се отървем от него, изваждаме лявата и дясната страна на последното равенство съответно от лявата и дясната страна на уравнението на правата с коефициента на наклона. В този случай получаваме . Това равенство е уравнение на права линия с даден наклон k, която минава през дадена точка.

Нека разгледаме един пример.

Пример.

Напишете уравнението на права, минаваща през точката, наклонът на тази права е -2.

Решение.

От състоянието, което имаме . Тогава уравнението на права линия с ъглов коефициент ще приеме формата .

Отговор:

Пример.

Напишете уравнението на права линия, ако е известно, че тя минава през точка и ъгълът на наклон спрямо положителната посока на оста Ox е равен на .

Решение.

Първо, нека изчислим наклона на правата, чието уравнение търсим (решихме този проблем в предишния параграф на тази статия). А-приорат . Сега имаме всички данни, за да напишем уравнението на права линия с ъглов коефициент:

Отговор:

Пример.

Напишете уравнението на права с ъглов коефициент, минаваща през точка, успоредна на правата.

Решение.

Очевидно ъглите на наклона на успоредните линии към оста Ox съвпадат (ако е необходимо, вижте статията успоредност на линиите), следователно ъгловите коефициенти на успоредните линии са равни. Тогава наклонът на правата линия, чието уравнение трябва да получим, е равен на 2, тъй като наклонът на правата линия е равен на 2. Сега можем да създадем необходимото уравнение на права линия с наклон:

Отговор:

Преход от уравнение на права с ъглов коефициент към други видове уравнение на права и обратно.

Въпреки цялото познаване, уравнението на права линия с ъглов коефициент не винаги е удобно за използване при решаване на проблеми. В някои случаи проблемите са по-лесни за решаване, когато уравнението на линия е представено в различна форма. Например, уравнението на права линия с ъглов коефициент не ви позволява незабавно да запишете координатите на насочващия вектор на правата линия или координатите на нормалния вектор на правата линия. Следователно трябва да се научите да преминавате от уравнението на права линия с ъглов коефициент към други видове уравнения на тази права линия.

От уравнението на права линия с ъглов коефициент е лесно да се получи каноничното уравнение на права линия върху равнина от формата . За да направим това, преместваме члена b от дясната страна на уравнението в лявата страна с противоположния знак, след което разделяме двете страни на полученото равенство на наклона k: . Тези действия ни водят от уравнението на права с ъглов коефициент към каноничното уравнение на права.

Пример.

Дайте уравнението на права линия с ъглов коефициент към каноничната форма.

Решение.

Нека извършим необходимите трансформации: .

Отговор:

Пример.

Правата линия се дава от уравнението на права линия с ъглов коефициент. Векторът нормален вектор ли е на тази права?

Решение.

За да разрешим този проблем, нека преминем от уравнението на права линия с ъглов коефициент към общото уравнение на тази права линия: . Знаем, че коефициентите на променливите x и y в общото уравнение на една права са съответните координати на нормалния вектор на тази права, т.е. нормалния вектор на правата . Очевидно е, че векторът е колинеарен на вектора, тъй като връзката е валидна (ако е необходимо, вижте статията). По този начин оригиналният вектор също е нормален вектор , и следователно е нормален вектор и оригиналната линия.

Отговор:

Да, така е.

А сега ще решим обратната задача - задачата за редуциране на уравнението на права линия върху равнина до уравнението на права линия с ъглов коефициент.

От общото уравнение на права линия на формата , в което е много лесно да се стигне до уравнение с коефициент на наклон. За да направите това, трябва да решите общото уравнение на правата по отношение на y. В този случай получаваме. Полученото равенство е уравнение на права линия с ъглов коефициент, равен на .

Задачите за намиране на производната на тангенс са включени в Единния държавен изпит по математика и се намират там всяка година. В същото време статистиката от последните години показва, че подобни задачи създават известни затруднения на завършилите. Ето защо, ако студент очаква да получи прилични резултати след преминаване на Единния държавен изпит, тогава той определено трябва да се научи как да се справя със задачи от раздела „Ъглов коефициент на допирателна като стойност на производната в точката на допирателна“, подготвен от специалисти на образователния портал Школково. След като разбере алгоритъма за решаването им, ученикът ще може успешно да преодолее сертификационния тест.

Основни моменти

Когато започвате да решавате USE задачи по тази тема, е необходимо да запомните основната дефиниция: производната на функция в точка е равна на наклона на допирателната към графиката на функцията в тази точка. Това е геометричното значение на производната.

Има още една важна дефиниция, която трябва да бъде опреснена. Звучи така: ъгловият коефициент е равен на тангенса на ъгъла на наклон на допирателната към абсцисната ос.

Кои други важни моменти си струва да се отбележат в тази тема? Когато решавате задачи за намиране на производната в Единния държавен изпит, трябва да запомните, че ъгълът, образуван от допирателната, може да бъде по-малък, повече от 90 градуса или равен на нула.

Как да се подготвим за изпита?

За да сте сигурни, че задачите в Единния държавен изпит по темата „Ъгловият коефициент на допирателната като стойност на производната в точката на допиране“ ви се дават доста лесно, когато се подготвяте за финалния тест, използвайте информацията за това раздел на образователния портал Школково. Тук ще намерите необходимия теоретичен материал, събран и нагледно представен от нашите специалисти, както и ще можете да се упражнявате в изпълнението на упражненията.

За всяка задача, например задачи по темата „Ъгловият коефициент на допирателната като тангенс на ъгъла на наклона“, записахме правилния отговор и алгоритъма за решение. В същото време учениците могат да изпълняват упражнения с различни нива на трудност онлайн. Ако е необходимо, задачата може да бъде запазена в секцията „Любими“, за да можете по-късно да обсъдите нейното решение с учителя.