Центрирани и нормализирани случайни променливи. Нормализирани случайни променливи

Разликата между произволна променлива и нейното математическо очакване се нарича отклонение или центрирана случайна променлива:

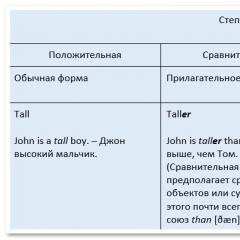
Редът на разпределение на центрирана произволна променлива е:

Имотицентрирана случайна променлива:

1. Математическото очакване на отклонението е 0:

2. Дисперсия на отклонението на произволна величина NSна математическото му очакване е равно на дисперсията на най-случайната променлива X:

С други думи, дисперсията на произволна променлива и дисперсията на нейното отклонение са равни.

4.2. Ако отклонението NS М (X)разделете на стандартно отклонение  (NS), тогава получаваме безразмерна центрирана случайна променлива, която се нарича стандартна (нормализирана) случайна променлива:

Имотистандартна случайна променлива:

Математическото очакване на стандартна случайна променлива е нула: М(З) =0.

Дисперсията на стандартната случайна променлива е 1: д(З) =1.

ЗАДАЧИ ЗА САМОСТОЯТЕЛНО РЕШЕНИЕ

В лотарията за 100 билета се теглят две неща, чиято цена е $210 и $60. Съставете закона за разпределение на спечелената сума за лице, което има: а) 1 билет, б) 2 билета. Намерете числените характеристики.

Двамата стрелци стрелят по целта веднъж. Случайна стойност NS- броят на точките, нокаутирани в един удар от първия стрелец, - има закон за разпределение:

З- количеството точки, избити от двете стрели. Определете числените характеристики.

Двама стрелци стрелят по целта си, като изстрелват един изстрел независимо един от друг. Вероятността за уцелване на целта за първия стрелец е 0,7, за втория - 0,8. Случайна стойност NS 1 - броят на попаденията на първия стрелец, NS 2  броят попадения на втория стрелец. Намерете закона на разпределението: а) общия брой попадения; б) случайна променлива З=3NS 1  2NS 2 ... Определете числените характеристики на общия брой попадения. Проверете изпълнението на свойствата на математическото очакване и дисперсия: М(3 х  2 Й)=3 М(х)  2 М(Й), д(3 х  2 Й)=9 д(х)+4 д(Й).

Случайна стойност NS- приходите на дружеството - има закон за разпределение:

Намерете закона за разпределение на произволна величина З- печалбата на дружеството. Определете нейните числени характеристики.

Случайни променливи NSи Имайтеса независими и имат същия закон за разпределение:

Случайните променливи имат ли същите закони за разпределение 2 NSи NS + Имайте ?

Докажете, че математическото очакване на стандартна случайна променлива е нула, а дисперсията е 1.

По-горе се запознахме със законите за разпределение на случайните величини. Всеки закон за разпределението описва изчерпателно свойствата на вероятностите на произволна променлива и прави възможно изчисляването на вероятностите за всякакви събития, свързани със случайна променлива. Въпреки това, в много практически въпроси няма нужда от такова пълно описание и често е достатъчно да се посочат само отделни числови параметри, които характеризират съществените характеристики на разпределението. Например средната стойност, около която са разпръснати стойностите на произволна променлива, някакво число, което характеризира големината на това разсейване. Тези числа са предназначени да изразят в сбита форма най-значимите характеристики на разпределението и се наричат числени характеристики на случайна величина.

Сред числовите характеристики на случайните променливи, на първо място, се разглеждат характеристиките, които фиксират позицията на случайната променлива върху числовата ос, т.е. някаква средна стойност на произволна променлива, около която са групирани възможните й стойности. От характеристиките на позицията в теорията на вероятностите най-важна роля играе очаквана стойност, което понякога се нарича просто средна стойност на произволна променлива.

Да предположим, че дискретният RV?, Поема стойностите x (, x 2, ..., x nс вероятности Р j, p 2, ... y Ptvтези. дадено от серия за разпространение

Възможно е в тези експерименти стойността х хнаблюдаваното Н (пъти, стойност х 2 - N 2пъти, ..., стойност x n - N nведнъж. Освен това + N 2 +... + N n = N.

Средноаритметично на резултатите от наблюдението

Ако нголям, т.е. н– „Оо, тогава

описващ разпределителния център. Средната стойност на произволната величина, получена по този начин, ще се нарече математическо очакване. Нека дадем словесна формулировка на определението.

Определение 3.8. Математическо очакване (MO) дискретният RV% е число, равно на сумата от произведенията на всичките му възможни стойности по вероятностите на тези стойности (нотация M;):

Сега разгледайте случая, когато броят на възможните стойности на дискретен RV е изброим, т.е. имаме ПП

Формулата за математическото очакване остава същата, само в горната граница на сумата NSсе заменя с оо, т.е.

В този случай вече получаваме серия, която може да се разминава, т.е. съответният SV ^ може да няма математическо очакване.

Пример 3.8. SV ?, дадено от разпределителната серия

Нека намерим MO на този SV.

Решение.А-приорат. тези. планина,не съществува.

По този начин, в случай на преброим брой стойности на RV, получаваме следната дефиниция.

Определение 3.9. Математическо очакванеили средната стойност, дискретно SV,с преброим брой стойности е число, равно на сумата от поредица от произведения на всичките му възможни стойности със съответните вероятности, при условие че тази серия се сближава абсолютно, т.е.

Ако тази серия се разминава или се сближава условно, тогава те казват, че RV ^ няма математическо очакване.

Нека преминем от дискретно RV към непрекъснато с плътност p (x).

Определение 3.10. Математическо очакванеили средната стойност, непрекъснат SVсе нарича число, равно на

при условие че този интеграл се сближава абсолютно.

Ако този интеграл се отклонява или сближава конвенционално, тогава те казват, че непрекъснатото RV?, Няма математическо очакване.

Забележка 3.8.Ако всички възможни стойности на случайната променлива J;

принадлежат само на интервала ( а; Б),тогава

Очакването не е единствената характеристика на позицията, използвана в теорията на вероятностите. Понякога се използват като мода и медиана.

Определение 3.11. мода SV ^ (обозначение Мот,)най-вероятната му стойност се нарича, т.е. тази, за която вероятността p iили плътност на вероятността p (x)достига най-високата стойност.

Определение 3.12. Медиана SV ?, (обозначение срещнах)се нарича неговата стойност, за която P (t> Met) = P (?> срещнах) = 1/2.

Геометрично, за непрекъснат SV, медианата е абсцисата на тази точка на оста о,за които площите вляво и вдясно от него са еднакви и равни на 1/2.

Пример 3.9. SVT,има обхват на разпространение

Намерете математическото очакване, модус и медиана на SV

Решение. МЪ,= 0-0,1 + 1 0,3 + 2 0,5 + 3 0,1 = 1,6. Л/о? = 2. Аз (?) Не съществува.

Пример 3.10. Непрекъснат% CB има плътност

Нека намерим математическото очакване, медианата и модата.

Решение.

p (x)достига своя максимум, тогава Очевидно медианата също е равна, тъй като площите от дясната и лявата страна на правата, минаваща през точката, са равни.

В допълнение към характеристиките на позицията в теорията на вероятностите се използват редица числени характеристики за различни цели. Сред тях от особено значение са моментите – началните и централните.

Определение 3.13. Началният момент на k-тия ред SV ?, наречено математическо очакване k-тостепен на това количество: = M (t> k).

От дефинициите на математическото очакване за дискретни и непрекъснати случайни променливи следва, че

Забележка 3.9.Очевидно отправната точка на 1-ви порядък е математическото очакване.

Преди да дефинираме централния момент, ние въвеждаме нова концепция за центрирана случайна променлива.

Определение 3.14. Центрирано SV е отклонението на произволна величина от нейното математическо очакване, т.е.

Лесно е да се види това

Центрирането на произволна променлива очевидно е еквивалентно на прехвърляне на началото в точка M ;. Моментите на центрирана случайна променлива се наричат фокусни точки.

Определение 3.15. Централният момент на k-тия ред SV% се нарича математическо очакване k-тоградуси на центрирана случайна променлива:

От дефиницията на математическото очакване следва, че

Очевидно за всяка произволна променлива ^ централният момент от 1-ви ред е равен на нула: с х= M (? 0) = 0.

Втората централна точка е от особено значение за практиката. от 2.Нарича се дисперсия.

Определение 3.16. Дисперсия SV ?, се нарича математическо очакване на квадрата на съответната центрирана величина (нотация Д?)

За да се изчисли дисперсията, следните формули могат да бъдат получени директно от определението:

Преобразувайки формула (3.4), можем да получим следната формула за изчисление DL ;.

SV дисперсията е характеристиката разпръскване, разсейването на стойностите на произволна променлива относно нейното математическо очакване.

Дисперсията има размерността на квадрата на произволна променлива, което не винаги е удобно. Следователно, за по-голяма яснота, е удобно да се използва число като характеристика на разсейване, чиято размерност съвпада с размерността на произволна променлива. За да направите това, квадратният корен се извлича от дисперсията. Получената стойност се извиква стандартно отклонениеслучайна величина. Ще го означим като a: a = l / w.

За неотрицателен SV?, като характеристика понякога се използва коефициентът на вариация, равно на съотношението на стандартното отклонение към математическото очакване:

Познавайки математическото очакване и стандартното отклонение на произволна променлива, можете да получите приблизителна представа за диапазона на възможните й стойности. В много случаи можем да предположим, че стойностите на случайната променлива% само понякога надхвърлят интервала M; ± За. Това правило за нормалното разпределение, което ще обосновем по-късно, се нарича правилото на трите сигма.

Математическото очакване и дисперсията са най-често използваните числени характеристики на произволна променлива. Някои от най-простите и доста очевидни свойства на тези числени характеристики следват от дефиницията на математическото очакване и дисперсия.

Най-простиятсвойства на математическото очакване и дисперсия.

1. Математическото очакване на неслучайна стойност се равно на стойността със себе си: M (s) = s.

Наистина, тъй като количеството сприема само една стойност с вероятност 1, тогава M (c) = с 1 = c.

2. Дисперсията на неслучайната величина c е равна на нула, т.е. D (c) = 0.

Наистина ли, Dc = M (s - Ms) 2 = M (s- s) 2 = М ( 0) = 0.

3. Неслучаен фактор може да бъде изваден от знака на математическото очакване: M (s ^) = sМ (?,).

Нека покажем валидността на това свойство с примера на дискретно RV.

Нека SV е дадено от разпределителния ред

Тогава

следователно,

Свойството се доказва по подобен начин за непрекъсната случайна величина.

4. Неслучаен фактор може да бъде изваден от знака на дисперсията в квадрата:

Колкото повече моменти на произволна променлива са известни, толкова по-подробно разбиране на закона за разпределението имаме.

В теорията на вероятностите и нейните приложения се използват още две числени характеристики на случайна променлива, базирани на централните моменти от 3-ти и 4-ти порядък, коефициент на асиметрия)