Приложение на интегралното смятане в механиката. Резюме: Приложение на диференциалното и интегралното смятане за решаване на физически и геометрични задачи в MATLab
Изпратете добрата си работа в базата знания е лесно. Използвайте формата по-долу
Студенти, докторанти, млади учени, които използват базата от знания в обучението и работата си, ще ви бъдат много благодарни.
Резюме на тема: "Интеграл и неговото приложение"
Ученици
пчелен мед. колеж
No 2 203 групи
Куликова Мария
Санкт Петербург 2010 г
Въведение
Интегралният символ е въведен от 1675 г., а интегралното смятане се изучава от 1696 г. Въпреки че интегралът се изучава главно от математиците, физиците също са допринесли за тази наука. Почти нито една формула на физиката не е пълна без диференциално и интегрално смятане. Затова реших да изследвам интеграла и неговото приложение.
История на интегралното смятане
Историята на понятието интеграл е тясно свързана с проблемите на намирането на квадратури. Математиците от Древна Гърция и Рим наричат задачите за повдигане на квадрат на една или друга плоска фигура като задачи за изчисляване на площи. Латинската дума quadratura се превежда като "квадратура". Необходимостта от специален термин се обяснява с факта, че в древни времена (и по-късно, до 18 век) идеите за реалните числа все още не са били достатъчно развити. Математиците оперират с техните геометрични двойници или скалари, които не могат да бъдат умножени. Затова задачите за намиране на площи трябваше да бъдат формулирани например по следния начин: „Построете квадрат, равен по размер на дадена окръжност“. (Както е добре известно, тази класическа задача за „квадратура на кръг“ не може да бъде решена с пергел и линейка.)
Символът t е въведен от Лайбниц (1675). Този знак е промяна на латинската буква S (първата буква на думата summ a) Самата дума интеграл е измислена от Й. Бернули (1690 г.). Вероятно идва от латинското integro, което се превежда като връщане към предишното състояние, възстановяване. (Наистина, операцията на интегриране „възстановява“ функцията, чието диференциране дава интегранта.) Може би произходът на термина интеграл е различен: думата цяло число означава цяло.
По време на кореспонденцията И. Бернули и Г. Лайбниц се съгласяват с предложението на Й. Бернули. След това през 1696 г. се появява името на нов клон на математиката - интегрално смятане (calculus integralis), което е въведено от И. Бернули.
Други добре известни термини, свързани с интегралното смятане, се появяват много по-късно. Наименованието противопроизводна функция, което сега се използва, замени по-ранната „примитивна функция“, въведена от Лагранж (1797). Латинската дума primitivus се превежда като "начален": F(x) = m f(x)dx - начален (или начален, или антипроизводен) за f (x), който се получава от F(x) чрез диференциране.
В съвременната литература множеството от всички първоизводни за функцията f(x) се нарича още неопределен интеграл. Тази концепция беше разграничена от Лайбниц, който забеляза, че всички антипроизводни функции се различават от произволна константа b, наречена определен интеграл (обозначението е въведено от C. Fourier (1768-1830), но Ойлер вече посочи границите на интегрирането).
Много значителни постижения на математиците от Древна Гърция при решаването на проблеми с намирането на квадратури (т.е. изчисляване на площи) на плоски фигури, както и кубатура (изчисляване на обеми) на тела, са свързани с използването на метода на изчерпване, предложен от Евдокс от Книд. (ок. 408 - ок. 355 пр. н. е.) .e.). Използвайки този метод, Евдокс доказва например, че площите на два кръга са свързани като квадратите на техните диаметри и че обемът на конус е равен на 1/3 от обема на цилиндър със същата основа и височина .
Методът на Евдокс е подобрен от Архимед. Основните етапи, характеризиращи метода на Архимед: 1) доказано е, че площта на кръга е по-малка от площта на всеки правилен многоъгълник, описан около него, но по-голяма от площта на всеки вписан; 2) доказано е, че при неограничено удвояване на броя на страните разликата в площите на тези многоъгълници клони към нула; 3) за да се изчисли площта на кръг, остава да се намери стойността, към която се стреми съотношението на площта на правилен многоъгълник с неограничено удвояване на броя на неговите страни.
С помощта на метода на изчерпване и редица други остроумни съображения (включително включващи модели на механиката) Архимед решава много проблеми. Той даде оценка за p (3.10/71 Архимед е предвидил много идеи за интегрално смятане. (Нека добавим, че на практика първите гранични теореми са доказани от него.) Но са необходими повече от хиляда и половина години, преди тези идеи да намерят ясен израз и да бъдат доведени до нивото на смятане. Математиците от 17-ти век, които получават много нови резултати, се учат от трудовете на Архимед. Активно се използва и друг метод - методът на неделимите, който също произхожда от Древна Гърция (свързва се преди всичко с атомистичните възгледи на Демокрит). Например, те си представиха криволинейния трапец (фиг. 1, а), съставен от вертикални сегменти с дължина f (x), на който въпреки това приписаха площ, равна на безкрайно малка стойност f (x) dx. В съответствие с това разбиране търсената площ се счита за равна на сумата безкраен брой безкрайно малки области. Понякога дори се подчертаваше, че отделните членове в тази сума са нули, но нули от специален вид, които, събрани в безкраен брой, дават точно определена положителна сума. На такава сега изглеждаща поне съмнителна основа И. Кеплер (1571-1630) в своите писания „Нова астрономия“. 1609 и „Стереометрия на винени бъчви“ (1615) правилно изчисляват редица области (например площта на фигура, ограничена от елипса) и обеми (тялото е нарязано на 6c крайно тънки плочи). Тези изследвания са продължени от италианските математици Б. Кавалиери (1598-1647) и Е. Торичели (1608-1647). Принципът, формулиран от Б. Кавалиери, въведен от него при някои допълнителни допускания, запазва своето значение и в наше време. Нека се изисква да се намери площта на фигурата, показана на фигура 1, b, където кривите, които ограничават фигурата отгоре и отдолу, имат уравненията y = f(x) и y=f(x)+c. Представлявайки фигура, съставена от „неделими“, по терминологията на Кавалиери, безкрайно тънки колони, забелязваме, че всички те имат обща дължина c. Премествайки ги във вертикална посока, можем да направим от тях правоъгълник с основа b-a и височина c. Следователно необходимата площ е равна на площта на получения правоъгълник, т.е. S \u003d S1 \u003d c (b - a). Общият принцип на Кавалиери за площите на равнинните фигури се формулира по следния начин: Нека линиите на определен пакет от паралели пресичат фигурите F1 и F2 по отсечки с еднаква дължина (фиг. 1, c). Тогава площите на фигурите Ф1 и Ф2 са равни. Подобен принцип работи в стереометрията и е полезен при намиране на обеми. През 17 век са направени много открития, свързани с интегралното смятане. И така, P. Fermat още през 1629 г. проблемът за повдигане на квадрат на всяка крива y \u003d xn, където n е цяло число (тоест той по същество извлича формулата m xndx \u003d (1 / n + 1) xn + 1) и на тази основа той решава редица задачи за намиране на центровете на тежестта. И. Кеплер, извеждайки своите известни закони за движението на планетите, всъщност разчита на идеята за приблизителна интеграция. И. Бароу (1630-1677), учителят на Нютон, се доближава до разбирането на връзката между интеграцията и диференциацията. Работите върху представянето на функциите под формата на степенни серии бяха от голямо значение. Но въпреки цялото значение на резултатите, получени от много изключително изобретателни математици от 17-ти век, смятането все още не е съществувало. Беше необходимо да се подчертаят общите идеи, залегнали в решаването на много конкретни проблеми, както и да се установи връзка между операциите на диференциация и интеграция, което дава доста общ алгоритъм. Това е направено от Нютон и Лайбниц, които независимо откриват факт, известен като формулата на Нютон-Лайбниц. Така най-накрая се оформи общият метод. Все още беше необходимо да се научим как да намираме антипроизводните на много функции, да даваме ново логическо смятане и т.н. Но основното вече е направено: създадено е диференциално и интегрално смятане. Методите на математическия анализ се развиват активно през следващия век (на първо място трябва да се споменат имената на Л. Ойлер, който завърши систематичното изследване на интегрирането на елементарни функции, и И. Бернули). В разработването на интегралното смятане участват руските математици М.В. Остроградски (1801-1862), В.Я. Буняковски (1804-1889), П.Л. Чебишев (1821-1894). От основно значение бяха по-специално резултатите на Чебишев, който доказа, че има интеграли, които не могат да бъдат изразени чрез елементарни функции. Едва през миналия век се появи строго изложение на теорията на интеграла. Решението на този проблем е свързано с имената на О. Коши, един от най-големите математици, немския учен Б. Риман (1826-1866), френския математик Г. Дарбу (1842-1917). Отговори на много въпроси, свързани със съществуването на площи и обеми на фигури, са получени със създаването на теорията на мярката от К. Джордан (1838-1922). Различни обобщения на концепцията за интеграла вече бяха предложени в началото на нашия век от френските математици А. Лебег (1875-1941) и А. Данжуа (1884-1974), съветският математик А.Я. Хинчинчин (1894-1959). Ако F(x) е една от първоизводните на функцията f(x) на интервала J, тогава първоизводната на този интервал има формата F(x)+C, където COR. Определение. Множеството от всички първоизводни на функцията f(x) в интервала J се нарича определен интеграл на функцията f(x) в този интервал и се означава с m f(x)dx. t f(x)dx = F(x)+C, където F(x) е някаква първоизводна на интервала J. f - подинтегрална функция, f(x) - интегрална функция, x - интегрална променлива, C - интегрална константа. Свойства на неопределения интеграл. (t f(x)dx) ў = t f(x)dx, t f(x)dx = F(x)+C, където F ў(x) = f(x) (t f(x)dx) ў= (F(x)+C) ў= f(x) t f ў(x)dx = f(x)+C - от определението. t k f (x)dx = k t fў(x)dx ако k е константа и F ў(x)=f(x), t k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k t fў(x)dx t (f(x)+g(x)+...+h(x))dx = t f(x)dx + t g(x)dx +...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = t dx = t ўdx = F(x)+G(x)+...+H(x)+C= t f(x)dx + t g(x)dx +...+ t h(x)dx, където C=C1+C2+C3+...+Cn. табличен начин. Метод на заместване. Ако интеграндът не е табличен интеграл, тогава е възможно (не винаги) да се приложи този метод. За целта са ви необходими: разделяне на интегралната функция на два фактора; посочете един от множителите на новата променлива; изразете втория фактор по отношение на нова променлива; напишете интеграла, намерете неговата стойност и извършете обратно заместване. Забележка: по-добре е да посочите функцията, която е свързана с оставащия израз, като нова променлива. 1. t xT(3x2-1)dx; Нека 3x2-1=t (tі0), вземете производната на двете части: y dt 1 1 y 1 1 t 2 2 1 ---W f- t 2 \u003d - f t 2dt \u003d - --- + C \u003d -C 3x2-1 + C t sin x cos 3x dx = t - t3dt = - - + C Нека cos x = t Метод за преобразуване на интегрант в сума или разлика: t sin 3x cos x dx = 1/2 t (sin 4x + sin 2x) dx = 1/8 cos 4x - ј cos 2x + C y x4+3x2+1 y 1 1 f dx = f(x2+2 - ---) dx = - x2 + 2x - arctg x + C x x2+1 x x2+1 3 Забележка: когато решавате този пример, е добре да направите полиноми "ъгъл". На части. Ако е невъзможно да вземете интеграла в дадена форма и в същото време е много лесно да намерите първоизводната на един фактор и производната на друг, тогава можете да използвате формулата. (u(x)v(x))"=u"(x)v(x)+u(x)v(x) u"(x)v(x)=(u(x)v(x)+u(x)v"(x) t u"(x)v(x)dx=t (u(x)v(x))"dx - t u(x)v"(x)dx t u"(x)v(x)dx=u(x)v(x)dx - t u(x)v"(x)dx t x cos (x) dx = t x dsin x = x sin x - t sin x dx = x sin x + cos x + C Определение. Фигурата, ограничена от графиката на непрекъсната знакопостоянна функция f(x), абсцисната ос и правите x=a, x=b, се нарича криволинеен трапец. Начини за намиране на площта на криволинейния трапец Теорема. Ако f(x) е непрекъсната и неотрицателна функция на сегмента , тогава площта на съответния криволинеен трапец е равна на нарастването на първоизводните. Дадено е: f(x) - непрекъснато за неопределено време. функция, xO. Докажете: S = F(b) - F(a), където F(x) е първоизводната на f(x). Доказателство: 1) Разгледайте спомагателната функция S(x). На всеки xO присвояваме онази част от криволинейния трапец, която лежи отляво на правата (фиг. 2), минаваща през точката с тази абциса и успоредна на оста y. Следователно S(a)=0 и S(b)=Str Нека докажем, че S(a) е първоизводната на f(x). D(f) = D(S) = S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), за Dx®0 DS е правоъгълник Dx®0 със страни Dx и f(x0) S "(x0) \u003d lim (Dx f (x0) / Dx) \u003d lim f (x0) \u003d f (x0): тъй като x0 е точка, тогава S (x) - Dx®0 Dx®0 антипроизводно f(x). Следователно, съгласно теоремата за общата форма на първоизводната, S(x)=F(x)+C. защото S(a)=0, тогава S(a) = F(a)+C S = S(b)=F(b)+C = F(b)-F(a) 1). Нека разделим отсечката на n равни части. Разделена стъпка (фиг. 3) Dx=(b-a)/n. В този случай Str=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+ f (xn)) За n®Ґ получаваме, че Str= Dx(f(x0)+f(x1)+...+f(xn)) Границата на тази сума се нарича определен интеграл. Сумата под границата се нарича интегрална сума. Определеният интеграл е границата на интегралната сума на сегмента като n®Ґ. Интегралната сума се получава като границата на сумата от произведенията на дължината на сегмента, получена чрез разделяне на домейна на функцията във всяка точка от този интервал. а - долна граница на интегриране; б - отгоре. Формула на Нютон-Лайбниц. Сравнявайки формулите за площта на криволинейния трапец, заключаваме: ако F е първоизводната на b на , тогава f(x)dx = F(b)-F(a) t f(x)dx = F(x) f = F(b) - F(a) Свойства на определен интеграл. t f(x)dx = t f(z)dz t f(x)dx = F(a) - F(a) = 0 t f(x)dx = - t f(x)dx t f(x)dx = F(a) - F(b) t f(x)dx = F(b) - F(a) = - (F(a) - F(b)) Ако a, b и c са произволни точки от интервала I, в които непрекъснатата функция f(x) има първоизводна, тогава t f(x)dx = t f(x)dx + t f(x)dx F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a) (това е свойството на адитивност на определен интеграл) Ако l и m са константи, тогава t (lf(x) +m j(x))dx = l t f(x)dx + m tj(x))dx - Това е свойството за линейност на определен интеграл. t (f(x)+g(x)+...+h(x))dx = t f(x)dx+ t g(x)dx+...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H (a)+Cn=b b b = t f(x)dx+ t g(x)dx+...+ t h(x)dx Комплект стандартни снимки (фиг. 4, 5, 6, 7, 8) Ориз. 4 Фиг. 5 Ориз. 6 Фиг. 7 защото f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0. Необходимо е: да се вземе предвид симетрията на функцията по отношение на оста OX. ABCD®A"B"CD b S (ABCD) \u003d S (A "B" CD) \u003d t -f (x) dx S= t f(x)dx = t g(x)dx S = t(f(x)-g(x))dx+t(g(x)-f(x))dx S= t (f(x)+m-g(x)-m)dx = t (f(x)-g(x))dx t ((f(x)-g(x))dx S= t (f(x)+m-g(x)-m)dx = T (f(x)-g(x))dx Ако върху сегмента f(x)іg(x), тогава площта между тези графики е равна на t ((f(x)-g(x))dx Функциите f(x) и g(x) са произволни и неотрицателни S=t f(x)dx - t g(x)dx = t (f(x)-g(x))dx Приложение на интеграла Във физиката. Силова работа (A=FScosa, cosa № 1) Ако върху частица действа сила F, кинетичната енергия не остава постоянна. В случая според нарастването на кинетичната енергия на частицата за време dt е равно на скаларното произведение Fds, където ds е изместването на частицата за време dt. Стойност се нарича работата, извършена от силата F. Нека точка се движи по оста OX под действието на сила, чиято проекция върху оста OX е функция f(x) (f-непрекъсната функция). Под действието на силата точката се премести от точка S1(a) до S2(b). Нека разделим сегмента на n сегмента с еднаква дължина Dx = (b - a)/n. Работата на силата ще бъде равна на сумата от работата на силата върху получените сегменти. защото f(x) -непрекъснато, тогава за малки работата на силата върху този сегмент е равна на f(a)(x1-a). По същия начин, на втория сегмент f(x1)(x2-x1), на n-тия сегмент - f(xn-1)(b-xn-1). Следователно работата върху е равна на: А » An = f(a)Dx +f(x1)Dx+...+f(xn-1)Dx= ((b-a)/n)(f(a)+f(x1)+...+f (xn-1)) Приблизителното равенство става точно, когато n®Ґ A = lim [(b-a)/n] (f(a)+...+f(xn-1))= t f(x)dx (по дефиниция) Нека пружина с твърдост C и дължина l е компресирана наполовина от дължината си. Определете големината на потенциалната енергия Ep е равна на работата A, извършена от силата -F (s) еластичността на пружината, когато е компресирана, тогава Ep \u003d A \u003d - t (-F (s)) dx От курса на механиката е известно, че F(s)= -Cs. От тук намираме En \u003d - t (-Cs) ds \u003d CS2 / 2 | = C/2 l2/4 Отговор: Cl2/8. Координати на центъра на масата Центърът на масата е точката, през която преминава резултантната на гравитацията за всяко пространствено разположение на тялото. Нека материалната хомогенна плоча o има формата на криволинеен трапец (x;y |aЈxЈb; 0ЈyЈf(x)) и функцията y=f(x) е непрекъсната върху , а площта на този криволинеен трапец е равна на S, тогава координатите на центъра на масата на плочата o се намират по формулите: x0 = (1/S) t x f(x) dx; y0 = (1/2S) t f 2(x) dx; Център на масата. Намерете центъра на масата на еднороден полукръг с радиус R. Начертайте полукръг в координатната система OXY (фиг. 9). От съображения за симетрия и хомогенност отбелязваме, че абсцисата на точка М Функцията, описваща полукръга, има формата: Тогава нека S = pR2/2 е площта на полукръга y = (1/2S) tC(R2-x2)dx = (1/pR2) tC(R2-x2)dx = -R -R R = (1/pR2)(R2x-x3/3)|= 4R/3p Отговор: M(0; 4R/3p) Пътят, изминат от материална точка Ако материалната точка се движи праволинейно със скорост u=u(t) и за времето T= t2-t1 (t2>t1) е изминала пътя S, то В геометрията Обемът е количествена характеристика на пространствено тяло. За единица обем се приема куб с ръб 1 mm (1di, 1m и т.н.). Броят на кубчетата от единица обем, поставени в дадено тяло, е обемът на тялото. Аксиоми на обема: Обемът е неотрицателна стойност. Обемът на едно тяло е равен на сбора от обемите на телата, които го изграждат. Нека намерим формулата за изчисляване на обема (фиг. 10): изберете оста OX в посоката на местоположението на това тяло; определяне на границите на местоположението на тялото спрямо OX; Нека въведем спомагателна функция S(x), която определя следното съответствие: на всеки x от отсечката, поставяме в съответствие площта на сечението на дадената фигура от равнината, минаваща през дадената точка x, перпендикулярна на оста OX. нека разделим сегмента на n равни части и начертаем равнина, перпендикулярна на оста OX през всяка точка от разделението, докато тялото ни ще бъде разделено на части. Според аксиомата V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx Dx®0, и Sk®Sk+1, а обемът на частта, затворена между две съседни равнини, е равен на обема на цилиндъра Vц=SonH. Имаме сумата от продуктите на стойностите на функцията в точките на разделяне по стъпката на разделяне, т.е. интегрална сума. По дефиницията на определен интеграл границата на тази сума като n®Ґ се нарича интеграл a V= t S(x)dx, където S(x) е сечението на равнината, преминаваща през b избрана точка, перпендикулярна на оста OX. За да намерите необходимия обем: 1). Изберете оста OX по удобен начин. 2). Определете границите на местоположението на това тяло спрямо оста. 3). Да се построи сечение на дадено тяло с равнина, перпендикулярна на оста OX и минаваща през съответната точка. 4). Изразете чрез известни количества функция, която изразява площта на дадено сечение. 5). Направете интеграл. 6). След като изчислите интеграла, намерете обема. Обем на фигурите на въртене Тялото, получено в резултат на въртенето на плоска фигура около някаква ос, се нарича фигура на въртене. Функцията S(x) на ротационната фигура има кръг. Ssec(x)=p f 2(x) Дължина на дъгата на плоска крива Нека функцията y = f(x) има непрекъсната производна y" = f "(x) на сегмента. В този случай дължината на дъгата l на „парчето“ от графиката на функцията y = f(x), xO може да се намери по формулата l \u003d t C (1 + f "(x) 2) dx 1. М.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд, "Алгебра и математически анализ", Москва, 1993 г 2. “Сборник задачи по математически анализ”, Москва, 1996г 3. И.В. Савелиев, „Курс по обща физика”, том 1, Москва, 1982 г 4. За подготовката на тази работа са използвани материали от сайта http://referatovbank.ru/. Идеи за интегрално смятане в трудовете на древните математици. Характеристики на метода на изчерпване. Историята на намирането на формулата за обем на тора на Кеплер. Теоретично обосноваване на принципа на интегралното смятане (принцип на Кавалиери). Понятието за определен интеграл. презентация, добавена на 05.07.2016 г История на интегралното смятане. Определение и свойства на двойния интеграл. Неговата геометрична интерпретация, изчисляване в декартови и полярни координати, свеждането му до повторения. Приложение в икономиката и геометрията за изчисляване на обеми и площи. курсова работа, добавена на 16.10.2013 г Определение на определен интеграл, неговите свойства. Дължината на дъгата на кривата. Площ на криволинеен трапец. Повърхностна площ на въртене. Области на фигури, ограничени от графики на функции, ограничени от линии, дадени от уравнения. Изчисляване на обеми на тела. контролна работа, добавена 02/10/2017 Историята на появата на понятието "интеграл" и интегрално смятане, неговите характеристики и значение. Интеграл като един от основните инструменти за работа с функции. Обосновка на необходимостта от изразяване на всички физически явления под формата на математическа формула. презентация, добавена на 19.05.2014 г Определение на криволинейния интеграл по координати, неговите основни свойства и изчисляване. Условие на независимост на криволинейния интеграл от пътя на интегриране. Изчисляване на площите на фигури чрез двоен интеграл. Използвайки формулата на Грийн. тест, добавен на 23.02.2011 г Методи за изчисляване на интеграли. Формули и проверка на неопределен интеграл. Площ на криволинеен трапец. Неопределен, определен и сложен интеграл. Основни приложения на интегралите. Геометричен смисъл на определени и неопределени интеграли. презентация, добавена на 15.01.2014 г Решаване на проблема за намиране на площта на криволинейния трапец. Определение и свойства на определен интеграл. Необходимо условие за интегрируемост и критерия на Дарбу. Интегрируемост на непрекъснати и монотонни функции. Доказателство за формулата на Нютон-Лайбниц. тест, добавен на 25.03.2011 г Изчисляване на площите на равнинни фигури. Намиране на определен интеграл на функция. Определяне на площта под кривата, площта на фигурата, затворена между кривите. Изчисляване на обемите на телата на въртене. Границата на интегралната сума на функция. Определяне на обема на цилиндър. презентация, добавена на 18.09.2013 г Понятието за определен интеграл, изчисляване на площта, обема на тялото и дължината на дъгата, статичния момент и центъра на тежестта на кривата. Изчисляване на площта в случай на правоъгълна криволинейна област. Приложение на криволинейни, повърхностни и тройни интеграли. курсова работа, добавена на 19.05.2011 г История на интегралното и диференциалното смятане. Приложения на определения интеграл за решаване на някои задачи на механиката и физиката. Моменти и масови центрове на равнинни криви, теорема на Гулден. Диференциални уравнения. Примери за решаване на проблеми в MatLab. "Омска държавна медицинска академия" Министерство на здравеопазването и социалното развитие на Руската федерация на тема: приложение на определен интеграл в медицината завършен от студент 1-ва година отделения по обща медицина група 102F Глушнева Н.А. Въведение Изключителен италиански физик и астроном, един от основателите на точното естествознание, Галилео Галилей (1564-1642) каза, че "Книгата на природата е написана на езика на математиката". Почти двеста години по-късно основателят на немската класическа философия Кант (1742-1804) твърди, че „Във всяка наука има толкова истина, колкото математика в нея“. Накрая, след почти сто и петдесет години, практически вече в наше време, немският математик и логик Давид Хилберт (1862-1943) заявява: „Математиката е основата на всички точни природни науки“. Леонардо да Винчи е казал: „Нека никой, който не е математик, не ме чете в моите основи.“ Опитвайки се да намери математическа обосновка на законите на природата, смятайки математиката за мощно средство за познание, той я прилага дори в такава наука като анатомията. Всеки има нужда от математика. И лекарите също. Поне за да разчетете правилно обичайната кардиограма. Без познаване на основите на математиката е невъзможно да бъдеш добър компютърен техник, да използваш възможностите на компютърната томография ... В крайна сметка съвременната медицина не може без най-сложната технология. Днес е невъзможно да се изследва хемодинамиката - движението на кръвта през съдовете без използването на интеграла. Дълго време катетеризацията на дясното сърце беше единственият метод за изследване, който позволяваше да се оцени състоянието на дясното сърце, да се получат характеристики на интракардиалния кръвен поток и да се определи налягането в дясната сърдечна и белодробната артерия. Въпреки това, по-близо до практиката. Първо, нека намерим линейната скорост на кръвния поток Промяна в линейната скорост на кръвния поток в различни съдове Това е пътят, изминат за единица време от частица кръв в съд. Линейната скорост в съдовете от различни видове е различна (виж фигурата) и зависи от обемната скорост на кръвния поток и площта на напречното сечение на съдовете. В практическата медицина линейната скорост на кръвния поток се измерва с помощта на ултразвукови и индикаторни методи, по-често се определя времето на пълно кръвообращение, което е 21-23 s. За да се определи, в кубиталната вена се въвежда индикатор (белязани с радиоактивен изотоп еритроцити, разтвор на метиленово синьо и др.) и се отбелязва времето на първото му появяване във венозната кръв на същия съд на другия крайник. Като начало, нека припомним, че интегралът е математически обект, възникнал исторически въз основа на необходимостта от решаване на различни приложни проблеми на физиката и технологиите. Това са физическите приложения на определен интеграл: изчисляване на пътя на материална точка, движеща се по праволинейна или криволинейна траектория със скоростта на нейното движение. Физичните величини, които се определят с помощта на интеграл, обикновено се наричат интегрални, а тези, чрез които се изразяват интегрални величини, се наричат диференциални. Например скоростта на тялото в точка е диференциална характеристика на тялото, а масата на тялото е интегрална характеристика. Диференциалните характеристики се определят от стойността в дадена точка и обикновено са различни в различните точки на пространството. Интегралните характеристики винаги изразяват свойствата на обектите, свързани с целия регион на пространството. Например масата характеризира цялото тяло като някакъв обект, заемащ област от пространството. Пътят, изминат от тялото, също е интегрална характеристика, тъй като характеризира цялата траектория, състояща се от много точки, а скоростта е различна във всяка точка от траекторията и характеризира всяка точка поотделно. Възниква въпросът - как да се изчисли интегралната скорост за целия съд (артерия или вена), като се знае линейната скорост на кръвния поток. Много е просто: имате нужда По-долу са изчисленията на ударния обем (ударен обем на сърцето (син.: систоличен кръвен обем, систоличен обем на сърцето, ударен обем на кръвта) - обемът на кръвта (в ml), изхвърлена от вентрикула на сърцето в една систола) - една от основните стойности в EHOkg, изчислена с помощта на интеграла на линейната скорост на кръвния поток. a - Схеми за изчисляване на ударния обем, a - използване на уравнението за непрекъснатост на потока, b - използване на уравнението за непрекъснатост на потока при наличие на значителна митрална регургитация. VTI = V cp ET, където CSA е площта на напречното сечение, VTI е линейният интеграл на скоростта на потока, V cp е средната скорост на потока в изходящия тракт на лявата камера, ET е времето на изтласкване. В случай на хемодинамично значима митрална регургитация (повече от 2-ра степен), общият ударен обем на лявата камера се изчислява по формулата: TSV=FSV+RSV [Интеграл на линейната скорост (FVI или VTI)] = [Време на кръвния поток (ET)] x [Средна скорост на кръвния поток (Vmean)]; Сърдечният дебит може да се определи от интеграла на линейната скорост на аортния и белодробния поток. В заключение бих искал да добавя, че работата ми не е предназначена за математик, който е добре запознат с интеграцията, а за всеки човек, който е проявил интерес към използването на интеграла в медицината. Затова се опитах да го направя възможно най-достъпен за възприемане и интересен дори за дете. Библиография: Открит урок по алгебра и началото на анализа в 11 клас с разширено изучаване на математика и физика „Приложение на методите на математическия анализ при решаване на практически задачи”. Учител: Вишневская Н.В. Цели на урока: 1. Повторете основните видове задачи, решени с методите на математическия анализ. 2. Повторете алгоритмите за решаване. 3. Анализирайте решението на проблеми с повишена трудност. 4. Решете икономически проблеми. План на урока: На дъската се анализират две задачи с повишена трудност (карти № 7 и № 5). Докато момчетата се подготвят, класът устно отговаря на въпросите: а) Области, в които се прилагат методите на математическия анализ; б) алгоритъм за решаване на проблеми чрез търсене на най-големите и най-малките стойности на функция; в) алгоритъм за решаване на задачи с помощта на определен интеграл. В същото време 6 души работят върху карти (№ 3, 4, 6, 8, 9, 10). Масите се запълват. Задачите се проверяват на дъската, учителят проверява правилността на решаването на задачи на карти. Икономическият проблем се анализира на дъската (карта № 1, 2). Работа по домашен контрол. Алгоритъм за решаване на задачи чрез търсене на най-голямата и най-малката стойност на функция. Алгоритъм за изчисляване на геометрични и физични величини с помощта на определен интеграл. Изразете желаната стойност като стойността в даден момент от функцията Е
.
Намерете производната fтази функция. изразяват функция Епод формата на определен интеграл от fи го изчислете. Заместваща стойност х = bнамерете желаната стойност. Домашни задачи (на дъската):
Два кораба се движат по две перпендикулярни прави, които се пресичат в една точка ОТНОСНО, към ОТНОСНО. В някакъв момент и двете са на 65 км ОТНОСНО, скоростта на първия е 15 км/ч, на втория 20 км/ч. От първия кораб тръгва моторна лодка, движеща се със скорост 25 km/h. а) Какво е най-краткото време, необходимо на лодката да пътува от първия кораб до втория? б) Какво е най-краткото време, необходимо на лодката да преплува от първия кораб до втория и да се върне обратно на първия кораб? V 1 = 15 км/ч 65 км С
1 ОТНОСНО
С
3 С
2
65 км V l = 25 км/ч V 2 = 20 км/ч Решение:
х- времето, изминало от момента, в който двата кораба са били на 65 км ОТНОСНОдо отплаването на лодката. В момента на тръгване на лодката първият кораб беше на разстояние Разграничете по отношение на х:
Отговор: а) 1 час; б) 3 часа. Котелът има формата на въртящ се параболоид. Радиусът на основата му Р= 3 м, дълб з\u003d 5 м. Котелът е пълен с течност, чието специфично тегло е 0,8 G / cm 3. Изчислете работата, която трябва да се извърши, за да се изпомпва течността от котела. при
при
Р= 3 м з= 5 м удари тегло = 0,8 g / cm 3 Изчислете работата, която трябва да се извърши, за да се изпомпва течността от котела. Решение:
В равнината на сечението хей AOBе парабола, чието уравнение Координати на точки INтрябва да удовлетворява това уравнение, т.е. Нека разделим параболоида на слоеве чрез равнини, успоредни на повърхността на течността. Нека дебелината на слоя на дълбочина ( з – y)е равно на dy. След това, като вземем приблизително слоя като цилиндър, получаваме неговия обем От уравнението на параболата Следователно, за да изпомпвате течност от дълбочина Отговор: Работа в клас.
Колко работа трябва да се изразходва, за да се разтегне пружината с 6 cm, ако сила от 1 kg я разтяга с 1 cm? Решение:
Според закона на Хук силата Екг, разтягане на пружината с х, е равно на х= 0,01 m Е= 1 кг Тогава Търсена работа Отговор: 0,18 kGm. Изчислете работата на силата Екогато една пружина се свие с 5 cm, ако е необходима сила от 1 kg, за да се свие с 1 cm. Решение:
Според закона на Хук х= 0,01 m Е= 1 кг Тогава Търсена работа Отговор: 0,125 kGm. Сила Е, с което електрическият заряд Където к- постоянен. Определете работата на силата Епри движение на заряд Решение:
Работата се определя по формулата При Отговор: Определете силата на налягането на водата върху вертикална стена с форма на полукръг с радиус Р= 6 m, чийто диаметър е на повърхността на водата. Решение:
Силата на натиска на флуида върху площ Сна дълбочина на потапяне хе равно на x C
dx
А Б
Разделяме полукръга с успоредни прави линии на ивици, които ще приемем като правоъгълник. Нека защрихованата лента има дължина AB, ширина dxи е дълбоко х Водно налягане върху лента в дълбочина х, ще бъде равно на . Оттук Специфичното тегло на водата 1 cm 3 \u003d 1 G, следователно теглото на 1 m 3 \u003d 1000 kg. 1 кг 1 бар = 0,987 атм. Отговор: 144000 кг. Скорост на движение на точката Решение:
Следователно Отговор: 512 m; 64 m/s Карта номер 1 (решено в клас на дъската)
Средни общи разходи за производство на сапун Връзката между годишните продажби, равни на годишното производство Q, и цената на сапуна Р(в хиляди рубли на тон) се описва с формулата След като продаде целия сапун, приготвен през годината на фиксирана цена, заводът получи максималната възможна печалба. Какви бяха приходите на компанията? Решение:
Експрес чрез Qпърво цената на сапуна от формулата Тогава печалба Жможе да се изрази: Нека намерим критичните точки на тази функция: Критични точки 100, -340, -120. Отрицателните корени нямат икономически смисъл. Q
Ж
Така че оптималният годишен обем сапун След това годишният доход Рще бъде: (хиляда рубли). Отговор: 1 милион рубли. Намерете налягането на водата върху правоъгълник, потопен вертикално във вода, ако е известно, че основата му е 8 m, височината е 12 m, горната основа е успоредна на водната повърхност и е на дълбочина 5 m. Решение:
5 м 8 м х
dx 12 м kGm. Отговор: Карта № 2 (по избор)
Производственият капацитет позволява на предприятието Linotron да произвежда не повече от 600 тона памучна вата годишно. Зависимост на стойността на общите разходи Връзка между годишните продажби на памучна вата, която е същата като годишния производствен обем, и цената на памучната вата Р(в хиляди рубли на тон) се описва от функцията Цената на ватата е определена на 1 януари 1995 г. и се ревизира едва на 1 януари следващата година. Намерете с точност до 1% рентабилността на производството по отношение на разходите, ако през 1995 г. предприятието получи максималната възможна печалба. Решение:
Използване на зависимости y y а 0b c x a 0b c x
Интегралното смятане възниква във връзка с решаването на задачи за определяне на площи и обеми. 2000 г. пр.н.е жителите на Египет и Вавилон вече знаеха как да определят приблизителната площ на кръг и знаеха правилото за изчисляване на обема на пресечена пирамида. Теоретичната обосновка на правилата за изчисляване на площи и обеми се появява за първи път сред древните гърци. Философът материалист Демокрит V век пр.н.е разглежда телата като състоящи се от голям брой малки частици. Тоест, конусът е набор от много тънки цилиндрични дискове с различни радиуси. Огромна роля в историята на интегралното смятане изигра проблемът за квадратурата на кръга(квадратура на кръг - изграждане на квадрат, чиято площ е равна на площта на даден кръг). Точната квадратура на няколко криволинейни фигури е открита от Хипократ (ср 5 век). Първият известен метод за изчисляване на интеграла е методът на изчерпване на Евдокс (ок. 370 г. пр.н.е.). Той се опита да намери области и обеми, като ги раздели на безкраен брой части, за които площта или обемът вече са известни. Този метод е подбран и разработен от Архимед, използван за изчисляване на площите на параболите и приблизително изчисляване на площта на кръг.В своето есе Квадратура на парабола Архимед използва метода на изчерпване, за да изчисли площта на сектор от парабола. Тези. Архимед е първият, който съставя суми, които в наше време се наричат интегрални суми. Първите значителни опити за разработване на интеграционните методи на Архимед, които бяха увенчани с успех, бяха направени през XVII век, когато, от една страна, е постигнат значителен напредък в областта на алгебрата, а от друга страна, икономиката, технологиите, естествените науки се развиват все по-интензивно и там са необходими обширни и задълбочени методи за изучаване и изчисляване на величини . При изчисляване на площта на криволинейния трапецНютон и Лайбниц стигат до концепциятаантипроизводна (или примитивна) функция за дадена производна функцияf(Х),КъдетоСЪСможе да е всичко. Тада се обадят днес
Работата по изучаването на основите на диференциалното и интегралното смятане започва през XIX век от трудовете на О. Коши и Б. Болцано. В същото време руските математици М. В. имат значителен принос в развитието на интегралното смятане. Остроградски, В.Я. Буняковски, В.Я. Чебишев. Това беше времето, когато съвременният математически анализ едва се създаваше. Това беше може би единствената епоха на математическото творчество по отношение на неговата интензивност и Ойлер обедини обширния, но разнороден материал на новия анализ в цялостна наука. С време, човек придобива все по-голяма власт над природата, но мечтата за полет до звездите остава също толкова неосъществима. Писатели на научна фантастика са споменавали ракети за космически полети. Тези ракети обаче бяха технически несъстоятелна мечта. Честта да отвори пътя към звездите за хората падна на нашия сънародник К. Е. Циолковски. Цяла плеяда учени, водени от S.P. Корольов. Особен интерес представляват задачи, които са прототип на задачи за изчисляване на траекториите на космически кораби, влизащи в дадена орбита, за намиране на височината и скоростта на издигане или спускане на тяло и някои други задачи с помощта на интегрално смятане. Задача 1. Дадена е скоростта на праволинейното движение на тялото уравнение . Намерете уравнението на пътя S, ако тялото е изминало 20m за време t = 2sec. Решение: Когато летите в космоса, е необходимо да вземете предвид всички фактори на околната среда около нас и за да стигнете там, където трябва, трябва да изчислите траекторията на движение, като използвате първоначалните данни. Всичко това трябва да се направи преди полета да се осъществи.През 2016 г. се навършват 55 години от полета в орбита на първия космонавт Юрий Алексеевич Гагарин. При изчисляването беше необходимо да се решат такива проблеми. Задача 2. Необходимо е да се изстреля ракета с тегло P \u003d 2 10 4 H (T)от повърхността на земята до височинач= 1500 км.Изчислете работата, необходима за изпълнението му. Решение.f - силата на привличане на тялото от Земята е функция на разстоянието до него хдо центъра на Земята: , където На повърхността на Земята, където силата на гравитацията е равна на теглото на тялото Р, А x = R- радиус на Земята, следователно, и При повдигане на ракета от повърхността на Земята на височина чпроменлива хпромени отх
= Rпреди х=
Р+
ч. Намираме търсената работа по формулата: Задача 3. сила в 10 Нопъва пружината 2 см. Каква работа е тя дали? Решение
.
Според закона на Хук силатаЕ , разтягане на пружината, е пропорционално на разтягането на пружината, т.е.Е =х.От условието на проблема k= 10/0,02(N/m),Че Е= 500x. работа: Задача 4. От дълбока минал= 100 ме необходимо клетката да се повдига равномерно с тежест R 1 = 10 4
з, който виси на въже, навито на барабан. Изчислете общата работа Пъленнеобходими за повдигане на клетката, ако теглото на един линеен метър въже R 2= 20з.
Решение
.
Работата по повдигането на клетката: и повдигането на въжето е пропорционално на теглото на въжето, т.е. Задача 5. Пружината се огъва под действието на сила от 1,5 10 4 зс 1 см. Колко работа трябва да се извърши, за да се деформира пружината с 3 cm? (Деформиращата сила е пропорционална на деформацията на пружината.) Решение
.
Е\u003d kx,Където х- деформация на пружината. При x = 0,01mние имаме: Издигането в открития космос е трудно и опасно, но не по-малко трудно е връщането на Земята, когато космическият кораб трябва да кацне със скорост не повече от 2 м/с. Само в този случай устройството, инструментите в него и най-важното членовете на екипажа няма да получат рязък силен удар. Константин Едуардович Циолковски решава да използва забавянето на космическия кораб от въздушната обвивка на Земята. Движейки се със скорост 8 m/s, космическият кораб не пада на Земята. Първият етап на спускане е включването на спирачен двигател за кратко време. Скоростта намалява с 0,2 km/s и веднага започва спускането. Помислете за пример за решаване на проблема за съставяне на закона за движение при дадени условия. Задача 6. Намерете закона за движение на свободно падащо тяло с постоянно ускорение g, ако тялото е било в покой в момента на движение. Решение:Известно е, че ускорението на праволинейно движещо се тяло е втората производна на пътя S по време T , или производна на скоростта спрямо времето T : , но, следователно, , откъде . Интегрираме: , и От условието: , откъдето намираме и скоростта на движение: . Нека намерим закона за движение на тялото: , или . Ние интегрираме: , . Според началните условия: , откъдето намираме Имаме уравнението на движението на падащо тяло: - това е позната формула на физиката. Задача 7. Тяло се хвърля вертикално нагоре с начална скорост Намерете уравнението на движението на това тяло (пренебрегвайте въздушното съпротивление). Решение:Да вземем: вертикалната посока нагоре е положителна, а ускорението на гравитацията, насочено надолу, е отрицателно. Имаме: откъде. Ние интегрираме: тогава . защото и след това C 1: Следващият пример показва изчисляването на траекторията за изхвърляне на отработени участъци, ненужни устройства, материали. В този случай те се изпращат на Земята, като са изчислили орбитата така, че при преминаване през атмосферните слоеве те изгарят, а неизгорелите остатъци падат на Земята (най-често в океана), без да причиняват вреда. Задача 8. Напишете уравнение за крива, минаваща през точка M (2; -3) и имаща допирателна с наклон .
Решение:Дадено е условието на задачата: Понякога строителите трябва да решават проблеми с изчисляването на площите на необичайни фигури, за които няма добре известни формули. В този случай интегралите отново идват на помощ.
.
Космонавтите и учените, работещи на орбиталната станция, за чистотата на експеримента решават и изследват много въпроси от астрономията, физиката, химията, медицината, биологията и др. Ще придружим следния проблем с литературен пример. Известният научно-фантастичен роман на Хърбърт Уелс "Войната на световете" описва атаката на марсианците на планетата Земя, които решили да разширят пренаселените си територии, като завземат нашите, т.к. Климатичните условия на Земята бяха подходящи. Започва завземането на територии и унищожаването на земляните, които получават помощ оттам, където изобщо не са очаквали. Нашите "местни" бактерии, с които вече сме се научили да се борим, влязоха в тялото на марсианците с въздух, храна, вода, намериха в него благоприятна среда за тяхното развитие и възпроизводство, бързо се адаптираха и, след като унищожиха марсианците, отървете Земята от нашествениците. Помислете за решението на проблема, което дава концепцията за това. Задача 10.Скоростта на възпроизвеждане на някои бактерии е пропорционална на броя на наличните бактерии в разглеждания момент t. Броят на бактериите се е утроил в рамките на 5 часа. Намерете зависимостта на броя на бактериите от времето. Решение:Нека x(t ) е броят на бактериите в момент t, а в началния момент след това скоростта на тяхното размножаване. По условие имаме: или следното: В известния роман на A.N. Толстой "Хиперболоид на инженер Гарин" Бих искал да почувствам, да почувствам какво е - хиперболоид? Какви са неговите размери, форма, повърхност, обем? Следващата задача е за това. Решение.Използваме формулата за изчисляване на обема на телата на въртене около оста OX с помощта на определен интеграл: Задача 12. Изчислете обема на тялото, образувано от въртене около оста OX на площта, ограничена от линиите y \u003d x 2 - 9И y = 0.
Икономическият смисъл на определен интеграл изразява обема на производството с известна функция f(t ) - производителността на труда в момента T . След това обемът на продукцията за периода се изчислява по формулата. Да разгледаме пример за предприятие. Задача 13. Намерете обема на произведената продукция за 4 години, ако функцията на Коб-Дъглас има формата Решение. Обемът на продуктите, произведени от предприятието, е равен на: Обобщавайки, можем да заключим, че използването на интеграла отваря големи възможности. Когато изучават геометрията, те разглеждат изчисляването на площите на плоски фигури, ограничени от сегменти (триъгълници, успоредници, трапеци, многоъгълници), и обемите на телата, получени по време на тяхното въртене. Определеният интеграл ви позволява да изчислите площите на сложни фигури, ограничени от всякакви криви линии, както и да намерите обемите на телата, получени чрез въртене на криволинейни трапеци около всяка ос. Бих искал също да отбележа, че използването на определен интеграл не се ограничава само до изчисляването на различни геометрични величини, но се използва и при решаване на задачи от различни области на физиката, аеродинамиката, астрономията, химията и медицината, астронавтиката, както и като икономически проблеми. Библиография:
слайд 2 Историята на понятието интеграл е тясно свързана с проблемите на намирането на квадратури, т.е. задачи за пресмятане на площи. Дори математиците от древна Гърция и Рим са се занимавали с изчисляването на повърхностите и обемите на телата. Първият европейски математик, който получи нови формули за площите на фигурите и обемите на телата, беше известният астроном И. Кеплер. След изследвания на редица учени (П. Ферма, Д. Уолис) И. Бароу открива връзката между задачите за намиране на площи и начертаване на допирателна (т.е. между интегриране и диференциране). Изследване на връзката между тези операции, свободно от геометричен език, е дадено от И. Нютон и Г. Лайбниц. Съвременната нотация на интеграла се връща към Лайбниц, който изрази идеята, че площта на криволинейния трапец е сумата от площите на безкрайно тънки ивици с ширина d и височина f(x). Самият интегрален знак представлява стилизирана латинска буква S (summa). Символът на интеграла е въведен от 1675 г., а проблемите на интегралното смятане се разглеждат от 1696 г. Въпреки че интегралът се изучава главно от математици, физиците също са допринесли за тази наука. Почти нито една формула на физиката не е пълна без диференциално и интегрално смятане. слайд 3 С името на Архимед (287-212 г. пр. н. е.) са свързани много значителни постижения на математиците от Древна Гърция при решаването на задачи за намиране на площи, както и обеми на тела.Развивайки идеите на своите предшественици, Архимед определя обиколката и площта на кръг, обемът и повърхността на топка. В трудовете си "За сферата и цилиндъра", "За спиралите", "За коноидите и сферите" той показа, че определянето на обемите на сфера, елипсоид, хиперболоид и параболоид на въртене се свежда до определяне на обем на конус и цилиндър. Архимед разработва и прилага методи, които предшестват тези, създадени през 17 век. интегрално смятане. Отне повече от една и половина хиляди години, преди идеите на Архимед да намерят ясен израз и да бъдат доведени до нивото на смятане. През 17 век математиците вече знаеха как да изчисляват площите на много фигури с извити граници и обемите на много тела. А общата теория е създадена през втората половина на 17 век. в трудовете на великия английски математик Исак Нютон (1643-1716) и великия немски математик Готфрид Лайбниц (1646-1716). Нютон и Лайбниц са основоположници на интегралното смятане. Те откриха важна теорема, която носи името им: където f(x) е функция, интегрируема в интервала, F(x) е една от нейните първоизводни. Разсъждението на Нютон и Лайбниц е несъвършено от гледна точка на съвременния математически анализ. През XVIII век. най-големият представител на математическия анализ, Леонард Ойлер, обобщи тези понятия в своите трудове. Едва в началото на XIX век. най-накрая бяха създадени концепциите за интегралното смятане. Обикновено се отбелязват заслугите на френския математик Огюстен Коши и немския математик Георг Риман. Самата дума интеграл е измислена от Й. Бернули (1690). Произлиза от латинското integro, което се превежда като връщане към предишното състояние, възстановяване. През 1696г се появява името на нов клон на математиката - интегрално смятане, който е въведен от И. Бернули. Наименованието противопроизводна функция, което сега се използва, замени по-ранната „примитивна функция“, въведена от Лагранж (1797). Нотацията за определен интеграл е въведена от Джоузеф Бернули, а долната и горната граница от Леонхард Ойлер. слайд 4 Математическите операции образуват двойки от две взаимно обратни операции, например събиране и изваждане, умножение и деление, повишаване на цяло положително число и извличане на корен. Диференцирането прави възможно дадена функция F(x) да намери своята производна F´(x). Има действие, обратно на диференцирането - това е интегриране - намиране на функцията F (x) по нейната известна производна f (x) \u003d F´ (x) или диференциала f (x) dx. Функцията F(x) се нарича първоизводна за функцията f(x), ако F´(x) = f(x) или dF(x)=f(x)dx. Ако функцията f(x) има първоизводната F(x), тогава той има безкраен набор от първоизводни и всички негови производни се съдържат в израза F(x) + С, където С е константа. Неопределеният интеграл на функция f(x) (или на израза f(x)dx) е множеството от всички нейни първоизводни. Запис ∫f(x)dx = F(x) +C. Тук ∫ е знакът на интеграла, f(x) е интегралната функция, f(x)dx е интегралната функция, x е интегралната променлива. Намирането на неопределен интеграл се нарича функционална интеграция. Свойства на неопределения интеграл Производната на неопределения интеграл е равна на интегранта: (∫ f(x)dx)´ = f(x) Диференциалът на неопределения интеграл е равен на интеграла: на диференциала на първоизводната е равно на самата антипроизводна и допълнителния член C:∫d (F(x)) = F(x) +C Постоянният фактор може да бъде изваден от знака на неопределения интеграл: алгебричната сума на краен брой функции е равна на алгебричната сума на интегралите на членовете: ∫ dx = ∫ dx ± ∫ dx слайд 5 Концепцията за определен интеграл се извежда чрез криволинейния трапец. Криволинейният трапец е фигура, ограничена от линиите y = f(x), y = 0, x=a, x=b. Определеният интеграл се изчислява с помощта на формулата на Нютон-Лайбниц. = F (x)|ba= F(b) – F(a) Общата нотация за определени и неопределени интеграли подчертава тясната връзка между тях: определен интеграл е число, а неопределен интеграл е набор от първоизводни функции. Връзката между определения и неопределения интеграл се изразява с формулата на Нютон-Лайбниц. Свойства на определен интеграл: Ако горната и долната граница на интегриране се сменят, тогава определеният интеграл ще запази абсолютната си стойност, но ще промени знака си на противоположния. Ако горната и долната граница на интегрирането са равни, тогава определеният интеграл е равен на нула. Ако сегментът на интегриране е разделен на няколко части, определеният интеграл върху сегмента ще бъде равен на сумата от определените интеграли на тези сегменти. Определеният интеграл на сумата от функции, дадени на интервала, е равен на сумата от определени интеграли на членовете на функциите. Постоянният множител към подинтегралната функция може да бъде изваден от знака на определен интеграл. Оценка на определения интеграл: ако m ≤ f(x) ≤ M on , тогава m (b – a) слайд 6 Нека функцията y=f(x) е непрекъсната на отсечката и f(x) ≥ 0. Фигурата, ограничена от графиката на функцията AB y=f(x), правите x=a, x=b и Оста Ox (виж фигурата) се нарича криволинейна трапец. Интегралната сума и нейните условия имат просто геометрично значение: продуктът е равен на площта на правоъгълник с основа и височина, а сумата е площта на защрихованата стъпаловидна фигура, показана на фигурата. Очевидно тази област зависи от разделянето на сегмента на частични сегменти и избора на броя точки на разделяне. Колкото по-малък е ∆ x, толкова по-близо е площта на стъпаловидната фигура до зоната на криволинейния трапец. Следователно границата на интегралната сума се приема като точната площ S на криволинейния трапец. По този начин, от геометрична гледна точка, определеният интеграл на неотрицателна функция е числено равен на площта на съответния криволинеен трапец. Слайд 7 1. Директно интегриране Директното интегриране обикновено се нарича изчисляване на неопределени интеграли чрез редуцирането им до таблични, като се използват основните свойства. Тук могат да възникнат следните случаи: 1) даденият интеграл се взема директно от формулата на съответния табличен интеграл; 2) след прилагане на свойствата този интеграл се редуцира до един или повече таблични интеграли; 3) даденият интеграл, след елементарни идентични трансформации върху интегранта и прилагане на свойства, се свежда до един или повече таблични интеграли. 2. Интегриране чрез метод на промяна на променлива (метод на заместване) Промяната на променлива в неопределения интеграл се извършва с помощта на два вида замествания: x = φ (t), където φ (t) е монотонна, непрекъснато диференцируема функция на новата променлива t. Формулата за промяна на променливата в този случай е ∫f(x) = ∫f [φ (t)] φ΄ (t) d(t); 2) u = ψ(x), където u е нова променлива. Промяната на формулата на променливата за това заместване е: ∫f [ψ(x)] ψ ΄(x) d(x) = ∫f (u) du v du, където u = φ (x), v = ψ(х ) са непрекъснато диференцируеми функции на x. Използвайки тази формула, намирането на интеграла ∫udv се свежда до намирането на друг интеграл ∫v du; прилагането му е целесъобразно в случаите, когато последният интеграл е или по-прост от първоначалния, или подобен на него. В този случай u се приема за такава функция, която се опростява при диференциране, а dv е онази част от интегранта, чийто интеграл е известен или може да бъде намерен. Слайд 8 Слайд 9 Как да намерите площта на показаните фигури? Слайд 10 слайд 11 В допълнение, определеният интеграл се използва за изчисляване на площите на равнинни фигури, обемите на телата на въртене и дължините на дъгите на кривите. слайд 12 Нека е дадено тяло с обем V и има такава права, че независимо коя равнина, перпендикулярна на тази права, вземем, ние знаем площта S на сечението на тялото с тази равнина. Но равнина, перпендикулярна на оста x, я пресича в някаква точка x. Следователно на всяко число x (от сегмента [a; b]) се присвоява едно число S (x) - площта на напречното сечение на тялото от тази равнина. Така на сегмента [a; b] е дадена функцията S(x). Ако функцията S е непрекъсната на отсечката [a; b] тогава е валидна формулата: слайд 13 Намерете площта на изобразените фигури 1 - 5. Отговори: 1) S = 2/3 (равномерност на функцията); 2) S = 1 (площ на правоъгълен триъгълник); 3) S = 4 (равенство на фигурите); 4) S = 2π (площ на полукръг); 5) S = 1 (площ на триъгълник). Слайд 14 Намерете сумата от площите на безкраен брой фигури, защриховани на фигурите. (Аргументът на всяка следваща функция се увеличава 2 пъти) Интересна задача! Отговор: sin nx=0 ; x=π/n; където n=1,2,4,8,16…; S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4 Отговор: 4. слайд 15 Верни отговори: I вариант: 2,3,1; II вариант: 2,4,2. слайд 16 Изчислете площта на фигурата, ограничена от линии (схематично изобразяващи функционални графики). 1) y = 6 + x – x2 и y = 6 – 2x; 2) y = 2x2 и y = x + 1; 3) y = 1 – x и y = 3 – 2x – x2; 4) y = x2 и y = . Отговор: 1) 4,5; 2) 9/8; 3) 4,5; 4) 1/3. Слайд 17 Намерете обема на тялото, получено при въртене около абсцисната ос на фигурата, ограничена от линии: 1) y = x2 + 1, x = 0, x = 1, y = 0; 2) y = , x = 1 , x = 4 , y = 0 ; 3) y = 2x, y = x + 3, x = 0, x = 1; 4) y \u003d x + 2, y \u003d 1, x = 0, x \u003d 2; 5) y2 - 4 x = 0, x - 2 = 0, x - 4 = 0, y = 0; 6) y2 - x + 1 = 0, x - 2 = 0, y = 0; 7) y \u003d - x2 + 2x, y \u003d 0; 8) y2 = 2 x, x - 2 = 0, y = 0; 9) y = , x = 3 , y = 0 ; 10) y \u003d 1 - x2, y \u003d 0. Отговор: 1) ; 2) 7,5; 3) 11 ; 4) 16 ⅔; 5) 24 ; 6) /2; 7) 16/15; 8) 4 ; 9) 2 ; 10) 16/15. Слайд 18 Намерете площта на фигурата, ограничена от линиите. 2) Фигурата, ограничена от линиите y=x+6, x=1, y=0, е разделена от параболата y=x 2+2x+4 на две части. Намерете площта на всяка част. 3) Намерете първоизводната F(x) на функцията f(x)=2x+4, чиято графика докосва правата y=6x+3. Изчислете площта на фигурата, ограничена от графиката на намерената първоизводна и правите линии y=6x+3 и y=0. Слайд 19 Какво действие се нарича интеграция? Коя функция се нарича първоизводна за функцията f(x)? Каква е разликата между различните първоизводни функции за дадена функция f(x)? Дайте дефиницията на неопределен интеграл. Как да проверя резултата от интеграцията? Каква е производната на неопределения интеграл? Какво е ∫ d(lnx8 - sin 3x)? Избройте методите на интеграция. Дайте дефиницията на определен интеграл. Формулирайте теоремата на Нютон-Лайбниц. Избройте свойствата на определения интеграл. Как да изчислим площта на плоска фигура с помощта на интеграла (направете словесен алгоритъм)? Избройте областите на приложение на интеграла, назовете количествата, които могат да бъдат изчислени с помощта на интеграла. Слайд 20 1) Изчислете площта на фигурата, ограничена от тези линии: y=x2 при x0, y=1, y=4, x=0 Решение: Тази фигура е симетрична на криволинеен трапец, ограничен от прави линии x=1, x=4, y=0 обратна функция y=x2, x0. Следователно тези фигури имат равни площи и 2) Намерете площта на фигурата, ограничена от линиите y=3x+1, y=9-x, y=x+1. Решение: Върховете на полученото ABC имат координати: A(0;1), B(2;7), C(4;5). Вижда се, че ABC е правоъгълник (произведението от наклоните на правите y=x+1 y=9-x е равно на -1). Следователно използването на интеграла за изчисляване на S(ABC) не е рационално. Винаги може да се намери като разлика в площите на триъгълници, за които са известни височината и основата, или можете да използвате метода на координатите. слайд 21 Намерете площите на фигури, ограничени от прави (1-7) y=x2 (x0), y=1, y=4, x=0 y= x2-4x+8, y=3x2-x3, ако x [ -2 ;3] y=x2-4x+sin2(x/2), y=-3-cos2(x/2), ако x y=3x+1, y=9-x, y=x+1 y= | x-2|, x|y|=2;x=1;x=3 y= arcsin x; y=0; х=0,5; x=1 При каква стойност на a правата x=a разделя площта на фигурата, ограничена от линиите y=2/x; х=1; х=3 в съотношение 1:3? Изчислете въз основа на геометричното му значение. слайд 22 Н. А. Колмогоров, "Алгебра и началото на анализа", Москва, Просвещение, 2000 г. М. И. Башмаков, "Алгебра и началото на анализа", Москва, ДРОФА, 2002 г. Ш. А. Алимов, "Алгебра и началото на анализа", 11 клас, Москва, ДРОФА, 2004 г. Л. В. Киселева, Ръководство по математика за студенти от медицински училища и колежи, Москва, FGOU "VUNMC Roszdrav", 2005 г. http://www.nerungri.edu.ru http://tambov.fio.ru http://www.zachetka.ru http://edu.of.ru http://festival.1september.ru
Вижте всички слайдовеОпределение и свойства на интеграла
Интеграция
Криволинеен трапец
Библиография
Подобни документи
Основното предимство на ехокардиографията (ЕхоКГ) е, че неинвазивно в реално време е възможно да се оцени размерът и движението на сърдечните структури, да се получат характеристики на интракардиалната хемодинамика и да се определи налягането в камерите на сърцето и белодробната артерия. Доказана е добра сравнимост на резултатите от ехокардиографията с данните, получени при сърдечна катетеризация.
Ехокардиографското изследване позволява не само да се установи наличието на белодробна хипертония, но и да се изключат редица заболявания, които причиняват вторична белодробна хипертония: дефекти на митралната клапа, вродени сърдечни дефекти, дилатативна кардиомиопатия, хроничен миокардит.Карта номер 7
– времето, необходимо на лодката да пътува от 1-ви кораб до 2-ри.
км от ОТНОСНО; в момента лодката пристига при 2-ри кораб, разстоянието между него и ОТНОСНОбеше равно на km; пътят на лодката е 
. Тогава по Питагоровата теорема
.
; 
; 
Карта номер 5
А Р
IN
dy
з
Ох х х
. Нека намерим параметъра А.
,
, следователно 
.
.
, Тогава 
, т.е. теглото на течния слой е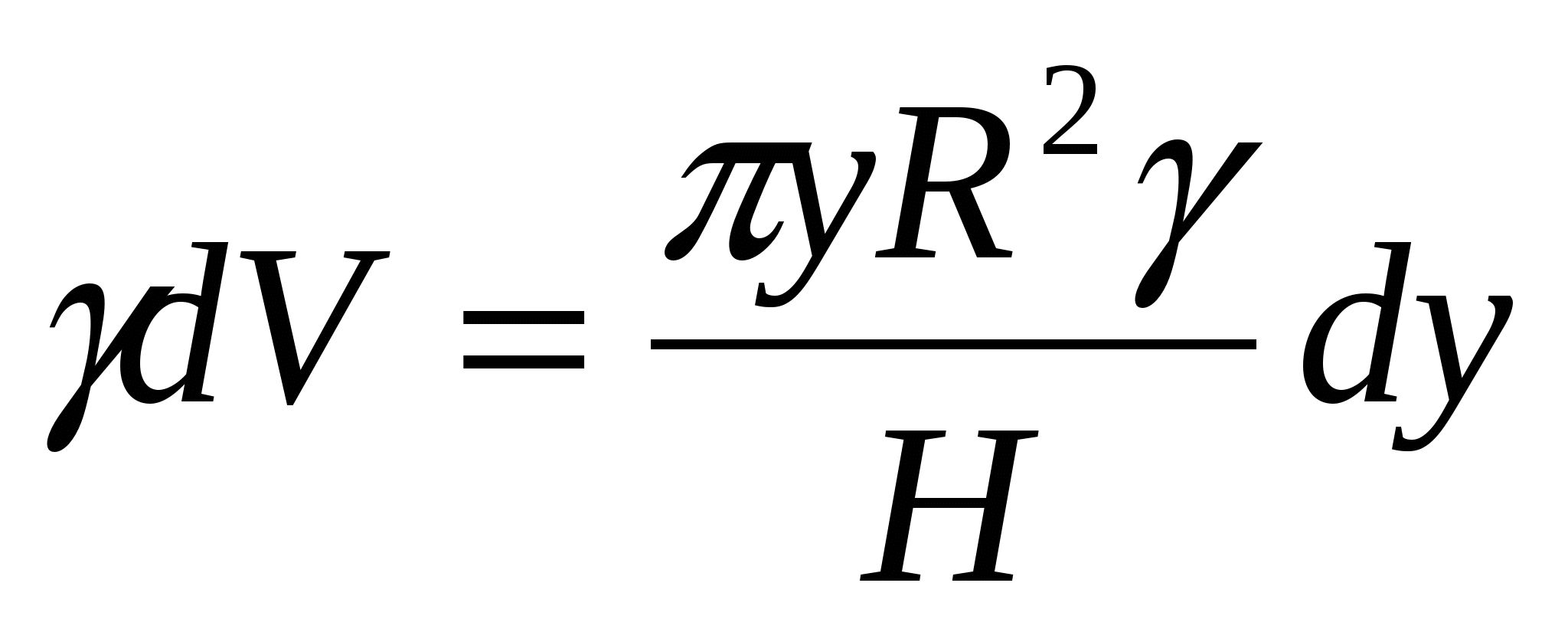 
.
, трябва да прекарате елементарна работа 
, 
. Тогава
, Тогава .
.
Карта номер 6
, k – коефициент на пропорционалност.
, следователно 
.
.
Карта номер 8
.
, следователно .
.
Карта номер 9
отблъсква заряда 
(от същия знак), разположен на разстояние от него r, се изразява с формулата
,
от точка 
, разделен от на разстояние 
, точно 
, далече от на разстояние 
, като приемем, че обвинението поставен в точката 
взети за отправна точка.
, . Тогава
.
получаваме 
.
.
Карта номер 3
, 
е специфичното тегло на течността.ОТНОСНО
.
,
,
,
.
;
9.81 нКарта номер 4
м/сек. Намери начин с, преминали през точката във времето T= 8 сек след началото на движението. Каква е средната скорост за този интервал?
, следователно 
, 
, 
.
.
.
(в хиляди рубли на тон) във фабриката за сапун Mukhinsky варират в зависимост от обема на годишното производство Q(в тонове) съгласно закона:
.
.
.
.
, 
.
;
.
t, тогава цената 
(хиляда рубли/т).Карта номер 10
, 
, 
м.
.
kGm.
(в хиляди рубли) от годишния обем на производството Q(в тонове) има формата
.
и , експрес.
формулаНютон-Лайбниц ви позволява да намалите доста сложното изчисление на определени интеграли, т.е. намиране на границите на интегрални суми, до сравнително проста операция за намиране на антипроизводни.Лайбниц притежава диференциалния символ a p По-късно се появява и интегралният символОпределен интегрален символвъвежда Ж. Фурие и термина "интеграл" (от латцяло число - цяло) е предложено от И. Бернули.
където 
Ние интегрираме: 
където 
Използвайки данните, намираме С = 4. Т.е. уравнението на движението на тялото има вида 
.
Тогава получаваме: работата за изстрелване на ракета е равна на 
.
Следователно цялата работа е завършена:
. Тогава извършената работа за деформиране е:
и Уравнение на скоростта: Намираме закона за движение на тялото: тъй като. и тогава 
където 
.Интегриране: 
или 
Когато и намерете 
, и Имаме уравнението на движението на тялото: или .
или 
Интегрирайки, имаме: 
При х = 2И y \u003d -3, C \u003d - 5, а траекторията на движение има формата: 
.
Задача 9. Изчислете площта на фигурата, ограничена от линии: и
Решение: Нека изградим чертеж (фиг. 1), за който ще решим система от уравнения. Нека намерим пресечните точки на линиите: A(-2;4) И B(4;16). Желаната площ е разликата между областите с границите на интеграция, a \u003d x 1 \u003d -2И в \u003d x 2 \u003d 4.Тогава имаме областта:
Да намерим С: и функция Известно е, че т.е. или откъдето коефициентът на пропорционалност е: и функцията има формата: 
.
Задача 11.Хипербола, ограничена от линии: y=0, x=
а, x = 2aсе върти около оста x. Намерете обема на получения хиперболоид (фиг. 2).
Уфолозите изучават фактите, цитирани от „очевидци“, казвайки, че са видели летящ космически кораб под формата на огромен светещ диск („чиния“), приблизително същата форма като на фигура 3. Помислете за решаване на проблема за определяне на обема на такова „ястие““.
Решение: При чертане на параболоид (фиг. 3) имаме границите на интегриране от х = -3преди х = 3. Нека заменим границите на интегриране поради симетрията на фигурата по отношение на оста y с х = 0И х = 3и удвоете резултата. Следователно обемът на диска е:
Историческа справка
Кратка история на интегралното смятане
Неопределен интеграл
Определен интеграл
Геометричният смисъл на определения интеграл
Интеграционни методи
Таблица на неопределените интеграли
Повторение на теоретичен материал
Продължаваме да повтаряме
Приложение на интеграла
Изчисляване на обеми на тела
ПРОВЕРЕТЕ СЕ!
Намери грешката!
Програмирано управление
Самостоятелна работа
Задачи за пресмятане на обеми
Задачи от изпита
Контролни въпроси
За любителите на математиката
Домашна работа
Библиография
Зареждане...