Ejemplo de matriz inversa de segundo orden. Matriz inversa en línea

Asignación de servicios. Usando este servicio en línea, puede encontrar sumas algebraicas, la matriz transpuesta AT, la matriz de unión y la matriz inversa.

Calculadora online. matriz inversa.

La solución se realiza directamente en el sitio (en línea) y es gratuita. Los resultados de los cálculos se presentan en un informe en formato Word y en formato Excel (es decir, es posible comprobar la solución). ver ejemplo de diseño.

Determinar si la matriz es cuadrada. Si no entonces matriz inversa no existe para ella.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

Sumas algebraicas.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Luego matriz inversa Se puede escribir como:

A-1=

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Encontrar la matriz inversa

La matriz A-1 se denomina matriz inversa con respecto a la matriz, si A*A-1 = , donde es la matriz identidad de orden ésimo. La matriz inversa solo puede existir para matrices cuadradas.

ver también Matriz inversa por el método de Jordano-Gauss

Algoritmo para encontrar la matriz inversa

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Hallar la matriz transpuesta AT.
Definición de sumas algebraicas. Reemplace cada elemento de la matriz con su complemento algebraico.
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz resultante se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

El siguiente algoritmo para encontrar la matriz inversa es similar al anterior, excepto por algunos pasos: primero se calculan los complementos algebraicos y luego se determina la matriz de unión.

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Definición de sumas algebraicas.
Llenar la matriz aliada (mutua, adjunta).
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz adjunta se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

Ejemplo 1. Escribimos la matriz de la forma:

Existe una matriz inversa si el determinante de la matriz es distinto de cero. Encuentre el determinante de la matriz:
= -1 (-1 4-(-2 5))-2 (2 4-(-2 (-2)))+3 (2 5-(-1 (-2))) = 10. El determinante es 10 y no es igual a cero. Sigamos con la solución.
Encontremos la matriz transpuesta:
Sumas algebraicas.

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Luego matriz inversa Se puede escribir como:

A-1=

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Otro algoritmo para encontrar la matriz inversa.

Presentamos otro esquema para encontrar la matriz inversa.

Encuentre el determinante de esta matriz cuadrada.
Encontramos sumas algebraicas a todos los elementos de la matriz.
Escribimos los complementos algebraicos de los elementos de las filas en las columnas (transposición).
Divide cada elemento de la matriz resultante por el determinante de la matriz.

Como ves, la operación de transposición se puede aplicar tanto al principio, sobre la matriz original, como al final, sobre las sumas algebraicas resultantes.

Caso especial: La inversa de la matriz identidad es la matriz identidad.

Ejemplo #2. Encuentra la matriz inversa de una matriz .
Solución.
1. Encuentra
.
2. Buscamos complementos algebraicos de cada elemento de la matriz A:
; ; .
Complementos algebraicos obtenidos de los elementos de la primera fila.

Encuentra la matriz inversa en línea

De manera similar, para los elementos de la segunda y tercera fila, obtenemos:
; ; .
; ; .
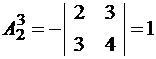Combinando 3 y 4 puntos, obtenemos la matriz inversa

.
Para probar, asegúrese de que A-1A = E.

Instrucción. Para obtener una solución, debe especificar la dimensión de la matriz. A continuación, en un nuevo cuadro de diálogo, complete la matriz.

Encontrar la matriz inversa

La matriz A-1 se denomina matriz inversa con respecto a la matriz, si A*A-1 = , donde es la matriz identidad de orden ésimo. La matriz inversa solo puede existir para matrices cuadradas.

Asignación de servicios. Usando este servicio en línea, puede encontrar sumas algebraicas, la matriz transpuesta AT, la matriz de unión y la matriz inversa. La solución se realiza directamente en el sitio (en línea) y es gratuita. Los resultados de los cálculos se presentan en un informe en formato Word y en formato Excel (es decir, es posible comprobar la solución). ver ejemplo de diseño.

Encontrar la matriz inversa en línea

ver también Matriz inversa por el método de Jordano-Gauss

Algoritmo para encontrar la matriz inversa

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Hallar la matriz transpuesta AT.
Definición de sumas algebraicas. Reemplace cada elemento de la matriz con su complemento algebraico.
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz resultante se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

El siguiente algoritmo para encontrar la matriz inversa es similar al anterior, excepto por algunos pasos: primero se calculan los complementos algebraicos y luego se determina la matriz de unión.

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Definición de sumas algebraicas.
Llenar la matriz aliada (mutua, adjunta).
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz adjunta se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

Ejemplo 1. Escribimos la matriz de la forma:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Luego matriz inversa Se puede escribir como:

A-1=

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Otro algoritmo para encontrar la matriz inversa.

Presentamos otro esquema para encontrar la matriz inversa.

Encuentre el determinante de esta matriz cuadrada.
Encontramos sumas algebraicas a todos los elementos de la matriz.
Escribimos los complementos algebraicos de los elementos de las filas en las columnas (transposición).
Divide cada elemento de la matriz resultante por el determinante de la matriz.

Como ves, la operación de transposición se puede aplicar tanto al principio, sobre la matriz original, como al final, sobre las sumas algebraicas resultantes.

Para probar, asegúrese de que A-1A = E.

Instrucción. Para obtener una solución, debe especificar la dimensión de la matriz. A continuación, en un nuevo cuadro de diálogo, complete la matriz.

Encontrar la inversa de una matriz es una parte importante de la sección de álgebra lineal. Con la ayuda de tales matrices, si existen, uno puede encontrar rápidamente una solución al sistema. ecuaciones lineales.

Una matriz se llama inversa de una matriz si se cumplen las siguientes igualdades.

Si el determinante de una matriz es distinto de cero, entonces se dice que la matriz es no especial o no singular.

Para que una matriz tenga inversa es necesario y suficiente que no sea degenerada.

Algoritmo para encontrar la matriz inversa

Tengamos una matriz cuadrada

y necesitas encontrar lo contrario. Para hacer esto, siga estos pasos:

1. Encuentra el determinante de la matriz. Si no es igual a cero, realice las siguientes acciones. De lo contrario, esta matriz es degenerada y no tiene inversa.

2. Hallar complementos algebraicos de elementos de matriz. Son iguales a los menores multiplicados por la potencia de la suma de la fila y la columna que buscamos.

3. Componer una matriz a partir de los complementos algebraicos de los elementos de la matriz matriz y transponerla. Esta matriz se llama matriz adjunta o unión y se denota por .

4. Dividir la matriz asociada en el determinante . La matriz resultante será inversa y tendrá las propiedades que se describen al principio del artículo.

Encuentre la matriz inversa a la matriz (Dubovik V.P., Yurik I.I.

Encontrar la matriz inversa

"Matemáticas Superiores. Colección de Problemas")

1) Encuentra el determinante de la matriz

Como el determinante no es igual a cero (), entonces existe la matriz inversa. Encontrar una matriz compuesta de sumas algebraicas

La matriz del complemento tomará la forma

Lo transponemos y obtenemos el adjunto

Divídelo por el determinante y obtén el inverso

Vemos que en el caso en que el determinante igual a uno está unido y las matrices inversas son las mismas.

2) Calcular el determinante de la matriz

Hallar la matriz de sumas algebraicas

La forma final de la matriz del complemento.

Transpóngalo y encuentre la matriz de unión.

Encontrar la matriz inversa

3) Calcular el determinante de la matriz. Para hacer esto, ampliémoslo a la primera línea. Como resultado, obtenemos dos términos distintos de cero

Encontramos la matriz de sumas algebraicas. El horario del determinante se dibuja a lo largo de las filas y columnas, en las que hay más elementos cero (indicados en negro).

La forma final de la matriz del complemento es la siguiente

transponerlo y encontrar la matriz asociada

Dado que el determinante de la matriz es igual a uno, la matriz inversa es la misma que la contigua. este ejemplo espalda.

Al calcular la matriz inversa, los errores asociados con signos incorrectos son típicos al calcular la matriz determinante y complementaria.

Matemáticas superiores » Matrices y determinantes » Matriz inversa » Cálculo de la matriz inversa mediante sumas algebraicas.

Algoritmo para calcular la matriz inversa usando sumas algebraicas: el método de la matriz asociada (unión).

La matriz $A^(-1)$ se llama la inversa de la matriz cuadrada $A$ si $A^(-1)\cdot A=A\cdot A^(-1)=E$, donde $E $ es la matriz identidad, cuyo orden es igual al orden de la matriz $A$.

Una matriz no singular es una matriz cuyo determinante no es igual a cero. En consecuencia, una matriz degenerada es aquella cuyo determinante es igual a cero.

La matriz inversa $A^(-1)$ existe si y solo si la matriz $A$ no es singular. Si la matriz inversa $A^(-1)$ existe, entonces es única.

Hay varias formas de encontrar la inversa de una matriz y veremos dos de ellas. Esta página cubrirá el método de matriz adjunta, que se considera estándar en la mayoría de los cursos. Matemáticas avanzadas. La segunda forma de encontrar la matriz inversa (método de las transformaciones elementales), que involucra el uso del método de Gauss o el método de Gauss-Jordan, se considera en la segunda parte.

Método de matriz adjunta (unión)

Sea dada la matriz $A_(n\times n)$. Para encontrar la matriz inversa $A^(-1)$, se requieren tres pasos:

Encuentre el determinante de la matriz $A$ y asegúrese de que $\Delta A\neq 0$, es decir que la matriz A es no degenerada.
Componga complementos algebraicos $A_(ij)$ de cada elemento de la matriz $A$ y anote la matriz $A_(n\times n)^(*)=\left(A_(ij) \right)$ de la matriz encontrada complementos algebraicos.
Escribe la matriz inversa teniendo en cuenta la fórmula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

La matriz $(A^(*))^T$ a menudo se denomina matriz adjunta (mutua, aliada) de $A$.

Si la decisión se toma manualmente, entonces el primer método es bueno solo para matrices de órdenes relativamente pequeños: el segundo (ejemplo No. 2), el tercero (ejemplo No. 3), el cuarto (ejemplo No. 4). Para encontrar la inversa de una matriz orden superior, se utilizan otros métodos. Por ejemplo, el método de Gauss, que se analiza en la segunda parte.

Ejemplo 1

Encuentra la matriz inversa a la matriz $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(matriz) \right)$.

matriz inversa

Dado que todos los elementos de la cuarta columna son iguales a cero, entonces $\Delta A=0$ (es decir, la matriz $A$ es degenerada). Dado que $\Delta A=0$, no existe una matriz inversa a $A$.

Ejemplo #2

Encuentra la matriz inversa a la matriz $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$.

Usamos el método de la matriz adjunta. Primero, encontremos el determinante de la matriz dada $A$:

$$ \Delta A=\izquierda| \begin(matriz) (cc) -5 y 7\\ 9 y 8 \end(matriz)\right|=-5\cdot 8-7\cdot 9=-103. $$

Como $\Delta A \neq 0$, entonces existe la matriz inversa, por lo que continuamos con la solución. Encontramos los complementos algebraicos de cada elemento de la matriz dada:

\begin(alineado) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(alineado)

Componga una matriz de complementos algebraicos: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponga la matriz resultante: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (la resultante matriz se suele denominar matriz adjunta o unión a la matriz $A$). Usando la fórmula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, tenemos:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(matriz) (cc) 8 & -7\\ -9 & -5 \end(matriz)\right) =\left(\begin(matriz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(matriz)\right) $$

Entonces se encuentra la matriz inversa: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \derecha) $. Para comprobar la verdad del resultado, basta con comprobar la verdad de una de las igualdades: $A^(-1)\cdot A=E$ o $A\cdot A^(-1)=E$. Comprobemos la igualdad $A^(-1)\cdot A=E$. Para trabajar menos con fracciones, sustituiremos la matriz $A^(-1)$ que no tiene la forma $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(matriz)\right)$ pero como $-\frac(1)(103)\cdot \left(\begin(matriz) (cc) 8 & -7\\ -9 & -5 \ end(matriz)\right)$:

Respuesta: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Ejemplo #3

Encuentra el inverso de la matriz $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$.

Empecemos por calcular el determinante de la matriz $A$. Entonces, el determinante de la matriz $A$ es:

$$ \Delta A=\izquierda| \begin(matriz) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(matriz) \right| = 18-36+56-12=26. $$

Como $\Delta A\neq 0$, entonces existe la matriz inversa, por lo que continuamos con la solución. Encontramos los complementos algebraicos de cada elemento de la matriz dada:

Componemos una matriz de sumas algebraicas y la transponemos:

$$ A^*=\left(\begin(matriz) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(matriz) \right); \; (A^*)^T=\left(\begin(matriz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(matriz) \right) $$

Usando la fórmula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, obtenemos:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(matriz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(matriz) \right)= \left(\begin(matriz) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(matriz) \right) $$

Entonces $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 y -3/26 y 37/26 \end(matriz) \right)$. Para comprobar la verdad del resultado, basta con comprobar la verdad de una de las igualdades: $A^(-1)\cdot A=E$ o $A\cdot A^(-1)=E$. Comprobemos la igualdad $A\cdot A^(-1)=E$. Para trabajar menos con fracciones, sustituiremos la matriz $A^(-1)$ que no tiene la forma $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, pero como $\frac(1)(26)\ cdot \left( \begin(matriz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(matriz) \right)$:

La verificación se pasó con éxito, la matriz inversa $A^(-1)$ se encontró correctamente.

Respuesta: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \end(array) \right)$.

Ejemplo #4

Encuentre la matriz inversa de $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(matriz) \right)$.

Para una matriz de cuarto orden, encontrar la matriz inversa usando sumas algebraicas es algo difícil. Sin embargo, tales ejemplos se encuentran en los trabajos de control.

Para encontrar la matriz inversa, primero debe calcular el determinante de la matriz $A$. La mejor manera de hacer esto en esta situación es expandir el determinante en una fila (columna). Seleccionamos cualquier fila o columna y encontramos el complemento algebraico de cada elemento de la fila o columna seleccionada.

Por ejemplo, para la primera fila obtenemos:

El determinante de la matriz $A$ se calcula mediante la siguiente fórmula:

$$ \Delta A=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14)= 6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

Matriz de complemento algebraico: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(matriz)\right)$.

Matriz adjunta: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 y -463\\ -112 y 4 y 36 y -96\end(matriz)\right)$

Matriz inversa:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(matriz) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(matriz) \right)= \left(\begin(matriz) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 y 1/25 y 9/25 y -24/25 \end(matriz) \right) $$

Examen:

Por lo tanto, la matriz inversa se encuentra correctamente.

Respuesta: $A^(-1)=\left(\begin(matriz) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(matriz) \right PS

En la segunda parte, se considerará otra forma de encontrar la matriz inversa, que implica el uso de transformaciones del método de Gauss o el método de Gauss-Jordan.

Clases en línea de matemáticas superiores

Encontrar la matriz inversa

La matriz A-1 se denomina matriz inversa con respecto a la matriz, si A*A-1 = , donde es la matriz identidad de orden ésimo. La matriz inversa solo puede existir para matrices cuadradas.

ver también Matriz inversa por el método de Jordano-Gauss

Algoritmo para encontrar la matriz inversa

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Hallar la matriz transpuesta AT.
Definición de sumas algebraicas. Reemplace cada elemento de la matriz con su complemento algebraico.
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz resultante se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

El siguiente algoritmo para encontrar la matriz inversa es similar al anterior, excepto por algunos pasos: primero se calculan los complementos algebraicos y luego se determina la matriz de unión.

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante matricial. Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Definición de sumas algebraicas.
Llenar la matriz aliada (mutua, adjunta).
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz adjunta se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

Ejemplo 1. Escribimos la matriz de la forma:

1,1 = (-1 4-5 (-2)) = 6

1,2 = -(2 4-(-2 (-2))) = -4

1,3 = (2 5-(-2 (-1))) = 8

2,1 = -(2 4-5 3) = 7

2,2 = (-1 4-(-2 3)) = 2

2,3 = -(-1 5-(-2 2)) = 1

3,1 = (2 (-2)-(-1 3)) = -1

3,2 = -(-1 (-2)-2 3) = 4

3,3 = (-1 (-1)-2 2) = -3
Luego matriz inversa Se puede escribir como:

A-1=

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Otro algoritmo para encontrar la matriz inversa.

Presentamos otro esquema para encontrar la matriz inversa.

Encuentre el determinante de esta matriz cuadrada.
Encontramos sumas algebraicas a todos los elementos de la matriz.
Escribimos los complementos algebraicos de los elementos de las filas en las columnas (transposición).
Divide cada elemento de la matriz resultante por el determinante de la matriz.

Como ves, la operación de transposición se puede aplicar tanto al principio, sobre la matriz original, como al final, sobre las sumas algebraicas resultantes.

Para probar, asegúrese de que A-1A = E.

Instrucción. Para obtener una solución, debe especificar la dimensión de la matriz. A continuación, en un nuevo cuadro de diálogo, complete la matriz.

La matriz A -1 se llama matriz inversa con respecto a la matriz A, si A * A -1 \u003d E, donde E es la matriz identidad de orden n. La matriz inversa solo puede existir para matrices cuadradas.

Asignación de servicios. Usando este servicio en línea, puede encontrar sumas algebraicas, matriz transpuesta A T , matriz de unión y matriz inversa. La solución se realiza directamente en el sitio (en línea) y es gratuita. Los resultados de los cálculos se presentan en un informe en formato Word y en formato Excel (es decir, es posible comprobar la solución). ver ejemplo de diseño.

Instrucción. Para obtener una solución, debe especificar la dimensión de la matriz. A continuación, en el nuevo cuadro de diálogo, complete la matriz A.

Véase también Matriz inversa por el método de Jordan-Gauss

Algoritmo para encontrar la matriz inversa

Encontrar la matriz transpuesta A T .
Definición de sumas algebraicas. Reemplace cada elemento de la matriz con su complemento algebraico.
Compilación de una matriz inversa a partir de sumas algebraicas: cada elemento de la matriz resultante se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.

Próximo algoritmo de matriz inversa similar al anterior, excepto por algunos pasos: primero se calculan los complementos algebraicos y luego se determina la matriz de unión C.

Determinar si la matriz es cuadrada. Si no, entonces no hay matriz inversa para ello.
Cálculo del determinante de la matriz A . Si no es igual a cero, continuamos la solución, de lo contrario, la matriz inversa no existe.
Definición de sumas algebraicas.
Rellenar la matriz de unión (mutua, adjunta) C .
Compilación de la matriz inversa a partir de sumas algebraicas: cada elemento de la matriz adjunta C se divide por el determinante de la matriz original. La matriz resultante es la inversa de la matriz original.
Haz una comprobación: multiplica la matriz original y la resultante. El resultado debe ser una matriz de identidad.

Ejemplo 1. Escribimos la matriz de la forma:

Sumas algebraicas. ∆ 1,2 = -(2 4-(-2 (-2))) = -4 ∆ 2,1 = -(2 4-5 3) = 7 ∆ 2,3 = -(-1 5-(-2 2)) = 1 ∆ 3,2 = -(-1 (-2)-2 3) = 4

A-1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Otro algoritmo para encontrar la matriz inversa.

Presentamos otro esquema para encontrar la matriz inversa.

Encuentre el determinante de la matriz cuadrada A dada.
Encontramos sumas algebraicas a todos los elementos de la matriz A .
Escribimos los complementos algebraicos de los elementos de las filas en las columnas (transposición).
Dividimos cada elemento de la matriz resultante por el determinante de la matriz A .

Como ves, la operación de transposición se puede aplicar tanto al principio, sobre la matriz original, como al final, sobre las sumas algebraicas resultantes.

un caso especial: La inversa, con respecto a la matriz identidad E , es la matriz identidad E .

Seguimos hablando de acciones con matrices. Es decir, en el transcurso del estudio de esta lección, aprenderá cómo encontrar la matriz inversa. Aprender. Incluso si las matemáticas son estrictas.

¿Qué es una matriz inversa? Aquí podemos hacer una analogía con los recíprocos: considere, por ejemplo, el número optimista 5 y su recíproco. El producto de estos números es igual a uno: . ¡Es lo mismo con las matrices! El producto de una matriz por su inversa es - matriz de identidad, que es la matriz análoga de la unidad numérica. Sin embargo, lo primero es lo primero, resolveremos un problema práctico importante, a saber, aprenderemos cómo encontrar esta matriz muy inversa.

¿Qué necesitas saber para poder encontrar la matriz inversa? Debes ser capaz de decidir determinantes. Debes entender lo que es la matriz y poder realizar algunas acciones con ellos.

Hay dos métodos principales para encontrar la matriz inversa:
vía sumas algebraicas Y usando transformaciones elementales.

Hoy estudiaremos la primera forma, más fácil.

Comencemos con lo más terrible e incomprensible. Considerar cuadrado matriz La matriz inversa se puede encontrar usando la siguiente fórmula:

Donde es el determinante de la matriz, es la matriz transpuesta de complementos algebraicos de los elementos correspondientes de la matriz.

El concepto de matriz inversa existe solo para matrices cuadradas, matrices "dos por dos", "tres por tres", etc.

Notación: Como probablemente ya notó, la inversa de una matriz se denota con un superíndice

Comencemos con el caso más simple: una matriz de dos por dos. La mayoría de las veces, por supuesto, se requiere "tres por tres", pero, sin embargo, recomiendo encarecidamente estudiar una tarea más simple para aprender el principio general de la solución.

Ejemplo:

Encuentra la inversa de una matriz

Nosotros decidimos. La secuencia de acciones se descompone convenientemente en puntos.

1) Primero encontramos el determinante de la matriz.

Si la comprensión de esta acción no es buena, lea el material ¿Cómo calcular el determinante?

¡Importante! Si el determinante de la matriz es CERO– matriz inversa NO EXISTE.

En el ejemplo bajo consideración, resultó que, lo que significa que todo está en orden.

2) Encuentra la matriz de menores.

Para solucionar nuestro problema, no es necesario saber qué es un menor, sin embargo, es recomendable leer el artículo Cómo calcular el determinante.

La matriz de menores tiene las mismas dimensiones que la matriz, es decir, en este caso.
El caso es pequeño, queda por encontrar cuatro números y ponerlos en lugar de asteriscos.

Volver a nuestra matriz
Veamos primero el elemento superior izquierdo:

como encontrarlo menor?
Y esto se hace así: MENTALMENTE tacha la fila y la columna en la que se encuentra este elemento:

el numero restante es menor del elemento dado, que escribimos en nuestra matriz de menores:

Considere el siguiente elemento de matriz:

Tache mentalmente la fila y la columna en la que se encuentra este elemento:

Lo que queda es el menor de este elemento, que escribimos en nuestra matriz:

De manera similar, consideramos los elementos de la segunda fila y encontramos sus menores:

Listo.

Es simple. En la matriz de menores se necesita SEÑALES DE CAMBIO para dos números:

¡Son estos números los que he encerrado en un círculo!

es la matriz de complementos algebraicos de los elementos correspondientes de la matriz.

Y solo algo...

4) Encuentra la matriz transpuesta de sumas algebraicas.

es la matriz transpuesta de complementos algebraicos de los elementos correspondientes de la matriz.

5) Respuesta.

Recuerda nuestra fórmula
Todo encontrado!

Entonces la matriz inversa es:

Es mejor dejar la respuesta como está. NO HAY NECESIDAD dividir cada elemento de la matriz por 2, ya que se obtendrán números fraccionarios. Este matiz se discute con más detalle en el mismo artículo. Acciones con matrices.

¿Cómo comprobar la solución?

La multiplicación de matrices debe realizarse ya sea

Examen:

ya mencionado matriz de identidad es una matriz con unidades en diagonal principal y ceros en otros lugares.

Por lo tanto, la matriz inversa se encuentra correctamente.

Si realiza una acción, el resultado también será una matriz de identidad. Este es uno de los pocos casos donde la multiplicación de matrices es permutable, más información detallada se puede encontrar en el artículo Propiedades de las operaciones sobre matrices. expresiones matriciales. También tenga en cuenta que durante la verificación, la constante (fracción) se adelanta y se procesa al final, después de la multiplicación de matrices. Esta es una toma estándar.

Pasemos a un caso más común en la práctica: la matriz de tres por tres:

Ejemplo:

Encuentra la inversa de una matriz

El algoritmo es exactamente el mismo que para el caso de dos por dos.

Encontramos la matriz inversa por la fórmula: , donde es la matriz transpuesta de complementos algebraicos de los elementos correspondientes de la matriz .

1) Encuentra el determinante de la matriz.

Aquí se revela el determinante. en la primera linea.

Además, no olvides eso, lo que significa que todo está bien. existe matriz inversa.

2) Encuentra la matriz de menores.

La matriz de menores tiene la dimensión "tres por tres" , y necesitamos encontrar nueve números.

Echaré un vistazo a un par de menores en detalle:

Considere el siguiente elemento de matriz:

MENTALMENTE tache la fila y la columna en la que se encuentra este elemento:

Los cuatro números restantes se escriben en el determinante "dos por dos"

Este determinante de dos por dos y es un menor del elemento dado. Necesita ser calculado:

Todo, se encuentra el menor, lo escribimos en nuestra matriz de menores:

Como habrás adivinado, hay nueve determinantes de dos por dos para calcular. El proceso, por supuesto, es tedioso, pero el caso no es el más difícil, puede ser peor.

Bueno, para consolidar, encontrar otro menor en las fotos:

Trate de calcular el resto de los menores usted mismo.

Resultado final:
es la matriz de menores de los elementos correspondientes de la matriz.

El hecho de que todos los menores resultaran negativos es pura coincidencia.

3) Encuentra la matriz de sumas algebraicas.

En la matriz de menores es necesario SEÑALES DE CAMBIO estrictamente para los siguientes elementos:

En este caso:

No se considera encontrar la matriz inversa para la matriz "cuatro por cuatro", ya que solo un maestro sádico puede dar tal tarea (para que el estudiante calcule un determinante "cuatro por cuatro" y 16 determinantes "tres por tres") . En mi práctica, solo hubo un caso de este tipo, y el cliente trabajo de control pagué caro mi tormento =).

En varios libros de texto, manuales, puede encontrar un enfoque ligeramente diferente para encontrar la matriz inversa, pero recomiendo usar el algoritmo de solución anterior. ¿Por qué? Porque la probabilidad de confundirse en cálculos y signos es mucho menor.

Este tema es uno de los más odiados entre los estudiantes. Peor, probablemente, sólo determinantes.

El truco es que el concepto mismo del elemento inverso (y no me refiero ahora solo a matrices) nos remite a la operación de multiplicación. Incluso en currículum escolar la multiplicación se considera una operación compleja, e incluso la multiplicación de matrices es un tema separado en general, al que tengo un párrafo completo y un video tutorial dedicado.

Hoy no entraremos en los detalles de los cálculos matriciales. Solo recuerda: cómo se denotan las matrices, cómo se multiplican y qué se sigue de esto.

Repaso: Multiplicación de matrices

En primer lugar, pongámonos de acuerdo en la notación. Una matriz $A$ de tamaño $\left[ m\times n \right]$ es simplemente una tabla de números con exactamente $m$ filas y $n$ columnas:

\=\underbrace(\left[ \begin(matriz) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matriz) \right])_(n)\]

Para no confundir filas y columnas accidentalmente en algunos lugares (créame, en el examen puede confundir uno con un dos, ¿qué podemos decir sobre algunas líneas allí?), solo mire la imagen:

Determinación de índices para celdas de matriz.

¿Lo que está sucediendo? Si colocamos el sistema de coordenadas estándar $OXY$ en la esquina superior izquierda y dirigimos los ejes para que cubran toda la matriz, entonces cada celda de esta matriz se puede asociar de manera única con las coordenadas $\left(x;y \right) $: este será el número de fila y el número de columna.

¿Por qué el sistema de coordenadas se coloca exactamente en la esquina superior izquierda? Sí, porque es a partir de ahí que comenzamos a leer cualquier texto. Es muy fácil de recordar.

¿Por qué el eje $x$ apunta hacia abajo y no hacia la derecha? Nuevamente, es simple: tome el sistema de coordenadas estándar (el eje $x$ va a la derecha, el eje $y$ sube) y gírelo para que encierre la matriz. Esta es una rotación de 90 grados en el sentido de las agujas del reloj; vemos su resultado en la imagen.

En general, descubrimos cómo determinar los índices de los elementos de la matriz. Ahora tratemos con la multiplicación.

Definición. Las matrices $A=\left[ m\times n \right]$ y $B=\left[ n\times k \right]$, cuando el número de columnas de la primera coincide con el número de filas de la segunda, son llamado consistente.

Es en ese orden. Se puede ser ambiguo y decir que las matrices $A$ y $B$ forman un par ordenado $\left(A;B \right)$: si son consistentes en este orden, entonces no es necesario que $B $ y $A$, esos. el par $\left(B;A \right)$ también es consistente.

Solo se pueden multiplicar matrices consistentes.

Definición. El producto de matrices consistentes $A=\left[ m\times n \right]$ y $B=\left[ n\times k \right]$ es la nueva matriz $C=\left[ m\times k \right ]$ , cuyos elementos $((c)_(ij))$ se calculan mediante la fórmula:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

En otras palabras: para obtener el elemento $((c)_(ij))$ de la matriz $C=A\cdot B$, debe tomar la fila $i$ de la primera matriz, la $j$ -ésima columna de la segunda matriz, y luego multiplique en pares los elementos de esta fila y columna. Sume los resultados.

Sí, esa es una definición dura. Varios hechos se desprenden inmediatamente de ella:

La multiplicación de matrices es, en términos generales, no conmutativa: $A\cdot B\ne B\cdot A$;
Sin embargo, la multiplicación es asociativa: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
E incluso distributivo: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
Y distributivo de nuevo: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

La distributividad de la multiplicación tuvo que describirse por separado para la suma del multiplicador izquierdo y derecho solo por la no conmutatividad de la operación de multiplicación.

Si, no obstante, resulta que $A\cdot B=B\cdot A$, tales matrices se denominan permutables.

Entre todas las matrices que se multiplican por algo allí, hay unas especiales, aquellas que, cuando se multiplican por cualquier matriz $A$, nuevamente dan $A$:

Definición. Una matriz $E$ se llama identidad si $A\cdot E=A$ o $E\cdot A=A$. En el caso de una matriz cuadrada $A$ podemos escribir:

La matriz identidad es un invitado frecuente en la resolución de ecuaciones matriciales. Y en general, un invitado frecuente en el mundo de las matrices. :)

Y debido a este $E$, a alguien se le ocurrió todo el juego que se escribirá a continuación.

¿Qué es una matriz inversa?

Dado que la multiplicación de matrices es una operación que consume mucho tiempo (tiene que multiplicar un montón de filas y columnas), el concepto de matriz inversa tampoco es el más trivial. Y necesita alguna explicación.

Definición clave

Bueno, es hora de saber la verdad.

Definición. La matriz $B$ se llama la inversa de la matriz $A$ si

La matriz inversa se denota por $((A)^(-1))$ (¡no debe confundirse con el grado!), por lo que la definición se puede reescribir así:

Parecería que todo es extremadamente simple y claro. Pero al analizar tal definición, surgen inmediatamente varias preguntas:

¿Existe siempre una matriz inversa? Y si no siempre, entonces, ¿cómo determinar: cuándo existe y cuándo no?
¿Y quién dijo que tal matriz es exactamente una? ¿Qué pasa si para alguna matriz original $A$ hay una multitud de inversas?
¿Cómo son todos estos "reveses"? ¿Y cómo los cuentas realmente?

En cuanto a los algoritmos de cálculo, hablaremos de esto un poco más adelante. Pero responderemos el resto de las preguntas ahora mismo. Dispongámoslos en forma de aserciones-lemas separados.

Propiedades básicas

Comencemos con cómo debería verse la matriz $A$ para que tenga $((A)^(-1))$. Ahora nos aseguraremos de que ambas matrices deben ser cuadradas y del mismo tamaño: $\left[ n\times n \right]$.

Lema 1. Dada una matriz $A$ y su inversa $((A)^(-1))$. Entonces ambas matrices son cuadradas y tienen el mismo orden $n$.

Prueba. Todo es simple. Sea la matriz $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Dado que el producto $A\cdot ((A)^(-1))=E$ existe por definición, las matrices $A$ y $((A)^(-1))$ son consistentes en ese orden:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( alinear)\]

Esta es una consecuencia directa del algoritmo de multiplicación de matrices: los coeficientes $n$ y $a$ son "tránsito" y deben ser iguales.

Al mismo tiempo, también se define la multiplicación inversa: $((A)^(-1))\cdot A=E$, por lo que las matrices $((A)^(-1))$ y $A$ son también consistente en este orden:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( alinear)\]

Por lo tanto, sin pérdida de generalidad, podemos asumir que $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Sin embargo, según la definición de $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, las dimensiones de las matrices son exactamente las mismas:

\[\begin(alinear) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Entonces resulta que las tres matrices - $A$, $((A)^(-1))$ y $E$ - son de tamaño cuadrado $\left[ n\times n \right]$. El lema está probado.

Bueno, eso ya es bueno. Vemos que sólo las matrices cuadradas son invertibles. Ahora asegurémonos de que la matriz inversa sea siempre la misma.

Lema 2. Dada una matriz $A$ y su inversa $((A)^(-1))$. Entonces esta matriz inversa es única.

Prueba. Comencemos por lo contrario: deje que la matriz $A$ tenga al menos dos instancias de inversas: $B$ y $C$. Entonces, de acuerdo con la definición, las siguientes igualdades son verdaderas:

\[\begin(alinear) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(alinear)\]

Del Lema 1 concluimos que las cuatro matrices $A$, $B$, $C$ y $E$ son cuadradas del mismo orden: $\left[ n\times n \right]$. Por lo tanto, el producto se define:

Dado que la multiplicación de matrices es asociativa (¡pero no conmutativa!), podemos escribir:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(alinear)\]

recibido solo variante posible: dos instancias de la matriz inversa son iguales. El lema está probado.

El razonamiento anterior repite casi palabra por palabra la prueba de la unicidad del elemento inverso para todos los números reales $b\ne 0$. La única adición significativa es tener en cuenta la dimensión de las matrices.

Sin embargo, todavía no sabemos nada acerca de si cualquier matriz cuadrada es invertible. Aquí el determinante viene en nuestra ayuda: esta es una característica clave para todas las matrices cuadradas.

Lema 3 . Dada una matriz $A$. Si existe la matriz $((A)^(-1))$ inversa a ella, entonces el determinante de la matriz original es distinto de cero:

\[\izquierda| A \right|\ne 0\]

Prueba. Ya sabemos que $A$ y $((A)^(-1))$ son matrices cuadradas de tamaño $\left[ n\times n \right]$. Por lo tanto, para cada uno de ellos es posible calcular el determinante: $\left| A \derecha|$ y $\izquierda| ((A)^(-1)) \derecho|$. Sin embargo, el determinante del producto es igual al producto de los determinantes:

\[\izquierda| A\cdot B \right|=\left| A \right|\cdot \left| B \derecha|\Flecha derecha \izquierda| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \derecho|\]

Pero según la definición de $A\cdot ((A)^(-1))=E$, y el determinante de $E$ siempre es igual a 1, entonces

\[\begin(alinear) & A\cdot ((A)^(-1))=E; \\ & \izquierda| A\cdot ((A)^(-1)) \right|=\left| E\derecho|; \\ & \izquierda| A \right|\cdot \left| ((A)^(-1)) \derecho|=1. \\ \end(alinear)\]

El producto de dos números es igual a uno solo si cada uno de estos números es diferente de cero:

\[\izquierda| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Entonces resulta que $\left| Un \right|\ne 0$. El lema está probado.

De hecho, este requisito es bastante lógico. Ahora analizaremos el algoritmo para encontrar la matriz inversa, y quedará completamente claro por qué, en principio, no puede existir una matriz inversa con un determinante cero.

Pero primero, formulemos una definición "auxiliar":

Definición. Una matriz degenerada es una matriz cuadrada de tamaño $\left[ n\times n \right]$ cuyo determinante es cero.

Por tanto, podemos afirmar que cualquier matriz invertible es no degenerada.

Cómo encontrar la matriz inversa

Ahora consideraremos un algoritmo universal para encontrar matrices inversas. En general, hay dos algoritmos generalmente aceptados, y también consideraremos el segundo hoy.

La que se considerará ahora es muy eficiente para matrices de tamaño $\left[ 2\times 2 \right]$ y - parcialmente - de tamaño $\left[ 3\times 3 \right]$. Pero a partir del tamaño $\left[ 4\times 4 \right]$ es mejor no usarlo. Por qué, ahora entenderás todo.

sumas algebraicas

Prepararse. Ahora habrá dolor. No, no te preocupes: una hermosa enfermera con falda, medias con encaje no viene a ti y no te pondrá una inyección en la nalga. Todo es mucho más prosaico: las sumas algebraicas y Su Majestad la "Matriz de la Unión" están llegando a usted.

Comencemos con el principal. Sea una matriz cuadrada de tamaño $A=\left[ n\times n \right]$ cuyos elementos se denominan $((a)_(ij))$. Entonces, para cada uno de estos elementos, se puede definir un complemento algebraico:

Definición. Complemento algebraico $((A)_(ij))$ al elemento $((a)_(ij))$ en la $i$-ésima fila y $j$-ésima columna de la matriz $A=\left [ n \times n \right]$ es una construcción de la forma

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Donde $M_(ij)^(*)$ es el determinante de la matriz obtenida del $A$ original al eliminar la misma $i$-ésima fila y $j$-ésima columna.

Otra vez. El complemento algebraico del elemento de la matriz con coordenadas $\left(i;j \right)$ se denota como $((A)_(ij))$ y se calcula según el esquema:

Primero, eliminamos la fila $i$ y la columna $j$-ésima de la matriz original. Obtenemos una nueva matriz cuadrada y denotamos su determinante como $M_(ij)^(*)$.
Luego multiplicamos este determinante por $((\left(-1 \right))^(i+j))$ - al principio esta expresión puede parecer alucinante, pero de hecho solo encontramos el signo delante de $ M_(ij)^(*) $.
Contamos, obtenemos un número específico. Esos. la suma algebraica es solo un número, no una nueva matriz, y así sucesivamente.

La matriz $M_(ij)^(*)$ en sí misma se denomina menor complementaria al elemento $((a)_(ij))$. Y en este sentido, la definición anterior de un complemento algebraico es un caso especial de una definición más compleja, la que consideramos en la lección sobre el determinante.

Nota IMPORTANTE. En realidad, en matemáticas "para adultos", las sumas algebraicas se definen de la siguiente manera:

Tomamos $k$ filas y $k$ columnas en una matriz cuadrada. En su intersección, obtenemos una matriz de tamaño $\left[ k\times k \right]$ — su determinante se llama menor de orden $k$ y se denota por $((M)_(k))$.

Luego tachamos estas $k$ filas y columnas $k$ "seleccionadas". Nuevamente, obtenemos una matriz cuadrada: su determinante se llama menor complementario y se denota por $M_(k)^(*)$.

Multiplica $M_(k)^(*)$ por $((\left(-1 \right))^(t))$, donde $t$ es (¡atención ahora!) la suma de los números de todas las filas seleccionadas y columnas Esta será la suma algebraica.

Eche un vistazo al tercer paso: ¡en realidad hay una suma de términos de $ 2k $! Otra cosa es que para $k=1$ obtenemos solo 2 términos - estos serán los mismos $i+j$ - las "coordenadas" del elemento $((a)_(ij))$, para el cual estamos buscando un complemento algebraico.

Así que hoy usamos una definición ligeramente simplificada. Pero como veremos más adelante, será más que suficiente. Mucho más importante es lo siguiente:

Definición. La matriz de unión $S$ a la matriz cuadrada $A=\left[ n\times n \right]$ es una nueva matriz de tamaño $\left[ n\times n \right]$, que se obtiene a partir de $A$ reemplazando $(( a)_(ij))$ por complementos algebraicos $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matriz) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matriz) \right]\]

El primer pensamiento que surge al momento de darse cuenta de esta definición es “¡esto es lo que tienes que contar en total!” Relájate: hay que contar, pero no tanto. :)

Bueno, todo esto es muy bonito, pero ¿por qué es necesario? Pero por qué.

teorema principal

Retrocedamos un poco. Recuerde, el Lema 3 establece que una matriz invertible $A$ siempre es no singular (es decir, su determinante es distinto de cero: $\left| A \right|\ne 0$).

Entonces, lo contrario también es cierto: si la matriz $A$ no es degenerada, entonces siempre es invertible. E incluso hay un esquema de búsqueda $((A)^(-1))$. Echale un vistazo:

Teorema de la matriz inversa. Sea dada una matriz cuadrada $A=\left[ n\times n \right]$, y su determinante es distinto de cero: $\left| Un \right|\ne 0$. Entonces la matriz inversa $((A)^(-1))$ existe y se calcula mediante la fórmula:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

Y ahora, todo lo mismo, pero con letra legible. Para encontrar la matriz inversa, necesitas:

Calcular el determinante $\left| A \right|$ y asegúrese de que no sea cero.
Compile la matriz de unión $S$, es decir cuenta 100500 sumas algebraicas $((A)_(ij))$ y ponlas en su lugar $((a)_(ij))$.
Transponga esta matriz $S$ y luego multiplíquela por algún número $q=(1)/(\left| A \right|)\;$.

¡Y eso es! Se encuentra la matriz inversa $((A)^(-1))$. Veamos ejemplos:

\[\left[ \begin(matriz) 3 & 1 \\ 5 & 2 \\\end(matriz) \right]\]

Solución. Comprobemos la reversibilidad. Calculemos el determinante:

\[\izquierda| A \derecha|=\izquierda| \begin(matriz) 3 & 1 \\ 5 & 2 \\\end(matriz) \right|=3\cdot 2-1\cdot 5=6-5=1\]

El determinante es diferente de cero. Entonces la matriz es invertible. Vamos a crear una matriz de unión:

Calculemos las sumas algebraicas:

\[\begin(alinear) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\derecho|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5\derecha|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \derecho|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\derecha|=3. \\ \end(alinear)\]

Atención: determinantes |2|, |5|, |1| y |3| son los determinantes de matrices de tamaño $\left[ 1\times 1 \right]$, no módulos. Esos. si los determinantes fueran números negativos, no es necesario eliminar el "menos".

En total, nuestra matriz de unión se ve así:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(matriz)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(matriz) \right])^(T))=\left[ \begin (matriz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(matriz) \right]\]

Bueno eso es todo. Problema resuelto.

Responder. $\left[ \begin(matriz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(matriz) \right]$

Una tarea. Encuentre la matriz inversa:

\[\left[ \begin(matriz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(matriz) \right] \]

Solución. Nuevamente, consideramos el determinante:

\[\begin(alinear) & \left| \begin(matriz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(matriz) \right|=\begin(matriz ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matriz)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

El determinante es diferente de cero: la matriz es invertible. Pero ahora será lo más chiquito: hay que contar hasta 9 (¡nueve, carajo!) sumas algebraicas. Y cada uno de ellos contendrá el calificador $\left[ 2\times 2 \right]$. Voló:

\[\begin(matriz) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matriz) 2 & -1 \\ 0 & 1 \\\end(matriz) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matriz) 0 & -1 \\ 1 & 1 \\\end(matriz) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matriz) 0 & 2 \\ 1 & 0 \\\end(matriz) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matriz) 1 & -1 \\ 0 & 2 \\\end(matriz) \right|=2; \\ \end(matriz)\]

En resumen, la matriz de unión se verá así:

Por tanto, la matriz inversa será:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matriz) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matriz) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(matriz) \right]\]

Bueno eso es todo. Aquí está la respuesta.

Responder. $\left[ \begin(matriz)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(matriz) \right PS

Como puede ver, al final de cada ejemplo, realizamos una verificación. Al respecto, una nota importante:

No sea perezoso para comprobar. Multiplica la matriz original por la inversa encontrada: deberías obtener $E$.

Es mucho más fácil y rápido realizar esta verificación que buscar un error en cálculos posteriores, cuando, por ejemplo, resuelve una ecuación matricial.

Forma alternativa

Como dije, el teorema de la matriz inversa funciona bien para los tamaños $\left[ 2\times 2 \right]$ y $\left[ 3\times 3 \right]$ (en último caso- ya no es tan "perfecto"), pero para matrices de gran tamaño, comienza la tristeza.

Pero no te preocupes: hay un algoritmo alternativo que se puede usar para encontrar tranquilamente el inverso incluso para la matriz $\left[ 10\times 10 \right]$. Pero, como suele ser el caso, para considerar este algoritmo, necesitamos un poco de base teórica.

Transformaciones elementales

Entre las diversas transformaciones de la matriz, hay varias especiales: se llaman elementales. Hay exactamente tres transformaciones de este tipo:

Multiplicación. Puede tomar la $i$-ésima fila (columna) y multiplicarla por cualquier número $k\ne 0$;
Adición. Agregue a la $i$-ésima fila (columna) cualquier otra $j$-ésima fila (columna) multiplicada por cualquier número $k\ne 0$ (por supuesto, $k=0$ también es posible, pero cuál es el punto de eso? ?Sin embargo, nada cambiará).
Permutación. Tome las filas (columnas) $i$-th y $j$-th y cámbielas.

Por qué estas transformaciones se llaman elementales (para matrices grandes no parecen tan elementales) y por qué solo hay tres de ellas: estas preguntas están más allá del alcance de la lección de hoy. Por lo tanto, no entraremos en detalles.

Otra cosa es importante: tenemos que realizar todas estas perversiones en la matriz asociada. Sí, sí, has oído bien. Ahora habrá una definición más, la última de la lección de hoy.

Matriz adjunta

Seguramente en la escuela resolviste sistemas de ecuaciones usando el método de la suma. Bueno, allí, reste otra línea de una línea, multiplique una línea por un número, eso es todo.

Entonces: ahora todo será igual, pero ya “de forma adulta”. ¿Listo?

Definición. Sean dadas la matriz $A=\left[ n\times n \right]$ y la matriz identidad $E$ del mismo tamaño $n$. Entonces la matriz asociada $\left[ A\left| E\bien. \right]$ es una nueva matriz $\left[ n\times 2n \right]$ que se ve así:

\[\izquierda[ A\izquierda| E\bien. \right]=\left[ \begin(matriz)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(matriz) \right]\]

En resumen, tomamos la matriz $A$, a la derecha le asignamos la matriz de identidad $E$ del tamaño requerido, las separamos con una barra vertical por belleza, aquí está la adjunta. :)

¿Cuál es el truco? Y esto es lo que:

Teorema. Sea la matriz $A$ invertible. Considere la matriz adjunta $\left[ A\left| E\bien. \derecho]$. si usa transformaciones elementales de cadenas llevarlo a la forma $\left[ E\left| Brillante. \right]$, es decir multiplicando, restando y reordenando filas para obtener de $A$ la matriz $E$ de la derecha, luego la matriz $B$ obtenida de la izquierda es la inversa de $A$:

\[\izquierda[ A\izquierda| E\bien. \right]\to \left[ E\left| Brillante. \derecha]\Flecha derecha B=((A)^(-1))\]

¡Es así de simple! En resumen, el algoritmo para encontrar la matriz inversa se ve así:

Escriba la matriz asociada $\left[ A\left| E\bien. \derecho]$;
Realice conversiones de cadenas elementales hasta que a la derecha en lugar de $A$ aparezca $E$;
Por supuesto, también aparecerá algo a la izquierda: una determinada matriz $B$. Esto será al revés;
BENEFICIOS! :)

Por supuesto, es mucho más fácil decirlo que hacerlo. Así que veamos un par de ejemplos: para los tamaños $\left[ 3\times 3 \right]$ y $\left[ 4\times 4 \right]$.

Una tarea. Encuentre la matriz inversa:

\[\left[ \begin(matriz)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(matriz) \right]\ ]

Solución. Componemos la matriz adjunta:

\[\left[ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(matriz) \right]\]

Como la última columna de la matriz original está llena de unos, reste la primera fila del resto:

\[\begin(alinear) & \left[ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(matriz) \right]\begin(matriz) \downarrow \\ -1 \\ -1 \\\end(matriz)\a \\ & \a \izquierda [ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(matriz) \right] \\ \end(alineación)\]

No hay más unidades, excepto la primera línea. Pero no lo tocamos, de lo contrario, las unidades recién eliminadas comenzarán a "multiplicarse" en la tercera columna.

Pero podemos restar la segunda línea dos veces de la última: obtenemos una unidad en la esquina inferior izquierda:

\[\begin(alinear) & \left[ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(matriz) \right]\begin(matriz) \ \\ \downarrow \\ -2 \\\end(matriz)\to \\ & \left [ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(matriz) \right] \\ \end(alineación)\]

Ahora podemos restar la última fila de la primera y dos veces de la segunda; de esta manera, "quitaremos a cero" la primera columna:

\[\begin(alinear) & \left[ \begin(matriz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(matriz) \right]\begin(matriz) -1 \\ -2 \\ \uparrow \\\end(matriz)\to \\ & \ a \left[ \begin(matriz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(matriz) \right] \\ \end(alinear)\]

Multiplica la segunda fila por −1 y luego resta 6 veces la primera y suma 1 vez a la última:

\[\begin(alinear) & \left[ \begin(matriz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(matriz) \right]\begin(matriz) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(matriz)\a \\ & \a \izquierda[ \begin(matriz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matriz) -6 \\ \updownarrow \\ +1 \\\end (matriz) \a \\ & \a \izquierda[ \begin(matriz)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(align)\]

Solo queda intercambiar las líneas 1 y 3:

\[\left[ \begin(matriz)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(matriz) \right]\]

¡Listo! A la derecha está la matriz inversa requerida.

Responder. $\left[ \begin(matriz)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(matriz) \right PS

Una tarea. Encuentre la matriz inversa:

\[\left[ \begin(matriz) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matriz) \right]\]

Solución. Nuevamente redactamos el adjunto:

\[\left[ \begin(matriz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(matriz) \right]\]

Pidamos prestado un poco, preocupémonos de cuánto tenemos que contar ahora... y empecemos a contar. Para empezar, ponemos a cero la primera columna restando la fila 1 de las filas 2 y 3:

\[\begin(alinear) & \left[ \begin(matriz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(matriz) \right]\begin(matriz) \downarrow \\ -1 \\ -1 \\ \ \\\end(matriz)\a \\ & \a \left[ \begin(matriz)(rrrr|rrrr) 1 & 4 y 2 y 3 y 1 y 0 y 0 y 0 \\ 0 y -6 y -1 y -5 y -1 y 1 y 0 y 0 \\ 0 y -5 y -1 y -2 y -1 y 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(matriz) \right] \\ \end(align)\]

Observamos demasiados "menos" en las líneas 2-4. Multiplique las tres filas por −1 y luego queme la tercera columna restando la fila 3 del resto:

\[\begin(alinear) & \left[ \begin(matriz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 y 1 y 0 y 0 \\ 0 y -5 y -1 y -2 y -1 y 0 y 1 y 0 \\ 0 y -10 y -2 y -5 y 0 y 0 y 0 y 1 \\ \end(matriz) \right]\begin(matriz) \ \\ \left| \cdot \left(-1 \right) \right. \\ \izquierda| \cdot \left(-1 \right) \right. \\ \izquierda| \cdot \left(-1 \right) \right. \\\end(matriz)\a \\ & \a \izquierda[ \begin(matriz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 y 1 y -1 y 0 y 0 \\ 0 y 5 y 1 y 2 y 1 y 0 y -1 y 0 \\ 0 y 10 y 2 y 5 y 0 y 0 y 0 y -1 \\ \end (matriz) \right]\begin(matriz) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matriz)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(matriz) \right] \\ \end(align)\]

Ahora es el momento de "freír" la última columna de la matriz original: restar la fila 4 del resto:

\[\begin(alinear) & \left[ \begin(matriz)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(matriz ) \right]\begin(matriz) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matriz)\a \\ & \a \left[ \begin(matriz)(rrrr|rrrr) 1 y -6 y 0 y 0 y -3 y 0 y 4 y -1 \\ 0 y 1 y 0 y 0 y 6 y -1 y -5 y 3 \\ 0 y 5 y 1 y 0 y 5 y 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(matriz) \right] \\ \end(align)\]

Tirada final: "quemar" la segunda columna restando la fila 2 de la fila 1 y 3:

\[\begin(alinear) & \left[ \begin(matriz)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \right]\begin(matriz) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matriz)\to \\ & \to \left[ \begin(matriz)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(matriz) \right] \\ \end(align)\]

Y de nuevo, la matriz identidad a la izquierda, así que la inversa a la derecha. :)

Responder. $\left[ \begin(matriz) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matriz) \right]$

Bueno eso es todo. Haz el control tú mismo, estoy descartado. :)

En este artículo, hablaremos sobre el método matricial para resolver un sistema de ecuaciones algebraicas lineales, encontraremos su definición y daremos ejemplos de la solución.

Definición 1

método de matriz inversa es el método utilizado para resolver SLAE cuando el número de incógnitas es igual al número de ecuaciones.

Ejemplo 1

Encuentre una solución a un sistema de n ecuaciones lineales con n incógnitas:

un 11 x 1 + un 12 x 2 + . . . + un 1 norte X norte = segundo 1 un norte 1 X 1 + un norte 2 X 2 + . . . + un norte norte X norte = segundo norte

Vista de registro de matriz : A × X = B

donde A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n es la matriz del sistema.

X = x 1 x 2 ⋮ x n - columna de incógnitas,

segundo = segundo 1 segundo 2 ⋮ segundo norte - columna de coeficientes libres.

De la ecuación que obtuvimos, necesitamos expresar X. Para hacer esto, multiplique ambos lados de la ecuación matricial de la izquierda por A - 1:

UNA - 1 × UNA × X = UNA - 1 × segundo .

Como A - 1 × A = E, entonces E × X = A - 1 × B o X = A - 1 × B.

Comentario

La matriz inversa a la matriz A tiene derecho a existir solo si la condición d e t A no es igual a cero. Por lo tanto, al resolver SLAE por el método de la matriz inversa, en primer lugar, se encuentra d e t A.

En el caso de que d e t A no sea igual a cero, el sistema tiene una única solución: utilizar el método de la matriz inversa. Si d e t A = 0, entonces el sistema no se puede resolver por este método.

Un ejemplo de resolución de un sistema de ecuaciones lineales utilizando el método de matriz inversa

Ejemplo 2

Resolvemos SLAE por el método de la matriz inversa:

2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2

¿Cómo decidir?

Escribimos el sistema en forma de ecuación matricial А X = B , donde

A \u003d 2 - 4 3 1 - 2 4 3 - 1 5, X \u003d x 1 x 2 x 3, B \u003d 1 3 2.

Expresamos a partir de esta ecuación X:

Encontramos el determinante de la matriz A:

det A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25

d e t А no es igual a 0, por lo tanto, el método de solución de matriz inversa es adecuado para este sistema.

Encontramos la matriz inversa A - 1 usando la matriz de unión. Calculamos las sumas algebraicas A i j a los elementos correspondientes de la matriz A:

A 11 \u003d (- 1) (1 + 1) - 2 4 - 1 5 \u003d - 10 + 4 \u003d - 6,

A 12 \u003d (- 1) 1 + 2 1 4 3 5 \u003d - (5 - 12) \u003d 7,

A 13 \u003d (- 1) 1 + 3 1 - 2 3 - 1 \u003d - 1 + 6 \u003d 5,

A 21 \u003d (- 1) 2 + 1 - 4 3 - 1 5 \u003d - (- 20 + 3) \u003d 17,

A 22 \u003d (- 1) 2 + 2 2 3 3 5 - 10 - 9 \u003d 1,

A 23 \u003d (- 1) 2 + 3 2 - 4 3 - 1 \u003d - (- 2 + 12) \u003d - 10,

A 31 \u003d (- 1) 3 + 1 - 4 3 - 2 4 \u003d - 16 + 6 \u003d - 10,

A 32 \u003d (- 1) 3 + 2 2 3 1 4 \u003d - (8 - 3) \u003d - 5,

A 33 \u003d (- 1) 3 + 3 2 - 4 1 - 2 \u003d - 4 + 4 \u003d 0.

Anotamos la matriz de unión A * , que está compuesta por complementos algebraicos de la matriz A:

UN * = - 6 7 5 17 1 - 10 - 10 - 5 0

Escribimos la matriz inversa según la fórmula:

A - 1 \u003d 1 d e t A (A *) T: A - 1 \u003d - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0,

Multiplicamos la matriz inversa A - 1 por la columna de términos libres B y obtenemos la solución del sistema:

X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1

Responder : x 1 = - 1; x 2 \u003d 0; x3 = 1

Si nota un error en el texto, resáltelo y presione Ctrl+Enter