Aplicación del cálculo integral en mecánica. Resumen: Aplicación del cálculo diferencial e integral a la resolución de problemas físicos y geométricos en MATLab
Enviar su buen trabajo en la base de conocimientos es sencillo. Utilice el siguiente formulario
Los estudiantes, estudiantes de posgrado y jóvenes científicos que utilicen la base de conocimientos en sus estudios y trabajos le estarán muy agradecidos.
Resumen sobre el tema: "Integral y su aplicación"
Estudiantes
Miel. colega
N° 2 203 grupos
María Kulikova
San Petersburgo 2010
Introducción
El símbolo integral se introdujo desde 1675 y el cálculo integral se estudia desde 1696. Aunque la integral es estudiada principalmente por matemáticos, los físicos también han contribuido a esta ciencia. Casi ninguna fórmula de la física está completa sin el cálculo diferencial e integral. Por eso, decidí explorar la integral y su aplicación.
Historia del calculo integral
La historia del concepto de integral está estrechamente relacionada con los problemas de encontrar cuadraturas. Los matemáticos de la antigua Grecia y Roma llamaron problemas de cálculo de áreas a los problemas de elevar al cuadrado una u otra figura plana. La palabra latina quadratura se traduce como "cuadratura". La necesidad de un término especial se explica por el hecho de que en la antigüedad (y más tarde, hasta el siglo XVIII), las ideas sobre los números reales aún no estaban suficientemente desarrolladas. Los matemáticos operaban con sus contrapartes geométricas o escalares que no se pueden multiplicar. Por lo tanto, las tareas para encontrar áreas debían formularse, por ejemplo, de la siguiente manera: "Construir un cuadrado del mismo tamaño que un círculo dado". (Este problema clásico de “la cuadratura de un círculo”, como es bien sabido, no se puede resolver con un compás y una regla.)
El símbolo t fue introducido por Leibniz (1675). Este signo es un cambio de la letra latina S (la primera letra de la palabra summ a) La palabra integral en sí fue acuñada por J. Bernoulli (1690). Probablemente provenga del latín integro, que se traduce como devolver a su estado anterior, restaurar. (De hecho, la operación de integración "recupera" la función cuya diferenciación produce el integrando.) Quizás el origen del término integral sea diferente: la palabra entero significa entero.
Durante la correspondencia, I. Bernoulli y G. Leibniz estuvieron de acuerdo con la propuesta de J. Bernoulli. Luego, en 1696, apareció el nombre de una nueva rama de las matemáticas: el cálculo integral (calculus integralis), que fue introducido por I. Bernoulli.
Otros términos muy conocidos relacionados con el cálculo integral aparecieron mucho más tarde. El nombre de función antiderivada actualmente en uso reemplazó a la anterior "función primitiva" introducida por Lagrange (1797). La palabra latina primitivus se traduce como "inicial": F(x) = m f(x)dx - inicial (o inicial, o antiderivada) de f (x), que se obtiene de F(x) por diferenciación.
En la literatura moderna, el conjunto de todas las primitivas de la función f(x) también se denomina integral indefinida. Este concepto fue distinguido por Leibniz, quien notó que todas las funciones antiderivadas se diferencian por una constante arbitraria b, llamada integral definida (la designación fue introducida por C. Fourier (1768-1830), pero Euler ya indicó los límites de integración).
Muchos logros importantes de los matemáticos griegos antiguos en la resolución de problemas de búsqueda de cuadraturas (es decir, cálculo de áreas) de figuras planas, así como de cubetura (cálculo de volúmenes) de cuerpos, están asociados con el uso del método de agotamiento propuesto por Eudoxo de Cnido (c .408 - c.355 a.C.). .e.). Con este método, Eudoxo demostró, por ejemplo, que las áreas de dos círculos están relacionadas como los cuadrados de sus diámetros, y que el volumen de un cono es igual a 1/3 del volumen de un cilindro que tiene la misma base y altura. .
El método de Eudoxo fue mejorado por Arquímedes. Las principales etapas que caracterizan el método de Arquímedes: 1) se demuestra que el área de un círculo es menor que el área de cualquier polígono regular descrito a su alrededor, pero mayor que el área de cualquier inscrito; 2) está demostrado que con una duplicación ilimitada del número de lados, la diferencia en las áreas de estos polígonos tiende a cero; 3) para calcular el área de un círculo, queda por encontrar el valor al que tiende la relación del área de un polígono regular con una duplicación ilimitada del número de sus lados.
Con la ayuda del método de agotamiento y una serie de otras consideraciones ingeniosas (incluidos los modelos mecánicos), Arquímedes resolvió muchos problemas. Dio una estimación de p (3,10/71 Arquímedes anticipó muchas ideas del cálculo integral. (Agreguemos que en la práctica los primeros teoremas de límite fueron demostrados por él.) Pero tuvieron que pasar más de mil años y medio antes de que estas ideas encontraran una expresión clara y fueran llevadas al nivel del cálculo. Los matemáticos del siglo XVII, que obtuvieron muchos resultados nuevos, aprendieron de los trabajos de Arquímedes. También se utilizó activamente otro método: el método de los indivisibles, que también se originó en la antigua Grecia (está asociado principalmente con las opiniones atomistas de Demócrito). Por ejemplo, imaginaron un trapecio curvilíneo (Fig. 1, a) compuesto por segmentos verticales de longitud f (x), al que, sin embargo, le atribuyeron un área igual a un valor infinitamente pequeño f (x) dx. De acuerdo con este entendimiento, el área requerida se consideró igual a la suma un número infinito de áreas infinitamente pequeñas. A veces incluso se subrayaba que los términos individuales de esta suma son ceros, pero ceros de un tipo especial que, sumados en un número infinito, dan una suma positiva bien definida. Sobre una base que ahora parece al menos dudosa, I. Kepler (1571-1630) en sus escritos “Nueva Astronomía”. 1609 y "Estereometría de barriles de vino" (1615) calcularon correctamente una serie de áreas (por ejemplo, el área de una figura limitada por una elipse) y volúmenes (el cuerpo se cortó en placas finitamente delgadas de 6c). Estos estudios fueron continuados por los matemáticos italianos B. Cavalieri (1598-1647) y E. Torricelli (1608-1647). El principio formulado por B. Cavalieri, introducido por él bajo algunos supuestos adicionales, conserva su importancia en nuestro tiempo. Sea necesario encontrar el área de la figura que se muestra en la Figura 1, b, donde las curvas que limitan la figura desde arriba y desde abajo tienen las ecuaciones y = f(x) y y=f(x)+c. Al representar una figura compuesta de columnas "indivisibles", en la terminología de Cavalieri, infinitamente delgadas, notamos que todas tienen una longitud común c. Moviéndolos en dirección vertical, podemos hacer un rectángulo con base b-a y altura c. Por lo tanto, el área requerida es igual al área del rectángulo resultante, es decir S \u003d S1 \u003d c (b - a). El principio general de Cavalieri para las áreas de figuras planas se formula de la siguiente manera: dejemos que las líneas de un determinado conjunto de paralelos crucen las figuras F1 y F2 a lo largo de segmentos de igual longitud (Fig. 1, c). Entonces las áreas de las figuras Ф1 y Ф2 son iguales. Un principio similar opera en estereometría y es útil para encontrar volúmenes. En el siglo 17 Se han realizado muchos descubrimientos relacionados con el cálculo integral. Entonces, P. Fermat ya en 1629 resolvió el problema de elevar al cuadrado cualquier curva y \u003d xn, donde n es un número entero (es decir, esencialmente derivó la fórmula m xndx \u003d (1 / n + 1) xn + 1), y Sobre esta base decidió una serie de tareas para encontrar los centros de gravedad. I. Kepler, al derivar sus famosas leyes del movimiento planetario, en realidad se basó en la idea de integración aproximada. I. Barrow (1630-1677), maestro de Newton, estuvo cerca de comprender la conexión entre integración y diferenciación. De gran importancia fueron los trabajos sobre la representación de funciones en forma de series de potencias. Sin embargo, a pesar de la importancia de los resultados obtenidos por muchos matemáticos extremadamente inventivos del siglo XVII, el cálculo aún no existía. Era necesario resaltar las ideas generales que subyacen a la solución de muchos problemas particulares, así como establecer una conexión entre las operaciones de diferenciación e integración, lo que da un algoritmo bastante general. Esto lo hicieron Newton y Leibniz, quienes descubrieron de forma independiente un hecho conocido como fórmula de Newton-Leibniz. Así, finalmente tomó forma el método general. Todavía era necesario aprender a encontrar las antiderivadas de muchas funciones, a realizar nuevos cálculos lógicos, etc. Pero lo principal ya está hecho: se ha creado el cálculo diferencial e integral. Los métodos de análisis matemático se desarrollaron activamente en el siglo siguiente (en primer lugar, cabe mencionar los nombres de L. Euler, que completó el estudio sistemático de la integración de funciones elementales, y I. Bernoulli). Los matemáticos rusos M.V. participaron en el desarrollo del cálculo integral. Ostrogradsky (1801-1862), V.Ya. Bunyakovsky (1804-1889), P.L. Chebyshev (1821-1894). De fundamental importancia fueron, en particular, los resultados de Chebyshev, quien demostró que hay integrales que no pueden expresarse en términos de funciones elementales. Una exposición rigurosa de la teoría de la integral apareció recién en el siglo pasado. La solución a este problema está asociada con los nombres de O. Cauchy, uno de los más grandes matemáticos, el científico alemán B. Riemann (1826-1866), el matemático francés G. Darboux (1842-1917). Las respuestas a muchas preguntas relacionadas con la existencia de áreas y volúmenes de figuras se obtuvieron con la creación de la teoría de la medida por K. Jordan (1838-1922). Varias generalizaciones del concepto de integral ya fueron propuestas a principios de nuestro siglo por los matemáticos franceses A. Lebesgue (1875-1941) y A. Denjoy (1884-1974), el matemático soviético A.Ya. Khinchinchin (1894-1959). Si F(x) es una de las primitivas de la función f(x) en el intervalo J, entonces la primitiva en este intervalo tiene la forma F(x)+C, donde COR. Definición. El conjunto de todas las primitivas de la función f(x) en el intervalo J se denomina integral definida de la función f(x) en este intervalo y se denota por m f(x)dx. t f(x)dx = F(x)+C, donde F(x) es alguna primitiva en el intervalo J. f - integrando, f(x) - integrando, x - variable de integración, C - constante de integración. Propiedades de la integral indefinida. (t f(x)dx) ў = t f(x)dx, t f(x)dx = F(x)+C, donde F ў(x) = f(x) (t f(x)dx) ў= (F(x)+C) ў= f(x) t f ў(x)dx = f(x)+C - de la definición. t k f (x)dx = k t fў(x)dx si k es una constante y F ў(x)=f(x), t k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k t fў(x)dx t (f(x)+g(x)+...+h(x))dx = t f(x)dx + t g(x)dx +...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = t dx = t ўdx = F(x)+G(x)+...+H(x)+C= t f(x)dx + t g(x)dx +...+ t h(x)dx, donde C=C1+C2+C3+...+Cn. forma tabular. Método de sustitución. Si el integrando no es una integral de tabla, entonces es posible (no siempre) aplicar este método. Para esto necesitas: dividir el integrando en dos factores; designar uno de los multiplicadores de la nueva variable; expresar el segundo factor en términos de una nueva variable; Escribe la integral, encuentra su valor y realiza la sustitución inversa. Nota: es mejor designar la función asociada con la expresión restante como una nueva variable. 1. txT(3x2-1)dx; Sea 3x2-1=t (tі0), tome la derivada de ambas partes: y dt 1 1 y 1 1 t 2 2 1 --- W f- t 2 \u003d - f t 2dt \u003d - --- + C \u003d -C 3x2-1 + C t sen x cos 3x dx = t - t3dt = - - + C Sea cos x = t Método para convertir un integrando en una suma o diferencia: t sen 3x cos x dx = 1/2 t (sen 4x + sen 2x) dx = 1/8 cos 4x - ј cos 2x + C y x4+3x2+1 y 1 1 f dx = f(x2+2 - ---) dx = - x2 + 2x - arctg x + C x x2+1 xx2+1 3 Nota: al resolver este ejemplo, es bueno hacer que los polinomios sean "ángulos". En partes. Si es imposible tomar la integral en una forma dada y, al mismo tiempo, es muy fácil encontrar la antiderivada de un factor y la derivada de otro, entonces puedes usar la fórmula. (u(x)v(x))"=u"(x)v(x)+u(x)v(x) u"(x)v(x)=(u(x)v(x)+u(x)v"(x) t u"(x)v(x)dx=t (u(x)v(x))"dx - t u(x)v"(x)dx t u"(x)v(x)dx=u(x)v(x)dx - t u(x)v"(x)dx t x cos (x) dx = t x dsen x = x sen x - t sen x dx = x sen x + cos x + C Definición. La figura delimitada por la gráfica de una función continua de signo constante f(x), el eje de abscisas y las rectas x=a, x=b, se llama trapezoide curvilíneo. Formas de encontrar el área de un trapecio curvilíneo Teorema. Si f(x) es una función continua y no negativa en el segmento , entonces el área del trapecio curvilíneo correspondiente es igual al incremento de las antiderivadas. Dado: f(x) - continua indefinidamente. función, xO. Demuestre: S = F(b) - F(a), donde F(x) es la antiderivada de f(x). Prueba: 1) Considere la función auxiliar S(x). A cada xO le asignamos la parte del trapecio curvilíneo que se encuentra a la izquierda de la recta (Fig. 2), que pasa por el punto con esta abscisa y es paralela al eje y. Por lo tanto S(a)=0 y S(b)=Str Demostremos que S(a) es la antiderivada de f(x). D(f) = D(S) = S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), para Dx®0 DS es un rectángulo Dx®0 con lados Dx y f(x0) S "(x0) \u003d lim (Dx f (x0) / Dx) \u003d lim f (x0) \u003d f (x0): dado que x0 es un punto, entonces S (x) - Dx®0 Dx®0 antiderivada f(x). Por lo tanto, según el teorema de la forma general de la antiderivada, S(x)=F(x)+C. Porque S(a)=0, entonces S(a) = F(a)+C S = S(b)=F(b)+C = F(b)-F(a) 1). Dividamos el segmento en n partes iguales. Paso dividido (Fig.3) Dx=(b-a)/n. En este caso Str=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+ f(xn)) Para n®Ґ obtenemos que Str= Dx(f(x0)+f(x1)+...+f(xn)) El límite de esta suma se llama integral definida. La suma bajo el límite se llama suma integral. La integral definida es el límite de la suma integral en el segmento como n®Ґ. La suma integral se obtiene como el límite de la suma de productos de la longitud del segmento obtenido al dividir el dominio de la función en cualquier punto de este intervalo. a - límite inferior de integración; segundo - arriba. Fórmula de Newton-Leibniz. Comparando las fórmulas para el área de un trapecio curvilíneo, concluimos: si F es la antiderivada de b en , entonces f(x)dx = F(b)-F(a) t f(x)dx = F(x) f = F(b) - F(a) Propiedades de una integral definida. tf(x)dx = tf(z)dz t f(x)dx = F(a) - F(a) = 0 tf(x)dx = - tf(x)dx t f(x)dx = F(a) - F(b) t f(x)dx = F(b) - F(a) = - (F(a) - F(b)) Si a, b y c son puntos del intervalo I en los que la función continua f(x) tiene una primitiva, entonces tf(x)dx = tf(x)dx + tf(x)dx F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a) (esta es la propiedad de aditividad de una integral definida) Si l y m son constantes, entonces t (lf(x) +m j(x))dx = l t f(x)dx + m tj(x))dx - Ésta es la propiedad de linealidad de una integral definida. t (f(x)+g(x)+...+h(x))dx = t f(x)dx+ t g(x)dx+...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H (a)+Cn=b b b = t f(x)dx+ t g(x)dx+...+ t h(x)dx Un conjunto de imágenes estándar (Fig. 4, 5, 6, 7, 8) Arroz. 4 figura. 5 Arroz. 6 figura. 7 Porque f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0. Es necesario: considerar la simetría de la función con respecto al eje OX. ABCD®A"B"CD b S (ABCD) \u003d S (A "B" CD) \u003d t -f (x) dx S= t f(x)dx = t g(x)dx S = t(f(x)-g(x))dx+t(g(x)-f(x))dx S= t (f(x)+mg(x)-m)dx = t (f(x)-g(x))dx t ((f(x)-g(x))dx S= t (f(x)+mg(x)-m)dx = T (f(x)-g(x))dx Si en el segmento f(x)іg(x), entonces el área entre estos gráficos es igual a t ((f(x)-g(x))dx Las funciones f(x) y g(x) son arbitrarias y no negativas S=t f(x)dx - t g(x)dx = t (f(x)-g(x))dx Aplicación de la integral En física. Trabajo de fuerza (A=FScosa, cosa No. 1) Si una fuerza F actúa sobre una partícula, la energía cinética no permanece constante. En este caso, según el incremento de la energía cinética de la partícula en el tiempo dt es igual al producto escalar Fds, donde ds es el desplazamiento de la partícula en el tiempo dt. Valor se llama trabajo realizado por la fuerza F. Dejemos que un punto se mueva a lo largo del eje OX bajo la acción de una fuerza cuya proyección sobre el eje OX es una función f(x) (función f-continua). Bajo la acción de la fuerza, el punto se movió del punto S1(a) al S2(b). Dividamos el segmento en n segmentos de la misma longitud Dx = (b - a)/n. El trabajo de la fuerza será igual a la suma del trabajo de la fuerza sobre los segmentos resultantes. Porque f(x) -continuo, entonces, para valores pequeños, el trabajo de la fuerza en este segmento es igual a f(a)(x1-a). De manera similar, en el segundo segmento f(x1)(x2-x1), en el enésimo segmento - f(xn-1)(b-xn-1). Por tanto, trabajar en es igual a: А » An = f(a)Dx +f(x1)Dx+...+f(xn-1)Dx= ((b-a)/n)(f(a)+f(x1)+...+f (xn-1)) La igualdad aproximada se vuelve exacta cuando n®Ґ A = lim [(b-a)/n] (f(a)+...+f(xn-1))= t f(x)dx (por definición) Sea un resorte de rigidez C y longitud l comprimido a la mitad de su longitud. Determine la magnitud de la energía potencial Ep es igual al trabajo A realizado por la fuerza -F (s) la elasticidad del resorte cuando se comprime, entonces Ep \u003d A \u003d - t (-F (s)) dx Por el curso de mecánica se sabe que F(s)= -Cs. Desde aquí encontramos En \u003d - t (-Cs) ds \u003d CS2 / 2 | = C/2l2/4 Respuesta: Cl2/8. Centro de coordenadas de masa El centro de masa es el punto por el que pasa la resultante de la gravedad para cualquier disposición espacial del cuerpo. Deje que la placa homogénea de material o tenga la forma de un trapecio curvilíneo (x;y |aЈxЈb; 0ЈyЈf(x)) y la función y=f(x) sea continua en , y el área de este trapezoide curvilíneo sea igual a S, entonces las coordenadas del centro de masa de la placa o se encuentran mediante las fórmulas: x0 = (1/S)txf(x)dx; y0 = (1/2S) t f 2(x) dx; Centro de masa. Encuentre el centro de masa de un semicírculo homogéneo de radio R. Dibuja un semicírculo en el sistema de coordenadas OXY (Fig. 9). Por razones de simetría y homogeneidad, observamos que la abscisa del punto M La función que describe el semicírculo tiene la forma: Sea S = pR2/2 el área del semicírculo, entonces y = (1/2S) tC(R2-x2)dx = (1/pR2) tC(R2-x2)dx = -R -R R = (1/pR2)(R2x-x3/3)|= 4R/3p Respuesta: M(0; 4R/3p) El camino recorrido por un punto material. Si el punto material se mueve rectilíneamente con la velocidad u=u(t) y durante el tiempo T= t2-t1 (t2>t1) ha pasado por la trayectoria S, entonces En geometría El volumen es una característica cuantitativa de un cuerpo espacial. Como unidad de volumen se toma un cubo con una arista de 1 mm (1di, 1m, etc.). El número de cubos de una unidad de volumen colocados en un cuerpo dado es el volumen del cuerpo. Axiomas de volumen: El volumen es un valor no negativo. El volumen de un cuerpo es igual a la suma de los volúmenes de los cuerpos que lo forman. Encontremos la fórmula para calcular el volumen (Fig.10): elija el eje OX en la dirección de la ubicación de este cuerpo; determinar los límites de la ubicación del cuerpo en relación con el buey; Introduzcamos una función auxiliar S(x) que define la siguiente correspondencia: a cada x del segmento, ponemos en correspondencia el área de la sección de la figura dada por el plano que pasa por el punto x dado perpendicular al eje OX. dividamos el segmento en n partes iguales y dibujemos un plano perpendicular al eje OX que pase por cada punto de la división, mientras nuestro cuerpo quedará dividido en partes. Según el axioma V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx Dx®0 y Sk®Sk+1, y el volumen de la pieza encerrada entre dos planos adyacentes es igual al volumen del cilindro Vц=SonH. Tenemos la suma de los productos de los valores de la función en los puntos de partición por el paso de partición, es decir importe integral. Según la definición de integral definida, el límite de esta suma como n®Ґ se llama integral a V= t S(x)dx, donde S(x) es la sección del plano que pasa por b punto seleccionado perpendicular al eje OX. Para encontrar el volumen que necesitas: 1). Elija el eje OX de forma cómoda. 2). Determine los límites de la ubicación de este cuerpo en relación con el eje. 3). Construya una sección de un cuerpo dado por un plano perpendicular al eje OX y que pase por el punto correspondiente. 4). Expresar en términos de cantidades conocidas una función que exprese el área de una sección determinada. 5). Haz una integral. 6). Después de calcular la integral, encuentra el volumen. Volumen de figuras de rotación. El cuerpo obtenido como resultado de la rotación de una figura plana alrededor de algún eje se llama figura de rotación. La función S(x) de la figura de rotación tiene un círculo. Ssec(x)=p f 2(x) Longitud de arco de una curva plana Sea la función y = f(x) tener una derivada continua y" = f "(x) en el intervalo. En este caso, la longitud del arco l del “trozo” de la gráfica de la función y = f(x), xO se puede encontrar mediante la fórmula l \u003d t C (1 + f "(x) 2) dx 1. M.Ya. Vilenkin, O.S. Ivashev-Musatov, S.I. Shvartsburd, “Álgebra y análisis matemático”, Moscú, 1993 2. “Colección de problemas de análisis matemático”, Moscú, 1996 3. I.V. Savelyev, “Curso de Física General”, Volumen 1, Moscú, 1982 4. Para la elaboración de este trabajo se utilizaron materiales del sitio http://referatovbank.ru/. Ideas de cálculo integral en las obras de los matemáticos antiguos. Características del método de agotamiento. La historia de la búsqueda de la fórmula del volumen del toro de Kepler. Fundamentación teórica del principio del cálculo integral (principio de Cavalieri). El concepto de integral definida. presentación, añadido el 05/07/2016 Historia del cálculo integral. Definición y propiedades de la integral doble. Su interpretación geométrica, cálculo en coordenadas cartesianas y polares, su reducción a lo repetido. Aplicación en economía y geometría para el cálculo de volúmenes y áreas. trabajo final, agregado el 16/10/2013 Definición de integral definida, sus propiedades. La longitud del arco de la curva. Área de un trapecio curvilíneo. Área superficial de rotación. Áreas de figuras delimitadas por gráficas de funciones delimitadas por rectas dadas por ecuaciones. Cálculo de volúmenes de cuerpos. trabajo de control, agregado 10/02/2017 La historia de la aparición del concepto de cálculo "integral" y integral, sus características y significado. Integral como una de las principales herramientas para trabajar con funciones. Justificación de la necesidad de expresar todos los fenómenos físicos en forma de fórmula matemática. presentación, agregado 19/05/2014 Definición de una integral curvilínea sobre coordenadas, sus principales propiedades y cálculo. Condición de independencia de la integral curvilínea del camino de integración. Calcular las áreas de figuras usando la integral doble. Usando la fórmula de Green. prueba, agregada el 23/02/2011 Métodos para calcular integrales. Fórmulas y verificación de la integral indefinida. Área de un trapecio curvilíneo. Integral indefinida, definida y compleja. Aplicaciones básicas de las integrales. Significado geométrico de integrales definidas e indefinidas. presentación, agregado 15/01/2014 Resolviendo el problema de encontrar el área de un trapecio curvilíneo. Definición y propiedades de una integral definida. Una condición necesaria para la integrabilidad y el criterio de Darboux. Integrabilidad de funciones continuas y monótonas. Prueba de la fórmula de Newton-Leibniz. prueba, agregada el 25/03/2011 Cálculo de las áreas de figuras planas. Encontrar una integral definida de una función. Determinación del área bajo la curva, el área de la figura encerrada entre las curvas. Cálculo de volúmenes de cuerpos de revolución. El límite de la suma integral de una función. Determinación del volumen de un cilindro. presentación, agregado 18/09/2013 El concepto de integral definida, el cálculo del área, volumen del cuerpo y la longitud del arco, el momento estático y el centro de gravedad de la curva. Cálculo del área en el caso de una región curvilínea rectangular. Aplicación de integrales curvilíneas, de superficie y triples. trabajo final, agregado el 19/05/2011 Historia del cálculo integral y diferencial. Aplicaciones de la integral definida a la solución de algunos problemas de mecánica y física. Momentos y centros de masa de curvas planas, teorema de Gulden. Ecuaciones diferenciales. Ejemplos de resolución de problemas en MatLab. "Academia Médica Estatal de Omsk" Ministerio de Salud y Desarrollo Social de la Federación de Rusia sobre el tema: aplicación de una integral definida En medicina completado por estudiante de 1er año departamentos de medicina general grupo 102F Glushneva N.A. Introducción El destacado físico y astrónomo italiano, uno de los fundadores de las ciencias naturales exactas, Galileo Galilei (1564-1642) dijo que "El Libro de la Naturaleza está escrito en el lenguaje de las matemáticas". Casi doscientos años después, el fundador de la filosofía clásica alemana, Kant (1742-1804), argumentó que "en cada ciencia hay tanta verdad como matemáticas". Finalmente, después de casi ciento cincuenta años, prácticamente ya en nuestro tiempo, el matemático y lógico alemán David Hilbert (1862-1943) afirmó: “Las matemáticas son la base de toda ciencia natural exacta”. Leonardo Da Vinci dijo: “Que nadie que no sea matemático me lea en mis fundamentos”. Tratando de encontrar una justificación matemática para las leyes de la naturaleza, considerando las matemáticas como un poderoso medio de conocimiento, las aplica incluso en una ciencia como la anatomía. Todo el mundo necesita matemáticas. Y los médicos también. Al menos para leer correctamente el cardiograma habitual. Sin conocimientos de los conceptos básicos de las matemáticas, es imposible ser un buen técnico en informática, aprovechar las posibilidades de la tomografía computarizada ... Después de todo, la medicina moderna no puede prescindir de la tecnología más compleja. Hoy en día es imposible estudiar la hemodinámica, el movimiento de la sangre a través de los vasos, sin el uso de la integral. Durante mucho tiempo, el cateterismo del corazón derecho fue el único método de investigación que permitía evaluar el estado del corazón derecho, obtener las características del flujo sanguíneo intracardíaco y determinar la presión en el corazón derecho y en las arterias pulmonares. Sin embargo, más cerca de la práctica. Primero, encontremos la velocidad lineal del flujo sanguíneo. Cambio en la velocidad lineal del flujo sanguíneo en varios vasos. Es el camino recorrido por unidad de tiempo por una partícula de sangre en un vaso. La velocidad lineal en vasos de diferentes tipos es diferente (ver figura) y depende de la velocidad volumétrica del flujo sanguíneo y del área de la sección transversal de los vasos. En la medicina práctica, la velocidad lineal del flujo sanguíneo se mide mediante ultrasonido y métodos indicadores, más a menudo se determina el tiempo de circulación sanguínea completa, que es de 21 a 23 s. Para determinarlo se introduce un indicador en la vena cubital (eritrocitos marcados con un isótopo radiactivo, solución de azul de metileno, etc.) y se anota el momento de su primera aparición en la sangre venosa del mismo vaso en la otra extremidad. Para empezar, recordemos que la integral es un objeto matemático que surgió históricamente de la necesidad de resolver diversos problemas aplicados de la física y la tecnología. Estas son las aplicaciones físicas de una integral definida: el cálculo de la trayectoria de un punto material que se mueve a lo largo de una trayectoria rectilínea o curvilínea a la velocidad de su movimiento. Aquellas cantidades físicas que se determinan mediante una integral se suelen denominar integrales, y aquellas cantidades a través de las cuales se expresan cantidades integrales se denominan diferenciales. Por ejemplo, la velocidad de un cuerpo en un punto es una característica diferencial de un cuerpo y la masa de un cuerpo es una característica integral. Las características diferenciales están determinadas por el valor en un punto y suelen ser diferentes en diferentes puntos del espacio. Las características integrales siempre expresan las propiedades de los objetos relacionados con toda la región del espacio. Por ejemplo, la masa caracteriza a todo el cuerpo como un objeto que ocupa una región del espacio. El camino recorrido por el cuerpo también es una característica integral, ya que caracteriza toda la trayectoria, que consta de muchos puntos, y la velocidad es diferente en cada punto de la trayectoria y caracteriza cada punto por separado. Surge la pregunta: cómo calcular la velocidad integral de todo el vaso (arteria o vena), conociendo la velocidad lineal del flujo sanguíneo. Es muy simple: necesitas A continuación se muestran los cálculos del volumen sistólico (volumen sistólico del corazón (sin.: volumen sanguíneo sistólico, volumen sistólico del corazón, volumen sistólico de la sangre) - el volumen de sangre (en ml) expulsada por el ventrículo del corazón en una sístole): uno de los valores principales en EHOkg, calculado utilizando la integral de la velocidad lineal del flujo sanguíneo. a - esquemas de cálculo del volumen sistólico, a - utilizando la ecuación de continuidad del flujo, b - utilizando la ecuación de continuidad del flujo en presencia de insuficiencia mitral significativa. VTI = V cp ET, donde CSA es el área de la sección transversal, VTI es la integral lineal de la velocidad del flujo, V cp es la velocidad promedio del flujo en el tracto de salida del ventrículo izquierdo, ET es el tiempo de eyección. En el caso de que exista insuficiencia mitral hemodinámicamente significativa (más de 2º grado), el volumen sistólico total del ventrículo izquierdo se calcula mediante la fórmula: TSV=FSV+RSV [Integral de velocidad lineal (FVI o VTI)] = [Tiempo de flujo sanguíneo (ET)] x [Velocidad media del flujo sanguíneo (Vmedia)]; El gasto cardíaco se puede determinar a partir de la integral de la velocidad lineal del flujo aórtico y pulmonar. En conclusión, me gustaría agregar que mi trabajo no está dirigido a un matemático que conozca bien la integración, sino a cualquier persona que haya mostrado interés en utilizar la integral en medicina. Por lo tanto, traté de hacerlo lo más accesible posible para la percepción e interesante incluso para un niño. Bibliografía: Una lección abierta de álgebra y los inicios del análisis en el grado 11 con un estudio ampliado de matemáticas y física. "Aplicación de métodos de análisis matemático en la resolución de problemas prácticos". Profesor: Vishnevskaya N.V. Objetivos de la lección: 1. Repetir los principales tipos de problemas resueltos mediante los métodos de análisis matemático. 2. Repita los algoritmos de solución. 3. Analizar la solución de problemas de mayor dificultad. 4. Resolver problemas económicos. Plan de estudios: En la pizarra se analizan dos tareas de mayor dificultad (tarjetas nº 7 y nº 5). Mientras los chicos se preparan, la clase responde oralmente las preguntas: a) Áreas donde se aplican métodos de análisis matemático; b) un algoritmo para resolver problemas buscando los valores mayor y menor de una función; c) un algoritmo para resolver problemas utilizando una integral definida. Al mismo tiempo, 6 personas trabajan con tarjetas (nº 3, 4, 6, 8, 9, 10). Las mesas se están llenando. Las tareas se verifican en la pizarra, el maestro verifica la corrección de la resolución de problemas en tarjetas. El problema económico se analiza en la pizarra (tarjeta nº 1, 2). Trabajos de control del hogar. Algoritmo para resolver problemas buscando los valores mayor y menor de una función. Algoritmo para calcular cantidades geométricas y físicas mediante una integral definida. Expresar el valor deseado como el valor en algún punto de la función. F
.
Encuentra la derivada F esta función. expresar una función F en forma de una integral definida de F y calcularlo. Valor sustitutivo X = b encontrar el valor deseado. Tareas caseras (en la pizarra):
Dos barcos se mueven a lo largo de dos líneas perpendiculares que se cruzan en un punto ACERCA DE, hacia ACERCA DE. En algún momento ambos se encuentran a 65 km de ACERCA DE, la velocidad del primero es de 15 km/h, la del segundo es de 20 km/h. Del primer barco parte una lancha a motor que se mueve a una velocidad de 25 km/h. a) ¿Cuál es el tiempo más corto que tarda el barco en viajar del primer barco al segundo? b) ¿Cuál es el tiempo más corto que le toma al bote nadar desde el primer barco al segundo y regresar al primer barco? V 1 = 15 kilómetros por hora 65 kilometros S
1 ACERCA DE
S
3 S
2
65 kilometros V l = 25 kilómetros por hora V 2 = 20 kilómetros por hora Solución:
X- el tiempo transcurrido desde el momento en que ambos barcos se encontraban a 65 km de ACERCA DE hasta la salida del barco. En el momento de la salida del barco, el primer barco se encontraba a una distancia Diferenciar con respecto a X:
Respuesta: a) 1 hora; b) 3 horas. La caldera tiene forma de paraboloide de revolución. El radio de su base. R= 3 m, profundidad h\u003d 5 m La caldera se llena con un líquido cuyo peso específico es 0,8 g / cm 3. Calcule el trabajo que se debe realizar para bombear el líquido fuera de la caldera. en
en
R= 3 metros h= 5 metros late peso = 0,8 g / cm 3 Calcule el trabajo que se debe realizar para bombear el líquido fuera de la caldera. Solución:
En el plano de la sección. hoy CUALQUIER OTRO NEGOCIO es una parábola cuya ecuación Coordenadas de puntos EN debe satisfacer esta ecuación, es decir Dividamos el paraboloide en capas por planos paralelos a la superficie del líquido. Deje que el espesor de la capa en profundidad ( h – y) es igual a dy. Luego, tomando aproximadamente la capa como un cilindro, obtenemos su volumen. De la ecuación de la parábola Por lo tanto, para bombear líquido desde una profundidad Respuesta: Trabajo de clase.
¿Cuánto trabajo se debe realizar para estirar el resorte 6 cm si una fuerza de 1 kg lo estira 1 cm? Solución:
Según la ley de Hooke, la fuerza F kg, estirando el resorte por X, es igual a X= 0,01m F= 1 kilogramo Entonces Trabajo buscado Respuesta: 0,18 kgm. Calcular el trabajo de fuerza. F cuando un resorte se comprime 5 cm, si se necesita una fuerza de 1 kg para comprimirlo 1 cm. Solución:
Según la ley de Hooke X= 0,01m F= 1 kilogramo Entonces Trabajo buscado Respuesta: 0,125 kgm. Fuerza F, con lo cual la carga eléctrica Dónde k- constante. Determinar el trabajo de la fuerza. F cuando se mueve la carga Solución:
El trabajo está determinado por la fórmula. En Respuesta: Determine la fuerza de presión del agua sobre una pared vertical que tiene la forma de un semicírculo de radio. R= 6 m, cuyo diámetro está en la superficie del agua. Solución:
La fuerza de la presión del fluido sobre un área. S a profundidad de inmersión X es igual a xC
dx
A B
Dividimos el semicírculo con rectas paralelas en tiras, que tomaremos como un rectángulo. Deje que la franja sombreada tenga longitud. AB, ancho dx y es profundo X Presión del agua sobre una franja en profundidad. X, será igual a . De aquí El peso específico del agua es 1 cm 3 = 1 g, por lo tanto el peso de 1 m 3 = 1000 kg. 1 kg 1 barra = 0,987 atm. Respuesta: 144000 kg. Velocidad de movimiento del punto Solución:
Por eso Respuesta: 512 metros; 64m/s Tarjeta número 1 (decidida en clase en la pizarra)
Costo total promedio de producción de jabón. Relación entre ventas anuales iguales a producción anual q y el precio del jabón R(en miles de rublos por tonelada) se describe mediante la fórmula Habiendo vendido todo el jabón elaborado durante el año a un precio fijo, la planta obtuvo el máximo beneficio posible. ¿Cuáles fueron los ingresos de la empresa? Solución:
expresar a través de q primero el precio del jabón de la fórmula entonces beneficio GRAMO se puede expresar: Encontremos los puntos críticos de esta función: Puntos críticos 100, -340, -120. Las raíces negativas no tienen sentido económico. q
GRAMO
Entonces el volumen anual óptimo de jabón Entonces el ingreso anual R será: (mil rublos). Respuesta: 1 millón de rublos. Encuentre la presión del agua sobre un rectángulo sumergido verticalmente en agua, si se sabe que su base mide 8 m, su altura es 12 m, la base superior es paralela a la superficie del agua y está a una profundidad de 5 m. Solución:
5 metros 8 metros X
dx 12 metros kgm. Respuesta: Tarjeta No. 2 (opcional)
Las capacidades de producción permiten a la empresa Linotron producir no más de 600 toneladas de algodón al año. Dependencia del valor de los costos totales. Relación entre las ventas anuales de algodón, que es igual al volumen de producción anual, y el precio del algodón R(en miles de rublos por tonelada) se describe mediante la función El precio del algodón se fija el 1 de enero de 1995 y no se revisa hasta el 1 de enero del año siguiente. Encuentre, con una precisión del 1%, la rentabilidad de la producción en términos de costos, si en 1995 la empresa recibe el máximo beneficio posible. Solución:
Usando dependencias y y a 0b c x a 0bcx
El cálculo integral surgió en relación con la solución de problemas de determinación de áreas y volúmenes. 2000 aC Los habitantes de Egipto y Babilonia ya sabían determinar el área aproximada de un círculo y conocían la regla para calcular el volumen de una pirámide truncada. La fundamentación teórica de las reglas para calcular áreas y volúmenes apareció por primera vez entre los antiguos griegos. El filósofo materialista Demócrito V Siglo aC Considera que los cuerpos están formados por un gran número de partículas pequeñas. Es decir, el cono es un conjunto de discos cilíndricos muy delgados y de diferentes radios. El problema de la cuadratura del círculo jugó un papel muy importante en la historia del cálculo integral.(cuadrar un círculo: construir un cuadrado cuyo área sea igual al área de un círculo dado). Hipócrates (centro) encontró la cuadratura exacta de varias figuras curvilíneas. siglo V). El primer método conocido para calcular la integral es el método de agotamiento de Eudoxo (ca. 370 a. C.). Intentó encontrar áreas y volúmenes, dividiéndolos en un número infinito de partes cuyo área o volumen ya se conocía. Este método fue recogido y desarrollado por Arquímedes, utilizado para calcular las áreas de parábolas y un cálculo aproximado del área de un círculo.En su ensayo Cuadratura de una parábola, Arquímedes utiliza el método de agotamiento para calcular el área de un sector de una parábola. Aquellos. Arquímedes fue el primero en compilar sumas, que hoy en día se denominan sumas integrales. Los primeros intentos importantes de desarrollar los métodos de integración de Arquímedes, que se vieron coronados por el éxito, se realizaron en XVII siglo, cuando, por un lado, se lograron avances significativos en el campo del álgebra y, por otro lado, la economía, la tecnología, las ciencias naturales se desarrollaron cada vez más intensamente, y allí se requirieron métodos extensos y profundos para estudiar y calcular cantidades. . Al calcular el área de un trapecio curvilíneo Newton y Leibniz llegan al concepto.función antiderivada (o primitiva) para una función derivada dadaF(X),DóndeCONpodría ser cualquier cosa. Ejército de reservallamar hoy
El trabajo sobre el estudio de los fundamentos del cálculo diferencial e integral comienza en XIX siglo por las obras de O. Cauchy y B. Bolzano. Al mismo tiempo, los matemáticos rusos M.V. hicieron una contribución significativa al desarrollo del cálculo integral. Ostrogradsky, V.Ya. Bunyakovsky, V.Ya. Chebyshev. Esta era la época en la que recién se estaba creando el análisis matemático moderno. Esta fue, quizás, la única época de creatividad matemática en términos de intensidad, y Euler unió el material extenso, pero dispar, del nuevo análisis en una ciencia integral. Con tiempo, El hombre adquirió cada vez más poder sobre la naturaleza, pero el sueño de volar a las estrellas seguía siendo igualmente irrealizable. Los escritores de ciencia ficción han mencionado los cohetes para vuelos espaciales. Sin embargo, estos misiles eran técnicamente un sueño equivocado. El honor de abrir el camino a las estrellas para las personas recayó en nuestro compatriota K. E. Tsiolkovsky. Toda una galaxia de científicos, liderados por S.P. Koroliov. De particular interés son los problemas que son el prototipo de los problemas para calcular las trayectorias de las naves espaciales que entran en una órbita determinada, para encontrar la altura y la velocidad de ascenso o descenso de un cuerpo y algunos otros problemas que utilizan el cálculo integral. Tarea 1. La velocidad del movimiento rectilíneo del cuerpo está dada. ecuación. Encuentre la ecuación del camino S si el cuerpo viajó 20 m en el tiempo t = 2 s. Solución: Al volar al espacio, es necesario tener en cuenta todos los factores del entorno que nos rodea y, para llegar a donde es necesario, es necesario calcular la trayectoria del movimiento utilizando los datos iniciales. Todo esto debe hacerse antes de que se realice el vuelo.En 2016 se cumple el 55 aniversario del vuelo a órbita del primer cosmonauta Yuri Alekseevich Gagarin. Al calcular, era necesario resolver tales problemas. Tarea 2. Es necesario lanzar un cohete que pese P \u003d 2 10 4 n (t) desde la superficie de la tierra hasta una alturah= 1500 kilómetros.Calcule el trabajo necesario para ejecutarlo. Solución.f - la fuerza de atracción del cuerpo por la Tierra es función de su distancia X al centro de la Tierra: , donde En la superficie de la Tierra donde la fuerza de gravedad es igual al peso del cuerpo R, A x = R- radio de la Tierra, por lo tanto, y Al elevar un cohete desde la superficie de la Tierra a una altura h variable X cambios deX
=R antes X=
R+
h. Encontramos el trabajo que buscamos mediante la fórmula: Tarea 3. fuerza en 10 norte estira la primavera 2 centímetros. que trabajo es ella ¿lo hace? Solución
.
Según la ley de Hooke, la fuerza F , estirar el resorte, es proporcional al estiramiento del resorte, es decirF =kh. De la condición del problema. k= 10/0,02(Nuevo Méjico), Eso F= 500x. Trabajo: Tarea 4. De una mina profundayo= 100 metroses necesario levantar la jaula uniformemente con un peso R 1 = 10 4
h, que cuelga de una cuerda enrollada en un tambor. Calcular el trabajo total Una completa necesaria para levantar la jaula si el peso de un metro lineal de cuerda R 2= 20h.
Solución
.
El trabajo para levantar la jaula: y para levantar la cuerda es proporcional al peso de la cuerda, es decir. Tarea 5. El resorte se dobla bajo la acción de una fuerza de 1,5 10 4 h por 1 cm. ¿Cuánto trabajo se debe hacer para deformar el resorte 3 cm? ( La fuerza de deformación es proporcional a la deflexión del resorte.) Solución
.
F\u003d kx,Dónde X- deflexión del resorte. En x = 0,01m tenemos: Es difícil e inseguro ascender al espacio exterior, pero no menos difícil es el regreso a la Tierra, cuando la nave espacial debe aterrizar a una velocidad de no más de 2 m/s. Solo en este caso, el dispositivo, los instrumentos que contiene y, lo más importante, los miembros de la tripulación no experimentarán un golpe fuerte y fuerte. Konstantin Eduardovich Tsiolkovsky decidió utilizar la desaceleración de la nave espacial por la capa de aire de la Tierra. Moviéndose a una velocidad de 8 m/s, la nave espacial no cae a la Tierra. La primera etapa del descenso consiste en activar el freno del motor durante un breve período de tiempo. La velocidad disminuye 0,2 km/s y el descenso comienza inmediatamente. Considere un ejemplo de cómo resolver el problema de elaborar la ley del movimiento en determinadas condiciones. Tarea 6. Encuentre la ley del movimiento de un cuerpo en caída libre con aceleración constante g, si el cuerpo estaba en reposo en el momento del movimiento. Solución:Se sabe que la aceleración de un cuerpo que se mueve rectilíneamente es la segunda derivada de la trayectoria S con respecto al tiempo. t , o derivada de la velocidad con respecto al tiempo t: , pero , por tanto, de dónde . Integramos: , y De la condición: , de donde encontramos y la velocidad de movimiento: . Encontremos la ley del movimiento del cuerpo: , o . Integramos: , . Según las condiciones iniciales: , de donde encontramos Tenemos la ecuación de movimiento de un cuerpo que cae: - esta es una fórmula familiar de la física. Tarea 7. Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial Encuentre la ecuación de movimiento de este cuerpo (desprecie la resistencia del aire). Solución:Tomemos: la dirección vertical hacia arriba es positiva y la aceleración de la gravedad, dirigida hacia abajo, es negativa. Tenemos: de dónde. Integramos: entonces. Porque y luego C 1: El siguiente ejemplo muestra el cálculo de la trayectoria para la descarga de secciones gastadas, dispositivos innecesarios y materiales. En este caso, se envían a la Tierra, habiendo calculado la órbita de modo que al pasar a través de las capas atmosféricas se quemen y los restos no quemados caigan a la Tierra (la mayoría de las veces al océano), sin causar daño. Tarea 8. Escribe una ecuación para una curva que pasa por el punto M (2; -3) y tiene una tangente con pendiente. .
Solución:La condición de la tarea está dada: A veces los constructores tienen que resolver problemas de cálculo de áreas de figuras inusuales para las que no existen fórmulas conocidas. En este caso, las integrales vuelven al rescate.
.
Los cosmonautas y científicos que trabajan en la estación orbital, para garantizar la pureza del experimento, resuelven e investigan muchas cuestiones de astronomía, física, química, medicina, biología, etc. Acompañaremos el siguiente problema con un ejemplo literario. La conocida novela de ciencia ficción de HG Wells "La guerra de los mundos" describe el ataque de los marcianos al planeta Tierra, quienes decidieron expandir sus territorios superpoblados capturando los nuestros, porque. Las condiciones climáticas de la Tierra eran adecuadas. Comenzó la toma de territorio y la destrucción de los terrícolas, quienes recibieron ayuda de donde no esperaban nada. Nuestras bacterias "nativas", con las que ya hemos aprendido a luchar, habiendo entrado en el cuerpo de los marcianos con aire, comida, agua, encontraron en él un ambiente favorable para su desarrollo y reproducción, se adaptaron rápidamente y, habiendo destruido a los marcianos, librar a la Tierra de los invasores. Considere la solución del problema que da el concepto de este. Tarea 10.La tasa de reproducción de algunas bacterias es proporcional al número de bacterias disponibles en el momento t considerado. La cantidad de bacterias se triplicó en 5 horas. Encuentre la dependencia del número de bacterias en el tiempo. Solución: Sea x(t ) es el número de bacterias en el momento t, y en el momento inicial luego la tasa de reproducción. Por condición, tenemos: o lo siguiente: En la famosa novela de A.N. Me gustaría sentir el "hiperboloide del ingeniero Garin" de Tolstoi, sentir lo que es: ¿un hiperboloide? ¿Cuáles son sus dimensiones, forma, superficie, volumen? La siguiente tarea trata sobre esto. Solución.Usamos la fórmula para calcular el volumen de los cuerpos de revolución alrededor del eje OX usando una integral definida: Tarea 12. Calcula el volumen del cuerpo formado por rotación alrededor del eje OX del área delimitada por las líneas. y \u003d x 2 - 9 Y y = 0.
El significado económico de una integral definida expresa el volumen de producción con una función conocida. pie ) - productividad laboral en este momento t . Luego, el volumen de producción para el período se calcula mediante la fórmula Consideremos un ejemplo de una empresa. Tarea 13. Encuentre el volumen de producción producido en 4 años si la función Cobb-Douglas tiene la forma Solución. El volumen de productos producidos por la empresa es igual a: En resumen, podemos concluir que el uso de la integral abre grandes oportunidades. Al estudiar geometría, consideran el cálculo de las áreas de figuras planas limitadas por segmentos lineales (triángulos, paralelogramos, trapecios, polígonos) y los volúmenes de los cuerpos obtenidos durante su rotación. La integral definida le permite calcular las áreas de figuras complejas delimitadas por líneas curvas, así como encontrar los volúmenes de cuerpos obtenidos al girar trapecios curvilíneos alrededor de cualquier eje. También me gustaría señalar que el uso de una integral definida no se limita solo al cálculo de varias cantidades geométricas, sino que también se usa para resolver problemas de diversos campos de la física, aerodinámica, astronomía, química y medicina, astronáutica, así como como problemas económicos. Bibliografía:
diapositiva 2 La historia del concepto de integral está estrechamente relacionada con los problemas de encontrar cuadraturas, es decir Tareas para calcular áreas. Incluso los matemáticos de la antigua Grecia y Roma se dedicaban a calcular las superficies y los volúmenes de los cuerpos. El primer matemático europeo que recibió nuevas fórmulas para las áreas de figuras y volúmenes de cuerpos fue el famoso astrónomo I. Kepler. Después de la investigación de varios científicos (P. Fermat, D. Wallis), I. Barrow descubrió la conexión entre los problemas de encontrar áreas y trazar una tangente (es decir, entre integración y diferenciación). I. Newton y G. Leibniz realizaron un estudio de la relación entre estas operaciones, libre del lenguaje geométrico. La notación moderna de la integral se remonta a Leibniz, quien expresó la idea de que el área de un trapecio curvilíneo es la suma de las áreas de franjas infinitamente delgadas de ancho d y altura f(x). El signo integral en sí es una letra latina estilizada S (summa). El símbolo de la integral se introdujo desde 1675 y las cuestiones del cálculo integral se abordaron desde 1696. Aunque la integral es estudiada principalmente por matemáticos, los físicos también han contribuido a esta ciencia. Casi ninguna fórmula de la física está completa sin el cálculo diferencial e integral. diapositiva 3 El nombre de Arquímedes (287-212 aC) está asociado con muchos logros importantes de los matemáticos de la antigua Grecia en la resolución de problemas de búsqueda de áreas, así como de volúmenes de cuerpos. Desarrollando las ideas de sus predecesores, Arquímedes determinó la circunferencia y el área. de un círculo, el volumen y superficie de una bola. En sus obras "Sobre la esfera y el cilindro", "Sobre las espirales", "Sobre los conoides y las esferas", demostró que la determinación de los volúmenes de una esfera, un elipsoide, un hiperboloide y un paraboloide de revolución se reduce a determinar la Volumen de un cono y un cilindro. Arquímedes desarrolló y aplicó métodos que anticiparon los creados en el siglo XVII. cálculo integral. Fueron necesarios más de mil quinientos años antes de que las ideas de Arquímedes encontraran una expresión clara y fueran llevadas al nivel del cálculo. En el siglo 17 Los matemáticos ya sabían calcular las áreas de muchas figuras con límites curvos y los volúmenes de muchos cuerpos. Y la teoría general fue creada en la segunda mitad del siglo XVII. en las obras del gran matemático inglés Issac Newton (1643-1716) y del gran matemático alemán Gottfried Leibniz (1646-1716). Newton y Leibniz son los fundadores del cálculo integral. Descubrieron un teorema importante que lleva su nombre: donde f(x) es una función integrable en el intervalo , F(x) es una de sus antiderivadas. El razonamiento dado por Newton y Leibniz es imperfecto desde el punto de vista del análisis matemático moderno. En el siglo XVIII. El mayor representante del análisis matemático, Leonard Euler, generalizó estos conceptos en sus obras. Sólo a principios del siglo XIX. Finalmente se crearon los conceptos de cálculo integral. Por lo general, se destacan los méritos del matemático francés Augustin Cauchy y del matemático alemán Georg Riemann. La palabra integral fue acuñada por J. Bernoulli (1690). Proviene del latín integro, que se traduce como devolver a su estado anterior, restaurar. En 1696 Apareció el nombre de una nueva rama de las matemáticas: el cálculo integral, que fue introducido por I. Bernoulli. El nombre de función antiderivada actualmente en uso reemplazó a la anterior "función primitiva" introducida por Lagrange (1797). La notación para una integral definida fue introducida por Joseph Bernoulli y los límites inferior y superior por Leonhard Euler. diapositiva 4 Las operaciones matemáticas forman pares de dos operaciones mutuamente inversas, por ejemplo, suma y resta, multiplicación y división, elevación a una potencia entera positiva y extracción de una raíz. La diferenciación permite que una función dada F(x) encuentre su derivada F´(x). Existe una acción inversa a la diferenciación, esto es integración, encontrar la función F (x) por su derivada conocida f (x) \u003d F´ (x) o el diferencial f (x) dx. La función F(x) se llama primitiva de la función f(x) si F´(x) = f(x) o dF(x)=f(x)dx. Si la función f(x) tiene la primitiva F(x), entonces tiene un conjunto infinito de antiderivadas, y todas sus antiderivadas están contenidas en la expresión F(x) + С, donde С es una constante. La integral indefinida de una función f(x) (o de la expresión f(x)dx) es el conjunto de todas sus primitivas. Notación ∫f(x)dx = F(x) +C. Aquí ∫ es el signo de la integral, f(x) es el integrando, f(x)dx es el integrando, x es la variable de integración. Encontrar una integral indefinida se llama integración de funciones. Propiedades de la integral indefinida La derivada de la integral indefinida es igual al integrando: (∫ f(x)dx)´ = f(x) El diferencial de la integral indefinida es igual al integrando: del diferencial de la antiderivada es igual a la propia primitiva y al término adicional C:∫d (F(x)) = F(x) +C El factor constante se puede sacar del signo de la integral indefinida: la suma algebraica de un número finito de funciones es igual a la suma algebraica de integrales de términos: ∫ dx = ∫ dx ± ∫ dx diapositiva 5 El concepto de integral definida se deriva a través de un trapezoide curvilíneo. Un trapecio curvilíneo es una figura delimitada por las rectas y = f(x), y = 0, x=a, x=b. La integral definida se calcula mediante la fórmula de Newton-Leibniz. = F (x)|ba= F(b) – F(a) La notación común para integrales definidas e indefinidas enfatiza la estrecha conexión entre ellas: una integral definida es un número y una integral indefinida es un conjunto de funciones antiderivadas. La relación entre la integral definida y la indefinida se expresa mediante la fórmula de Newton-Leibniz. Propiedades de una integral definida: si se intercambian los límites superior e inferior de integración, entonces la integral definida conservará su valor absoluto, pero cambiará su signo al opuesto. Si los límites superior e inferior de integración son iguales, entonces la integral definida es igual a cero. Si el segmento de integración se divide en varias partes, la integral definida del segmento será igual a la suma de las integrales definidas de estos segmentos. La integral definida de la suma de funciones dadas en el intervalo es igual a la suma de integrales definidas de los términos de las funciones. El factor constante del integrando se puede sacar del signo de una integral definida. Evaluación de la integral definida: si m ≤ f(x) ≤ M on , entonces m (b – a) diapositiva 6 Sea la función y=f(x) continua en el segmento y f(x) ≥ 0. La figura acotada por la gráfica de la función AB y=f(x), las rectas x=a, x=b y la El eje del buey (ver figura) se llama trapecio curvilíneo. La suma integral y sus términos tienen un significado geométrico simple: el producto es igual al área de un rectángulo con base y altura, y la suma es el área de la figura escalonada sombreada que se muestra en la figura. Obviamente, esta área depende de la división del segmento en segmentos parciales y de la elección del número de puntos de división. Cuanto menor sea ∆ x, más cerca estará el área de la figura escalonada del área del trapezoide curvilíneo. Por tanto, el límite de la suma integral se toma como el área exacta S del trapecio curvilíneo. Así, desde un punto de vista geométrico, la integral definida de una función no negativa es numéricamente igual al área del trapecio curvilíneo correspondiente. Diapositiva 7 1. Integración directa La integración directa generalmente se denomina cálculo de integrales indefinidas reduciéndolas a tabulares utilizando las propiedades básicas. Aquí pueden surgir los siguientes casos: 1) la integral dada se toma directamente de la fórmula de la integral tabular correspondiente; 2) después de aplicar las propiedades, esta integral se reduce a una o más integrales de tabla; 3) la integral dada, después de transformaciones elementales idénticas sobre el integrando y la aplicación de propiedades, se reduce a una o más integrales de tabla. 2. Integración por método de cambio de variable (método de sustitución) El cambio de una variable en la integral indefinida se realiza mediante sustituciones de dos tipos: x = φ (t), donde φ (t) es una función monótona y continuamente diferenciable de la nueva variable t. La fórmula para el cambio de variable en este caso es ∫f(x) = ∫f [φ (t)] φ΄ (t) d(t); 2) u = ψ(x), donde u es una nueva variable. La fórmula de cambio de variable para esta sustitución es: ∫f [ψ(x)] ψ ΄(x) d(x) = ∫f (u) du v du, donde u = φ (x), v = ψ(х ) son funciones continuamente diferenciables de x. Usando esta fórmula, encontrar la integral ∫udv se reduce a encontrar otra integral ∫v du; su aplicación es conveniente en los casos en que la última integral es más simple que la original o similar a ella. En este caso, se considera que u es una función que simplifica la diferenciación, y dv es la parte del integrando cuya integral se conoce o se puede encontrar. Diapositiva 8 Diapositiva 9 ¿Cómo encontrar el área de las figuras mostradas? Diapositiva 10 diapositiva 11 Además, la integral definida se utiliza para calcular las áreas de figuras planas, los volúmenes de cuerpos de revolución y las longitudes de arcos de curvas. diapositiva 12 Sea un cuerpo de volumen V, y existe una recta tal que, sea cual sea el plano perpendicular a esta recta que tomemos, conocemos el área S de la sección del cuerpo por este plano. Pero un plano perpendicular al eje x lo corta en algún punto x. Por lo tanto, a cada número x (del segmento [a; b]) se le asigna un único número S (x), el área de la sección transversal del cuerpo por este plano. Así, en el segmento [a; b] se da la función S(x). Si la función S es continua en el segmento [a; b] entonces la fórmula es válida: diapositiva 13 Encuentre el área de las figuras representadas 1 - 5. Respuestas: 1) S = 2/3 (uniformidad de la función); 2) S = 1 (área de un triángulo rectángulo); 3) S = 4 (igualdad de cifras); 4) S = 2π (área de un semicírculo); 5) S = 1 (área de un triángulo). Diapositiva 14 Encuentra la suma de las áreas de un número infinito de figuras sombreadas en las figuras. (El argumento de cada función siguiente aumenta 2 veces) ¡Una tarea interesante! Respuesta: pecado nx=0; x=π/n; donde n=1,2,4,8,16…; S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4 Respuesta: 4. diapositiva 15 Respuestas correctas: I opción: 2,3,1; II opción: 2,4,2. diapositiva 16 Calcule el área de la figura delimitada por líneas (que representa esquemáticamente gráficos de funciones). 1) y = 6 + x – x2 y y = 6 – 2x; 2) y = 2x2 y y = x + 1; 3) y = 1 – xey = 3 – 2x – x2; 4) y = x2 y y = . Respuesta: 1) 4,5; 2) 9/8; 3) 4,5; 4) 1/3. Diapositiva 17 Encuentre el volumen del cuerpo obtenido al rotar alrededor del eje de abscisas de la figura delimitada por líneas: 1) y = x2 + 1, x = 0, x = 1, y = 0; 2) y = , x = 1 , x = 4 , y = 0 ; 3) y = 2x, y = x + 3, x = 0, x = 1; 4) y = x + 2, y = 1, x = 0, x = 2; 5) y2 - 4 x = 0, x - 2 = 0, x - 4 = 0, y = 0; 6) y2 - x + 1 = 0, x - 2 = 0, y = 0; 7) y \u003d - x2 + 2x, y \u003d 0; 8) y2 = 2 x, x - 2 = 0, y = 0; 9) y = , x = 3 , y = 0 ; 10) y \u003d 1 - x2, y \u003d 0. Respuesta: 1) ; 2) 7,5; 3) 11 ; 4) 16 ⅔; 5) 24 ; 6) /2; 7) 16/15; 8) 4; 9) 2; 10) 16/15. Diapositiva 18 Encuentra el área de la figura delimitada por las rectas 2) La figura delimitada por las rectas y=x+6, x=1, y=0 se divide por la parábola y=x 2+2x+4 en dos partes. Encuentra el área de cada parte. 3) Encuentra la primitiva F(x) de la función f(x)=2x+4 cuya gráfica toca la recta y=6x+3. Calcula el área de la figura acotada por la gráfica de la antiderivada encontrada y las rectas y=6x+3 e y=0. Diapositiva 19 ¿Qué acción se llama integración? ¿Qué función se llama antiderivada para la función f(x)? ¿Cuál es la diferencia entre diferentes funciones antiderivadas para una función dada f(x)? Dé la definición de integral indefinida. ¿Cómo comprobar el resultado de la integración? ¿Cuál es la derivada de la integral indefinida? ¿Qué es ∫ d(lnx8 - sen 3x)? Enumere los métodos de integración. Dé la definición de integral definida. Formule el teorema de Newton-Leibniz. Enumera las propiedades de la integral definida. ¿Cómo calcular el área de una figura plana usando la integral (hacer un algoritmo verbal)? Enumere las áreas de aplicación de la integral, nombre las cantidades que se pueden calcular utilizando la integral. Diapositiva 20 1) Calcula el área de la figura acotada por estas rectas: y=x2 en x0, y=1, y=4, x=0 función inversa y=x2, x0. Por lo tanto, estas figuras tienen áreas iguales y 2) Encuentra el área de la figura delimitada por las rectas y=3x+1, y=9-x, y=x+1. Solución: Los vértices del ABC resultante tienen coordenadas: A(0;1), B(2;7), C(4;5). Se puede observar que ABC es rectangular (el producto de las pendientes de las rectas y=x+1 y=9-x es igual a -1). Por tanto, el uso de la integral para calcular S(ABC) no es racional. Siempre se puede encontrar como la diferencia en las áreas de triángulos cuya altura y base se conocen, o puedes usar el método de coordenadas. diapositiva 21 Encuentre las áreas de las figuras acotadas por las rectas (1-7) y=x2 (x0), y=1, y=4, x=0 y= x2-4x+8, y=3x2-x3, si x [ -2 ;3] y=x2-4x+sin2(x/2), y=-3-cos2(x/2), si x y=3x+1, y=9-x, y=x+1 y= | x-2|, x|y|=2;x=1;x=3 y= arcosen x; y=0; x=0,5; x=1 ¿A qué valor de a la recta x=a divide el área de la figura delimitada por las rectas y=2/x; x=1; x=3 en una proporción de 1:3? Calcula en función de su significado geométrico. diapositiva 22 N. A. Kolmogorov, "El álgebra y los inicios del análisis", Moscú, Prosveshchenie, 2000. M. I. Bashmakov, "Álgebra y los inicios del análisis", Moscú, DROFA, 2002 Sh.A. Alimov, "Álgebra y el comienzo del análisis", 11º grado, Moscú, DROFA, 2004 L. V. Kiseleva, Manual de matemáticas para estudiantes de facultades y facultades de medicina, Moscú, FGOU "VUNMC Roszdrav", 2005 http://www.nerungri.edu.ru http://tambov.fio.ru http://www.zachetka.ru http://edu.of.ru http://festival.1september.ru
Ver todas las diapositivasDefinición y propiedades de la integral.
Integración
trapezoide curvilíneo
Bibliografía
Documentos similares
La principal ventaja de la ecocardiografía (EchoCG) es que de forma no invasiva y en tiempo real es posible evaluar el tamaño y el movimiento de las estructuras cardíacas, obtener características de la hemodinámica intracardíaca y determinar la presión en las cámaras del corazón y la arteria pulmonar. Se ha demostrado una buena comparabilidad de los resultados de la ecocardiografía con los datos obtenidos durante el cateterismo cardíaco.
Un estudio ecocardiográfico permite no solo detectar la presencia de hipertensión pulmonar, sino también excluir una serie de enfermedades que causan hipertensión pulmonar secundaria: defectos de la válvula mitral, defectos cardíacos congénitos, miocardiopatía dilatada, miocarditis crónica.Tarjeta número 7
– el tiempo que tarda el barco en viajar del primer barco al segundo.
kilómetros desde ACERCA DE; en el momento en que el barco llega al segundo barco, la distancia entre éste y ACERCA DE era igual a km; el camino del barco es 
. Entonces por el teorema de Pitágoras
.
; 
; 
Tarjeta número 5
A R
EN
dy
h
Ah x x
. Busquemos el parámetro A.
,
, por eso 
.
.
, Entonces 
, es decir. el peso de la capa líquida es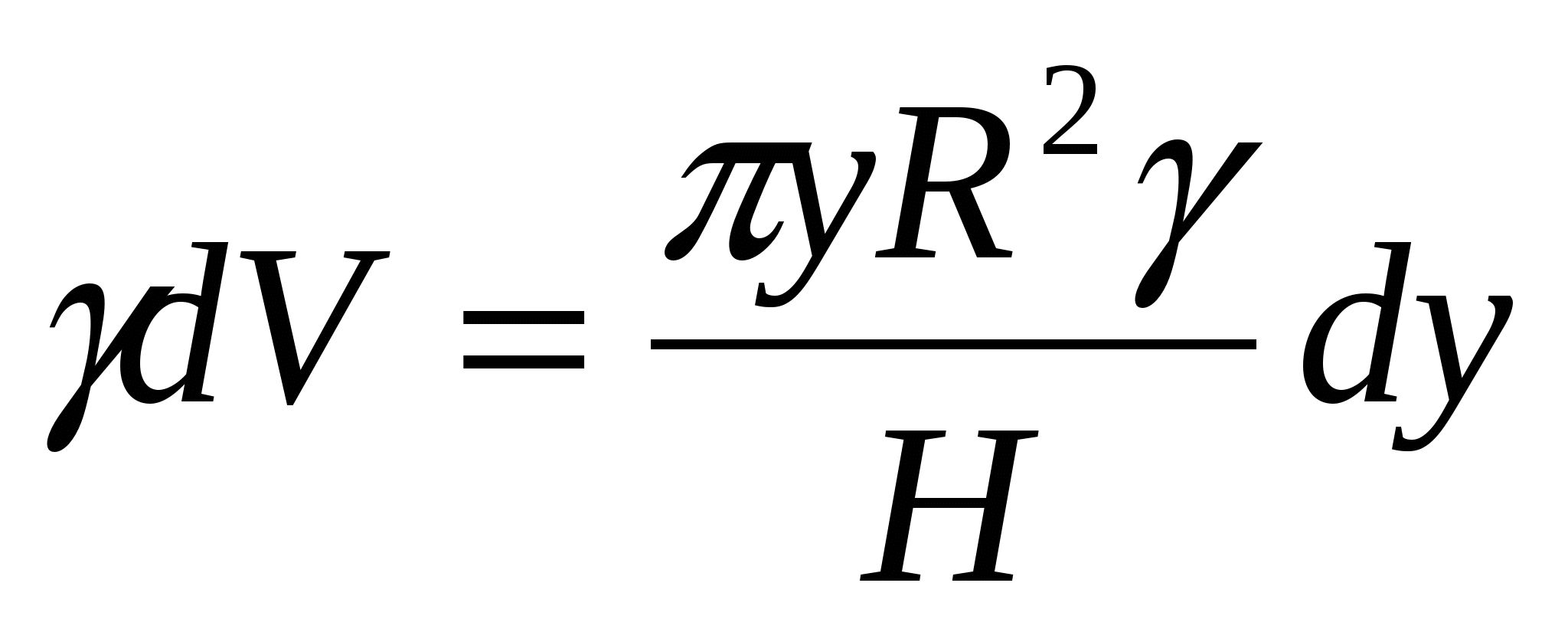 
.
, necesitas gastar trabajo elemental 
, 
. Entonces
, Entonces .
.
Tarjeta número 6
, k – coeficiente de proporcionalidad.
, por eso 
.
.
Tarjeta número 8
.
, por eso .
.
Tarjeta número 9
repele la carga 
(del mismo signo), ubicado a cierta distancia de él r, se expresa mediante la fórmula
,
desde un punto 
, separado de en la distancia 
, exactamente 
, lejos de en la distancia 
, suponiendo que la carga colocado en el punto 
tomado como punto de partida.
, . Entonces
.
obtenemos 
.
.
Tarjeta número 3
, 
es la gravedad específica del líquido.ACERCA DE
.
,
,
,
.
;
9,81 norteTarjeta número 4
m/seg. encontrar una manera s, pasado por el momento t= 8 segundos después del inicio del movimiento. ¿Cuál es la velocidad promedio para este intervalo?
, por eso 
, 
, 
.
.
.
(en miles de rublos por tonelada) en la fábrica de jabón Mukhinsky varían según el volumen de producción anual q(en toneladas) según la ley:
.
.
.
.
, 
.
;
.
t, entonces el precio 
(miles de rublos/t).Tarjeta número 10
, 
, 
metro.
.
kgm.
(en miles de rublos) del volumen de producción anual q(en toneladas) tiene la forma
.
y , expresar.
fórmula Newton-Leibniz le permite reducir el cálculo bastante complejo de ciertas integrales, es decir encontrar los límites de sumas integrales, a una operación relativamente simple de encontrar antiderivadas.Leibniz posee el símbolo diferencial una p Posteriormente también apareció el símbolo integral.Símbolo integral definidointrodujo J. Fourier, y el término "integral" (del latín entero - entero) fue propuesto por I. Bernoulli.
dónde 
Integramos: 
dónde 
Usando los datos, encontramos С = 4. Es decir, la ecuación de movimiento del cuerpo tiene la forma 
.
Entonces obtenemos: el trabajo para lanzar un cohete es igual a 
.
Por lo tanto, el trabajo completo está completo:
. Entonces el trabajo realizado para deformar es:
y Ecuación de velocidad: encontramos la ley del movimiento del cuerpo: desde. y luego 
dónde 
.Integrar: 
o 
cuando y encontrar 
, y tenemos la ecuación del movimiento corporal: o .
o 
Integrando tenemos: 
En x = 2 Y y \u003d -3, c \u003d - 5, y la trayectoria del movimiento tiene la forma: 
.
Tarea 9. Calcula el área de la figura delimitada por líneas: y
Solución: Construyamos un dibujo (Fig. 1), para el cual resolveremos un sistema de ecuaciones. Encontremos los puntos de intersección de las rectas: A(-2;4) Y B(4;16). El área deseada es la diferencia entre las áreas con los límites de integración, a \u003d x 1 \u003d -2 Y en \u003d x 2 \u003d 4. Entonces tenemos el área:
Encontremos С: y función Se sabe que t.e. o de donde el coeficiente de proporcionalidad es: y la función tiene la forma: 
.
Tarea 11.Hipérbolalimitado por líneas: y=0,x=
a, x = 2agira alrededor del eje x. Encuentre el volumen del hiperboloide resultante (Fig. 2).
Los ufólogos están estudiando los hechos que citan los "testigos presenciales", que dicen que vieron una nave espacial voladora en forma de un enorme disco luminoso ("plato"), aproximadamente de la misma forma que en la Figura 3. Considere resolver el problema de determinar el volumen de tal “plato” ".
Solución: Al dibujar un paraboloide (Fig. 3), tenemos los límites de integración de x = -3 antes x = 3. Reemplacemos los límites de integración debidos a la simetría de la figura con respecto al eje y por x = 0 Y x = 3 y duplicar el resultado. Por tanto, el volumen del disco es:
Referencia histórica
Una breve historia del cálculo integral
Integral indefinida
Integral definida
El significado geométrico de la integral definida.
Métodos de integración
Tabla de integrales indefinidas
Repetición de material teórico.
seguimos repitiendo
Aplicación de la integral
Cálculo de volúmenes de cuerpos.
¡COMPRUEBA TU MISMO!
¡Encuentra el error!
control programado
Trabajo independiente
Tareas para calcular volúmenes.
Tareas del examen.
Preguntas de control
Para los amantes de las matemáticas
Tarea
Bibliografía
Cargando...