Funkcja gęstości normalnie rozproszonej zmiennej losowej. Normalna dystrybucja i jego parametry

W wielu wyzwań związanych z normalnie rozproszonymi losowymi wartościami konieczne jest określenie prawdopodobieństwa zmienna losowa , podporządkowany do normalnego prawa z parametrami, do witryny z wcześniej. Aby obliczyć to prawdopodobieństwo, używamy ogólnego wzoru

gdzie - rozmiar rozkładu wielkości.

Znajdź funkcję rozkładu zmiennej losowej rozprowadzonej zgodnie z normalnym prawem z parametrami. Wartość gęstości dystrybucji to:

Stąd znajdziemy funkcję dystrybucji

. (6.3.3)

Wykonamy w integralnej (6.3.3), zastępując zmienną

i dajemy to na myśl:

(6.3.4)

Integralny (6.3.4) nie jest wyrażony funkcje podstawoweAle można go obliczyć za pośrednictwem specjalnej funkcji wyrażającą specyficzną integralną z wyrażenia lub (tzw. Z całością prawdopodobieństwa), dla którego stół jest kompilowany. Istnieje wiele odmian takich funkcji, na przykład:

;

itp. Który z tych funkcji używa - kwestia smaku. Wybieramy jako taką funkcję.

. (6.3.5)

Nie jest trudno zobaczyć, że ta funkcja jest niczym oprócz funkcji dystrybucji dla normalnej zmiennej losowej rozproszonej z parametrami.

Zgadzamy się zadzwonić do funkcji normalna funkcja Dystrybucja. Dodatek (tabela 1) pokazuje tabele wartości tabeli.

Wyraź funkcję dystrybucji (6.3.3) wartości za pomocą parametrów i dzięki normalnej funkcji dystrybucji. Oczywiście

Teraz znajdziemy prawdopodobieństwo przychodzącego losowej wariancji na stronie. Według wzoru (6.3.1)

W ten sposób wyraziliśmy prawdopodobieństwo przychodzącego zmiennej losowej rozpowszechnionej zgodnie z normalnym prawem z dowolnymi parametrami, poprzez standardową funkcję dystrybucji odpowiadającej najprostszym normalnym prawu parametry 0.1. Należy pamiętać, że argumenty funkcji w wzorze (6.3.7) mają bardzo proste znaczenie: istnieje odległość od prawego końca witryny do środka dyspersji, wyrażona w średnie odchylenia kwadratowe; - Ta sama odległość dla lewego końca witryny, a ta odległość jest uważana za dodatnie, jeśli koniec znajduje się po prawej stronie centrum dyspersji i ujemnego, jeśli po lewej stronie.

Podobnie jak każda funkcja dystrybucji, funkcja ma właściwości:

3. - Funkcja funkcji.

Ponadto, z symetrii normalnego rozkładu z parametrami w stosunku do początku współrzędnej, wynika z tego

Korzystając z tego właściwości, w rzeczywistości możliwe byłoby ograniczenie tabel funkcji tylko z dodatnimi wartościami argumentu, ale w celu uniknięcia nadmiaru operacji (odejmowanie od jednego), w tabeli 1 aplikacji, wartości są ważne zarówno dla argumentów pozytywnych, jak i negatywnych.

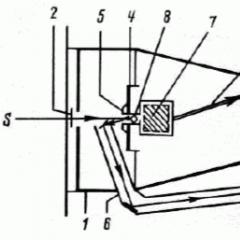
W praktyce zadanie obliczania prawdopodobieństwa wprowadzenia normalnie rozproszonej zmiennej losowej do obszaru jest często symetryczne względem środka rozpraszającego. Rozważaj taką część długości (rys. 6.3.1). Obliczamy podobny do wejścia do tej sekcji według wzoru (6.3.7):

Biorąc pod uwagę nieruchomość (6.3.8) funkcji i dając lewą część wzoru (6.3.9) bardziej zwarty wygląd, otrzymujemy formułę prawdopodobieństwa zmiennej losowej, rozpowszechniane zgodnie z normalnym prawem do obszaru, symetryczne W stosunku do centrum rozpraszania:

. (6.3.10)

Niech następujący zadanie. Odkładamy z centrum dyspersji kolejnych segmentów długości (rys. 6.3.2) i obliczamy prawdopodobieństwo przychodzącego losowej wariancji w każdym z nich. Ponieważ krzywa normalnego prawa jest symetryczna, wystarczy odłożyć takie segmenty tylko w jedną stronę.

Według formuły (6.3.7) znajdziemy:

(6.3.11)

Jak widać z tych danych, prawdopodobieństwa wprowadzenia każdego z następujących segmentów (piątą, szóstą itp.) Dokładnością 0,001 są zero.

Otaczanie prawdopodobieństw do wejścia w segmenty do 0,01 (do 1%), otrzymamy trzy liczby, które są łatwe do zapamiętania:

0,34; 0,14; 0,02.

Suma tych trzech wartości wynosi 0,5. Oznacza to, że dla normalnej zmiennej losowej rozproszonej, wszystkie dyspersje (z dokładnością do procentu) jest ułożone na stronie.

Pozwala to na poznanie średniego odchylenia kwadratowego i matematycznego oczekiwania zmiennej losowej, wstępnie wskazują interwał swoich praktycznie możliwych wartości. Ta metoda oszacowania zakresu możliwych wartości zmiennej losowej jest znana statystyki matematyczne Pod nazwą "Zasada trzech Sigma". Z trzech zasad SIGMA, szacowana metoda określania średniego odchylenia kwadratowego zmiennej jest również następującej: podjąć maksymalne praktycznie możliwe odchylenie od średniej i podzielić go do trzech. Oczywiście ten szorstki odbiór może być zalecany tylko wtedy, gdy nie ma innych, dokładniejszych sposobów określania.

Przykład 1. Zmienna losowa, rozproszona zgodnie z normą normalną, jest błąd pomiaru pewnej odległości. W pomiarze, systematyczny błąd jest dozwolony do przeszacowania o 1,2 (m); Średnie odchylenie kwadratowe błędu pomiaru wynosi 0,8 (m). Znajdź prawdopodobieństwo, że odchylenie wartości mierzonej od prawdziwości nie przekroczy wartości bezwzględnej 1,6 lit. m).

Decyzja. Błąd pomiaru Istnieje wartość losowa podwładna do normalnego prawa z parametrami i. Konieczne jest znalezienie prawdopodobieństwa tej wielkości na stronie przed wcześniej. Według formuły (6.3.7) mamy:

Korzystanie z tabel funkcji (aplikacja, tabela 1), znajdziemy:

; ,

Przykład 2. Znajdź to samo prawdopodobieństwo, co w poprzednim przykładzie, ale pod warunkiem, że nie ma błędu systematycznego.

Decyzja. W Formule (6.3.10), wierząc, znajdziemy:

Przykład 3. W celu zapewnienia rodzaju pasa (autostrady), której szerokość wynosi 20 m, strzelanie w kierunku prostopadle do autostrady. Dążący jest prowadzony w linii środkowej autostrady. Średnie odchylenie kwadratowe w kierunku fotografowania jest równe m. Istnieje błąd systematyczny w kierunku wypalania: tydzień 3 m. Znajdź prawdopodobieństwo wejścia do autostrady w jednym strzale.

W teorii prawdopodobieństwa uwzględniono wystarczająco dużą liczbę zróżnicowanych przepisów dystrybucyjnych. Aby rozwiązać problemy związane z budową kart kontrolnych, tylko niektóre z nich są interesujące. Najważniejsze z nich jest prawo dystrybucji normalnejktóry jest używany do budowania kart kontrolnych używanych w znak ilościowy. Kiedy mamy do czynienia z ciągłą zmienną losową. Prawo normalne zajmuje szczególną pozycję między innymi przepisami. Wynika to z faktu, że po pierwsze, najczęściej występują w praktyce, a po drugie, jest to marginalne prawo, do którego zbliża się inne prawa dystrybucyjne z bardzo typowymi typowymi warunkami. Jeśli chodzi o drugą okoliczność, w teorii prawdopodobieństw, udowodniono, że suma wystarczająco duża liczba niezależnych (lub słabo zależnych) zmiennych losowych podporządkowanych, jak bardzo przepisy dystrybucji (z zastrzeżeniem bardzo niesztywnych ograniczeń ), w przybliżeniu obeys normalne prawo, a to jest dokładniejsze, tym większa liczba zmiennych losowych jest sumowana. Większość ludzi napotkała w praktyce zmiennych losowych, takich jak błędy pomiarowe, można przedstawić jako sumę bardzo większej liczby stosunkowo małych warunków - błędy podstawowe, z których każda jest spowodowana przez działanie jednego powodu, niezależnie od reszta. Normalne prawo przejawia się w przypadkach, gdy zmienna losowa H. Jest to wynik dużej liczby różnych czynników. Każdy czynnik oddzielnie o wielkości H. wpływa na lekko i nie możesz określić, który ma wpływ więcej niżniż reszta.

Normalna dystrybucja(dystrybucja Laplace Gauss.) - Dystrybucja prawdopodobieństwa ciągłej zmiennej losowej H. taka, że \u200b\u200bgęstość dystrybucji prawdopodobieństwa, gdy - ¥<х< + ¥ принимает действительное значение:

Ejr. (3)

Oznacza to, że normalny rozkład charakteryzuje się dwoma parametrami M i S, gdzie m - wartość oczekiwana; S- odchylenie standardowe rozkładu normalnego.

S. 2 - Jest to dyspersja normalnego rozkładu.

Oczekiwanie matematyczne M charakteryzuje położenie środka dystrybucyjnego, a odchylenie standardowe S (SBE) jest charakterystyką dyspersją (fig. 3).

f (x) f (x)

Rysunek 3 - Funkcje gęstości normalnej dystrybucji z:

a) różne oczekiwania matematyczne M; b) Różne narciarskie s.

Tak więc wartość μ określone przez położenie krzywej dystrybucji na osi odcięcia. Wymiar μ - taki sam jak wymiarowość zmiennej losowej X.. Wraz ze wzrostem oczekiwań matematycznych, tłum funkcji przesuwa równolegle w prawo. Z malejącą dyspersją s 2 Gęstość jest coraz bardziej skoncentrowana wokół M, podczas gdy funkcja dystrybucji staje się bardziej fajna.

Wartość σ definiuje kształt krzywej dystrybucji. Ponieważ obszar pod krzywą dystrybucji powinien zawsze pozostać równa jednostka., Wraz ze wzrostem σ, krzywa dystrybucji staje się bardziej płaska. Na rys. 3.1 przedstawia trzy krzywe w różnych σ: σ1 \u003d 0,5; σ2 \u003d 1,0; σ3 \u003d 2.0.

Rysunek 3.1 - Funkcje gęstości normalnej dystrybucji zróżne narciarskie s.

Funkcja dystrybucji (zintegrowana funkcja) ma formularz (rys. 4):

(4)

Figura 4 - Zintegrowana (a) i różnicowa (b) Funkcja rozkładu normalnego

Jest to szczególnie ważne dla transformacji liniowej normalnie rozproszonej zmiennej losowej. H.Po uzyskaniu zmiennej losowej Z. Z oczekiwaniami matematycznymi 0 i dyspersji 1. Taka transformacja nazywa się racjonowaniem:

Można go przeprowadzić dla każdej zmiennej losowej. Rational pozwala na wszystkie możliwe warianty rozkładu normalnego w celu zmniejszenia jednego przypadku: M \u003d 0, S \u003d 1.

Normalny rozkład z M \u003d 0, S \u003d 1 zwany normalny rozkład normalny (znormalizowany).

Standardowa normalna dystrybucja (Standardowy rozkład Laplas-Gaussa lub znormalizowanej dystrybucji normalnej) jest rozkład prawdopodobieństwa znormalizowanej normalnej zmiennej losowej Z., której gęstość dystrybucji jest:

kiedy - ¥.<z.< + ¥

Wartości funkcji. F Z) Określony przez wzór:

(7)

Wartości funkcji. F Z) i gęstość f z) Znormalizowany rozkład normalny jest obliczany i zmniejsza się do tabel (tabulated). Stół składa się tylko do wartości dodatnich z.więc:

F (–z) \u003d 1–F Z) (8)

Korzystając z tych tabel, można zdefiniować nie tylko wartości funkcji i gęstości znormalizowanego rozkładu normalnego dla określonego z., ale także wartości funkcji ogólnej dystrybucji normalnej, jak:

; (9)

. 10)

W wielu wyzwań związanych z normalnie rozproszonymi wartościami losowymi konieczne jest określenie prawdopodobieństwa zmiennej losowej H., podporządkowany do normalnego prawa z parametrami M i S, do określonego obszaru. Taka sekcja może być na przykład pole tolerancji do parametru z górnej wartości U. Nizhny. L..

Prawdopodobieństwo wprowadzenia interwału h. 1 be. h. 2 można określić o wzorze:

Tak więc prawdopodobieństwo losowej wariancji (wartość parametru) H. W polu Tolerancji jest określona przez formułę

Możesz znaleźć prawdopodobieństwo, że zmienna losowa H. Okazuje się być w μ K.s. . Uzyskane wartości dla k. \u003d 1,2 i 3 są następujące (wyglądają również na fig. 5):

Tak więc, jeśli jakakolwiek wartość pojawia się poza trzyczęściową częścią, w której istnieje 99,73% wszystkich możliwych wartości, a prawdopodobieństwo takiego zdarzenia jest bardzo małe (1: 270), należy uznać, że w obliczu rozważanego wartości Być zbyt małym lub zbyt dużym. Nie z powodu przypadkowej zmienności, ale ze względu na niezbędne zakłócenia w samym procesie, zdolny do powodowania zmian w charakteru dystrybucji.

Nazywany jest również fabuła leżącego wewnątrz obwodników trójstronnych statystyczny obszar tolerancji odpowiednia maszyna lub proces.

Przykład pliku

Rozważ normalny rozkład. Za pomocą funkcji. MS Excel. Norm.Rasp () Konstruujemy wykresy funkcji dystrybucji i gęstości prawdopodobieństwa. Wygenerujmy szereg liczb losowych rozproszonych zgodnie z normalnym prawem, ocenimy parametry dystrybucji, średniej i odchylenia standardowego .

Normalna dystrybucja (Również zwany dystrybucją Gaussa) jest najważniejsza jak w teorii, więc w zastosowaniach systemów sterowania aplikacjami. Znaczenie znaczenia Normalna dystrybucja (pol. Normalna Dystrybucja) W wielu dziedzinach nauki wynika z teorii prawdopodobieństwa.

Definicja : Wartość losowa X. dystrybuowane przez Normalne prawo Jeśli ma:

Normalna dystrybucja Zależy od dwóch parametrów: μ (MJ) - IS i σ ( sigma) - Jest (odchylenie standardowe). Parametr μ określa pozycję środka gęstości prawdopodobieństwa Normalna dystrybucja i σ - rozproszony w stosunku do środka (medium).

Uwaga : Na temat efektu parametrów μ i σ w formularzu dystrybucyjnym określono w artykule o i w Przykładowy plik na efekcie arkuszy parametrów Możesz zmienić kształt krzywej.

Normalna dystrybucja w MS Excel

W MS Excel, zaczynając w 2010 roku Normalna dystrybucja Istnieje norma norm. Arp (), Nazwa angielska - Norm.Dist (), co pozwala obliczyć gęstości prawdopodobieństwa (patrz Formuła powyżej) i Integralna funkcja dystrybucji (Prawdopodobieństwo, że wartość losowa X, dystrybuowana przez Normalne prawo zajmie wartość mniejszą lub równą X). Obliczenia w tym ostatnim przypadku są wykonane zgodnie z następującym wzorem:

Powyższa dystrybucja ma oznaczenie N. (μ; σ). Często używają oznaczenia N. (μ; σ 2).

Uwaga : Pani Excel 2010 w Excelu była tylko norma NormSp (), która umożliwia obliczenie funkcji dystrybucji i gęstość prawdopodobieństwa. Normrasp () pozostawiony w MS Excel 2010 za zgodność.

Standardowa normalna dystrybucja

Standardowa normalna dystrybucja nazywa normalna dystrybucja C μ \u003d 0 i σ \u003d 1. Powyższa dystrybucja ma oznaczenie N. (0;1).

Uwaga : W literaturze dla losowej zmiennej dystrybuowanej przez Standard normalne prawo Specjalne oznaczenie Z jest naprawione.

Ktoś normalna dystrybucja może zostać przekonwertowany na standard za pomocą zmiennej wymiany Z. =( X. -μ)/σ . Ten proces konwersji jest nazywany Normalizacja .

Uwaga : MS Excel ma funkcję normalizacji () (), która wykonuje powyższą konwersję. Chociaż w MS Excel ta transformacja jest wywoływana z jakiegoś powodu Normalizacja . Formuły \u003d (x-μ) / σ i \u003d Normalizacja (x; μ; σ) Zwróć ten sam wynik.

W MS Excel 2010 dla Istnieje specjalna funkcja norm. Str.sp () i jego przestarzałą wersję norm Normstrap () wykonywania podobnych obliczeń.

Będziemy zademonstrować, w jaki sposób proces standaryzacji jest realizowany w MS Excel Normalna dystrybucja N. (1,5; 2).

Aby to zrobić, obliczymy prawdopodobieństwo, że zmienna losowa rozprowadzona przez Normalne prawo N (1,5; 2) , mniej lub równe 2,5. Formuła wygląda tak: \u003d Normy. RASP (2,5; 1,5; 2; prawda) \u003d 0,691462. Wymieniając zmienną Z. =(2,5-1,5)/2=0,5 , Napisz formułę do obliczania Standardowa normalna dystrybucja: \u003d Norm.st.Rasp (0,5; prawda) =0,691462.

Naturalnie oba formuły dają te same wyniki (patrz Przykładowy przykładowy przykład).

Zwróć uwagę na to normalizacja tylko C. (argument całka równa prawdzie), a nie gęstości prawdopodobieństwa .

Uwaga : W literaturze dla funkcji obliczają prawdopodobieństwo zmiennej losowej dystrybucji przez Standard normalne prawo Specjalne oznaczenie F (Z). W MS Excel ta funkcja jest obliczana przez formułę \u003d Norm.st.sp (z; prawda) . Obliczenia są wykonane przez formułę

Ze względu na parytet funkcji Dystrybucje F (x), a mianowicie f (x) \u003d f (s), funkcja Standardowa normalna dystrybucja Ma właściwość F (-x) \u003d 1-F (x).

Funkcje odwrotne

Funkcjonować Norm.St.sp (x; prawda) Oblicza prawdopodobieństwo P, że wartość losowa x będzie miała wartość mniejszą lub równą x. Ale często konieczne jest przeprowadzenie odwrotnej kalkulacji: znając prawdopodobieństwo p, wymagane jest obliczenie wartości X. Obliczona wartość X jest nazywana Standard Normalna dystrybucja .

W MS Excel, aby obliczyć Kwantyjny Korzystanie z funkcji norms.stro.ob () i norm.

Funkcje Graphics.

Plik przykładowy zawiera Grafika gęstości dystrybucji prawdopodobieństwo I. Integralna funkcja dystrybucji .

Jak wiesz, około 68% wartości wybranych z agregatu normalna dystrybucja są w ciągu 1 odchylenia standardowego (σ) z μ (oczekiwania średniego lub matematycznego); Około 95% - w ciągu 2 σ, a w ciągu 3 σ jest już 99% wartości. Upewnić się, że Standardowa normalna dystrybucja Możesz napisać formułę:

= Norm.ST.Spasp (1; prawda) -Norm.st.Rasp (-1; Prawda)

co zwróci wartość 68,2689% - jest to dokładnie odsetek wartości w zakresie +/- 1 odchylenia standardowego od Średni (cm. Wykres wykresu w przykładowym pliku).

Ze względu na parytet funkcji Standardowa normalna gęstość Dystrybucja: FA. ( X.)= FA. (s) funkcjonować Standardowa normalna dystrybucja Ma właściwość F (-x) \u003d 1-F (x). Dlatego powyższa formuła może być uproszczona:

= 2 * Norm.ST.Rasp (1; Prawda) -1

Dla arbitralnego Funkcje rozkładu normalnego N (μ; σ) Podobne obliczenia powinny być wykonane przez wzór:

2 * Norms.RSP (μ + 1 * σ; μ; σ; prawda) -1

Powyższe obliczenia prawdopodobieństw są wymagane dla.

Uwaga : Aby ułatwić pisanie formuły w pliku przykładowym są tworzone dla parametrów dystrybucji: μ i σ.

Generacja liczb losowych

Wygenerujmy 3 tablicę 100 liczb o różnych μ i σ. Aby to zrobić w oknie Pokolenie losowe liczby Ustaw następujące wartości dla każdej pary parametrów:

Uwaga : Jeśli ustawisz opcję Losowa dyspersja ( Losowe nasienie) Możesz wybrać określony losowy zestaw liczb generowanych. Na przykład, ustawiając tę \u200b\u200bopcję do 25, możesz wygenerować te same zestawy liczb losowych na różnych komputerach (chyba że, oczywiście inne parametry dystrybucyjne pasują). Wartość opcji może podjąć całe wartości od 1 do 32 767. Nazwa opcji Losowa dyspersja może pomylić. Lepiej byłoby to przetłumaczyć jako Ustaw numer z liczbami losowymi .

W rezultacie będziemy mieć 3 kolumny liczb, na podstawie którego można ocenić parametry rozkładu, z którego wykonano próbkę: μ i σ . Oszacowanie dla μ można wykonać za pomocą funkcji SRNAVOV () i dla σ - za pomocą standardowej funkcji klonowej (), zobacz.

Uwaga : Aby wygenerować tablicę liczb rozprowadzonych przez Normalne prawo , możesz użyć formuły \u003d Normy. Prof (klej (); μ; σ) . Funkcja samoprzylepna () generuje od 0 do 1, co odpowiada wraz z zakresem zmiany prawdopodobieństwa (patrz Plik przykładowy wytwarzanie liści).

Zadania

Zadanie 1 . Firma produkuje nylonowe nici średniej wytrzymałości 41 MPa i odchylenie standardowego 2 MPa. Konsument chce zdobyć wątki o trwałość co najmniej 36 MPa. Oblicz prawdopodobieństwo, że autobusy dokonane przez firmę dla konsumenta będą zgodne z wymaganiami lub ich przekroczyć. Rozwiązanie1. : = 1-normy. Kolekcje (36; 41; 2; Prawda)

Zadanie2. . Enterprise produkuje rury, średnia średnica zewnętrzna wynosi 20,20 mm, a odchylenie standardowe wynosi 0,25 mm. Zgodnie z warunkami technicznymi rury są rozpoznawane jako odpowiednie, jeśli średnica mieści się w zakresie 20,00 +/- 0,40 mm. Jaka proporcja produkowanych rur robi to? Rozwiązanie2. : = Norm.Rasp (20,00 + 0,40; 20.20; 0,25; prawda) - Norms.RSP (20.00.00.40; 20.20; 0,25) Figura poniżej, powierzchnia wartości średnicy jest podświetlona, \u200b\u200bco spełnia specyfikacje specyfikacji.

Rozwiązanie jest podane Przykładowe zadania lekcji .

Zadanie3. . Enterprise produkuje rury, średnia średnica zewnętrzna wynosi 20,20 mm, a odchylenie standardowe wynosi 0,25 mm. Średnica zewnętrzna nie powinna przekraczać pewnej wartości (zakłada się, że dolna granica nie jest ważna). Jaka górna granica w specyfikacjach technicznych powinna być zainstalowana tak, że 97,5% wszystkich produkowanych produktów pasuje do tego? Rozwiązanie3. : = Norma. Produkt (0,975; 20.20; 0,25) \u003d 20,6899 lub \u003d Norm.St.ob (0,975) * 0,25 + 20,2 (Wykonane "oznaczenie", patrz wyżej)

Zadanie 4. . Znalezienie parametrów. Normalna dystrybucja Według wartości 2 (lub). Załóżmy, że wiadomo, że wartość losowa ma normalny rozkład, ale jego parametry nie są znane, ale tylko 2nd percentyl (na przykład 0,5- percentyl . Mediana i 0,95th. percentyl). Dlatego Znany, a potem wiemy, tj. μ. Aby znaleźć, musisz użyć. Rozwiązanie daje B. Przykładowe zadania lekcji .

Uwaga : Do pani Excel 2010 w Excelu były normy () i Normster () (), które są równoważne normom. Produkcja () i normy. Normobra () i Normsman () pozostają w MS Excel 2010 i więcej tylko do kompatybilności.

Liniowe kombinacje normalnie rozproszonych zmiennych losowych

Wiadomo, że liniowa kombinacja normalnie rozproszonych zmiennych losowych X. ( JA.) z parametrami μ. ( JA.) i σ. ( JA.) Jest również dystrybuowany normalnie. Na przykład, jeśli wartość losowa Y \u003d X (1) + x (2), to będzie miał rozkład z parametrami μ (1) + μ (2) i Root (σ (1) ^ 2 + σ (2) ^ 2). Upewnij się, że MS Excel.

Definicja. Normalnanazywany rozkładem prawdopodobieństwem ciągłej zmiennej losowej, która jest opisana przez gęstość prawdopodobieństwa

Nazywane jest również normalne prawo dystrybucji prawo Gaussa..

Prawo normalne zajmuje centralne miejsce w teorii prawdopodobieństwa. Wynika to z faktu, że prawo niniejsze objawia się we wszystkich przypadkach, w których wartość losowa jest wynikiem dużej liczby różnych czynników. Wszystkie inne prawa dystrybucyjne zbliżają się do normalnego prawa.

Można go łatwo wykazać, że parametry i gęstość rozkładu są odpowiednio oczekiwaniem matematycznym i średnim odchyleniem kwadratowym losowej zmiennej X.

Znajdź funkcję dystrybucji F (x).

Nazywany jest wykres gęstości dystrybucji normalnej normalna krzywalub krzywa Gaussa..

Normalna krzywa ma następujące właściwości:

1) Funkcja jest określona na całej osi numerycznej.

2) dla wszystkich h. Funkcja dystrybucji trwa tylko wartości dodatnie.

3) Oś Och jest poziomą asymptota wykresu gęstości prawdopodobieństwa, ponieważ z nieograniczonym wzrostem wartości bezwzględnej argumentu h.Wartość funkcji dąży do zera.

4) Znajdujemy funkcję ekstremum.

Dlatego dla y '\u003e 0 dla x.< m i y '< 0 dla x\u003e m. potem w punkcie x \u003d T. Funkcja ma maksymalną równą.

5) Funkcja jest symetryczna o bezpośrednim x \u003d A.dlatego różnica

(x - A.) Zawarte w funkcji gęstości dystrybucji na placu.

6) Aby znaleźć punkty rozpadania wykresu, znajdujemy drugą pochodną funkcji gęstości.

Dla x \u003d m. + S I. x \u003d m. - S Druga pochodna wynosi zero, a podczas przełączania tych punktów zmienia znak, tj. W tych punktach funkcja ma fleksję.

W tych punktach wartość funkcji jest równa.

Konstruujemy wykres funkcji gęstości rozkładu.

Wykresy są zbudowane t. \u003d 0 i trzy możliwe wartości średniego odchylenia kwadratatycznego S \u003d 1, S \u003d 2 i S \u003d 7. Jak widać, ze wzrostem wartości średniego odchylenia kwadratowego, wykres staje się bardziej łagodny i maksymalna wartość maleje.

Jeśli ale \u003e 0, harmonogram przesunie się w kierunku pozytywnym ale < 0 – в отрицательном.

Dla ale \u003d 0 i S \u003d 1 krzywa zwana norma normalna. Równanie znormalizowanej krzywej:

W przypadku zwięzłości mówi się, że współpracownicy prawa n (m, s), tj. X ~ n (m, s). Parametry M i S pokrywa się z podstawowymi właściwościami dystrybucji: m \u003d m x, s \u003d s x \u003d. Jeśli SV X ~ N (0, 1), to nazywa się znormalizowana normalna wielkość. Fr znormalizowana normalna wielkość zwana funkcja Laplasa. i wskazany AS. F (x). Dzięki nim możliwe jest obliczenie prawdopodobieństw czasowych dla dystrybucji normalnej N (M, S):

P (x 1 £ x< x 2) = Ф - Ф .

Podczas rozwiązywania zadań w normalnym dystrybucji często konieczne jest użycie wartości tabel funkcji Laplace. Ponieważ funkcja Laplace jest ważna F (s) = 1 - F (x)Wtedy wystarczy mieć wartości tabeli funkcji F (x) Tylko dla wartości pozytywnych argumentów.

W przypadku prawdopodobieństwa wejścia do symetrycznego w stosunku do oczekiwań matematycznych, interwał formuły: p (| x - m x |< e) = 2×F (E / s) - 1.

Centralne chwile dystrybucji normalnej spełniają powtarzający się stosunek: M N +2 \u003d (N + 1) S 2 m N, N \u003d 1, 2, .... Wynika z tego, że wszystkie centralne momenty zrzęda nieparzystego są zero (od m 1 \u003d 0).

Znajdź prawdopodobieństwo przychodzącego zmiennej losowej rozprowadzonej zgodnie z normalną ustawą w danym przedziale.

Oznaczać

Dlatego Integralna nie jest wyrażona przez funkcje podstawowe, funkcja jest wprowadzana do uwzględnienia.

,

który jest nazywany funkcja Laplasa.lub integralne prawdopodobieństwa.

Wartości tej funkcji, gdy różne wartości h. Rozważane i podane są w specjalnych tabelach.

Wykres funkcji Laplace jest pokazany poniżej.

Laplace oferuje następujące właściwości:

2) f (- h.) \u003d - f ( h.);

Nazywana jest również funkcja Laplace funkcja błędu. i oznacz ERF. x..

Wciąż używany norma normalnafunkcja Laplace, która jest związana z funkcją Laplace według stosunku:

Wykres normalnej funkcji Laplas jest pokazany poniżej.

Rozważając normalne prawo dystrybucyjne, ważne wydarzenie prywatne jest przydzielane, znane jako rządzi trzej sigm.

Piszemy prawdopodobieństwo, że odchylenie normalnie rozproszonej zmiennej losowej z oczekiwań matematycznych jest mniej określona wartość RE:

Jeśli weźmiesz d \u003d 3S, otrzymujemy użycie wartości funkcji Laplace za pomocą tabel:

Te. Prawdopodobieństwo, że losowa wartość odbiega od jego matematycznego oczekiwania o wartość większą niż trzykrotnie przeciętne odchylenie kwadratowe jest prawie równe zero.

Ta zasada jest nazywana zasada trzech sigm.

Nie praktykuje tego, że uważa się, że jeśli w przypadku jakiejkolwiek zmiennej losowej, wykonuje się reguła trzech sigm, wówczas ta wartość losowa ma normalny rozkład.

Przykład. Pociąg składa się z 100 wagonów. Masa każdego samochodu - zmienna losowa, rozproszona zgodnie z normalnym prawem z oczekiwaniami matematycznymi ale \u003d 65 ton i średnie odchylenie kwadratowe S \u003d 0,9 t. Lokomotywa może nosić masę nie więcej niż 6600 ton, w przeciwnym razie konieczne jest szkolenie drugiej lokomotywy. Znajdź prawdopodobieństwo, że druga lokomotywa nie jest wymagana.

Druga lokomotywa nie będzie wymagana, jeśli odchylenie masy kompozycji z oczekiwanych (100 × 65 \u003d 6500) nie przekracza 6600 - 6500 \u003d 100 ton.

Dlatego Masa każdej padliny ma normalny rozkład, a następnie masa całej kompozycji będzie również dystrybuowana normalnie.

Dostajemy:

Przykład. Normalnie rozproszona zmienność losowa X jest ustawiana przez jego parametry - a \u003d 2 -oczekiwania matematyczne i S \u003d 1 - średnie odchylenie kwadratowe. Wymagane jest napisanie gęstości prawdopodobieństwa i konstruowania jego harmonogramu, znajdzie prawdopodobieństwo, czy przyjmie wartość od interwału (1; 3), znajdź prawdopodobieństwo, że X zostanie odrzucony (moduł) z oczekiwania matematycznego nie więcej niż 2.

Gęstość dystrybucji to:

Zbuduj harmonogram:

Znajdź prawdopodobieństwo przychodzącego losowej wariancji do interwału (1; 3).

Znajdujemy prawdopodobieństwo odchylenia losowej zmiennej z oczekiwań matematycznych o wartość, nie większa niż 2.

Ten sam wynik można uzyskać za pomocą znormalizowanej funkcji Laplace.

Wykład 8 Prawo dużych liczb(Sekcja 2)

Zaplanuj wykłady

Centralny limit twierdzenie (ogólny preparat i prywatny formulacja dla niezależnych zmiennych losowych równo rozłożonych).

Nierówność chebyseva.

Prawo dużych liczb w formie Czebyszewa.

Koncepcja częstotliwości zdarzeń.

Statystyczne zrozumienie prawdopodobieństwa.

Prawo dużych liczb w formie Bernoulli.

Badanie wzorów statystycznych umożliwiło ustalenie, że w pewnych warunkach całkowite zachowanie dużej liczby zmiennych losowych prawie traci losowy charakter i staje się naturalny (innymi słowy, przypadkowe odchylenia z niektórych zachowań średnich są wzajemnie spłacane). W szczególności, jeśli wpływ na ilość poszczególnych terminów jest równomiernie niewielki, ilość dystrybucji kwoty zbliża się do normalności. Sformułowanie matematyczne tego oświadczenia podano w grupie zwanych twierdzeń prawo dużych liczb.

Prawo dużych liczb - Zasada ogólna, z racji, której wspólne działanie czynników losowych prowadzi do kilku bardzo ogólnych warunków do wyniku, co jest prawie niezależne od przypadku. Pierwszym przykładem tej zasady jest zbliżenie częstości występowania ofensywy zdarzenie losowe Wraz z jego prawdopodobieństwem, ze wzrostem liczby testów (często stosowanych w praktyce, na przykład, stosując częstotliwość występowania jakichkolwiek cech respondenta w próbce jako selektywnej oceny odpowiedniego prawdopodobieństwa).

Istota prawo dużych liczb To jest to, kiedy duża liczba Niezależne eksperymenty częstotliwość wyglądu niektórych zdarzeń jest bliska jego prawdopodobieństwa.

Centralny limit twierdzenie (CPT) (w brzmieniu Lapunowa A.m. dla równo rozłożonej SV). If IF Waren Independent SV X 1, X 2, ..., XN, ... mają takie samo prawo dystrybucyjne o skończonej charakterystyce numerycznej M \u003d M i D \u003d S 2, a następnie z N ® ¥, Prawo dystrybucji SV jest nieograniczone zbliża się do normalnego prawa N (n × m,).

Następstwo. Jeśli w stanie twierdzenia Następnie w N ® ¥ prawo dystrybucji CV Y jest nieograniczony zbliża się do normalnego prawa N (M, S /).

Moavover Laplace Twierdzenie.Niech SV K jest liczbą "sukcesów" w n testach zgodnie z programem Bernoulliego. Następnie w N ® ¥ i ustaloną wartością prawdopodobieństwa "sukcesu" w jednym badaniu p, prawo dystrybucji CV K jest nieograniczone zbliża się do normalnego prawa N (n × p,).

Następstwo. Jeśli, w stanie twierdzenia, zamiast C / N, częstotliwość "sukcesu" w n testom zgodnie z programem Bernoulli, jego prawo transakcyjne z N ® ¥ i stała wartość p jest nieograniczona zbliża się do normalnego prawa n (P,).

Komentarz. Niech SV K jest liczbą "sukcesów" w n testach zgodnie z programem Bernoulliego. Prawo dystrybucji takiego praw biominy. Następnie, w N ® ¥, prawo biodowca ma dwa dystrybucje limitu:

n dystrybucja Poisson. (dla N ® ¥ i L \u003d n × p \u003d const);

n dystrybucja Gaussa. N (n × p,) (z n ® ¥ i p \u003d const).

Przykład. Prawdopodobieństwo "sukcesu" w jednym badaniu jest tylko p \u003d 0,8. Ile trzeba przetestować testy, aby z prawdopodobieństwem co najmniej 0,9 można spodziewać się, że obserwowana częstotliwość "sukcesu" w badaniach według schematu Bernoulliego odbiega od prawdopodobieństwa P bez więcej niż e \u003d 0,01?

Decyzja. Dla porównania będziemy rozwiązać problem na dwa sposoby.

W porównaniu z innymi rodzajami dystrybutorów. Główna funkcja Dystrybucja ta jest taka, że \u200b\u200bwszystkie inne prawa dystrybucji dążą do tego prawa z nieskończoną powtórzeniem liczby testów. Jak dostaje ta dystrybucja?

Wyobraź sobie, że biorąc pod uwagę ręczny dynamometr, znajduje się w młodszych miejscach twojego miasta. I wszyscy, którzy przechodzą, proponujesz mierzyć swoją siłę, ściskając dynamometr z prawą lub lewą ręką. Odczyty dynamometru są starannie hamujące. Po chwili, wystarczająco duże ilości Testy, zakładasz osi odcięcia dynamometru i ilość osób, które "ściśnięte" są świadectwem osi rzędnej. Otrzymane punkty dołączyły do \u200b\u200bgładkiej linii. Rezultatem jest krzywa pokazana na rys. 9.8. Wygląd tej krzywej nie będzie szczególnie zmieniony przez zwiększenie czasu doświadczenia. Ponadto z jakiegoś momentu nowe wartości określają tylko krzywą bez zmiany jej kształtu.

Figa. 9.8.

Teraz przejdziemy z naszym dynametrem w sali sportowej i powtórzymy eksperyment. Teraz maksymalna krzywa przesuwa się w prawo, lewy koniec będzie nieco zaciśnięty, podczas gdy prawy koniec będzie ostrzejszy (rys. 9.9).

Figa. 9.9.

Należy zauważyć, że maksymalna częstotliwość drugiego rozkładu (punkt b) będzie niższa niż maksymalna częstotliwość pierwszej dystrybucji (punkt A). Można to wyjaśnić faktem, że łączna liczba osób odwiedzających halę sportową będzie mniejsza niż liczba osób, które przeszedł w pobliżu eksperymentatora w pierwszym przypadku (w centrum miasta w wystarczająco ludzkim miejscu). Maksymalny przesunięty w prawo, ponieważ hale sportowe uczestniczyli fizycznie bardziej silni ludzie W porównaniu do ogólnego tła.

I wreszcie odwiedź szkołę, przedszkola i domy opieki z tym samym celem: zidentyfikować ręce odwiedzających do tych miejsc. I znowu krzywa dystrybucji będzie miał podobną formę, ale teraz, oczywiście jego lewy koniec będzie bardziej stromy, a prawo jest bardziej dokręcone. A zarówno w drugim przypadku maksimum (pkt C) będzie niższy niż punkt A (rys. 9.10).

Figa. 9.10.

Jest to wspaniała właściwość normalnej dystrybucji - aby zachować formę krzywej gęstości rozkładu prawdopodobieństwa (rys. 8 - 10) zauważono i opisano w 1733 r. Przez MOAVR, a następnie zbadany przez Gaussa.

W badania naukowe, w technice, w masowych zjawiskach lub eksperymentach, jeśli chodzi o wielokrotne powtarzające się wartości losowe w stałych warunkach doświadczenia, mówi się, że wyniki testów doświadczają losowego rozpraszania z zastrzeżeniem prawa normalnej krzywej rozkładu

(21)

Gdzie jest najczęstszym wydarzeniem. Z reguły, we wzorze (21) zamiast parametru. Co więcej, długość jest serią eksperymentalną, tym mniej parametru będzie różni się od oczekiwań matematycznych. Obszar pod krzywą (rys. 9.11) jest równą jednostką. Obszar, który spełnia interwał osi odcięcia jest numerycznie równy prawdopodobieństwu losowego wyniku w tym przedziale.

Figa. 9.11.

Funkcja normalnej dystrybucji ma formularz

(22)

Należy pamiętać, że normalna krzywa (rys. 9.11) jest symetryczna w odniesieniu do bezpośredniego i asymptotycznego zbliżania się do osi Och.

Oblicz oczekiwanie matematyczne na normalne prawo

(23)

Właściwości rozkładu normalnego

Rozważ podstawowe właściwości tej najważniejszej dystrybucji.

Właściwość 1.. Funkcja gęstości dystrybucji normalnej (21) oznaczania na całej osi odcięcia.

Nieruchomość 2.. Funkcja gęstości rozkładu normalnego (21) jest większa niż zero dla dowolnej powierzchni definicji ().

Nieruchomość 3.. Z nieskończonym wzrostem (spadek) funkcja dystrybucji (21) ma tendencję do zera .

Nieruchomość 4.. W przypadku funkcji dystrybucji, zestaw (21) największa wartość równy

(24)

Nieruchomość 5.. Wykres funkcyjny (rys. 9.11) jest symetryczny na bezpośrednim.

Nieruchomość 6.. Wykres funkcyjny (Rys. 9.11) ma dwa punkty rozpuszczania symetryczne stosunkowo proste:

(25)

Nieruchomość 7.. Wszystkie dziwne chwile centralne są zero. Należy zauważyć, że przy użyciu właściwości 7 asymetria funkcji jest określana przez wzór. Jeśli stwierdza się, że badana dystrybucja jest symetrycznie stosunkowo prosta. Jeśli mówią, że wiersz jest przesuwany w prawo (bardziej powszechny prawy gałąź wykresu lub dokręcone). Jeśli uważa się, że wiersz jest przesunięty w lewo (bardziej powszechna oddział grafiki Rysunek 9.12).

Figa. 9.12.

Nieruchomość 8.. Nadmiar rozkładu wynosi 3. Często w praktyce są obliczane i w pobliżu tej wartości do zera określać "kompresję" lub "rozmycie" wykresu (rys. 9.13). A ponieważ jest to związane, a następnie ostatecznie charakteryzuje stopień rozpraszania częstotliwości danych. Jak również określa