Застосування інтегрального обчислення у механіці. Застосування диференціального та інтегрального обчислення до вирішення фізичних та геометричних завдань у MATLab
Надіслати свою гарну роботу до бази знань просто. Використовуйте форму нижче
Студенти, аспіранти, молоді вчені, які використовують базу знань у своєму навчанні та роботі, будуть вам дуже вдячні.
Реферат на тему: «Інтеграл та його застосування»
Студентки
мед. коледжу
№2 203 групи
Куликової Марії
Санкт - Петербург 2010 рік
Вступ
Символ інтеграла запроваджено з 1675 р., а питаннями інтегрального обчислення займаються з 1696 р. Хоча інтеграл вивчають, переважно, вчені-математики, а й фізики зробили свій внесок у цю науку. Майже жодна формула фізики не обходиться без диференціального та інтегрального обчислень. Тому я вирішила дослідити інтеграл і його застосування.
Історія інтегрального обчислення
Історія поняття інтеграла тісно пов'язана із завданнями знаходження квадратур. Завданнями про квадратуру тієї чи іншої плоскої постаті математики Стародавню Грецію і Риму називали завдання обчислення площ. Латинське слово quadratura перекладається як "надання квадратної форми". Необхідність у спеціальному терміні пояснюється тим, що в античний час (і пізніше, аж до XVIII століття) ще не були досить розвинені уявлення про дійсні числа. Математики оперували з їх геометричними аналогами чи скалярними величинами, які не можна перемножувати. Тому й завдання перебування площ доводилося формулювати, наприклад, так: «Побудувати квадрат, рівновеликий даному колу». (Ця класична задача «про квадратуру кола» кола» не може, як відомо, бути вирішена за допомогою циркуля та лінійки.)
Символ т введений Лейбніцем (1675). Цей знак є зміною латинської літери S (першої літери слова summ a) Саме слово інтеграл вигадав Я. Бернуллі (1690). Ймовірно, воно походить від латинського integro, яке перекладається як приводити до колишнього стану, відновлювати. (Дійсно, операція інтегрування «відновлює» функцію, диференціюванням якої отримано підінтегральну функцію.) Можливо, походження терміна інте грало інше: слово integer означає цілий.
У ході листування І. Бернуллі та Г. Лейбніц погодився з пропозицією Я. Бернуллі. Тоді ж, у 1696 р., з'явилася і назва нової гілки математико-інтегрального обчислення (calculus integralis), яку запровадив І. Бернуллі.
Інші відомі терміни, що стосуються інтегрального числення, з'явилися помітно пізніше. Назва, що вживається зараз, первісна функція замінило більш її раннє «примітивна функція», яке ввів Лагранж (1797 р.). Латинське слово primitivus перекладається як «початковий»: F(x) = т f(x)dx - початкова (чи первісна, чи первісна) для f(x), яка виходить із F(x) диференціюванням.
У сучасній літературі безліч всіх первісних для функції f(х) називається також невизначеним інтегралом. Це поняття виділив Лейбніц, який помітив, що всі первісні функції відрізняються довільною постійною b, називають певним інтегралом (позначення ввів К. Фур'є (1768-1830), але межі інтегрування вказував вже Ейлер).
Багато значних досягнень математиків Стародавню Грецію у вирішенні завдань перебування квадратур (тобто. обчислення площ) плоских постатей, і навіть кубатур (обчислення обсягів) тіл пов'язані із застосуванням методу вичерпування, запропонованим Евдоксом Книдским (бл. 408 - бл. 355 до зв. .е.). За допомогою цього методу Евдокс довів, наприклад, що площі двох кіл відносяться як квадрати їх діаметрів, а об'єм конуса дорівнює 1/3 об'єму циліндра, що має таку ж основу та висоту.
Метод Євдокса було вдосконалено Архімедом. Основні етапи, що характеризують метод Архімеда: 1) доводиться, що площа кола менше площі будь-якого описаного біля нього правильного багатокутника, але більше площі будь-якого вписаного; 2) доводиться, що при необмеженому подвоєнні числа сторін різниця площ цих багатокутників прагне нуля; 3) для обчислення площі кола залишається знайти значення, якого прагне відношення площі правильного багатокутника при необмеженому подвоєнні числа його сторін.
За допомогою методу вичерпування, цілої низки інших дотепних міркувань (у тому числі із залученням моделей механіки) Архімед вирішив багато завдань. Він оцінив число p (3.10/71 Архімед передбачив багато ідей інтегрального обчислення. (Додамо, що й перші теореми про межах були доведені им.) Але знадобилося понад півтори тисячі років, як ці ідеї знайшли чітке вираження і було доведено рівня обчислення. Математики XVII століття, отримали багато нових результатів, навчалися на працях Архімеда. Активно застосовувався й інший метод - метод неподільних, який також зародився у Стародавній Греції (він пов'язаний насамперед з атомістичними поглядами Демокріта). Наприклад, криволінійну трапецію (рис. 1, а) вони уявляли собі складеною з вертикальних відрізків довжиною f(х), яким, тим щонайменше, приписували площу, рівну нескінченно малій величині f(х)dx . Відповідно до такого розуміння шукана площа вважалася рівною сумі нескінченно великої кількості нескінченно малих площ. Іноді навіть підкреслювалося, що окремі доданки у цій сумі - нулі, але нулі особливого роду, які, складені у нескінченному числі, дають цілком певну позитивну суму. На такій здається тепер щонайменше сумнівній основі І. Кеплер (1571-1630) у своїх творах "Нова астрономія". 1609 і «Стереометрія винних бочок» (1615) правильно обчислив ряд площ (наприклад, площа фігури обмеженої еліпсом) і обсягів (тіло розрізалося на 6ecкінцево тонкі пластинки). Ці дослідження були продовжені італійськими математиками Б. Кавальєрі (1598-1647) та Е. Торрічеллі (1608-1647). Зберігає своє значення і в наш час сформульований Б. Кавальєрі принцип, запроваджений ним за деяких додаткових припущень. Нехай потрібно знайти площу фігури, зображеної на малюнку 1 б, де криві, що обмежують фігуру зверху і знизу, мають рівняння y = f(x) та y=f(x)+c. Представляючи фігуру складеної з «неподільних», за термінологією Кавальєрі, нескінченно тонких стовпчиків, помічаємо, що вони мають загальну довжину с. Пересуваючи їх у вертикальному напрямку, можемо скласти з них прямокутник з основою b-а та висотою с. Тому потрібна площа дорівнює площі отриманого прямокутника, тобто. S = S1 = c (b – а). Загальний принцип Кавальєрі для площ плоских фігур формулюється так: Нехай прямі деякого пучка паралельних перетинають фігури Ф1 та Ф2 за відрізками рівної довжини (рис. 1, в). Тоді площі фігур Ф1 та Ф2 рівні. Аналогічний принцип діє в стереометрії і виявляється корисним при знаходженні обсягів. У XVII ст. було зроблено багато відкриття, що стосуються інтегрального числення. Так, П.Ферма вже у 1629 р. задачу квадратури будь-якої кривої у = хn, де п - ціле (тобто по суті вивів формулу т хndx = (1/n+1)хn+1), і на цій основі вирішив ряд завдань перебування центрів тяжкості. І. Кеплер під час виведення своїх знаменитих законів руху планет фактично спирався на ідею наближеного інтегрування. І. Барроу (1630-1677), вчитель Ньютона, близько підійшов до розуміння зв'язку інтегрування та диференціювання. Велике значення мали роботи з представлення функцій у вигляді статечних рядів. Проте за всієї значимості результатів, отриманих багатьма надзвичайно винахідливими математиками XVII століття обчислення ще був. Необхідно було виділити загальні ідеї, що лежать в основі вирішення багатьох приватних завдань, а також встановити зв'язок операцій диференціювання та інтегрування, що дає досить загальний алгоритм. Це зробили Ньютон і Лейбніц, які відкрили незалежно один від одного факт, відомий під назвою формули Ньютона - Лейбніца. Тим самим було остаточно оформився загальний метод. Належало ще навчитися знаходити першорядні багато функцій, дати логічні нового обчислення і т.п. Але головне вже було зроблено: диференційне та інтегральне числення створено. Методи математичного аналізу активно розвивалися у наступному столітті (насамперед слід назвати імена Л. Ейлера, який завершив систематичне дослідження інтегрування елементарних функцій, та І. Бернуллі). У розвитку інтегрального числення взяли участь російські математики М.В. Остроградський (1801-1862), В.Я. Буняковський (1804-1889), П.Л. Чебишев (1821-1894). Принципове значення мали, зокрема, результати Чебишева, який доказав, що є інтеграли, не виразні через елементарні функції. Суворий виклад теорії інтеграла виник лише у минулому столітті. Вирішення цього завдання пов'язане з іменами О. Коші, одного з найбільших математиків, німецького вченого Б. Рімана (1826-1866), французького математика Г. Дарбу (1842-1917). Відповіді на багато питань, пов'язаних із існуванням площ та обсягів фігур, були отримані зі створенням К. Жорданом (1838-1922) теорії міри. Різні узагальнення поняття інтеграла вже на початку нашого століття були запропоновані французькими математиками А. Лебегом (1875-1941) та А. Данжуа (1884-1974), радянським математиком А.Я. Хінчинчин (1894-1959). Якщо F(x) - одна з первісних функцій f(x) на проміжку J, то первісна на цьому проміжку має вигляд F(x)+C, де CОР. Визначення. Безліч всіх первісних функцій f(x) на проміжку J називається певним інтегралом від функції f(x) на цьому проміжку і позначається т f(x)dx. т f(x)dx = F(x)+C, де F(x) - деяка первісна на проміжку J. f - підінтегральна функція, f(x) - підінтегральний вираз, x - змінна інтеграція, C - постійна інтегрування. Властивості невизначеного інтегралу. (т f(x)dx) у = т f(x)dx, т f(x)dx = F(x)+C, де F у(x) = f(x) (т f (x) dx) у = (F (x) + C) у = f (x) т f у (x) dx = f (x) + C - з визначення. т k f (x) dx = k f f (x) dx якщо k - постійна і F у (x) = f (x), т k f (x) dx = f (x) dx = k (F (x) dx + C1) = k т f (x) dx т (f(x)+g(x)+...+h(x))dx = т f(x)dx + тg(x)dx +...+ т h(x)dx т (f(x)+g(x)+...+h(x))dx = т dx = т уdx = F(x)+G(x)+...+H(x)+C= т f(x)dx + g(x)dx +...+ т h(x)dx, де C=C1+C2+C3+...+Cn. Табличний метод. Спосіб підстановки. Якщо підінтегральна функція не є табличним інтегралом, можливо (не завжди) застосувати цей спосіб. Для цього треба: розбити підінтегральну функцію на два множники; позначити один із множників нової змінної; виразити другий множник через нову змінну; скласти інтеграл, знайти його значення та виконати зворотну підстановку. Примітка: за нову змінну краще позначити ту функцію, яка пов'язана з виразом, що залишився. 1. т xЦ(3x2-1)dx; Нехай 3x2-1=t (tі0), візьмемо похідну від обох частин: у dt 1 1 у 1 1 t 2 2 1 ---Ш ф-t 2 = - ф t 2dt = - --- + C = -Ц 3x2-1 + C т sin x cos 3x dx = т - t3dt = - - + C Нехай cos x = t Метод перетворення підінтегральної функції на суму чи різницю: т sin 3x cos x dx = 1/2 т (sin 4x + sin 2x) dx = 1/8 cos 4x - ј cos 2x + C у x4+3x2+1 у 1 1 ф dx = ф(x2+2 - ---) dx = - x2 + 2x - arctg x + C х x2+1 х x2+1 3 Примітка: при вирішенні цього прикладу робити багаточлени ”кутом”. По частинах. Якщо в заданому вигляді взяти інтеграл неможливо, а в той же час, дуже легко перебуває первісна одного множника і похідна іншого, можна використовувати формулу. (u(x)v(x))"=u"(x)v(x)+u(x)v(x) u"(x)v(x)=(u(x)v(x)+u(x)v"(x) т u"(x)v(x)dx=т (u(x)v(x))"dx - т u(x)v"(x)dx т u"(x)v(x)dx=u(x)v(x)dx - т u(x)v"(x)dx т x cos (x) dx = т x dsin x = x sin x - т sin x dx = x sin x + cos x + C Визначення. Фігура, обмежена графіком безперервної, знакопостійної функції f(x), віссю абцис і прямими x=a, x=b називається криволінійною трапецією. Способи знаходження площі криволінійної трапеції Теорема. Якщо f(x) безперервна та невід'ємна функція на відрізку , то площа відповідної криволінійної трапеції дорівнює приросту первісних. Дано: f (x) - безперервна неопр. функція, xО. Довести: S = F(b) - F(a), де F(x) - первісна f(x). Доведення: 1) Розглянемо допоміжну функцію S(x). Кожному xО поставимо у відповідність ту частину криволінійної трапеції, яка лежить лівіше за пряму (рис. 2), що проходить через точку з цією абцисою і паралельно осі ординат. Отже S(a)=0 і S(b)=Sтр Доведемо, що S(a) - первісна f(x). D(f) = D(S) = S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), при Dx®0 DS - прямокутник Dx®0 зі сторонами Dx та f(x0) S"(x0) = lim(Dx f(x0) / Dx) = lim f(x0)=f(x0): тому що x0 точка, то S(x) - Dx®0 Dx®0 є первісною f(x). Отже, за теоремою про загальний вигляд первісної S(x)=F(x)+C. Т.к. S(a)=0, то S(a) = F(a)+C S = S(b) = F(b) + C = F(b)-F(a) 1). Розіб'ємо відрізок на n рівних частин. Крок розбиття (рис. 3) Dx=(b-a)/n. При цьому Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+f (xn)) При n®Ґ отримаємо, що Sтр= Dx(f(x0)+f(x1)+...+f(xn)) Межу цієї суми називають певним інтегралом. Сума, що стоїть під межею, називається інтегральною сумою. Певний інтеграл – це межа інтегральної суми на відрізку при n®Ґ. Інтегральна сума виходить як межа суми творів довжини відрізка, отриманого при розбиття області визначення функції в якійсь точці цього інтервалу. a - нижня межа інтегрування; b – верхній. Формула Ньютона-Лейбніца. Порівнюючи формули площі криволінійної трапеції робимо висновок: якщо F - первісна для b на , то т f(x)dx = F(b)-F(a) т f(x)dx = F(x) F = F(b) - F(a) Властивості певного інтегралу. т f(x)dx = т f(z)dz т f(x)dx = F(a) - F(a) = 0 т f(x)dx = - т f(x)dx т f(x)dx = F(a) - F(b) f(x)dx = F(b) - F(a) = - (F(a) - F(b)) Якщо a, b та c будь-які точки проміжку I, на якому безперервна функція f(x) має первісну, то т f(x)dx = f(x)dx + f(x)dx F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a) (Це властивість адитивності певного інтегралу) Якщо l і m постійні величини, то т (lf (x) + m j (x)) dx = l t f (x) dx + m tj (x)) dx - Це властивість лінійності певного інтегралу. т (f(x)+g(x)+...+h(x))dx = т f(x)dx+ т g(x)dx+...+ т h(x)dx т (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H (a) + Cn = b b b = f (x) dx + g (x) dx + ... + h (x) dx Набір стандартних картинок (рис. 4, 5, 6, 7, 8) Мал. 4 Мал. 5 Мал. 6 Мал. 7 Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0. Треба розглянути симетрію функції щодо осі OX. ABCD®A"B"CD b S(ABCD)=S(A"B"CD) = т-f(x)dx S = т f (x) dx = т g (x) dx S = т(f(x)-g(x))dx+т(g(x)-f(x))dx S = т (f(x)+m-g(x)-m)dx = т (f(x)-g(x))dx т ((f(x)-g(x))dx S = т (f(x)+m-g(x)-m)dx = Т(f(x)-g(x))dx Якщо на відрізку f(x)ig(x), то площа між цими графіками дорівнює т ((f(x)-g(x))dx Функції f(x) і g(x) довільні та невід'ємні S = f(x)dx - т g(x)dx = т(f(x)-g(x))dx Застосування інтегралу У фізиці. Робота сили (A = FScosa, cosa № 1) Якщо на частку діє сила F, кінетична енергія не залишається постійною. У цьому випадку згідно приріст кінетичної енергії частки за час dt дорівнює скалярному добутку Fds, де ds - переміщення частки за час dt. Величина називається роботою, що здійснюється силою F. Нехай точка рухається осі ОХ під дією сили, проекція якої на вісь ОХ є функція f(x) (f-безперервна функція). Під дією сили точка перемістилася з точки S1(a) до S2(b). Розіб'ємо відрізок на n відрізків, однакової довжини Dx = (b - a)/n. Робота сили дорівнюватиме сумі робіт сили на отриманих відрізках. Т.к. f(x) -безперервна, то при малому робота сили на цьому відрізку дорівнює f(a)(x1-a). Аналогічно на другому відрізку f(x1)(x2-x1), на n-му відрізку - f(xn-1)(b-xn-1). Отже робота на рівні: А » An = f(a)Dx +f(x1)Dx+...+f(xn-1)Dx= ((b-a)/n)(f(a)+f(x1)+...+f (xn-1)) Приблизна рівність переходить у точну за n®Ґ А = lim [(b-a)/n] (f(a)+...+f(xn-1))= т f(x)dx (за визначенням) Нехай пружина жорсткості С та довжини l стиснута на половину своєї довжини. Визначити величину потенційної енергії Ер дорівнює роботі A, що чиниться силою -F(s) пружність пружини при її стисканні, то Eп = A = - т (-F(s)) dx З курсу механіки відомо, що F(s)=-Cs. Звідси знаходимо Еп = - т (-Cs) ds = CS2/2 | = C/2 l2/4 Відповідь: Cl2/8. Координати центру мас Центр мас - точка, через яку проходить рівнодіюча сил тяжіння при будь-якому просторовому розташуванні тіла. Нехай матеріальна однорідна пластина має форму криволінійної трапеції (x;y |aЈxЈb; 0ЈyЈf(x)) і функція y=f(x) безперервна на , а площа цієї криволінійної трапеції дорівнює S, тоді координати центру мас пластини про знаходять за формулами: x0 = (1/S) т x f(x) dx; y0 = (1/2S) f 2(x) dx; Центр мас. Знайти центр мас однорідного півкола радіусу R. Зобразимо півколо у системі координат OXY (рис. 9). З міркувань симетрії та однорідності помічаємо, що абсцис точки M Функція, що описує півколо має вигляд: Нехай S = pR2/2 - площа півкола, тоді y = (1/2S) тЦ(R2-x2)dx = (1/pR2) тЦ(R2-x2)dx = -R -R R = (1/pR2)(R2x-x3/3)|= 4R/3p Відповідь: M(0; 4R/3p) Шлях, пройдений матеріальною точкою Якщо матеріальна точка рухається прямолінійно зі швидкістю u = u (t) і за час T = t2-t1 (t2> t1) пройшла шлях S, то У геометрії Об'єм – кількісна характеристика просторового тіла. За одиницю виміру обсягу приймають куб з ребром 1мм(1ді, 1м і т.д.). Кількість кубів одиничного обсягу розміщених у цьому тілі – об'єм тіла. Аксіоми об'єму: Обсяг – це невід'ємна величина. Обсяг тіла дорівнює сумі обсягів тіл, що його складають. Знайдемо формулу для обчислення обсягу (рис. 10): виберемо вісь ОХ за напрямом розташування цього тіла; визначимо межі розташування тіла щодо ОХ; введемо допоміжну функцію S(x), що задає таку відповідність: кожному x з відрізка поставимо у відповідність площу перерізу даної фігури площиною, що проходить через задану точку x перпендикулярно осі ОХ. розіб'ємо відрізок на n рівних частин і через кожну точку розбиття проведемо площину перпендикулярну до осі ОХ, при цьому наше тіло розіб'ється на частини. По аксіомі V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx Dx®0, а Sk®Sk+1, а об'єм частини, укладеної між двома сусідніми площинами, дорівнює об'єму циліндра Vц=SоснH. Маємо суму творів значень функцій у точках розбиття на крок розбиття, тобто. інтегральну суму. За визначенням певного інтегралу, межа цієї суми при n®Ґ називається інтегралом a V= т S(x)dx, де S(x) - переріз площини, що проходить через b обрану точку перпендикулярно до осі ОХ. Для знаходження обсягу треба: 1). Вибрати зручним способом вісь ОХ. 2). Визначити межі розташування цього тіла щодо осі. 3). Побудувати переріз даного тіла площиною перпендикулярно до осі ОХ і проходить через відповідну точку. 4). Виразити через відомі величини функцію, що виражає площу даного перерізу. 5). Скласти інтеграл. 6). Обчисливши інтеграл, знайти обсяг. Обсяг фігур обертання Тіло, отримане в результаті обертання плоскої фігури щодо якоїсь осі, називають фігурою обертання. Функція S(x) у фігури обертання є коло. Sсіч(x)=p f 2(x) Довжина дуги плоскої кривої. Нехай на відрізку функція y = f(x) має безперервну похідну y" = f"(x). В цьому випадку довжину дуги l "шматка" графіка функції y = f(x), xО можна знайти за формулою l = т Ц(1+f"(x)2)dx 1. М.Я. Віленкін, О.С. Івашев-Мусатов, С.І. Шварцбурд, "Алгебра та математичний аналіз", Москва, 1993 р. 2. "Збірник завдань з математичного аналізу", Москва, 1996 р. 3. І.В. Савельєв, "Курс загальної фізики", том 1, Москва, 1982 р. 4. Для підготовки даної роботи було використані матеріали із російського сайту internet Ідеї інтегрального обчислення у працях древніх математиків. Особливості методу вичерпування. Історія знаходження формули обсягу тора Кеплера. Теоретичне обґрунтування принципу інтегрального обчислення (принцип Кавальєрі). Поняття певного інтегралу. презентація , доданий 05.07.2016 Історія інтегрального обчислення. Визначення та властивості подвійного інтеграла. Його геометрична інтерпретація, обчислення в декартових та полярних координатах, зведення його до повторного. Застосування економіки та геометрії для обчислення обсягів і площ. курсова робота , доданий 16.10.2013 Визначення певного інтегралу, його властивості. Довжина дуги кривої. Площа криволінійної трапеції. Площа поверхні обертання. Площа фігур, обмежених графіками функцій, обмежених лініями, заданими рівняннями. Обчислення обсягів тел. контрольна робота , доданий 10.02.2017 Історія появи поняття "інтеграла" та інтегрального обчислення, його особливості та значення. Інтеграл як один із основних інструментів роботи з функціями. Обгрунтування необхідності вираження всіх фізичних явищ як математичної формули. презентація , додано 19.05.2014 Визначення криволінійного інтеграла за координатами, його основні властивості та обчислення. Умова незалежності криволінійного інтеграла від шляху інтегрування. Обчислення площ фігур за допомогою подвійного інтегралу. Використання формули Гріна. контрольна робота , доданий 23.02.2011 Способи обчислення інтегралів. Формули та перевірка невизначеного інтеграла. Площа криволінійної трапеції. Невизначений, певний та складний інтеграл. Основні застосування інтегралів. Геометричний зміст певного та невизначеного інтегралів. презентація , доданий 15.01.2014 Розв'язання задачі знаходження площі криволінійної трапеції. Визначення та властивості певного інтегралу. Необхідна умова інтегрованості та критерій Дарбу. Інтегрованість безперервних та монотонних функцій. Доказ формули Ньютона Лейбніца. контрольна робота , доданий 25.03.2011 Обчислення площ плоских фігур. Знаходження певного інтегралу функції. Визначення площі під кривою площі фігури, укладеної між кривими. Обчислення обсягів тіл обертання. Межа інтегральної суми функції. Визначення об'єму циліндра. презентація , додано 18.09.2013 Поняття певного інтеграла, розрахунок площі, об'єму тіла та довжини дуги, статичного моменту та центру тяжкості кривої. Обчислення площі у разі прямокутної криволінійної області. Застосування криволінійного, поверхневого та потрійного інтегралів. курсова робота , доданий 19.05.2011 Історія інтегрального та диференціального обчислення. Програми певного інтеграла до вирішення деяких завдань механіки та фізики. Моменти та центри мас плоских кривих, теорема Гульдена. Диференційне рівняння. Приклади розв'язання задач у MatLab. "Омська державна медична академія" Міністерства охорони здоров'я та соціального розвитку Російської Федерації на тему: застосування певного інтегралу в медицині виконала студент 1 курсу відділення Лікувальна справа група 102Ф Глушнєва Н.А. Вступ Видатний італійський фізик і астроном, один із засновників точного природознавства, Галілео Галілей (1564-1642) говорив, що "Книга природи написана мовою математики". Майже через двісті років родоначальник німецької класичної філософії Кант (1742-1804) стверджував, що "У всякій науці стільки істини, скільки в ній математики". Зрештою, ще через майже сто п'ятдесят років, практично вже в наш час, німецький математик і логік Давид Гільберт (1862-1943) констатував: "Математика - основа найточнішого природознавства". Леонардо Да Вінчі казав: «Хай не читає мене в основах моїх той, хто не математик». Намагаючись знайти математичне обґрунтування законів природи, вважаючи математику могутнім засобом пізнання, він застосовує її навіть у такій науці, як анатомія. Математика всім потрібна. І медикам також. Хоча б для того, щоби грамотно прочитати звичайну кардіограму. Без знання азів математики не можна бути докою в комп'ютерній техніці, використовувати можливості комп'ютерної томографії... Адже сучасна медицина не може обходитися без найскладнішої техніки. На сьогодні неможливо вивчення гемодинаміки-руху крові по судинах без застосування інтегралу. Протягом тривалого часу катетеризація правих відділів серця була єдиним методом дослідження, що дозволяв оцінювати стан правих відділів серця, отримувати характеристики внутрішньосерцевого кровотоку, визначати тиск у правих відділах серця та легеневої артерії. Однак ближче до практики. Для початку знайдемо лінійну швидкість кровотоку Зміна лінійної швидкості кровотоку у різних судинах Це шлях, який проходить в одиницю часу частинкою крові в судині. Лінійна швидкість у судинах різного типу різна (див. малюнок) і залежить від об'ємної швидкості кровотоку та площі поперечного перерізу судин. У практичній медицині лінійну швидкість кровотоку вимірюють за допомогою ультразвукового та індикаторного методів, частіше визначають час повного кругообігу крові, який дорівнює 21-23 с. Для його визначення в ліктьову вену вводять індикатор (еритроцити, мічені радіоактивним ізотопом, розчин метиленового синього та ін) і відзначають час його першої появи у венозній крові цієї судини в іншій кінцівці. Для початку згадаємо, що інтеграл-це математичний об'єкт, який виник історично на основі потреби вирішення різних прикладних завдань фізики та техніки. Це і фізичні додатки певного інтеграла: обчислення шляху матеріальної точки, що рухається прямолінійною або криволінійною траєкторією за швидкістю її руху. Ті фізичні величини, що визначаються з допомогою інтегралу - зазвичай називаються інтегральними, а ті величини, якими виражаються інтегральні величини - диференціальними. Наприклад, швидкість тіла у точці – це диференціальна характеристика тіла, а маса тіла – інтегральна. Диференціальні характеристики визначаються значенням у точці і зазвичай різні у різних точках простору. Інтегральні характеристики завжди виражають властивості об'єктів, які стосуються цілої області простору. Наприклад, маса характеризує тіло цілком як деякий об'єкт, що займає область простору. Шлях, пройдений тілом - це теж інтегральна характеристика, оскільки вона характеризує цілу траєкторію, що складається з безлічі точок, а швидкість різна в кожній точці траєкторії і характеризує кожну точку окремо. Виникає питання - як же обчислити інтегральну швидкість для цілої судини (артерії або вени), знаючи лінійну швидкість кровотоку. Дуже просто: потрібно Нижче наведені розрахунки ударного об'єму (ударний об'єм серця (син.: систолічний об'єм крові, систолічний об'єм серця, ударний об'єм крові) - об'єм крові (в мл), що викидається шлуночком серця за одну систолу) - однією з основних величин в ЕХОкг, що розраховуються при допомоги інтеграла лінійної швидкості кровотоку. а - Схеми розрахунку ударного обсягу, а - з використанням рівняння безперервності потоку; б - з використанням рівняння безперервності потоку за наявності значної мітральної регургітації. VTI = V cp ЕТ, де CSA - площа поперечного перерізу, VTI - інтеграл лінійної швидкості потоку, V cp - середня швидкість потоку у виносному тракті лівого шлуночка, ЕТ - час викиду. У тому випадку, коли є гемодинамічно значуща мітральна регургітація (більше 2-го ступеня), тотальний ударний об'єм лівого шлуночка розраховується за формулою: TSV = FSV + RSV, [Інтеграл лінійної швидкості (FVI, або VTI)] = [Час кровотоку (ET)] х [Середня швидкість кровотоку (Vmean)]; Серцевий викид може бути визначений інтегралом лінійної швидкості аортального і легеневого потоку. На завершення хочу додати, що моя робота розрахована не на математика, від і до того, що розбирається в інтегруванні, а на будь-яку людину, яка виявила інтерес до застосування інтеграла в медицині. Тому я намагалася зробити її максимально доступною для сприйняття та цікавою навіть дитині. Список літератури: Відкритий урок з алгебри та початків аналізу в 11 класі з розширеним вивченням математики та фізики «Застосування методів математичного аналізу під час вирішення практичних завдань». Вчитель: Вишневська Н.В. Цілі уроку: 1. Повторити основні типи завдань, які вирішуються методами математичного аналізу. 2. Повторити алгоритми розв'язання. 3. Розібрати розв'язання задач підвищеної проблеми. 4. Вирішити економічні завдання. План проведення уроку: На дошці розбираються два завдання підвищеної проблеми (картки № 7 і № 5). Поки хлопці готуються, клас усно відповідає на запитання: а) Області, де використовуються методи математичного аналізу; б) алгоритм розв'язання задач шляхом пошуку найбільших та найменших значень функції; в) алгоритм розв'язання задач за допомогою певного інтегралу. У цей час 6 людина працюють за картками (№ 3, 4, 6, 8, 9, 10). Заповнюються таблиці. Перевіряються завдання на дошці, вчитель перевіряє правильність розв'язання карток. Розбирається на дошці економічне завдання (картка №1, 2). Домашня контрольна робота Алгоритм розв'язання задач шляхом пошуку найбільших та найменших значень функції. Алгоритм обчислення геометричних та фізичних величин за допомогою певного інтегралу. Виражають шукану величину як значення в деякій точці функції F
.
Знаходять похідну fцієї функції. Виражають функцію Fу вигляді певного інтеграла від fта обчислюють його. Підставляючи значення х = bзнаходять потрібну величину. Домашні завдання (на дошці):
Два кораблі рухаються двома перпендикулярними прямими, що перетинаються в точці Про, по напрямку до Про. У якийсь момент часу обидва знаходяться за 65 км від Прошвидкість першого дорівнює 15 км/год, другого – 20 км/год. Від першого корабля відходить моторний човен, що рухається зі швидкістю 25 км/год. а) За який найменший час катер може доплисти від першого корабля до другого? б) За який найменший час катер може доплисти від першого корабля до другого і повернутися на перший корабель? V 1 = 15 км/год 65 км S
1 Про
S
3 S
2
65 км Vл = 25 км/год V 2 = 20 км/год Рішення:
х– час, що минув від того моменту, коли обидва кораблі перебували за 65 км від Про, До моменту відправлення катера. У момент відправлення катера 1-й корабель був на відстані Продиференціюємо по х:
Відповідь: а) 1 год; б) 3:00. Котел має форму параболоїда обертання. Радіус його заснування R= 3 м, глибина Н= 5 м. Котел наповнений рідиною, питома вага якої 0,8 г/см 3 . Обчислити роботу, яку потрібно зробити, щоб викачати рідину з казана. у
у
R= 3 м Н= 5 м уд. вага = 0,8 Г/см 3 Обчислити роботу, яку потрібно зробити, щоб викачати рідину з казана. Рішення:
У площині перерізу хОу АОВ– парабола, рівняння якої Координати точки Уповинні задовольняти цього рівняння, тобто. Розділимо параболоїд на шари площинами, паралельними поверхні рідини. Нехай товщина шару на глибині ( Н – у)дорівнює dy. Тоді, приймаючи приблизно шар за циліндр, отримаємо його об'єм З рівняння параболи Отже, щоб викачати рідину з глибини Відповідь: Робота у класі.
Яку роботу потрібно витратити, щоб розтягнути пружину на 6 см, якщо сила 1 кг розтягує її на 1 см? Рішення:
Відповідно до закону Гука сила FкГ, що розтягує пружину на х, дорівнює х= 0,01 м F= 1 кг Тоді Шукана робота Відповідь: 0,18 кгм. Обчислити роботу сили Fпри стиску пружини на 5 см, якщо для стиснення її на 1 см потрібна сила в 1 кг. Рішення:
За законом Гука х= 0,01 м F= 1 кг Тоді Шукана робота Відповідь: 0,125 кгм. Сила F, з якою електричний заряд де k- Постійна. Визначити роботу сили Fпри переміщенні заряду Рішення:
Робота визначається за формулою При Відповідь: Визначити силу тиску води на вертикальну стінку, що має форму півкола радіусу R= 6 м, діаметр якого лежить на поверхні води. Рішення:
Сила тиску рідини на майданчик площею Sпри глибині занурення хдорівнює х З
dх
А В
Півколо паралельними прямими розділимо на смужки, які приймемо за прямокутник. Нехай заштрихована смужка має довжину АВ, ширину dxі знаходиться на глибині х Тиск води на смужку, що знаходиться на глибині х, буде одно. Звідси Питома вага води 1 см 3 = 1 Г, отже вага 1 м 3 = 1000 кг. 1 кг 1 бар = 0,987 атм. Відповідь: 144000 кг. Швидкість руху точки Рішення:
Отже Відповідь: 512 м; 64 м/с. Картка № 1 (вирішується у класі на дошці)
Середні сукупні витрати виробництва мила Зв'язок між річним обсягом продажів, що дорівнює величині річного випуску Q, і ціною мила Р(В тис. рублів за тонну) описується формулою Реалізувавши за фіксованою ціною все зварене мило за рік, завод отримав максимально можливий прибуток. Якою була при цьому виручка підприємства? Рішення:
Виразимо через Qспочатку ціну мила з формули Тоді прибуток Gможна висловити: Знайдемо критичні точки цієї функції: Критичні точки 100 -340 -120. Негативне коріння немає економічного сенсу. Q
G
Значить оптимальний річний обсяг мила Тоді річний виторг Rскладе: (тис. руб.). Відповідь: 1 млн. руб. Знайти величину тиску води на прямокутник, вертикально занурений у воду, якщо відомо, що його основа дорівнює 8 м, висота 12 м, верхня основа паралельно поверхні води і знаходиться на глибині 5 м. Рішення:
5 м 8 м х
dx 12 м кГм. Відповідь: Картка №2 (додаткова)
Виробничі потужності дозволяють підприємству «Лінотрон» випускати трохи більше 600 тонн вати на рік. Залежність величини сукупних витрат Зв'язок між річним обсягом продажів вати, який збігається з обсягом річного виробництва, та ціною на вату Р(В тис. рублів за тонну) описується функцією Ціна на вату встановлюється 1 січня 1995 року та переглядається лише 1 січня наступного року. Знайдіть з точністю до 1% рентабельність виробництва з витрат, якщо за 1995 підприємство отримає максимально можливий прибуток. Рішення:
Використовуючи залежності у у a 0b c x a 0b c x
Інтегральне обчислення виникло у зв'язку з вирішенням завдань визначення площ та обсягів. За 2000 років до н. жителі Єгипту та Вавилону вже вміли визначати приблизно площу кола і знали правило для обчислення обсягу усіченої піраміди. Теоретичне обґрунтування правил обчислення площ та обсягів уперше з'явилися у давніх греків. Філософ-матеріаліст Демокріт в V віці до н.е. розглядає тіла, які складаються з великої кількості малих частинок. Тобто конус є безліч дуже тонких циліндричних дисків різних радіусів. Величезну роль історії інтегрального обчислення зіграла завдання квадратуру кола(квадратура кола – побудова квадрата, площа якого дорівнює площі даного кола). Точну квадратуру кількох криволінійних постатей знайшов Гіппократ (середина V століття). Першим відомим методом для обчислення інтегралу є метод вичерпання Евдокса (приблизно 370 до н.е.). Він намагався знайти площі та обсяги, розриваючи їх на безліч частин, для яких площа чи обсяг вже відомий. Цей метод був підхоплений та розвинений Архімедом, використовувався для розрахунку площ парабол та наближеного розрахунку площі кола.У своєму творі "Квадратура параболи" Архімед користується методом вичерпування для обчислення площі сектора параболи. Тобто. Архімед вперше складає суми, які нашого часу називають інтегральними сумами. Перші значні спроби розвитку інтеграційних методів Архімеда, що увінчалися успіхом, були зроблені в XVII столітті, коли, з одного боку, було досягнуто значних успіхів у галузі алгебри, з другого боку – дедалі інтенсивніше розвивалися економіка, техніка, природознавство, а там були потрібні великі і глибокі методи вивчення і обчислення величин. При обчисленні площі криволінійної трапеціїНьютон і Лейбніц приходять до поняттяпервісної (або примітивної) функції для даної похідної функціїf(х),деЗмогло бути будь-яким. Тадо званої сьогодні
Роботи з дослідження основ диференціального та інтегрального обчислень починаються у XIX столітті працями О. Коші та Б. Больцано. Тоді ж у розвиток інтегрального обчислення зробили значний внесок російські вчені-математики М.В. Остроградський, В.Я. Буняковський, В.Я. Чебишів. Це був час, коли сучасний математичний аналіз лише створювався. Це була, мабуть, єдина за своєю інтенсивністю епоха математичної творчості, а Ейлер об'єднав великий, але розрізнений матеріал нового аналізу цілу науку. З часом, людина набувала все більшої влади над природою, але мрія про політ до зірок залишалася такою ж нездійсненною. Письменники-фантасти згадували ракети реалізації космічного польоту. Однак ці ракети були технічно невиправданою мрією. Честь відкрити людям дорогу до зірок випала частку нашого співвітчизника К. Е. Ціолковського. Над завданнями створення штучного супутника Землі, розрахунків траєкторії виходу їх у орбіту працювала ціла плеяда вчених, на чолі з С.П. Корольовим. Особливо цікавими є завдання, які є прообразом завдань на розрахунки траєкторій виходу космічних апаратів на задану орбіту, на знаходження висоти та швидкості підйому або спуску тіла та деякі інші завдання з використанням інтегрального обчислення. Завдання 1. Швидкість прямолінійного руху тіла задана рівнянням. Знайти рівняння шляху S, якщо за час t = 2сек тіло пройшло 20м. Рішення: При польоті в космос, треба врахувати всі фактори навколишнього середовища, і щоб потрапити куди потрібно, потрібно розрахувати траєкторію руху, використовуючи вихідні дані. Все це потрібно зробити перед тим, як відбудеться політ.2016 року виповнюється 55 років від дня польоту на орбіту першого космонавта Юрія Олексійовича Гагаріна. При розрахунках доводилося вирішувати такі завдання. Завдання 2. Необхідно запустити ракету вагою Р = 2 · 10 4 Н (Т)з поверхні Землі на висотуh= 1500 км.Обчислити роботу необхідну її запуску. Рішення.f – сила тяжіння тіла Землею є функція від його відстані хдо центру Землі: , де На поверхні Землі де сила тяжіння дорівнює вазі тіла Р, а х = R- радіус Землі, тому При підйомі ракети з поверхні Землі на висоту hзмінна хзмінюється відx
= Rдо x=
R+
h. Шукану роботу знаходимо за формулою: Завдання 3. Сила в 10 Нрозтягує пружину на 2 см. Яку роботу вона чи здійснює при цьому? Рішення
.
За законом Гука, сила F , що розтягує пружину, пропорційна розтягуванню пружини, тобто.F =кх.З умови завдання до= 10/0,02(Н/м),то F= 500х. Робота: Завдання 4. З шахти глибиноюl= 100 мтреба підняти рівномірно кліти вагою Р 1 = 10 4
Н, що висить на канаті, намотаний на барабан. Обчислити повну роботу А повно, необхідну для підняття кліті, якщо вага одного погонного метра каната Р 2= 20Н.
Рішення
.
Робота з підняття кліті: а підняття каната пропорційна вазі каната, тобто. Завдання 5. Ресора прогинається під дією сили 1,5 · 10 4 Нна 1см. Яку роботу треба витратити на деформацію ресори на 3 см? (Деформуюча сила пропорційна прогину ресори.) Рішення
.
F=кх,де х- прогин ресори. При х = 0,01ммаємо: Складний і небезпечний підйом у космічний простір, але не менших труднощів таїть повернення на Землю, коли апарат космічного корабля повинен приземлитися зі швидкістю не більше 2 м/с. Тільки в цьому випадку апарат, прилади в ньому, а головне члени екіпажу, не зазнають різкого жорсткого удару. Костянтин Едуардович Ціолковський вирішив використати гальмування космічного корабля повітряною оболонкою Землі. Рухаючись із швидкістю 8 м/с, космічний апарат не падає на Землю. Перша стадія спуску – включення на короткий час гальмівного двигуна. Швидкість зменшується на 0,2 км/с і відразу починається спуск. Розглянемо приклад розв'язання задачі на складання закону руху за заданих умов. Завдання 6. Знайти закон руху вільно падаючого тіла при постійному прискоренні g, якщо в момент руху тіло перебувало у спокої. Рішення:Відомо, що прискорення прямолінійно рухомого тіла є другою похідною шляху S за часом t , або похідна від швидкості за часом t: але, отже, звідки. Інтегруємо: , і З умови: , звідки знайдемо і швидкість руху: . Знайдемо закон руху тіла: , або . Інтегруємо: , . За початковими умовами: звідки знайдемо Маємо рівняння руху падаючого тіла: - це знайома формула фізики. Завдання 7. Тіло кинуто вертикально вгору з початковою швидкістю Знайти рівняння руху цього тіла (опір повітря знехтувати). Рішення:Приймемо: напрямок по вертикалі вгору – за позитивне, а прискорення сили тяжіння, як спрямоване вниз, – за негативне. Маємо: , звідки . Інтегруємо: то . Т.к. і то З 1: Наступний приклад показує розрахунок траєкторії скидання відпрацьованих секцій, непотрібних приладів, матеріалів. У цьому випадку їх відправляють на Землю, розрахувавши орбіту так, щоб при проходженні через атмосферні шари вони згоріли, а залишки, що не згоріли, впали на Землю (найчастіше - в океан), не завдавши при цьому шкоди. Завдання 8. Скласти рівняння кривої, що проходить через точку М (2; -3) і має дотичну з кутовим коефіцієнтом .
Рішення:За умови завдання дано: Будівельникам іноді доводиться вирішувати завдання з обчислення площ незвичайних фігур, котрим немає загальновідомих формул. І тут знову рятують інтеграли.
.
Космонавти та вчені, працюючи на орбітальній станції, для чистоти експерименту вирішують та досліджують багато питань астрономії, фізики, хімії, медицини, біології тощо. Супроводимо наступне завдання літературним прикладом. У відомому фантастичному романі Герберта Уеллса «Війна світів» описується напад марсіан на планету Земля, які вирішили розширити свої перенаселені території рахунок захоплення наших, т.к. Кліматичні умови Землі були відповідними. Почалося захоплення території та знищення землян, які отримали допомогу звідти, звідки зовсім не очікували. Наші «рідні» бактерії, з якими ми вже навчилися боротися, потрапивши в організм марсіан з повітрям, їжею, водою, знайшли в ньому сприятливе середовище для свого розвитку та розмноження, швиденько адаптувалися і, знищивши марсіан, позбавили Землю загарбників. Розглянемо розв'язання задачі, що дає уявлення про це. Завдання 10.Швидкість розмноження деяких бактерій пропорційна кількості бактерій, наявних в даний час t. Кількість бактерій потроїлася протягом 5год. Знайти залежність кількості бактерій від часу. Рішення:Нехай x (t ) є кількість бактерій у момент часу t, а початковий момент тоді швидкість їх розмноження. За умовою маємо: або слід. У знаменитому романі О.М. Толстого «Гіперболоїд інженера Гаріна» хотілося б відчути, відчути, що це таке – гіперболоїд? Які у нього розміри, форма, поверхня, об'єм? Наступне завдання – про це. Рішення.Використовуємо формулу для обчислення об'єму тіл обертання навколо осі ОХ за допомогою певного інтеграла: Завдання 12. Обчислити об'єм тіла, утвореного обертанням навколо осі ОХ площі, обмеженою лініями у = х 2 - 9і у = 0.
Економічний зміст певного інтегралу виражає обсяг виробленої продукції за відомої функції f(t ) - продуктивність праці в момент t . Тоді обсяг продукції за проміжок обчислюється за формулою Розглянемо приклад для підприємства. Завдання 13. Знайти обсяг продукції, виробленої за 4 роки, якщо функція Кобба-Дугласа має вигляд Рішення. Обсяг виробленої підприємством продукції дорівнює: Підбиваючи підсумки можна дійти невтішного висновку, що застосування інтегралу розкриває великі можливості. При вивченні геометрії розглядають обчислення площ плоских фігур обмежених відрізками прямих (трикутників, паралелограмів, трапецій, багатокутників) та обсягів тіл, отриманих при їх обертанні. Певний інтеграл дозволяє обчислювати площі складних фігур, обмежених будь-якими кривими лініями, а також знаходити об'єми тіл, які отримують при обертанні криволінійних трапецій навколо осі. Також хочеться відзначити, що застосування певного інтегралу не обмежується лише обчисленням різних геометричних величин, але використовується і при вирішенні завдань з різних галузей фізики, аеродинаміки, астрономії, хімії та медицини, космонавтики, а також економічних завдань. Список літератури:
Слайд 2 Історія поняття інтеграла тісно пов'язані з завданнями перебування квадратур, тобто. завданнями на обчислення площ. Обчисленнями площ поверхонь та обсягів тіл займалися ще математики Стародавньої Греції та Риму. Першим європейським математиком, який отримав нові формули для площ фігур та обсягів тіл, був знаменитий астроном І. Кеплер. Після досліджень низки вчених (П.Ферма, Д.Валліса) І. Барроу відкрив зв'язок між завданнями відшукання площ та проведенням дотичної (тобто між інтегруванням та диференціюванням). Дослідження зв'язку між цими операціями, вільне від геометричної мови, було дано І. Ньютоном і Г. Лейбніцем. Сучасне позначення інтеграла перегукується з Лейбницу, в якого воно висловлювало думку, що площа криволінійної трапеції є сума площ нескінченно тонких смужок шириною d і висоти f(x). Сам знак інтеграла є стилізованою латинською літерою S(summa). Символ інтеграла запроваджено з 1675р., а питаннями інтегрального обчислення займаються з 1696р. Хоча інтеграл вивчають, переважно, ученые–математики, а й фізики зробили свій внесок у цю науку. Майже жодна формула фізики не обходиться без диференціального та інтегрального обчислень. Слайд 3 Багато значних досягнень математиків Стародавню Грецію у вирішенні завдань перебування площ, і навіть обсягів тіл пов'язані з ім'ям Архімеда(287-212 до зв. е.) Розвиваючи ідеї попередників Архімед визначив довжину кола і площу кола, обсяг і поверхню кулі. У роботах «Про кулю і циліндр», «Про спіралі», «Про коноїди та сфери», він показав, що визначення обсягів кулі, еліпсоїда, гіперболоїда та параболоїда обертання зводиться до визначення обсягу конуса та циліндра. Архімед розробив і застосував методи, що передбачили створене XVII в. інтегральне обчислення. Потрібно було понад півтори тисячі років, перш ніж ідеї Архімеда знайшли чітке вираження і були доведені до обчислення. У XVII ст. математики вже вміли обчислювати площі багатьох постатей із кривими кордонами та обсяги багатьох тіл. А загальна теорія була створена у другій половині XVII ст. у працях великого англійського математика Іссака Ньютона (1643-1716) та великого німецького математика Готфріда Лейбніца (1646-1716). Ньютон та Лейбніц є засновниками інтегрального обчислення. Вони відкрили важливу теорему, яка носить їхнє ім'я: де f(x) – функція, що інтегрується на відрізку , F(x) – одна з її першорядних. Міркування, які наводили Ньютон і Лейбніц, недосконалі з погляду сучасного математичного аналізу. У XVIII ст. Найбільший представник математичного аналізу Леонард Ейлер ці поняття узагальнив у своїх працях. Тільки на початку ХІХ ст. було остаточно створено поняття інтегрального обчислення. Зазвичай зазначають заслуги французького математика Огюстена Коші і німецького математика Георга Рімана. Саме слово інтеграл придумав Я.Бернуллі (1690). Воно походить від латинського integro, яке перекладається як приводити до колишнього стану, відновлювати. У1696р. з'явилася й назва нової гілки математики – інтегральне числення, яке запровадив І.Бернуллі. Назва, що вживається зараз, первісна функція замінило більш раннє «примітивна функція», яке ввів Лагранж (1797 р.). Позначення певного інтеграла запровадив Йосип Бернуллі, а нижні та верхні межі Леонард Ейлер. Слайд 4 Математичні операції утворюють пари двох взаємно зворотних дій, наприклад, додавання та віднімання, множення і розподіл, зведення в цілий позитивний ступінь та вилучення кореня. Диференціювання дає можливість заданої функції F(х) знаходити її похідну F´(х). Існує дія, зворотне диференціювання - це інтегрування - знаходження функції F(х) за відомою її похідною f(x) = F'(х) або диференціалу f(x)dx. Функція F(х) називається першоподібною для функції f(x), якщо F'(х) = f(x) або dF(x)=f(x)dx. то вона має безліч первісних, причому всі її первісні містяться у виразі F(х) +С, де С - постійна. Невизначеним інтегралом від функції f(x)(або від виразу f(x)dx) називається сукупність її первісних. Позначення ∫f(x)dx = F(х) +С. Тут ∫ – знак інтеграла, f(x) – підінтегральна функція, f(x)dx – підінтегральний вираз, х – змінна інтегрування. Знаходження невизначеного інтеграла називається інтегруванням функції. Властивості невизначеного інтеграла Похідна від невизначеного інтеграла дорівнює підінтегральної функції: (∫ f(x)dx)´ = f(x) Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу: d (∫ f(x)dx) = f(x) dx Інтеграл від диференціала першоподібної дорівнює найпершою і додатковому доданку С:∫d (F(x)) = F(х) +С Постійний множник можна виносити за знак невизначеного інтеграла: ∫a f(x) dx =a ∫f(x) dx Інтеграл від алгебраїчної суми кінцевого числа функцій дорівнює сумі алгебри інтегралів від доданків: ∫ dx = ∫ dx ± ∫ dx Слайд 5 Поняття певного інтегралу виводиться через криволінійну трапецію. Криволінійною трапецією називається фігура, обмежена лініями y = f(x), y = 0, x=a, x=b. Площа криволінійної трапеції виражається інтегральною сумою або числом, яке називається певним інтегралом. Певний інтеграл обчислюється за формулою Ньютона Лейбніца. = F(x)|ba= F(b) – F(a) Спільність позначення певного та невизначеного інтегралів підкреслює тісний зв'язок між ними: певний інтеграл – це число, а невизначений інтеграл – сукупність первісних функцій. Зв'язок між певним та невизначеним інтегралом виражається формулою Ньютона – Лейбніца. Властивості певного інтеграла: Якщо верхній і нижній межі інтегрування поміняти місцями, певний інтеграл збереже абсолютну величину, але змінить свій знак на протилежний. Якщо верхня та нижня межі інтегрування рівні, то певний інтеграл дорівнює нулю. Якщо відрізок інтегрування розбити на кілька частин, певний інтеграл на відрізку дорівнюватиме сумі певних інтегралів цих відрізків. Певний інтеграл від суми функцій, заданих на відрізку, дорівнює сумі певних інтегралів від доданків. Постійний множник підінтегральної функції можна виносити за знак певного інтеграла. Оцінка певного інтеграла: якщо m ≤ f(x) ≤ M на , то m (b – a) Слайд 6 Нехай функція y=f(x) безперервна на відрізку і f(x) ≥ 0. Фігура, обмежена графіком АВ функції y=f(x), прямими x=a, x=b та віссю Ох (див. рисунок), називається криволінійною трапецією. Інтегральна сума та її доданки мають простий геометричний зміст: добуток дорівнює площі прямокутника з основою і висотою, а сума являє собою площу заштрихованої ступінчастої фігури, зображеної на малюнку. Очевидно, що ця площа залежить від розбиття відрізка на часткові відрізки та вибору кількості точок розбиття. Що менше ∆ х, то площа ступінчастої фігури ближче до площі криволінійної трапеції. Отже, за точну площу S криволінійної трапеції приймається межа інтегральної суми. Таким чином, з геометричної точки зору, певний інтеграл від невід'ємної функції чисельно дорівнює площі відповідної криволінійної трапеції. Слайд 7 1. Безпосереднє інтегрування Безпосереднім інтегруванням називається обчислення невизначених інтегралів шляхом приведення їх до табличних із застосуванням основних властивостей. Тут можуть бути такі випадки: 1) даний інтеграл береться безпосередньо за формулою відповідного табличного інтеграла; 2) даний інтеграл після застосування властивостей наводиться до одного або кількох табличних інтегралів; 3) даний інтеграл після елементарних тотожних перетворень над підінтегральною функцією та застосуванням властивостей наводиться до одного або кількох табличних інтегралів. 2. Інтегрування методом заміни змінної (спосібом підстановки) Заміна змінної в невизначеному інтегралі проводиться за допомогою підстановок двох видів: х = φ(t), де φ(t) – монотонна, безперервно диференційована функція нової змінної t. Формула заміни змінної у разі має вигляд ∫f(x) = ∫f [φ (t)] φ΄ (t) d(t); 2) u = ψ(x), де u – нова змінна. Формула заміни змінної за такої підстановки: ∫f [ψ(х)] ψ ΄(х) d(х) = ∫f(u) du 3. Інтегрування частинами Інтегруванням частинами називається знаходження інтеграла за формулою ∫udv = uv - ∫ v du, де u = φ(x), v = ψ(х) – безперервно диференційовані функції від х. З допомогою цієї формули знаходження інтеграла ∫udv зводиться до пошуку іншого інтеграла ∫v du; її застосування доцільно у випадках, коли останній інтеграл або простіше вихідного, або подібний. При цьому за u береться така функція, яка при диференціюванні спрощується, а за dv - та частина підінтегрального виразу, інтеграл від якого відомий або може бути знайдений. Слайд 8 Слайд 9 Як знайти площі зображених фігур? Слайд 10 Слайд 11 Крім цього, певний інтеграл використовується для обчислення площ плоских фігур, обсягів тіл обертання, довжин дуг кривих. Слайд 12 Нехай задано тіло об'ємом V, причому є така пряма, що, яку б площину, перпендикулярну до цієї прямої, ми не взяли, нам відома площа S перерізу тіла цією площиною. Але площина, перпендикулярна до осі Ох, перетинає її в деякій точці х. Отже, кожному числу х (з відрізка [а; b]) поставлене у відповідність однину S (х) - площа перерізу тіла цією площиною. Тим самим було на відрізку [а; b] задана функція S(x). Якщо функція S неперервна на відрізку [а; b] то справедлива формула: Слайд 13 Знайдіть площу зображених фігур 1 – 5. Відповіді: 1) S = 2/3 (парність функції); 2) S = 1 (площа прямокутного трикутника); 3) S = 4 (рівність фігур); 4) S = 2π (площа півкола); 5) S = 1 (площа трикутника). Слайд 14 Знайти суму площ нескінченної кількості фігур, що заштриховані на малюнках. (Аргумент кожної наступної функції збільшується у 2 рази) Цікаве завдання! Відповідь: sin nx = 0; x=π/n; де n = 1,2,4,8,16 ...; S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4 Відповідь: 4. Слайд 15 Вірні відповіді: I варіант: 2,3,1; ІІ варіант: 2,4,2. Слайд 16 Обчисліть площу фігури, обмежену лініями (схематично зобразивши графіки функцій). 1) y = 6 + x - x2 і y = 6 - 2x; 2) y = 2x2 і y = x + 1; 3) y = 1 - x і y = 3 - 2x - x2; 4) y = x2 та y = . Відповідь: 1) 4,5; 2) 9/8; 3) 4,5; 4) 1/3. Слайд 17 Знайдіть об'єм тіла, отриманого при обертанні навколо осі абсцис фігури, обмеженої лініями: 1) y = x2 + 1, x = 0, x = 1, y = 0; 2) y = x = 1 x = 4 y = 0; 3) y = 2x, y = x + 3, x = 0, x = 1; 4) y = x + 2, y = 1, x = 0, x = 2; 5) у2 - 4 х = 0, х - 2 = 0, х - 4 = 0, у = 0; 6) у2 - х + 1 = 0, х - 2 = 0, у = 0; 7) y = - x2 + 2х, у = 0; 8) у2 = 2 х, х - 2 = 0, у = 0; 9) y = , x = 3, y = 0; 10) у = 1 - x2, у = 0. Відповідь: 1); 2) 7,5 ; 3) 11; 4) 16 ⅔; 5) 24 ; 6) /2; 7) 16/15; 8) 4 ; 9) 2 ; 10) 16/15. Слайд 18 Знайти площу фігури, обмеженої лініями 2) Фігура, обмежена лініями y=x+6, x=1, y=0 ділиться параболою y=x2+2x+4 на частини. Знайти площу кожної частини. 3) Знайти ту первісну F(x) функції f(x)=2x+4, графік якої стосується прямої у=6х+3. Обчислити площу фігури, обмеженою графіком знайденої первісної і прямими у=6х+3 і у=0. Слайд 19 Яка дія називається інтегруванням? Яка функція називається первісною для функції f(x)? Чим відрізняються одна від одної різні первісні функції цієї функції f(x)? Дайте визначення невизначеного інтегралу. Як перевірити результат інтегрування? Чому дорівнює похідна від невизначеного інтегралу? Чому дорівнює ∫ d(lnx8 – sin 3x)? Перерахуйте методи інтегрування. Дайте визначення певного інтегралу. Сформулюйте теорему Ньютона Лейбніца. Перелічіть властивості певного інтегралу. Як обчислити площу плоскої фігури за допомогою інтегралу (складайте словесний алгоритм)? Перерахуйте сфери застосування інтеграла, назвіть величини, які можна обчислити за допомогою інтеграла. Слайд 20 1) Обчислити площу фігури, обмеженої даними лініями: y=x2 при x0, y=1, y=4, x=0 Рішення: Дана фігура симетрична криволінійної трапеції, обмеженої прямими х=1, х=4, у=0, графіком функції, зворотної у = х2, x0. Тому ці фігури мають рівні площі і 2) Знайти площу фігури, обмеженої прямими у=3х+1, у=9-х, у=х+1. Рішення: Вершини отриманого ABC мають координати: А(0;1), В(2;7), С(4;5). Можна помітити, що ABC - прямокутний (твір кутових коефіцієнтів прямих у=х+1 у=9-х дорівнює -1). Тому застосування інтегралу для обчислення S(ABC) не є раціональним. Її завжди можна знайти як різницю площ трикутників, у яких відомі висота і основа або можна використовувати координатний метод. Слайд 21 Знайти площі фігур, обмежених лініями (1-7) у = х2 (х 0), у = 1, у = 4, х = 0 у = х2-4х +8, у = 3х2-х3, якщо х [-2 ;3] у=х2-4х+sin2(x/2), y=-3-cos2(x/2), якщо х у=3х+1, у=9-х, у=х+1 у=| x-2|, x|y|=2;x=1;x=3 y= arcsin x; у = 0; x = 0,5; x=1 При якому значенні а пряма х=а ділить площу фігури, обмеженою лініями у=2/х; х = 1; х=3 щодо 1:3? Обчислити виходячи з його геометричного змісту. Слайд 22 Н. А. Колмогоров, «Алгебра та початку аналізу», Москва, Просвітництво, 2000р. М. І. Башмаков, «Алгебра та початку аналізу», Москва, ДРОФА, 2002р. Ш.А.Алімов, «Алгебра та початку аналізу», 11 кл., Москва, ДРОФА, 2004р. Л. В. Кисельова, Посібник з математики для студентів медичних училищ та коледжів, Москва, ФГОУ «ВУНМЦ Росздрава», 2005р. http://www.nerungri.edu.ru http://tambov.fio.ru http://www.zachetka.ru http://edu.of.ru http://festival.1september.ru
Переглянути всі слайдиВизначення та властивості інтегралу
Інтегрування
Криволінійна трапеція
Список літератури
Подібні документи
Основна перевага ехокардіографічного дослідження (ЕхоКГ) полягає в тому, що неінвазивно в реальному режимі часу можна оцінити розміри та рух серцевих структур, отримати характеристики внутрішньосерцевої гемодинаміки, визначити тиск у камерах серця та легеневої артерії. Доведено хорошу сумісність результатів ЕхоКГ-дослідження з даними, отриманими при катетеризації серця.
ЕхоКГ-дослідження дозволяє не тільки виявити наявність легеневої гіпертензії, але й виключити низку захворювань, що є причиною вторинної легеневої гіпертензії: вади мітрального клапана, вроджені вади серця, дилатаційна кардіоміопатія, хронічний міокардит.Картка № 7
 – час, який потрібний катеру на шлях від 1-го корабля до 2-го.
– час, який потрібний катеру на шлях від 1-го корабля до 2-го. км від Про; в момент прибуття катера на другий корабель, відстань між ним і Продорівнювало км; шлях катера дорівнює
км від Про; в момент прибуття катера на другий корабель, відстань між ним і Продорівнювало км; шлях катера дорівнює  . Тоді за теоремою Піфагора
. Тоді за теоремою Піфагора .
.


 ;
; 
 ;
; 
Картка № 5
![]()
 А R
У
А R
У


 dy
Н
dy
Н

О х х
 . Знайдемо параметр а.
. Знайдемо параметр а.
 ,
,
 , отже
, отже  .
.
 .
.
 тоді
тоді  , тобто. вага шару рідини дорівнює
, тобто. вага шару рідини дорівнює 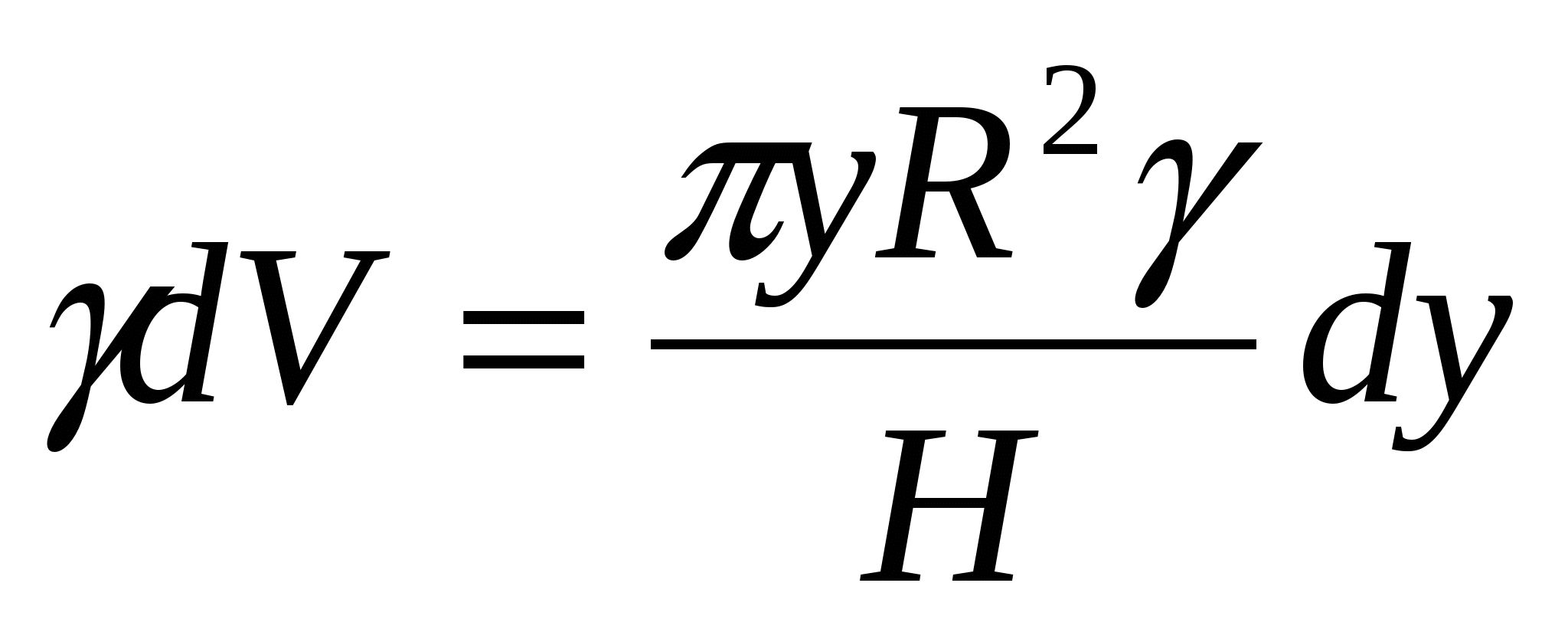 .
.
 , потрібно витратити елементарну роботу
, потрібно витратити елементарну роботу  ,
,  . Тоді
. Тоді тоді.
тоді. .
.
Картка № 6
 , k - Коефіцієнт пропорційності.
, k - Коефіцієнт пропорційності. , отже
, отже  .
.
 .
.
Картка № 8
 .
.
 , отже
, отже  .
.
 .
.
Картка № 9
 відштовхує заряд
відштовхує заряд  (того ж знака), що знаходиться від нього на відстані r, виражається формулою
(того ж знака), що знаходиться від нього на відстані r, виражається формулою ,
,
 з точки
з точки  , віддаленої від
, віддаленої від  на відстані
на відстані  , в точку
, в точку  , віддалену від
, віддалену від  на відстані
на відстані  вважаючи, що заряд
вважаючи, що заряд  поміщений у точці
поміщений у точці  , прийнятої початку відліку.
, прийнятої початку відліку. ,
,  . Тоді
. Тоді .
.
 отримаємо
отримаємо  .
.
 .
.
Картка № 3
 ,
,  - Питома вага рідини.
- Питома вага рідини.Про

 .
.

 ,
,
 ,
,
 ,
,

 .
.
 ;
;
 9,81 н
9,81 нКартка № 4
 м/с. Знайти шлях s, пройдений точкою за час Т= 8 с після початку руху. Чому дорівнює середня швидкість руху за цей проміжок?
м/с. Знайти шлях s, пройдений точкою за час Т= 8 с після початку руху. Чому дорівнює середня швидкість руху за цей проміжок? , отже
, отже  ,
,  ,
,  .
.
 .
.
 .
.
 (у тис. рублів на тонну) на Мухинському миловарному заводі змінюються залежно від обсягу річного випуску Q(у тоннах) згідно із законом:
(у тис. рублів на тонну) на Мухинському миловарному заводі змінюються залежно від обсягу річного випуску Q(у тоннах) згідно із законом: .
.
 .
.
 .
.
 .
.
 ,
,  .
.



 ;
;
 .
.
 т, тоді ціна
т, тоді ціна  (Тис. руб. / Т).
(Тис. руб. / Т).Картка № 10
 ,
,  ,
,  м.
м. .
.
 кГм.
кГм. (У тис. рублів) від річного обсягу виробництва Q(у тоннах) має вигляд
(У тис. рублів) від річного обсягу виробництва Q(у тоннах) має вигляд .
.
 і , висловимо.
і , висловимо.











![]() формулаНьютона-Лейбніца дозволяє зводити досить складне обчислення певних інтегралів, тобто. знаходження меж інтегральних сум, до порівняно простий операції відшукання первісних.Лейбницю належить символ диференціалуа п пізніше з'явився і символ інтегралаСимвол певного інтегралуувів Ж. Фур'є, а термін «інтеграл» (від латинського integer - цілий) було запропоновано І. Бернуллі.
формулаНьютона-Лейбніца дозволяє зводити досить складне обчислення певних інтегралів, тобто. знаходження меж інтегральних сум, до порівняно простий операції відшукання первісних.Лейбницю належить символ диференціалуа п пізніше з'явився і символ інтегралаСимвол певного інтегралуувів Ж. Фур'є, а термін «інтеграл» (від латинського integer - цілий) було запропоновано І. Бернуллі.![]() звідки
звідки ![]() Інтегруємо:
Інтегруємо: ![]() звідки
звідки ![]() Використовуючи дані, знайдемо С = 4. Тобто. рівняння руху тіла має вигляд
Використовуючи дані, знайдемо С = 4. Тобто. рівняння руху тіла має вигляд ![]() .
.
 Тоді отримуємо: робота для запуску ракети дорівнює
Тоді отримуємо: робота для запуску ракети дорівнює ![]()
 .
.
 Отже, повна робота повна:
Отже, повна робота повна:![]() . Тоді робота для деформації дорівнює:
. Тоді робота для деформації дорівнює:
![]() і рівняння швидкості: Знаходимо закон руху тіла: т.к. і тоді
і рівняння швидкості: Знаходимо закон руху тіла: т.к. і тоді ![]() звідки
звідки ![]() .Інтегруємо:
.Інтегруємо: ![]() або
або ![]() При і знайдемо
При і знайдемо ![]() , і маємо рівняння руху тіла: або .
, і маємо рівняння руху тіла: або .![]() або
або ![]() Інтегруючи, маємо:
Інтегруючи, маємо: ![]() При х = 2і у = -3, С = - 5, а траєкторія руху має вигляд:
При х = 2і у = -3, С = - 5, а траєкторія руху має вигляд: ![]() .
.
 Завдання 9. Обчислити площу фігури, обмежену лініями: і
Завдання 9. Обчислити площу фігури, обмежену лініями: і Рішення: Виконаємо побудову креслення (рис. 1), для чого вирішимо систему рівнянь. Знайдемо точки перетину ліній: А(-2;4) та В(4;16). Шукана площа є різницею площ з межами інтегрування, а = х 1 = -2і в = х 2 = 4.Тоді маємо площу:
Рішення: Виконаємо побудову креслення (рис. 1), для чого вирішимо систему рівнянь. Знайдемо точки перетину ліній: А(-2;4) та В(4;16). Шукана площа є різницею площ з межами інтегрування, а = х 1 = -2і в = х 2 = 4.Тоді маємо площу:![]() Знайдемо З: і функція Відомо, що. або звідки коефіцієнт пропорційності дорівнює: а функція має вигляд:
Знайдемо З: і функція Відомо, що. або звідки коефіцієнт пропорційності дорівнює: а функція має вигляд: ![]() .
.
 Завдання 11.Гіпербола, обмежена лініями: у = 0, х =
aх = 2аобертається навколо осі ОХ. Знайти обсяг отриманого гіперболоїда (рис.2).
Завдання 11.Гіпербола, обмежена лініями: у = 0, х =
aх = 2аобертається навколо осі ОХ. Знайти обсяг отриманого гіперболоїда (рис.2).
 Вчені-уфологи займаються вивченням фактів, які наводять «очевидці», розповідаючи про те, що бачили космічний корабель, що летить, у вигляді величезного світиться диска («тарілки»), приблизно такої форми як на малюнку 3. Розглянемо розв'язання задачі з визначення обсягу такої «тарілки ».
Вчені-уфологи займаються вивченням фактів, які наводять «очевидці», розповідаючи про те, що бачили космічний корабель, що летить, у вигляді величезного світиться диска («тарілки»), приблизно такої форми як на малюнку 3. Розглянемо розв'язання задачі з визначення обсягу такої «тарілки ». Рішення: При виконанні креслення параболоїда (рис.3) маємо межі інтегрування від х = -3до х = 3. Замінимо межі інтегрування з симетричності фігури щодо осі ОУ на х = 0і х = 3, а результат удвох. Отже, об'єм диска дорівнює:
Рішення: При виконанні креслення параболоїда (рис.3) маємо межі інтегрування від х = -3до х = 3. Замінимо межі інтегрування з симетричності фігури щодо осі ОУ на х = 0і х = 3, а результат удвох. Отже, об'єм диска дорівнює:![]()
Історична довідка
Коротка історія інтегрального обчислення
Невизначений інтеграл
Визначений інтеграл
Геометричний зміст певного інтегралу
Методи інтегрування
Таблиця невизначених інтегралів
Повторення теоретичного матеріалу
Продовжуємо повторювати
Застосування інтегралу
Обчислення обсягів тіл
ПЕРЕВІР СЕБЕ!
Знайди помилку!
Програмований контроль
Самостійна робота
Завдання на обчислення обсягів
Завдання з ЄДІ
Контрольні питання
Для любителів математики
Домашнє завдання
Список літератури


