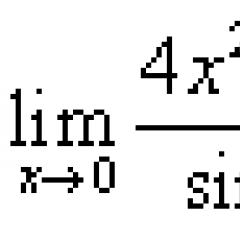Втората забележителна граница. Първата забележителна граница: примери за намиране, проблеми и подробни решения Limit cos 1 x
Има няколко забележителни лимита, но най-известните са първият и вторият забележителни лимити. Забележителното при тези лимити е, че те се използват широко и с тяхна помощ могат да се намерят други лимити, които се срещат в много проблеми. Това ще направим в практическата част на този урок. За да се решат проблемите, като се сведат до първата или втората забележителна граница, няма нужда да се разкриват съдържащите се в тях несигурности, тъй като стойностите на тези граници отдавна са изведени от велики математици.
Първата прекрасна границасе нарича границата на съотношението на синуса на безкрайно малка дъга към същата дъга, изразено в радианова мярка:
Нека да преминем към решаването на проблеми на първата забележителна граница. Забележка: ако има тригонометрична функция под знака за граница, това е почти сигурен знак, че този израз може да бъде намален до първата забележителна граница.
Пример 1.Намерете границата.
Решение. Вместо това заместване хнула води до несигурност:
![]() .
.
Знаменателят е синус, следователно изразът може да бъде приведен до първата забележителна граница. Да започнем трансформацията:
![]() .
.
Знаменателят е синус от три X, но числителят има само едно X, което означава, че трябва да получите три X в числителя. За какво? Да представя 3 х = аи вземете израза.
И стигаме до вариант на първата забележителна граница:
защото няма значение коя буква (променлива) в тази формула стои вместо X.
Умножаваме X по три и веднага разделяме:
 .
.
В съответствие с първото забелязано забележително ограничение, заместваме дробния израз:
Сега най-накрая можем да решим тази граница:
 .
.
Пример 2.Намерете границата.
Решение. Директното заместване отново води до несигурността „нула, разделена на нула“:
![]() .
.
За да получим първата забележителна граница, е необходимо х под знака за синус в числителя и само х в знаменателя да имат еднакъв коефициент. Нека този коефициент е равен на 2. За да направите това, представете си текущия коефициент за x, както е показано по-долу, извършвайки операции с дроби, получаваме:
 .
.
Пример 3.Намерете границата.
Решение. При заместване отново получаваме несигурността „нула, разделена на нула“:
 .
.
Вероятно вече разбирате, че от оригиналния израз можете да получите първата прекрасна граница, умножена по първата прекрасна граница. За да направим това, разлагаме квадратите на x в числителя и синуса в знаменателя на еднакви множители и за да получим еднакви коефициенти за x и синуса, разделяме x в числителя на 3 и веднага умножаваме от 3. Получаваме:
 .
.
Пример 4.Намерете границата.
Решение. Отново получаваме несигурността „нула, разделена на нула“:
![]() .
.
Можем да получим съотношението на първите две забележителни граници. Разделяме и числителя, и знаменателя на x. След това, така че коефициентите за синуси и xes да съвпадат, умножаваме горното x по 2 и веднага разделяме на 2, а долното x умножаваме по 3 и веднага делим на 3. Получаваме:

Пример 5.Намерете границата.
Решение. И отново несигурността на „нула, разделена на нула“:
Спомняме си от тригонометрията, че тангенсът е отношението на синус към косинус, а косинусът на нулата е равен на едно. Извършваме трансформациите и получаваме:
 .
.
Пример 6.Намерете границата.
Решение. Тригонометричната функция под знака на граница отново предполага използването на първата забележителна граница. Представяме го като съотношението на синус към косинус.
Първата забележителна граница често се използва за изчисляване на граници, съдържащи синус, аркуссинус, тангенс, арктангенс и произтичащите несигурности на нула, разделена на нула.
Формула
Формулата за първата забележителна граница е: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Отбелязваме, че за $ \alpha\to 0 $ получаваме $ \sin\alpha \to 0 $, следователно имаме нули в числителя и знаменателя. Следователно формулата на първата забележителна граница е необходима, за да разкрие несигурностите $ \frac(0)(0) $.
За да се приложи формулата, трябва да бъдат изпълнени две условия:
- Изразите, съдържащи се в синуса и знаменателя на дробта, са еднакви
- Изразите в синуса и знаменателя на дроб клонят към нула
внимание! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Въпреки че изразите под синуса и в знаменателя са еднакви, обаче $ 2x ^2+1 = 1 $, при $ x\to 0 $. Второто условие не е изпълнено, така че НЕ МОЖЕТЕ да приложите формулата!
Последствия
Доста рядко в задачите можете да видите чисто първо чудесно ограничение, в което веднага да запишете отговора. На практика всичко изглежда малко по-сложно, но за такива случаи ще бъде полезно да знаете последствията от първото забележително ограничение. Благодарение на тях можете бързо да изчислите необходимите лимити.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Примери за решения
Нека разгледаме първата забележителна граница, примери за нейното решение за изчисляване на граници, съдържащи тригонометрични функции и несигурност $ \bigg[\frac(0)(0)\bigg] $
| Пример 1 |
| Изчислете $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Решение |
|
Нека погледнем границата и забележим, че тя съдържа синус. След това заместваме $ x = 0 $ в числителя и знаменателя и получаваме нулата на несигурността, разделена на нула: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ Вече два знака, че трябва да приложим чудесна граница, но има малък нюанс: не можем веднага да приложим формулата, тъй като изразът под знака синус се различава от израза в знаменателя. И имаме нужда те да бъдат равни. Следователно, използвайки елементарни трансформации на числителя, ние го превръщаме в $2x$. За да направим това, ще извадим двете от знаменателя на дробта като отделен фактор. Изглежда така: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Моля имайте предвид, че в края $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ беше получено съгласно формулата. Ако не можете да разрешите проблема си, изпратете го до нас. Ние ще предоставим подробно решение. Ще можете да видите напредъка на изчислението и да получите информация. Това ще ви помогне да получите оценката си от вашия учител навреме! |
| Отговор |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Пример 2 |
| Намерете $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Решение |
|
Както винаги, първо трябва да знаете вида на несигурността. Ако е нула, разделена на нула, тогава обръщаме внимание на наличието на синус: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Тази несигурност ни позволява да използваме формулата на първата забележителна граница, но изразът от знаменателя не е равен на аргумента на синуса? Следователно формулата не може да се приложи директно. Необходимо е дробта да се умножи и раздели на аргумента на синуса: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Сега записваме свойствата на границите: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Второто ограничение отговаря точно на формулата и е равно към едно: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Заместваме отново $ x = 0 $ в дроб и получаваме несигурността $ \frac(0)(0) $. За да го премахнете, достатъчно е да извадите $ x $ извън скобите и да го намалите с: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Отговор |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Пример 4 |
| Изчислете $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Решение |
|
Нека започнем изчислението със замяната $ x=0 $. В резултат на това получаваме несигурността $ \frac(0)(0) $. Границата съдържа синус и тангенс, което подсказва за възможно развитие на ситуацията, използвайки формулата на първата забележителна граница. Нека трансформираме числителя и знаменателя на дробта във формула и следствие: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Сега виждаме, че в числителя и знаменателя има изрази, които отговарят на формулата и последствията. Аргументът на синуса и аргумента на тангенса са еднакви за съответните знаменатели $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Отговор |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
Статията: „Първата забележителна граница, примери за решения“ говори за случаите, в които е препоръчително да използвате тази формула и нейните последствия.
Първото забележително ограничение е следното равенство:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Тъй като за $\alpha\to(0)$ имаме $\sin\alpha\to(0)$, те казват, че първата забележителна граница разкрива несигурност от формата $\frac(0)(0)$. Най-общо казано във формула (1), вместо променливата $\alpha$, всеки израз може да бъде поставен под знака синус и в знаменателя, стига да са изпълнени две условия:
- Изразите под знака синус и в знаменателя едновременно клонят към нула, т.е. има несигурност от формата $\frac(0)(0)$.
- Изразите под знака синус и в знаменателя са еднакви.
Следствията от първата забележителна граница също често се използват:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \край (уравнение)
На тази страница са решени единадесет примера. Пример № 1 е посветен на доказателството на формули (2)-(4). Примери № 2, № 3, № 4 и № 5 съдържат решения с подробни коментари. Примери № 6-10 съдържат решения практически без коментари, тъй като в предишните примери са дадени подробни обяснения. Решението използва някои тригонометрични формули, които могат да бъдат намерени.
Позволете ми да отбележа, че наличието на тригонометрични функции, съчетани с несигурността $\frac (0) (0)$, не означава непременно прилагането на първата забележителна граница. Понякога са достатъчни прости тригонометрични трансформации - например вж.
Пример №1
Докажете, че $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
а) Тъй като $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, тогава:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Тъй като $\lim_(\alpha\to(0))\cos(0)=1$ и $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Че:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
б) Нека направим промяната $\alpha=\sin(y)$. Тъй като $\sin(0)=0$, тогава от условието $\alpha\to(0)$ имаме $y\to(0)$. В допълнение, има околност на нула, в която $\arcsin\alpha=\arcsin(\sin(y))=y$, така че:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
Равенството $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ е доказано.
в) Нека направим замяната $\alpha=\tg(y)$. Тъй като $\tg(0)=0$, тогава условията $\alpha\to(0)$ и $y\to(0)$ са еквивалентни. В допълнение, има околност на нула, в която $\arctg\alpha=\arctg\tg(y))=y$, следователно, въз основа на резултатите от точка а), ще имаме:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
Равенството $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ е доказано.
Равенствата a), b), c) често се използват заедно с първата забележителна граница.
Пример №2
Изчислете границата $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) ( x+7))$.
Тъй като $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ и $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, т.е. и числителят и знаменателят на дробта едновременно клонят към нула, тогава тук имаме работа с несигурност от формата $\frac(0)(0)$, т.е. Свършен. Освен това е ясно, че изразите под знака синус и в знаменателя съвпадат (т.е. и е изпълнено):
Така че и двете условия, изброени в началото на страницата, са изпълнени. От това следва, че формулата е приложима, т.е. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.
Отговор: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Пример №3
Намерете $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Тъй като $\lim_(x\to(0))\sin(9x)=0$ и $\lim_(x\to(0))x=0$, тогава имаме работа с несигурност от формата $\frac (0 )(0)$, т.е. Свършен. Изразите под знака синус и в знаменателя обаче не съвпадат. Тук трябва да коригирате израза в знаменателя до желаната форма. Трябва изразът $9x$ да бъде в знаменателя, тогава той ще стане верен. По същество пропускаме множител от $9$ в знаменателя, който не е толкова труден за въвеждане – просто умножете израза в знаменателя по $9$. Естествено, за да компенсирате умножението с $9$, ще трябва незабавно да разделите на $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Сега изразите в знаменателя и под знака за синус съвпадат. И двете условия за границата $\lim_(x\to(0))\frac(\sin(9x))(9x)$ са изпълнени. Следователно $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. А това означава, че:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Отговор: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Пример №4
Намерете $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Тъй като $\lim_(x\to(0))\sin(5x)=0$ и $\lim_(x\to(0))\tg(8x)=0$, тук имаме работа с несигурност на формата $\frac(0)(0)$. Въпреки това, формата на първата забележителна граница е нарушена. Числител, съдържащ $\sin(5x)$, изисква знаменател от $5x$. В тази ситуация най-лесният начин е да разделите числителя на $5x$ и веднага да умножите по $5x$. Освен това ще извършим подобна операция със знаменателя, като умножим и разделим $\tg(8x)$ на $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Намалявайки с $x$ и извеждайки константата $\frac(5)(8)$ извън граничния знак, получаваме:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Имайте предвид, че $\lim_(x\to(0))\frac(\sin(5x))(5x)$ напълно удовлетворява изискванията за първата забележителна граница. За намиране на $\lim_(x\to(0))\frac(\tg(8x))(8x)$ е приложима следната формула:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Отговор: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Пример №5
Намерете $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Тъй като $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (не забравяйте, че $\cos(0)=1$) и $\ lim_(x\to(0))x^2=0$, тогава имаме работа с несигурност от формата $\frac(0)(0)$. Въпреки това, за да приложите първата забележителна граница, трябва да се отървете от косинуса в числителя, преминавайки към синуси (за да приложите след това формулата) или тангенси (за да приложите след това формулата). Това може да стане със следната трансформация:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Да се върнем на лимита:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
Дробта $\frac(\sin^2(5x))(x^2)$ вече е близо до формата, необходима за първата забележителна граница. Нека поработим малко с дробта $\frac(\sin^2(5x))(x^2)$, коригирайки я до първата забележителна граница (обърнете внимание, че изразите в числителя и под синуса трябва да съвпадат):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Да се върнем на въпросния лимит:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Отговор: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Пример №6
Намерете границата $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Тъй като $\lim_(x\to(0))(1-\cos(6x))=0$ и $\lim_(x\to(0))(1-\cos(2x))=0$, тогава имаме работа с несигурност $\frac(0)(0)$. Нека го разкрием с помощта на първата забележителна граница. За да направим това, нека преминем от косинуси към синуси. Тъй като $1-\cos(2\alpha)=2\sin^2(\alpha)$, тогава:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Преминавайки към синуси в дадената граница, ще имаме:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Отговор: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Пример № 7
Изчислете ограничението $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ при $\alpha\neq \ бета$.
Подробни обяснения бяха дадени по-рано, но тук просто отбелязваме, че отново има несигурност $\frac(0)(0)$. Нека преминем от косинуси към синуси, използвайки формулата
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Използвайки тази формула, получаваме:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\дясно| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ бета(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x) \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ алфа^2-\бета^2)(2)\cdot(1)\cdot(1) =\frac(\бета^2-\алфа^2)(2). $$
Отговор: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ алфа^2)(2)$.
Пример № 8
Намерете границата $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Тъй като $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (не забравяйте, че $\sin(0)=\tg(0)=0$) и $\ lim_(x\to(0))x^3=0$, тогава тук имаме работа с несигурност от формата $\frac(0)(0)$. Нека го разбием по следния начин:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Отговор: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Пример №9
Намерете границата $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Тъй като $\lim_(x\to(3))(1-\cos(x-3))=0$ и $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, тогава има несигурност от формата $\frac(0)(0)$. Преди да пристъпите към нейното разширяване, е удобно да направите промяна на променливата по такъв начин, че новата променлива да клони към нула (обърнете внимание, че във формулите променливата $\alpha \to 0$). Най-лесният начин е да въведете променливата $t=x-3$. Въпреки това, в името на удобството на по-нататъшните трансформации (тази полза може да се види в хода на решението по-долу), струва си да направите следната замяна: $t=\frac(x-3)(2)$. Отбелязвам, че и двете замени са приложими в този случай, просто втората замяна ще ви позволи да работите по-малко с дроби. Тъй като $x\to(3)$, тогава $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Отговор: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Пример №10
Намерете границата $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2 )$.
Отново имаме работа с несигурност $\frac(0)(0)$. Преди да пристъпите към нейното разширяване, удобно е да направите промяна на променливата по такъв начин, че новата променлива да клони към нула (обърнете внимание, че във формулите променливата е $\alpha\to(0)$). Най-лесният начин е да въведете променливата $t=\frac(\pi)(2)-x$. Тъй като $x\to\frac(\pi)(2)$, тогава $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Отговор: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Пример №11
Намерете границите $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
В този случай не е нужно да използваме първата прекрасна граница. Моля, обърнете внимание, че и първата, и втората граница съдържат само тригонометрични функции и числа. Често в примери от този вид е възможно да се опрости изразът, разположен под знака за граница. Освен това, след гореспоменатото опростяване и намаляване на някои фактори, несигурността изчезва. Дадох този пример само с една цел: да покажа, че наличието на тригонометрични функции под знака за граница не означава непременно използването на първата забележителна граница.
Тъй като $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (не забравяйте, че $\sin\frac(\pi)(2)=1$ ) и $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (нека ви напомня, че $\cos\frac(\pi)(2)=0$), тогава имаме занимаващи се с несигурност от формата $\frac(0)(0)$. Това обаче не означава, че ще трябва да използваме първия прекрасен лимит. За да се разкрие несигурността, достатъчно е да се вземе предвид, че $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Подобно решение има в книгата с решения на Демидович (№ 475). Що се отнася до втората граница, както в предишните примери в този раздел, имаме несигурност от формата $\frac(0)(0)$. Защо възниква? Възниква, защото $\tg\frac(2\pi)(3)=-\sqrt(3)$ и $2\cos\frac(2\pi)(3)=-1$. Ние използваме тези стойности, за да трансформираме изразите в числителя и знаменателя. Целта на нашите действия е да запишем сумата в числителя и знаменателя като произведение. Между другото, често в рамките на подобен тип е удобно да промените променлива, направена по такъв начин, че новата променлива да клони към нула (вижте например примери № 9 или № 10 на тази страница). В този пример обаче няма смисъл от замяна, въпреки че при желание замяната на променливата $t=x-\frac(2\pi)(3)$ не е трудна за изпълнение.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
Както можете да видите, не трябваше да прилагаме първото прекрасно ограничение. Разбира се, можете да направите това, ако желаете (вижте бележката по-долу), но не е необходимо.
Какво е решението, използвайки първата забележителна граница? Покажи скрий
Използвайки първата забележителна граница, получаваме:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\десен))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ дясно))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Отговор: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Събрани са формули, свойства и теореми, използвани при решаването на проблеми, които могат да бъдат решени с помощта на първата забележителна граница. Дадени са подробни решения на примери, използващи първата забележителна граница на неговите последствия.
СъдържаниеВижте също: Доказателство за първото забележително ограничение и неговите последствия
Приложни формули, свойства и теореми
Тук ще разгледаме примери за решения на проблеми, включващи изчисляване на граници, които използват първата забележителна граница и последствията от нея.
По-долу са изброени формулите, свойствата и теоремите, които най-често се използват в този тип изчисления.
- Първото забележително ограничение и неговите последствия:
. - Тригонометрични формули за синус, косинус, тангенс и котангенс:
;
;
;
в , ;
;
;
;
;
;
.
Примери за решения
Пример 1
За това.
1. Изчислете лимита.
Тъй като функцията е непрекъсната за всички x, включително в точката, тогава
.
2. Тъй като функцията не е дефинирана (и следователно не е непрекъсната) за , трябва да се уверим, че съществува пунктирана околност на точката, на която . В нашия случай, при. Следователно това условие е изпълнено.
3. Изчислете границата. В нашия случай той е равен на първата забележителна граница:
.
По този начин,
.
По същия начин намираме границата на функцията в знаменателя:
;
в ;
.
И накрая, прилагаме аритметичните свойства на ограничението на функцията:
.
Да кандидатстваме.
В . От таблицата на еквивалентните функции намираме:
в ; при .
Тогава .
Пример 2
Намерете границата:
.
Решение, използващо първата забележителна граница
В , , . Това е несигурността на формата 0/0 .
Нека трансформираме функцията отвъд граничния знак:
.
Нека направим промяна на променливата. От и за , тогава
.
По същия начин имаме:
.
Тъй като функцията косинус е непрекъсната на цялата числова ос, тогава
.
Прилагаме аритметичните свойства на границите:
.
Решение, използващо еквивалентни функции
Нека приложим теоремата за замяна на функции с еквивалентни в лимита на частното.
В . От таблицата на еквивалентните функции намираме:
в ; при .
Тогава .
Пример 3
Намерете границата:
.
Нека заместим числителя и знаменателя на дробта:
;
.
Това е несигурността на формата 0/0
.
Нека се опитаме да решим този пример, като използваме първата чудесна граница. Тъй като стойността на променливата в него клони към нула, ще направим замяна, така че новата променлива да клони не към , а към нула. За да направим това, преминаваме от x към нова променлива t, като правим заместването , . След това в , .
Първо трансформираме функцията отвъд граничния знак, като умножим числителя и знаменателя на дробта по:
.
Нека заместим и използваме тригонометричните формули, дадени по-горе.
;
;
.
Функцията е непрекъсната при . Намираме неговата граница:
.
Нека трансформираме втората дроб и приложим първата чудесна граница:
.
Направихме заместване в числителя на дробта.
Прилагаме свойството на границата на продукт от функции:
.
Пример 4
Намерете границата:
.
В , , . Имаме несигурност на формата 0/0 .
Нека трансформираме функцията под знака за граница. Нека приложим формулата:
.
Нека заместим:
.
Нека трансформираме знаменателя:
.
Тогава
.
Тъй като и за , правим заместването и прилагаме теоремата за границата на сложна функция и първата забележителна граница:
.
Прилагаме аритметичните свойства на границата на функция:
.
Пример 5
Намерете границата на функцията:
.
Лесно е да се види, че в този пример имаме несигурност на формата 0/0
. За да го разкрием, прилагаме резултата от предишната задача, според който
.
Нека въведем обозначението:
(A5.1). Тогава
(A5.2) .
От (A5.1) имаме:
.
Нека го заместим в оригиналната функция:
,
Където ,
,
;
;
;
.
Използваме (A5.2) и непрекъснатостта на функцията косинус. Прилагаме аритметичните свойства на границата на функция.
,
тук m е различно от нула число, ;
;
;
.
Пример 6
Намерете границата:
.
Когато , числителят и знаменателят на дробта клонят към 0
. Това е несигурността на формата 0/0
. За да го разширим, трансформираме числителя на дробта:
.
Нека приложим формулата:
.
Нека заместим:
;
,
Където .
Нека приложим формулата:
.
Нека заместим:
;
,
Където .
Числител на дроб:
.
Функцията зад знака за ограничение ще приеме формата:
.
Нека намерим границата на последния фактор, като вземем предвид неговата непрекъснатост при :
.
Нека приложим тригонометричната формула:
.
Да заместим
. Тогава
.
Нека разделим числителя и знаменателя на , приложим първото забележително ограничение и едно от неговите последствия:
.
Накрая имаме:
.
Бележка 1: Можете също да приложите формулата
.
Тогава .
|
Първата забележителна граница. Извеждането на първата забележителна граница представлява интерес от гледна точка на приложението на теорията за границите и затова ви я предлагаме почти цялата. Нека разгледаме поведението на функцията |
След това ясно зоната DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
S D MOA = 
S MOA =  =
= S D C OA =
S D C OA = 
Връщайки се към споменатото неравенство и удвоявайки го, получаваме:
грях х < х < tg х.
След разделяне по срок грех х:
 или
или 
Тъй като  , след това променливата
, след това променливата  се сключва между две количества, които имат еднаква граница, т.е. , въз основа на теоремата за границата на междинната функция от предходния параграф, имаме:
се сключва между две количества, които имат еднаква граница, т.е. , въз основа на теоремата за границата на междинната функция от предходния параграф, имаме:
-първата прекрасна граница .
Пример.Изчислете границите на функциите, като използвате първата забележителна граница:





Отговор. 1) 1, 2) 0, 3)

Упражнение:Изчислете границата на функция, като използвате първата забележителна граница:

Отговор: -2.
Втората забележителна граница.
За да изведем втората забележителна граница, въвеждаме дефиницията на числото д:
Определение.
Променлива граница  при
при  нарече номерд
:
нарече номерд
:
- Втората прекрасна граница
Номер д– ирационално число. Стойността му до десет истински знака след десетичната запетая обикновено се закръгля до един истински знак след десетичната запетая:
д= 2,7182818284..."2,7.
Теорема. функция  прих
клонящ към безкрайност, клонящ към границатад
:
прих
клонящ към безкрайност, клонящ към границатад
:

Пример.Изчислете границите на функциите:

Решение.
Според свойствата на границите границата на степента е равна на степента на границата, т.е.:


Освен това по подобен начин може да се докаже, че 


Отговор. 1)д 3 , 2)д 2 , 3)д 4 .
Упражнение.Изчислете границата на функцията, като използвате втората забележителна граница:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ОТНОСНО  отговор: e -5
отговор: e -5
Непрекъснатост на функция Непрекъснатост на функция в точка
Определение. функцияf ( х ), х Î ( а ; b ) х О Î ( а ; b ), ако границата на функциятаf ( х ) в точкатах О съществува и е равна на стойността на функцията в тази точка:
 .
.
Според това определение непрекъснатостта на функцията f(х) в точката х Оозначава, че са изпълнени следните условия:
функция f(х) трябва да се определи в точката х О ;
y функция f(х) трябва да има ограничение в точката х О ;
граница на функция f(х) в точката х Отрябва да съответства на стойността на функцията в този момент.
Пример.
функция f(х)
=
х 2
определена на цялата числова ос и непрекъсната в точка х= 1 защото f( 1)
= 1 и 
Непрекъснатост на функция върху множество
Определение. функцияf(x), се нарича непрекъснат на интервала(а; б), ако е непрекъсната във всяка точка от този интервал.
Ако една функция е непрекъсната в дадена точка, тогава тази точка се нарича точка на непрекъснатост на тази функция. В случаите, когато границата на функция в дадена точка не съществува или нейната стойност не съвпада със стойността на функцията в дадена точка, тогава функцията се нарича прекъсната в тази точка, а самата точка се нарича прекъсната. точка на функцията f(x).
Свойства на непрекъснатите функции.
1) Сумата от краен брой функции, непрекъснати в точка а,
2) Произведение на краен брой функции, непрекъснати в точка а,има функция, която е непрекъсната в тази точка.
3) Съотношението на краен брой функции, непрекъснати в точка а,е функция, която е непрекъсната в тази точка, ако стойността на функцията в знаменателя е различна от нула в точката А.
Пример.
функция f(х) = х П, Където н Î н, е непрекъснат на цялата числова ос. Този факт може да бъде доказан с помощта на свойство 2 и непрекъснатостта на функцията f(х) = х.
функция f(х) = sх П (с– константа) е непрекъснат на цялата числова ос, въз основа на свойство 2 и пример 1.
Теорема 1. Полиномът е функция, която е непрекъсната на цялата числова ос.
Теорема 2 . Всяка дробна рационална функция е непрекъсната във всяка точка от своята дефиниционна област.
Пример.

Определение
функцияf
(
х
)
наречено непрекъснато в точках = а
, ако в този момент нарастването му  клони към нула, когато аргументът нараства
клони към нула, когато аргументът нараства  клони към нула, или с други думи: функцияf
(Х)
наречено непрекъснато в точках = а
, ако в този момент безкрайно малко увеличение на аргумента съответства на безкрайно малко увеличение на функцията, т.е. ако
клони към нула, или с други думи: функцияf
(Х)
наречено непрекъснато в точках = а
, ако в този момент безкрайно малко увеличение на аргумента съответства на безкрайно малко увеличение на функцията, т.е. ако 
 при
при  . За да направите това, разгледайте кръг с радиус 1; нека означим централния ъгъл на MOB с х, при което
. За да направите това, разгледайте кръг с радиус 1; нека означим централния ъгъл на MOB с х, при което  .
.