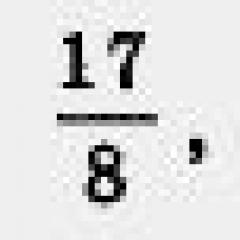Аритметичен квадратен корен и неговите свойства. Корен от n-та степен: дефиниции, нотация, примери Концепцията за корен квадратен от отрицателно число

Пак погледнах табелата... И, да тръгваме!

Да започнем с нещо просто:

Само минутка. това, което означава, че можем да го напишем така:

Схванах го? Ето следващия за вас:

Корените на получените числа не са ли точно извлечени? Няма проблем – ето няколко примера:

Ами ако има не два, а повече множители? Същото! Формулата за умножение на корени работи с произволен брой фактори:

Вече напълно сам:

Отговори:Много добре! Съгласете се, всичко е много лесно, основното е да знаете таблицата за умножение!

Коренно деление

Подредихме умножението на корените, сега нека преминем към свойството на делението.

Нека ви напомня, че общата формула изглежда така:

Което означава, че коренът на частното е равен на частното на корените.

Е, нека да разгледаме някои примери:

Това е цялата наука. Ето един пример:

Всичко не е толкова гладко, колкото в първия пример, но, както виждате, няма нищо сложно.

Ами ако срещнете този израз:

Просто трябва да приложите формулата в обратна посока:

И ето един пример:

Може да срещнете и този израз:

Всичко е същото, само тук трябва да запомните как да превеждате дроби (ако не си спомняте, погледнете темата и се върнете!). Помниш ли? Сега да решим!

Сигурен съм, че сте се справили с всичко, сега нека се опитаме да вдигнем корените до степен.

степенуване

Какво се случва, ако квадратният корен се повдигне на квадрат? Просто е, запомнете значението на корен квадратен от число - това е число, чийто корен квадратен е равен на.

И така, ако повдигнем на квадрат число, чийто квадратен корен е равен, какво получаваме?

Добре, разбира се, !

Нека да разгледаме примери:

Просто е, нали? Ами ако коренът е на различна степен? Всичко е наред!

Следвайте същата логика и запомнете свойствата и възможните действия със степени.

Прочетете теорията по темата "" и всичко ще ви стане пределно ясно.

Например, ето един израз:

В този пример степента е четна, но какво ще стане, ако е нечетна? Отново приложете свойствата на експонентите и факторизирайте всичко:

Всичко изглежда ясно с това, но как да извлечете корена на число на степен? Ето например това:

Доста просто, нали? Ами ако степента е повече от две? Следваме същата логика, използвайки свойствата на степените:

Е, всичко ясно ли е? След това решете сами примерите:

А ето и отговорите:

Влизане под знака на корена

Какво ли не се научихме да правим с корените! Остава само да се упражнявате да въвеждате числото под корена!

Наистина е лесно!

Да кажем, че имаме записано число

Какво можем да направим с него? Е, разбира се, скрийте тройката под корена, като помните, че тройката е корен квадратен от!

Защо имаме нужда от това? Да, само за да разширим нашите възможности при решаване на примери:

Как ви харесва това свойство на корените? Прави ли живота много по-лесен? За мен е точно така! само Трябва да помним, че можем да въвеждаме само положителни числа под знака за квадратен корен.

Решете сами този пример -
успяхте ли Да видим какво трябва да получите:

Много добре! Успяхте да въведете номера под корен! Нека да преминем към нещо също толкова важно - нека да разгледаме как да сравняваме числа, съдържащи квадратен корен!

Сравнение на корените

Защо трябва да се научим да сравняваме числа, които съдържат квадратен корен?

Много просто. Често в големи и дълги изрази, срещани на изпита, получаваме ирационален отговор (помните ли какво е това? Вече говорихме за това днес!)

Трябва да поставим получените отговори на координатната линия, например, за да определим кой интервал е подходящ за решаване на уравнението. И тук възниква проблемът: в изпита няма калкулатор, а без него как можете да си представите кое число е по-голямо и кое по-малко? Това е!

Например, определете кое е по-голямо: или?

Не можете да кажете веднага. Е, нека използваме свойството disassembled за въвеждане на число под знака на корена?

Тогава продължете:

Е, очевидно, колкото по-голямо е числото под знака на корена, толкова по-голям е самият корен!

Тези. ако, тогава,.

От това твърдо заключаваме, че. И никой няма да ни убеди в обратното!

Извличане на корени от големи числа

Преди това въведохме множител под знака на корена, но как да го премахнем? Просто трябва да го разделите на фактори и да извлечете това, което извлечете!

Възможно е да се поеме по различен път и да се разшири в други фактори:

Не е лошо, нали? Всеки от тези подходи е правилен, решете както желаете.

Факторингът е много полезен при решаването на такива нестандартни проблеми като този:

Да не се страхуваме, а да действаме! Нека разложим всеки фактор под корена на отделни фактори:

Сега опитайте сами (без калкулатор! Няма да бъде на изпита):

това ли е краят Нека не спираме на половината път!

Това е всичко, не е толкова страшно, нали?

Се случи? Браво, точно така!

Сега опитайте този пример:

Но примерът е труден за разбиване, така че не можете веднага да разберете как да подходите към него. Но, разбира се, можем да се справим.

Е, да започнем факторизирането? Нека веднага да отбележим, че можете да разделите число на (помнете знаците за делимост):

Сега опитайте сами (отново без калкулатор!):

Е, проработи ли? Браво, точно така!

Нека обобщим

Корен квадратен (аритметичен корен квадратен) от неотрицателно число е неотрицателно число, чийто квадрат е равен на.
.
Ако просто вземем корен квадратен от нещо, винаги получаваме един неотрицателен резултат.
Свойства на аритметичен корен:
Когато сравнявате квадратни корени, трябва да запомните, че колкото по-голямо е числото под знака на корена, толкова по-голям е самият корен.

Как е квадратният корен? Всичко е ясно?

Опитахме се да ви обясним без никакви проблеми всичко, което трябва да знаете на изпита за корен квадратен.

Твой ред е. Пишете ни дали тази тема е трудна за вас или не.

Научихте ли нещо ново или вече всичко беше ясно?

Пишете в коментарите и успех на изпитите!

Разгледайте уравнението x 2 = 4. Решете го графично. За да направите това, в една координатна система изграждаме парабола y = x 2 и права линия y = 4 (фиг. 74). Те се пресичат в две точки A (- 2; 4) и B (2; 4). Абсцисите на точки A и B са корените на уравнението x 2 = 4. И така, x 1 = - 2, x 2 = 2.

Разсъждавайки по абсолютно същия начин, намираме корените на уравнението x 2 = 9 (вижте фиг. 74): x 1 = - 3, x 2 = 3.

Сега нека се опитаме да решим уравнението x 2 = 5; геометрична илюстрация е показана на фиг. 75. Ясно е, че това уравнение има два корена x 1 и x 2 и тези числа, както и в предишните два случая, са равни по абсолютна стойност и противоположни по знак (x 1 - - x 2) - Но за разлика от предишното случаи , където корените на уравнението са намерени без затруднения (и те могат да бъдат намерени без използване на графики), с уравнението x 2 = 5 това не е така: според чертежа не можем да посочим стойностите на корени, можем само да установим, че единият корен е разположен малко вляво има 2 точки, а вторият е малко вдясно

точки 2.

Кое е това число (точка), което се намира точно вдясно от точка 2 и което на квадрат дава 5? Ясно е, че това не е 3, тъй като 3 2 = 9, т.е. оказва се повече от необходимото (9 > 5).

Това означава, че числото, което ни интересува, се намира между числата 2 и 3. Но между числата 2 и 3 има безкраен брой рационални числа, напр. и т.н. Може би сред тях ще има фракция като ? Тогава няма да имаме проблеми с уравнението x 2 - 5, можем да го запишем

Но тук ни очаква неприятна изненада. Оказва се, че няма дроб, за която да е валидно равенството
Доказателството на изложеното твърдение е доста трудно. Въпреки това го представяме, защото е красиво и поучително и е много полезно да се опитаме да го разберем.

Да приемем, че има несъкратима дроб, за която равенството е в сила. Тогава, т.е. m 2 = 5n 2. Последното равенство означава, че естественото число m 2 се дели на 5 без остатък (в частното ще бъде n2).

Следователно числото m 2 завършва или с числото 5, или с числото 0. Но тогава естественото число m също завършва или с числото 5, или с числото 0, т.е. числото m се дели на 5 без остатък. С други думи, ако числото m се раздели на 5, тогава частното ще доведе до някакво естествено число k. Това означава,
че m = 5k.
Виж сега:
m2 = 5n2;
Нека заместим 5k вместо m в първото равенство:

(5k) 2 = 5n 2, т.е. 25k 2 = 5n 2 или n 2 = 5k 2.
Последното равенство означава, че числото. 5n 2 се дели на 5 без остатък. Разсъждавайки по-горе, стигаме до извода, че числото n също се дели на 5 без остатък.
И така, m се дели на 5, n се дели на 5, което означава, че дробта може да бъде намалена (с 5). Но ние предположихме, че дробта е несъкратима. Какъв е проблема? Защо, след като разсъждавахме правилно, стигнахме до абсурда или, както често казват математиците, получихме противоречие Да, защото първоначалната предпоставка беше неправилна, сякаш имаше несъкратима дроб, за която важи равенството!
Оттук заключаваме: няма такава дроб.
Методът на доказателство, който току-що използвахме, се нарича в математиката метод на доказателство от противно. Същността му е следната. Трябва да докажем определено твърдение и приемаме, че то не е вярно (математиците казват: „предположете обратното“ - не в смисъл на „неприятно“, а в смисъл на „противно на това, което се изисква“).
Ако в резултат на правилно разсъждение стигнем до противоречие с условието, тогава заключаваме: нашето предположение е невярно, което означава, че това, което трябваше да докажем, е вярно.

Така че, разполагайки само с рационални числа (и все още не знаем други числа), не можем да решим уравнението x 2 = 5.
След като се сблъскаха с такава ситуация за първи път, математиците осъзнаха, че трябва да измислят начин да я опишат на математически език. Те въведоха нов символ, който нарекоха квадратен корен и използвайки този символ, корените на уравнението x 2 = 5 бяха записани, както следва:

Той гласи: „корен квадратен от 5“). Сега за всяко уравнение от формата x 2 = a, където a > O, можете да намерите корените - те са числа , (фиг. 76).

Нека подчертаем също, че числото не е нито цяло число, нито дроб.
Това означава, че това не е рационално число, то е число от ново естество; ние ще говорим конкретно за такива числа по-късно, в глава 5.
Засега нека просто отбележим, че новото число е между числата 2 и 3, тъй като 2 2 = 4, което е по-малко от 5; 3 2 = 9, а това е повече от 5. Можете да изясните:

Всъщност 2,2 2 = 4,84< 5, а 2,3 2 = 5,29 >5. Вие също можете
посочете:

наистина, 2,23 2 = 4,9729< 5, а 2,24 2 = 5,0176 > 5.
На практика обикновено се смята, че числото е равно на 2,23 или е равно на 2,24, само че това не е обикновено равенство, а приблизително равенство, което се обозначава със символа "."
Така,

Докато обсъждахме решението на уравнението x 2 = a, се натъкнахме на доста типично състояние на нещата за математиката. Озовавайки се в нестандартна, необичайна (както обичат да казват космонавтите) ситуация и не намирайки изход от нея с познатите средства, математиците измислят нов термин и ново обозначение (нов символ) за математическия модел, който те за пръв път срещнат; с други думи, те въвеждат ново понятие и след това изучават свойствата на това
концепции. Така новото понятие и неговото обозначение стават собственост на математическия език. Ние действахме по същия начин: въведохме термина „корен квадратен от числото a“, въведохме символ за обозначаването му и малко по-късно ще проучим свойствата на новото понятие. Досега знаем само едно нещо: ако a > 0,
тогава е положително число, удовлетворяващо уравнението x 2 = a. С други думи, това е положително число, което, когато се повдигне на квадрат, дава числото a.
Тъй като уравнението x 2 = 0 има корен x = 0, ние се съгласихме да приемем, че
Сега сме готови да дадем строга дефиниция.
Определение. Корен квадратен от неотрицателно число a е неотрицателно число, чийто квадрат е равен на a.

Това число се означава с числото и се нарича радикално число.
Така че, ако a е неотрицателно число, тогава:

Ако< О, то уравнение х 2 = а не имеет корней, говорить в этом случае о квадратном корне из числа а не имеет смысла.
Следователно изразът има смисъл само за a > 0.
Казват, че - същият математически модел (същата връзка между неотрицателни числа
(a и b), но само вторият е описан на по-прост език от първия (използва по-прости символи).

Операцията за намиране на корен квадратен от неотрицателно число се нарича извличане на квадратен корен. Тази операция е обратна на повдигането на квадрат. Сравнете:

Моля, обърнете внимание отново, че в таблицата се появяват само положителни числа, както е посочено в определението за квадратен корен. И въпреки че например (- 5) 2 = 25 е истинско равенство, преминете от него към нотация, използвайки квадратен корен (т.е. запишете това.)
забранено е. A-приори, . е положително число, което означава .
Често казват не „корен квадратен“, а „корен аритметичен квадратен“. Пропускаме термина „аритметика“ за краткост.

Г) За разлика от предишните примери, не можем да посочим точната стойност на числото. Ясно е само, че е по-голямо от 4, но по-малко от 5, тъй като

4 2 = 16 (това е по-малко от 17) и 5 2 = 25 (това е повече от 17).
Въпреки това, приблизителната стойност на числото може да бъде намерена с помощта на микрокалкулатор, който съдържа операцията за извличане на корен квадратен; тази стойност е 4,123.
Така,
Числото, подобно на числото, обсъдено по-горе, не е рационално.
д) Не може да се изчисли, тъй като корен квадратен от отрицателно число не съществува; записът е безсмислен. Предложената задача е неправилна.
д) тъй като 31 > 0 и 31 2 = 961. В такива случаи трябва да използвате таблица с квадрати на естествени числа или микрокалкулатор.
g) тъй като 75 > 0 и 75 2 = 5625.
В най-простите случаи стойността на квадратния корен се изчислява веднага: и т.н. В по-сложни случаи трябва да използвате таблица с квадрати на числа или да извършите изчисления с помощта на микрокалкулатор. Но какво ще стане, ако нямате маса или калкулатор под ръка? Нека отговорим на този въпрос, като решим следния пример.

Пример 2.Изчисли
Решение.
Първи етап.Не е трудно да се досетите, че отговорът ще бъде 50 с опашка. Всъщност 50 2 = 2500 и 60 2 = 3600, докато числото 2809 е между числата 2500 и 3600.

Втора фаза.Да намерим „опашката“, т.е. последната цифра на желаното число. Дотук знаем, че ако се вземе коренът, тогава отговорът може да бъде 51, 52, 53, 54, 55, 56, 57, 58 или 59. Трябва да проверим само две числа: 53 и 57, тъй като само те, когато се повдигне на квадрат, резултатът ще бъде четирицифрено число, завършващо на 9, същото число, което завършва на 2809.
Имаме 532 = 2809 - това е, от което се нуждаем (имахме късмет, веднага ударихме окото на бика). Значи = 53.
Отговор:

53
Пример 3.Страните на правоъгълен триъгълник са 1 cm и 2 cm. Колко е хипотенузата на триъгълника? (Фиг.77)

Решение.

Нека използваме теоремата на Питагор, известна от геометрията: сумата от квадратите на дължините на катетите на правоъгълен триъгълник е равна на квадрата на дължината на неговата хипотенуза, т.е. a 2 + b 2 = c 2, където a , b са катетите, c е хипотенузата на правоъгълния триъгълник.

означава,

Този пример показва, че въвеждането на квадратни корени не е прищявка на математиците, а обективна необходимост: в реалния живот има ситуации, чиито математически модели съдържат операция за извличане на квадратен корен. Може би най-важната от тези ситуации е свързана с
решаване на квадратни уравнения. Досега, когато срещахме квадратни уравнения ax 2 + bx + c = 0, ние или факторизирахме лявата страна (което не винаги се получаваше), или използвахме графични методи (което също не е много надеждно, макар и красиво). Всъщност, за да намерите
корени x 1 и x 2 на квадратното уравнение ax 2 + bx + c = 0 в математическите формули се използват

съдържащи, както се вижда, знака за квадратен корен. Тези формули се използват на практика, както следва. Нека, например, трябва да решим уравнението 2x 2 + bx - 7 = 0. Тук a = 2, b = 5, c = - 7. Следователно,
b2 - 4ac = 5 2 - 4 . 2. (- 7) = 81. След това намираме . означава,

По-горе отбелязахме, че това не е рационално число.
Математиците наричат такива числа ирационални. Всяко число от формата е ирационално, ако не може да се извади корен квадратен. Например, и т.н. - ирационални числа. В Глава 5 ще говорим повече за рационални и ирационални числа. Рационалните и ирационалните числа заедно съставляват множеството от реални числа, т.е. наборът от всички онези числа, с които работим в реалния живот (всъщност,
ност). Например, всички това са реални числа.
Точно както дефинирахме концепцията за квадратен корен по-горе, можем също да дефинираме концепцията за кубичен корен: кубичният корен на неотрицателно число a е неотрицателно число, чийто куб е равен на a. С други думи, равенството означава, че b 3 = a.

Всичко това ще изучаваме в курса по алгебра за 11 клас.

Площта на квадратен парцел е 81 dm². Намерете неговата страна. Да предположим, че дължината на страната на квадрата е хдециметри. Тогава площта на парцела е х² квадратни дециметра. Тъй като според условието тази площ е равна на 81 dm², тогава х² = 81. Дължината на страната на квадрат е положително число. Положително число, чийто квадрат е 81, е числото 9. При решаването на задачата беше необходимо да се намери числото x, чийто квадрат е 81, т.е. да се реши уравнението х² = 81. Това уравнение има два корена: х 1 = 9 и х 2 = - 9, тъй като 9² = 81 и (- 9)² = 81. И двете числа 9 и - 9 се наричат квадратен корен от 81.

Забележете, че един от квадратните корени х= 9 е положително число. Нарича се аритметичен квадратен корен от 81 и се обозначава с √81, така че √81 = 9.

Аритметичен корен квадратен от число Ае неотрицателно число, чийто квадрат е равен на А.

Например, числата 6 и - 6 са корен квадратен от числото 36. Числото 6 обаче е аритметичен корен квадратен от 36, тъй като 6 е неотрицателно число и 6² = 36. Числото - 6 не е аритметичен корен.

Аритметичен корен квадратен от число Асе обозначава по следния начин: √ А.

Знакът се нарича знак за аритметичен квадратен корен; А- наречен радикален израз. Израз √ АПрочети така: аритметичен квадратен корен от число А.Например √36 = 6, √0 = 0, √0,49 = 0,7. В случаите, когато е ясно, че говорим за аритметичен корен, те накратко казват: „корен квадратен от А«.

Актът на намиране на корен квадратен от число се нарича извличане на квадратен корен. Това действие е обратното на повдигането на квадрат.

Можете да повдигнете всяко число на квадрат, но не можете да извлечете квадратни корени от което и да е число. Например, невъзможно е да се извлече корен квадратен от числото - 4. Ако такъв корен съществува, тогава, обозначавайки го с буквата х, ще получим неправилното равенство x² = - 4, тъй като има неотрицателно число отляво и отрицателно число отдясно.

Израз √ Аима смисъл само когато a ≥ 0. Определението за корен квадратен може да бъде написано накратко, както следва: √ a ≥ 0, (√А)² = А. Равенство (√ А)² = Авалидно за a ≥ 0. По този начин, за да се гарантира, че корен квадратен от неотрицателно число Аравно на b, т.е. във факта, че √ А =b, трябва да проверите дали са изпълнени следните две условия: b ≥ 0, b² = А.

Корен квадратен от дроб

Нека изчислим. Забележете, че √25 = 5, √36 = 6 и нека проверим дали равенството е в сила.

защото и , тогава равенството е вярно. Така, .

Теорема:Ако А≥ 0 и b> 0, тоест коренът на дробта е равен на корена на числителя, разделен на корена на знаменателя. Изисква се да се докаже, че: и .

Тъй като √ А≥0 и √ b> 0, тогава .

За свойството да се повдига дроб на степен и определението за квадратен корен теоремата е доказана. Нека да разгледаме няколко примера.

Изчислете, като използвате доказаната теорема .

Втори пример: Докажете това , Ако А ≤ 0, b < 0. .

Друг пример: Изчислете.

Преобразуване на квадратен корен

Премахване на множителя под знака на корена. Нека изразът бъде даден. Ако А≥ 0 и b≥ 0, тогава използвайки теоремата за корена на произведението, можем да напишем:

Тази трансформация се нарича премахване на фактора от знака за корен. Нека да разгледаме един пример;

Изчислете при х= 2. Директно заместване х= 2 в радикалния израз води до сложни изчисления. Тези изчисления могат да бъдат опростени, ако първо премахнете факторите под знака за корен: . Замествайки сега x = 2, получаваме:.

Така че, при премахване на фактора под знака на корена, радикалният израз се представя под формата на продукт, в който един или повече фактори са квадрати на неотрицателни числа. След това приложете теоремата за корена на произведението и вземете корена на всеки фактор. Нека разгледаме пример: Опростете израза A = √8 + √18 - 4√2, като извадите факторите в първите два члена от под знака за корен, получаваме:. Нека подчертаем това равенство валидно само когато А≥ 0 и b≥ 0. ако А < 0, то .

В тази статия ще представим понятие корен от число. Ще продължим последователно: ще започнем с квадратния корен, оттам ще преминем към описанието на кубичния корен, след което ще обобщим понятието корен, като дефинираме n-тия корен. В същото време ще въведем определения, обозначения, ще дадем примери за корени и ще дадем необходимите обяснения и коментари.

Корен квадратен, корен квадратен аритметичен

За да разберете дефиницията на корен от число и по-специално на корен квадратен, трябва да имате . В този момент често ще срещаме втората степен на числото - квадрата на числото.

Да започнем с дефиниции на корен квадратен.

Определение

Корен квадратен от aе число, чийто квадрат е равен на a.

За да донесе примери за квадратни корени, вземем няколко числа, например 5, −0.3, 0.3, 0, и ги повдигнем на квадрат, получаваме съответно числата 25, 0.09, 0.09 и 0 (5 2 =5·5=25, (−0,3) 2 =(−0,3)·(−0,3)=0,09, (0,3) 2 =0,3·0,3=0,09 и 0 2 =0·0=0 ). Тогава, по дефиницията, дадена по-горе, числото 5 е корен квадратен от числото 25, числата −0,3 и 0,3 са корен квадратен от 0,09, а 0 е корен квадратен от нула.

Трябва да се отбележи, че не за всяко число a съществува a, чийто квадрат е равен на a. А именно, за всяко отрицателно число a няма реално число b, чийто квадрат да е равен на a. Всъщност равенството a=b 2 е невъзможно за всяко отрицателно a, тъй като b 2 е неотрицателно число за всяко b. По този начин, няма квадратен корен от отрицателно число в множеството от реални числа. С други думи, в множеството от реални числа квадратният корен от отрицателно число не е дефиниран и няма значение.

Това води до логичен въпрос: „Има ли квадратен корен от a за всяко неотрицателно a“? Отговорът е да. Този факт може да бъде оправдан от конструктивния метод, използван за намиране на стойността на квадратния корен.

Тогава възниква следващият логичен въпрос: „Какъв е броят на всички квадратни корени от дадено неотрицателно число a - едно, две, три или дори повече“? Ето отговора: ако a е нула, тогава единственият квадратен корен от нула е нула; ако a е някакво положително число, тогава броят на квадратните корени на числото a е две, а корените са . Нека оправдаем това.

Нека започнем със случая a=0. Първо, нека покажем, че нулата наистина е корен квадратен от нула. Това следва от очевидното равенство 0 2 =0·0=0 и дефиницията на квадратния корен.

Сега нека докажем, че 0 е единственият квадратен корен от нула. Нека използваме обратния метод. Да предположим, че има някакво ненулево число b, което е квадратен корен от нула. Тогава трябва да е изпълнено условието b 2 =0, което е невъзможно, тъй като за всяко ненулево b стойността на израза b 2 е положителна. Стигнахме до противоречие. Това доказва, че 0 е единственият квадратен корен от нула.

Нека да преминем към случаите, когато а е положително число. По-горе казахме, че винаги има квадратен корен от всяко неотрицателно число, нека квадратният корен от a е числото b. Да кажем, че има число c, което също е квадратен корен от a. Тогава по дефиницията на квадратен корен равенствата b 2 =a и c 2 =a са верни, от което следва, че b 2 −c 2 =a−a=0, но тъй като b 2 −c 2 =( b−c)·( b+c) , тогава (b−c)·(b+c)=0 . Полученото равенство е валидно свойства на операциите с реални числавъзможно само когато b−c=0 или b+c=0 . Така числата b и c са равни или противоположни.

Ако приемем, че има число d, което е друг корен квадратен от числото a, тогава чрез разсъждения, подобни на вече дадените, се доказва, че d е равно на числото b или числото c. И така, броят на квадратните корени от положително число е две, а квадратните корени са противоположни числа.

За удобство при работа с квадратни корени, отрицателният корен е „отделен“ от положителния. За целта се въвежда дефиниция на аритметичен квадратен корен.

Определение

Аритметичен корен квадратен от неотрицателно число ае неотрицателно число, чийто квадрат е равен на a.

Нотацията за аритметичния корен квадратен от a е . Знакът се нарича знак за аритметичен квадратен корен. Нарича се още радикален знак. Следователно понякога можете да чуете и „корен“, и „радикал“, което означава един и същ обект.

Извиква се числото под знака за аритметичен квадратен корен радикално число, а изразът под знака за корен е радикален израз, докато терминът „радикално число“ често се заменя с „радикален израз“. Например в записа числото 151 е радикално число, а в записа изразът a е радикален израз.

При четене думата „аритметика“ често се пропуска, например записът се чете като „корен квадратен от седем точка двадесет и девет“. Думата „аритметика“ се използва само когато искат да подчертаят, че говорим конкретно за положителен корен квадратен от число.

В светлината на въведената нотация, от дефиницията на аритметичен квадратен корен следва, че за всяко неотрицателно число a .

Квадратни корени от положително число a се записват с помощта на аритметичния знак за квадратен корен като и . Например квадратният корен от 13 е и . Аритметичният корен квадратен от нула е нула, т.е. За отрицателни числа a няма да придаваме значение на нотацията, докато не изучим комплексни числа. Например изразите и са безсмислени.

Въз основа на дефиницията на квадратния корен се доказват свойствата на квадратния корен, които често се използват в практиката.

В заключение на този параграф отбелязваме, че квадратните корени на числото a са решения на формата x 2 =a по отношение на променливата x.

Кубичен корен от число

Определение за кубичен коренна числото a се дава подобно на определението за квадратен корен. Само че се основава на концепцията за куб от число, а не за квадрат.

Определение

Кубичен корен от aе число, чийто куб е равен на a.

Да дадем примери за кубични корени. За да направите това, вземете няколко числа, например 7, 0, −2/3, и ги кубирайте: 7 3 =7·7·7=343, 0 3 =0·0·0=0, . Тогава, въз основа на определението за кубичен корен, можем да кажем, че числото 7 е кубичен корен от 343, 0 е кубичен корен от нула и −2/3 е кубичен корен от −8/27.

Може да се покаже, че кубичният корен от число, за разлика от квадратния корен, винаги съществува не само за неотрицателно a, но и за всяко реално число a. За да направите това, можете да използвате същия метод, който споменахме при изучаването на квадратни корени.

Освен това има само един кубичен корен от дадено число a. Нека докажем последното твърдение. За да направите това, разгледайте три случая поотделно: a е положително число, a=0 и a е отрицателно число.

Лесно е да се покаже, че ако a е положително, кубичният корен на a не може да бъде нито отрицателно число, нито нула. Наистина, нека b е кубичен корен от a, тогава по дефиниция можем да запишем равенството b 3 =a. Ясно е, че това равенство не може да бъде вярно за отрицателно b и за b=0, тъй като в тези случаи b 3 =b·b·b ще бъде съответно отрицателно число или нула. Така че кубичният корен на положително число a е положително число.

Да предположим сега, че в допълнение към числото b има друг кубичен корен от числото a, нека го обозначим с. Тогава c 3 =a. Следователно b 3 −c 3 =a−a=0, но b 3 −c 3 =(b−c)·(b 2 +b·c+c 2)(това е формулата за съкратено умножение разлика от кубчета), откъдето (b−c)·(b 2 +b·c+c 2)=0. Полученото равенство е възможно само когато b−c=0 или b 2 +b·c+c 2 =0. От първото равенство имаме b=c, а второто равенство няма решения, тъй като лявата му страна е положително число за всякакви положителни числа b и c като сбор от три положителни члена b 2, b·c и c 2. Това доказва уникалността на кубичния корен на положително число a.

Когато a=0, кубичният корен на числото a е само числото нула. Наистина, ако приемем, че има число b, което е различен от нула кубичен корен от нула, тогава трябва да е валидно равенството b 3 =0, което е възможно само когато b=0.

За отрицателно a могат да бъдат дадени аргументи, подобни на случая за положително a. Първо, показваме, че кубичният корен на отрицателно число не може да бъде равен нито на положително число, нито на нула. Второ, приемаме, че има втори кубичен корен от отрицателно число и показваме, че той задължително ще съвпадне с първия.

И така, винаги има кубичен корен от всяко дадено реално число а и то уникален.

Да дадем дефиниция на аритметичен кубичен корен.

Определение

Аритметичен кубичен корен от неотрицателно число aе неотрицателно число, чийто куб е равен на a.

Аритметичният кубичен корен на неотрицателно число a се означава като , знакът се нарича знак на аритметичния кубичен корен, числото 3 в тази нотация се нарича коренов индекс. Числото под знака на корена е радикално число, изразът под знака за корен е радикален израз.

Въпреки че аритметичният кубичен корен е дефиниран само за неотрицателни числа a, също така е удобно да се използват обозначения, в които отрицателните числа се намират под знака за аритметичен кубичен корен. Ще ги разбираме по следния начин: , където a е положително число. Например, .

Ще говорим за свойствата на кубичните корени в общата статия свойства на корените.

Изчисляването на стойността на кубичен корен се нарича извличане на кубичен корен; това действие се обсъжда в статията извличане на корени: методи, примери, решения.

За да завършим тази точка, нека кажем, че кубичният корен на числото a е решение на формата x 3 =a.

n-ти корен, аритметичен корен от степен n

Нека обобщим понятието корен от число - въвеждаме дефиниция на n-ти коренза n.

Определение

n-ти корен от aе число, чиято n-та степен е равна на a.

От тази дефиниция става ясно, че коренът от първа степен на числото a е самото число a, тъй като при изучаване на степента с естествен показател взехме a 1 =a.

По-горе разгледахме специални случаи на корен n-ти за n=2 и n=3 - корен квадратен и корен кубичен. Тоест квадратният корен е корен от втора степен, а кубичният корен е корен от трета степен. За да изучаваме корени от n-та степен за n=4, 5, 6, ..., е удобно да ги разделим на две групи: първата група - корени от четни степени (т.е. за n = 4, 6, 8 , ...), втората група - корени на нечетни степени (т.е. с n=5, 7, 9, ...). Това се дължи на факта, че корените на четните степени са подобни на квадратните корени, а корените на нечетните степени са подобни на кубичните корени. Нека се справим с тях един по един.

Да започнем с корените, чиято степен са четните числа 4, 6, 8, ... Както вече казахме, те са подобни на корен квадратен от числото a. Тоест, коренът на всяка четна степен на числото a съществува само за неотрицателно a. Освен това, ако a=0, тогава коренът на a е единствен и равен на нула, а ако a>0, тогава има два корена с четна степен на числото a и те са противоположни числа.

Нека обосновем последното твърдение. Нека b е четен корен (означаваме го като 2·m, където m е някакво естествено число) на числото a. Да предположим, че има число c - друг корен от степен 2·m от числото a. Тогава b 2·m −c 2·m =a−a=0 . Но ние знаем формата b 2 m −c 2 m = (b−c) (b+c) (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2), тогава (b−c)·(b+c)· (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2)=0. От това равенство следва, че b−c=0, или b+c=0, или b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2 =0. Първите две равенства означават, че числата b и c са равни или b и c са противоположни. И последното равенство е валидно само за b=c=0, тъй като от лявата му страна има израз, който е неотрицателен за всякакви b и c като сбор от неотрицателни числа.

Що се отнася до корените от n-та степен за нечетно n, те са подобни на кубичния корен. Тоест, коренът на всяка нечетна степен на числото a съществува за всяко реално число a и за дадено число a той е уникален.

Уникалността на корен от нечетна степен 2·m+1 от числото a се доказва по аналогия с доказателството за уникалността на кубичния корен от a. Само че тук вместо равенство a 3 −b 3 =(a−b)·(a 2 +a·b+c 2)използва се равенство от вида b 2 m+1 −c 2 m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m). Изразът в последната скоба може да бъде пренаписан като b 2 m +c 2 m +b c (b 2 m−2 +c 2 m−2 + b c (b 2 m−4 +c 2 m−4 +b c (…+(b 2 +c 2 +b c)))). Например при m=2 имаме b 5 −c 5 =(b−c)·(b 4 +b 3 ·c+b 2 ·c 2 +b·c 3 +c 4)= (b−c)·(b 4 +c 4 +b·c·(b 2 +c 2 +b·c)). Когато и a и b са положителни или и двете отрицателни, техният продукт е положително число, тогава изразът b 2 +c 2 +b·c в най-високите вложени скоби е положителен като сбор от положителните числа. Сега, преминавайки последователно към изразите в скоби на предишните степени на вложеност, се убеждаваме, че те също са положителни като сбор от положителни числа. В резултат на това получаваме, че равенството b 2 m+1 −c 2 m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)=0възможно само когато b−c=0, тоест когато числото b е равно на числото c.

Време е да разберем записа на корените на n-та степен. За целта се дава дефиниция на аритметичен корен от n-та степен.

Определение

Аритметичен корен от n-та степен на неотрицателно число aе неотрицателно число, чиято n-та степен е равна на a.

Концепцията за корен квадратен от неотрицателно число

Разгледайте уравнението x2 = 4. Решете го графично. За да направите това в една система координатиДа построим парабола y = x2 и права линия y = 4 (фиг. 74). Те се пресичат в две точки A (- 2; 4) и B (2; 4). Абсцисите на точки A и B са корените на уравнението x2 = 4. Така че x1 = - 2, x2 = 2.

Разсъждавайки по абсолютно същия начин, намираме корените на уравнението x2 = 9 (виж фиг. 74): x1 = - 3, x2 = 3.

Сега нека се опитаме да решим уравнението x2 = 5; геометрична илюстрация е показана на фиг. 75. Ясно е, че това уравнение има два корена x1 и x2 и тези числа, както в предишните два случая, са равни по абсолютна стойност и противоположни по знак (x1 - - x2) - Но за разлика от предишните случаи, където корените на уравнението бяха намерени без затруднения (и те могат да бъдат намерени без използване на графики), това не е случаят с уравнението x2 = 5: от чертежа не можем да посочим стойностите на корените, можем само да установим, че един коренсе намира малко вляво от точка - 2, а втората е разположена малко вдясно от точка 2.

Но тук ни очаква неприятна изненада. Оказва се, че няма такова нещо дроби DIV_ADBLOCK32">

Да предположим, че има несъкратима дроб, за която равенството е в сила https://pandia.ru/text/78/258/images/image007_16.jpg" alt=".jpg" width="55" height="36">!}, т.е. m2 = 5n2. Последното равенство означава това естествено число m2 се дели на 5 без остатък (в частното става n2).

Следователно числото m2 завършва или с числото 5, или с числото 0. Но тогава естественото число m също завършва или с числото 5, или с числото 0, т.е. числото m се дели на 5 без остатък. С други думи, ако числото m се раздели на 5, тогава частното ще доведе до някакво естествено число k. Това означава, че m = 5k.

Виж сега:

Нека заместим 5k вместо m в първото равенство:

(5k)2 = 5n2, т.е. 25k2 = 5n2 или n2 = 5k2.

Последното равенство означава, че числото. 5n2 се дели на 5 без остатък. Разсъждавайки по-горе, стигаме до извода, че числото n също се дели на 5 без остатък.

И така, m се дели на 5, n се дели на 5, което означава, че дробта може да бъде намалена (с 5). Но ние предположихме, че дробта е несъкратима. Какъв е проблема? Защо, след като сме разсъждавали правилно, сме стигнали до абсурд или, както често казват математиците, сме получили противоречие, защото първоначалната предпоставка е неправилна, сякаш има несъкратима дроб, за която е валидно равенството! ).

Ако в резултат на правилно разсъждение стигнем до противоречие с условието, тогава заключаваме: нашето предположение е невярно, което означава, че това, което трябваше да докажем, е вярно.

И така, имайки само рационални числа(и все още не знаем други числа), няма да можем да решим уравнението x2 = 5.

След като се сблъскаха с такава ситуация за първи път, математиците осъзнаха, че трябва да измислят начин да я опишат на математически език. Те въведоха нов символ, който нарекоха квадратен корен и използвайки този символ, корените на уравнението x2 = 5 бяха записани, както следва: ). Сега за всяко уравнение от формата x2 = a, където a > O, можете да намерите корените - те са числа https://pandia.ru/text/78/258/images/image012_6.jpg" alt=".jpg" width="32" height="31">!}нито цяло, нито част.
Това означава, че това не е рационално число, то е число от ново естество; ние ще говорим конкретно за такива числа по-късно, в глава 5.
Засега нека просто отбележим, че новото число е между числата 2 и 3, тъй като 22 = 4, което е по-малко от 5; Z2 = 9, а това е повече от 5. Можете да изясните:

Моля, обърнете внимание отново, че в таблицата се появяват само положителни числа, както е посочено в определението за квадратен корен. И въпреки че, например, = 25 е истинско равенство, преминете от него към записване с квадратен корен (т.е. напишете това. .jpg" alt=".jpg" width="42" height="30">!}е положително число, което означава https://pandia.ru/text/78/258/images/image025_3.jpg" alt=".jpg" width="35" height="28">!}. Ясно е само, че е по-голямо от 4, но по-малко от 5, тъй като 42 = 16 (това е по-малко от 17) и 52 = 25 (това е повече от 17).
Въпреки това, приблизителната стойност на числото може да се намери с помощта на микро калкулатор, който съдържа операция за квадратен корен; тази стойност е 4,123.

Числото, подобно на числото, обсъдено по-горе, не е рационално.
д) Не може да се изчисли, тъй като корен квадратен от отрицателно число не съществува; записът е безсмислен. Предложената задача е неправилна.
д) https://pandia.ru/text/78/258/images/image029_1.jpg" alt="Задача" width="80" height="33 id=">!}, тъй като 75 > 0 и 752 = 5625.

В най-простите случаи стойността на квадратния корен се изчислява веднага:

https://pandia.ru/text/78/258/images/image031_2.jpg" alt="Задача" width="65" height="42 id=">!}
Решение.
Първи етап.Не е трудно да се досетите, че отговорът ще бъде 50 с опашка. Всъщност 502 = 2500 и 602 = 3600, докато числото 2809 е между числата 2500 и 3600.