Calculate triple integral in spherical coordinates online. Triple integral calculation

Let us have two rectangular coordinate systems in space and
, and a system of functions

(1)

which establish a one-to-one correspondence between points in some areas
And
in these coordinate systems. Let us assume that the functions of system (1) have
continuous partial derivatives. The determinant made up of these partial derivatives

,

is called the Jacobian (or Jacobi determinant) of the system of functions (1). We will assume that
V
.

Under the assumptions made above, the following general formula for changing variables in a triple integral holds:

As in the case of the double integral, the mutual uniqueness of system (1) and the condition
may be violated at individual points, on individual lines and on individual surfaces.

System of functions (1) for each point
matches a single point
. These three numbers
are called curvilinear coordinates of a point . Points of space
, for which one of these coordinates retains a constant value, form the so-called. coordinate surface.

II Triple integral in cylindrical coordinates

The cylindrical coordinate system (CSS) is determined by the plane
, in which a polar coordinate system is specified and the axis
, perpendicular to this plane. Cylindrical coordinates of a point
, Where
– polar coordinates of the point – projections t glasses to the plane
, A – these are the coordinates of the projection of the point per axis
or
.

In plane
Let's enter Cartesian coordinates in the usual way, direct the applicate axis along the axis
CSK. Now it is not difficult to obtain formulas connecting cylindrical coordinates with Cartesian ones:

(3)

These formulas map the area to the entire space
.

The coordinate surfaces in the case under consideration will be:

1)
– cylindrical surfaces with generatrices parallel to the axis
, whose guides are circles in the plane
, centered at point ;

2)

;

3)
– planes parallel to the plane
.

Jacobian of system (3):

.

The general formula in the case of CSK takes the form:

Note 1 . The transition to cylindrical coordinates is recommended in the case when the area of ​​integration is a circular cylinder or cone, or a paraboloid of revolution (or parts thereof), and the axis of this body coincides with the axis of the applicate
.

Note 2. Cylindrical coordinates can be generalized in the same way as polar coordinates in a plane.

Example 1. Calculate the triple integral of a function

by region
, representing the inner part of the cylinder
, bounded by a cone
and paraboloid
.

Solution. We have already considered this area in §2, example 6, and obtained a standard entry in the DPSC. However, calculating the integral in this region is difficult. Let's go to CSK:

.

Projection
body
to the plane
- it's a circle
. Therefore, the coordinate varies from 0 to
, A – from 0 to R. Through an arbitrary point
draw a straight line parallel to the axis
. The straight line will go into
on a cone, but will come out on a paraboloid. But the cone
has the equation in the CSC
, and the paraboloid
- the equation
. So we have

III Triple integral in spherical coordinates

The spherical coordinate system (SCS) is determined by the plane
, in which the UCS is specified, and the axis
, perpendicular to the plane
.

Spherical coordinates of a point space is called a triple of numbers
, Where – polar angle of projection of a point onto a plane
,– angle between axis
and vector
And
.

In plane
let's introduce Cartesian coordinate axes
And
in the usual way, and the applicate axis is compatible with the axis
. The formulas connecting spherical coordinates with Cartesian ones are as follows:

(4)

These formulas map the area to the entire space
.

Jacobian of the system of functions (4):

.

There are three families of coordinate surfaces:

1)
– concentric spheres with the center at the origin;

2)
– half-planes passing through the axis
;

3)
– circular cones with a vertex at the origin of coordinates, the axis of which is the axis
.

Formula for transition to SSC in triple integral:

Note 3. The transition to the SCS is recommended when the domain of integration is a ball or part of it. In this case, the equation of the sphere
goes into. Like the CSK discussed earlier, the CSK is “tied” to the axis
. If the center of the sphere is shifted by a radius along the coordinate axis, then we obtain the simplest spherical equation when displaced along the axis
:

Note 4. It is possible to generalize the SSC:

with Jacobian
. This system of functions will translate the ellipsoid

to "parallelepiped"

Example 2. Find the average distance of points on a ball of radius from its center.

Solution. Recall that the average value of the function
in area
is the triple integral of a function over a region divided by the volume of the region. In our case

So we have

The triple integral is written as follows:

Calculate triple integral - means finding a number equal to the volume of the body V or, what is the same thing - areas V .

Almost everyone can understand the meaning of calculating a triple integral "the hard way." More precisely - “under the skin”, and even more precisely - in its respiratory organs - the lungs. Regardless of whether you know it or not, there are over 700 million alveoli in the human lungs - vesicular formations entwined with a network of capillaries. Gas exchange occurs through the walls of the alveoli. Therefore, we can reason like this: the volume of gas in the lungs can be represented as some compact area. And this volume consists of small volumes concentrated in the alveoli. The key role in this comparison is played by the huge number of alveoli in the lungs: as we will see in the next paragraph, through such a “huge number of small things” the concept of a triple integral is mathematically formulated.

Why is the triple integral used to find the volume of a body? V? Let the area V divided into n arbitrary areas Δ vi, and this designation means not only each small area, but also its volume. In each such small area, an arbitrary point is selected Mi, A f(Mi)- function value f(M) at this point. Now we will maximize the number of such small areas, and the largest diameter Δ vi- on the contrary, reduce. We can compose an integral sum of the form

If the function f(M) = f(x, y, z) is continuous, it will exist integral sum limit the type indicated above. This limit is called triple integral .

In this case the function f(M) = f(x, y, z) called domain integrable V ; V- area of ​​integration; x, y, z- integration variables, dv(or dx dy dz ) - element of volume.

Calculation of the triple integral by reducing the multiplicity

As in the case of double integrals, the calculation of triple integrals reduces to the calculation of integrals of lower multiplicity.

Consider a three-dimensional region V. Below and above (that is, in height) this area is limited by surfaces z = z1 (x, y) And z = z2 (x, y) . On the sides (that is, in width), the area is limited by surfaces y = y1 (x) And y = y2 (x) . And finally, in depth (if you are looking at the area in the direction of the axis Ox) - surfaces x = a And x = b

To apply the transition to integrals of lower multiplicity, it is required that the three-dimensional domain V was correct. It is correct when the line is parallel to the axis Oz, crosses the region boundary V at no more than two points. Regular three-dimensional regions are, for example, a cuboid, an ellipsoid, and a tetrahedron. The figure below shows a rectangular parallelepiped, which we will encounter in the first problem-solving example.

To visualize the difference between correctness and incorrectness, we add that the surfaces of the region along the height of the correct region should not be concave inward. The figure below is an example of an incorrect area V- a single-sheet hyperboloid, the surface of which is straight, parallel to the axis Oz(red), intersects at more than two points.

We will only consider the correct areas.

So the area V- correct. Then for any function f(x, y, z) , continuous in the region V, the formula is valid

This formula allows you to reduce the calculation of the triple integral to the sequential calculation of the internal definite integral over the variable z(at constant x And y) and the outer double integral over a two-dimensional domain D .

Passing from the double integral to the repeated one, we obtain the following formula for calculating the triple integral:

Thus, to calculate a triple integral, you need to sequentially evaluate three definite integrals.

These integrals are calculated from the innermost (over the variable z) to the outermost one (by variable x). To make the sequence of calculations easier to understand, three “nested” integrals can be written as follows:

.

From this entry it is already clear that:

• first you need to integrate the function f(x, y, z) by variable z, and take the equations as integration limits z = z1 (x, y) And z = z2 (x, y) surfaces delimiting the area V below and above;
• y y = y1 (x) And y = y2 (x) surfaces delimiting the area V from the sides;
• integrate the result obtained at the previous step over the variable x, and take the equations as integration limits x = a And x = b surfaces delimiting the area V in depth.

Example 1. Let us go from a triple integral to an iterated integral

-

sequences of three definite integrals. Evaluate this iterated integral.

Solution. The calculation of the iterated integral always starts from the last integral:

.

Let's calculate the second integral - over the variable y:

.

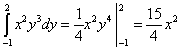x:

.

Answer: This repeated integral and its corresponding triple integral are equal to 10.

Example 2. Calculate triple integral

,

Where V- parallelepiped bounded by planes x = − 1 , x = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Solution. The limits of integration for all three definite integrals are uniquely specified by the equations of the surfaces bounding the parallelepiped. Therefore, we immediately reduce this triple integral to a sequence of three definite integrals:

.

z

.

We calculate the integral “in the middle” - over the variable y. We get;

.

Now we calculate the outermost integral - over the variable x:

Answer: This triple integral is -2.

Example 3. Calculate triple integral

,

Where Vx + y + z = 1 and coordinate planes x = 0 , y = 0 , z= 0 . Region V projected onto a plane xOy into a triangle D, as shown in the figure below.

Solution. Let us first set the limits of integration. For the integral over a variable z the lower limit of integration is uniquely specified: z= 0 . To get the upper limit, we express z from x + y + z = 1 . We get 1 − x − y. For the integral over a variable y the lower limit of integration is uniquely specified: y= 0 . To obtain the upper limit, we express y from x + y + z = 1 , while considering that z= 0 (since the line is located in the plane xOy). We get: 1 − x .

We reduce this triple integral to a sequence of three definite integrals:

.

We calculate the innermost integral - over a variable z, considering x and y constants. We get:

.

y. We get:

x:

Answer: This triple integral is equal to 1/8.

Calculate the triple integral yourself and then look at the solution

Example 4. Calculate triple integral

,

Where V- a pyramid bounded by a plane x + y + z = 1 and coordinate planes x = 0 , y = 0 , z = 0 .

Arrangement of integration limits when passing to a sequence of three integrals

It happens that students who do not have any special difficulties directly calculating integrals cannot get used to setting the limits of integration when moving from a triple integral to a sequence of three definite integrals. This matter does require some training. In the first example, the domain of integration V was a parallelepiped, with which everything is clear: it is bounded on all sides by planes, which means that the limits of integration are uniquely defined by the equations of the planes. In the second example - a pyramid: here it was necessary to think a little more and express one of the limits from the equation. And if the area V are they limited by non-flat surfaces? It is, of course, necessary to inspect the area in a certain way V .

Let's start with a "more terrible" example in order to feel the "situation close to combat."

Example 5. Arrange the limits of integration when passing from a triple integral, in which the region V- ellipsoid

.

Solution. Let the center of the ellipsoid be the origin, as shown in the figure above. Let's look at the ellipsoid from below. It is limited from below by a surface, which is that part of the surface of the ellipsoid that is located below the plane xOy z and the resulting expression with a minus sign will be the lower limit of integration over the variable z:

.

Now let's look at the ellipsoid from above. Here it is limited by a surface, which is that part of the ellipsoid’s surface that is located above the axis xOy. Therefore, we need to express from the ellipsoid equation z and the resulting expression will be the upper limit of integration over the variable z:

.

Projection of an ellipsoid onto a plane xOy is an ellipsoid. His equation:

To obtain the lower limit of integration over a variable y, need to be expressed y from the ellipsoid equation and take the resulting expression with a minus sign:

.

For the upper limit of integration over a variable y the same expression with a plus sign:

Regarding integration over a variable x, then the area V limited in depth by planes. Therefore, the limits of integration over a variable x can be represented as the coordinates of the rear and front boundaries of the area. In the case of an ellipsoid, they will be the values ​​of the semi-axis lengths taken with negative and positive signs a: x1 = − a And x2 = a .

Thus, the sequence of integrals for calculating the volume of an ellipsoid is as follows:

,

where “yrek first”, “yrek second”, “zet first” and “zet second” are the expressions obtained above. If you have the desire and courage to calculate this integral and thus the volume of the ellipsoid, then here is the answer: 4 πabc/3 .

The following examples are not as scary as the one just discussed. Moreover, they involve not only setting the limits of integration, but also calculating the triple integral itself. Test what you've learned by following the solution to the scary example. You still have to think when setting limits.

Example 6. Calculate triple integral

if the region of integration is limited by planes x + y = 1 , x + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Solution. The “resort” example is compared to example 5, since the limits of integration over “Y” and “Z” are uniquely defined. But we will have to deal with the limits of integration over "X". Projection of the domain of integration onto the plane xOy is a trapezoid ABCD.

In this example, it is more advantageous to project the trapezoid onto the axis Oy, otherwise, to calculate the triple integral, you will have to divide the figure into three parts. In Example 4 we started examining the integration region from below, and this is the usual procedure. But in this example, we begin the inspection from the side, or, if it’s easier, we put the figure on its side and consider that we are looking at it from below. We can find the limits of integration over "X" purely algebraically. To do this, we express “x” from the first and second equations given in the example condition. From the first equation we obtain the lower limit 1 − y, from the second - upper 4 − 2 y. Let us reduce this triple integral to a sequence of three definite integrals:

.

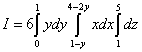Attention! In this example, the outermost integral is not over the “x” variable, but over the “y” variable, and the “average” integral is over the “x” variable! Here we applied a change in the order of integration, which we became familiar with when studying the double integral. This is due to the fact that, as already mentioned, we began to examine the integration region not from below, but from the side, that is, we projected it not onto the axis Ox, per axis Oy.

We calculate the innermost integral - over a variable z, considering x and y constants. We get:

We calculate the average integral - over a variable x. We get:

.

Finally, we calculate the outermost integral - over the variable y:

Answer: This triple integral is equal to 43.

Example 7. Calculate triple integral

,

if the region of integration is limited to surfaces x = 0 , y = 0 , z = 2 , x + y + z = 4 .

Solution. Region V(pyramid MNRP) is correct. Projection area V to the plane xOy is a triangle AOB.

The lower limits of integration for all variables are specified in the example condition. Let's find the upper limit of integration over "X". To do this, we express “x” from the fourth equation, considering “y” equal to zero and “ze” equal to two. We get x= 2 . Let's find the upper limit of integration over the "game". To do this, let’s express “Y” from the same fourth equation, considering “Z” to be equal to two, and “X” to be a variable value. We get y = 2 − x. And finally, we find the upper limit of integration over the variable “z”. To do this, let’s express “zet” from the same fourth equation, considering “y” and “zet” to be variable quantities. We get z = 4 − x − y .

Let us reduce this triple integral to a sequence of three definite integrals:

.

We calculate the innermost integral - over a variable z, considering x and y constants. We get:

.

We calculate the average integral - over a variable y. We get:

.

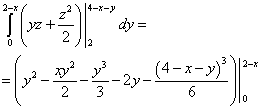We calculate the outermost integral - over a variable x and finally we find this triple integral:

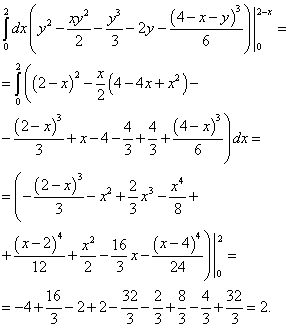
Answer: This triple integral is equal to 2.

Change of variables in the triple integral and cylindrical coordinates

If the projection of the integration domain onto any of the coordinate planes is a circle or part of a circle, then the triple integral is easier to calculate by passing to cylindrical coordinates. The cylindrical coordinate system is a generalization polar coordinate system to space. In a cylindrical coordinate system, a point M characterized by three quantities ( r, φ , z), Where r- distance from the origin to the projection N points M to the plane xOy, φ - angle between vector ON and positive axis direction Ox, z- applicate point M(picture below).

Rectangular coordinates x, y, z with cylindrical coordinates r, φ , z connect formulas

x = r cos φ ,

y = r sin φ ,

z = z .

In order to move to cylindrical coordinates in a triple integral, you need to express the integrand as a function of variables r, φ , z:

That is, the transition from rectangular to cylindrical coordinates is carried out as follows:

The triple integral in cylindrical coordinates is calculated in the same way as in Cartesian rectangular coordinates, by transforming it into a sequence of three definite integrals:

Example 8. Calculate triple integral

transition to cylindrical coordinates, where V- area limited by surfaces and.

Solution. Since the area V to the plane xOy is projected into a circle, then the coordinate φ varies from 0 to 2 π , and the coordinate r- from r=0 to r=1. A constant value in space corresponds to a cylinder. Considering the intersection of this cylinder with the region V, we get a change in ordinate z from z = r up to z= 1 . Let's move on to cylindrical coordinates and get.

1. Cylindrical coordinates represent the connection of polar coordinates in the xy plane with the usual Cartesian applicate z (Fig. 3).

Let M(x, y, z) be an arbitrary point in xyz space, P be the projection of point M onto the xy plane. Point M is uniquely determined by a triple of numbers - polar coordinates of point P, z - applicate of point M. Formulas connecting them with Cartesian ones have the form

Jacobian mapping (8)

Example 2.

Calculate integral

where T is the area limited by surfaces

Solution. Let us move in the integral to spherical coordinates using formulas (9). Then the domain of integration can be specified by the inequalities

And that means

Example 3 Find the volume of the body limited by:

We have: x 2 +y 2 +z 2 =8 - sphere of radius R= v8 with center at point O(000),

The upper part of the cone z 2 =x 2 +y 2 with the axis of symmetry Oz and the vertex at point O (Fig. 2.20).

Let's find the line of intersection of the sphere and the cone:

And since according to the condition z? 0, then

Circle R=2 lying in the z=2 plane.

Therefore, according to (2.28)

where the region U is bounded above

(part of the sphere),

(part of a cone);

region U is projected on the Oxy plane into region D - a circle of radius 2.

Therefore, it is advisable to go over to cylindrical coordinates in the triple integral using formulas (2.36):

The limits of change q, r are found in the area D v of the complete circle R = 2 with the center at point O, thereby: 0? q? 2р, 0? r? 2. Thus, the region U in cylindrical coordinates is given by the following inequalities:

notice, that

The procedure for calculating a triple integral is similar to the corresponding operation for a double integral. To describe it, we introduce the concept of a regular three-dimensional region:

Definition 9.1. A three-dimensional region V bounded by a closed surface S is called regular if:

1. any straight line parallel to the Oz axis and drawn through an internal point of the region intersects S at two points;
2. the entire region V is projected onto the Oxy plane into a regular two-dimensional region D;
3. any part of the region V, cut off from it by a plane parallel to any of the coordinate planes, has properties 1) and 2).

Let us consider a regular region V, bounded below and above by the surfaces z=χ(x,y) and z=ψ(x,y) and projected onto the Oxy plane into the regular region D, inside which x varies from a to b, limited by the curves y=φ1(x) and y=φ2(x) (Fig. 1). Let us define a continuous function f(x, y, z) in domain V.

Definition 9.2. Let us call the triple integral of the function f(x, y, z) over the region V an expression of the form:

The triple integral has the same properties as the double integral. We list them without proof, since they are proved similarly to the case of a double integral.

Calculation of the triple integral.

Theorem 9.1. The triple integral of the function f(x,y,z) over a regular domain V is equal to the triple integral over the same domain:

. (9.3)

Proof.

Let us divide the region V by planes parallel to the coordinate planes into n regular regions. Then from property 1 it follows that

where is the triple integral of the function f(x,y,z) over the region.

Using formula (9.2), the previous equality can be rewritten as:

From the condition of continuity of the function f(x,y,z) it follows that the limit of the integral sum on the right side of this equality exists and is equal to the triple integral. Then, passing to the limit at , we obtain:

Q.E.D.

Comment.

Similar to the case of a double integral, it can be proven that changing the order of integration does not change the value of the triple integral.

Example. Let us calculate the integral where V is a triangular pyramid with vertices at points (0, 0, 0), (1, 0, 0), (0, 1, 0) and (0, 0, 1). Its projection onto the Oxy plane is a triangle with vertices (0, 0), (1, 0) and (0, 1). The region is limited from below by the plane z = 0, and from above by the plane x + y + z = 1. Let’s move on to the threefold integral:

Factors that do not depend on the integration variable can be taken out of the sign of the corresponding integral:

Curvilinear coordinate systems in three-dimensional space.

1. Cylindrical coordinate system.

The cylindrical coordinates of the point P(ρ,φ,z) are the polar coordinates ρ, φ of the projection of this point onto the Oxy plane and the applicate of this point z (Fig. 2).

Formulas for the transition from cylindrical to Cartesian coordinates can be specified as follows:

x = ρ cosφ, y = ρ sinφ, z = z. (9.4)

1. Spherical coordinate system.

In spherical coordinates, the position of a point in space is determined by the linear coordinate ρ - the distance from the point to the origin of the Cartesian coordinate system (or the pole of the spherical system), φ - the polar angle between the positive semi-axis Ox and the projection of the point onto the Oxy plane, and θ - the angle between the positive semi-axis of the axis Oz and segment OP (Fig. 3). Wherein

Let us set the formulas for the transition from spherical to Cartesian coordinates:

x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9.5)

Jacobian and its geometric meaning.

Let us consider the general case of changing variables in a double integral. Let a region D be given in the Oxy plane, bounded by a line L. Let us assume that x and y are single-valued and continuously differentiable functions of new variables u and v:

x = φ(u, v), y = ψ(u, v). (9.6)

Let us consider the rectangular coordinate system Ouv, the point P΄(u, v) of which corresponds to the point P(x, y) from the region D. All such points form a region D΄ in the Ouv plane, bounded by the line L΄. We can say that formulas (9.6) establish a one-to-one correspondence between the points of the regions D and D΄. In this case, the lines u = const and

v = const in the Ouv plane will correspond to some lines in the Oxy plane.

Let us consider a rectangular area ΔS΄ in the Ouv plane, bounded by the straight lines u = const, u+Δu = const, v = const and v+Δv = const. It will correspond to a curved area ΔS in the Oxy plane (Fig. 4). The areas of the areas under consideration will also be denoted by ΔS΄ and ΔS. In this case, ΔS΄ = Δu Δv. Let's find the area ΔS. Let us denote the vertices of this curvilinear quadrilateral P1, P2, P3, P4, where

P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);

P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);

P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);

P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).

Let us replace the small increments Δu and Δv with the corresponding differentials. Then

In this case, the quadrilateral P1 P2 P3 P4 can be considered a parallelogram and its area can be determined using the formula from analytical geometry:

(9.7)

Definition 9.3. The determinant is called the functional determinant or Jacobian of the functions φ(x, y) and ψ(x, y).

Passing to the limit at in equality (9.7), we obtain the geometric meaning of the Jacobian:

that is, the module of the Jacobian is the limit of the ratio of the areas of infinitesimal areas ΔS and ΔS΄.

Comment. In a similar way, we can define the concept of a Jacobian and its geometric meaning for an n-dimensional space: if x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un),…, xn = φ(u1 , u2,…, un), then

(9.8)

In this case, the module of the Jacobian gives a limit to the ratio of the “volumes” of small regions of the spaces x1, x2,..., xn and u1, u2,..., un.

Change of variables in multiple integrals.

Let us study the general case of change of variables using the example of a double integral.

Let a continuous function z = f(x,y) be given in domain D, each value of which corresponds to the same value of the function z = F(u, v) in domain D΄, where

F(u, v) = f(φ(u, v), ψ(u, v)). (9.9)

Consider the integral sum

where the integral sum on the right is taken over the domain D΄. Passing to the limit at , we obtain a formula for transforming coordinates in the double integral.

Transformation of double integral of rectangular coordinates, to polar coordinates
, related to rectangular coordinates by the relations
,
, is carried out according to the formula

If the domain of integration
limited to two beams
,
(
), coming out of the pole, and two curves
And
, then the double integral is calculated using the formula

.

Example 1.3. Calculate the area of ​​the figure bounded by these lines:
,
,
,
.

Solution. To calculate the area of ​​an area
Let's use the formula:
.

.

1.2. Triple integrals

The basic properties of triple integrals are similar to the properties of double integrals.

In Cartesian coordinates, the triple integral is usually written as follows:

.

If
, then the triple integral over the area numerically equal to the volume of the body :

.

Triple integral calculation

Let the domain of integration bounded below and above, respectively, by single-valued continuous surfaces
,
, and the projection of the region to the coordinate plane
there is a flat area
(Fig. 1.6).

.

Example 1.4. Calculate
, Where - a body limited by planes:

Triple integral in cylindrical coordinates

When moving from Cartesian coordinates
to cylindrical coordinates
(Fig. 1.9) associated with
relations
,
,
, and

Region
, bounded by a curve
, will take the form, or
, while the polar angle
. As a result we have

.

2. Elements of field theory

Let us first recall the methods for calculating curvilinear and surface integrals.

Calculation of a curvilinear integral over coordinates of functions defined on a curve , reduces to calculating a definite integral of the form

if the curve specified parametrically
corresponds to the starting point of the curve , A
- its end point.

Calculation of the surface integral of a function
, defined on a two-sided surface , comes down to calculating a double integral, for example, of the form

if the surface , given by the equation
, is uniquely projected onto the plane
to the region
. Here - angle between unit normal vector to the surface and axis
:

Side of the surface required by the problem conditions is determined by the choice of the appropriate sign in formula (2.3).

Definition 2.1. Vector field
called the vector function of a point
along with its scope:

Vector field
characterized by a scalar quantity – divergence:

Definition 2.2. Flow vector field
through the surface called the surface integral:

Where - unit normal vector to the selected side of the surface , A
- scalar product of vectors And .

Definition 2.3. Circulation vector field

By closed curve called a curvilinear integral

Where
.

Ostrogradsky-Gauss formula establishes a connection between the vector field flow through a closed surface and field divergence:

Where - surface bounded by a closed contour , A is the unit normal vector to this surface. The direction of the normal must be consistent with the direction of the contour traversal .

Example 2.1. Calculate Surface Integral

,

Where - outer part of the cone
(
), cut off by a plane
(Figure 2.1).

Solution. Surface uniquely projected into the region
plane
, and the integral is calculated using formula (2.2).

Region
there is a circle
. Therefore, in the last integral we move to polar coordinates, while
,
:

Example 2.2. Find the divergence and curl of a vector field
.

Solution. Using formula (2.4) we obtain

The rotor of a given vector field is found using formula (2.5)

Example 2.3. Find the flux of a vector field
through part of the plane :
, located in the first octant (the normal forms an acute angle with the axis
).

Where
- plane projection on
(Fig. 2.4).

Example 2.4. Compute the flux of a vector field through a closed surface , formed by the plane
and part of the cone
(
) (Fig. 2.2).

Solution. Let us use the Ostrogradsky-Gauss formula (2.8)

.

Let's find the divergence of the vector field according to formula (2.4):

Where
is the volume of the cone over which integration is carried out. Let's use the well-known formula to calculate the volume of a cone
(- radius of the base of the cone, - his high). In our case we get
. Finally we get

.

Example 2.5. Calculate the circulation of a vector field
along the contour , formed by the intersection of surfaces
And
(
). Check the result using the Stokes formula.

Solution. The intersection of these surfaces is a circle
,
(Fig. 2.1). The traversal direction is usually chosen so that the area limited by it remains to the left. Let's write the parametric equations of the contour :

and the parameter varies from before
. Using formula (2.7), taking into account (2.1) and (2.10), we obtain

.

Let us now apply the Stokes formula (2.9). As a surface , stretched on the contour , you can take part of the plane
. Normal direction
to this surface is consistent with the direction of the contour traversal . The curl of a given vector field is calculated in Example 2.2:
. Therefore, the desired circulation

Where
- area of ​​the region
.
- circle radius
, where