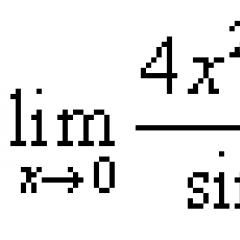The second remarkable limit. The first remarkable limit: examples of finding, problems and detailed solutions Limit cos 1 x
There are several remarkable limits, but the most famous are the first and second remarkable limits. The remarkable thing about these limits is that they are widely used and with their help one can find other limits encountered in numerous problems. This is what we will do in the practical part of this lesson. To solve problems by reducing them to the first or second remarkable limit, there is no need to reveal the uncertainties contained in them, since the values of these limits have long been deduced by great mathematicians.
The first remarkable limit is called the limit of the ratio of the sine of an infinitesimal arc to the same arc, expressed in radian measure:
Let's move on to solving problems at the first remarkable limit. Note: if there is a trigonometric function under the limit sign, this is an almost sure sign that this expression can be reduced to the first remarkable limit.
Example 1. Find the limit.
Solution. Substitution instead x zero leads to uncertainty:
![]() .
.
The denominator is sine, therefore, the expression can be brought to the first remarkable limit. Let's start the transformation:
![]() .
.
The denominator is the sine of three X, but the numerator has only one X, which means you need to get three X in the numerator. For what? To introduce 3 x = a and get the expression .
And we come to a variation of the first remarkable limit:
because it doesn’t matter which letter (variable) in this formula stands instead of X.
We multiply X by three and immediately divide:
 .
.
In accordance with the first remarkable limit noticed, we replace the fractional expression:
Now we can finally solve this limit:
 .
.
Example 2. Find the limit.
Solution. Direct substitution again leads to the “zero divided by zero” uncertainty:
![]() .
.
To get the first remarkable limit, it is necessary that the x under the sine sign in the numerator and just the x in the denominator have the same coefficient. Let this coefficient be equal to 2. To do this, imagine the current coefficient for x as below, performing operations with fractions, we obtain:
 .
.
Example 3. Find the limit.
Solution. When substituting, we again get the uncertainty “zero divided by zero”:
 .
.
You probably already understand that from the original expression you can get the first wonderful limit multiplied by the first wonderful limit. To do this, we decompose the squares of the x in the numerator and the sine in the denominator into identical factors, and in order to get the same coefficients for the x and sine, we divide the x in the numerator by 3 and immediately multiply by 3. We get:
 .
.
Example 4. Find the limit.
Solution. Once again we get the uncertainty “zero divided by zero”:
![]() .
.
We can obtain the ratio of the first two remarkable limits. We divide both the numerator and the denominator by x. Then, so that the coefficients for sines and xes coincide, we multiply the upper x by 2 and immediately divide by 2, and multiply the lower x by 3 and immediately divide by 3. We get:

Example 5. Find the limit.
Solution. And again the uncertainty of “zero divided by zero”:
We remember from trigonometry that tangent is the ratio of sine to cosine, and the cosine of zero is equal to one. We carry out the transformations and get:
 .
.
Example 6. Find the limit.
Solution. The trigonometric function under the sign of a limit again suggests the use of the first remarkable limit. We represent it as the ratio of sine to cosine.
The first remarkable limit is often used to calculate limits containing sine, arcsine, tangent, arctangent and the resulting uncertainties of zero divided by zero.
Formula
The formula for the first remarkable limit is: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
We note that for $ \alpha\to 0 $ we get $ \sin\alpha \to 0 $, thus we have zeros in the numerator and denominator. Thus, the formula of the first remarkable limit is needed to reveal the uncertainties $ \frac(0)(0) $.
To apply the formula, two conditions must be met:
- The expressions contained in the sine and the denominator of the fraction are the same
- Expressions in the sine and denominator of a fraction tend to zero
Attention! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Although the expressions under the sine and in the denominator are the same, however $ 2x^2+1 = 1 $, at $ x\to 0 $. The second condition is not met, so you CANNOT apply the formula!
Consequences
Quite rarely in tasks you can see a pure first wonderful limit in which you could immediately write down the answer. In practice, everything looks a little more complicated, but for such cases it will be useful to know the consequences of the first remarkable limit. Thanks to them, you can quickly calculate the required limits.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Examples of solutions
Let's consider the first remarkable limit, examples of its solution for calculating limits containing trigonometric functions and uncertainty $ \bigg[\frac(0)(0)\bigg] $
| Example 1 |
| Calculate $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Solution |
|
Let's look at the limit and notice that it contains a sine. Next, we substitute $ x = 0 $ into the numerator and denominator and get the uncertainty zero divided by zero: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0) $$ Already two signs that we need to apply a wonderful limit, but there is a small nuance: we cannot immediately apply the formula, since the expression under the sine sign differs from the expression in the denominator. And we need them to be equal. Therefore, using elementary transformations of the numerator, we will turn it into $2x$. To do this, we will take the two out of the denominator of the fraction as a separate factor. It looks like this: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Please note , that at the end $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ was obtained according to the formula. If you cannot solve your problem, then send it to us. We will provide detailed solution. You will be able to view the progress of the calculation and gain information. This will help you get your grade from your teacher in a timely manner! |
| Answer |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Example 2 |
| Find $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Solution |
|
As always, you first need to know the type of uncertainty. If it is zero divided by zero, then we pay attention to the presence of a sine: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ This uncertainty allows us to use the formula of the first remarkable limit, but the expression from the denominator is not equal to the argument of the sine? Therefore, the formula cannot be applied “head-on”. It is necessary to multiply and divide the fraction by the argument of the sine: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x-x^4)(x ^3+2x)) = $$ Now we write down the properties of the limits: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x-x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ The second limit fits the formula exactly and is equal to one: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x)(2x-x^4) = $$ Substitute again $ x = 0 $ into a fraction and we get the uncertainty $ \frac(0)(0) $. To eliminate it, it is enough to take $ x $ out of brackets and reduce it by: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Answer |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Example 4 |
| Calculate $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Solution |
|
Let's start the calculation with the substitution $ x=0 $. As a result, we obtain the uncertainty $ \frac(0)(0) $. The limit contains a sine and a tangent, which hints at a possible development of the situation using the formula of the first remarkable limit. Let's transform the numerator and denominator of the fraction into a formula and consequence: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Now we see that in the numerator and denominator there are expressions that fit the formula and consequences. The sine argument and the tangent argument are the same for the corresponding denominators $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Answer |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
The article: “The first remarkable limit, examples of solutions” talked about cases in which it is advisable to use this formula and its consequences.
The first remarkable limit is the following equality:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Since for $\alpha\to(0)$ we have $\sin\alpha\to(0)$, they say that the first remarkable limit reveals an uncertainty of the form $\frac(0)(0)$. Generally speaking, in formula (1), instead of the variable $\alpha$, any expression can be placed under the sine sign and in the denominator, as long as two conditions are met:
- The expressions under the sine sign and in the denominator simultaneously tend to zero, i.e. there is uncertainty of the form $\frac(0)(0)$.
- The expressions under the sine sign and in the denominator are the same.
Corollaries from the first remarkable limit are also often used:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(equation)
Eleven examples are solved on this page. Example No. 1 is devoted to the proof of formulas (2)-(4). Examples No. 2, No. 3, No. 4 and No. 5 contain solutions with detailed comments. Examples No. 6-10 contain solutions with virtually no comments, because detailed explanations were given in previous examples. The solution uses some trigonometric formulas that can be found.
Let me note that the presence of trigonometric functions coupled with the uncertainty $\frac (0) (0)$ does not necessarily mean the application of the first remarkable limit. Sometimes simple trigonometric transformations are sufficient - for example, see.
Example No. 1
Prove that $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha )(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Since $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, then:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Since $\lim_(\alpha\to(0))\cos(0)=1$ and $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , That:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Let's make the replacement $\alpha=\sin(y)$. Since $\sin(0)=0$, then from the condition $\alpha\to(0)$ we have $y\to(0)$. In addition, there is a neighborhood of zero in which $\arcsin\alpha=\arcsin(\sin(y))=y$, so:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ has been proven.
c) Let's make the replacement $\alpha=\tg(y)$. Since $\tg(0)=0$, then the conditions $\alpha\to(0)$ and $y\to(0)$ are equivalent. In addition, there is a neighborhood of zero in which $\arctg\alpha=\arctg\tg(y))=y$, therefore, based on the results of point a), we will have:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ has been proven.
Equalities a), b), c) are often used along with the first remarkable limit.
Example No. 2
Calculate the limit $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.
Since $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ and $\lim_( x\to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. and both the numerator and denominator of the fraction simultaneously tend to zero, then here we are dealing with an uncertainty of the form $\frac(0)(0)$, i.e. done. In addition, it is clear that the expressions under the sine sign and in the denominator coincide (i.e., and is satisfied):
So, both conditions listed at the beginning of the page are met. It follows from this that the formula is applicable, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7))=1$.
Answer: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Example No. 3
Find $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Since $\lim_(x\to(0))\sin(9x)=0$ and $\lim_(x\to(0))x=0$, then we are dealing with an uncertainty of the form $\frac(0 )(0)$, i.e. done. However, the expressions under the sine sign and in the denominator do not coincide. Here you need to adjust the expression in the denominator to the desired form. We need the expression $9x$ to be in the denominator, then it will become true. Essentially, we're missing a factor of $9$ in the denominator, which isn't that hard to enter—just multiply the expression in the denominator by $9$. Naturally, to compensate for multiplication by $9$, you will have to immediately divide by $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Now the expressions in the denominator and under the sine sign coincide. Both conditions for the limit $\lim_(x\to(0))\frac(\sin(9x))(9x)$ are satisfied. Therefore, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. And this means that:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Answer: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Example No. 4
Find $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Since $\lim_(x\to(0))\sin(5x)=0$ and $\lim_(x\to(0))\tg(8x)=0$, here we are dealing with uncertainty of the form $\frac(0)(0)$. However, the form of the first remarkable limit is violated. A numerator containing $\sin(5x)$ requires a denominator of $5x$. In this situation, the easiest way is to divide the numerator by $5x$, and immediately multiply by $5x$. In addition, we will perform a similar operation with the denominator, multiplying and dividing $\tg(8x)$ by $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Reducing by $x$ and taking the constant $\frac(5)(8)$ outside the limit sign, we get:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Note that $\lim_(x\to(0))\frac(\sin(5x))(5x)$ fully satisfies the requirements for the first remarkable limit. To find $\lim_(x\to(0))\frac(\tg(8x))(8x)$ the following formula is applicable:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Answer: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Example No. 5
Find $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Since $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (remember that $\cos(0)=1$) and $\lim_(x\to(0))x^2=0$, then we are dealing with uncertainty of the form $\frac(0)(0)$. However, in order to apply the first remarkable limit, you should get rid of the cosine in the numerator, moving on to sines (in order to then apply the formula) or tangents (in order to then apply the formula). This can be done with the following transformation:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Let's go back to the limit:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
The fraction $\frac(\sin^2(5x))(x^2)$ is already close to the form required for the first remarkable limit. Let's work a little with the fraction $\frac(\sin^2(5x))(x^2)$, adjusting it to the first remarkable limit (note that the expressions in the numerator and under the sine must match):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Let's return to the limit in question:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Answer: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Example No. 6
Find the limit $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Since $\lim_(x\to(0))(1-\cos(6x))=0$ and $\lim_(x\to(0))(1-\cos(2x))=0$, then we are dealing with uncertainty $\frac(0)(0)$. Let us reveal it with the help of the first remarkable limit. To do this, let's move from cosines to sines. Since $1-\cos(2\alpha)=2\sin^2(\alpha)$, then:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Passing to sines in the given limit, we will have:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Answer: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Example No. 7
Calculate the limit $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ subject to $\alpha\neq\ beta$.
Detailed explanations were given earlier, but here we simply note that again there is uncertainty $\frac(0)(0)$. Let's move from cosines to sines using the formula
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Using this formula, we get:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\right| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Answer: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alpha^2)(2)$.
Example No. 8
Find the limit $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Since $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (remember that $\sin(0)=\tg(0)=0$) and $\lim_(x\to(0))x^3=0$, then here we are dealing with uncertainty of the form $\frac(0)(0)$. Let's break it down as follows:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Answer: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Example No. 9
Find the limit $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Since $\lim_(x\to(3))(1-\cos(x-3))=0$ and $\lim_(x\to(3))(x-3)\tg\frac(x -3)(2)=0$, then there is uncertainty of the form $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable $\alpha \to 0$). The easiest way is to introduce the variable $t=x-3$. However, for the sake of convenience of further transformations (this benefit can be seen in the course of the solution below), it is worth making the following replacement: $t=\frac(x-3)(2)$. I note that both replacements are applicable in this case, it’s just that the second replacement will allow you to work less with fractions. Since $x\to(3)$, then $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Answer: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Example No. 10
Find the limit $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2 )$.
Once again we are dealing with uncertainty $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable is $\alpha\to(0)$). The easiest way is to introduce the variable $t=\frac(\pi)(2)-x$. Since $x\to\frac(\pi)(2)$, then $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Example No. 11
Find the limits $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
In this case we don't have to use the first wonderful limit. Please note that both the first and second limits contain only trigonometric functions and numbers. Often in examples of this kind it is possible to simplify the expression located under the limit sign. Moreover, after the aforementioned simplification and reduction of some factors, the uncertainty disappears. I gave this example for only one purpose: to show that the presence of trigonometric functions under the limit sign does not necessarily mean the use of the first remarkable limit.
Since $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (remember that $\sin\frac(\pi)(2)=1$ ) and $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (let me remind you that $\cos\frac(\pi)(2)=0$), then we have dealing with uncertainty of the form $\frac(0)(0)$. However, this does not mean that we will need to use the first wonderful limit. To reveal the uncertainty, it is enough to take into account that $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
There is a similar solution in Demidovich’s solution book (No. 475). As for the second limit, as in the previous examples in this section, we have an uncertainty of the form $\frac(0)(0)$. Why does it arise? It arises because $\tg\frac(2\pi)(3)=-\sqrt(3)$ and $2\cos\frac(2\pi)(3)=-1$. We use these values to transform the expressions in the numerator and denominator. The goal of our actions is to write down the sum in the numerator and denominator as a product. By the way, often within a similar type it is convenient to change a variable, made in such a way that the new variable tends to zero (see, for example, examples No. 9 or No. 10 on this page). However, in this example there is no point in replacing, although if desired, replacing the variable $t=x-\frac(2\pi)(3)$ is not difficult to implement.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
As you can see, we didn't have to apply the first wonderful limit. Of course, you can do this if you want (see note below), but it is not necessary.
What is the solution using the first remarkable limit? show\hide
Using the first remarkable limit we get:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ right))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Formulas, properties and theorems used in solving problems that can be solved using the first remarkable limit are collected. Detailed solutions of examples using the first remarkable limit of its consequences are given.
ContentSee also: Proof of the first remarkable limit and its consequences
Applied formulas, properties and theorems
Here we will look at examples of solutions to problems involving calculating limits that use the first remarkable limit and its consequences.
Listed below are the formulas, properties and theorems that are most often used in this type of calculation.
- The first remarkable limit and its consequences:
. - Trigonometric formulas for sine, cosine, tangent and cotangent:
;
;
;
at , ;
;
;
;
;
;
.
Examples of solutions
Example 1
For this.
1. Calculate the limit.
Since the function is continuous for all x, including at the point, then
.
2. Since the function is not defined (and, therefore, is not continuous) for , we need to make sure that there exists a punctured neighborhood of the point on which . In our case, at . Therefore this condition is met.
3. Calculate the limit. In our case, it is equal to the first remarkable limit:
.
Thus,
.
Similarly, we find the limit of the function in the denominator:
;
at ;
.
And finally, we apply the arithmetic properties of the function limit:
.
Let's apply.
At . From the table of equivalent functions we find:
at ; at .
Then .
Example 2
Find the limit:
.
Solution using the first remarkable limit
At , , . This is the uncertainty of the form 0/0 .
Let's transform the function beyond the limit sign:
.
Let's make a change of variable. Since and for , then
.
Similarly we have:
.
Since the cosine function is continuous on the entire number line, then
.
We apply the arithmetic properties of limits:
.
Solution using equivalent functions
Let us apply the theorem on replacing functions with equivalent ones in the quotient limit.
At . From the table of equivalent functions we find:
at ; at .
Then .
Example 3
Find the limit:
.
Let's substitute the numerator and denominator of the fraction:
;
.
This is the uncertainty of the form 0/0
.
Let's try to solve this example using the first wonderful limit. Since the value of the variable in it tends to zero, we will make a substitution so that the new variable tends not to , but to zero. To do this, we move from x to a new variable t, making the substitution , . Then at , .
We first transform the function beyond the limit sign by multiplying the numerator and denominator of the fraction by:
.
Let's substitute and use the trigonometric formulas given above.
;
;
.
The function is continuous at . We find its limit:
.
Let's transform the second fraction and apply the first wonderful limit:
.
We made a substitution in the numerator of the fraction.
We apply the property of the limit of a product of functions:
.
Example 4
Find the limit:
.
At , , . We have uncertainty of the form 0/0 .
Let's transform the function under the limit sign. Let's apply the formula:
.
Let's substitute:
.
Let's transform the denominator:
.
Then
.
Since and for , we make the substitution and apply the theorem on the limit of a complex function and the first remarkable limit:
.
We apply the arithmetic properties of the limit of a function:
.
Example 5
Find the limit of the function:
.
It is easy to see that in this example we have an uncertainty of the form 0/0
. To reveal it, we apply the result of the previous problem, according to which
.
Let us introduce the notation:
(A5.1). Then
(A5.2) .
From (A5.1) we have:
.
Let's substitute it into the original function:
,
Where ,
,
;
;
;
.
We use (A5.2) and the continuity of the cosine function. We apply the arithmetic properties of the limit of a function.
,
here m is a non-zero number, ;
;
;
.
Example 6
Find the limit:
.
When , the numerator and denominator of the fraction tend to 0
. This is the uncertainty of the form 0/0
. To expand it, we transform the numerator of the fraction:
.
Let's apply the formula:
.
Let's substitute:
;
,
Where .
Let's apply the formula:
.
Let's substitute:
;
,
Where .
Numerator of fraction:
.
The function behind the limit sign will take the form:
.
Let's find the limit of the last factor, taking into account its continuity at :
.
Let's apply the trigonometric formula:
.
Let's substitute
. Then
.
Let's divide the numerator and denominator by , apply the first remarkable limit and one of its consequences:
.
Finally we have:
.
Note 1: You could also apply the formula
.
Then .
|
The first remarkable limit. The derivation of the first remarkable limit is of interest from the point of view of the application of the theory of limits, and therefore we offer you it almost in its entirety. Let's consider the behavior of the function |
Then clearly the area DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
S D MOA = 
S MOA =  =
= S D C OA =
S D C OA = 
Returning to the mentioned inequality and doubling it, we get:
sin x < x < tg x.
After division by term sin x:
 or
or 
Because the  , then the variable
, then the variable  is concluded between two quantities that have the same limit, i.e. , based on the theorem on the limit of the intermediate function of the previous paragraph, we have:
is concluded between two quantities that have the same limit, i.e. , based on the theorem on the limit of the intermediate function of the previous paragraph, we have:
-first wonderful limit .
Example. Calculate the limits of the functions using the first remarkable limit:





Answer. 1) 1, 2) 0, 3)

Exercise: Calculate the limit of a function using the first remarkable limit:

Answer: -2.
The second remarkable limit.
To derive the second remarkable limit, we introduce the definition of the number e:
Definition.
Variable Limit  at
at  called a numbere
:
called a numbere
:
- The second wonderful limit
Number e– irrational number. Its value to ten true decimal places is usually rounded to one true decimal place:
e= 2.7182818284..."2.7.
Theorem. Function  atX
tending to infinity, tending to the limite
:
atX
tending to infinity, tending to the limite
:

Example. Calculate the limits of the functions:

Solution.
According to the properties of limits, the limit of the degree is equal to the degree of the limit, i.e.:


Moreover, in a similar way it can be proven that 


Answer. 1)e 3 , 2)e 2 , 3)e 4 .
Exercise. Calculate the limit of the function using the second remarkable limit:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ABOUT  answer: e -5
answer: e -5
Continuity of a function Continuity of a function at a point
Definition. Functionf ( x ), x Î ( a ; b ) x O Î ( a ; b ), if the limit of the functionf ( x ) at the pointX O exists and is equal to the value of the function at this point:
 .
.
According to this definition, the continuity of the function f(x) at the point X O means the following conditions are met:
function f(x) must be defined at the point X O ;
y function f(x) there must be a limit at the point X O ;
limit of a function f(x) at the point X O must match the value of the function at this point.
Example.
Function f(x)
=
x 2
defined on the entire number line and continuous at a point X= 1 because f( 1)
= 1 and 
Continuity of a function on a set
Definition. Functionf(x), is called continuous on the interval(a; b), if it is continuous at every point of this interval.
If a function is continuous at some point, then this point is called the point of continuity of this function. In cases where the limit of a function at a given point does not exist or its value does not coincide with the value of the function at a given point, then the function is called discontinuous at this point, and the point itself is called a discontinuity point of the function f(x).
Properties of continuous functions.
1) The sum of a finite number of functions continuous at a point A,
2) Product of a finite number of functions continuous at a point A, there is a function that is continuous at this point.
3) The ratio of a finite number of functions continuous at a point A, is a function that is continuous at this point if the value of the function in the denominator is different from zero at the point A.
Example.
Function f(x) = x P, Where n Î N, is continuous on the entire number line. This fact can be proven using property 2 and the continuity of the function f(x) = x.
Function f(x) = sx P (With– constant) is continuous on the entire number line, based on property 2 and example 1.
Theorem 1. A polynomial is a function that is continuous on the entire number line.
Theorem 2 . Any fractional rational function is continuous at every point of its domain of definition.
Example.

Definition
Functionf
(
x
)
called continuous at a pointx = a
, if at this point its increment  tends to zero when the argument increment
tends to zero when the argument increment  tends to zero, or in other words: functionf
(X)
called continuous at a pointx = a
, if at this point an infinitesimal increment of the argument corresponds to an infinitesimal increment of the function, i.e. if
tends to zero, or in other words: functionf
(X)
called continuous at a pointx = a
, if at this point an infinitesimal increment of the argument corresponds to an infinitesimal increment of the function, i.e. if 
 at
at  . To do this, consider a circle of radius 1; let us denote the central angle of the MOB by X, wherein
. To do this, consider a circle of radius 1; let us denote the central angle of the MOB by X, wherein  .
.