Find the length of side ab online. Equation of a straight line with slope
Numerically equal to the tangent of the angle (constituting the smallest rotation from the Ox axis to the Oy axis) between the positive direction of the abscissa axis and the given straight line.
The tangent of an angle can be calculated as the ratio of the opposite side to the adjacent side. k is always equal to , that is, the derivative of the equation of a straight line with respect to x.
For positive values of the slope k and zero shift coefficient b the straight line will lie in the first and third quadrants (in which x And y both positive and negative). At the same time, large values of the angular coefficient k a steeper straight line will correspond, and a flatter one will correspond to smaller ones.
Straight and perpendicular if , and parallel if .
Notes
Wikimedia Foundation. 2010.
- Iphit (king of Elis)
- List of Decrees of the President of the Russian Federation “On awarding state awards” for 2001
See what “Angular coefficient of a straight line” is in other dictionaries:
slope (direct)- - Topics oil and gas industry EN slope... Technical Translator's Guide
Slope factor- (mathematical) number k in the equation of a straight line on the plane y = kx+b (see Analytical geometry), characterizing the slope of the straight line relative to the x-axis. In the rectangular coordinate system of U.K. k = tan φ, where φ is the angle between ... ... Great Soviet Encyclopedia
Equations of a line
ANALYTIC GEOMETRY- a section of geometry that studies the simplest geometric objects using elementary algebra based on the coordinate method. The creation of analytical geometry is usually attributed to R. Descartes, who outlined its foundations in the last chapter of his... ... Collier's Encyclopedia
Reaction time- Reaction time (RT) measurement is probably the most venerable subject in empirical psychology. It originated in the field of astronomy, in 1823, with the measurement of individual differences in the speed of perception of a star crossing a telescope line. These … Psychological Encyclopedia
MATHEMATICAL ANALYSIS- a branch of mathematics that provides methods for quantitative research of various processes of change; deals with the study of the rate of change (differential calculus) and the determination of the lengths of curves, areas and volumes of figures limited by curved contours and ... Collier's Encyclopedia
Straight- This term has other meanings, see Direct (meanings). The straight line is one of the basic concepts of geometry, that is, it does not have an exact universal definition. In a systematic presentation of geometry, a straight line is usually taken as one... ... Wikipedia
Straight line- Image of straight lines in a rectangular coordinate system Straight line is one of the basic concepts of geometry. In a systematic presentation of geometry, a straight line is usually taken as one of the initial concepts, which is only indirectly defined... ... Wikipedia
Direct- Image of straight lines in a rectangular coordinate system Straight line is one of the basic concepts of geometry. In a systematic presentation of geometry, a straight line is usually taken as one of the initial concepts, which is only indirectly defined... ... Wikipedia
Minor shaft- Not to be confused with the term "Ellipsis". Ellipse and its foci Ellipse (ancient Greek ἔλλειψις deficiency, in the sense of lack of eccentricity up to 1) the locus of points M of the Euclidean plane for which the sum of the distances from two given points is F1... ... Wikipedia
Let on a plane where there is a rectangular Cartesian coordinate system, a straight line l passes through point M 0 parallel to the direction vector A (Fig. 96).
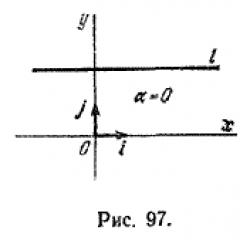
If straight l crosses the O axis X(at point N), then at an angle of a straight line l with O axis X we will understand the angle α by which it is necessary to rotate the O axis X around point N in the direction opposite to clockwise rotation, so that the O axis X coincided with a straight line l. (This refers to an angle less than 180°.)
This angle is called inclination angle straight. If straight l parallel to the O axis X, then the angle of inclination is assumed to be zero (Fig. 97).
The tangent of the angle of inclination of a straight line is called slope of a straight line and is usually denoted by the letter k:
tan α = k. (1)
If α = 0, then k= 0; this means that the line is parallel to the O axis X and its slope is zero.
If α = 90°, then k= tan α does not make sense: this means that a straight line perpendicular to the O axis X(i.e. parallel to the O axis at), has no slope.
The slope of a line can be calculated if the coordinates of any two points on this line are known. Let two points on a line be given: M 1 ( x 1 ; at 1) and M 2 ( x 2 ; at 2) and let, for example, 0< α < 90°, а x 2 > x 1 , at 2 > at 1 (Fig. 98).
Then from the right triangle M 1 PM 2 we find
$$ k=tga = \frac(|M_2 P|)(|M_1 P|) = \frac(y_2 - y_1)(x_2 - x_1) $$
$$ k=\frac(y_2 - y_1)(x_2 - x_1) \;\; (2)$$
It is similarly proven that formula (2) is also true in the case of 90°< α < 180°.
Formula (2) becomes meaningless if x 2 - x 1 = 0, i.e. if straight l parallel to the O axis at. There is no slope coefficient for such straight lines.
Task 1. Determine the angular coefficient of the prim passing through the points
M 1 (3; -5) and M 2 (5; -7).
Substituting the coordinates of points M 1 and M 2 into formula (2), we obtain
\(k=\frac(-7-(-5))(5-3)\) or k = -1
Task 2. Determine the slope of the straight line passing through the points M 1 (3; 5) and M 2 (3; -2).
Because x 2 - x 1 = 0, then equality (2) loses its meaning. There is no slope for this straight line. The straight line M 1 M 2 is parallel to the O axis at.
Task 3. Determine the slope of the line passing through the origin and point M 1 (3; -5)
In this case, point M 2 coincides with the origin. Applying formula (2), we obtain
$$ k=\frac(y_2 - y_1)(x_2 - x_1)=\frac(0-(-5))(0-3)= -\frac(5)(3); \;\; k= -\frac(5)(3) $$
Let's create an equation of a straight line with an angle coefficient k, passing through the point
M 1 ( x 1 ; at 1). According to formula (2), the angular coefficient of a straight line is found from the coordinates of its two points. In our case, point M 1 is given, and as the second point we can take any point M( X; at) the desired straight line.
If point M lies on a straight line that passes through point M 1 and has an angular coefficient k, then by virtue of formula (2) we have
$$ \frac(y-y_1)(x-x_1)=k \;\; (3) $$
If point M does not lie on a line, then equality (3) does not hold. Consequently, equality (3) is the equation of the line passing through the point M 1 ( x 1 ; at 1) with slope k; this equation is usually written as
y- y 1 = k(x - x 1). (4)
If the straight line intersects the O axis at at some point (0; b), then equation (4) takes the form
at - b = k (X- 0),
y = kx + b. (5)
This equation is called equation of a straight line with slope k and initial ordinate b.
Task 4. Find the angle of inclination of the straight line √3 x + 3at - 7 = 0.
Let us reduce this equation to the form
$$ y= =\frac(1)(\sqrt3)x + \frac(7)(3) $$
Hence, k= tan α = - 1 / √ 3, whence α = 150°
Task 5. Write an equation for a straight line passing through point P(3; -4) with an angle coefficient k = 2 / 5
Substituting k = 2 / 5 , x 1 = 3, y 1 = - 4 into equation (4), we get
at - (- 4) = 2 / 5 (X- 3) or 2 X - 5at - 26 = 0.
Task 6. Write an equation for a straight line passing through point Q (-3; 4) and a component with the positive direction of the O axis X angle 30°.
If α = 30°, then k= tan 30° = √ 3 / 3 . Substituting into equation (4) the values x 1 , y 1 and k, we get
at -4 = √ 3 / 3 (x+ 3) or √3 x-3y + 12 + 3√3 = 0.
In mathematics, one of the parameters that describes the position of a line on the Cartesian coordinate plane is the angular coefficient of this line. This parameter characterizes the slope of the straight line to the abscissa axis. To understand how to find the slope, first recall the general form of the equation of a straight line in the XY coordinate system.
In general, any straight line can be represented by the expression ax+by=c, where a, b and c are arbitrary real numbers, but a 2 + b 2 ≠ 0.
Using simple transformations, such an equation can be brought to the form y=kx+d, in which k and d are real numbers. The number k is the slope, and the equation of a line of this type is called an equation with a slope. It turns out that to find the slope, you simply need to reduce the original equation to the form indicated above. For a more complete understanding, consider a specific example:
Problem: Find the slope of the line given by the equation 36x - 18y = 108
Solution: Let's transform the original equation.
Answer: The required slope of this line is 2.
If, during the transformation of the equation, we received an expression like x = const and as a result we cannot represent y as a function of x, then we are dealing with a straight line parallel to the X axis. The angular coefficient of such a straight line is equal to infinity.
For lines expressed by an equation like y = const, the slope is zero. This is typical for straight lines parallel to the abscissa axis. For example:
Problem: Find the slope of the line given by the equation 24x + 12y - 4(3y + 7) = 4
Solution: Let's bring the original equation to its general form
24x + 12y - 12y + 28 = 4
It is impossible to express y from the resulting expression, therefore the angular coefficient of this line is equal to infinity, and the line itself will be parallel to the Y axis.
Geometric meaning
For a better understanding, let's look at the picture:
In the figure we see a graph of a function like y = kx. To simplify, let’s take the coefficient c = 0. In the triangle OAB, the ratio of side BA to AO will be equal to the angular coefficient k. At the same time, the ratio BA/AO is the tangent of the acute angle α in the right triangle OAB. It turns out that the angular coefficient of the straight line is equal to the tangent of the angle that this straight line makes with the abscissa axis of the coordinate grid.
Solving the problem of how to find the angular coefficient of a straight line, we find the tangent of the angle between it and the X axis of the coordinate grid. Boundary cases, when the line in question is parallel to the coordinate axes, confirm the above. Indeed, for a straight line described by the equation y=const, the angle between it and the abscissa axis is zero. The tangent of the zero angle is also zero and the slope is also zero.
For straight lines perpendicular to the x-axis and described by the equation x=const, the angle between them and the X-axis is 90 degrees. The tangent of a right angle is equal to infinity, and the angular coefficient of similar straight lines is also equal to infinity, which confirms what was written above.
Tangent slope
A common task often encountered in practice is also to find the slope of a tangent to the graph of a function at a certain point. A tangent is a straight line, therefore the concept of slope is also applicable to it.
To figure out how to find the slope of a tangent, we will need to recall the concept of derivative. The derivative of any function at a certain point is a constant numerically equal to the tangent of the angle that is formed between the tangent at the specified point to the graph of this function and the abscissa axis. It turns out that to determine the angular coefficient of the tangent at the point x 0, we need to calculate the value of the derivative of the original function at this point k = f"(x 0). Let's look at the example:
Problem: Find the slope of the line tangent to the function y = 12x 2 + 2xe x at x = 0.1.
Solution: Find the derivative of the original function in general form
y"(0.1) = 24. 0.1 + 2. 0.1. e 0.1 + 2. e 0.1
Answer: The required slope at point x = 0.1 is 4.831
The figure shows the angle of inclination of the straight line and indicates the value of the angular coefficient for various options for the location of the straight line relative to the rectangular coordinate system.
Finding the slope of a straight line with a known angle of inclination to the Ox axis does not present any difficulties. To do this, it is enough to recall the definition of the angular coefficient and calculate the tangent of the angle of inclination.
Example.
Find the slope of the straight line if its angle of inclination to the abscissa axis is equal to .
Solution.
By condition . Then, by definition of the slope of a straight line, we calculate 
.
Answer:
The task of finding the angle of inclination of a straight line to the x-axis with a known slope is a little more complicated. Here it is necessary to take into account the sign of the slope. When the angle of inclination of the straight line is acute and is found as . When the angle of inclination of the straight line is obtuse and can be determined by the formula 
.
Example.
Determine the angle of inclination of the straight line to the abscissa axis if its slope is equal to 3.
Solution.
Since by condition the angular coefficient is positive, the angle of inclination of the straight line to the Ox axis is acute. We calculate it using the formula.
Answer:
Example.
The slope of the straight line is . Determine the angle of inclination of the straight line to the Ox axis.
Solution.
Let's denote k is the angular coefficient of the straight line, - the angle of inclination of this straight line to the positive direction of the Ox axis. Because 
, then we use the formula to find the angle of inclination of the line of the following form . We substitute the data from the condition into it: .
Answer:
Equation of a straight line with an angular coefficient.
Equation of a straight line with slope has the form , where k is the slope of the line, b is some real number. Using the equation of a straight line with an angular coefficient, you can specify any straight line that is not parallel to the Oy axis (for a straight line parallel to the ordinate axis, the angular coefficient is not defined).
Let's understand the meaning of the phrase: “a straight line on a plane in a fixed coordinate system is given by an equation with an angular coefficient of the form “.” This means that the equation is satisfied by the coordinates of any point on the line and is not satisfied by the coordinates of any other points on the plane. Thus, if, when substituting the coordinates of a point, the correct equality is obtained, then the straight line passes through this point. Otherwise, the point does not lie on the line.
Example.
The straight line is given by an equation with a slope. Do the points also belong to this line?
Solution.
Let's substitute the coordinates of the point into the original equation of the straight line with the slope: 
. We have obtained the correct equality, therefore, point M 1 lies on the line.
When substituting the coordinates of a point, we get an incorrect equality: 
. Thus, point M 2 does not lie on the line.
Answer:
Dot M 1 belongs to the line, M 2 does not.
It should be noted that a straight line defined by the equation of a straight line with an angular coefficient passes through the point, since when we substitute its coordinates into the equation we obtain the correct equality: .
Thus, the equation of a straight line with an angular coefficient defines on the plane a straight line passing through a point and forming an angle with the positive direction of the abscissa axis, and .
As an example, let us depict a straight line defined by the equation of a straight line with an angle coefficient of the form . This line passes through a point and has a slope 
radians (60 degrees) to the positive direction of the Ox axis. Its slope is equal to .
Equation of a straight line with slope passing through a given point.
Now we will solve a very important problem: we will obtain the equation of a straight line with a given slope k and passing through the point .
Since the line passes through the point, the equality is true 
. We don't know the number b. To get rid of it, we subtract the left and right sides of the last equality from the left and right sides of the equation with the slope, respectively. In this case we get 
. This equality is equation of a straight line with a given slope k, which passes through a given point.
Let's look at an example.
Example.
Write the equation of a line passing through the point, the slope of this line is -2.
Solution.
From the condition we have 
. Then the equation of a straight line with an angular coefficient will take the form .
Answer:
Example.
Write the equation of a straight line if it is known that it passes through a point and the angle of inclination to the positive direction of the Ox axis is equal to .
Solution.
First, let's calculate the slope of the line whose equation we are looking for (we solved this problem in the previous paragraph of this article). A-priory 
. Now we have all the data to write down the equation of a straight line with an angle coefficient:
Answer:
Example.
Write the equation of a line with an angular coefficient passing through a point parallel to the line.
Solution.
Obviously, the angles of inclination of parallel lines to the Ox axis coincide (if necessary, see the article parallelism of lines), therefore, the angular coefficients of parallel lines are equal. Then the slope of the straight line, the equation of which we need to obtain, is equal to 2, since the slope of the straight line is equal to 2. Now we can create the required equation of a straight line with a slope:
Answer:
Transition from the equation of a line with an angle coefficient to other types of equation of a line and vice versa.
Despite all the familiarity, the equation of a straight line with an angular coefficient is not always convenient to use when solving problems. In some cases, problems are easier to solve when the equation of a line is presented in a different form. For example, the equation of a straight line with an angular coefficient does not allow you to immediately write down the coordinates of the directing vector of the straight line or the coordinates of the normal vector of the straight line. Therefore, you should learn to move from the equation of a straight line with an angle coefficient to other types of equations of this straight line.
From the equation of a straight line with an angular coefficient it is easy to obtain the canonical equation of a straight line on a plane of the form 
. To do this, we move the term b from the right side of the equation to the left side with the opposite sign, then divide both sides of the resulting equality by the slope k: . These actions lead us from the equation of a line with an angle coefficient to the canonical equation of a line.
Example.
Give the equation of a straight line with an angle coefficient 
to the canonical form.
Solution.
Let's perform the necessary transformations: .
Answer:
Example.
A straight line is given by the equation of a straight line with an angular coefficient. Is the vector a normal vector of this line?
Solution.
To solve this problem, let's move from the equation of a straight line with an angle coefficient to the general equation of this straight line: 
. We know that the coefficients of the variables x and y in the general equation of a line are the corresponding coordinates of the normal vector of this line, that is, the normal vector of the line 
. It is obvious that the vector is collinear to the vector, since the relation is valid (if necessary, see the article). Thus, the original vector is also a normal line vector , and, therefore, is a normal vector and the original line.
Answer:
Yes it is.
And now we will solve the inverse problem - the problem of reducing the equation of a straight line on a plane to the equation of a straight line with an angle coefficient.
From the general straight line equation of the form 
, in which it is very easy to go to an equation with a slope coefficient. To do this, you need to solve the general equation of the line with respect to y. In this case we get . The resulting equality is an equation of a straight line with an angular coefficient equal to .
Problems on finding the derivative of a tangent are included in the Unified State Examination in mathematics and are found there every year. At the same time, statistics from recent years show that such tasks cause certain difficulties for graduates. Therefore, if a student expects to get decent scores after passing the Unified State Exam, then he should definitely learn how to cope with problems from the section “Angle coefficient of a tangent as the value of the derivative at the point of tangency,” prepared by specialists of the Shkolkovo educational portal. Having understood the algorithm for solving them, the student will be able to successfully overcome the certification test.
Basic moments
When starting to solve USE problems on this topic, it is necessary to remember the basic definition: the derivative of a function at a point is equal to the slope of the tangent to the graph of the function at this point. This is the geometric meaning of the derivative.
There is another important definition that needs to be refreshed. It sounds like this: the angular coefficient is equal to the tangent of the angle of inclination of the tangent to the abscissa axis.
What other important points are worth noting in this topic? When solving problems on finding the derivative in the Unified State Examination, it is necessary to remember that the angle formed by the tangent can be less than, more than 90 degrees, or equal to zero.
How to prepare for the exam?
To ensure that tasks in the Unified State Examination on the topic “The angular coefficient of a tangent as the value of the derivative at the point of tangency” are given to you quite easily, when preparing for the final test, use the information on this section on the Shkolkovo educational portal. Here you will find the necessary theoretical material, collected and clearly presented by our specialists, and you will also be able to practice performing the exercises.
For each task, for example, problems on the topic “The angular coefficient of a tangent as the tangent of the angle of inclination,” we wrote down the correct answer and solution algorithm. At the same time, students can perform exercises of varying difficulty levels online. If necessary, the task can be saved in the “Favorites” section so that you can later discuss its solution with the teacher.
Loading...