Encuentra la longitud del lado ab en línea. Ecuación de una recta con pendiente
Numéricamente igual a la tangente del ángulo (que constituye la rotación más pequeña del eje Ox al eje Oy) entre la dirección positiva del eje de abscisas y la línea recta dada.
La tangente de un ángulo se puede calcular como la relación entre el lado opuesto y el lado adyacente. k es siempre igual a , es decir, la derivada de la ecuación de una recta con respecto a X.
Para valores positivos de la pendiente. k y coeficiente de desplazamiento cero b la línea recta se ubicará en el primer y tercer cuadrante (en el que X Y y tanto positivos como negativos). Al mismo tiempo, grandes valores del coeficiente angular. k A una línea recta más pronunciada le corresponderá y a una más plana le corresponderán otras más pequeñas.
Recta y perpendicular si, y paralela si.
Notas
Fundación Wikimedia. 2010.
- Ifit (rey de Elis)
- Lista de Decretos del Presidente de la Federación de Rusia "Sobre la concesión de premios estatales" para 2001
Vea qué es el "coeficiente angular de una línea recta" en otros diccionarios:
pendiente (directa)- - Temas industria del petróleo y gas ES pendiente... Guía del traductor técnico
factor de pendiente- número (matemático) k en la ecuación de una línea recta en el plano y = kx+b (ver Geometría analítica), que caracteriza la pendiente de la línea recta con respecto al eje x. En el sistema de coordenadas rectangular del Reino Unido k = tan φ, donde φ es el ángulo entre... ... Gran enciclopedia soviética
Ecuaciones de una recta
GEOMETRÍA ANALÍTICA- una sección de geometría que estudia los objetos geométricos más simples utilizando álgebra elemental basada en el método de coordenadas. La creación de la geometría analítica suele atribuirse a R. Descartes, quien esbozó sus fundamentos en el último capítulo de su... ... Enciclopedia de Collier
Tiempo de reacción- La medición del tiempo de reacción (RT) es probablemente el tema más venerable de la psicología empírica. Tiene su origen en el campo de la astronomía, en 1823, con la medición de las diferencias individuales en la velocidad de percepción de una estrella que cruza la línea de un telescopio. Estos … Enciclopedia psicológica
ANÁLISIS MATEMÁTICO- una rama de las matemáticas que proporciona métodos para la investigación cuantitativa de diversos procesos de cambio; se ocupa del estudio de la tasa de cambio (cálculo diferencial) y de la determinación de las longitudes de curvas, áreas y volúmenes de figuras limitadas por contornos curvos y... Enciclopedia de Collier
Derecho- Este término tiene otros significados, ver Directo (significados). La línea recta es uno de los conceptos básicos de la geometría, es decir, no tiene una definición universal exacta. En una presentación sistemática de la geometría, una línea recta generalmente se toma como una... ... Wikipedia
Línea recta- Imagen de líneas rectas en un sistema de coordenadas rectangulares La línea recta es uno de los conceptos básicos de la geometría. En una presentación sistemática de la geometría, se suele tomar una línea recta como uno de los conceptos iniciales, que sólo se define indirectamente... ... Wikipedia
Directo- Imagen de líneas rectas en un sistema de coordenadas rectangulares La línea recta es uno de los conceptos básicos de la geometría. En una presentación sistemática de la geometría, se suele tomar una línea recta como uno de los conceptos iniciales, que sólo se define indirectamente... ... Wikipedia
eje menor- No confundir con el término "Elipsis". Elipse y sus focos Elipse (griego antiguo ἔλλειψις deficiencia, en el sentido de falta de excentricidad hasta 1) el lugar geométrico de los puntos M del plano euclidiano para el cual la suma de las distancias desde dos puntos dados es F1... ... Wikipedia
Sea en un plano donde hay un sistema de coordenadas cartesiano rectangular, una línea recta yo pasa por el punto M 0 paralelo al vector director A (Figura 96).
si es heterosexual yo cruza el eje O X(en el punto N), luego en un ángulo de línea recta yo con eje O X entenderemos el ángulo α por el cual es necesario girar el eje O X alrededor del punto N en la dirección opuesta a la rotación en el sentido de las agujas del reloj, de modo que el eje O X coincidió con una línea recta yo. (Esto se refiere a un ángulo inferior a 180°).
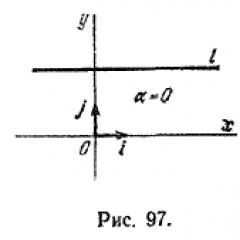
Este ángulo se llama ángulo de inclinación derecho. si es heterosexual yo paralelo al eje O X, entonces se supone que el ángulo de inclinación es cero (Fig. 97).
La tangente del ángulo de inclinación de una recta se llama pendiente de una recta y generalmente se indica con la letra k:
bronceado α = k. (1)
Si α = 0, entonces k= 0; esto significa que la línea es paralela al eje O X y su pendiente es cero.
Si α = 90°, entonces k= tan α no tiene sentido: esto significa que una línea recta perpendicular al eje O X(es decir, paralelo al eje O en), no tiene pendiente.
La pendiente de una recta se puede calcular si se conocen las coordenadas de dos puntos cualesquiera de esta recta. Sean dados dos puntos de una recta: M 1 ( X 1 ; en 1) y M2 ( X 2 ; en 2) y sea, por ejemplo, 0< α < 90°, а X 2 > X 1 , en 2 > en 1 (figura 98).
Luego del triángulo rectángulo M 1 PM 2 encontramos
$$ k=tga = \frac(|M_2 P|)(|M_1 P|) = \frac(y_2 - y_1)(x_2 - x_1) $$
$$ k=\frac(y_2 - y_1)(x_2 - x_1) \;\; (2)$$
De manera similar se demuestra que la fórmula (2) también es cierta en el caso de 90°< α < 180°.
La fórmula (2) deja de tener sentido si X 2 - X 1 = 0, es decir, si es recto yo paralelo al eje O en. No existe un coeficiente de pendiente para tales líneas rectas.
Tarea 1. Determine el coeficiente angular del prim que pasa por los puntos.
M1 (3; -5) y M2 (5; -7).
Sustituyendo las coordenadas de los puntos M 1 y M 2 en la fórmula (2), obtenemos
\(k=\frac(-7-(-5))(5-3)\) o k = -1
Tarea 2. Determine la pendiente de la recta que pasa por los puntos M 1 (3; 5) y M 2 (3; -2).
Porque X 2 - X 1 = 0, entonces la igualdad (2) pierde su significado. Esta recta no tiene pendiente. La recta M 1 M 2 es paralela al eje O en.
Tarea 3. Determine la pendiente de la recta que pasa por el origen y el punto M 1 (3; -5)
En este caso el punto M 2 coincide con el origen. Aplicando la fórmula (2), obtenemos
$$ k=\frac(y_2 - y_1)(x_2 - x_1)=\frac(0-(-5))(0-3)= -\frac(5)(3); \;\; k= -\frac(5)(3) $$
Creemos una ecuación de una línea recta con un coeficiente de ángulo. k, pasando por el punto
m 1 ( X 1 ; en 1). Según la fórmula (2), el coeficiente angular de una línea recta se encuentra a partir de las coordenadas de sus dos puntos. En nuestro caso, se da el punto M 1, y como segundo punto podemos tomar cualquier punto M( X; en) la línea recta deseada.
Si el punto M se encuentra en una línea recta que pasa por el punto M 1 y tiene un coeficiente angular k, entonces en virtud de la fórmula (2) tenemos
$$ \frac(y-y_1)(x-x_1)=k \;\; (3) $$
Si el punto M no se encuentra en una recta, entonces la igualdad (3) no se cumple. En consecuencia, la igualdad (3) es la ecuación de la recta que pasa por el punto M 1 ( X 1 ; en 1) con pendiente k; esta ecuación generalmente se escribe como
y- y 1 = k(X - X 1). (4)
Si la recta corta al eje O en en algún momento (0; b), entonces la ecuación (4) toma la forma
en - b = k (X- 0),
y = kx + b. (5)
Esta ecuación se llama ecuación de una recta de pendiente k y ordenada inicial b.
Tarea 4. Encuentra el ángulo de inclinación de la recta √3 x + 3en - 7 = 0.
Reduzcamos esta ecuación a la forma
$$ y= =\frac(1)(\sqrt3)x + \frac(7)(3) $$
Por eso, k= tan α = - 1 / √ 3, de donde α = 150°
Tarea 5. Escribe una ecuación para una línea recta que pasa por el punto P(3; -4) con un coeficiente angular k = 2 / 5
Sustituyendo k = 2 / 5 , X 1 = 3, y 1 = - 4 en la ecuación (4), obtenemos
en - (- 4) = 2 / 5 (X- 3) o 2 X - 5en - 26 = 0.
Tarea 6. Escribe una ecuación para una línea recta que pasa por el punto Q (-3; 4) y una componente con la dirección positiva del eje O. Xángulo de 30°.
Si α = 30°, entonces k= tan 30° = √ 3 / 3 . Sustituyendo en la ecuación (4) los valores X 1 , y 1 y k, obtenemos
en -4 = √ 3 / 3 (X+ 3) o √3 X-3y + 12 + 3√3 = 0.
En matemáticas, uno de los parámetros que describe la posición de una recta en el plano cartesiano es el coeficiente angular de esta recta. Este parámetro caracteriza la pendiente de la línea recta hacia el eje de abscisas. Para entender cómo encontrar la pendiente, primero recuerde la forma general de la ecuación de una línea recta en el sistema de coordenadas XY.
En general, cualquier línea recta se puede representar mediante la expresión ax+by=c, donde a, b y c son números reales arbitrarios, pero a 2 + b 2 ≠ 0.
Usando transformaciones simples, dicha ecuación se puede llevar a la forma y=kx+d, en la que k y d son números reales. El número k es la pendiente, y la ecuación de una recta de este tipo se llama ecuación con pendiente. Resulta que para encontrar la pendiente, simplemente necesitas reducir la ecuación original a la forma indicada arriba. Para una comprensión más completa, considere un ejemplo específico:
Problema: Encuentra la pendiente de la recta dada por la ecuación 36x - 18y = 108
Solución: Transformemos la ecuación original.
Respuesta: La pendiente requerida de esta recta es 2.
Si al transformar la ecuación obtuvimos una expresión como x = const y como resultado no podemos representar y en función de x, entonces estamos ante una línea recta paralela al eje X. El coeficiente angular de tal. una línea recta es igual al infinito.
Para rectas expresadas por una ecuación como y = const, la pendiente es cero. Esto es típico de líneas rectas paralelas al eje de abscisas. Por ejemplo:
Problema: Encuentra la pendiente de la recta dada por la ecuación 24x + 12y - 4(3y + 7) = 4
Solución: llevemos la ecuación original a su forma general.
24x + 12y - 12y + 28 = 4
Es imposible expresar y a partir de la expresión resultante, por lo tanto, el coeficiente angular de esta línea es igual al infinito y la línea misma será paralela al eje Y.
Significado geométrico
Para una mejor comprensión, veamos la imagen:
En la figura vemos una gráfica de una función como y = kx. Para simplificar, tomemos el coeficiente c = 0. En el triángulo OAB, la relación entre el lado BA y AO será igual al coeficiente angular k. Al mismo tiempo, la relación BA/AO es la tangente del ángulo agudo α en el triángulo rectángulo OAB. Resulta que el coeficiente angular de la recta es igual a la tangente del ángulo que forma esta recta con el eje de abscisas de la cuadrícula de coordenadas.
Resolviendo el problema de cómo encontrar el coeficiente angular de una línea recta, encontramos la tangente del ángulo entre ella y el eje X de la cuadrícula de coordenadas. Los casos límite, cuando la línea en cuestión es paralela a los ejes de coordenadas, confirman lo anterior. De hecho, para una línea recta descrita por la ecuación y=const, el ángulo entre ella y el eje de abscisas es cero. La tangente del ángulo cero también es cero y la pendiente también es cero.
Para líneas rectas perpendiculares al eje de abscisas y descritas por la ecuación x=const, el ángulo entre ellas y el eje X es de 90 grados. La tangente de un ángulo recto es igual al infinito, y el coeficiente angular de rectas semejantes también es igual al infinito, lo que confirma lo escrito anteriormente.
pendiente tangente
Una tarea común que se encuentra a menudo en la práctica es también encontrar la pendiente de una tangente a la gráfica de una función en un punto determinado. Una tangente es una recta, por lo que también le es aplicable el concepto de pendiente.
Para saber cómo encontrar la pendiente de una tangente, necesitaremos recordar el concepto de derivada. La derivada de cualquier función en un punto determinado es una constante numéricamente igual a la tangente del ángulo que se forma entre la tangente en el punto especificado a la gráfica de esta función y el eje de abscisas. Resulta que para determinar el coeficiente angular de la tangente en el punto x 0, necesitamos calcular el valor de la derivada de la función original en este punto k = f"(x 0). Veamos el ejemplo:
Problema: Encuentra la pendiente de la recta tangente a la función y = 12x 2 + 2xe x en x = 0,1.
Solución: encuentre la derivada de la función original en forma general.
y"(0.1) = 24. 0.1 + 2. 0.1. e 0.1 + 2. e 0.1
Respuesta: La pendiente requerida en el punto x = 0,1 es 4,831
La figura muestra el ángulo de inclinación de la línea recta e indica el valor del coeficiente angular para varias opciones para la ubicación de la línea recta con respecto al sistema de coordenadas rectangular.
Encontrar la pendiente de una línea recta con un ángulo de inclinación conocido con respecto al eje Ox no presenta ninguna dificultad. Para hacer esto, basta con recordar la definición del coeficiente angular y calcular la tangente del ángulo de inclinación.
Ejemplo.
Encuentra la pendiente de la recta si su ángulo de inclinación con respecto al eje de abscisas es igual a .
Solución.
Por condición. Luego, por definición de la pendiente de una recta, calculamos 
.
Respuesta:
La tarea de encontrar el ángulo de inclinación de una línea recta con respecto al eje x con una pendiente conocida es un poco más complicada. Aquí hay que tener en cuenta la señal de la pendiente. Cuando el ángulo de inclinación de la recta es agudo y se encuentra como . Cuando el ángulo de inclinación de la recta es obtuso y puede determinarse mediante la fórmula 
.
Ejemplo.
Determine el ángulo de inclinación de la recta con respecto al eje de abscisas si su pendiente es igual a 3.
Solución.
Dado que por condición el coeficiente angular es positivo, el ángulo de inclinación de la línea recta con respecto al eje Ox es agudo. Lo calculamos usando la fórmula.
Respuesta:
Ejemplo.
La pendiente de la recta es . Determine el ángulo de inclinación de la línea recta con respecto al eje Ox.
Solución.
denotemos k es el coeficiente angular de la línea recta, - el ángulo de inclinación de esta línea recta con respecto a la dirección positiva del eje Ox. Porque 
, luego usamos la fórmula para encontrar el ángulo de inclinación de la recta de la siguiente forma . Sustituimos los datos de la condición en ella: .
Respuesta:
Ecuación de una recta con coeficiente angular.
Ecuación de una recta con pendiente tiene la forma , donde k es la pendiente de la recta, b es algún número real. Usando la ecuación de una línea recta con un coeficiente angular, puede especificar cualquier línea recta que no sea paralela al eje Oy (para una línea recta paralela al eje de ordenadas, el coeficiente angular no está definido).
Entendamos el significado de la frase: “una línea recta en un plano en un sistema de coordenadas fijo está dada por una ecuación con un coeficiente angular de la forma “.” Esto significa que la ecuación se satisface con las coordenadas de cualquier punto de la recta y no se satisface con las coordenadas de ningún otro punto del plano. Así, si al sustituir las coordenadas de un punto se obtiene la igualdad correcta, entonces la recta pasa por este punto. De lo contrario, el punto no se encuentra en la recta.
Ejemplo.
La recta viene dada por una ecuación con pendiente. ¿Los puntos también pertenecen a esta línea?
Solución.
Sustituyamos las coordenadas del punto en la ecuación original de la recta con pendiente: 
. Hemos obtenido la igualdad correcta, por tanto, el punto M 1 se encuentra en la recta.
Al sustituir las coordenadas de un punto, obtenemos una igualdad incorrecta: 
. Por tanto, el punto M 2 no se encuentra en la recta.
Respuesta:
Punto M 1 pertenece a la línea, M 2 no.
Cabe señalar que por el punto pasa una recta definida por la ecuación de una recta con coeficiente angular, ya que cuando sustituimos sus coordenadas en la ecuación obtenemos la igualdad correcta: .
Así, la ecuación de una recta con coeficiente angular define en el plano una recta que pasa por un punto y forma un ángulo con la dirección positiva del eje x, y .
Como ejemplo, representemos una línea recta definida por la ecuación de una línea recta con un coeficiente angular de la forma. Esta recta pasa por un punto y tiene pendiente. 
radianes (60 grados) en la dirección positiva del eje Ox. Su pendiente es igual a .
Ecuación de una recta con pendiente que pasa por un punto dado.
Ahora resolveremos un problema muy importante: obtendremos la ecuación de una recta de pendiente k dada y que pasa por el punto .
Como la recta pasa por el punto, la igualdad es verdadera. 
. No sabemos el número b. Para deshacernos de él, restamos los lados izquierdo y derecho de la última igualdad de los lados izquierdo y derecho de la ecuación de la recta con el coeficiente de pendiente, respectivamente. En este caso obtenemos 
. Esta igualdad es ecuación de una recta con una pendiente dada k, que pasa por un punto dado.
Veamos un ejemplo.
Ejemplo.
Escribe la ecuación de una recta que pasa por el punto, la pendiente de esta recta es -2.
Solución.
De la condición que tenemos 
. Entonces la ecuación de una recta con coeficiente angular tomará la forma.
Respuesta:
Ejemplo.
Escribe la ecuación de una recta si se sabe que pasa por un punto y el ángulo de inclinación hacia la dirección positiva del eje Ox es igual a .
Solución.
Primero, calculemos la pendiente de la recta cuya ecuación buscamos (este problema lo resolvimos en el párrafo anterior de este artículo). priorato 
. Ahora tenemos todos los datos para escribir la ecuación de una recta con coeficiente de ángulo:
Respuesta:
Ejemplo.
Escribe la ecuación de una recta con un coeficiente angular que pasa por un punto paralelo a la recta.
Solución.
Obviamente, los ángulos de inclinación de las rectas paralelas al eje Ox coinciden (si es necesario, ver el artículo paralelismo de rectas), por lo tanto, los coeficientes angulares de las rectas paralelas son iguales. Entonces la pendiente de la recta, cuya ecuación necesitamos obtener, es igual a 2, ya que la pendiente de la recta es igual a 2. Ahora podemos crear la ecuación requerida de una línea recta con pendiente:
Respuesta:
Transición de la ecuación de una recta con coeficiente de ángulo a otros tipos de ecuación de una recta y viceversa.
A pesar de toda la familiaridad, la ecuación de una línea recta con un coeficiente angular no siempre es conveniente de utilizar al resolver problemas. En algunos casos, los problemas son más fáciles de resolver cuando la ecuación de una recta se presenta en una forma diferente. Por ejemplo, la ecuación de una línea recta con un coeficiente angular no le permite escribir inmediatamente las coordenadas del vector director de la línea recta o las coordenadas del vector normal de la línea recta. Por tanto, conviene aprender a pasar de la ecuación de una recta con un coeficiente de ángulo a otros tipos de ecuaciones de esta recta.
A partir de la ecuación de una recta con coeficiente angular es fácil obtener la ecuación canónica de una recta en un plano de la forma 
. Para hacer esto, movemos el término b del lado derecho de la ecuación al lado izquierdo con el signo opuesto, luego dividimos ambos lados de la igualdad resultante por la pendiente k: . Estas acciones nos llevan de la ecuación de una recta con coeficiente de ángulo a la ecuación canónica de una recta.
Ejemplo.
Da la ecuación de una línea recta con un coeficiente de ángulo. 
a la forma canónica.
Solución.
Realicemos las transformaciones necesarias: .
Respuesta:
Ejemplo.
Una línea recta viene dada por la ecuación de una línea recta con un coeficiente angular. ¿Es el vector un vector normal de esta recta?
Solución.
Para solucionar este problema, pasemos de la ecuación de una recta con coeficiente de ángulo a la ecuación general de esta recta: 
. Sabemos que los coeficientes de las variables x e y en la ecuación general de una recta son las coordenadas correspondientes del vector normal de esta recta, es decir, el vector normal de la recta. 
. Es obvio que el vector es colineal con el vector, ya que la relación es válida (si es necesario, consulte el artículo). Por tanto, el vector original también es un vector lineal normal. , y, por tanto, es un vector normal y la recta original.
Respuesta:
Sí, lo es.
Y ahora resolveremos el problema inverso: el problema de reducir la ecuación de una línea recta en un plano a la ecuación de una línea recta con un coeficiente de ángulo.
De la ecuación general de línea recta de la forma 
, en el que es muy fácil pasar a una ecuación con un coeficiente de pendiente. Para hacer esto, necesitas resolver la ecuación general de la recta con respecto a y. En este caso obtenemos. La igualdad resultante es una ecuación de una recta con un coeficiente angular igual a .
Los problemas para encontrar la derivada de una tangente se incluyen en el Examen Estatal Unificado de Matemáticas y se encuentran allí todos los años. Al mismo tiempo, las estadísticas de los últimos años muestran que estas tareas plantean ciertas dificultades a los graduados. Por lo tanto, si un estudiante espera obtener calificaciones decentes después de aprobar el Examen Estatal Unificado, entonces definitivamente debería aprender a resolver los problemas de la sección "Coeficiente angular de una tangente como valor de la derivada en el punto de tangencia", preparada por especialistas del portal educativo Shkolkovo. Habiendo comprendido el algoritmo para su resolución, el alumno podrá superar con éxito la prueba de certificación.
Momentos básicos
Al comenzar a resolver problemas USE sobre este tema, es necesario recordar la definición básica: la derivada de una función en un punto es igual a la pendiente de la tangente a la gráfica de la función en este punto. Este es el significado geométrico de la derivada.
Hay otra definición importante que es necesario actualizar. Suena así: el coeficiente angular es igual a la tangente del ángulo de inclinación de la tangente al eje de abscisas.
¿Qué otros puntos importantes vale la pena destacar en este tema? Al resolver problemas para encontrar la derivada en el Examen Estatal Unificado, es necesario recordar que el ángulo formado por la tangente puede ser menor, mayor que 90 grados o igual a cero.
¿Cómo prepararse para el examen?
Para que las tareas del Examen Estatal Unificado sobre el tema "El coeficiente angular de una tangente como valor de la derivada en el punto de tangencia" le resulten bastante fáciles, cuando se prepare para la prueba final, utilice la información de este Sección del portal educativo de Shkolkovo. Aquí encontrarás el material teórico necesario, recopilado y claramente presentado por nuestros especialistas, y también podrás practicar la realización de los ejercicios.
Para cada tarea, por ejemplo, problemas sobre el tema "El coeficiente angular de una tangente como tangente del ángulo de inclinación", escribimos la respuesta correcta y el algoritmo de solución. Al mismo tiempo, los estudiantes pueden realizar ejercicios de distintos niveles de dificultad en línea. Si es necesario, la tarea se puede guardar en la sección “Favoritos” para luego discutir su solución con el profesor.
Cargando...