Zastosowanie rachunku całkowego w mechanice. Streszczenie: Zastosowanie rachunku różniczkowego i całkowego do rozwiązywania problemów fizycznych i geometrycznych w programie MATLab
Wyślij swoją dobrą pracę do bazy wiedzy jest prosta. Skorzystaj z poniższego formularza
Studenci, doktoranci, młodzi naukowcy, którzy wykorzystują bazę wiedzy w swoich studiach i pracy, będą Państwu bardzo wdzięczni.
Streszczenie na temat: „Całka i jej zastosowanie”
Studenci
Miód. Szkoła Wyższa
Nr 2 203 grupy
Kulikowa Maria
Petersburg 2010
Wstęp
Symbol całki wprowadzono w 1675 r., a rachunek całkowy badano od 1696 r. Chociaż całką zajmują się głównie matematycy, fizycy również wnieśli swój wkład w tę naukę. Prawie żadna formuła fizyki nie jest kompletna bez rachunku różniczkowego i całkowego. Dlatego zdecydowałem się zbadać całkę i jej zastosowanie.
Historia rachunku całkowego
Historia pojęcia całki jest ściśle związana z problemami znajdowania kwadratur. Matematycy starożytnej Grecji i Rzymu nazywali problemy kwadratury jednej lub drugiej płaskiej figury problemami obliczania obszarów. Łacińskie słowo quadratura tłumaczy się jako „kwadrat”. Potrzebę specjalnego terminu tłumaczy się faktem, że w czasach starożytnych (a później, aż do XVIII wieku) idee dotyczące liczb rzeczywistych nie były jeszcze wystarczająco rozwinięte. Matematycy operowali swoimi geometrycznymi odpowiednikami, czyli skalarami, których nie można pomnożyć. Dlatego zadania na znalezienie pól należało sformułować np. w następujący sposób: „Zbuduj kwadrat o wielkości równej danemu okręgowi”. (Tego klasycznego problemu „kwadratury koła” nie można, jak dobrze wiadomo, rozwiązać za pomocą kompasu i linijki.)
Symbol t wprowadził Leibniz (1675). Znak ten jest odmianą łacińskiej litery S (pierwsza litera słowa summ a).Samo słowo całka zostało ukute przez J. Bernoulliego (1690). Prawdopodobnie pochodzi od łacińskiego integro, które tłumaczy się jako przywrócenie do poprzedniego stanu, przywrócenie. (Istotnie, operacja całkowania „odzyskuje” funkcję, której różniczkowanie daje całkę.) Być może pochodzenie terminu całka jest inne: słowo liczba całkowita oznacza całość.
W trakcie korespondencji I. Bernoulli i G. Leibniz zgodzili się z propozycją J. Bernoulliego. Następnie w 1696 r. pojawiła się nazwa nowej gałęzi matematyki - rachunku całkowego (calculus integralis), którą wprowadził I. Bernoulli.
Inne znane terminy związane z rachunkiem całkowym pojawiły się znacznie później. Używana obecnie nazwa funkcja pierwotna zastąpiła wcześniejszą „funkcję pierwotną” wprowadzoną przez Lagrange'a (1797). Łacińskie słowo primitivus tłumaczy się jako „inicjał”: F(x) = m f(x)dx - inicjał (lub inicjał lub funkcja pierwotna) dla f (x), który otrzymuje się z F(x) przez różniczkowanie.
We współczesnej literaturze zbiór wszystkich funkcji pierwotnych funkcji f(x) nazywany jest także całką nieoznaczoną. Koncepcję tę wyróżnił Leibniz, który zauważył, że wszystkie funkcje pierwotne różnią się dowolną stałą b, zwaną całką oznaczoną (oznaczenie wprowadził C. Fourier (1768-1830), ale Euler wskazał już granice całkowania).
Wiele znaczących osiągnięć matematyków starożytnej Grecji w rozwiązywaniu problemów znajdowania kwadratur (czyli obliczania pól) figur płaskich, a także kubatur (obliczania objętości) ciał, wiąże się ze stosowaniem metody wyczerpania zaproponowanej przez Eudoksosa z Knidos (ok. 408 - ok. 355 p.n.e.). .e.). Za pomocą tej metody Eudoksos udowodnił na przykład, że pola dwóch kół są powiązane jako kwadraty ich średnic oraz że objętość stożka jest równa 1/3 objętości walca o tej samej podstawie i wysokości .
Archimedes udoskonalił metodę Eudoksosa. Główne etapy charakteryzujące metodę Archimedesa: 1) udowodniono, że powierzchnia koła jest mniejsza niż powierzchnia dowolnego wielokąta foremnego opisanego wokół niego, ale większa niż powierzchnia dowolnego wpisanego; 2) udowodniono, że przy nieograniczonym podwojeniu liczby boków różnica pól tych wielokątów dąży do zera; 3) aby obliczyć pole koła, pozostaje znaleźć wartość, do której zmierza stosunek pola powierzchni wielokąta foremnego przy nieograniczonym podwojeniu liczby jego boków.
Za pomocą metody wyczerpania i szeregu innych dowcipnych rozważań (w tym z wykorzystaniem modeli mechaniki) Archimedes rozwiązał wiele problemów. Podał oszacowanie p (3,10/71 Archimedes przewidział wiele idei rachunku całkowego. (Dodajmy, że w praktyce udowodnił on pierwsze twierdzenia graniczne.) Ale minęło ponad tysiąc i pół roku, zanim idee te znalazły jasny wyraz i zostały sprowadzone na poziom rachunku różniczkowego. Matematycy XVII wieku, którzy uzyskali wiele nowych wyników, nauczyli się z dzieł Archimedesa. Aktywnie stosowano także inną metodę – metodę niepodzielności, która również wywodzi się ze starożytnej Grecji (kojarzona jest przede wszystkim z atomistycznymi poglądami Demokryta). Na przykład wyobrazili sobie trapez krzywoliniowy (ryc. 1, a) złożony z pionowych odcinków o długości f (x), któremu jednak przypisali obszar równy nieskończenie małej wartości f (x) dx. Zgodnie z tym zrozumieniem wymaganą powierzchnię uznano za równą sumie nieskończonej liczby nieskończenie małych obszarów. Czasem nawet podkreślano, że poszczególnymi wyrazami tej sumy są zera, ale zera szczególnego rodzaju, które dodane w nieskończonej liczbie dają dobrze określoną sumę dodatnią. Na takiej obecnie co najmniej wątpliwej podstawie I. Kepler (1571-1630) w swoich pismach „Nowa astronomia”. 1609 i „Stereometria beczek na wino” (1615) poprawnie obliczyły liczbę pól (na przykład pole figury ograniczone elipsą) i objętości (korpus pocięto na 6c skończenie cienkich płytek). Badania te kontynuowali matematycy włoscy B. Cavalieri (1598-1647) i E. Torricelli (1608-1647). Zasada sformułowana przez B. Cavalieri, wprowadzona przez niego przy pewnych dodatkowych założeniach, zachowuje swoje znaczenie w naszych czasach. Niech konieczne będzie znalezienie obszaru figury pokazanej na rysunku 1, b, gdzie krzywe ograniczające figurę od góry i od dołu mają równania y = f(x) i y=f(x)+c. Przedstawiając figurę złożoną z „niepodzielnych”, w terminologii Cavalieriego, nieskończenie cienkich kolumn, zauważamy, że wszystkie mają wspólną długość c. Przesuwając je w kierunku pionowym, możemy z nich zrobić prostokąt o podstawie b-a i wysokości c. Dlatego wymagany obszar jest równy obszarowi powstałego prostokąta, tj. S \u003d S1 \u003d c (b - a). Ogólna zasada Cavalieriego dotycząca pól figur płaskich jest sformułowana w następujący sposób: Niech linie pewnej wiązki równoległości przecinają figury F1 i F2 wzdłuż odcinków o równej długości (ryc. 1, c). Wtedy pola figur Ф1 i Ф2 są równe. Podobna zasada działa w stereometrii i jest przydatna przy znajdowaniu objętości. W XVII wieku dokonano wielu odkryć związanych z rachunkiem całkowym. Tak więc P. Fermat już w 1629 r. Problem kwadratury dowolnej krzywej y \u003d xn, gdzie n jest liczbą całkowitą (to znaczy zasadniczo wyprowadził wzór m xndx \u003d (1 / n + 1) xn + 1), oraz na tej podstawie podjął szereg zadań mających na celu znalezienie środków ciężkości. I. Kepler, wyprowadzając swoje słynne prawa ruchu planet, w rzeczywistości oparł się na idei przybliżonej integracji. I. Barrow (1630-1677), nauczyciel Newtona, był bliski zrozumienia związku pomiędzy integracją a różnicowaniem. Duże znaczenie miały prace nad przedstawieniem funkcji w postaci szeregów potęgowych. Jednak pomimo całego znaczenia wyników uzyskanych przez wielu niezwykle pomysłowych matematyków XVII wieku, rachunek różniczkowy jeszcze nie istniał. Należało podkreślić ogólne idee leżące u podstaw rozwiązania wielu szczegółowych problemów, a także ustalić związek pomiędzy operacjami różniczkowania i całkowania, co daje dość ogólny algorytm. Dokonali tego Newton i Leibniz, którzy niezależnie odkryli fakt znany jako wzór Newtona-Leibniza. W ten sposób ogólna metoda w końcu nabrała kształtu. Należało jeszcze nauczyć się znajdować funkcje pierwotne wielu funkcji, tworzyć nowe rachunki logiczne i tak dalej. Ale najważniejsze już zostało zrobione: stworzono rachunek różniczkowy i całkowy. Metody analizy matematycznej były aktywnie rozwijane w następnym stuleciu (przede wszystkim należy wymienić nazwiska L. Eulera, który ukończył systematyczne badania integracji funkcji elementarnych, oraz I. Bernoulliego). Rosyjscy matematycy M.V. brali udział w rozwoju rachunku całkowego. Ostrogradski (1801-1862), V.Ya. Bunyakovsky (1804-1889), P.L. Czebyszewa (1821-1894). Zasadnicze znaczenie miały zwłaszcza wyniki Czebyszewa, który udowodnił, że istnieją całki, których nie można wyrazić w postaci funkcji elementarnych. Rygorystyczne przedstawienie teorii całki pojawiło się dopiero w ubiegłym stuleciu. Rozwiązanie tego problemu kojarzone jest z nazwiskami O. Cauchy'ego, jednego z najwybitniejszych matematyków, niemieckiego naukowca B. Riemanna (1826-1866), francuskiego matematyka G. Darboux (1842-1917). Odpowiedzi na wiele pytań związanych z istnieniem pól i objętości figur uzyskano wraz z utworzeniem teorii miary przez K. Jordana (1838-1922). Różne uogólnienia pojęcia całki zaproponowali już na początku naszego stulecia francuscy matematycy A. Lebesgue (1875–1941) i A. Denjoy (188–4–1974), radziecki matematyk A.Ya. Chinczyczin (1894-1959). Jeżeli F(x) jest jedną z funkcji pierwotnych funkcji f(x) na przedziale J, to funkcja pierwotna na tym przedziale ma postać F(x)+C, gdzie COR. Definicja. Zbiór wszystkich funkcji pierwotnych funkcji f(x) na przedziale J nazywamy całką oznaczoną funkcji f(x) na tym przedziale i oznaczamy przez m f(x)dx. t f(x)dx = F(x)+C, gdzie F(x) jest jakąś funkcją pierwotną na przedziale J. f – całka, f(x) – całka, x – zmienna całkująca, C – stała całkowania. Własności całki nieoznaczonej. (t f(x)dx) ў = t f(x)dx, t f(x)dx = F(x)+C, gdzie F ў(x) = f(x) (t f(x)dx) ў= (F(x)+C) ў= f(x) t f ў(x)dx = f(x)+C - z definicji. t k fa (x)dx = k t fў(x)dx jeśli k jest stałą i F ў(x)=f(x), t k fa (x)dx = k F(x)dx = k(F(x)dx+C1)= k t fў(x)dx t (f(x)+g(x)+...+h(x))dx = t f(x)dx + t g(x)dx +...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = t dx = t ўdx = F(x)+G(x)+...+H(x)+C= t f(x)dx + t g(x)dx +...+ t h(x)dx, gdzie C=C1+C2+C3+...+Cn. sposób tabelaryczny. Metoda substytucyjna. Jeśli podcałka nie jest całką tablicową, to możliwe jest (nie zawsze) zastosowanie tej metody. Do tego potrzebujesz: podzielić całkę na dwa czynniki; wyznacz jeden z mnożników nowej zmiennej; wyrazić drugi czynnik w postaci nowej zmiennej; zapisz całkę, znajdź jej wartość i wykonaj podstawienie odwrotne. Uwaga: dla nowej zmiennej lepiej jest wyznaczyć funkcję związaną z pozostałym wyrażeniem. 1. txT(3x2-1)dx; Niech 3x2-1=t (tі0), weź pochodną obu części: y dt 1 1 y 1 1 t 2 2 1 ---W f- t 2 \u003d - f t 2dt \u003d - --- + C \u003d -C 3x2-1 + C t grzech x cos 3x dx = t - t3dt = - - + C Niech cos x = t Metoda konwersji całki na sumę lub różnicę: t sin 3x cos x dx = 1/2 t (sin 4x + sin 2x) dx = 1/8 cos 4x - ј cos 2x + C y x4+3x2+1 y 1 1 f dx = f(x2+2 - ---) dx = - x2 + 2x - łuk x + C x x2+1 x x2+1 3 Uwaga: rozwiązując ten przykład, dobrze jest uczynić wielomiany „kątami”. W częściach. Jeżeli w danej postaci nie da się przyjąć całki, a jednocześnie bardzo łatwo jest znaleźć funkcję pierwotną jednego czynnika i pochodną drugiego, wówczas można skorzystać ze wzoru. (u(x)v(x))"=u"(x)v(x)+u(x)v(x) u"(x)v(x)=(u(x)v(x)+u(x)v"(x) t u"(x)v(x)dx=t (u(x)v(x))"dx - t u(x)v"(x)dx t u"(x)v(x)dx=u(x)v(x)dx - t u(x)v"(x)dx t x cos (x) dx = t x dsin x = x grzech x - t grzech x dx = x grzech x + cos x + C Definicja. Figurę ograniczoną wykresem ciągłej funkcji ze stałym znakiem f(x), osią odciętych i liniami prostymi x=a, x=b nazywamy trapezem krzywoliniowym. Sposoby znajdowania obszaru trapezu krzywoliniowego Twierdzenie. Jeśli f(x) jest ciągłą i nieujemną funkcją na odcinku , wówczas obszar odpowiedniego trapezu krzywoliniowego jest równy przyrostowi funkcji pierwotnych. Dane: f(x) - ciągłe w nieskończoność. funkcja, x0. Udowodnij: S = F(b) - F(a), gdzie F(x) jest funkcją pierwotną f(x). Dowód: 1) Rozważmy funkcję pomocniczą S(x). Każdemu xO przypisujemy tę część trapezu krzywoliniowego, która leży na lewo od prostej (ryc. 2), przechodzącej przez punkt z tą odciętą i równoległą do osi y. Stąd S(a)=0 i S(b)=Str Udowodnimy, że S(a) jest funkcją pierwotną f(x). D(f) = D(S) = S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), dla Dx®0 DS jest prostokątem Dx®0 o bokach Dx i f(x0) S "(x0) \u003d lim (Dx f (x0) / Dx) \u003d lim f (x0) \u003d f (x0): ponieważ x0 jest punktem, to S (x) - Dx®0 Dx®0 funkcja pierwotna f(x). Zatem z twierdzenia o postaci ogólnej funkcji pierwotnej S(x)=F(x)+C. Ponieważ S(a)=0, wówczas S(a) = F(a)+C S = S(b)=F(b)+C = F(b)-F(a) 1). Podzielmy odcinek na n równych części. Krok podzielony (ryc. 3) Dx=(b-a)/n. W tym przypadku Str=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®When = lim Dx(f(x0)+f(x1)+...+ f (xn)) Dla n®When otrzymujemy, że Str= Dx(f(x0)+f(x1)+...+f(xn)) Granicę tej sumy nazywamy całką oznaczoną. Suma poniżej limitu nazywana jest sumą całkowitą. Całka oznaczona jest granicą sumy całkowej odcinka jako n®though. Sumę całkową otrzymuje się jako granicę sumy iloczynów długości odcinka otrzymanej przez podzielenie dziedziny funkcji w dowolnym punkcie tego przedziału. a - dolna granica całkowania; b - góra. Wzór Newtona-Leibniza. Porównując wzory na powierzchnię trapezu krzywoliniowego, dochodzimy do wniosku: jeśli F jest funkcją pierwotną b na , to f(x)dx = F(b)-F(a) t f(x)dx = F(x) f = F(b) - F(a) Własności całki oznaczonej. t f(x)dx = t f(z)dz t f(x)dx = F(a) - F(a) = 0 t f(x)dx = - t f(x)dx t f(x)dx = F(a) - F(b) t f(x)dx = F(b) - F(a) = - (F(a) - F(b)) Jeżeli a, b i c są dowolnymi punktami przedziału I, w których funkcja ciągła f(x) ma funkcję pierwotną, to t f(x)dx = t f(x)dx + t f(x)dx F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a) (jest to właściwość addytywności całki oznaczonej) Jeśli l i m są stałymi, to t (lf(x) +m j(x))dx = l t f(x)dx + m tj(x))dx - Jest to właściwość liniowości całki oznaczonej. t (f(x)+g(x)+...+h(x))dx = t f(x)dx+ t g(x)dx+...+ t h(x)dx t (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H (a)+Cn=b b b = t f(x)dx+ t g(x)dx+...+ t h(x)dx Zestaw standardowych zdjęć (ryc. 4, 5, 6, 7, 8) Ryż. 4 Ryc. 5 Ryż. 6 Ryc. 7 Ponieważ k(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0. Konieczne jest: rozważenie symetrii funkcji względem osi OX. ABCD®A"B"CD b S (ABCD) \u003d S (A „B” CD) \u003d t -f (x) dx S= t f(x)dx = t g(x)dx S = t(f(x)-g(x))dx+t(g(x)-f(x))dx S= t (f(x)+m-g(x)-m)dx = t (f(x)-g(x))dx t ((f(x)-g(x))dx S= t (f(x)+m-g(x)-m)dx = T (f(x)-g(x))dx Jeśli na odcinku f(x)іg(x), to obszar pomiędzy tymi wykresami jest równy t ((f(x)-g(x))dx Funkcje f(x) i g(x) są dowolne i nieujemne S=t f(x)dx - t g(x)dx = t (f(x)-g(x))dx Zastosowanie całki W fizyce. Praca przymusowa (A=FScosa, cosa nr 1) Jeśli na cząstkę działa siła F, energia kinetyczna nie pozostaje stała. W tym wypadku wg przyrost energii kinetycznej cząstki w czasie dt jest równy iloczynowi skalarnemu Fds, gdzie ds jest przemieszczeniem cząstki w czasie dt. Wartość nazywa się pracą wykonaną przez siłę F. Niech punkt porusza się wzdłuż osi OX pod działaniem siły, której rzut na oś OX jest funkcją f(x) (f-funkcja ciągła). Pod działaniem siły punkt przesunął się z punktu S1(a) do S2(b). Podzielmy odcinek na n odcinków o tej samej długości Dx = (b - a)/n. Praca siły będzie równa sumie pracy siły na powstałych odcinkach. Ponieważ f(x) -ciągły, to dla małych praca siły na tym odcinku jest równa f(a)(x1-a). Podobnie na drugim odcinku f(x1)(x2-x1), na n-tym odcinku - f(xn-1)(b-xn-1). Zatem praca nad jest równa: А » An = f(a)Dx +f(x1)Dx+...+f(xn-1)Dx= ((b-a)/n)(f(a)+f(x1)+...+f (xn-1)) Przybliżona równość staje się dokładna, gdy n®When A = lim [(b-a)/n] (f(a)+...+f(xn-1))= t f(x)dx (z definicji) Niech sprężyna o sztywności C i długości l zostanie ściśnięta o połowę swojej długości. Określ wielkość energii potencjalnej Ep równej pracy A wykonanej przez siłę -F (s) sprężystość sprężyny po jej ściśnięciu, następnie Ep \u003d A \u003d - t (-F (s)) dx Z przebiegu mechaniki wiadomo, że F(s)= -Cs. Stąd znajdziemy En \u003d - t (-Cs) ds \u003d CS2 / 2 | = C/2 l2/4 Odpowiedź: Cl2/8. Współrzędne środka masy Środek masy to punkt, przez który przechodzi wypadkowa ciężkości dla dowolnego przestrzennego układu ciała. Niech materiałowa płyta jednorodna o ma kształt krzywoliniowego trapezu (x;y |aЈxЈb; 0ЈyЈf(x)), a funkcja y=f(x) jest ciągła na , a pole tego krzywoliniowego trapezu jest równe S, wówczas współrzędne środka masy płyty o wyznacza się ze wzorów: x0 = (1/S) t x f(x) dx; y0 = (1/2S) t fa 2(x) dx; Centrum Mszy. Znajdź środek masy jednorodnego półkola o promieniu R. Narysuj półkole w układzie współrzędnych OXY (ryc. 9). Ze względu na symetrię i jednorodność zauważamy, że odcięta punktu M Funkcja opisująca półkole ma postać: Niech S = pR2/2 będzie zatem polem półkola y = (1/2S) tC(R2-x2)dx = (1/pR2) tC(R2-x2)dx = -R -R R = (1/pR2)(R2x-x3/3)|= 4R/3p Odpowiedź: M(0; 4R/3p) Ścieżka przebyta przez punkt materialny Jeżeli punkt materialny porusza się prostoliniowo z prędkością u=u(t) i przez czas T= t2-t1 (t2>t1) minął drogę S, to W geometrii Objętość jest ilościową cechą ciała przestrzennego. Za jednostkę objętości przyjmuje się sześcian o krawędzi 1 mm (1di, 1m itd.). Liczba sześcianów o jednostkowej objętości umieszczonych w danym ciele to objętość tego ciała. Aksjomaty objętości: Objętość jest wartością nieujemną. Objętość ciała jest równa sumie objętości ciał, które je tworzą. Znajdźmy wzór na obliczenie objętości (ryc. 10): wybierz oś OX w kierunku położenia tego ciała; określić granice położenia ciała względem OX; Wprowadźmy funkcję pomocniczą S(x), która definiuje następującą korespondencję: do każdego x z odcinka podstawiamy odpowiednio pole przekroju danej figury przez płaszczyznę przechodzącą przez dany punkt x prostopadłą do osi OX. podzielmy odcinek na n równych części i narysujmy płaszczyznę prostopadłą do osi OX przez każdy punkt podziału, podczas gdy nasze ciało zostanie podzielone na części. Zgodnie z aksjomatem V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx Dx®0 i Sk®Sk+1, a objętość części zawartej pomiędzy dwiema sąsiednimi płaszczyznami jest równa objętości walca Vц=SonH. Mamy sumę iloczynów wartości funkcji w punktach podziału według kroku podziału, tj. kwota całkowita. Z definicji całki oznaczonej granicę tej sumy jako n® `` nazywamy całką a V= t S(x)dx, gdzie S(x) to odcinek przechodzącej płaszczyzny b wybrany punkt prostopadły do osi OX. Aby znaleźć potrzebną głośność: 1). Wybierz oś OX w wygodny sposób. 2). Określ granice położenia tego ciała względem osi. 3). Skonstruuj przekrój danego ciała przez płaszczyznę prostopadłą do osi OX i przechodzącą przez odpowiedni punkt. 4). Wyraź w znanych ilościach funkcję wyrażającą pole danego przekroju. 5). Zrób całkę. 6). Po obliczeniu całki znajdź objętość. Objętość figur obrotowych Ciało powstałe w wyniku obrotu płaskiej figury wokół jakiejś osi nazywa się figurą obrotową. Funkcja S(x) figury obrotu ma okrąg. Ssec(x)=p fa 2(x) Długość łuku płaskiej krzywej Niech funkcja y = f(x) ma ciągłą pochodną y” = f”(x) na przedziale. W tym przypadku długość łuku l „kawałka” wykresu funkcji y = f(x), xO można znaleźć ze wzoru l \u003d t C (1 + f "(x) 2) dx 1. M.Ya. Vilenkin, OS Iwaszew-Musatow, S.I. Shvartsburd, „Algebra i analiza matematyczna”, Moskwa, 1993 2. „Zbiór problemów analizy matematycznej”, Moskwa, 1996 3. I.V. Savelyev, „Kurs fizyki ogólnej”, tom 1, Moskwa, 1982 4. Do przygotowania tej pracy wykorzystano materiały ze strony http://referatovbank.ru/. Idee rachunku całkowego w dziełach starożytnych matematyków. Cechy metody wyczerpania. Historia znajdowania wzoru na objętość torusa Keplera. Teoretyczne uzasadnienie zasady rachunku całkowego (zasada Cavalieriego). Pojęcie całki oznaczonej. prezentacja, dodano 07.05.2016 Historia rachunku całkowego. Definicja i własności całki podwójnej. Jego interpretacja geometryczna, obliczenia we współrzędnych kartezjańskich i biegunowych, redukcja do powtórzenia. Zastosowanie w ekonomii i geometrii do obliczania objętości i powierzchni. praca semestralna, dodano 16.10.2013 Definicja całki oznaczonej, jej własności. Długość łuku krzywej. Powierzchnia trapezu krzywoliniowego. Powierzchnia obrotu. Pola figur ograniczone wykresami funkcji ograniczonymi liniami określonymi przez równania. Obliczanie objętości ciał. prace kontrolne, dodano 02.10.2017 Historia pojawienia się pojęcia rachunku „całkowego” i całkowego, jego cechy i znaczenie. Integral jako jedno z głównych narzędzi pracy z funkcjami. Uzasadnienie konieczności wyrażania wszelkich zjawisk fizycznych w formie wzoru matematycznego. prezentacja, dodano 19.05.2014 Definicja całki krzywoliniowej po współrzędnych, jej główne własności i obliczanie. Warunek niezależności całki krzywoliniowej od ścieżki całkowania. Obliczanie pól figur przy użyciu całki podwójnej. Korzystając ze wzoru Greena. test, dodano 23.02.2011 Metody obliczania całek. Wzory i weryfikacja całki nieoznaczonej. Powierzchnia trapezu krzywoliniowego. Całka nieoznaczona, oznaczona i zespolona. Podstawowe zastosowania całek. Znaczenie geometryczne całek oznaczonych i nieoznaczonych. prezentacja, dodano 15.01.2014 Rozwiązanie problemu znalezienia pola trapezu krzywoliniowego. Definicja i własności całki oznaczonej. Warunek konieczny całkowalności i kryterium Darboux. Całkowalność funkcji ciągłych i monotonicznych. Dowód wzoru Newtona-Leibniza. test, dodano 25.03.2011 Obliczanie pól figur płaskich. Znajdowanie całki oznaczonej funkcji. Wyznaczanie pola pod krzywą, pola figury zawartej pomiędzy krzywymi. Obliczanie objętości ciał obrotowych. Granica sumy całkowej funkcji. Wyznaczanie objętości cylindra. prezentacja, dodano 18.09.2013 Pojęcie całki oznaczonej, obliczanie pola, objętości ciała i długości łuku, momentu statycznego i środka ciężkości krzywej. Obliczanie powierzchni w przypadku prostokątnego obszaru krzywoliniowego. Zastosowanie całek krzywoliniowych, powierzchniowych i potrójnych. praca semestralna, dodana 19.05.2011 Historia rachunku całkowego i różniczkowego. Zastosowanie całki oznaczonej do rozwiązywania niektórych problemów mechaniki i fizyki. Momenty i środki mas krzywych płaskich, twierdzenie Guldena. Równania różniczkowe. Przykłady rozwiązywania problemów w MatLabie. „Państwowa Akademia Medyczna w Omsku” Ministerstwo Zdrowia i Rozwoju Społecznego Federacji Rosyjskiej na temat: zastosowanie całki oznaczonej w medycynie ukończył student I roku oddziały medycyny ogólnej grupa 102F Głuszniewa N.A. Wstęp Wybitny włoski fizyk i astronom, jeden z twórców nauk ścisłych, Galileo Galilei (1564-1642) stwierdził, że „Księga Natury jest napisana językiem matematyki”. Prawie dwieście lat później twórca niemieckiej filozofii klasycznej Kant (1742-1804) argumentował, że „w każdej nauce jest tyle prawdy, ile matematyki”. Wreszcie po prawie stu pięćdziesięciu latach, praktycznie już w naszych czasach, niemiecki matematyk i logik David Hilbert (1862-1943) stwierdził: „Matematyka jest podstawą wszystkich ścisłych nauk przyrodniczych”. Leonardo Da Vinci powiedział: „Niech nikt, kto nie jest matematykiem, nie czyta mi moich podstaw”. Próbując znaleźć matematyczne uzasadnienie dla praw natury, uznając matematykę za potężny środek wiedzy, stosuje ją nawet w takiej nauce jak anatomia. Każdy potrzebuje matematyki. I lekarze też. Przynajmniej po to, aby poprawnie odczytać zwykły kardiogram. Bez znajomości podstaw matematyki nie da się być dobrym informatykiem, korzystać z możliwości tomografii komputerowej... Wszak współczesna medycyna nie może obejść się bez najbardziej skomplikowanej technologii. Dziś nie można badać hemodynamiki - ruchu krwi w naczyniach bez użycia całki. Przez długi czas cewnikowanie prawego serca było jedyną metodą badawczą, która umożliwiała ocenę stanu prawego serca, uzyskanie charakterystyki wewnątrzsercowego przepływu krwi oraz określenie ciśnienia w prawym sercu i tętnicach płucnych. Jednak bliżej praktyki. Najpierw znajdźmy prędkość liniową przepływu krwi Zmiana prędkości liniowej przepływu krwi w różnych naczyniach Jest to droga, którą w jednostce czasu przebywa cząstka krwi w naczyniu. Prędkość liniowa w naczyniach różnych typów jest różna (patrz rysunek) i zależy od prędkości objętościowej przepływu krwi i pola przekroju poprzecznego naczyń. W medycynie praktycznej prędkość liniową przepływu krwi mierzy się metodami ultradźwiękowymi i wskaźnikowymi, częściej określa się czas pełnego krążenia krwi, który wynosi 21-23 s. Aby to określić, do żyły łokciowej wprowadza się wskaźnik (erytrocyty znakowane izotopem radioaktywnym, roztworem błękitu metylenowego itp.) i odnotowuje się czas jego pierwszego pojawienia się we krwi żylnej tego samego naczynia w drugiej kończynie. Na początek przypomnijmy, że całka jest przedmiotem matematycznym, który powstał historycznie na podstawie konieczności rozwiązywania różnych stosowanych problemów fizyki i technologii. Oto fizyczne zastosowania całki oznaczonej: obliczenie drogi punktu materialnego poruszającego się po trajektorii prostoliniowej lub krzywoliniowej z prędkością jego ruchu. Te wielkości fizyczne, które są określane za pomocą całki, nazywane są zwykle całkami, a wielkości, za pomocą których wyrażane są wielkości całkowite, nazywane są różniczkami. Na przykład prędkość ciała w punkcie jest cechą różnicową ciała, a masa ciała jest cechą integralną. Charakterystyki różniczkowe są określane przez wartość w punkcie i zwykle są różne w różnych punktach przestrzeni. Charakterystyki integralne zawsze wyrażają właściwości obiektów odnoszące się do całego obszaru przestrzeni. Na przykład masa charakteryzuje całe ciało jako jakiś obiekt zajmujący obszar przestrzeni. Droga, którą przebywa ciało, jest również cechą integralną, ponieważ charakteryzuje całą trajektorię składającą się z wielu punktów, a prędkość jest inna w każdym punkcie trajektorii i charakteryzuje każdy punkt z osobna. Powstaje pytanie - jak obliczyć prędkość całkową dla całego naczynia (tętnicy lub żyły), znając prędkość liniową przepływu krwi. To bardzo proste: potrzebujesz Poniżej obliczenia objętości wyrzutowej (objętość wyrzutowa serca (syn.: skurczowa objętość krwi, skurczowa objętość serca, wyrzutowa objętość krwi) - objętość krwi (w ml) wyrzucanej przez komorę serca w jednym skurczu) – jedna z głównych wartości w EHOkg, obliczana na podstawie całki z liniowej prędkości przepływu krwi. a - Schematy obliczania objętości wyrzutowej, a - przy użyciu równania ciągłości przepływu, b - przy użyciu równania ciągłości przepływu w przypadku znacznej niedomykalności mitralnej. VTI = V cp ET, gdzie CSA to pole przekroju poprzecznego, VTI to liniowa całka prędkości przepływu, V cp to średnia prędkość przepływu w drodze odpływu z lewej komory, ET to czas wyrzutu. W przypadku, gdy występuje hemodynamicznie istotna niedomykalność mitralna (ponad 2 stopień), całkowitą objętość wyrzutową lewej komory oblicza się ze wzoru: TSV=FSV+RSV [Całka prędkości liniowej (FVI lub VTI)] = [Czas przepływu krwi (ET)] x [Średnia prędkość przepływu krwi (Vmean)]; Pojemność minutową serca można wyznaczyć na podstawie całki prędkości liniowej przepływu aortalnego i płucnego. Na zakończenie dodam, że moja praca nie jest przeznaczona dla matematyka dobrze zorientowanego w integracji, ale dla każdej osoby, która wykazała zainteresowanie wykorzystaniem całki w medycynie. Dlatego starałam się, aby była ona jak najbardziej przystępna dla percepcji i ciekawa nawet dla dziecka. Bibliografia: Otwarta lekcja algebry i początków analizy w klasie 11 z rozszerzoną nauką matematyki i fizyki „Zastosowanie metod analizy matematycznej w rozwiązywaniu problemów praktycznych”. Nauczyciel: Vishnevskaya N.V. Cele Lekcji: 1. Powtórz główne typy problemów rozwiązywanych metodami analizy matematycznej. 2. Powtórz algorytmy rozwiązania. 3. Analizować rozwiązania problemów o podwyższonym stopniu trudności. 4. Rozwiązuj problemy gospodarcze. Plan lekcji: Na tablicy analizowane są dwa zadania o podwyższonym stopniu trudności (karty nr 7 i nr 5). Podczas gdy chłopaki się przygotowują, klasa ustnie odpowiada na pytania: a) Obszary, w których stosowane są metody analizy matematycznej; b) algorytm rozwiązywania problemów poprzez wyszukiwanie największych i najmniejszych wartości funkcji; c) algorytm rozwiązywania problemów z wykorzystaniem całki oznaczonej. Jednocześnie 6 osób pracuje nad kartkami (nr 3, 4, 6, 8, 9, 10). Stoły się zapełniają. Zadania sprawdzane są na tablicy, nauczyciel sprawdza poprawność rozwiązania problemów na kartkach. Problem gospodarczy analizowany jest na tablicy (karta nr 1, 2). Kontrola domu. Algorytm rozwiązywania problemów poprzez wyszukiwanie największych i najmniejszych wartości funkcji. Algorytm obliczania wielkości geometrycznych i fizycznych za pomocą całki oznaczonej. Wyraź żądaną wartość jako wartość w pewnym punkcie funkcji F
.
Znajdź pochodną F tę funkcję. wyrazić funkcję F w postaci całki oznaczonej F i oblicz to. Wartość zastępcza X = B znajdź żądaną wartość. Zadania domowe (na tablicy):
Dwa statki poruszają się po dwóch prostopadłych liniach, które przecinają się w jednym punkcie O, w kierunku O. W pewnym momencie oba są oddalone o 65 km O prędkość pierwszego wynosi 15 km/h, drugiego 20 km/h. Z pierwszego statku odpływa motorówka, poruszająca się z prędkością 25 km/h. a) Jaki jest najkrótszy czas podróży łodzi z pierwszego statku na drugi? b) Jaki jest najkrótszy czas przepłynięcia łodzi z pierwszego statku na drugi i powrotu na pierwszy statek? V 1 = 15 km/h 65 km S
1 O
S
3 S
2
65 km V l = 25 km/h V 2 = 20 km/h Rozwiązanie:
X- czas, jaki upłynął od chwili, gdy oba statki znajdowały się w odległości 65 km O aż do wypłynięcia łodzi. W momencie wypłynięcia łodzi pierwszy statek był w oddali Różnić się pod względem X:
Odpowiedź: a) 1 godzina; b) 3 godziny. Kocioł ma kształt paraboloidy obrotowej. Promień jego podstawy R= 3 m, głębokość H\u003d 5 m. Kocioł jest wypełniony cieczą, której ciężar właściwy wynosi 0,8 G / cm3. Oblicz pracę, jaką należy wykonać, aby wypompować ciecz z kotła. Na
Na
R= 3 m H= 5 m bije waga = 0,8 g / cm 3 Oblicz pracę, jaką należy wykonać, aby wypompować ciecz z kotła. Rozwiązanie:
W płaszczyźnie przekroju hej AOB jest parabolą, której równanie Współrzędne punktu W musi spełniać to równanie, tj. Podzielmy paraboloidę na warstwy płaszczyznami równoległymi do powierzchni cieczy. Niech grubość warstwy na głębokości ( H – y) jest równe dy. Następnie, biorąc warstwę w przybliżeniu za walec, uzyskujemy jej objętość Z równania paraboli Dlatego, aby wypompować ciecz z głębokości Odpowiedź: Praca klasowa.
Ile pracy należy włożyć, aby rozciągnąć sprężynę o 6 cm, jeśli siła 1 kg rozciągnie ją o 1 cm? Rozwiązanie:
Według prawa Hooke’a siła F kg, rozciągając sprężynę o X, jest równe X= 0,01 m F= 1 kg Następnie Szukana praca Odpowiedź: 0,18 kGm. Oblicz pracę siły F gdy sprężyna jest ściśnięta o 5 cm, jeśli do jej ściśnięcia o 1 cm potrzebna jest siła 1 kg. Rozwiązanie:
Zgodnie z prawem Hooke’a X= 0,01 m F= 1 kg Następnie Szukana praca Odpowiedź: 0,125 kGm. Siła F, z którym ładunek elektryczny Gdzie k- stała. Wyznacz pracę siły F podczas przenoszenia ładunku Rozwiązanie:
Pracę określa się według wzoru Na Odpowiedź: Wyznacz siłę nacisku wody na pionową ścianę mającą kształt półkola o promieniu R= 6 m, którego średnica znajduje się na powierzchni wody. Rozwiązanie:
Siła ciśnienia płynu na powierzchnię S na głębokości zanurzenia X jest równe x C
dx
A B
Półkole równoległymi liniami prostymi dzielimy na paski, które przyjmiemy jako prostokąt. Niech zacieniony pasek będzie miał długość AB, szerokość dx i jest głęboki X Ciśnienie wody na listwie na głębokości X, będzie równe . Stąd Ciężar właściwy wody 1 cm 3 \u003d 1 G, a zatem ciężar 1 m 3 \u003d 1000 kg. 1 kg 1 bar = 0,987 atm. Odpowiedź: 144000 kg. Prędkość ruchu punktu Rozwiązanie:
Stąd Odpowiedź: 512 m; 64 m/s Karta nr 1 (ustalana na zajęciach na tablicy)
Średni całkowity koszt produkcji mydła Zależność między roczną sprzedażą równą rocznej produkcji Q i cenę mydła R(w tysiącach rubli za tonę) opisuje wzór Sprzedając całe uwarzone w ciągu roku mydło po ustalonej cenie, zakład uzyskał maksymalny możliwy zysk. Jakie były przychody firmy? Rozwiązanie:
Wyraź przez Q najpierw cena mydła z przepisu Potem zysk G może być wyrażone: Znajdźmy punkty krytyczne tej funkcji: Punkty krytyczne 100, -340, -120. Negatywne korzenie nie mają ekonomicznego sensu. Q
G
Czyli optymalna roczna ilość mydła Potem roczny dochód R będzie: (tysiąc rubli). Odpowiedź: 1 milion rubli. Znajdź ciśnienie wody na prostokącie zanurzonym pionowo w wodzie, jeśli wiadomo, że jego podstawa ma długość 8 m, wysokość 12 m, górna podstawa jest równoległa do powierzchni wody i znajduje się na głębokości 5 m. Rozwiązanie:
5 m 8 m X
dx 12 m kGm. Odpowiedź: Karta nr 2 (opcjonalnie)
Zdolności produkcyjne pozwalają przedsiębiorstwu Linotron wyprodukować nie więcej niż 600 ton waty rocznie. Zależność wartości kosztów całkowitych Zależność pomiędzy roczną sprzedażą waty, która odpowiada rocznej wielkości produkcji, a ceną waty R(w tysiącach rubli za tonę) opisuje funkcja Cenę waty ustala się na dzień 1 stycznia 1995 r. i koryguje się ją dopiero 1 stycznia następnego roku. Znajdź z dokładnością do 1% opłacalność produkcji pod względem kosztów, jeśli w 1995 roku przedsiębiorstwo uzyska maksymalny możliwy zysk. Rozwiązanie:
Korzystanie z zależności tak, tak A 0b do x a 0bcx
Rachunek całkowy powstał w związku z rozwiązaniem problemów wyznaczania pól i objętości. 2000 p.n.e mieszkańcy Egiptu i Babilonu wiedzieli już, jak określić przybliżoną powierzchnię koła i znali zasadę obliczania objętości ściętej piramidy. Teoretyczne uzasadnienie zasad obliczania powierzchni i objętości pojawiło się po raz pierwszy wśród starożytnych Greków. Materialistyczny filozof Demokryt V wiek p.n.e uważa, że ciała składają się z dużej liczby małych cząstek. Oznacza to, że stożek jest zbiorem bardzo cienkich cylindrycznych dysków o różnych promieniach. Ogromną rolę w historii rachunku całkowego odegrał problem kwadratury koła(kwadratowanie koła - zbudowanie kwadratu, którego pole jest równe polu danego koła). Dokładną kwadraturę kilku krzywoliniowych figur odkrył Hipokrates (w środku V wiek). Pierwszą znaną metodą obliczania całki jest metoda wyczerpania Eudoksosa (ok. 370 p.n.e.). Próbował znaleźć pola i objętości, dzieląc je na nieskończoną liczbę części, dla których pole lub objętość jest już znana. Metodę tę przejął i opracował Archimedes, służącą do obliczania obszarów paraboli i przybliżonego obliczania pola koła.W swoim eseju Kwadratura paraboli Archimedes stosuje metodę wyczerpania do obliczenia pola sektora paraboli. Te. Archimedes jako pierwszy zestawił sumy, które w naszych czasach nazywane są sumami całkowitymi. Pierwsze znaczące próby opracowania metod integracyjnych Archimedesa zostały uwieńczone sukcesem XVII stulecia, kiedy z jednej strony nastąpił znaczny postęp w dziedzinie algebry, a z drugiej strony ekonomia, technologia, nauki przyrodnicze rozwijały się tam coraz intensywniej i potrzebne były tam rozbudowane i głębokie metody badania i obliczania wielkości . Przy obliczaniu powierzchni trapezu krzywoliniowego Newton i Leibniz dochodzą do tej koncepcjifunkcja pierwotna (lub pierwotna) dla danej funkcji pochodnejF(X),GdzieZmoże być cokolwiek. Tazadzwonić dzisiaj
Prace nad badaniem podstaw rachunku różniczkowego i całkowego rozpoczynają się w XIX wieku przez dzieła O. Cauchy’ego i B. Bolzano. Jednocześnie rosyjscy matematycy M.V. wnieśli znaczący wkład w rozwój rachunku całkowego. Ostrogradski, V.Ya. Bunyakovsky, V.Ya. Czebyszew. Był to czas, kiedy dopiero powstawała nowoczesna analiza matematyczna. Była to być może jedyna pod względem intensywności epoka kreatywności matematycznej i Euler połączył obszerny, ale odmienny materiał nowej analizy w naukę integralną. Z czasem, człowiek zdobywał coraz większą władzę nad naturą, ale marzenie o lataniu do gwiazd pozostawało równie nierealne. Pisarze science fiction wspominali o rakietach do lotów kosmicznych. Jednak te rakiety były technicznie niezdrowym marzeniem. Zaszczyt otwarcia ludziom drogi do gwiazd przypadł na los naszego rodaka K. E. Ciołkowskiego. Cała galaktyka naukowców pod przewodnictwem S.P. Korolow. Szczególnie interesujące są problemy będące prototypem problemów obliczania trajektorii statku kosmicznego wchodzącego na daną orbitę, wyznaczania wysokości i prędkości wznoszenia lub opadania ciała oraz niektórych innych problemów z wykorzystaniem rachunku całkowego. Zadanie 1. Dana jest prędkość ruchu prostoliniowego ciała równanie. Znajdź równanie drogi S, jeśli ciało przebyło 20 m w czasie t = 2 sek. Rozwiązanie: Lecąc w kosmos, należy wziąć pod uwagę wszystkie czynniki otaczającego nas środowiska, a aby dotrzeć tam, gdzie trzeba, należy obliczyć trajektorię ruchu na podstawie danych początkowych. Wszystko to należy zrobić przed lotem.W 2016 roku przypada 55. rocznica lotu na orbitę pierwszego kosmonauty Jurija Aleksiejewicza Gagarina. Podczas obliczeń konieczne było rozwiązanie takich problemów. Zadanie 2. Konieczne jest wystrzelenie rakiety ważącej P \u003d 2 10 4 H (T) od powierzchni ziemi na wysokośćH= 1500 km.Oblicz pracę potrzebną do jego wykonania. Rozwiązanie.f - siła przyciągania ciała przez Ziemię jest funkcją jego odległości X do środka Ziemi: , gdzie Na powierzchni Ziemi, gdzie siła ciężkości jest równa ciężarowi ciała R, A x = R- zatem promień Ziemi i Podczas podnoszenia rakiety z powierzchni Ziemi na wysokość H zmienny X zmiany odX
= R zanim X=
R+
H. Pracę, której szukamy, znajdujemy korzystając ze wzoru: Zadanie 3. siła w 10 N rozciąga sprężynę 2cm. Jaką ona ma pracę czy to? Rozwiązanie
.
Według prawa Hooke’a siła F , naciągnięcie sprężyny, jest proporcjonalne do naciągnięcia sprężyny, tj.F =kh. Od stanu problemu k= 10/0,02(N/m), To F= 500x. Stanowisko: Zadanie 4. Z głębi kopalnil= 100 mkonieczne jest równomierne podniesienie klatki z ciężarem R 1 = 10 4
H, który wisi na linie nawiniętej na bęben. Oblicz całkowitą pracę Pełna potrzebne do podniesienia klatki, jeżeli ciężar wynosi jeden metr bieżący liny R2= 20H.
Rozwiązanie
.
Praca przy podnoszeniu klatki: oraz przy podnoszeniu liny jest proporcjonalna do ciężaru liny, tj. Zadanie 5. Sprężyna ugina się pod działaniem siły 1,5 10 4 H o 1 cm. Ile pracy należy wykonać, aby odkształcić sprężynę o 3 cm? ( Siła odkształcająca jest proporcjonalna do ugięcia sprężyny.) Rozwiązanie
.
F\u003d kx,Gdzie X- ugięcie sprężyny. Na x = 0,01 m mamy: Wylot w przestrzeń kosmiczną jest trudny i niebezpieczny, ale nie mniej trudny jest powrót na Ziemię, gdy statek kosmiczny musi wylądować z prędkością nie większą niż 2 m/s. Tylko w tym przypadku urządzenie, znajdujące się w nim instrumenty i, co najważniejsze, członkowie załogi nie doznają ostrego, mocnego uderzenia. Konstantin Eduardowicz Ciołkowski postanowił wykorzystać hamowanie statku kosmicznego przez powłokę powietrzną Ziemi. Poruszając się z prędkością 8 m/s, statek kosmiczny nie spada na Ziemię. Pierwszym etapem zjazdu jest włączenie na krótki czas hamulca silnika. Prędkość spada o 0,2 km/s i natychmiast rozpoczyna się zniżanie. Rozważmy przykład rozwiązania problemu sformułowania prawa ruchu w danych warunkach. Zadanie 6. Znajdź zasadę ruchu swobodnie spadającego ciała ze stałym przyspieszeniem g, jeśli w chwili ruchu ciało znajdowało się w spoczynku. Rozwiązanie:Wiadomo, że przyspieszenie ciała poruszającego się prostoliniowo jest drugą pochodną drogi S po czasie T lub pochodna prędkości po czasie T : , ale zatem , skąd . Całkujemy: , i Z warunku: , skąd znajdujemy i prędkość ruchu: . Znajdźmy prawo ruchu ciała: , lub . Integrujemy: , . Zgodnie z warunkami początkowymi: , skąd znajdujemy Mamy równanie ruchu spadającego ciała: - jest to znany wzór z fizyki. Zadanie 7. Ciało rzucono pionowo w górę z prędkością początkową Znajdź równanie ruchu tego ciała (pomiń opór powietrza). Rozwiązanie:Załóżmy, że kierunek pionowy w górę jest dodatni, a przyspieszenie ziemskie skierowane w dół jest ujemne. Mamy: skąd. Integrujemy: następnie . Ponieważ a następnie C 1: Poniższy przykład pokazuje obliczenie trajektorii zrzutu zużytych sekcji, niepotrzebnych urządzeń, materiałów. W tym przypadku są one wysyłane na Ziemię, po obliczeniu orbity tak, aby podczas przechodzenia przez warstwy atmosfery wypaliły się, a niespalone pozostałości spadły na Ziemię (najczęściej do oceanu), nie wyrządzając szkody. Zadanie 8. Napisz równanie krzywej przechodzącej przez punkt M (2; -3) i mającej styczną z nachyleniem .
Rozwiązanie:Podano warunek zadania: Konstruktorzy czasami muszą rozwiązać problemy z obliczaniem obszarów nietypowych figur, dla których nie ma dobrze znanych wzorów. W tym przypadku całki znów przychodzą na ratunek.
.
Kosmonauci i naukowcy pracujący na stacji orbitalnej, dla czystości eksperymentu, rozwiązują i badają wiele zagadnień z astronomii, fizyki, chemii, medycyny, biologii itp. Następującemu problemowi towarzyszyć będziemy przykład literacki. Znana powieść science fiction HG Wellsa „Wojna światów” opisuje atak Marsjan na planetę Ziemia, którzy postanowili rozszerzyć swoje przeludnione terytoria, zdobywając nasze, ponieważ. Warunki klimatyczne na Ziemi były odpowiednie. Rozpoczęło się zajmowanie terytorium i niszczenie Ziemian, którzy otrzymali pomoc tam, gdzie wcale się nie spodziewali. Nasze „rodzime” bakterie, z którymi nauczyliśmy się już walczyć, wchodząc do ciała Marsjan z powietrzem, pożywieniem i wodą, znalazły w nim sprzyjające środowisko dla ich rozwoju i rozmnażania, szybko się przystosowały i po zniszczeniu Marsjan, uwolnić Ziemię od najeźdźców. Rozważ rozwiązanie problemu, który daje koncepcję tego. Zadanie 10.Tempo rozmnażania się niektórych bakterii jest proporcjonalne do liczby bakterii dostępnych w rozpatrywanym czasie t. Liczba bakterii potroiła się w ciągu 5 godzin. Znajdź zależność liczby bakterii od czasu. Rozwiązanie: Niech x(t ) to liczba bakterii w chwili t, a w chwili początkowej tempo ich rozmnażania. Według warunku mamy: lub co następuje: W słynnej powieści A.N. „Hiperboloida inżyniera Garina” Tołstoja Chciałbym poczuć, poczuć, co to jest – hiperboloida? Jakie są jego wymiary, kształt, powierzchnia, objętość? Następne zadanie dotyczy tego. Rozwiązanie.Ze wzoru obliczamy objętość ciał obrotowych wokół osi OX za pomocą całki oznaczonej: Zadanie 12. Oblicz objętość ciała powstałego w wyniku obrotu wokół osi OX obszaru ograniczonego liniami y \u003d x 2 - 9 I y = 0.
Znaczenie ekonomiczne całki oznaczonej wyraża wielkość produkcji o znanej funkcji f(t ) - wydajność pracy w tej chwili T . Następnie wielkość produkcji w danym okresie oblicza się według wzoru. Rozważmy przykład dla przedsiębiorstwa. Zadanie 13. Znajdź wielkość produkcji wyprodukowanej w ciągu 4 lat, jeśli funkcja Cobba-Douglasa ma postać Rozwiązanie. Wolumen produktów wytwarzanych przez przedsiębiorstwo jest równy: Podsumowując, możemy stwierdzić, że zastosowanie całki otwiera ogromne możliwości. Studiując geometrię, uwzględniają obliczanie pól figur płaskich ograniczonych odcinkami linii (trójkąty, równoległoboki, trapezy, wielokąty) oraz objętości ciał uzyskane podczas ich obrotu. Całka oznaczona pozwala obliczyć pola figur złożonych ograniczonych dowolnymi liniami zakrzywionymi, a także znaleźć objętości ciał uzyskane przez obrót trapezów krzywoliniowych wokół dowolnej osi. Pragnę również zauważyć, że zastosowanie całki oznaczonej nie ogranicza się tylko do obliczania różnych wielkości geometrycznych, ale jest również wykorzystywane przy rozwiązywaniu problemów z różnych dziedzin fizyki, aerodynamiki, astronomii, chemii i medycyny, astronautyki, a także jak problemy gospodarcze. Bibliografia:
slajd 2 Historia pojęcia całki jest ściśle związana z problemami znajdowania kwadratur, tj. zadania obliczania powierzchni. Nawet matematycy starożytnej Grecji i Rzymu zajmowali się obliczaniem pól powierzchni i objętości ciał. Pierwszym europejskim matematykiem, który otrzymał nowe wzory na pola figur i objętości ciał, był słynny astronom I. Kepler. Po badaniach szeregu naukowców (P. Fermat, D. Wallis) I. Barrow odkrył związek pomiędzy problemami znajdowania obszarów a rysowaniem stycznej (tj. pomiędzy integracją a różniczkowaniem). Wolne od języka geometrycznego badanie relacji między tymi operacjami przeprowadzili I. Newton i G. Leibniz. Współczesny zapis całki sięga czasów Leibniza, który wyraził pogląd, że pole krzywoliniowego trapezu jest sumą pól nieskończenie cienkich pasków o szerokości d i wysokości f(x). Sam znak integralny to stylizowana łacińska litera S (summa). Symbol całki wprowadzono od 1675 r., a zagadnienia rachunku całkowego zaczęto stosować od 1696 r. Chociaż całką zajmują się głównie matematycy, fizycy również wnieśli swój wkład w tę naukę. Prawie żadna formuła fizyki nie jest kompletna bez rachunku różniczkowego i całkowego. slajd 3 Wiele znaczących osiągnięć matematyków starożytnej Grecji w rozwiązywaniu problemów znajdowania obszarów, a także objętości ciał wiąże się z imieniem Archimedesa (287-212 p.n.e.) Archimedes rozwijając idee swoich poprzedników, określił obwód i powierzchnię koła, objętość i powierzchnia kuli. W swoich pracach „O kuli i cylindrze”, „O spiralach”, „O stożkach i kulach” pokazał, że wyznaczanie objętości kuli, elipsoidy, hiperboloidy i paraboloidy obrotowej sprowadza się do określenia objętości objętość stożka i walca. Archimedes opracował i zastosował metody, które wyprzedzały metody stworzone w XVII wieku. rachunek całkowy. Minęło ponad półtora tysiąca lat, zanim idee Archimedesa znalazły jasny wyraz i zostały sprowadzone na poziom rachunku różniczkowego. W XVII wieku matematycy wiedzieli już, jak obliczać pola wielu figur o zakrzywionych granicach i objętości wielu ciał. A ogólna teoria powstała w drugiej połowie XVII wieku. w dziełach wielkiego angielskiego matematyka Izaaka Newtona (1643-1716) i wielkiego niemieckiego matematyka Gottfrieda Leibniza (1646-1716). Newton i Leibniz są twórcami rachunku całkowego. Odkryli ważne twierdzenie, które nosi ich nazwę: gdzie f(x) jest funkcją całkowalną na przedziale , F(x) jest jedną z jej funkcji pierwotnych. Rozumowanie podane przez Newtona i Leibniza jest niedoskonałe z punktu widzenia współczesnej analizy matematycznej. W XVIII wieku. największy przedstawiciel analizy matematycznej, Leonard Euler, uogólnił te koncepcje w swoich pracach. Dopiero na początku XIX w. ostatecznie powstały koncepcje rachunku całkowego. Zwykle odnotowuje się zasługi francuskiego matematyka Augustina Cauchy'ego i niemieckiego matematyka Georga Riemanna. Samo słowo całka ukuł J. Bernoulli (1690). Pochodzi od łacińskiego integro, co tłumaczy się jako przywrócenie do poprzedniego stanu, przywrócenie. W 1696 r pojawiła się nazwa nowej gałęzi matematyki - rachunku całkowego, którą wprowadził I. Bernoulli. Używana obecnie nazwa funkcja pierwotna zastąpiła wcześniejszą „funkcję pierwotną” wprowadzoną przez Lagrange'a (1797). Zapis całki oznaczonej wprowadził Joseph Bernoulli, a granicę dolną i górną Leonhard Euler. slajd 4 Operacje matematyczne tworzą pary dwóch wzajemnie odwrotnych operacji, na przykład dodawanie i odejmowanie, mnożenie i dzielenie, podnoszenie do dodatniej potęgi całkowitej i wyodrębnianie pierwiastka. Różniczkowanie pozwala danej funkcji F(x) znaleźć jej pochodną F´(x). Istnieje działanie odwrotne do różniczkowania - jest to integracja - znalezienie funkcji F (x) przez jej znaną pochodną f (x) \u003d F´ (x) lub różniczkę f (x) dx. Funkcja F(x) nazywana jest funkcją pierwotną funkcji f(x), jeżeli F´(x) = f(x) lub dF(x)=f(x)dx. Jeżeli funkcja f(x) ma funkcję pierwotną F(x), to ma nieskończony zbiór funkcji pierwotnych, a wszystkie jego funkcje pierwotne zawarte są w wyrażeniu F(x) + С, gdzie С jest stałą. Całka nieoznaczona funkcji f(x) (lub wyrażenia f(x)dx) jest zbiorem wszystkich jej funkcji pierwotnych. Notacja ∫f(x)dx = F(x) +C. Tutaj ∫ jest znakiem całki, f(x) jest całką, f(x)dx jest całką, x jest zmienną całkującą. Znalezienie całki nieoznaczonej nazywa się całkowaniem funkcji. Własności całki nieoznaczonej Pochodna całki nieoznaczonej jest równa całce: (∫ f(x)dx)´ = f(x) Różniczka całki nieoznaczonej jest równa całce: różniczki funkcji pierwotnej wynosi równy samej funkcji pierwotnej i członowi dodatkowemu C:∫d (F(x)) = F(x) +C Ze znaku całki nieoznaczonej można wyjąć współczynnik stały: suma algebraiczna skończonej liczby funkcji wynosi równa sumie algebraicznej całek wyrazów: ∫ dx = ∫ dx ± ∫ dx slajd 5 Pojęcie całki oznaczonej wyprowadza się za pomocą trapezu krzywoliniowego. Trapez krzywoliniowy to figura ograniczona liniami y = f(x), y = 0, x=a, x=b. Całkę oznaczoną oblicza się za pomocą wzoru Newtona – Leibniza. = F (x)|ba= F(b) – F(a) Wspólny zapis całek oznaczonych i nieoznaczonych podkreśla ścisły związek między nimi: całka oznaczona jest liczbą, a całka nieoznaczona jest zbiorem funkcji pierwotnych. Związek między całką oznaczoną i nieoznaczoną wyraża wzór Newtona-Leibniza. Właściwości całki oznaczonej: Jeśli zamienimy górną i dolną granicę całkowania, to całka oznaczona zachowa swoją wartość bezwzględną, ale zmieni swój znak na przeciwny. Jeżeli górna i dolna granica całkowania są równe, to całka oznaczona jest równa zeru. Jeśli odcinek całkowania podzielimy na kilka części, całka oznaczona na tym segmencie będzie równa sumie całek oznaczonych tych odcinków. Całka oznaczona sumy funkcji podanych na przedziale jest równa sumie całek oznaczonych wyrazów funkcji. Stały czynnik całki można odjąć od znaku całki oznaczonej. Obliczanie całki oznaczonej: jeśli m ≤ f(x) ≤ M na , to m (b – a) slajd 6 Niech funkcja y=f(x) będzie ciągła na odcinku i f(x) ≥ 0. Figura ograniczona wykresem funkcji AB y=f(x), proste x=a, x=b i Oś wołu (patrz rysunek) nazywa się trapezem krzywoliniowym. Suma całkowa i jej terminy mają proste znaczenie geometryczne: iloczyn jest równy obszarowi prostokąta o podstawie i wysokości, a suma to obszar zacienionej figury schodkowej pokazanej na rysunku. Oczywiście obszar ten zależy od podziału odcinka na odcinki cząstkowe i wyboru liczby punktów podziału. Im mniejszy ∆ x, tym obszar figury schodkowej jest bliżej obszaru trapezu krzywoliniowego. Dlatego za granicę sumy całkowej przyjmuje się dokładne pole S trapezu krzywoliniowego. Zatem z geometrycznego punktu widzenia całka oznaczona funkcji nieujemnej jest liczbowo równa powierzchni odpowiedniego trapezu krzywoliniowego. Slajd 7 1. Całkowanie bezpośrednie Całkowanie bezpośrednie nazywa się zwykle obliczaniem całek nieoznaczonych poprzez sprowadzenie ich do postaci tabelarycznych przy użyciu podstawowych własności. Mogą tu wystąpić następujące przypadki: 1) podaną całkę wzięto bezpośrednio ze wzoru na odpowiednią całkę tabelaryczną; 2) po zastosowaniu właściwości całkę tę redukuje się do jednej lub większej liczby całek tabelarycznych; 3) podaną całkę, po elementarnych identycznych przekształceniach po całce i zastosowaniu własności, redukuje się do jednej lub większej liczby całek tablicowych. 2. Całkowanie metodą zmiany zmiennej (metoda podstawieniowa) Zamiana zmiennej w całkę nieoznaczoną odbywa się za pomocą dwóch rodzajów podstawień: x = φ (t), gdzie φ (t) jest monotoniczną, różniczkowalną w sposób ciągły funkcją nowa zmienna t. Wzór na zmianę zmiennej w tym przypadku to ∫f(x) = ∫f [φ (t)] φ΄ (t) d(t); 2) u = ψ(x), gdzie u jest nową zmienną. Zmiana wzoru zmiennej na to podstawienie wynosi: ∫f [ψ(x)] ψ ΄(x) d(x) = ∫f (u) du v du, gdzie u = φ (x), v = ψ(х ) są ciągle różniczkowalnymi funkcjami x . Korzystając z tego wzoru, znalezienie całki ∫udv sprowadza się do znalezienia innej całki ∫v du; jego zastosowanie jest celowe w przypadkach, gdy ostatnia całka jest albo prostsza od pierwotnej, albo do niej podobna. W tym przypadku u przyjmuje się taką funkcję, która upraszcza różniczkowanie, a dv jest tą częścią całki, której całka jest znana lub może zostać znaleziona. Slajd 8 Slajd 9 Jak znaleźć obszar pokazanych figur? Slajd 10 slajd 11 Ponadto całka oznaczona służy do obliczania pól figur płaskich, objętości ciał obrotowych i długości łuków krzywych. slajd 12 Niech będzie dane bryła o objętości V i istnieje taka prosta, że niezależnie od tego, jaką płaszczyznę prostopadłą do tej prostej przyjmiemy, znamy pole S przekroju bryły przez tę płaszczyznę. Ale płaszczyzna prostopadła do osi x przecina ją w pewnym punkcie x. Dlatego każdej liczbie x (z odcinka [a; b]) przypisana jest pojedyncza liczba S (x) - pole przekroju ciała przez tę płaszczyznę. Zatem na odcinku [a; b] podana jest funkcja S(x). Jeżeli funkcja S jest ciągła na odcinku [a; b] wówczas obowiązuje wzór: slajd 13 Znajdź obszar przedstawionych figur 1 - 5. Odpowiedzi: 1) S = 2/3 (równość funkcji); 2) S = 1 (obszar prostokątnego trójkąta); 3) S = 4 (równość liczb); 4) S = 2π (pole półkola); 5) S = 1 (obszar trójkąta). Slajd 14 Znajdź sumę pól nieskończonej liczby figur zacieniowanych na figurach. (Argument każdej kolejnej funkcji zwiększa się 2 razy) Ciekawe zadanie! Odpowiedź: grzech nx=0 ; x=π/n; gdzie n=1,2,4,8,16…; S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4 Odpowiedź: 4. slajd 15 Prawidłowe odpowiedzi: I opcja: 2,3,1; II opcja: 2,4,2. slajd 16 Oblicz obszar figury ograniczony liniami (schematycznie przedstawiającymi wykresy funkcji). 1) y = 6 + x – x2 i y = 6 – 2x; 2) y = 2x2 i y = x + 1; 3) y = 1 – x i y = 3 – 2x – x2; 4) y = x2 i y = . Odpowiedź: 1) 4,5; 2) 9/8; 3) 4,5; 4) 1/3. Slajd 17 Znajdź objętość ciała uzyskaną przez obrót wokół osi odciętej figury ograniczonej liniami: 1) y = x2 + 1, x = 0, x = 1, y = 0; 2) y = , x = 1 , x = 4 , y = 0 ; 3) y = 2x, y = x + 3, x = 0, x = 1; 4) y \u003d x + 2, y \u003d 1, x \u003d 0, x \u003d 2; 5) y2 - 4 x = 0, x - 2 = 0, x - 4 = 0, y = 0; 6) y2 - x + 1 = 0, x - 2 = 0, y = 0; 7) y \u003d - x2 + 2x, y \u003d 0; 8) y2 = 2 x, x - 2 = 0, y = 0; 9) y = , x = 3 , y = 0 ; 10) y \u003d 1 - x2, y \u003d 0. Odpowiedź: 1) ; 2) 7,5; 3) 11 ; 4) 16 ⅔; 5) 24 ; 6) /2; 7) 16/15; 8) 4 ; 9) 2 ; 10) 16/15. Slajd 18 Znajdź obszar figury ograniczony liniami 2) Figura ograniczona liniami y=x+6, x=1, y=0 jest podzielona przez parabolę y=x 2+2x+4 na dwie części. Znajdź obszar każdej części. 3) Znajdź funkcję pierwotną F(x) funkcji f(x)=2x+4, której wykres styka się z prostą y=6x+3. Oblicz pole figury ograniczone wykresem znalezionej funkcji pierwotnej i liniami prostymi y=6x+3 i y=0. Slajd 19 Jakie działanie nazywa się integracją? Jaką funkcję nazywamy funkcją pierwotną dla funkcji f(x)? Jaka jest różnica między różnymi funkcjami pierwotnymi dla danej funkcji f(x)? Podaj definicję całki nieoznaczonej. Jak sprawdzić wynik całkowania? Jaka jest pochodna całki nieoznaczonej? Ile wynosi ∫ d(lnx8 – sin 3x)? Wymień metody integracji. Podaj definicję całki oznaczonej. Sformułuj twierdzenie Newtona-Leibniza. Podaj własności całki oznaczonej. Jak obliczyć powierzchnię płaskiej figury za pomocą całki (utwórz algorytm słowny)? Wymień obszary zastosowania całki, podaj wielkości, które można obliczyć za pomocą całki. Slajd 20 1) Oblicz pole figury ograniczone tymi liniami: y=x2 przy x0, y=1, y=4, x=0 funkcja odwrotna y=x2, x0. Dlatego te figury mają równe pola i 2) Znajdź obszar figury ograniczony liniami y=3x+1, y=9-x, y=x+1. Rozwiązanie: Wierzchołki powstałego ABC mają współrzędne: A(0;1), B(2;7), C(4;5). Można zauważyć, że ABC jest prostokątny (iloczyn nachylenia prostych y=x+1 y=9-x jest równy -1). Dlatego użycie całki do obliczenia S(ABC) nie jest racjonalne. Zawsze można go znaleźć jako różnicę w polach trójkątów, których wysokość i podstawa są znane, lub można zastosować metodę współrzędnych. slajd 21 Znajdź pola figur ograniczonych liniami (1-7) y=x2 (x0), y=1, y=4, x=0 y= x2-4x+8, y=3x2-x3, jeśli x [ -2 ;3] y=x2-4x+sin2(x/2), y=-3-cos2(x/2), jeśli x y=3x+1, y=9-x, y=x+1 y= | x-2|, x|y|=2;x=1;x=3 y= arcsin x; y=0; x=0,5; x=1 Przy jakiej wartości a linia x=a dzieli obszar figury ograniczony liniami y=2/x; x=1; x=3 w stosunku 1:3? Oblicz na podstawie jego znaczenia geometrycznego. slajd 22 N. A. Kołmogorow, „Algebra i początki analizy”, Moskwa, Prosveshchenie, 2000. M. I. Bashmakov, „Algebra i początki analizy”, Moskwa, DROFA, 2002 Sh.A. Alimov, „Algebra i początki analizy”, 11. klasa, Moskwa, DROFA, 2004 L. V. Kiseleva, Podręcznik matematyki dla studentów szkół i uczelni medycznych, Moskwa, FGOU „VUNMC Roszdrav”, 2005 http://www.nerungri.edu.ru http://tambov.fio.ru http://www.zachetka.ru http://edu.of.ru http://festival.1september.ru
Wyświetl wszystkie slajdyDefinicja i własności całki
Integracja
Trapez krzywoliniowy
Bibliografia
Podobne dokumenty
Główną zaletą echokardiografii (EchoCG) jest możliwość nieinwazyjnej oceny w czasie rzeczywistym wielkości i ruchu struktur serca, uzyskania charakterystyki hemodynamiki wewnątrzsercowej oraz określenia ciśnienia w komorach serca i tętnicy płucnej. Wykazano dobrą porównywalność wyników badania echokardiograficznego z danymi uzyskanymi podczas cewnikowania serca.
Badanie echokardiograficzne pozwala nie tylko wykryć obecność nadciśnienia płucnego, ale także wykluczyć szereg chorób powodujących wtórne nadciśnienie płucne: wady zastawki mitralnej, wrodzone wady serca, kardiomiopatię rozstrzeniową, przewlekłe zapalenie mięśnia sercowego.Numer karty 7
 – czas potrzebny łodzi na przebycie podróży z pierwszego statku na drugi.
– czas potrzebny łodzi na przebycie podróży z pierwszego statku na drugi. km od O; w momencie, gdy łódź dopływa do drugiego statku, odległość między nim a O było równe km; jest droga łodzi
km od O; w momencie, gdy łódź dopływa do drugiego statku, odległość między nim a O było równe km; jest droga łodzi  . Następnie z twierdzenia Pitagorasa
. Następnie z twierdzenia Pitagorasa .
.


 ;
; 
 ;
; 
Numer karty 5
![]()
 A R
W
A R
W


 dy
H
dy
H

Och, x x
 . Znajdźmy parametr A.
. Znajdźmy parametr A.
 ,
,
 , stąd
, stąd  .
.
 .
.
 , Następnie
, Następnie  , tj. masa warstwy cieczy wynosi
, tj. masa warstwy cieczy wynosi 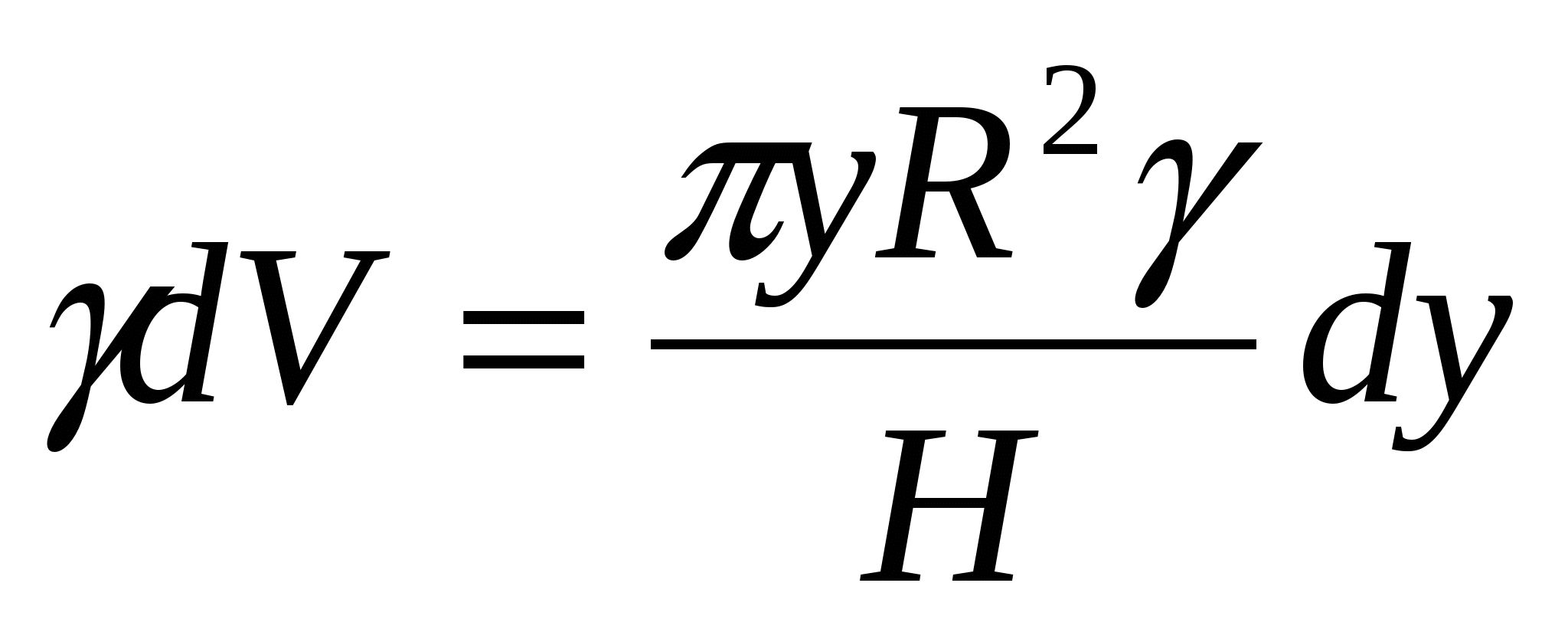 .
.
 , musisz spędzić elementarną pracę
, musisz spędzić elementarną pracę  ,
,  . Następnie
. Następnie , Następnie .
, Następnie . .
.
Karta numer 6
 , k – współczynnik proporcjonalności.
, k – współczynnik proporcjonalności. , stąd
, stąd  .
.
 .
.
Numer karty 8
 .
.
 , stąd
, stąd  .
.
 .
.
Numer karty 9
 odpycha ładunek
odpycha ładunek  (tego samego znaku), znajdującego się w pewnej odległości od niego R, wyraża się wzorem
(tego samego znaku), znajdującego się w pewnej odległości od niego R, wyraża się wzorem ,
,
 z punktu
z punktu  , oddzielony od
, oddzielony od  na odległość
na odległość  , Dokładnie
, Dokładnie  , z dala od
, z dala od  na odległość
na odległość  , przy założeniu, że opłata
, przy założeniu, że opłata  umieszczony w punkcie
umieszczony w punkcie  przyjąć za punkt wyjścia.
przyjąć za punkt wyjścia. ,
,  . Następnie
. Następnie .
.
 dostajemy
dostajemy  .
.
 .
.
Numer karty 3
 ,
,  jest ciężarem właściwym cieczy.
jest ciężarem właściwym cieczy.O

 .
.

 ,
,
 ,
,
 ,
,

 .
.
 ;
;
 9,81 n
9,81 nNumer karty 4
 m/sek. Znaleźć drogę S, minęło w pewnym momencie T= 8 sekund po rozpoczęciu ruchu. Jaka jest średnia prędkość w tym przedziale?
m/sek. Znaleźć drogę S, minęło w pewnym momencie T= 8 sekund po rozpoczęciu ruchu. Jaka jest średnia prędkość w tym przedziale? , stąd
, stąd  ,
,  ,
,  .
.
 .
.
 .
.
 (w tysiącach rubli za tonę) w fabryce mydła Mukhinsky różnią się w zależności od wielkości rocznej produkcji Q(w tonach) zgodnie z prawem:
(w tysiącach rubli za tonę) w fabryce mydła Mukhinsky różnią się w zależności od wielkości rocznej produkcji Q(w tonach) zgodnie z prawem: .
.
 .
.
 .
.
 .
.
 ,
,  .
.



 ;
;
 .
.
 t, potem cena
t, potem cena  (tysiąc rubli/t).
(tysiąc rubli/t).Numer karty 10
 ,
,  ,
,  M.
M. .
.
 kGm.
kGm. (w tysiącach rubli) rocznej wielkości produkcji Q(w tonach) ma postać
(w tysiącach rubli) rocznej wielkości produkcji Q(w tonach) ma postać .
.
 i ekspresowe.
i ekspresowe.











![]() formuła Newton-Leibniz pozwala zredukować dość złożone obliczenia niektórych całek, tj. znajdowanie granic sum całkowitych, po stosunkowo prostą operację znajdowania funkcji pierwotnych.Leibniz jest właścicielem symbolu różniczkowego str Później pojawił się także symbol całkowyZdecydowany symbol całkiwprowadził J. Fourier i termin „całka” (z łac liczba całkowita - całość) zaproponował I. Bernoulli.
formuła Newton-Leibniz pozwala zredukować dość złożone obliczenia niektórych całek, tj. znajdowanie granic sum całkowitych, po stosunkowo prostą operację znajdowania funkcji pierwotnych.Leibniz jest właścicielem symbolu różniczkowego str Później pojawił się także symbol całkowyZdecydowany symbol całkiwprowadził J. Fourier i termin „całka” (z łac liczba całkowita - całość) zaproponował I. Bernoulli.![]() Gdzie
Gdzie ![]() Integrujemy:
Integrujemy: ![]() Gdzie
Gdzie ![]() Korzystając z danych, znajdujemy С = 4. Oznacza to, że równanie ruchu ciała ma postać
Korzystając z danych, znajdujemy С = 4. Oznacza to, że równanie ruchu ciała ma postać ![]() .
.
 Wtedy otrzymujemy: praca potrzebna do wystrzelenia rakiety jest równa
Wtedy otrzymujemy: praca potrzebna do wystrzelenia rakiety jest równa ![]()
 .
.
 Zatem całe zadanie zostało ukończone:
Zatem całe zadanie zostało ukończone:![]() . Zatem praca wykonana przy odkształceniu wynosi:
. Zatem praca wykonana przy odkształceniu wynosi:
![]() i Równanie prędkości: Znajdujemy prawo ruchu ciała: ponieważ. i wtedy
i Równanie prędkości: Znajdujemy prawo ruchu ciała: ponieważ. i wtedy ![]() Gdzie
Gdzie ![]() .Zintegrować:
.Zintegrować: ![]() Lub
Lub ![]() Kiedy i znajdź
Kiedy i znajdź ![]() , i Mamy równanie ruchu ciała: lub .
, i Mamy równanie ruchu ciała: lub .![]() Lub
Lub ![]() Całkując mamy:
Całkując mamy: ![]() Na x = 2 I y \u003d -3, C \u003d - 5, a trajektoria ruchu ma postać:
Na x = 2 I y \u003d -3, C \u003d - 5, a trajektoria ruchu ma postać: ![]() .
.
 Zadanie 9. Oblicz obszar figury ograniczony liniami: i
Zadanie 9. Oblicz obszar figury ograniczony liniami: i Rozwiązanie: Zbudujmy rysunek (ryc. 1), dla którego rozwiążemy układ równań. Znajdźmy punkty przecięcia linii: A(-2;4) I B(4;16). Pożądany obszar to różnica między obszarami z granicami integracji, a \u003d x 1 \u003d -2 I w \u003d x 2 \u003d 4. Następnie mamy obszar:
Rozwiązanie: Zbudujmy rysunek (ryc. 1), dla którego rozwiążemy układ równań. Znajdźmy punkty przecięcia linii: A(-2;4) I B(4;16). Pożądany obszar to różnica między obszarami z granicami integracji, a \u003d x 1 \u003d -2 I w \u003d x 2 \u003d 4. Następnie mamy obszar:![]() Znajdźmy С: i funkcję Wiadomo, że t.e. lub skąd współczynnik proporcjonalności wynosi: a funkcja ma postać:
Znajdźmy С: i funkcję Wiadomo, że t.e. lub skąd współczynnik proporcjonalności wynosi: a funkcja ma postać: ![]() .
.
 Zadanie 11.Hiperbolaograniczona liniami: y=0, x=
A, x = 2aobraca się wokół osi x. Znajdź objętość powstałego hiperboloidu (ryc. 2).
Zadanie 11.Hiperbolaograniczona liniami: y=0, x=
A, x = 2aobraca się wokół osi x. Znajdź objętość powstałego hiperboloidu (ryc. 2).
 Ufolodzy badają fakty, które cytują „naoczni świadkowie”, mówiąc, że widzieli latający statek kosmiczny w postaci ogromnego świetlistego dysku („czaszy”), w przybliżeniu takiego samego jak na ryc. 3. Rozważ rozwiązanie problemu określenia objętości takie „danie” „.
Ufolodzy badają fakty, które cytują „naoczni świadkowie”, mówiąc, że widzieli latający statek kosmiczny w postaci ogromnego świetlistego dysku („czaszy”), w przybliżeniu takiego samego jak na ryc. 3. Rozważ rozwiązanie problemu określenia objętości takie „danie” „. Rozwiązanie: Rysując paraboloidę (ryc. 3), mamy granice całkowania x = -3 zanim x = 3. Zamieńmy granice całkowania wynikające z symetrii figury względem osi y przez x = 0 I x = 3 i podwoić wynik. Zatem objętość dysku wynosi:
Rozwiązanie: Rysując paraboloidę (ryc. 3), mamy granice całkowania x = -3 zanim x = 3. Zamieńmy granice całkowania wynikające z symetrii figury względem osi y przez x = 0 I x = 3 i podwoić wynik. Zatem objętość dysku wynosi:![]()
Odniesienie historyczne
Krótka historia rachunku całkowego
Całka nieoznaczona
Określona całka
Geometryczne znaczenie całki oznaczonej
Metody integracji
Tabela całek nieoznaczonych
Powtórzenie materiału teoretycznego
Powtarzamy
Zastosowanie całki
Obliczanie objętości ciał
SPRAWDŹ SIĘ!
Znajdź błąd!
Zaprogramowane sterowanie
Niezależna praca
Zadania obliczania objętości
Zadania z egzaminu
Pytania kontrolne
Dla miłośników matematyki
Praca domowa
Bibliografia


