Коэффициент корреляции равный 1 означает что. Статистика и обработка данных в психологии(продолжение)

» Статистика

Статистика и обработка данных в психологии
(продолжение)

Корреляционный анализ

При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.

Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.

До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот.

С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве-Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (r s), который применяется к порядковым данным, т.е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.

Коэффициент корреляции

Коэффициент корреляции - это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:

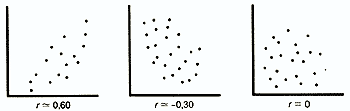
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n- 2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных (h =n -2=6) при вычислении r (см. табл. 4 в Приложении) и 7 пар данных (h =n-2= 5) при вычислении r s (табл. 5 в Приложении).

Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента r s требовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные - менее точно.

Коэффициент корреляции Браве-Пирсона (r) - этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу (у разных авторов она может выглядеть по-разному)

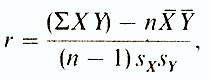
где ΣXY - сумма произведений данных из каждой пары;
n-число пар;
X - средняя для данных переменной X;
Y - средняя для данных переменной Y
S x - стандартное отклонение для распределения х;
S y - стандартное отклонение для распределения у

Коэффициент корреляции рангов Спирмена (r s ) - это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений.

Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами.

Дело в том, что при использовании коэффициента корреляции рангов Спирмена (r s) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к +1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к -1, можно говорить о полной обратной зависимости.

Коэффициент r s вычисляют по формуле

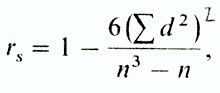
где d - разность между рангами сопряженных значений признаков (независимо от ее знака), а - число пар.

Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые).

Резюме

Итак, мы рассмотрели различные параметрические и непараметрические статистические методы, используемые в психологии. Наш обзор был весьма поверхностным, и главная задача его заключалась в том, чтобы читатель понял, что статистика не так страшна, как кажется, и требует в основном здравого смысла. Напоминаем, что данные «опыта», с которыми мы здесь имели дело, - вымышленные и не могут служить основанием для каких-либо выводов. Впрочем, подобный эксперимент стоило бы действительно провести. Поскольку для этого опыта была выбрана сугубо классическая методика, такой же статистический анализ можно было бы использовать во множестве различных экспериментов. В любом случае нам кажется, что мы наметили какие-то главные направления, которые могут оказаться полезны тем, кто не знает, с чего начать статистический анализ полученных результатов.

Литература

Годфруа Ж. Что такое психология. - М., 1992.
Chatillon G., 1977. Statistique en Sciences humaines, Trois-Rivieres, Ed. SMG.
Gilbert N.. 1978. Statistiques, Montreal, Ed. HRW.
Moroney M.J., 1970. Comprendre la statistique, Verviers, Gerard et Cie.
Siegel S., 1956. Non-parametric Statistic, New York, MacGraw-Hill Book Co.

Приложение Таблицы

Примечания. 1) Для больших выборок или уровня значимости меньше 0,05 следует обратиться к таблицам в пособиях по статистике.

2) Таблицы значений других непараметрических критериев можно найти в специальных руководствах (см. библиографию).

Таблица 1. Значения критерия t Стьюдента
h	0,05
1	6,31
2	2,92
3	2,35
4	2,13
5	2,02
6	1,94
7	1,90
8	1,86
9	1,83
10	1,81
11	1,80
12	1,78
13	1,77
14	1,76
15	1,75
16	1,75
17	1,74
18	1,73
19	1,73
20	1,73
21	1,72
22	1,72
23	1,71
24	1,71
25	1,71
26	1,71
27	1,70
28	1,70
29	1,70
30	1,70
40	1,68
¥	1,65

Таблица 2. Значения критерия χ 2
h	0,05
1	3,84
2	5,99
3	7,81
4	9,49
5	11,1
6	12,6
7	14,1
8	15,5
9	16,9
10	18,3

Таблица 3. Достоверные значения Z
р	Z
0,05	1,64
0,01	2,33

Таблица 4. Достоверные (критические) значения r
h =(N-2)		р= 0,05 (5%)
3		0,88
4		0,81
5		0,75
6		0,71
7		0,67
8		0,63
9		0,60
10		0,58
11		0.55
12		0,53
13		0,51
14		0,50
15		0,48
16		0,47
17		0,46
18		0,44
19		0,43
20		0,42

Таблица 5. Достоверные (критические) значения r s
h =(N-2)	р = 0,05
2	1,000
3	0,900
4	0,829
5	0,714
6	0,643
7	0,600
8	0,564
10	0,506
12	0,456
14	0,425
16	0,399
18	0,377
20	0,359
22	0,343
24	0,329
26	0,317
28	0,306

С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве - Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (r s ), который применяется к порядковым данным, т. е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.

Коэффициент корреляции

Коэффициент корреляции - это величина, которая может варьировать в пределах от -1 до 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

Переменная

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n -2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных ( = п - 2 = 6) при вычислении r (табл. В.4) и 7 пар данных ( = п - 2 = 5) при вычислении r s (табл. 5 в дополнении Б. 5).

Коэффициент Браве – Пирсона

Для вычисления этого коэффициента применяют следующую формулу (у разных авторов она может выглядеть по-разному):

где XY - сумма произведений данных из каждой пары;

n - число пар;

- средняя для данных переменной X ;

Средняя для данных переменной Y ;

S Х - x ;

s Y - стандартное отклонение для распределения у.

Теперь мы можем использовать этот коэффициент для того, чтобы установить, существует ли связь между временем реакции испытуемых и эффективностью их действий. Возьмем, например, фоновый уровень контрольной группы.

n = 15  15,8  13,4 = 3175,8;

(n – 1)S x S y = 14  3,07  2,29 = 98,42;

r =

Отрицательное значение коэффициента корреляции может означать, что чем больше время реакции, тем ниже эффективность. Однако величина его слишком мала для того, чтобы можно было говорить о достоверной связи между этим двумя переменными.

nXY= ………

(n - 1)S X S Y = ……

Какой вывод можно сделать из этих результатов? Если вы считаете, что между переменными есть связь, то какова она - прямая или обратная? Достоверна ли она [см. табл. 4 (в дополнении Б. 5) с критическими значениями r ]?

Коэффициент корреляции рангов Спирмена r s

Дело в том, что при использовании коэффициента корреляции рангов Спирмена (r s ) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к + 1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к - 1, можно говорить о полной обратной зависимости.

Коэффициент r s вычисляют по формуле

где d- разность между рангами сопряженных значений признаков (независимо от ее знака), а n -число пар.

Поскольку именно так обстоит дело с распределением значений эффективности и времени реакции в экспериментальной группе после воздействия, можно повторить расчеты, которые вы уже проделали для этой группы, только теперь не для коэффициента r , а для показателя r s . Это позволит посмотреть, насколько различаются эти два показателя*.

* Следует помнить, что

1) для числа попаданий 1-й ранг соответствует самой высокой, а 15-й-самой низкой результативности, тогда как для времени реакции 1-й ранг соответствует самому короткому времени, а 15-й-самому долгому;

2) данным ex aequo придается средний ранг.

Таким образом, как и в случае коэффициента r, получен положительный, хотя и недостоверный, результат. Какой же из двух результатов правдоподобнее: r = -0,48 или r s = +0,24? Такой вопрос может встать лишь в том случае, если результаты достоверны.

Поскольку в экспериментальной группе после воздействия был получен коэффициент r s , равный 0,24, подобная тенденция здесь, очевидно, не прослеживается. Попробуйте самостоятельно разобраться в данных для контрольной группы после воздействия, зная, что d 2 = 122,5:

; достоверно ли?

Каков ваш вывод?………………………………… ……………………………………………………………

…………………………………………………………………………………………………………………….

Существуют три главных раздела статистики: описательная статистика, индуктивная статистика и корреляционный анализ.

7.3.1. Коэффициенты корреляции и детерминации. Можно количественно определить тесноту связи между факторами и ее направленность (прямую или обратную), вычислив:

1) если нужно определить носящую линейный характер взаимосвязь между двумя факторами, - парный коэффициент корреляции : в 7.3.2 и 7.3.3 рассмотрены операции вычисления парного линейного коэффициента корреляции по Бравэ–Пирсону (r ) и парного рангового коэффициента корреляции по Спирмену (r );

2) если мы хотим определить взаимосвязь между двумя факторами, но зависимость эта явно нелинейная - то корреляционное отношение ;

3) если мы хотим, определить связь между одним фактором и некоторой совокупностью других факторов - то (или, что то же самое, «коэффициент множественной корреляции»);

4) если мы хотим выявить изолированно связь одного фактора только с конкретным другим, входящим в группу факторов, воздействующих на первый, для чего приходится считать влияние всех остальных факторов неизменным - то частный (парциальный) коэффициент корреляции .

Любой коэффициент корреляции (r, r) не может по абсолютной величине превышать 1, то есть –1 < r (r) < 1). Если получено значение 1, то это значит, что рассматриваемая зависимость не статистическая, а функциональная, если 0 - корреляции нет вообще.

Знак при коэффициенте корреляции определяет направленность связи: знак «+» (либо отсутствие знака) означает, что связь прямая (положительная ), знак «–» - что связь обратная (отрицательная ). К тесноте связи знак никакого отношения не имеет

Коэффициент корреляции характеризует статистическую взаимосвязь. Но часто нужно определить другого типа зависимость, а именно: каков вклад некоторого фактора в формирование другого связанного с ним фактора. Такого рода зависимость с некоторой долей условности характеризуется коэффициентом детерминации (D ), определяемым по формуле D = r 2 ´100% (где r - коэффициент корреляции по Бравэ–Пирсону, см. 7.3.2). Если измерения проводились в шкале порядка (шкале рангов) , то с некоторым ущербом для достоверности можно вместо значения r подставить в формулу значение r (коэффициента корреляции по Спирмену, см. 7.3.3).

Например, если мы получили как характеристику зависимости фактора Б от фактора А коэффициент корреляции r = 0,8 или r = –0,8, то D = 0,8 2 ´100% = 64%, то есть около 2½ 3. Следовательно, вклад фактора А и его изменений в формирование фактора Б составляет примерно 2½ 3 от суммарного вклада всех вообще факторов.

7.3.2. Коэффициент корреляции по Бравэ-Пирсону. Процедуру вычисления коэффициента корреляции по Бравэ–Пирсону (r ) можно применять только в тех случаях, когда связь рассматривается на базе выборок, имеющих нормальное распределение частот (нормальное распределение ) и полученных измерениями в шкалах интервалов или отношений. Расчетная формула этого коэффициента корреляции:

å (x i – )(y i – )

r = .

n×s x ×s y

Что показывает коэффициент корреляции? Во-первых, знак при коэффициенте корреляции показывает направленность связи, а именно: знак «–» свидетельствует о том, что связь обратная , или отрицательная (имеет место тенденция: с убыванием значений одного фактора соответствующие значения другого фактора растут, а с возрастанием - убывают), а отсутствие знака или знак «+» свидетельствуют о прямой , или положительной связи (имеет место тенденция: с увеличением значений одного фактора увеличиваются и значения другого, а с уменьшением - уменьшаются). Во-вторых, абсолютная (не зависящая от знака) величина коэффициента корреляции говорит о тесноте (силе) связи. Принято считать (в достаточной мере условно): при значениях r < 0,3 корреляция очень слабая , нередко ее просто не принимают в расчет, при 0,3 £ r < 5 корреляция слабая , при 0,5 £ r < 0,7) - средняя , при 0,7 £ r £ 0,9) - сильная и, наконец, при r > 0,9 - очень сильная. В нашем случае (r » 0,83) связь обратная (отрицательная) и сильная.

Напомним: значения коэффициента корреляции могут находиться в интервале от –1 до +1. Выход значения r за эти пределы свидетельствует о том, что в расчетах допущена ошибка . Если r = 1, то это значит, что связь не статистическая, а функциональная - чего в спорте, биологии, медицине практически не бывает. Хотя при небольшом количестве измерений случай ный подбор значений, дающий картину функциональной связи, возможен, но такой случай тем менее вероятен, чем больше объем сопоставляемых выборок (n), то есть количество пар сравниваемых измерений.

Расчетная таблица (табл. 7,1)строится соответственно формуле.

Таблица 7.1.

Расчетная таблица для вычисления по Бравэ–Пирсону

x i	y i	(x i – )	(x i – ) 2	(y i – )	(y i – ) 2	(x i – )(y i – )
13,2	4,75	0,2	0,04	–0,35	0,1225	– 0,07
13,5	4,7	0,5	0,25	– 0,40	0,1600	– 0,20
12,7	5,10	– 0,3	0,09	0,00	0,0000	0,00
12,5	5,40	– 0,5	0,25	0,30	0,0900	– 0,15
13,0	5,10	0,0	0,00	0,00	0.0000	0,00
13,2	5,00	0,1	0,01	– 0,10	0,0100	– 0,02
13,1	5,00	0,1	0,01	– 0,10	0,0100	– 0,01
13,4	4,65	0,4	0,16	– 0,45	0,2025	– 0,18
12,4	5,60	– 0,6	0,36	0,50	0,2500	– 0,30
12,3	5,50	– 0,7	0,49	0,40	0,1600	– 0,28
12,7	5,20	–0,3	0,09	0,10	0,0100	– 0,03
åx i =137 =13,00	åy i =56,1 =5,1		å(x i – ) 2 = =1,78		å(y i – ) 2 = = 1,015	å(x i – )(y i – )= = –1,24

Поскольку s х = ï ï = ï ï» 0,42, а

s y =ï ï» 0,32, r » –1,24ï (11´0,42´0,32)» –1,24ï 1,48 » –0,83 .

Иными словами, нужно очень твердо знать, что коэффициент корреляции не может по абсолютной величине превосходить 1,0. Это нередко позволяет избежать грубейших ошибок, точнее - найти и исправить допущенные при подсчетах ошибки.

7.3.3. Коэффициент корреляции по Спирмену . Как уже было сказано, применять коэффициент корреляции по Бравэ–Пирсону (r) можно только в тех случаях, когда анализируемые факторы по распределению частот близки к нормальному и значения вариант получены измерениями обязательно в шкале отношений или в шкале интервалов, что бывает, если они выражены физическими единицами. В остальных случаях находят коэффициент корреляции по Спирмену (r ). Впрочем, этот коэффициент можно применять и в случаях, когда разрешено (и желательно! ) применять коэффициент корреляции по Бравэ-Пирсону. Но следует иметь в виду, что процедура определения коэффициента по Бравэ-Пирсону обладает большей мощностью («разрешающей способностью »), поэтому r более информативен, чем r . Даже при большом n отклонение r может быть порядка ±10%.

Таблица 7.2 Расчетная формула коэффици-

x i y i R x R y |d R | d R 2 ента корреляции по Спирмену

13,2 4,75 8,5 3,0 5,5 30,25 r = 1 – . Вос

13,5 4,70 11,0 2,0 9,0 81,00 пользуемся нашим примером

12,7 5,10 4,5 6,5 2,0 4,00 для расчета r , но построим

12,5 5,40 3,0 9,0 6,0 36,00 иную таблицу (табл.7.2).

13,0 5,10 6,0 6,5 0,5 0,25 Подставим значения:

13,2 5,00 8,5 4,5 4,0 16,00 r = 1– =

13,1 5,00 7,0 4,5 2,5 6,25 =1– 2538:1320 » 1–1,9 » – 0,9.

13,4 4,65 10,0 1,0 9,0 81,00 Мы видим: r оказался немного

12,4 5,60 2,0 11,0 9,0 81,00 больше, чем r , но это разли-

12,3 5,50 1,0 10,0 9,0 81,00 чие не очень велико. Ведь при

12,7 5,20 4,5 8,0 3,5 12,25 таком малом n значения r и r

åd R 2 = 423 очень уж приблизительны, мало достоверны, их действительное значение может колебаться в широких пределах, поэтому различие r иr в 0,1 малосущественно. Обычно r рассматривают как аналог r , но только менее точный . Знаки при r и r показывает направленность связи.

7.3.4. Применение и проверка достоверности коэффициентов корреляции. Определение степени корреляционной зависимости между факторами необходимо для управления развитием нужного нам фактора: для этого приходится влиять на другие факторы, существенно влияющие на него, и нужно знать меру их действенности. Знать про взаимосвязь факторов нужно для разработки или выбора готовых тестов: информативность теста определяется корреляцией его результатов с проявлениями интересующего нас признака или свойства. Без знания корреляций невозможны любые формы отбора.

Выше было отмечено, что в спортивной и вообще педагогической, медицинской и даже экономической и социологической практике большой интерес представляет определение того вклада , который один фактор вносит в формирование другого . Это связано с тем, что помимо рассматриваемого фактора-причины на целевой (интересующий нас) фактор действуют, давая каждый тот или иной вклад в него, и другие.

Считается, что мерой вклада каждого фактора-причины может служить коэффициент детерминации D i = r 2 ´100%. Так, например, если r = 0,6, т.е. связь между факторами А и Б средняя, то D = 0,6 2 ´100% = 36%. Зная, таким образом, что вклад фактора А в формирование фактора Б приблизительно 1½ 3, можно, например уделять целенаправленному развитию этого фактора приблизительно 1½ 3 тренировочного времени. Если же коэффициент корреляции r = 0,4 , то D = r 2 100% =16%, или примерно 1½ 6 - в два с лишним раза меньше, и уделять его развитию по этой логике следует соответственно лишь 1½ 6 часть тренировочного времени.

Величины D i для разных существенных факторов дают приблизительное представление о количественном взаимоотношении их влияний на интересующий нас целевой фактор, ради совершенствования которого мы, собственно, и работаем над другими факторами (например, прыгун в длину с разбега работает над повышением скорости своего спринтерского бега, так как оно является тем фактором, который дает самый значительный вклад в формирование результата в прыжках).

Напомним, что определяя D можно вместо r поставить r , хотя, конечно, точность определения оказывается ниже.

На основе выборочного (рассчитанного по выборочным данным) коэффициента корреляции нельзя делать вывод о достоверности факта наличия связи между рассматриваемыми факторами вообще. Для того, чтобы сделать такой вывод с той или иной степенью обоснованности, используют стандартные критерии значимости корреляции . Их применение предполагает линейную зависимость между факторами и нормальное распределение частот в каждом из них (имея в виду не выборочное, а генеральное их представление).

Можно, например, применить t-критерии Стьюдента. Его рас-

четная формула: t p = –2 , где k - исследуемый выборочный коэффициент корреляции, a n - объем сопоставляемых выборок. Полученное расчетное значение t-критерия (t р)сравнивают с табличным при выбранном нами уровне значимости и числе степеней свободы n = n – 2. Чтобы избавиться от расчетной работы, можно воспользоваться специальной таблицей критических значений выборочных коэффициентов корреляции (см. выше), соответствующих наличию достоверной связи между факторами (с учетом n и a ).

Таблица 7.3.

Граничные значений достоверности выборочного коэффициента корреляции

Число степеней свободы при определении коэффициентов корреляции принимают равным 2 (т.е. n = 2) Указанные в табл. 7.3 значения имеют нижней границей доверительного интервала истинного коэффициента корреляции 0, то есть при таких значениях нельзя утверждать, что корреляция вообще имеет место. При значении выборочного коэффициента корреляции выше указанного в таблице можно при соответствующем уровне значимости считать, что истинный коэффициент корреляции не равен нулю.

Но ответ на вопрос, есть ли реальная связь между рассматриваемыми факторами, оставляет место для другого вопроса: в каком интервале лежит истинное значение коэффициента корреляции, каким он может быть на самом деле, при бесконечно большом n ? Этот интервал для любого конкретного значения r и n сопоставляемых факторов можно рассчитать, но удобнее пользоваться системой графиков (номограммой ), где каждая пара кривых, построенная для не которого указанного над ними n , соответствует границам интервала.

Рис. 7.4. Доверительные границы выборочного коэффициента корреляции (a = 0,05). Каждая кривая соответствует указанному над ней n .

Обратясь к номограмме на рис. 7.4, можно определить интервал значений истинного коэффициента корреляции для вычисленных значений выборочного коэффициента корреляции при a = 0,05.

7.3.5. Корреляционные отношения. Если парная корреляция нелинейна , нельзя вычислять коэффициент корреляции, определяют корреляционные отношения . Обязательное требование: признаки должны быть измерены в шкале отношений или в шкале интервалов. Можно вычислять корреляционную зависимость фактора X от фактора Y и корреляционную зависимость фактора Y от фактора X - они различаются. При небольшом объеме n рассматриваемых выборок, представляющих факторы, для вычисления корреляционных отношений можно пользоваться формулами:

корреляционное отношение h x ½ y = ;

корреляционное отношение h y ½ x = .

Здесь и - средние арифметические выборок X и Y, и - внутриклассовые средние арифметические. Tо есть - среднее арифметическое тех значений в выборке фактора Х, с которыми сопряжены одинаковые значения в выборке фактора Y (например, если в факторе X имеются значения 4, 6, и 5, с которыми в выборке фактора Y сопряжены 3 варианты с одинаковым значением 9, то = (4+6+5)½ 3 = 5). Соответственно - среднее арифметическое тех значений в выборке фактора Y, с которыми сопряжены одинаковые значения в выборке фактора Х. Приведем пример и проведем расчет:

Х: 75 77 78 76 80 79 83 82 ; Y: 42 42 43 43 43 44 44 45 .

Таблица 7.4

Расчетная таблица

х i	y i	x y	х i – х	(х i – х ) 2	х i – х y	(x i – x y ) 2
			–4		–1
			–2
			–3		–2
			–1

					–3


x=79	y=43			S=76		S=28

Следовательно, h y ½ x = » 0,63.

7.3.6. Частные и множественный коэффициенты корреляции. Чтобы оценить зависимость между 2-мя факторами, вычисляя коэффициенты корреляции, мы как бы по умолчанию предполагаем, что никакие другие факторы на эту зависимость никакого воздействия не оказывают. В реальности дело обстоит не так. Так, на зависимость между весом и ростом очень существенно влияют калорийность питания, величина систематической физической нагрузки, наследственность и др. Когда нужно при оценке связи между 2-мя факторами учесть существенное влияние других факторов и в то же время как бы изолироваться от них, считая их неизменными , вычисляют частные (иначе - парциальные ) коэффициенты корреляции.

Пример: нужно оценить парные зависимости между 3-мя существенно действующими факторами X, Y и Z. Обозначим r XY (Z) частный (парциальный) коэффициент корреляции между факторами X и Y (при этом величину фактора Z считаем неизменной), r ZX (Y) - частный коэффициент корреляции между факторами Z и X (при неизменном значении фактора Y), r YZ (X) - частный коэффициент корреляции между факторами Y и Z (при неизменном значении фактора X). Используя вычисленные простые парные (по Бравэ-Пирсону) коэффициенты корреляции r XY , r XZ и r YZ , м

ожно вычислить частные (парциальные) коэффициенты корреляции по формулам:

r XY – r XZ ´r YZ r XZ – r XY ´r ZY r ZY –r ZX ´r YZ

r XY (Z) = ; r XZ (Y) = ; r ZY (Х) =

Ö(1–r 2 XZ)(1–r 2 YZ) Ö(1– r 2 XY)(1–r 2 ZY) Ö(1–r 2 ZX)(1–r 2 YX)

И частные коэффициенты корреляции могут принимать значения от –1 до +1. Возведя их в квадрат, получают соответствующие частные коэффициенты детерминации , называемые также частными мерами определенности (умножив на 100, выразим в %%). Частные коэффициенты корреляции больше или меньше отличаются от простых (полных) парных коэффициентов, что зависит от силы влияния на них 3-го фактора (как бы неизменного). Нулевая гипотеза (Н 0), то есть гипотеза об отсутствии связи (зависимости) между факторами X и Y, проверяется (при общем количество признаков k ) вычислением t-критерия по формуле: t Р = r XY (Z) ´ (n –k) 1 ½ 2 ´ (1–r 2 XY (Z)) –1 ½ 2 .

Если t Р < t a n , гипотеза принимается (считаем, что зависимости нет), если же t Р ³ t a n - гипотеза опровергается, то есть считается, что зависимость действительно имеет место. t a n берется по таблице t -критерия Стьюдента, причем k - количество учитываемых факторов (в нашем примере 3), число степеней свободы n = n – 3. Другие частные коэффициенты корреляции проверяют аналогично (в формулу вместо r XY (Z) подставляют соответственно r XZ (Y) или r ZY (X)).

Таблица 7.5

Исходные данные

Ö (1 – 0,71 2)(1 – 0,71 2) Ö (1 – 0,5)(1 – 0,5)

Для оценки зависимости фактора Х от совместного действия нескольких факторов (здесь факторы Y и Z), вычисляют значения простых парных коэффициентов корреляции и, используя их, вычисляют множественный коэффициент корреляции r X (YZ) :

Ö r 2 XY + r 2 XZ – 2r XY ´ r XZ ´ r YZ

r X (YZ) = .

Ö 1 – r 2 YZ

7.2.7. Коэффициент ассоциации. Нередко требуется количественно оценить зависимость между качественными признаками, т.е. такими признаками, которые нельзя представить (охарактеризовать) количественно, которые неизмеримы . Например, стоит задача выяснить, существует ли зависимость между спортивной специализацией занимающихся и такими личностными свойствами, как интравертность (направленность личности на явления собственного субъективного мира) и экстравертность (направленность личности на мир внешних объектов). Условные обозначения представим в табл. 7.6.

Таблица 7.6.

X (лет)	Y (раз)	Z (раз)	X (лет)	Y (раз)	Z (раз)

Признак 1 Признак 2	Интравертность	Экстравертность
Спортивные игры	а	b
Гимнастика	с	d

Очевидно, что числами, имеющимися в нашем распоряжении, здесь могут быть только частоты распределений. В таком случае вычисляют коэффициент ассоциации (другое название «коэффициент сопряженности »). Рассмотрим простейший случай: связь между двумя парами признаков, при этом вычисленный коэффициент сопряженности называют тетрахорическим (см. табл.).

Таблица 7.7.

а =20	b = 15	a + b = 35
с =15	d = 5	c + d = 20
a + c = 35	b + d = 20	n = 55

Вычисления производим по формуле:

ad – bc 100 – 225 –123

Вычисление коэффициентов ассоциации (коэффициентов сопряжения) при большем количестве признаков связано с расчетами по аналогичной матрице соответствующего порядка.

Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).

Пр1.:

График зависимости застенчивости и дипресивности. Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.

Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.

Используется две системы классификации корреляционных связей по их силе: общая и частная.

Общая классификация корреляционных связей:1) сильная, или тесная при коэффициенте корреляции r>0,70;2) средняя при 0,500,70, а не просто корреляция высокого уровня значимости.

В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.

	Дихотомическая шкала (1/0)	Ранговая (порядковая) шкала
Дихотомическая шкала (1/0)	Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона.		Бисериальная корреляция
Ранговая (порядковая) шкала	Рангово-бисериальная корреляция.	Ранговый коэффициент корреляции Спирмена или Кендалла.
Интервальная и абсолютная шкала	Бисериальная корреляция	Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент	Коэффициент корреляции Пирсона (коэффициент линейной корреляции)

При r =0 линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии параллельны осям координат.

Равенство r =0 говорит лишь об отсутствии линейной корреляционной зависимости (некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.

Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.

В SPSS: 11.3.2 Коэффициенты корреляции

До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения - большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.

В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале - коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.

Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:

· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

· Перенесите переменную sex в список строк, а переменную psyche - в список столбцов.

· Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.

· В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.

Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:

/ СПСС 10

Задание № 10 Корреляционный анализ

Понятие корреляции

Корреляция или коэффициент корреляции – это статистический показательвероятностной связи между двумя переменными, измеренными по количественным шкалам. В отличие от функциональной связи, при которой каждому значению одной переменной соответствуетстрого определенное значение другой переменной,вероятностная связь характеризуется тем, что каждому значению одной переменной соответствуетмножество значений другой переменной, Примером вероятностной связи является связь между ростом и весом людей. Ясно, что один и тот же рост может быть у людей разного веса и наоборот.

Корреляция представляет собой величину, заключенную в пределах от -1 до + 1, и обозначается буквой r. Причем, если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой. Значение корреляции менее 0,2 рассматривается как слабая корреляция, свыше 0,5 – высокая. Если коэффициент корреляции отрицательный, это означает наличие обратной связи: чем выше значение одной переменной, тем ниже значение другой.

В зависимости от принимаемых значений коэффициента rможно выделить различные виды корреляции:

Строгая положительная корреляция определяется значениемr=1. Термин «строгая» означает, что значение одной переменной однозначно определяются значениями другой переменной, а термин «положительная» - что с возрастанием значений одной переменной значения другой переменной также возрастают.

Строгая корреляция является математической абстракцией и практически не встречается в реальных исследованиях.

Положительная корреляция соответствует значениям 0

Отсутствие корреляции определяется значениемr=0. Нулевой коэффициент корреляции говорит о том, что значения переменных никак не связаны между собой.

Отсутствие корреляции H o : 0 r xy =0 формулируется как отражениенулевой гипотезы в корреляционном анализе.

Отрицательная корреляция : -1

Строгая отрицательная корреляция определяется значениемr= -1. Она также, как и строгая положительная корреляция, является абстракцией и не находит выражение в практических исследованиях.

Таблица 1

Виды корреляции и их определения

Метод вычисления коэффициента корреляции зависит от вида шкалы, по которой измерены значения переменной.

Коэффициент корреляции r Пирсона является основным и может использоваться для переменных с номинальной и частично упорядоченными, интервальными шкалами, распределение значений по которым соответствует нормальному (корреляция моментов произведения). Коэффициент корреляции Пирсона дает достаточно точные результаты и в случаях анормальных распределений.

Для распределений, не являющихся нормальными, предпочтительнее пользоваться коэффициентами ранговой корреляции Спирмена и Кендалла. Ранговыми они являются потому, что программа предварительно ранжирует коррелируемые переменные.

Корреляцию rСпирмена программаSPSSвычисляет следующим образом: сначала переменные переводятся в ранги, а затем к рангам применяется формулаrПирсона.

В основе корреляции, предложенной М. Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых. Если у пары испытываемых изменение по Х совпадают по направлению с изменением по Yсовпадает, то это свидетельствует о положительной связи. Если не совпадает – то об отрицательной связи. Данный коэффициент применяется преимущественно психологами, работающими с малыми выборками. Так как социологи работают с большими массивами данных, то перебор пар, выявление разности относительных частот и инверсий всех пар испытуемых в выборке затруднителен. Наиболее распространенным является коэф. Пирсона.

Поскольку коэффициент корреляции rПирсона является основным и может использоваться (с некоторой погрешностью в зависимости от типа шкалы и уровня анормальности в распределении) для всех переменных, измеренных по количественным шкалам, рассмотрим примеры его использования и сравним полученные результаты с результатами измерений по другим коэффициентам корреляции.

Формула вычисления коэффициента r - Пирсона:

r xy = ∑ (Xi-Xср)∙(Yi-Yср) / (N-1)∙σ x ∙σ y ∙

Где: Xi, Yi- Значения двух переменных;

Xср, Yср- средние значения двух переменных;

σ x , σ y – стандартные отклонения,

N- количество наблюдений.

Парные корреляции

Например, мы хотели бы выяснить, как соотносятся ответы между различными видами традиционных ценностей в представлениях студентов об идеальном месте работы (переменные: а9.1, а9.3, а9.5, а9.7), а затем о соотношении либеральных ценностях (а9.2, а9.4. а9.6, а9.8) . Данные переменные измерены по 5 – членным упорядоченным шкалам.

Используем процедуру: «Анализ», «Корреляции»,«Парные». По умолчанию коэф. Пирсона установлен в диалоговом окне. Используем коэф. Пирсона

В окно отбора переносятся тестируемые переменные: а9.1, а9.3, а9.5, а9.7

Путем нажатия ОК получаем расчет:

Корреляции


а9.1.т. Насколько важно иметь достаточно времени для семьи и личной жизни?	Корреляция Пирсона
	Знч.(2-сторон)

а9.3.т. Насколько важно не бояться потерять свою работу?	Корреляция Пирсона
	Знч.(2-сторон)

а9.5.т. Насколько важно иметь такого начальника, который будет советоваться с Вами, принимая то или иное решение?	Корреляция Пирсона
	Знч.(2-сторон)

а9.7.т. Насколько важно работать в слаженном коллективе, ощущать себя его частью?	Корреляция Пирсона
	Знч.(2-сторон)

** Корреляция значима на уровне 0.01 (2-сторон.).

Таблица количественных значений построенной корреляционной матрицы

Частные корреляции:

Для начала построим парную корреляцию между указанными двумя переменными:

Корреляции



с8. Ощущают близость с теми, кто живет рядом с вами, соседями	Корреляция Пирсона
	Знч.(2-сторон)

с12. Ощущают близость со своей семьей	Корреляция Пирсона
	Знч.(2-сторон)


**. Корреляция значима на уровне 0.01 (2-сторон.).

Затем используем процедуру построения частной корреляции: «Анализ», «Корреляции»,«Частные».

Предположим, что ценность «Важно самостоятельно определять и изменять порядок своей работы» во взаимосвязи с указанными переменными окажется тем решающим фактором, под влияние которого ранее выявленная связь исчезнет, либо окажется малозначимой.

Корреляции

Исключенные переменные			с8. Ощущают близость с теми, кто живет рядом с вами, соседями	с12. Ощущают близость со своей семьей

с16. Ощущают близость с людьми, котрые имеют тот же достаток, что и вы	с8. Ощущают близость с теми, кто живет рядом с вами, соседями	Корреляция
		Значимость (2-сторон.)

	с12. Ощущают близость со своей семьей	Корреляция
		Значимость (2-сторон.)

Как видно из таблицы под влиянием контрольной переменной связь несколько снизилась: с 0, 120 до 0, 102. Однако, это незначительно снижение не позволяет утверждать, что ране выявленная связь является отражением ложной корреляции, т.к. она остается достаточно высокой и позволяет с нулевой погрешностью опровергать нулевую гипотезу.

Коэффициент корреляции

Наиболее точный способ определения тесноты и характера корреляционной связи - нахождение коэффициента корреляции. Коэффициент корреляции есть число определяемое по формуле:

где r ху - коэффициент корреляции;

x i -значения первого признака;

у i -значения второго признака;

Средняя арифметическая значений первого признака

Средняя арифметическая значений второго признака

Для пользования формулой (32) построим таблицу, которая обеспечит необходимую последовательность в подготовке чисел для нахождения числителя и знаменателя коэффициента корреляции.

Как видно из формулы (32), последовательность действий такая: находим средние арифметические обоих признаков х и у, находим разность между значениями признака и его средней (х і - ) и у і - ), затем находим их произведение (х і - ) (у і - ) – суммa пocлeдних дает числитель коэффициента корреляции. Для нахождения его знаменателя следует разности (x i - )и (у і - ) возвести в квадрат, найти их суммы и извлечь корень квадратный из их произведения.

Так для примера 31 нахождение коэффициента корреляции в соответствии с формулой (32) можно представить следующим образом (табл. 50).

Полученное число коэффициента корреляции дает возможность установить наличие, тесноту и характер связи.

1. Если коэффициент корреляции равен нулю, связь между признаками отсутствует.

2. Если коэффициент корреляции равен единице, связь между признаками столь велика, что превращается в функциональную.

3. Абсолютная величина коэффициента корреляции не выходит за пределы интервала от нуля до единицы:

Это дает возможность ориентироваться на тесноту связи: чем величина коэффициента ближе к нулю, тем связь слабее, а чем ближе к единице, тем связь теснее.

4. Знак коэффициента корреляции «плюс» означает прямую корреляцию, знак «минус»-обратную.

Таблица50

х і	у і	(х і - )	(у і - )	(х і - )(у і - )	(х і - )2	(у і - )2
14,00	12,10	-1,70	-2,30	+3,91	2,89	5,29
14,20	13,80	-1,50	-0,60	+0,90	2,25	0,36
14,90	14,20	-0,80	-0,20	+0,16	0,64	0,04
15,40	13,00	-0,30	-1,40	+0,42	0,09	1,96
16,00	14,60	+0,30	+0,20	+0,06	0,09	0,04
17,20	15,90	+1,50	+2,25	2,25
18,10	17,40	+2,40	+2,00	+4,80	5,76	4,00
109,80	101,00		12,50	13,97	13,94

Таким образом, вычисленный в примере 31 коэффициент корреляции r xy = +0,9. позволяет сделать такие выводы: существует корреляционная связь между величиной мышечной силы правой и левой кистей у исследуемых школьников (коэффициент r xy =+0,9 отличен от нуля), связь очень тесная (коэффициент r xy =+0,9 близок к единице), корреляция прямая (коэффициент r xy = +0,9 положителен), т. е. с увеличением мышечной силы одной из кистей увеличивается сила другой кисти.

При вычислении коэффициента корреляции и пользовании его свойствами следует учесть, что выводы дают корректные результаты в том случае, когда признаки распределены нормально и когда рассматривается взаимосвязь между большим количеством значений обоих признаков.

В рассмотренном примере 31 анализированы только 7 значений обоих признаков, что, конечно, недостаточно для подобных исследований. Напоминаем здесь еще раз, что примеры, в данной книге вообще и в этой главе в частности, носят характер иллюстрации методов, а не подробного изложения каких-либо научных экспериментов. Вследствие этого рассмотрено небольшое число значений признаков, измерения округлены - все это делается для того, чтобы громоздкими вычислениями не затемнять идею метода.

Особое внимание следует обратить на существо рассматриваемой взаимосвязи. Коэффициент корреляции не может привести к верным результатам исследования, если анализ взаимосвязи между признаками проводится формально. Возвратимся еще раз к примеру 31. Оба рассмотренных признака представляли собой значения мышечной силы правой и левой кистей. Представим себе, что под признаком x i в примере 31 (14,0; 14,2; 14,9... ...18,1) мы понимает длину случайно пойманных рыб в сантиметрах, а под признаком у і (12,1; 13,8; 14,2... ...17,4) -вес приборов в лаборатории в килограммах. Формально воспользовавшись аппаратом вычислений для нахождения коэффициента корреляции и получив в этом случае также r xy =+0>9, мы должны были заключить, что между длиной рыб и весом приборов существует тесная связь прямого характера. Бессмысленность такого вывода очевидна.

Чтобы избежать формального подхода к пользованию коэффициентом корреляции, следует любым другим методом - математическим, логическим, экспериментальным, теоретическим - выявить возможность существования корреляционной связи между признаками, то есть обнаружить органическое единство признаков. Только после этого можно приступать к пользованию корреляционным анализом и устанавливать величину и характер взаимосвязи.

В математической статистике существует еще понятие множественной корреляции - взаимосвязи между тремя и более признаками. В этих случаях пользуются коэффициентом множественной корреляции, состоящим из парных коэффициентов корреляции, описанных выше.

Например, коэффициент корреляции трех признаков-х і , у і , z і - есть:

где R xyz -коэффициент множественной корреляции, выражающий, как признак х i зависит от признаков у і и z i ;

r xy -коэффициент корреляции между признаками x i и y i ;

r xz -коэффициент корреляции между признаками Xi и Zi;

r yz - коэффициент корреляции между признаками y i , z i

Корреляционный анализ это:

Корреляционный анализ

Корреля́ция - статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.

Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи - например, для независимых случайных величин). Отрицательная корреляция - корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция - корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.

Автокорреляция - статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса - со сдвигом по времени.

Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом .

Коэффициент корреляции

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике - это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.

Коэффициент корреляции Пирсона

Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:

Пусть X ,Y - две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

где cov обозначает ковариацию, а D - дисперсию, или, что то же самое,

где символ обозначает математическое ожидание.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).

Коэффициент корреляции Кенделла

Используется для измерения взаимной неупорядоченности.

Коэффициент корреляции Спирмена

Свойства коэффициента корреляции

Неравенство Коши - Буняковского:

если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна

, и следствием неравенства Коши - Буняковского будет: . , где . Более того в этом случае знаки и k совпадают: .

Корреляционный анализ

Корреляционный анализ - метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции ) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.

Цель корреляционного анализа - обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют . В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная , если одна переменная растёт, а вторая уменьшается, корреляция отрицательная .

Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = s i n (x ) и B = c o s (x ), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону s i n 2(x ) + c o s 2(x ) = 1.

Ограничения корреляционного анализа

Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).

Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных . Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.

Область применения

Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Ложная корреляция

Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.

В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.

См. также

Автокорреляционная функция
Взаимнокорреляционная функция
Ковариация
Коэффициент детерминации
Регрессионный анализ

Wikimedia Foundation. 2010.

Пр1.:

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

Используется две системы классификации корреляционных связей по их силе: общая и частная.

В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.

	Дихотомическая шкала (1/0)	Ранговая (порядковая) шкала
Дихотомическая шкала (1/0)	Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона.		Бисериальная корреляция
Ранговая (порядковая) шкала	Рангово-бисериальная корреляция.	Ранговый коэффициент корреляции Спирмена или Кендалла.
Интервальная и абсолютная шкала	Бисериальная корреляция	Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент	Коэффициент корреляции Пирсона (коэффициент линейной корреляции)

В SPSS: 11.3.2 Коэффициенты корреляции

· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

· Перенесите переменную sex в список строк, а переменную psyche - в список столбцов.

Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:

/ Теория. Коэффициент корреляции

Коэффициент корреляции - двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.

К настоящему времени разработано великое множество различных коэффициентов корреляции. Однако самые важные меры связи - Пирсона, Спирмена и Кендалла . Их общей особенностью является то, что они отражают взаимосвязь двух признаков , измеренных в количественной шкале - ранговой или метрической .

Вообще говоря, любое эмпирическое исследование сосредоточено на изучении взаимосвязей двух или более переменных .

Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь - нелинейная . Если увеличение одной переменной связано с увеличением другой, то связь - положительная ( прямая ) ; если увеличение одной переменной связано с уменьшением другой, то связь - отрицательная ( обратная ) . Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция - монотонная ; в противном случае функцию называют немонотонной .

Функциональные связи являются идеализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных - веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.

При изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот).

Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной - идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых. Вряд ли на этом основании кому-то придет в голову отрицать факт наличия строгой функциональной связи между длиной и весом тела.

Итак, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков.

Наглядное представление о характере вероятностной связи дает диаграмма рассеивания - график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку. В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.

Можно ввести три градации величин корреляции по силе связи:

r < 0,3 - слабая связь (менее 10% от общей доли дисперсии);

0,3 < r < 0,7 - умеренная связь (от 10 до 50% от общей доли дисперсии);

r > 0,7 - сильная связь (50% и более от общей доли дисперсии).

Частная корреляция

Часто бывает так, что две переменные коррелируют друг с другом только за счет того, что обе они меняются под влиянием некоторой третьей переменной. То есть, на самом деле связь между соответствующими свойствами этих двух переменных отсутствует, но проявляется в статистической взаимосвязи, или корреляции, под влиянием общей причины третьей переменной).

Таким образом, если корреляция между двумя переменными уменьшается, при фиксируемой третьей случайной величине, то это означает, что их взаимозависимость возникает частично через воздействие этой третьей переменной. Если же частная корреляция равна нулю или очень мала, то можно сделать вывод о том, что их взаимозависимость целиком обусловлена собственным воздействием и никак не связана с третьей переменной.

Также, если частная корреляция больше первоначальной корреляции между двумя переменными, то можно сделать вывод о том, что другие переменные ослабили связь, или "скрыли" корреляцию.

К тому же необходимо помнить о том, что корреляция не есть причинность . Исходя из этого, мы не имеем права безапелляционно говорить о наличии причинной связи: некоторая совершенно отличная от рассматриваемых в анализе переменная может быть источником этой корреляции. Как при обычной корреляции, так и при частных корреляциях предположение о причинности должно всегда иметь собственные внестатистические основания.

Коэффициент корреляции Пирсона

r- Пирсона применяется для изучения взаимосвязи двух метрических переменных , измеренных на одной и той же выборке . Существует множество ситуаций, в которых уместно его применение. Влияет ли интеллект на успеваемость на старших курсах университета? Связан ли размер заработной платы работника с его доброжелательностью к коллегам? Влияет ли настроение школьника на успешность решения сложной арифметической задачи? Для ответа на подобные вопросы исследователь должен измерить два интересующих его показателя у каждого члена выборки.

На величину коэффициента корреляции не влияет то, в каких единицах измерения представлены признаки. Следовательно, любые линейные преобразования признаков (умножение на константу, прибавление константы) не меняют значения коэффициента корреляции. Исключением является умножение одного из признаков на отрицательную константу: коэффициент корреляции меняет свой знак на противоположный.

Корреляция Пирсона есть мера линейной связи между двумя переменными . Она позволяет определить , насколько пропорциональна изменчивость двух переменных . Если переменные пропорциональны друг другу, то графически связь между ними можно представить в виде прямой линии с положительным (прямая пропорция) или отрицательным (обратная пропорция) наклоном.

На практике связь между двумя переменными, если она есть, является вероятностной и графически выглядит как облако рассеивания эллипсоидной формы. Этот эллипсоид, однако, можно представить (аппроксимировать) в виде прямой линии, или линии регрессии. Линия регрессии - это прямая, построенная методом наименьших квадратов: сумма квадратов расстояний (вычисленных по оси Y) от каждой точки графика рассеивания до прямой является минимальной.

Особое значение для оценки точности предсказания имеет дисперсия оценок зависимой переменной. По сути, дисперсия оценок зависимой переменной Y - это та часть ее полной дисперсии, которая обусловлена влиянием независимой переменной X. Иначе говоря, отношение дисперсии оценок зависимой переменной к ее истинной дисперсии равно квадрату коэффициента корреляции.

Квадрат коэффициента корреляции зависимой и независимой переменных представляет долю дисперсии зависимой переменной, обусловленной влиянием независимой переменной, и называется коэффициентом детерминации . Коэффициент детерминации, таким образом, показывает, в какой степени изменчивость одной переменной обусловлена (детерминирована) влиянием другой переменной.

Коэффициент детерминации обладает важным преимуществом по сравнению с коэффициентом корреляции. Корреляция не является линейной функцией связи между двумя переменными. Поэтому, среднее арифметическое коэффициентов корреляции для нескольких выборок не совпадает с корреляцией, вычисленной сразу для всех испытуемых из этих выборок (т.е. коэффициент корреляции не аддитивен). Напротив, коэффициент детерминации отражает связь линейно и поэтому является аддитивным: допускается его усреднение для нескольких выборок.

Дополнительную информацию о силе связи дает значение коэффициента корреляции в квадрате - коэффициент детерминации: это часть дисперсии одной переменной, которая может быть объяснена влиянием другой переменной. В отличие от коэффициента корреляции коэффициент детерминации линейно возрастает с увеличением силы связи.

Коэффициенты корреляции Спирмена и τ-Кендалла (ранговые корреляции). Если обе переменные, между которыми изучается связь, представлены в порядковой шкале, или одна из них - в порядковой, а другая - в метрической, то применяются ранговые коэффициенты корреляции: Спирмена или τ - Кенделла . И тот , и другой коэффициент требует для своего применения предварительного ранжирования обеих переменных .

Коэффициент ранговой корреляции Спирмена - это непараметрический метод , который используется с целью статистического изучения связи между явлениями . В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Если члены группы численностью были ранжированы сначала по переменной x, затем – по переменной y, то корреляцию между переменными x и y можно получить, просто вычислив коэффициент Пирсона для двух рядов рангов. При условии отсутствия связей в рангах (т.е. отсутствия повторяющихся рангов) по той и другой переменной, формула для Пирсона может быть существенно упрощена в вычислительном отношении и преобразована в формулу, известную как Спирмена .

Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции .

Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений . Данный метод может быть использован не только для количественно выраженных данных , но также и в случаях , когда регистрируемые значения определяются описательными признаками различной интенсивности .

Коэффициент ранговой корреляции Спирмена при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений

Альтернативу корреляции Спирмена для рангов представляет корреляция τ-Кендалла . В основе корреляции, предложенной М.Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по x совпадает по направлению с изменением по y, то это свидетельствует о положительной связи, если не совпадает - то об отрицательной связи.

Коэффициенты корреляции были специально разработаны для численного определения силы и направления связи между двумя свойствами, измеренными в числовых шкалах (метрических или ранговых).

Как уже упоминалось, максимальной силе связи соответствуют значения корреляции +1 (строгая прямая или прямо пропорциональная связь) и -1 (строгая обратная или обратно пропорциональная связь), отсутствию связи соответствует корреляция, равная нулю.

Дополнительную информацию о силе связи дает значение коэффициента детерминации: это часть дисперсии одной переменной, которая может быть объяснена влиянием другой переменной.

Тема 12 Корреляционный анализ

Функциональная зависимость и корреляция . Еще Гиппократ в VI в. до н. э. обратил внимание на наличие связи между телосложением и темпераментом людей, между строением тела и предрасположенностью к тем или иным заболеваниям. Определенные виды подобной связи выявлены также в животном и растительном мире. Так, существует зависимость между телосложением и продуктивностью у сельскохозяйственных животных; известна связь между качеством семян и урожайностью культурных растений и т.д. Что же касается подобных зависимостей в экологии, то существуют зависимости между содержанием тяжелых металлов в почве и снежном покрове от их концентрации в атмосферном воздухе и т.п. Поэтому естественно стремление использовать эту закономерность в интересах человека, придать ей более или менее точное количественное выражение.

Как известно, для описания связей между переменными величинами применяют математические понятие функции f , которая ставит в соответствие каждому определенному значению независимой переменной x определенное значение зависимой переменной y , т.е. . Такого рода однозначные зависимости между переменными величинамиx и y называют функциональными . Однако такого рода связи в природных объектах встречаются далеко не всегда. Поэтому зависимость между биологическими, а также и экологическими признаками имеет не функциональный, а статистический характер, когда в массе однородных индивидов определенному значению одного признака, рассматриваемого в качестве аргумента, соответствует не одно и то же числовое значение, а целая гамма распределяющихся в вариационный ряд числовых значений другого признака, рассматриваемого в качестве зависимой переменной, или функции. Такого рода зависимость между переменными величинами называется корреляционной или корреляцией..

Функциональные связи легко обнаружить и измерить на единичных и групповых объектах, однако этого нельзя проделать с корреляционными связями, которые можно изучать только на групповых объектах методами математической статистики. Корреляционная связь между признаками бывает линейной и нелинейной, положительной и отрицательной. Задача корреляционного анализа сводится к установлению направления и формы связи между варьирующими признаками, измерению ее тесноты и, наконец, к проверке достоверности выборочных показателей корреляции.

Зависимость между переменными X и Y можно выразить аналитически (с помощью формул и уравнений) и графически (как геометрическое место точек в системе прямоугольных координат). График корреляционной зависимости строят по уравнению функции или , которая называетсярегрессией . Здесь и – средние арифметические, найденные при условии, чтоX или Y примут некоторые значения x или y . Эти средние называются условными .

11.1. Параметрические показатели связи

Коэффициент корреляции . Сопряженность между переменными величинами x и y можно установить, сопоставляя числовые значения одной из них с соответствующими значениями другой. Если при увеличении одной переменной увеличивается другая, это указывает на положительную связь между этими величинами, и наоборот, когда увеличение одной переменной сопровождается уменьшением значения другой, это указывает на отрицательную связь .

Для характеристики связи, ее направления и степени сопряженности переменных применяют следующие показатели:

линейной зависимость – коэффициент корреляции ;

нелинейный – корреляционной отношение .

Для определения эмпирического коэффициента корреляции используют следующую формулу:

. (1)

Здесь s x и s y – средние квадратические отклонения.

Коэффициент корреляции можно вычислить, не прибегая к расчету средних квадратических отклонений, что упрощает вычислительную работу, по следующей аналогичной формуле:

. (2)

Коэффициент корреляции – безразмерное число, лежащее в пределах от –1 до +1. При независимом варьировании признаков, когда связь между ними полностью отсутствует, . Чем сильнее сопряженность между признаками, тем выше значение коэффициента корреляции. Следовательно, при этот показатель характеризует не только наличие, но и степень сопряженности между признаками. При положительной или прямой связи, когда большим значениям одного признака соответствуют большие же значения другого, коэффициент корреляции имеет положительный знак и находится в пределах от 0 до +1, при отрицательной или обратной связи, когда большим значениям одного признака соответствуют меньшие значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до –1.

Коэффициент корреляции нашел широкое применение в практике, но он не является универсальным показателем корреляционных связей, так как способен характеризовать только линейные связи, т.е. выражаемые уравнением линейной регрессии (см. тему 12). При наличии нелинейной зависимости между варьирующими признаками применяют другие показатели связи, рассмотренных ниже.

Вычисление коэффициента корреляции . Это вычисление производят разными способами и по-разному в зависимости от числа наблюдений (объема выборки). Рассмотрим отдельно специфику вычисления коэффициента корреляции при наличии малочисленных выборок и выборок большого объема.

Малые выборки . При наличии малочисленных выборок коэффициент корреляции вычисляют непосредственно по значениям сопряженных признаков, без предварительной группировки выборочных данных в вариационные ряды. Для этого служат приведенные выше формулы (1) и (2). Более удобными, особенно при наличии многозначных и дробных чисел, которыми выражаются отклонения вариант х i и y i от средних и , служат следующие рабочие формулы:

где ;

;

Здесь x i и y i – парные варианты сопряженных признаков x и y ; и –средние арифметические; – разность между парными вариантами сопряженных признаковx и y ; n – общее число парных наблюдений, или объем выборочной совокупности.

Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра ρ и как величина случайная сопровождается ошибкой:

Отношение выборочного коэффициента корреляции к своей ошибке служит критерием для проверки нулевой гипотезы – предположения о том, что в генеральной совокупности этот параметр равен нулю, т.е. . Нулевую гипотезу отвергают на принятом уровне значимостиα , если

Значения критических точек t st для разных уровней значимости α и чисел степеней свободы приведены в табл.1 Приложений.

Установлено, что при обработке малочисленных выборок (особенно когда n < 30 ) расчет коэффициента корреляции по формулам (1) – (3) дает несколько заниженные оценки генерального параметра ρ , т.е. необходимо внести следующую поправку:

z-преобразование Фишера . Правильное применение коэффициента корреляции предполагает нормальное распределение двумерной совокупности сопряженных значений случайных величин x и y . Из математической статистики известно, что при наличии значительной корреляции между переменными величинами, т.е. когда R xy > 0,5 выборочное распределение коэффициента корреляции для большего числа малых выборок, взятых из нормально распределяющейся генеральной совокупности, значительно отклоняются от нормальной кривой.

Учитывая это обстоятельство, Р. Фишер нашел более точный способ оценки генерального параметра по значению выборочного коэффициента корреляции. Этот способ сводится к замене R xy преобразованной величиной z, которая связана с эмпирическим коэффициентом корреляции, следующим образом:

Распределение величины z является почти неизменным по форме, так как мало зависит от объема выборки и от значения коэффициента корреляции в генеральной совокупности, и приближается к нормальному распределению.

Критерием достоверности показателя z является следующее отношение:

Нулевая гипотеза отвергается на принятом уровне значимости α и числе степеней свободы . Значения критических точекt st приведены в табл.1 Приложений.

Применение z-преобразования позволяет с большей уверенностью оценивать статистическую значимость выборочного коэффициента корреляции, а также и разность между эмпирическими коэффициентами , когда в этом возникает необходимость.

Минимальный объем выборки для точной оценки коэффициента корреляции. Можно рассчитать объем выборки для заданного значения коэффициента корреляции, который был бы достаточен для опровержения нулевой гипотезы (если корреляция между признаками Y и X действительно существует). Для этого служит следующая формула:

где n – искомый объем выборки; t – величина, заданная по принятому уровню значимости (лучше для α = 1%); z – преобразованный эмпирический коэффициент корреляции.

Большие выборки . При наличии многочисленных исходных данных их приходится группировать в вариационные ряды и, построив корреляционную решетку, разность по ее клеткам (ячейкам) общие частоты сопряженных рядов. Корреляционная решетка образуется пересечением строк и столбцов, число которых равно числу групп или классов коррелируемых рядов. Классы располагаются в верхней строке и в первой (слева) столбце корреляционной таблицы, а общие частоты, обозначаемые символом f xy , – в клетках корреляционной решетки, составляющей основную часть корреляционной таблицы.

Классы, помещенные в верхней строке таблицы, обычно располагаются слева направо в возрастающем порядке, а в первом столбце таблицы – сверху вниз в убывающем порядке. При таком расположении классов вариационных рядов их общие частоты (при наличии положительной связи между признаками Y и X ) будут распределяться по клеткам решетки в виде эллипса по диагонали от нижнего левого угла к верхнему правому углу решетки или (при наличии отрицательной связи между признаками) в направлении от верхнего левого угла к нижнему правому углу решетки. Если же частоты f xy распределяются по клеткам корреляционной решетки более или менее равномерно, не образуя фигуры эллипса, это будет указывать на отсутствие корреляции между признаками.

Распределение частот f xy по клеткам корреляционной решетки дает лишь общее представление о наличии или отсутствии связи между признаками. Судить о тесноте или менее точно лишь по значению и знаку коэффициента корреляции . При вычислении коэффициента корреляции с предварительной группировки выборочных данных в интервальные вариационные ряды не следует брать слишком широкие классовые интервалы. Грубая группировка гораздо сильнее сказывается на значении коэффициента корреляции, чем это имеет место при вычислении средних величин и показателей вариации.

Напомним, что величина классового интервала определяется по формуле

где x max , x min – максимальная и минимальная варианты совокупности; К – число классов, на которые следует разбить вариацию признака. Опыт показал, что в области корреляционного анализа величину К можно поставить в зависимость от объема выборки примерно следующим образом (табл.1).

Таблица 1

Объем выборки	Значение К
50 ≥ n > 30
100 ≥ n > 50
200 ≥ n > 100
300 ≥ n > 200

Как и другие статистические характеристики, вычисляемые с предварительной группировкой исходных данных в вариационные ряды, коэффициент корреляции определяют разными способами, дающими совершенно идентичные результаты.

Способ произведений . Коэффициент корреляции можно вычислить используя основные формулы (1) или (2), внеся в них поправку на повторяемость вариант в димерной совокупности. При этом, упрощая символику, отклонения вариант от их средних обозначим через а , т.е. и . Тогда формула (2) с учетом повторяемости отклонений примет следующее выражение:

Достоверность этого показателя оценивается с помощью критерия Стьюдента, который представляет отношение выборочного коэффициента корреляции к своей ошибке, определяемой по формуле

Отсюда и если эта величина превышает стандартное значение критерия Стьюдентаt st для степени свободы и уровне значимостиα (см. Таблицу 2 Приложений), то нулевую гипотезу отвергают.

Способ условных средних . При вычислении коэффициента корреляции отклонения вариант (“классов”) можно находить не только от средних арифметических и , но и от условных средних А х и A y . При этом способе в числитель формулы (2) вносят поправку и формула приобретает следующий вид:

где f xy – частоты классов одного и другого рядов распределения; и , т.е. отклонения классов от условных средних, отнесенные к величине классовых интерваловλ ; n – общее число парных наблюдений, или объем выборки; и – условные моменты первого порядка, гдеf x – частоты ряда Х , аf y – частоты ряда Y ; s x и s y – средние квадратические отклонения рядов X и Y , вычисляемые по формуле .

Способ условных средних имеет преимущество перед способом произведений, так как позволяет избегать операции с дробными числами и придавать один и тот же (положительный) знак отклонениям a x и a y , что упрощает технику вычислительной работы, особенно при наличии многозначных чисел.

Оценка разности между коэффициентами корреляции . При сравнении коэффициентов корреляции двух независимых выборок нулевая гипотеза сводится к предположению о том, что в генеральной совокупности разница между этими показателями равна нулю. Иными словами, следует исходить из предположения, что разница, наблюдаемая между сравниваемыми эмпирическими коэффициентами корреляции, возникла случайно.

Для проверки нулевой гипотезы служит t-критерий Стьюдента, т.е. отношение разности между эмпирическими коэффициентами корреляции R 1 и R 2 к своей статистической ошибке, определяемой по формуле:

где s R1 и s R2 – ошибки сравниваемых коэффициентов корреляции.

Нулевая гипотеза опровергается при условии, что для принятого уровне значимостиα и числе степеней свободы .

Известно, что более точную оценку достоверности коэффициента корреляции получают при переводе R xy в число z . Не является исключением и оценка разности между выборочными коэффициентами корреляции R 1 и R 2 , особенно в тех случаях, когда последние вычислены на выборках сравнительно небольшого объема (n < 100 ) и по своему абсолютному значению значительно превышают 0,50.

Разность оценивают с помощью t-критерия Стьюдента, который строят по отношению этой разности к своей ошибке, вычисляемой по формуле

Нулевую гипотезу отвергают, если для и принятого уровня значимостиα.

Корреляционное отношение . Для измерения нелинейной зависимости между переменными x и y используют показатель, который называют корреляционным отношением , который описывает связь двусторонне. Конструкция корреляционного отношения предполагает сопоставление двух видов вариации: изменчивости отдельных наблюдений по отношению к частным средним и вариации самих частных средних по сравнению с общей средней величиной. Чем меньшую часть составит первый компонент по отношению ко второму, тем теснота связи окажется большей. В пределе, когда никакой вариации отдельных значений признака возле частных средних не будет наблюдаться, теснота связи окажется предельно большой. Аналогичным образом, при отсутствии изменчивости частных средних теснота связи окажется минимальной. Так как это соотношение вариации может быть рассмотрено для каждого из двух признаков, получается два показателя тесноты связи – h yx и h xy . Корреляционное отношение является величиной относительной и может принимать значения от 0 до 1. При этом коэффициенты корреляционного отношения обычно не равны друг другу, т.е. . Равенство между этими показателями осуществимо только при строго линейной зависимости между признаками. Корреляционное отношение является универсальным показателем: оно позволяет характеризировать любую форму корреляционной связи – и линейную, и нелинейную.

Коэффициенты корреляционного отношения h yx и h xy определяют рассмотренными выше способами, т.е. способом произведений и способом условных средних.

Способ произведений . Коэффициенты корреляционного отношения h yx и h xy определяют по следующим формулам:

где и – групповые дисперсии,

а и – общие дисперсии.

Здесь и – общие средние арифметические, а и – групповые средние арифметические;f yi – частоты ряда Y , а f xi – частоты ряда X ; k – количество классов; n – количество варьирующих признаков.

Рабочие формулы для расчета коэффициентов корреляционного отношения следующие:

Способ условных средних . Определяя коэффициенты корреляционного отношения по формулам (15), отклонения классовых вариант x i и y i можно брать не только от средних арифметических и , но и от условных средних А х и A y . В таких случаях групповые и общие девиаты рассчитываются по формулам и , а также, и , где и .

В развернутом виде формулы (15) выглядят следующим образом:

;

. (17)

В этих формулах и – отклонения классов от условных средних, сокращенные на величину классовых интервалов; значенияa y и a x выражаются числами натурального ряда: 0, 1, 2, 3, 4, … .Остальные символы объяснены выше.

Сравнивая способ произведений со способом условных средних, нельзя не заметить преимущество первого способа, особенно в тех случаях, когда приходится иметь дело с многозначными числами. Как и другие выборочные показатели, корреляционное отношение является оценкой своего генерального параметра и, как величина случайная, сопровождается ошибкой, определяемой по формуле

Достоверность оценки корреляционного отношения можно проверить по t-критерию Стьюдента. H 0 -гипотеза исходит из предположения, что генеральный параметр равен нулю, т.е. должно выполнятся следующее условие:

для числа степеней свободы и уровня значимостиα.

Коэффициент детерминации . Для истолкования значений, принимаемых показателями тесноты корреляционной связи, используют коэффициенты детерминации , которые показывают, какая доля вариации одного признака зависит от варьирования другого признака. При наличии линейной связи коэффициентом детерминации служит квадрат коэффициента корреляции R2 xy , а при нелинейной зависимости между признаками y и x – квадрат корреляционного отношения h2 yx . Коэффициенты детерминации дают основание построить следующую примерную шкалу, позволяющую судить о тесноте связи между признаками: при связь считается средней; указывает на слабую связь и лишь при можно судить о сильной связи, когда около 50 % вариации признакаY зависит от вариации признака X .

Оценка формы связи . При строго линейной зависимости между переменными величинами y и x осуществляется равенство . В таких случаях коэффициенты корреляционного отношения совпадают со значением коэффициента корреляции. Совпадут при этом по своему значению и коэффициенты детерминации, т.е. . Следовательно, по разности между этими величинами можно судить о форме корреляционной зависимости между переменнымиy и x :

Очевидно, что при линейной связи между переменными y и x показатель γ будет равен нулю; если же связь между переменными y и x нелинейная, γ > 0.

Показатель γ является оценкой генерального параметра и, как величина случайная, нуждается в проверке достоверности. При этом исходят из предположения о том, что связь между величинами y и x линейна (нулевая гипотеза). Проверить эту гипотезу позволяет F-критерий Фишера:

где a – численность групп, или классов вариационного ряда; N – объем выборки. Нулевую гипотезу отвергают, если для (находят по горизонтали табл.2 Приложений), (находят в первом столбце той же таблицы) и принятого уровня значимостиα.

Определение значимости корреляции

Классификации коэффициентов корреляции

Коэффициенты корреляции характеризуются силой и значимостью.

Классификация коэффициентов корреляции по силе.

Классификация коэффициентов корреляции по значимости.

Не следует путать 2 этих классификации, так как они определяют разные характеристики. Сильная корреляция может оказаться случайной и, стало быть, недостоверной. Особенно часто это случается в выборке с малым объемом. А в большой выборке даже слабая корреляция может оказаться высокозначимой.

После вычисления коэффициента корреляции необходимо выдвинуть статистические гипотезы:

Н 0: показатель корреляции значимо не отличается от нуля (является случайным).

Н 1: показатель корреляции значимо отличается от нуля (является неслучайным).

Проверка гипотез осуществляется сравнением полученных эмпирических коэффициентов с табличными критическими значениями. Если эмпирическое значение достигает критического или превышает его, то нулевая гипотеза отвергается: r эмп ≥ r кр Но, Þ Н 1 . В таких случаях делают вывод, что обнаружена достоверность различий.

Если эмпирическое значение не превышает критического, то нулевая гипотеза не отвергается: r эмп < r кр Þ Н 0 . В таких случаях делают вывод, что достоверность различий не установлена.

/ Статистика / Корреляция

Вычисление матрицы парных коэффициентов

корреляции

Для расчета матрицы парных коэффициентов корреляции следует вызвать меню Корреляционные матрицы модуля Основ ные статистики .

Рис. 1 Панель модуля основные статистики

Основные этапы проведения корреляционного анализа в системе SТАТІSТІСА рассмотрим на данных примера (см. рис. 2). Исходные данные представляют собой результаты наблюдений за деятельностью 23 предприятий одной из отрас-лей промышленности.

Рис.2 Исходные данные

Графы таблицы содержат следующие показатели:

РЕНТАБЕЛ - рентабельность, %;

ДОЛЯ РАБ - удельный вес рабочих в составе ППП, ед.;

ФОНДООТД - фондоотдача, ед.;

ОСНФОНДЫ - среднегодовая стоимость основных производственных фондов, млн руб.;

НЕПРРАСХ - непроизводственные расходы, тыс. руб. Требуется исследовать зависимость рентабельности от дрУ"

гих показателей.

Предположим, что рассматриваемые признаки в генераль-ной совокупности подчиняются нормальному закону распределения, а данные наблюдений представляют собой выборку из совокупности.

Вычислим парные коэффициенты корреляции между всеми переменными. После выбора строки Корреляционные матрицы на экране появится диалоговое окно Корреляции Пирсона . Название обусловлено тем, что впервые этот коэффициент был Пирсоном, Эджвортом и Велдоном.

Выберем переменные для анализа. Для этого в диалоговом окне имеются две кнопки: Квадр. матрица (один список) и Прямоуг. матрица (два списка).

Рис. 3 Диалоговое окно корреляционного анализа

Первая кнопка предназначена для вычисления матрицы обыч. ного симметричного вида с парными коэффициентами корреля-ции всех сочетаний переменных. Если при анализе используют-ся все показатели, то в диалоговом окне выбора переменных можно нажать кнопку Выбрать все. (Если переменные идут не подряд, их можно выбрать щелчком мыши с одновременно нажатой клавишей Ctrl )

Если нажать кнопку Подроб. диалогового окна, то для каж-дой переменной будут отображаться длинные имена. Щелкнув эту кнопку еще раз (она примет название Кратко ), получим короткие имена.

Кнопка Информация открывает окно для выбранной пере-менной, в котором можно просмотреть ее характеристики: длинное имя, формат отображения, отсортированный список значе-ний, описательные статистики (количество значений, среднее, стандартное отклонение).

После выбора переменных нажмем ОК или кнопку Корре ляции диалогового окна Корреляции Пирсона . На экране появится рассчитанная корреляционная матрица.

Значимые коэффициенты корреляции на экране выделяются красным цветом.

В нашем примере показатель рентабельности оказался наиболее связан с показателями фондоотдача (связь прямая) и производственные расходы (обратная связь, предполагающая реньшение V с увеличением X). Но насколько тесно взаимоязаны признаки? Тесной считается связь при значениях коэфциента по модулю больше чем 0.7 и слабой - меньше 0.3. таким образом, при дальнейшем построении уравнения регрессии следует ограничиться показателями «Фондоотдача» и «Непроизводственные расходы» как наиболее информативными.

Однако в нашем примере наблюдается явление мультиколшрности, когда существует связь между самими независимыми переменными (парный коэффициент корреляции по модулю больше чем 0.8).

Опция прямоугольная матрица (два списка переменных) открывает диалоговое окно выбора двух списков переменных. Поместим как на рисунке

В результате получаем прямоугольную корреляционную матрицу, содержащую лишь коэффициенты корреляции с зависимой переменной.

Если установлена опция Корр. Матрицу (выдел. значимые), то после нажатия кнопкиКорреляция будет построена матрица с коэф., выделенными на уровне значимостир .

Если выбрана опция Подробная таблица результатов , то, на-жав кнопку Корреляции , получим таблицу, которая содержит не только коэффициенты корреляции, но также средние, стан-дартные отклонения, коэффициенты уравнения регрессии, сво-бодный член в уравнении регрессии и другие статистики

Когда переменные имеют небольшую относительную вариацию (отношение стандартного отклонения к среднему меньше чем 0.0000000000001), требуется более высокая степень оценки. Ее можно задать, пометив галочкой опцию Вычисления с повы-шенной точностью диалогового окна Корреляции Пирсона.

Режим работы с пропущенными данными определяется оп-цией Построчное удаление ПД. Если ее выбрать, то SТАТІSТІСА проигнорирует все наблюдения, имеющие пропуски. В против-ном случае производится их попарное удаление.

Помеченный галочкой режим Отображать длинные имена переменных приведет к получению таблицы с длинными имена-ми переменных.

Графическое изображение корреляционных зависимостей

Диалоговое окно Корреляции Пирсона содержит ряд кнопок для получения графического изображения корреляционных зависимостей.

Опция 2М рассеяния строит последовательность диаграмм Рассеяния для каждой выбранной переменной. Окно для их выбора идентично рисунку 6. Слева следует указать висимые переменные, справа независимую - РЕНТАБЕЛ. Нажав ОК, получим график, на котором будет изображена одогнанная регрессионная прямая и доверительные границы рогноза.

Линейный коэффициент корреляции дает наиболее объективную оценку тесноты связи, если расположение точек в системе координат напоминает прямую линию или вытянутый эллипс, если же точки расположены в виде кривой, то коэффициент орреляции дает заниженную оценку.

На основе графика мы можем еще раз подтвердить взаимосвязь между показателями рентабельности и фондоотдачи, как данные наблюдений расположились в виде наклонного эллипса. Надо сказать, что связь считается тем теснее, чем бли-же точки к главной оси эллипса.

В нашем примере изменение показателя фондоотдачи на единицу приведет к изменению рентабельности на 5.7376%.

Посмотрим влияние показателя непроизводственных расходов на значение рентабельности. Для этого построим аналогичный график

Анализируемые данные уже меньше напоминают по своей форме эллипс, да и коэффициент корреляции несколько ниже. Найденное значение коэффициента регрессии показывает, что при увеличении непроизводственных расходов на 1 тысячу рублей рентабельность уменьшается на 0.7017%.

Следует заметить, что построение множественной регрессии (рассмотренное в последующих главах), когда уравнение со-держит одновременно оба признака, приводит к другим значе-ниям коэффициентов регрессии, что объясняется взаимодействи-ем объясняющих переменных между собой.

При использовании кнопки С именами точки на диаграмме рассеяния приобретут соответствующие им номера или имена, если они предварительно заданы.

Следующая опция с указанием графика Матричный строит атрицу диаграмм рассеяния для выбранных переменных.

ждый графический элемент этой матрицы содержит корреля-яонные поля, образуемые соответствующими переменными с

поженной на них линией регрессии.

При анализе матрицы диаграмм рассеяния следует обратить внимание на те графики, линии регрессии которых имеют суще-ственный наклон к оси X, что позволяет предположить суще-ствование взаимозависимости между соответствующими при-знаками.

Опция ЗМ рассеяния строит трехмерное корреляционное поле для выбранных переменных. Если использована кнопка С именами, точки на диаграмме рассеяния будут помечены номерами или именами соответствующих наблюдений, если они их имеют.

Графическая опция Поверхность строит ЗМ диаграмму рассеяния для выбранной тройки переменных вместе с подогнанной поверхностью второго порядка.

Опция Категор. диаграммы рассеяния в свою очередь строит каскад корреляционных полей для выбранных показателей.

После нажатия соответствующей кнопки программа попросит пользователя составить два их набора из отобранных ранее с помощью кнопки Переменные. Затем на экране появится новое

окно запроса для задания группирующей переменной, на основе которой будут классифицированы все имеющиеся наблюдения.

Результатом является построение корреляционных полей в резе групп наблюдений для каждой пары переменных, отне-яных к разным спискам

3.4. Расчет частных и множественных коэффици ентов корреляции

Для расчета частных и множественных коэффициентов кор. реляции вызовем модуль Множественная регрессия , используя кнопку переключателя модулей. На экране появится следующее диалоговое окно:

Нажав кнопку Переменные , выберем переменные для анализа: слева зависимую - рентабельность , а справа независимые - фондоотдача и непроизводственные расходы . Остальные переменные не будут участвовать в дальнейшем анализе - на основе проведения корреляционного анализа они признаны не-информативными для регрессионной модели.

В поле Файл ввода в качестве входных данных предлагаются обычные исходные данные, представляющие собой таблицу с переменными и наблюдениями, или корреляционная матрица. Корреляционную матрицу можно предварительно создать в самом модуле Множественная регрессия или вычислить с помо-щью опции Быстрые основные статистики.

При работе с файлом исходных данных можно задать ре-жим работы с пропусками:

Построчное удаление. При выборе этой опции в анализе используются только те наблюдения, которые не имеют пропущенных значений во всех выбранных переменных.

Замена средним. Пропущенные значения в каждой переменной заменяются средним, вычисленным по имеющимся комплектным наблюдениям.

Попарное удаление пропущенных данных. Если выбрана эта опция, то при вычислении парных корреляций удаля-ются наблюдения, имеющие пропущенные значения в соответствующих парах переменных.

В поле Тип регрессии пользователь может выбрать стандартную или фиксированную нелинейную регрессию. По умолчачанию выбирается стандартный анализ множественной регрессии, при котором вычисляется стандартная корреляционная матрица всех выбранных переменных.

Режим Фиксированная нелинейная регрессия позволяет осуществить различные преобразования независимых переменных. Опция Провести анализ по умолчанию использует установки, соответствующие определению стандартной регрессионной рдели, включающей свободный член. Если эта опция отменена, то при щелчке мышью по кнопке ОК стартовой панели эется диалоговое окно Определение модели, в котором вы эжете выбрать как тип регрессионного анализа (например, пошаговый, гребневый и др.), так и другие опции.

Установив флажок строки опции Показывать описательные описательные , корр. матрицы и щелкнув ОК, получим диалоговое окно со статистическими характеристиками данных.

В нем вы можете просмотреть подробные описательные статистики (в том числе количество наблюдений, по которым был вычислен коэффициент корреляции для каждой пары переменных). Чтобы продолжить анализ и открыть диалоговое окно Определители модели, нажмите ОК.

Если анализируемые показатели имеют чрезвычайно малую относительную дисперсию, вычисляемую как общая дисперсия, деленная на среднее, то следует установить флажок около опции Вычисления с повышенной точностью для получения более точных значений элементов корреляционной матрицы.

Установив все необходимые параметры в диалоговом окне Множественная регрессия , нажмем ОК и получим результаты требуемых вычислений.

По данным нашего примера множественный коэффициент корреляции получился равным 0.61357990 и соответственно коэффициент детерминации - 0.37648029. Таким образом, лишь 37,6% дисперсии показателя «рентабельность» объясняется из-менением показателей «фондоотдачи» и «непроизводственных расходов». Такое низкое значение свидетельствует о недостаточ-ном числе факторов, введенных в модель. Попробуем изменить количество независимых переменных, дополнив список пере-менной «Основные фонды» (введение в модель показателя «доля рабочих в ППП» приводит к мультиколлениарности, что явля-ется недопустимым). Коэффициент детерминации несколько повысился, но не настолько, чтобы существенно улучшить результаты - его значение составило около 41%. Очевидно, наша дача требует дополнительных исследований по выявлению факторов, влияющих на рентабельность.

Значимость множественного коэффициента корреляции про-ряется по таблице Ф-критерия Фишера. Гипотеза о его значимости отвергается, если значение вероятности отклонения превышает заданный уровень (чаще всего берут а=0.1, 0.05; 0.01 0.001). В нашем примере р=0.008882 < 0.05, что свидетельствует о значимости коэффициента.

Таблица результатов содержит следующие графы:

Коэффициент Бета (в) - стандартизованный коэффициент регрессии ддя соответствующей переменной;

Частная корреляция - частные коэффициенты корреля-ции между соответствующей переменной и зависимой, при фиксировании влияния остальных, входящих в модель.

Частный коэффициент корреляции между рентабельностью и фондоотдачей в нашем примере равен 0.459899. Это означает, после ввода в модель показателя непроизводственных рас-эв влияние фондоотдачи на рентабельность несколько сни-пось - с 0.49 (значение парного коэффициента корреляции) 0.46. Аналогичный коэффициент для показателя непроизвод-аенных расходов также снизился - с 0.46 (значение парного коэффициента корреляции) до 0.42 (берут значение по модулю), характеризует изменение связи с зависимой переменной че ввода в модель показателя фондоотдачи.

Получастная корреляция - корреляция между нескорректированной зависимой переменной и соответствующей не-зависимой с учетом влияния остальных, включенных в модель.

Толерантность (определяется как 1 минус квадрат множественной корреляции между соответствующей переменной и всеми независимыми переменными в уравнении регрес- сии).

Коэффициент детерминации - квадрат коэффициента множественной корреляции между соответствующей независимой переменной и всеми остальными переменными, входящими в регрессионное уравнение.

1-значения - расчетное значение критерия Стьюдента для проверки гипотезы о значимости частного коэффициента корреляции с указанным (в скобках) числом степеней свободы.

р-уровень! - вероятность отклонения гипотезы о значимости частного коэффициента корреляции.

В нашем случае полученное значение р для первого коэффициента (0.031277) меньше выбранного =0.05. Значение вто-рого коэффициента его несколько превышает (0.050676), что говорит о его незначимости на этом уровне. Но он значим, например, при =0.1 (в десяти случаях из ста гипотеза окажется все-таки неверна).