Ъглите на триъгълника винаги са. Научна електронна библиотека

Теорема. Сумата на вътрешните ъгли на триъгълника е равна на два преки ъгли.

Вземете някакъв вид триъгълник AVS (фиг. 208). Означават вътрешните си ъгли с числа 1, 2 и 3. Нека докажем това

∠1 + ∠2 + ∠3 \u003d 180 °.

Нарежете няколко върха на триъгълника, например, в, директно mn успоредно на AU.

На върха в получихме три ъгъл: ∠4, ∠2 и ∠5. Тяхното количество е разгърнато ъгъл, следователно е равно на 180 °:

∠4 + ∠2 + ∠5 \u003d 180 °.

Но ∠4 \u003d ∠1 е вътрешният проход на основните ъгли с паралелно директно mn и високоговорители и secant av.

∠5 \u003d ∠3 е вътрешният гръб на подлежащите ъгли с паралелен директен mn и високоговорители и южното слънце.

Така че, ∠4 и ∠5 могат да бъдат заменени с равен ∠1 и ∠3.

Следователно, ∠1 + ∠2 + ∠3 \u003d 180 °. Теорема се доказва.

2. Имот на външния ъгъл на триъгълника.

В действителност, в триъгълника на ABC (фиг. 209) ∠1 + ∠2 \u003d 180 ° - ∠3, но също така и ∠VD, външният ъгъл на този триъгълник, не в съседство с ∠1 и ∠2, също е 180 ° - ∠3.

По този начин:

∠1 + ∠2 \u003d 180 ° - ∠3;

∠bcd \u003d 180 ° - ∠3.

Следователно, ∠1 + ∠2 \u003d ∠BCD.

Полученото свойство на външния ъгъл на триъгълника изяснява съдържанието на предишната доказана теорема на външния ъгъл на триъгълника, в който се твърди само, че външният ъгъл на триъгълника е по-голям от всеки вътрешен ъгъл на триъгълника, а не свързани с него; Сега е установено, че външният ъгъл е равен на сумата както на вътрешните ъгли, които не са свързани с него.

3. Имотът на правоъгълен триъгълник с ъгъл от 30 °.

Да предположим, че правоъгълният триъгълник на ъгловия ъгъл В е равен на 30 ° (фиг. 210). Тогава другият, освен остър ъгъл, ще бъде 60 °.

Доказваме, че високоговорителите на високоговорителите са равни на половината от хипотенузата на AV. Ще продължим катацата с високоговорителите за върха на директния ъгъл С и отложим сегмента cm, равен на сегмента на AU. Точката m да се свърже с точка V. Полученият триъгълник на WMM е равен на д-р триъгълник. Следователно виждаме, че всеки ъгъл на AVM триъгълника е равен на 60 °, следователно, този триъгълник е равностранен.

Високоговорителите на високоговорителите са равни на половината съм, и тъй като съм равен на AB, тогава говорителите ще бъдат равни на половината от хипотенуса.

Цели и задачи:

Образование:

• повторете и обобщете знанието на триъгълника;
• докаже теорема за сумата на ъглите на триъгълника;
• на практика да бъдат убедени от верността на формулировката на теоремата;
• научете се да прилагате знанията, придобити при решаване на задачи.

Разработване:

• разработване на геометрично мислене, интерес към темата, когнитивната и творческата дейност на учениците, математическата реч, способността за самостоятелно получават знания.

Образование:

• разработка лични качества Ученици, като целенасоченост, постоянство, точност, способност за работа в екипа.

Оборудване: Мултимедиен проектор, триъгълници от цветна хартия, CMC "Live Mathematics", компютър, екрана.

Подготвителен етап: Учителят дава задачата на ученика да се подготви исторически сертификат На теоремата "сумата на ъглите на триъгълника".

Вид на урока: Изучаване на нов материал.

По време на класовете

I. Организационен момент

Поздрав. Психологическо отношение на учениците да работят.

II. Тренировка

С геометрична фигура "триъгълник" се срещнахме по предишни уроци. Да повторим какво знаем за триъгълника?

Учениците работят в групи. На тях им се дава възможност да общуват помежду си, всеки независимо изгради процеса на знание.

Какво стана? Всяка група изразява своите предложения, учителят ги пише на борда. Обсъждането на резултатите се извършва:

Снимка 1.

III. Ние формулираме задачата на урока

Така че, за триъгълника знаем доста много. Но не всички. Всеки от вас на бюрото има триъгълници и транспорт. Какво мислите, каква задача можем да формулираме?

Учениците формулират задачата на урока - да намерят сумата на ъглите на триъгълника.

IV. Обяснение на новия материал

Практическа част(допринася за актуализирането на знанията и уменията на знанието). Гледайте измерванията на ъглите, като използвате транспорта и ги намерите. Резултати Запис в бележника (чуйте получените отговори). Разбираме, че сумата на ъглите на всички се оказа, че е различна (тя може да се окаже, защото неточно поставянето на транспорта, небрежно извършено преброяване и т.н.).

Извършване на пунктирани линии и разберете какво все още е равно на сумата на триъгълните ъгли:

но)
Фигура 2.

б)
Фигура 3.

в)
Фигура 4.

д)
Фигура 5.

д)
Фигура 6.

След извършване на практическа работа, учениците формулират отговора: сумата на ъглите на триъгълника е равна на степен на разширен ъгъл, т.е. 180 °.

Учител: По математика практическа работа Това прави възможно само да се направи някакво изявление, но трябва да се докаже. Одобрението, правосъдието, което е установено с доказателства, се нарича теорема. Коя теорема можем да формулираме и докажем?

Ученици: Сумата на ъглите на триъгълника е 180 градуса.

Историческа справка:Имотът на ъглите на триъгълника е създаден в Древен Египет. Доказателството, посочено в съвременните учебници, се съдържа в коментарите на свързването към "началото на" евклидея. Границата твърди, че това доказателство (фиг. 8) е отворено от питагорейците (5 V. пр. Хр. Д.). Първата книга "началото" Евклид определя друго доказателство за теоремата на сумата на ъглите на триъгълника, което е лесно да се разбере с помощта на чертежа (фиг. 7):

Фигура 7.

Фигура 8.

Чертежите се маркират на екрана през проектора.

Учителят предлага да се докаже теорема с помощта на рисунки.

Тогава доказателството се извършва с помощта на UMC "Live Mathematics". Учителят на компютъра проектира доказателство за теоремата.

Теоремата на сумата на ъглите на триъгълника: "Сумата на ъглите на триъгълника е 180 °"

Фигура 9.

Доказателство:

но)

Фигура 10.

б)

Фигура 11.

в)

Фигура 12.

Учениците в тетрадката правят кратък запис на доказателството за теорема:

Теорема: Сумата от ъглите на триъгълника е 180 °.

Фигура 13.

Дадено:Δ ABS.

Докажи A + B + C \u003d 180 °.

Доказателство:

Какво е необходимо да се докаже.

V. Физически. Минута.

VI. Обяснение на новия материал (продължение)

Последствията от теоремата на сумата на ъглите на триъгълника произтичат самостоятелно, тя допринася за развитието на способността да се формулира собствената си гледна точка, изразяват и твърдят:

Във всеки триъгълник или всички ъгли са остри, или два остри ъгли, а третата глупава или директна.

Ако в триъгълника всички ъгли са остри, тогава се нарича otterugal.

Ако един от ъглите на триъгълника е глупав, тогава се нарича глупак.

Ако един от ъглите на триъгълника е прав, тогава се нарича правоъгълна.

Теоремата на сумата на ъглите на триъгълника ви позволява да класифицирате триъгълниците не само от двете страни, но и в ъглите. (В хода на въвеждането на видове триъгълници масата е изпълнена с ученици)

маса 1

Тип триъгълник	Isosceles.	Равностранен	Гъвкав
Правоъгълна
Глупак
Счупване

VII. Закрепване на изследвания материал.

1. Решаване на задачи орално:

(Чертежите се маркират на екрана през проектора)

(Допълнение)

Визуална геометрия 7. Подкрепете абстрактен номер 4 сумата на ъглите на триъгълника.

Голям френски учен от XVII век Blaise Pascal. В детството, обичан да се забърква геометрични фигури. Той беше запознат с транспорта и знаеше как да измерва ъглите. Младият изследовател забеляза, че всички триъгълници са сумата от три ъгли, същото е 180 °. - Как да го докажем? - помисли си Паскал. "В крайна сметка е невъзможно да се провери количеството ъгли във всички триъгълници - техния безкраен комплект". После отсече с ножици два ъгъла на триъгълника и ги прикрепи към третия ъгъл. Оказа се подробен ъгъл, за който е известно, че е 180 °. Това беше първото му откритие. Допълнителна съдба Момчето вече беше предварително определено.

В тази нишка ще се запознаете с пет признака на равенство на правоъгълните триъгълници и, може би, с най-популярната собственост на правоъгълен триъгълник с ъгъл от 30 °. Звучи така: корените, лежащият срещу ъгъл от 30 °, е равен на половината от хипотенузата. Споделяне на равностранена височина на триъгълника, ние веднага получаваме доказателство за този имот.

Теорема. Сумата от ъглите на триъгълника е 180 °. За да докажете, прекарайте директна, паралелна база през върха. Тъмните ъгли са равни и сивите ъгли са равни като кръстосания под паралелните прави линии. Тъмен ъгъл, сив ъгъл и ъгъл на горната форма на подробен ъгъл, тяхното количество е 180 °. От теоремата следва, че ъглите на равностранения триъгълник са равни на 60 ° и че сумата на острите ъгли на правоъгълния триъгълник е 90 °.

Външен ъгъл Триъгълникът се нарича ъгъл в непосредствена близост до ъгъла на триъгълника. Ето защо, понякога ъглите на самия триъгълник се наричат \u200b\u200bвътрешни ъгли.

Теорема на външния триъгълник. Външният ъгъл на триъгълника е равен на сумата на двата вътрешни, несравнима с нея. Всъщност външният ъгъл и два вътрешни, не в непосредствена близост, допълват ъгъла на рязане до 180 °. От теоремата следва, че външен ъгъл е повече от всеки вътрешен, който не е свързан с него.

Теорема за връзката между страните и ъглите на триъгълника. В триъгълника срещу повечето страни по-голям ъгъл и срещу по-големия ъгъл лежи най-голямата страна. Следователно следва: 1) ролки по-малко хипотенуза. 2) перпендикулярно по-малко наклонено.

Разстояние от точка до директно . Тъй като перпендикулярът е по-малък от всички наклонени, изразходвани от една и съща точка, дължината му се поема над разстоянието от точката за директно.

Неравенството на триъгълника . Дължината на всяка страна на триъгълника е по-малка от сумата на другите две от нейните страни, т.е. но< b + с , б.< а + с , от< а + б. . Следствие. Дължината на скрапа е по-голяма от сегмента, свързващ краищата му.

Признаци на равенство
Правоъгълни триъгълници

В две категории. Ако две категории от един правоъгълен триъгълник са съответно равни на две категории друг триъгълник, тогава такива триъгълници са равни.

Върху Кастан и съседен остър ъгъл. Ако ролките и съседните острия ъгъл на един правоъгълен триъгълник са съответно равни на катетъра и остър ъгъл на друг триъгълник в непосредствена близост до него, тогава такива триъгълници са равни.

Върху катету и противоположния остър ъгъл. Ако ролките и противоположният ъгъл на един правоъгълен триъгълник са съответно равни на катето и противоположния остър ъгъл на друг триъгълник, тогава такива триъгълници са равни.

Върху хипотенуза и остър ъгъл. Ако хипотенузата и остър ъгъл на един правоъгълен триъгълник са съответно равни на хипотенузата и остър ъгъл на друг триъгълник, тогава такива триъгълници са равни.

Доказателството на тези знаци се свежда веднага до един от признаците на равенството на триъгълниците.

Върху пеметрите и хипотенузата. Ако катат и хипотенуза на един правоъгълен триъгълник са съответно равни на утежната и хипотента на друг правоъгълен триъгълник, тогава такива триъгълници са равни.

Доказателства. Правим триъгълници равни на митниците. Получаваме уравнителен триъгълник. Неговата височина, проведена от върха, ще бъде медиана. Тогава триъгълниците са равни на вторите лодки, а триъгълниците са равни на три страни.

Теорема върху собствеността на категорията, разположена срещу ъгъл от 30 °. Корен, лежащ под ъгъл от 30 °, е половин хипотен. Доказва пълнотата на триъгълника към равностранен.

Теорема върху свойствата на ъгъла на бисейра. Всяка точка от ъгъла бисектор е равна на нейните страни. Ако точката е равно на отстрани от страната на ъгъла, тогава тя лежи върху бисекта на ъгъла. Доказано е от държането на две перпендикулярно на страните на ъгъла и разглеждането на правоъгълните триъгълници.

Второ прекрасна точка . Триъгълните бисектори се пресичат в една точка.

Разстояние между паралелно право. Теорема. Всички точки на всяка от двете паралелни линии са на еднакво разстояние от друга линия. Теорема трябва да определи разстоянието между паралелно направо.

Дефиниция. Разстоянието между две паралелно право е разстоянието от всяка точка на един от паралелните директни към друга права линия.

Подробни теореми за доказателства

Това е референтен абстрактен номер 4 в геометрията в степен 7. Изберете допълнителни действия:

Триъгълник . Остър, глупав и правоъгълен триъгълник.

Картети и хипотензи. Равен и равностранен триъгълник.

Сумата на ъглите на триъгълника.

Външен триъгълник ъгъл. Признаци на равенството на триъгълниците.

Чудесни линии и точки в триъгълника: височини, медиани,

bissctrix, Median.д. перпендикулярно, ортоцентър,

центърът на тежестта, центъра на описания кръг, центърът на вписания кръг.

Питагорова теорема. Аспектното съотношение в произволен финнет.

Триъгълник - Това е многоъгълник с три страни (или три ъгъла). Страните на триъгълника са обозначени с малки букви, които съвпадат главни буквиобозначаващи върховете.

Ако всичките три ъгли са остри (фиг.20), тогава това остър триъгълник . Ако някой от ъглите е директен(° С, фиг.21), това е право триъгълникШпакловка Страниа, Б.Генериране на прав ъгъл се нарича скелеШпакловка страна ° С.противопоставя се на правия ъгъл, наречен хипотенуза. Ако е такава ъгли глупави (b, фиг.22), това е глупав триъгълник.


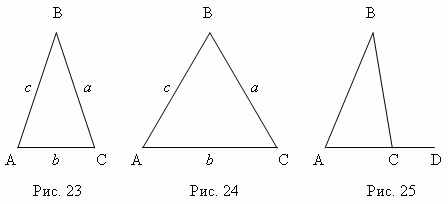
ABC триъгълник (фиг.23) - isosceles., ако две Неговите партии са равни (а.= ° С.); Тези равни страни се наричат странатретата страна се нарича база Триъгълник. ТриъгълникABC (фиг.24) - равностранен, ако всичко Неговите партии са равни (а. = б. = ° С. ). Общо взето ( а. ≠ б. ≠ ° С.) . \\ t скален триъгълник .

Основните свойства на триъгълниците. Във всеки триъгълник:

1. Анти-мнозинството е против мнозинството и обратно.

2. Срещу равните страни лъжат равни ъгли, и обратно.

По-специално, всички ъгли в равностранен Триъгълникът е равен.

3. Сумата на ъглите на триъгълника е равна на 180 º .

От последните две свойства следва, че всеки ъгъл в равностранен

Триъгълникът е 60. º.

4. Продължаване на една от страните на триъгълника (AC, фиг.25), получаване външен

BCD Ъгъл . Външният ъгъл на триъгълника е равен на сумата на вътрешните ъгли,

Не е свързано с него : BCD \u003d A + B.

5. . \\ T страната на триъгълника е по-малка от сумата на другите две и повече

Тяхната разлика (а. < б. + ° С., а. > б. – ° С.;б. < а. + ° С., б. > а. – ° С.;° С. < а. + б.,° С. > а. – б.).

Признаци на равенството на триъгълниците.

Триъгълниците са равни, ако са съответно равни:

А. ) Две страни и ъгъл между тях;

Б. ) Два ъгъла и до тях в непосредствена близост до тях;

в) три страни.

Признаци на равенство на правоъгълните триъгълници.

Две правоъгълна Триъгълникът е равен, ако е изпълнено едно от следните условия:

1) равен на техните катетри;

2) Кататът и хипотенузата на един триъгълник са равни на катето и хипотенузата на другия;

3) хипотенуза и остър ъгъл на един триъгълник са равни на хипотенузе и острия ъгъл на другия;

4) Catat и съседният остър ъгъл на един триъгълник са равни на катето и съседния остър ъгъл на другия;

5) Catat и противоположният остър ъгъл на един триъгълник са равни на катето и противоположен острен ъгъл на другия.

Чудесни линии и точки в триъгълника.

Височина триъгълник еперпендикулярно,понижени от всички върха в обратна посока ( или продължаването му). Тази страна се наричаосновата на триъгълника . Три височини на триъгълника винаги се пресичатв една точка, Наречен orthocentro.триъгълник. Ортоцентър на острия-короналния триъгълник (точкаО. , Фиг.26) се намира вътре в триъгълника иorthocentre Stupagol триъгълник (точкаО. , Фиг.27) – отвън; Ортоцентърът на правоъгълния триъгълник съвпада с върха на директния ъгъл.

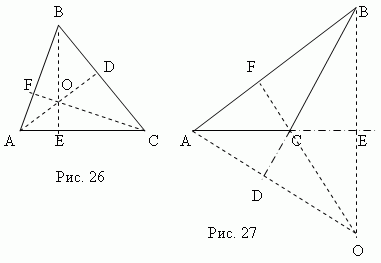
Медиана - това е раздел Свързване на всеки върха на триъгълника от средната страна. Три триъгълни медиана (AD, BE, CF, фиг.28) пресичане в една точка О. винаги лежащ в триъгълники да бъдеш център на тежестта. Тази точка разделя всеки медианат по отношение на 2: 1, като се брои от върха.

Бисектор - това е изрязани бизоцериъгъл от върха до точката пресичане с противоположната страна. Трима бисекторни триъгълници (AD, BE, CF, фиг.29) пресичане в една точка О, винаги лежащ в триъгълники това е център, вписан в кръг (виж раздел "в-разгърнати описаните полигони ").

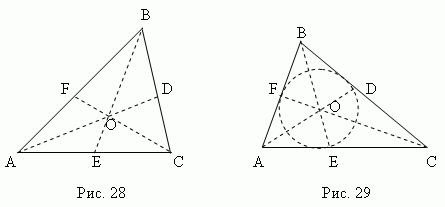
Bissectrix разделя противоположната страна на частите, пропорционални на съседните партии Шпакловка Например, на фиг.29AE: CE \u003d AB: BC.

Общински перпендикулярни - Това е перпендикулярно проведено от средното ниво Нарежете точки (страни). Три медиански перпендикулярен триъгълник abc (Ko, mo, no, фиг.30 ) се пресичат в една точка, която е център описан кръг (Точки k, m, n - средните страни на триъгълника ABC).

В острия триъгълник този момент се намира вътре в триъгълника; в глупак - отвън; в правоъгълна - в средата на хипотенузата. Ортоинтер, център на тежестта, център на описания и център, включен в центъра улова само в равностранен триъгълник.

Питагорова теорема. В правоъгълна триъгълна квадратна дължинахипотензите са равни на сумата на квадратите на магията на катетите.

Доказателството на питагоровата теорема очевидно следва от фиг.31. Помислете за правоъгълен триъгълникABC с кей а, Б.и хипотенуза ° С..

Да построим квадрат AKMB. Използване на хипотенузаAB. настрана. Тогавапродължете от страна на правоъгълия триъгълникАВС така да получите квадрат CDEF. чиято страна е равнаa + b.Сега е ясно, че площадът на площадаCDEF е равен на ( a + B.) 2 . От друга страна, това районът е равен на суматаквадрат четири правоъгълни триъгълника и квадратен AKMB, т.е.

° С. 2 + 4 (aB. / 2) = ° С. 2 + 2 ab,

следователно

° С. 2 + 2 aB.= (a + B.) 2 ,

и накрая имаме:

° С. 2 = А. 2 + Б. 2 .

Аспектното съотношение в произволен триъгълник.

Като цяло (за произволен триъгълник) имаме:

° С. 2 = А. 2 + Б. 2 – 2aB.· защото. ° С,

където C. - ъгъл между странитеа. и б. .

\u003e\u003e Геометрия: сумата на ъглите на триъгълника. Пълни уроци

Урок по тема: Сумата на ъглите на триъгълника.

Цели Урок:

• Консолидация и проверка на знанията на учениците по темата: "сумата на ъглите на триъгълника";
• Доказателство за свойствата на ъглите на триъгълника;
• Прилагане на този имот при решаването на най-простите задачи;
• Използване на исторически материал за развитие когнитивна дейност ученици;
• Поставяне на уменията на точността при изграждане на рисунки.

Задачи Урок:

• Проверете уменията на учениците за решаване на проблеми.

План на урока:

1. Триъгълник;
2. Теорема на сумата на ъглите на триъгълника;
3. Примерни задачи.

Триъгълник.

Файл: O.gif Триъгълник- най-простият полигон с 3 върха (ъгли) и 3 страни; Част от равнината, ограничена от три точки, и три сегмента, двойки свързват тези точки.
Три точки на място, които не лежат на една права линия, съответства на един и само един самолет.
Всеки многоъгълник може да бъде разделен на триъгълници - този процес се нарича триангулация.
Има част от математиката, изцяло посветена на изучаването на моделите на триъгълниците - Тригонометрия.

Теорема на сумата на ъглите на триъгълника.

Файл: T.gif Теорема на сумата на ъглите на триъгълника е класическата теоремна евклидова геометрия, твърди, че ъгълът на триъгълните ъгли е 180 °.

Доказателства :

Нека δ abc бъде даден. Ние извършваме през Vertex B Direct, паралелен (AC) и отбелязваме от точка D, така че точките А и д лъжат от различни страни от директната пр. Хр. След това ъгълът (DBC) и ъгълът (ACB) са равни по отношение на паралелния директ BD и AC и втората (BC). След това сумата на триъгълните ъгли в върховете B и C е равна на ъгъла (ABD). Но ъгълът (ABD) и ъгълът (BAC) в горната част на ABC триъгълник са вътрешно едностранно с паралелен директен BD и AC, а вторият (AB) и тяхната сума е 180 °. Следователно сумата на ъглите на триъгълника е 180 °. Теорема се доказва.

Последствия.

Външният ъгъл на триъгълника е равен на сумата от два ъгъла на триъгълника, който не е свързан с него.

Доказателство:

Нека δ abc бъде даден. Точка D се намира на права линия, така че А да е между С и Г. Тогава лошото е външен до ъгъла на триъгълника в горната част А и А + Bad \u003d 180 °. Но + В + С \u003d 180 °, и следователно, В + С \u003d 180 ° - А. Следователно BAD \u003d B + C. Изследването е доказано.

Последствия.

Външният ъгъл на триъгълника е по-голям от всеки триъгълник, който не е свързан с него.

Задача.

Външният ъгъл на триъгълника се нарича ъгъл, в непосредствена близост до някакъв ъгъл на този триъгълник. Докажете, че външният ъгъл на триъгълника е равен на сумата от два ъгъла на триъгълника, който не е свързан с него.
(Фиг. 1)

Решение:

Позволявам Δ ABS ∠das - външен (фиг. 1). Тогава ∠das \u003d 180 ° -∠vas (чрез свойствата на съседните ъгли), от теоремата на сумата на ъглите на триъгълника ∠V + ∠с \u003d 180 ° -∠VAS. От тези равенства получаваме ∠das \u003d ∠v + ∠

Интересен факт:

Сумата на ъглите на триъгълника " :

В геометрията на Лобачевски сумата на ъглите на триъгълника винаги е по-малка от 180. В геометрията на еуклид тя винаги е равна на 180. В геометрията на Riemann сумата на ъглите на триъгълника винаги е по-голяма от 180.

От историята на математиката:

Euclidean (III B BC) В работата на "начало" води такава дефиниция: "паралелно същността на директните, които са в една и съща равнина и продължават в двете страни, не се срещат помежду си".
Posidochi (i b bc) "Две прави линии, разположени в една и съща равнина, се справят един от друг"
Древен гръцки учен PAPP (III B BC) въвежда символ на паралелен директен знак \u003d. Впоследствие английски икономист Ricardo (1720-1823) Този символ се използва като знак за равенство.
Само през XVIII век започва да използва символа на паралелизма на директния знак ||.
Нито един момент не се прекъсва от оживена връзка между поколенията, всеки ден асимилираме опита, придобит от нашите предци. Древните гърци въз основа на наблюдения и от практическия опит направиха заключения, изразени хипотези и след това на срещи на учени - симпозиуми (буквално "празник") - тези хипотези се опитаха да оправдаят и докажат. По това време одобрението беше: "Истината е родена в спора."

Въпроси:

1. Какво е триъгълник?
2. Какво прави теоремата за сумата на ъглите на триъгълника?
3. Какъв е външният ъгъл на триъгълника?