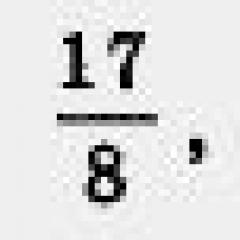Raíz cuadrada aritmética y sus propiedades. Raíz de enésimo grado: definiciones, notación, ejemplos El concepto de raíz cuadrada de un número negativo

Volví a mirar el cartel... ¡Y vamos!

Comencemos con algo simple:

Solo un minuto. esto, lo que significa que podemos escribirlo así:

¿Entiendo? Aquí tienes el siguiente:

¿No se extraen exactamente las raíces de los números resultantes? No hay problema, aquí hay algunos ejemplos:

¿Qué pasa si no hay dos, sino más multiplicadores? ¡Lo mismo! La fórmula para multiplicar raíces funciona con cualquier número de factores:

Ahora completamente solo:

Respuestas:¡Bien hecho! De acuerdo, todo es muy fácil, ¡lo principal es conocer la tabla de multiplicar!

División de raíces

Hemos resuelto la multiplicación de raíces, ahora pasemos a la propiedad de la división.

Permítanme recordarles que la fórmula general se ve así:

Lo que significa que la raíz del cociente es igual al cociente de las raíces.

Bueno, veamos algunos ejemplos:

Eso es todo lo que es la ciencia. He aquí un ejemplo:

No todo es tan sencillo como en el primer ejemplo, pero, como puedes ver, no hay nada complicado.

¿Qué pasa si te encuentras con esta expresión?

Sólo necesitas aplicar la fórmula en la dirección opuesta:

Y aquí hay un ejemplo:

También puedes encontrarte con esta expresión:

Todo es igual, solo que aquí debes recordar cómo traducir fracciones (si no lo recuerdas, ¡mira el tema y regresa!). ¿Te acuerdas? ¡Ahora decidamos!

Estoy seguro de que lo has hecho todo, ahora intentemos levantar las raíces un poco.

exponenciación

¿Qué pasa si la raíz cuadrada se eleva al cuadrado? Es simple, recuerda el significado de la raíz cuadrada de un número: este es un número cuya raíz cuadrada es igual a.

Entonces, si elevamos al cuadrado un número cuya raíz cuadrada es igual, ¿qué obtenemos?

Bueno, ¡por supuesto!

Veamos ejemplos:

Es simple, ¿verdad? ¿Qué pasa si la raíz está en un grado diferente? ¡Está bien!

Sigue la misma lógica y recuerda las propiedades y posibles acciones con grados.

Lea la teoría sobre el tema "" y todo le quedará muy claro.

Por ejemplo, aquí hay una expresión:

En este ejemplo, el grado es par, pero ¿y si es impar? Nuevamente, aplica las propiedades de los exponentes y factoriza todo:

Todo parece claro con esto, pero ¿cómo extraer la raíz de un número a una potencia? Aquí, por ejemplo, está esto:

Bastante simple, ¿verdad? ¿Qué pasa si el título es más de dos? Seguimos la misma lógica usando las propiedades de los grados:

Bueno, ¿está todo claro? Luego resuelve los ejemplos tú mismo:

Y aquí están las respuestas:

Entrando bajo el signo de la raíz.

¡Qué no hemos aprendido a hacer con las raíces! ¡Todo lo que queda es practicar ingresando el número debajo del signo raíz!

¡Es realmente fácil!

Digamos que tenemos un número escrito.

¿Qué podemos hacer con él? Bueno, por supuesto, esconde el tres debajo de la raíz, ¡recordando que el tres es la raíz cuadrada de!

¿Porqué necesitamos esto? Sí, solo para ampliar nuestras capacidades a la hora de resolver ejemplos:

¿Qué te parece esta propiedad de las raíces? ¿Hace la vida mucho más fácil? ¡Para mí, eso es exactamente correcto! Solo Debemos recordar que sólo podemos introducir números positivos bajo el signo de la raíz cuadrada.

Resuelva este ejemplo usted mismo:
¿Lograste? Veamos qué deberías conseguir:

¡Bien hecho! ¡Logró ingresar el número debajo del signo raíz! Pasemos a algo igualmente importante: ¡veamos cómo comparar números que contienen una raíz cuadrada!

Comparación de raíces

¿Por qué necesitamos aprender a comparar números que contienen una raíz cuadrada?

Muy simple. A menudo, en expresiones grandes y largas que encontramos en el examen, recibimos una respuesta irracional (¿recuerdas qué es esto? ¡Ya hablamos de esto hoy!)

Necesitamos colocar las respuestas recibidas en la línea de coordenadas, por ejemplo, para determinar qué intervalo es adecuado para resolver la ecuación. Y aquí surge el problema: no hay calculadora en el examen, y sin ella, ¿cómo imaginar qué número es mayor y cuál es menor? ¡Eso es todo!

Por ejemplo, determine cuál es mayor: ¿o?

No puedes saberlo de inmediato. Bueno, usemos la propiedad desensamblada de ingresar un número debajo del signo raíz.

Entonces adelante:

Bueno, obviamente, cuanto mayor sea el número debajo del signo de la raíz, ¡mayor será la raíz misma!

Aquellos. si, entonces, .

De esto concluimos firmemente que. ¡Y nadie nos convencerá de lo contrario!

Extraer raíces de grandes cantidades

Antes de esto, ingresamos un multiplicador bajo el signo de la raíz, pero ¿cómo eliminarlo? ¡Solo necesitas factorizarlo en factores y extraer lo que extraes!

Fue posible tomar un camino diferente y expandirse hacia otros factores:

No está mal, ¿verdad? Cualquiera de estos enfoques es correcto, decide como desees.

La factorización es muy útil para resolver problemas no estándar como este:

¡No tengamos miedo, sino actuemos! Descompongamos cada factor bajo la raíz en factores separados:

Ahora pruébalo tú mismo (¡sin calculadora! No estará en el examen):

¿Es este el final? ¡No nos detengamos a mitad de camino!

Eso es todo, no da tanto miedo, ¿verdad?

¿Sucedió? ¡Bien hecho, así es!

Ahora prueba este ejemplo:

Pero el ejemplo es un hueso duro de roer, por lo que no se puede descubrir de inmediato cómo abordarlo. Pero, por supuesto, podemos manejarlo.

Bueno, ¿empecemos a factorizar? Notemos de inmediato que puedes dividir un número por (recuerda los signos de divisibilidad):

Ahora, pruébalo tú mismo (¡nuevamente, sin calculadora!):

Bueno, ¿funcionó? ¡Bien hecho, así es!

resumámoslo

1. Una raíz cuadrada (raíz cuadrada aritmética) de un número no negativo es un número no negativo cuyo cuadrado es igual a.
   .
2. Si simplemente sacamos la raíz cuadrada de algo, siempre obtenemos un resultado no negativo.
3. Propiedades de una raíz aritmética:
4. Al comparar raíces cuadradas, es necesario recordar que cuanto mayor sea el número bajo el signo de la raíz, mayor será la raíz misma.

¿Cómo es la raíz cuadrada? ¿Todo claro?

Intentamos explicarte sin complicaciones todo lo que necesitas saber en el examen sobre la raíz cuadrada.

Es tu turno. Escríbenos si este tema te resulta difícil o no.

¿Aprendiste algo nuevo o ya estaba todo claro?

¡Escribe en los comentarios y buena suerte en tus exámenes!

Considera la ecuación x 2 = 4. Resuélvela gráficamente. Para hacer esto, en un sistema de coordenadas, construimos una parábola y = x 2 y una línea recta y = 4 (Fig. 74). Se cruzan en dos puntos A (- 2; 4) y B (2; 4). Las abscisas de los puntos A y B son las raíces de la ecuación x 2 = 4. Entonces, x 1 = - 2, x 2 = 2.

Razonando exactamente de la misma manera, encontramos las raíces de la ecuación x 2 = 9 (ver Fig. 74): x 1 = - 3, x 2 = 3.

Ahora intentemos resolver la ecuación x 2 = 5; En la figura se muestra una ilustración geométrica. 75. Está claro que esta ecuación tiene dos raíces x 1 y x 2, y estos números, como en los dos casos anteriores, son iguales en valor absoluto y opuestos en signo (x 1 - - x 2) - Pero a diferencia de la anterior casos, donde las raíces de la ecuación se encontraron sin dificultad (y se pudieron encontrar sin usar gráficas), con la ecuación x 2 = 5 este no es el caso: según el dibujo, no podemos indicar los valores de las raíces, solo podemos establecer que una raíz está ubicada ligeramente hacia la izquierda, hay 2 puntos, y la segunda está un poco hacia la derecha.

puntos 2.

¿Cuál es este número (punto) que se ubica justo a la derecha del punto 2 y que al cuadrado da 5? Está claro que esto no es 3, ya que 3 2 = 9, es decir resulta más de lo necesario (9 > 5).

Esto significa que el número que nos interesa se encuentra entre los números 2 y 3. Pero entre los números 2 y 3 hay una infinidad de números racionales, por ejemplo etc. Quizás entre ellos habrá una fracción como ? Entonces no tendremos ningún problema con la ecuación x 2 - 5, podemos escribir que

Pero aquí nos espera una desagradable sorpresa. Resulta que no existe ninguna fracción para la cual se cumpla la igualdad.
La prueba de lo dicho es bastante difícil. Sin embargo, lo presentamos porque es hermoso e instructivo, y es muy útil para intentar comprenderlo.

Supongamos que existe una fracción irreducible para la cual se cumple la igualdad. Entonces, es decir m 2 = 5n 2. La última igualdad significa que el número natural m 2 es divisible por 5 sin resto (en el cociente será n2).

En consecuencia, el número m 2 termina con el número 5 o con el número 0. Pero entonces el número natural m también termina con el número 5 o con el número 0, es decir el número m es divisible por 5 sin resto. En otras palabras, si el número m se divide por 5, entonces el cociente será algún número natural k. Esto significa,
que m = 5k.
Ahora mira:
metro 2 = 5norte 2 ;
Sustituyamos 5k en lugar de m en la primera igualdad:

(5k) 2 = 5n 2, es decir 25k 2 = 5n 2 o n 2 = 5k 2.
La última igualdad significa que el número. 5n 2 es divisible por 5 sin resto. Razonando como arriba, llegamos a la conclusión de que el número n también es divisible por 5 sin resto.
Entonces, m es divisible por 5, n es divisible por 5, lo que significa que la fracción se puede reducir (por 5). Pero supusimos que la fracción era irreducible. ¿Qué pasa? Por qué, habiendo razonado correctamente, llegamos al absurdo o, como suelen decir los matemáticos, obtuvimos una contradicción. ¡Sí, porque la premisa inicial era incorrecta, como si existiera una fracción irreducible para la cual se cumple la igualdad!
De ahí concluimos: no existe tal fracción.
El método de prueba que acabamos de utilizar se llama en matemáticas método de prueba por contradicción. Su esencia es la siguiente. Necesitamos probar una determinada afirmación y asumimos que no se cumple (los matemáticos dicen: "supongamos lo contrario", no en el sentido de "desagradable", sino en el sentido de "lo contrario de lo requerido").
Si, como resultado de un razonamiento correcto, llegamos a una contradicción con la condición, entonces concluimos: nuestra suposición es falsa, lo que significa que lo que necesitábamos demostrar es verdadero.

Entonces, al tener solo números racionales (y aún no conocemos otros números), no podemos resolver la ecuación x 2 = 5.
Al encontrarse por primera vez con una situación así, los matemáticos se dieron cuenta de que tenían que encontrar una manera de describirla en lenguaje matemático. Introdujeron un nuevo símbolo, al que llamaron raíz cuadrada, y usando este símbolo, las raíces de la ecuación x 2 = 5 se escribieron de la siguiente manera:

Dice: “raíz cuadrada de 5”). Ahora, para cualquier ecuación de la forma x 2 = a, donde a > O, puedes encontrar las raíces; son números. , (Figura 76).

Recalquemos también que el número no es ni entero ni fraccionario.
Esto significa que no es un número racional, es un número de nueva naturaleza; hablaremos específicamente de dichos números más adelante, en el Capítulo 5.
Por ahora, sólo notemos que el nuevo número está entre los números 2 y 3, ya que 2 2 = 4, que es menor que 5; 3 2 = 9, y esto es más que 5. Puedes aclarar:

De hecho, 2,2 2 = 4,84< 5, а 2,3 2 = 5,29 >5. Tú también puedes
especificar:

de hecho, 2,23 2 = 4,9729< 5, а 2,24 2 = 5,0176 > 5.
En la práctica, generalmente se cree que el número es 2,23 o 2,24, solo que esta no es una igualdad ordinaria, sino una igualdad aproximada, que se denota con el símbolo "".
Entonces,

Mientras discutíamos la solución de la ecuación x 2 = a, nos encontramos con una situación bastante típica de las matemáticas. Al encontrarse en una situación no estándar, anormal (como les gusta decir a los cosmonautas) y al no encontrar una salida por medios conocidos, los matemáticos idean un nuevo término y una nueva designación (un nuevo símbolo) para el modelo matemático que encontrado por primera vez; en otras palabras, introducen un nuevo concepto y luego estudian las propiedades de este.
conceptos. Así, el nuevo concepto y su designación pasan a ser propiedad del lenguaje matemático. Actuamos de la misma manera: introdujimos el término “raíz cuadrada del número a”, introdujimos un símbolo para designarlo y un poco más tarde estudiaremos las propiedades del nuevo concepto. Hasta ahora sólo sabemos una cosa: si a > 0,
entonces es un número positivo que satisface la ecuación x 2 = a. En otras palabras, es un número positivo que al elevarlo al cuadrado produce el número a.
Dado que la ecuación x 2 = 0 tiene una raíz x = 0, acordamos suponer que
Ahora estamos listos para dar una definición estricta.
Definición. La raíz cuadrada de un número no negativo a es un número no negativo cuyo cuadrado es igual a a.

Este número se denota por el número y se llama número radical.
Entonces, si a es un número no negativo, entonces:

si un< О, то уравнение х 2 = а не имеет корней, говорить в этом случае о квадратном корне из числа а не имеет смысла.
Por tanto, la expresión sólo tiene sentido para a > 0.
Ellos dijeron eso - el mismo modelo matemático (la misma relación entre números no negativos
(a y b), pero sólo el segundo se describe en un lenguaje más simple que el primero (usa símbolos más simples).

La operación de encontrar la raíz cuadrada de un número no negativo se llama raíz cuadrada. Esta operación es la inversa de elevar al cuadrado. Comparar:

Tenga en cuenta nuevamente que en la tabla solo aparecen números positivos, como se especifica en la definición de raíz cuadrada. Y aunque, por ejemplo, (- 5) 2 = 25 es una igualdad verdadera, pasa de ella a la notación usando la raíz cuadrada (es decir, escribe eso).
está prohibido. A-priorato, . es un número positivo, lo que significa .
A menudo no dicen "raíz cuadrada", sino "raíz cuadrada aritmética". Omitimos el término "aritmética" por brevedad.

D) A diferencia de los ejemplos anteriores, no podemos indicar el valor exacto del número. Sólo está claro que es mayor que 4, pero menor que 5, ya que

4 2 = 16 (esto es menos de 17) y 5 2 = 25 (esto es más de 17).
Sin embargo, el valor aproximado del número se puede encontrar utilizando una microcalculadora, que contiene la operación de extraer la raíz cuadrada; este valor es 4,123.
Entonces,
El número, como el número comentado anteriormente, no es racional.
e) No se puede calcular, ya que no existe la raíz cuadrada de un número negativo; la entrada no tiene sentido. La tarea propuesta es incorrecta.
e) ya que 31 > 0 y 31 2 = 961. En tales casos, hay que utilizar una tabla de cuadrados de números naturales o una microcalculadora.
g) ya que 75 > 0 y 75 2 = 5625.
En los casos más simples, el valor de la raíz cuadrada se calcula inmediatamente: etc. En casos más complejos, hay que utilizar una tabla de cuadrados de números o realizar cálculos con una microcalculadora. ¿Pero qué pasa si no tienes una mesa o una calculadora a mano? Respondamos a esta pregunta resolviendo el siguiente ejemplo.

Ejemplo 2. Calcular
Solución.
Primera etapa. No es difícil adivinar que la respuesta será 50 con cola. De hecho, 50 2 = 2500 y 60 2 = 3600, mientras que el número 2809 está entre los números 2500 y 3600.

Segunda fase. Encontremos la "cola", es decir el último dígito del número deseado. Hasta ahora sabemos que si se saca la raíz, entonces la respuesta puede ser 51, 52, 53, 54, 55, 56, 57, 58 o 59. Sólo necesitamos verificar dos números: 53 y 57, ya que solo ellos, al elevarlo al cuadrado, dará como resultado un número de cuatro dígitos que termina en 9, el mismo número que termina en 2809.
Tenemos 532 = 2809: esto es lo que necesitamos (tuvimos suerte, inmediatamente dimos en el blanco). Entonces = 53.
Respuesta:

53
Ejemplo 3. Los lados de un triángulo rectángulo miden 1 cm y 2 cm. ¿Cuál es la hipotenusa del triángulo? (Figura 77)

Solución.

Usemos el teorema de Pitágoras, conocido por la geometría: la suma de los cuadrados de las longitudes de los catetos de un triángulo rectángulo es igual al cuadrado de la longitud de su hipotenusa, es decir, a 2 + b 2 = c 2, donde a , b son los catetos, c es la hipotenusa del triángulo rectángulo.

Medio,

Este ejemplo muestra que la introducción de raíces cuadradas no es un capricho de los matemáticos, sino una necesidad objetiva: en la vida real hay situaciones cuyos modelos matemáticos contienen la operación de extraer una raíz cuadrada. Quizás la más importante de estas situaciones se relaciona con
resolver ecuaciones cuadráticas. Hasta ahora, cuando nos encontrábamos con ecuaciones cuadráticas ax 2 + bx + c = 0, factorizábamos el lado izquierdo (lo que no siempre funcionaba) o usábamos métodos gráficos (que tampoco son muy fiables, aunque bonitos). De hecho, para encontrar
Se utilizan las raíces x 1 y x 2 de la ecuación cuadrática ax 2 + bx + c = 0 en fórmulas matemáticas

que contiene, como puede verse, el signo de la raíz cuadrada. Estas fórmulas se utilizan en la práctica de la siguiente manera. Supongamos, por ejemplo, que necesitamos resolver la ecuación 2x ​​2 + bx - 7 = 0. Aquí a = 2, b = 5, c = - 7. Por lo tanto,
b2 - 4ac = 5 2 - 4 . 2. (- 7) = 81. A continuación encontramos . Medio,

Hemos señalado anteriormente que no es un número racional.
Los matemáticos llaman irracionales a estos números. Cualquier número de esta forma es irracional si no se puede sacar la raíz cuadrada. Por ejemplo, etc. - Numeros irracionales. En el Capítulo 5 hablaremos más sobre números racionales e irracionales. Los números racionales e irracionales juntos forman el conjunto de los números reales, es decir el conjunto de todos esos números que operamos en la vida real (de hecho,
ness). Por ejemplo, todos estos son números reales.
Así como definimos el concepto de raíz cuadrada anteriormente, también podemos definir el concepto de raíz cúbica: una raíz cúbica de un número no negativo a es un número no negativo cuyo cubo es igual a a. En otras palabras, la igualdad significa que b 3 = a.

Todo esto lo estudiaremos en el curso de álgebra de 11º grado.

El área de un terreno cuadrado es de 81 dm². Encuentra su lado. Supongamos que la longitud del lado del cuadrado es X decímetros. Entonces el área de la parcela es X² decímetros cuadrados. Dado que, según la condición, esta área es igual a 81 dm², entonces X² = 81. La longitud de un lado de un cuadrado es un número positivo. Un número positivo cuyo cuadrado es 81 es el número 9. Al resolver el problema, era necesario encontrar el número x cuyo cuadrado es 81, es decir resolver la ecuación X² = 81. Esta ecuación tiene dos raíces: X 1 = 9 y X 2 = - 9, ya que 9² = 81 y (- 9)² = 81. Ambos números 9 y - 9 se llaman raíces cuadradas de 81.

Tenga en cuenta que una de las raíces cuadradas X= 9 es un número positivo. Se llama raíz cuadrada aritmética de 81 y se denota √81, por lo que √81 = 9.

Raíz cuadrada aritmética de un número A es un número no negativo cuyo cuadrado es igual a A.

Por ejemplo, los números 6 y - 6 son raíces cuadradas del número 36. Sin embargo, el número 6 es una raíz cuadrada aritmética de 36, ya que 6 es un número no negativo y 6² = 36. El número - 6 no es un raíz aritmética.

Raíz cuadrada aritmética de un número A denotado de la siguiente manera: √ A.

El signo se llama signo de raíz cuadrada aritmética; A- llamó expresión radical. Expresión √ A leer así: raíz cuadrada aritmética de un número A. Por ejemplo, √36 = 6, √0 = 0, √0,49 = 0,7. En los casos en los que está claro que estamos hablando de una raíz aritmética, dicen brevemente: “la raíz cuadrada de A«.

El acto de encontrar la raíz cuadrada de un número se llama raíz cuadrada. Esta acción es la inversa de elevar al cuadrado.

Puedes elevar al cuadrado cualquier número, pero no puedes extraer raíces cuadradas de ningún número. Por ejemplo, es imposible extraer la raíz cuadrada del número - 4. Si tal raíz existiera, entonces, denotándola con la letra X, obtendríamos la igualdad incorrecta x² = - 4, ya que hay un número no negativo a la izquierda y un número negativo a la derecha.

Expresión √ A sólo tiene sentido cuando un ≥ 0. La definición de raíz cuadrada se puede escribir brevemente de la siguiente manera: √ un ≥ 0, (√A)² = A. Igualdad (√ A)² = A valido para un ≥ 0. Por tanto, para garantizar que la raíz cuadrada de un número no negativo A es igual b, es decir, en el hecho de que √ A =b, debe comprobar que se cumplan las dos condiciones siguientes: segundo ≥ 0, b² = A.

Raíz cuadrada de una fracción

Calculemos. Tenga en cuenta que √25 = 5, √36 = 6, y comprobemos si se cumple la igualdad.

Porque y , entonces la igualdad es verdadera. Entonces, .

Teorema: Si A≥ 0 y b> 0, es decir, la raíz de la fracción es igual a la raíz del numerador dividida por la raíz del denominador. Se requiere demostrar que: y .

Desde √ A≥0 y √ b> 0, entonces.

Sobre la propiedad de elevar una fracción a una potencia y la definición de raíz cuadrada el teorema está demostrado. Veamos algunos ejemplos.

Calcula usando el teorema probado. .

Segundo ejemplo: Demuestre que , Si A ≤ 0, b < 0. .

Otro ejemplo: Calcular.

.

Conversión de raíz cuadrada

Quitando el multiplicador de debajo del signo raíz. Dejemos que se dé la expresión. Si A≥ 0 y b≥ 0, entonces usando el teorema de la raíz del producto podemos escribir:

Esta transformación se llama eliminar el factor del signo raíz. Veamos un ejemplo;

Calcular en X= 2. Sustitución directa X= 2 en la expresión radical conduce a cálculos complejos. Estos cálculos se pueden simplificar si primero elimina los factores debajo del signo raíz: . Sustituyendo ahora x = 2, obtenemos:.

Entonces, al quitar un factor de debajo del signo de la raíz, la expresión radical se representa como un producto en el que uno o más factores son cuadrados de números no negativos. Luego aplica el teorema de la raíz del producto y saca la raíz de cada factor. Consideremos un ejemplo: Simplificamos la expresión A = √8 + √18 - 4√2 quitando los factores en los dos primeros términos debajo del signo de la raíz, obtenemos:. Destaquemos que la igualdad válido sólo cuando A≥ 0 y b≥ 0. si A < 0, то .

En este artículo presentaremos concepto de raíz de un número. Procederemos de forma secuencial: comenzaremos con la raíz cuadrada, de allí pasaremos a la descripción de la raíz cúbica, luego de lo cual generalizaremos el concepto de raíz, definiendo la raíz enésima. Al mismo tiempo, introduciremos definiciones, notaciones, daremos ejemplos de raíces y daremos las explicaciones y comentarios necesarios.

Raíz cuadrada, raíz cuadrada aritmética

Para comprender la definición de raíz de un número, y de la raíz cuadrada en particular, es necesario tener . En este punto, a menudo nos encontraremos con la segunda potencia de un número: el cuadrado de un número.

Empecemos con definiciones de raíz cuadrada.

Definición

raíz cuadrada de a es un número cuyo cuadrado es igual a a.

para poder traer ejemplos de raíces cuadradas, tomamos varios números, por ejemplo, 5, −0.3, 0.3, 0, y los elevamos al cuadrado, obtenemos los números 25, 0.09, 0.09 y 0, respectivamente (5 2 =5·5=25, (−0,3) 2 =(−0,3)·(−0,3)=0,09, (0.3)2 =0.3·0.3=0.09 y 0 2 =0·0=0 ). Entonces, según la definición dada anteriormente, el número 5 es la raíz cuadrada del número 25, los números −0,3 y 0,3 son las raíces cuadradas de 0,09 y 0 es la raíz cuadrada de cero.

Cabe señalar que no para cualquier número a existe un cuyo cuadrado sea igual a a. Es decir, para cualquier número negativo a no existe ningún número real b cuyo cuadrado sea igual a a. De hecho, la igualdad a=b 2 es imposible para cualquier a negativo, ya que b 2 es un número no negativo para cualquier b. De este modo, No existe raíz cuadrada de un número negativo en el conjunto de los números reales.. En otras palabras, en el conjunto de los números reales la raíz cuadrada de un número negativo no está definida y no tiene significado.

Esto lleva a una pregunta lógica: “¿Existe una raíz cuadrada de a para cualquier a no negativa”? La respuesta es sí. Este hecho puede justificarse por el método constructivo utilizado para encontrar el valor de la raíz cuadrada.

Entonces surge la siguiente pregunta lógica: "¿Cuál es el número de todas las raíces cuadradas de este número no negativo a: uno, dos, tres o incluso más"? Aquí está la respuesta: si a es cero, entonces la única raíz cuadrada de cero es cero; Si a es un número positivo, entonces el número de raíces cuadradas del número a es dos y las raíces son . Justifiquemos esto.

Comencemos con el caso a=0 . Primero, demostremos que cero es efectivamente la raíz cuadrada de cero. Esto se desprende de la igualdad obvia 0 2 =0·0=0 y la definición de la raíz cuadrada.

Ahora demostremos que 0 es la única raíz cuadrada de cero. Usemos el método opuesto. Supongamos que hay un número b distinto de cero que es la raíz cuadrada de cero. Entonces se debe cumplir la condición b 2 =0, lo cual es imposible, ya que para cualquier b distinto de cero el valor de la expresión b 2 es positivo. Hemos llegado a una contradicción. Esto prueba que 0 es la única raíz cuadrada de cero.

Pasemos a los casos en los que a es un número positivo. Dijimos anteriormente que siempre hay una raíz cuadrada de cualquier número no negativo, sea la raíz cuadrada de a el número b. Digamos que existe un número c, que también es raíz cuadrada de a. Entonces, por la definición de raíz cuadrada, las igualdades b 2 =a y c 2 =a son verdaderas, de lo cual se sigue que b 2 −c 2 =a−a=0, pero como b 2 −c 2 =( b−c)·( b+c) , entonces (b−c)·(b+c)=0 . La igualdad resultante es válida. propiedades de las operaciones con números reales posible sólo cuando b−c=0 o b+c=0 . Por tanto, los números b y c son iguales o opuestos.

Si suponemos que existe un número d, que es otra raíz cuadrada del número a, entonces, mediante razonamientos similares a los ya dados, se demuestra que d es igual al número b o al número c. Entonces, el número de raíces cuadradas de un número positivo es dos y las raíces cuadradas son números opuestos.

Para facilitar el trabajo con raíces cuadradas, la raíz negativa se “separa” de la positiva. Para ello se introduce definición de raíz cuadrada aritmética.

Definición

Raíz cuadrada aritmética de un número no negativo a es un número no negativo cuyo cuadrado es igual a a.

La notación para la raíz cuadrada aritmética de a es. El signo se llama signo de raíz cuadrada aritmética. También se le llama signo radical. Por lo tanto, a veces se puede escuchar tanto “raíz” como “radical”, que significa el mismo objeto.

El número bajo el signo de la raíz cuadrada aritmética se llama número radical, y la expresión bajo el signo raíz es expresión radical, mientras que el término “número radical” a menudo se reemplaza por “expresión radical”. Por ejemplo, en la notación el número 151 es un número radical y en la notación la expresión a es una expresión radical.

Al leer, la palabra "aritmética" a menudo se omite; por ejemplo, la entrada se lee como "la raíz cuadrada de siete coma veintinueve". La palabra “aritmética” se utiliza sólo cuando se quiere enfatizar que estamos hablando específicamente de la raíz cuadrada positiva de un número.

A la luz de la notación introducida, de la definición de raíz cuadrada aritmética se deduce que para cualquier número no negativo a .

Las raíces cuadradas de un número positivo a se escriben usando el signo aritmético de raíz cuadrada como y. Por ejemplo, las raíces cuadradas de 13 son y. La raíz cuadrada aritmética de cero es cero, es decir, . Para los números negativos a, no le daremos significado a la notación hasta que estudiemos números complejos. Por ejemplo, las expresiones y no tienen sentido.

A partir de la definición de raíz cuadrada, se prueban las propiedades de las raíces cuadradas, que se utilizan a menudo en la práctica.

Como conclusión de este punto, observamos que las raíces cuadradas del número a son soluciones de la forma x 2 =a con respecto a la variable x.

raíz cúbica de un número

Definición de raíz cúbica del número a se da de manera similar a la definición de la raíz cuadrada. Solo que se basa en el concepto de cubo de un número, no de cuadrado.

Definición

Raíz cúbica de un es un número cuyo cubo es igual a a.

vamos a dar ejemplos de raíces cúbicas. Para hacer esto, tome varios números, por ejemplo, 7, 0, −2/3, y cúbralos al cubo: 7 3 =7·7·7=343, 0 3 =0·0·0=0, . Luego, basándonos en la definición de raíz cúbica, podemos decir que el número 7 es la raíz cúbica de 343, 0 es la raíz cúbica de cero y −2/3 es la raíz cúbica de −8/27.

Se puede demostrar que la raíz cúbica de un número, a diferencia de la raíz cuadrada, siempre existe, no sólo para a no negativo, sino también para cualquier número real a. Para hacer esto, puedes usar el mismo método que mencionamos al estudiar raíces cuadradas.

Además, sólo existe una única raíz cúbica de un número dado a. Probemos la última afirmación. Para ello, considere tres casos por separado: a es un número positivo, a=0 y a es un número negativo.

Es fácil demostrar que si a es positivo, la raíz cúbica de a no puede ser ni un número negativo ni cero. De hecho, sea b la raíz cúbica de a, entonces, por definición, podemos escribir la igualdad b 3 =a. Está claro que esta igualdad no puede ser cierta para b negativo y para b=0, ya que en estos casos b 3 =b·b·b será un número negativo o cero, respectivamente. Entonces la raíz cúbica de un número positivo a es un número positivo.

Ahora supongamos que además del número b hay otra raíz cúbica del número a, denotémoslo c. Entonces c 3 =a. Por lo tanto, b 3 −c 3 =a−a=0, pero b 3 −c 3 =(b−c)·(b 2 +b·c+c 2)(esta es la fórmula de multiplicación abreviada diferencia de cubos), de donde (b−c)·(b 2 +b·c+c 2)=0. La igualdad resultante es posible sólo cuando b−c=0 o b 2 +b·c+c 2 =0. De la primera igualdad tenemos b=c, y la segunda igualdad no tiene soluciones, ya que su lado izquierdo es un número positivo para cualquier número positivo byc como suma de tres términos positivos b 2, b·c y c 2. Esto prueba la unicidad de la raíz cúbica de un número positivo a.

Cuando a=0, la raíz cúbica del número a es solo el número cero. De hecho, si suponemos que hay un número b, que es una raíz cúbica de cero distinta de cero, entonces debe cumplirse la igualdad b 3 =0, lo cual es posible sólo cuando b=0.

Para a negativo, se pueden dar argumentos similares a los del caso para a positivo. Primero, demostramos que la raíz cúbica de un número negativo no puede ser igual ni a un número positivo ni a cero. En segundo lugar, suponemos que existe una segunda raíz cúbica de un número negativo y demostramos que necesariamente coincidirá con la primera.

Entonces, siempre hay una raíz cúbica de cualquier número real a y única.

vamos a dar definición de raíz cúbica aritmética.

Definición

Raíz cúbica aritmética de un número no negativo a es un número no negativo cuyo cubo es igual a a.

La raíz cúbica aritmética de un número no negativo a se denota como , el signo se llama signo de la raíz cúbica aritmética, el número 3 en esta notación se llama índice raíz. El número debajo del signo raíz es número radical, la expresión bajo el signo raíz es expresión radical.

Aunque la raíz cúbica aritmética se define sólo para números a no negativos, también es conveniente utilizar notaciones en las que los números negativos se encuentran bajo el signo de la raíz cúbica aritmética. Los entenderemos de la siguiente manera: , donde a es un número positivo. Por ejemplo, .

Hablaremos de las propiedades de las raíces cúbicas en el artículo general Propiedades de las raíces.

Calcular el valor de una raíz cúbica se llama extraer una raíz cúbica; esta acción se analiza en el artículo extracción de raíces: métodos, ejemplos, soluciones.

Para concluir este punto, digamos que la raíz cúbica del número a es una solución de la forma x 3 =a.

raíz enésima, raíz aritmética de grado n

Generalicemos el concepto de raíz de un número: introducimos definición de raíz enésima por n.

Definición

raíz enésima de a es un número cuya enésima potencia es igual a a.

De esta definición se desprende claramente que la raíz de primer grado del número a es el propio número a, ya que al estudiar el grado con exponente natural tomamos a 1 =a.

Arriba vimos casos especiales de la raíz enésima para n=2 y n=3: raíz cuadrada y raíz cúbica. Es decir, una raíz cuadrada es una raíz de segundo grado y una raíz cúbica es una raíz de tercer grado. Para estudiar raíces de enésimo grado para n=4, 5, 6, ..., conviene dividirlas en dos grupos: el primer grupo, raíces de grados pares (es decir, para n = 4, 6, 8 , ...), el segundo grupo - raíces en grados impares (es decir, con n=5, 7, 9, ...). Esto se debe al hecho de que las raíces de potencias pares son similares a las raíces cuadradas y las raíces de potencias impares son similares a las raíces cúbicas. Tratemos con ellos uno por uno.

Empecemos por las raíces cuyas potencias son los números pares 4, 6, 8,... Como ya dijimos, son parecidas a la raíz cuadrada del número a. Es decir, la raíz de cualquier grado par del número a existe sólo para a no negativo. Además, si a=0, entonces la raíz de a es única e igual a cero, y si a>0, entonces hay dos raíces de grado par del número a, y son números opuestos.

Justifiquemos la última afirmación. Sea b una raíz par (la denotamos como 2·m, donde m es algún número natural) del número a. Supongamos que hay un número c, otra raíz de grado 2·m del número a. Entonces b 2·m −c 2·m =a−a=0 . Pero conocemos la forma b 2 m −c 2 m = (b−c) (b+c) (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2), entonces (b−c)·(b+c)· (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2)=0. De esta igualdad se deduce que b−c=0, o b+c=0, o b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2 =0. Las dos primeras igualdades significan que los números b y c son iguales o b y c son opuestos. Y la última igualdad es válida sólo para b=c=0, ya que en su lado izquierdo hay una expresión que es no negativa para cualquier b y c como suma de números no negativos.

En cuanto a las raíces de enésimo grado para n impar, son similares a la raíz cúbica. Es decir, la raíz de cualquier grado impar del número a existe para cualquier número real a, y para un número dado a es única.

La unicidad de una raíz de grado impar 2·m+1 del número a se demuestra por analogía con la prueba de la unicidad de la raíz cúbica de a. Solo aquí en lugar de igualdad. a 3 −b 3 =(a−b)·(a 2 +a·b+c 2) se utiliza una igualdad de la forma b 2 m+1 −c 2 m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m). La expresión en el último paréntesis se puede reescribir como b 2 m +c 2 m +b c (b 2 m−2 +c 2 m−2 + b c (b 2 m−4 +c 2 m−4 +bc c (…+(b 2 +c 2 +bc c)))). Por ejemplo, con m=2 tenemos b 5 −c 5 =(b−c)·(b 4 +b 3 ·c+b 2 ·c 2 +b·c 3 +c 4)= (b−c)·(b 4 +c 4 +b·c·(b 2 +c 2 +b·c)). Cuando a y b son ambos positivos o ambos negativos, su producto es un número positivo, entonces la expresión b 2 +c 2 +b·c en el paréntesis anidado más alto es positiva como la suma de los números positivos. Ahora, pasando secuencialmente a las expresiones entre paréntesis de los grados de anidamiento anteriores, estamos convencidos de que también son positivas como suma de números positivos. Como resultado, obtenemos que la igualdad b 2 m+1 −c 2 m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)=0 posible sólo cuando b−c=0, es decir, cuando el número b es igual al número c.

Es hora de entender la notación de raíces enésimas. Para ello se da definición de raíz aritmética de enésimo grado.

Definición

Raíz aritmética del enésimo grado de un número no negativo a es un número no negativo cuya enésima potencia es igual a a.

El concepto de raíz cuadrada de un número no negativo.

Considera la ecuación x2 = 4. Resuélvela gráficamente. Para hacer esto en un sistema coordenadas Construyamos una parábola y = x2 y una recta y = 4 (Fig. 74). Se cruzan en dos puntos A (- 2; 4) y B (2; 4). Las abscisas de los puntos A y B son las raíces de la ecuación x2 = 4. Entonces, x1 = - 2, x2 = 2.

Razonando exactamente de la misma manera, encontramos las raíces de la ecuación x2 = 9 (ver Fig. 74): x1 = - 3, x2 = 3.

Ahora intentemos resolver la ecuación x2 = 5; En la figura se muestra una ilustración geométrica. 75. Es claro que esta ecuación tiene dos raíces x1 y x2, y estos números, como en los dos casos anteriores, son iguales en valor absoluto y opuestos en signo (x1 - - x2) - Pero a diferencia de los casos anteriores, donde las Las raíces de la ecuación se encontraron sin dificultad (y se pudieron encontrar sin usar gráficas), este no es el caso de la ecuación x2 = 5: del dibujo no podemos indicar los valores de las raíces, solo podemos establecer que uno raíz se encuentra ligeramente a la izquierda del punto - 2, y el segundo se encuentra ligeramente a la derecha del punto 2.

Pero aquí nos espera una desagradable sorpresa. Resulta que no existe tal cosa fracciones DIV_ADBLOCK32">

Supongamos que hay una fracción irreducible para la cual se cumple la igualdad https://pandia.ru/text/78/258/images/image007_16.jpg" alt=".jpg" width="55" height="36">!}, es decir, m2 = 5n2. La última igualdad significa que número natural m2 es divisible por 5 sin resto (en el cociente se convierte en n2).

En consecuencia, el número m2 termina en el número 5 o en el número 0. Pero entonces el número natural m también termina en el número 5 o en el número 0, es decir, el número m es divisible por 5 sin resto. En otras palabras, si el número m se divide por 5, entonces el cociente será algún número natural k. Esto significa que m = 5k.

Ahora mira:

Sustituyamos 5k en lugar de m en la primera igualdad:

(5k)2 = 5n2, es decir, 25k2 = 5n2 o n2 = 5k2.

La última igualdad significa que el número. 5n2 es divisible por 5 sin resto. Razonando como arriba, llegamos a la conclusión de que el número n también es divisible por 5 sin resto.

Entonces, m es divisible por 5, n es divisible por 5, lo que significa que la fracción se puede reducir (por 5). Pero supusimos que la fracción era irreducible. ¿Qué pasa? Por qué, habiendo razonado correctamente, llegamos al absurdo o, como suelen decir los matemáticos, obtuvimos una contradicción. ¡Sí, porque la premisa inicial era incorrecta, como si existiera una fracción irreducible para la cual se cumple la igualdad! ).

Si, como resultado de un razonamiento correcto, llegamos a una contradicción con la condición, entonces concluimos: nuestra suposición es falsa, lo que significa que lo que necesitábamos demostrar es verdadero.

Entonces, teniendo sólo numeros racionales(y aún no conocemos otros números), no podremos resolver la ecuación x2 = 5.

Al encontrarse por primera vez con una situación así, los matemáticos se dieron cuenta de que tenían que encontrar una manera de describirla en lenguaje matemático. Introdujeron un nuevo símbolo, al que llamaron raíz cuadrada, y usando este símbolo, las raíces de la ecuación x2 = 5 se escribieron de la siguiente manera: ). Ahora, para cualquier ecuación de la forma x2 = a, donde a > O, puedes encontrar las raíces: son números.https://pandia.ru/text/78/258/images/image012_6.jpg" alt=".jpg" width="32" height="31">!} ni un todo ni una fracción.
Esto significa que no es un número racional, es un número de nueva naturaleza; hablaremos específicamente de dichos números más adelante, en el Capítulo 5.
Por ahora, sólo notemos que el nuevo número está entre los números 2 y 3, ya que 22 = 4, que es menor que 5; Z2 = 9, y esto es más que 5. Puedes aclarar:

Tenga en cuenta nuevamente que en la tabla solo aparecen números positivos, como se especifica en la definición de raíz cuadrada. Y aunque, por ejemplo, = 25 es una igualdad verdadera, pasa de ella a la notación usando la raíz cuadrada (es decir, escribe eso. .jpg" alt=".jpg" width="42" height="30">!} es un número positivo, lo que significa https://pandia.ru/text/78/258/images/image025_3.jpg" alt=".jpg" width="35" height="28">!}. Solo está claro que es mayor que 4, pero menor que 5, ya que 42 = 16 (esto es menor que 17) y 52 = 25 (esto es más de 17).
Sin embargo, el valor aproximado del número se puede encontrar usando microcalculadora, que contiene la operación de raíz cuadrada; este valor es 4,123.

El número, como el número comentado anteriormente, no es racional.
e) No se puede calcular, ya que no existe la raíz cuadrada de un número negativo; la entrada no tiene sentido. La tarea propuesta es incorrecta.
mi) https://pandia.ru/text/78/258/images/image029_1.jpg" alt="Tarea" width="80" height="33 id=">!}, ya que 75 > 0 y 752 = 5625.

En los casos más simples, el valor de la raíz cuadrada se calcula inmediatamente:

https://pandia.ru/text/78/258/images/image031_2.jpg" alt="Tarea" width="65" height="42 id=">!}
Solución.
Primera etapa. No es difícil adivinar que la respuesta será 50 con cola. De hecho, 502 = 2500 y 602 = 3600, mientras que el número 2809 está entre los números 2500 y 3600.