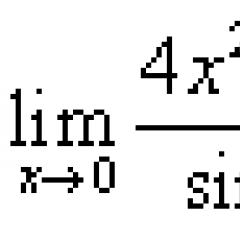El segundo límite destacable. El primer límite notable: ejemplos de hallazgo, problemas y soluciones detalladas Límite cos 1 x
Hay varios límites notables, pero los más famosos son el primer y segundo límites notables. Lo destacable de estos límites es que se utilizan ampliamente y con su ayuda se pueden encontrar otros límites que se encuentran en numerosos problemas. Esto es lo que haremos en la parte práctica de esta lección. Para resolver problemas reduciéndolos al primer o segundo límite notable, no es necesario revelar las incertidumbres contenidas en ellos, ya que los grandes matemáticos han deducido durante mucho tiempo los valores de estos límites.
El primer límite maravilloso. Se llama límite de la relación del seno de un arco infinitesimal al mismo arco, expresado en medida en radianes:
Pasemos a resolver problemas en el primer límite destacable. Nota: si hay una función trigonométrica debajo del signo de límite, este es un signo casi seguro de que esta expresión se puede reducir al primer límite destacable.
Ejemplo 1. Encuentra el límite.
Solución. Sustitución en lugar X cero conduce a la incertidumbre:
![]() .
.
El denominador es seno, por tanto, la expresión se puede llevar al primer límite notable. Comencemos la transformación:
![]() .
.
El denominador es el seno de tres X, pero el numerador tiene solo una X, lo que significa que necesitas obtener tres X en el numerador. ¿Para qué? para presentar 3 X = a y obtener la expresión.
Y llegamos a una variación del primer límite destacable:
porque no importa qué letra (variable) en esta fórmula esté en lugar de X.
Multiplicamos X por tres e inmediatamente dividimos:
 .
.
De acuerdo con el primer límite notable observado, reemplazamos la expresión fraccionaria:
Ahora finalmente podemos resolver este límite:
 .
.
Ejemplo 2. Encuentra el límite.
Solución. La sustitución directa nuevamente conduce a la incertidumbre de “cero dividido por cero”:
![]() .
.
Para obtener el primer límite notable, es necesario que la x bajo el signo del seno en el numerador y solo la x en el denominador tengan el mismo coeficiente. Sea este coeficiente igual a 2. Para hacer esto, imagine el coeficiente actual para x como se muestra a continuación, realizando operaciones con fracciones, obtenemos:
 .
.
Ejemplo 3. Encuentra el límite.
Solución. Al sustituir, obtenemos nuevamente la incertidumbre “cero dividido por cero”:
 .
.
Probablemente ya entiendas que a partir de la expresión original puedes obtener el primer límite maravilloso multiplicado por el primer límite maravilloso. Para hacer esto, descomponemos los cuadrados de x en el numerador y el seno en el denominador en factores idénticos, y para obtener los mismos coeficientes para x y seno, dividimos x en el numerador por 3 e inmediatamente multiplicamos por 3. Obtenemos:
 .
.
Ejemplo 4. Encuentra el límite.
Solución. Una vez más obtenemos la incertidumbre “cero dividido por cero”:
![]() .
.
Podemos obtener la relación de los dos primeros límites notables. Dividimos tanto el numerador como el denominador por x. Luego, para que los coeficientes de los senos y las x coincidan, multiplicamos la x superior por 2 e inmediatamente la dividimos por 2, y multiplicamos la x inferior por 3 e inmediatamente la dividimos por 3. Obtenemos:

Ejemplo 5. Encuentra el límite.
Solución. Y nuevamente la incertidumbre del “cero dividido por cero”:
Recordamos de la trigonometría que la tangente es la relación entre el seno y el coseno, y el coseno de cero es igual a uno. Realizamos las transformaciones y obtenemos:
 .
.
Ejemplo 6. Encuentra el límite.
Solución. La función trigonométrica bajo el signo de un límite sugiere nuevamente el uso del primer límite destacable. Lo representamos como la relación entre seno y coseno.
El primer límite destacable se utiliza a menudo para calcular límites que contienen seno, arcoseno, tangente, arcotangente y las incertidumbres resultantes de cero dividido por cero.
Fórmula
La fórmula para el primer límite notable es: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Observamos que para $ \alpha\to 0 $ obtenemos $ \sin\alpha \to 0 $, por lo tanto tenemos ceros en el numerador y denominador. Por lo tanto, se necesita la fórmula del primer límite notable para revelar las incertidumbres $ \frac(0)(0) $.
Para aplicar la fórmula se deben cumplir dos condiciones:
- Las expresiones contenidas en el seno y el denominador de la fracción son iguales
- Las expresiones en el seno y denominador de una fracción tienden a cero
¡Atención! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Aunque las expresiones bajo el seno y en el denominador son las mismas, sin embargo $ 2x ^2+1 = 1 $, para $ x\a 0 $. ¡La segunda condición no se cumple, por lo que NO PUEDES aplicar la fórmula!
Consecuencias
Muy raramente, en las tareas se puede ver un primer límite maravilloso puro en el que se puede escribir inmediatamente la respuesta. En la práctica, todo parece un poco más complicado, pero en estos casos será útil conocer las consecuencias del primer límite destacable. Gracias a ellos, podrás calcular rápidamente los límites requeridos.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Ejemplos de soluciones
Consideremos el primer límite notable, ejemplos de su solución para calcular límites que contienen funciones trigonométricas e incertidumbre $ \bigg[\frac(0)(0)\bigg] $
| Ejemplo 1 |
| Calcular $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Solución |
|
Miremos el límite y notemos que contiene un seno. Luego, sustituimos $ x = 0 $ en el numerador y denominador y obtenemos la incertidumbre cero dividida por cero: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ Ya hay dos signos de que necesitamos aplicar un límite maravilloso, pero hay un pequeño matiz: no podemos aplicar la fórmula de inmediato, ya que la expresión bajo el signo del seno difiere de la expresión en el denominador. Y necesitamos que sean iguales. Por lo tanto, usando transformaciones elementales del numerador, lo convertiremos en $2x$. Para ello, sacaremos los dos del denominador de la fracción como factor independiente. Se ve así: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Por favor tenga en cuenta que al final $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ se obtuvo según la fórmula. Si no puede resolver su problema, envíenoslo. Proporcionaremos una solución detallada. Podrás ver el progreso del cálculo y obtener información. ¡Esto te ayudará a obtener tu calificación de tu maestro de manera oportuna! |
| Respuesta |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Ejemplo 2 |
| Encuentra $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Solución |
|
Como siempre, primero hay que saber el tipo de incertidumbre. Si es cero dividido por cero, entonces prestamos atención a la presencia de un seno: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ ¿Esta incertidumbre nos permite usar la fórmula del primer límite notable, pero la expresión del denominador no es igual al argumento del seno? Por tanto, la fórmula no se puede aplicar “de frente”. Es necesario multiplicar y dividir la fracción por el argumento del seno: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Ahora anotamos las propiedades de los límites: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ El segundo límite se ajusta exactamente a la fórmula y es igual a uno: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Sustituimos nuevamente $ x = 0 $ en una fracción y obtenemos la incertidumbre $ \frac(0)(0) $. Para eliminarlo basta con sacar $ x $ de paréntesis y reducirlo por: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Respuesta |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Ejemplo 4 |
| Calcular $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Solución |
|
Comencemos el cálculo con la sustitución $ x=0 $. Como resultado, obtenemos la incertidumbre $ \frac(0)(0) $. El límite contiene un seno y una tangente, lo que insinúa un posible desarrollo de la situación utilizando la fórmula del primer límite destacable. Transformemos el numerador y denominador de la fracción en fórmula y consecuencia: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Ahora vemos que en el numerador y denominador hay expresiones que se ajustan a la fórmula y consecuencias. El argumento seno y el argumento tangente son los mismos para los denominadores correspondientes. $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Respuesta |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
El artículo: “El primer límite destacable, ejemplos de soluciones” hablaba de casos en los que es aconsejable utilizar esta fórmula y sus consecuencias.
El primer límite destacable es la siguiente igualdad:
\begin(ecuación)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(ecuación)
Dado que para $\alpha\to(0)$ tenemos $\sin\alpha\to(0)$, dicen que el primer límite notable revela una incertidumbre de la forma $\frac(0)(0)$. En términos generales, en la fórmula (1), en lugar de la variable $\alpha$, se puede colocar cualquier expresión bajo el signo del seno y en el denominador, siempre que se cumplan dos condiciones:
- Las expresiones bajo el signo del seno y en el denominador tienden simultáneamente a cero, es decir hay incertidumbre de la forma $\frac(0)(0)$.
- Las expresiones bajo el signo del seno y en el denominador son las mismas.
También se utilizan a menudo corolarios del primer límite notable:
\begin(ecuación) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(ecuación) \begin(ecuación) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(ecuación)
En esta página se resuelven once ejemplos. El ejemplo nº 1 está dedicado a la demostración de las fórmulas (2)-(4). Los ejemplos No. 2, No. 3, No. 4 y No. 5 contienen soluciones con comentarios detallados. Los ejemplos 6 a 10 contienen soluciones prácticamente sin comentarios, porque en ejemplos anteriores se dieron explicaciones detalladas. La solución utiliza algunas fórmulas trigonométricas que se pueden encontrar.
Permítanme señalar que la presencia de funciones trigonométricas junto con la incertidumbre $\frac (0) (0)$ no significa necesariamente la aplicación del primer límite destacable. A veces son suficientes transformaciones trigonométricas simples, por ejemplo, ver.
Ejemplo No. 1
Demuestre que $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Dado que $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, entonces:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Dado que $\lim_(\alpha\to(0))\cos(0)=1$ y $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , Eso:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Hagamos el cambio $\alpha=\sin(y)$. Dado que $\sin(0)=0$, entonces de la condición $\alpha\to(0)$ tenemos $y\to(0)$. Además, hay una vecindad de cero en la que $\arcsin\alpha=\arcsin(\sin(y))=y$, entonces:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
Se ha demostrado la igualdad $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$.
c) Hagamos el reemplazo $\alpha=\tg(y)$. Dado que $\tg(0)=0$, entonces las condiciones $\alpha\to(0)$ y $y\to(0)$ son equivalentes. Además, existe una vecindad de cero en la cual $\arctg\alpha=\arctg\tg(y))=y$, por lo tanto, con base en los resultados del punto a), tendremos:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
Se ha demostrado la igualdad $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
Las igualdades a), b), c) se utilizan a menudo junto con el primer límite destacable.
Ejemplo No. 2
Calcula el límite $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) (x+7))$.
Dado que $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ y $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, es decir y el numerador y denominador de la fracción tienden simultáneamente a cero, entonces aquí estamos tratando con una incertidumbre de la forma $\frac(0)(0)$, es decir hecho. Además, está claro que las expresiones bajo el signo del seno y en el denominador coinciden (es decir, y se satisfacen):
Entonces, se cumplen ambas condiciones enumeradas al principio de la página. De esto se deduce que la fórmula es aplicable, es decir $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.
Respuesta: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Ejemplo No. 3
Encuentre $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Dado que $\lim_(x\to(0))\sin(9x)=0$ y $\lim_(x\to(0))x=0$, entonces estamos tratando con una incertidumbre de la forma $\frac (0 )(0)$, es decir hecho. Sin embargo, las expresiones bajo el signo del seno y en el denominador no coinciden. Aquí debe ajustar la expresión en el denominador a la forma deseada. Necesitamos que la expresión $9x$ esté en el denominador; entonces será verdadera. Básicamente, nos falta un factor de $9$ en el denominador, que no es tan difícil de ingresar: simplemente multiplica la expresión en el denominador por $9$. Naturalmente, para compensar la multiplicación por $9$, tendrás que dividir inmediatamente por $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Ahora las expresiones en el denominador y bajo el signo del seno coinciden. Ambas condiciones para el límite $\lim_(x\to(0))\frac(\sin(9x))(9x)$ se cumplen. Por lo tanto, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. Y esto significa que:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Respuesta: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Ejemplo No. 4
Encuentre $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Dado que $\lim_(x\to(0))\sin(5x)=0$ y $\lim_(x\to(0))\tg(8x)=0$, aquí estamos tratando con incertidumbre de la forma $\frac(0)(0)$. Sin embargo, se viola la forma del primer límite destacable. Un numerador que contiene $\sin(5x)$ requiere un denominador de $5x$. En esta situación, la forma más sencilla es dividir el numerador por $5x$ e inmediatamente multiplicarlo por $5x$. Además, realizaremos una operación similar con el denominador, multiplicando y dividiendo $\tg(8x)$ por $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Reduciendo por $x$ y tomando la constante $\frac(5)(8)$ fuera del signo del límite, obtenemos:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Tenga en cuenta que $\lim_(x\to(0))\frac(\sin(5x))(5x)$ satisface completamente los requisitos para el primer límite notable. Para encontrar $\lim_(x\to(0))\frac(\tg(8x))(8x)$ se aplica la siguiente fórmula:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Respuesta: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Ejemplo No. 5
Encuentre $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Dado que $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (recuerde que $\cos(0)=1$) y $\ lim_(x\to(0))x^2=0$, entonces estamos tratando con una incertidumbre de la forma $\frac(0)(0)$. Sin embargo, para aplicar el primer límite destacable, debes deshacerte del coseno en el numerador, pasando a los senos (para luego aplicar la fórmula) o tangentes (para luego aplicar la fórmula). Esto se puede hacer con la siguiente transformación:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Volvamos al límite:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
La fracción $\frac(\sin^2(5x))(x^2)$ ya está cerca de la forma requerida para el primer límite notable. Trabajemos un poco con la fracción $\frac(\sin^2(5x))(x^2)$, ajustándola al primer límite destacable (nota que las expresiones en el numerador y debajo del seno deben coincidir):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Volvamos al límite en cuestión:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0) ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Respuesta: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Ejemplo No. 6
Encuentra el límite $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Dado que $\lim_(x\to(0))(1-\cos(6x))=0$ y $\lim_(x\to(0))(1-\cos(2x))=0$, entonces estamos lidiando con la incertidumbre $\frac(0)(0)$. Revelémoslo con la ayuda del primer límite destacable. Para hacer esto, pasemos de cosenos a senos. Dado que $1-\cos(2\alpha)=2\sin^2(\alpha)$, entonces:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Pasando a senos en el límite dado, tendremos:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Respuesta: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Ejemplo No. 7
Calcular el límite $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ sujeto a $\alpha\neq \beta$.
Anteriormente se dieron explicaciones detalladas, pero aquí simplemente observamos que nuevamente hay incertidumbre $\frac(0)(0)$. Pasemos de cosenos a senos usando la fórmula
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Usando esta fórmula, obtenemos:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\derecha| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Respuesta: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.
Ejemplo No. 8
Encuentra el límite $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Dado que $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (recuerde que $\sin(0)=\tg(0)=0$) y $\ lim_(x\to(0))x^3=0$, entonces aquí estamos tratando con una incertidumbre de la forma $\frac(0)(0)$. Desglosémoslo de la siguiente manera:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Respuesta: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Ejemplo No. 9
Encuentra el límite $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Dado que $\lim_(x\to(3))(1-\cos(x-3))=0$ y $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, entonces hay incertidumbre de la forma $\frac(0)(0)$. Antes de proceder a su expansión, conviene hacer un cambio de variable de tal forma que la nueva variable tienda a cero (nótese que en las fórmulas la variable $\alpha \to 0$). La forma más sencilla es introducir la variable $t=x-3$. Sin embargo, por conveniencia para futuras transformaciones (este beneficio se puede ver en el curso de la solución a continuación), vale la pena realizar el siguiente reemplazo: $t=\frac(x-3)(2)$. Observo que ambos reemplazos son aplicables en este caso, solo que el segundo reemplazo te permitirá trabajar menos con fracciones. Desde $x\to(3)$, entonces $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\derecha| =\left|\begin(alineado)&t=\frac(x-3)(2);\\&t\to(0)\end(alineado)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Respuesta: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Ejemplo No. 10
Encuentra el límite $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2 )$.
Una vez más estamos lidiando con la incertidumbre $\frac(0)(0)$. Antes de proceder a su expansión, conviene hacer un cambio de variable de tal forma que la nueva variable tienda a cero (nótese que en las fórmulas la variable es $\alpha\to(0)$). La forma más sencilla es introducir la variable $t=\frac(\pi)(2)-x$. Dado que $x\to\frac(\pi)(2)$, entonces $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\izquierda|\frac(0)(0)\derecha| =\left|\begin(alineado)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(alineado)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Respuesta: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Ejemplo No. 11
Encuentra los límites $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
En este caso no tenemos que utilizar el primer límite maravilloso. Tenga en cuenta que tanto el primer como el segundo límite contienen solo números y funciones trigonométricas. A menudo, en ejemplos de este tipo es posible simplificar la expresión situada bajo el signo de límite. Además, tras la mencionada simplificación y reducción de algunos factores, la incertidumbre desaparece. Di este ejemplo con un solo propósito: mostrar que la presencia de funciones trigonométricas bajo el signo del límite no significa necesariamente el uso del primer límite destacable.
Dado que $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (recuerde que $\sin\frac(\pi)(2)=1$ ) y $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (déjame recordarte que $\cos\frac(\pi)(2)=0$), entonces tenemos tratando con incertidumbre de la forma $\frac(0)(0)$. Sin embargo, esto no significa que debamos utilizar el primer límite maravilloso. Para revelar la incertidumbre, basta tener en cuenta que $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Hay una solución similar en el libro de soluciones de Demidovich (núm. 475). En cuanto al segundo límite, como en los ejemplos anteriores de esta sección, tenemos una incertidumbre de la forma $\frac(0)(0)$. ¿Por qué surge? Surge porque $\tg\frac(2\pi)(3)=-\sqrt(3)$ y $2\cos\frac(2\pi)(3)=-1$. Usamos estos valores para transformar las expresiones en el numerador y denominador. El objetivo de nuestras acciones es escribir la suma en el numerador y denominador como producto. Por cierto, a menudo dentro de un tipo similar es conveniente cambiar una variable, de tal manera que la nueva variable tienda a cero (ver, por ejemplo, los ejemplos No. 9 o No. 10 en esta página). Sin embargo, en este ejemplo no tiene sentido reemplazar, aunque si se desea, reemplazar la variable $t=x-\frac(2\pi)(3)$ no es difícil de implementar.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
Como puede ver, no tuvimos que aplicar el primer límite maravilloso. Por supuesto, puedes hacer esto si lo deseas (ver nota a continuación), pero no es necesario.
¿Cuál es la solución utilizando el primer límite notable? mostrar ocultar
Usando el primer límite notable obtenemos:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ derecha))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Respuesta: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Se recogen fórmulas, propiedades y teoremas utilizados en la resolución de problemas que pueden resolverse utilizando el primer límite destacable. Se dan soluciones detalladas de ejemplos que utilizan el primer límite notable de sus consecuencias.
ContenidoVer también: Prueba del primer límite destacable y sus consecuencias.
Fórmulas, propiedades y teoremas aplicados.
Aquí veremos ejemplos de soluciones a problemas que implican el cálculo de límites que utilizan el primer límite notable y sus consecuencias.
A continuación se enumeran las fórmulas, propiedades y teoremas que se utilizan con mayor frecuencia en este tipo de cálculo.
- El primer límite destacable y sus consecuencias:
. - Fórmulas trigonométricas para seno, coseno, tangente y cotangente:
;
;
;
en , ;
;
;
;
;
;
.
Ejemplos de soluciones
Ejemplo 1
Para esto.
1. Calcula el límite.
Dado que la función es continua para todo x, incluso en el punto, entonces
.
2. Dado que la función no está definida (y, por lo tanto, no es continua) para , debemos asegurarnos de que exista una vecindad perforada del punto en el que . En nuestro caso, en . Por lo tanto se cumple esta condición.
3. Calcula el límite. En nuestro caso, es igual al primer límite destacable:
.
De este modo,
.
De manera similar, encontramos el límite de la función en el denominador:
;
en ;
.
Y finalmente aplicamos las propiedades aritméticas de la función límite:
.
Apliquemos.
En . De la tabla de funciones equivalentes encontramos:
en ; en .
Entonces .
Ejemplo 2
Encuentra el límite:
.
Solución utilizando el primer límite destacable.
En , , . Esta es la incertidumbre de la forma. 0/0 .
Transformemos la función más allá del signo de límite:
.
Hagamos un cambio de variable. Desde y para, entonces
.
De manera similar tenemos:
.
Dado que la función coseno es continua en toda la recta numérica, entonces
.
Aplicamos las propiedades aritméticas de los límites:
.
Solución usando funciones equivalentes
Apliquemos el teorema de sustitución de funciones por funciones equivalentes en el límite del cociente.
En . De la tabla de funciones equivalentes encontramos:
en ; en .
Entonces .
Ejemplo 3
Encuentra el límite:
.
Sustituyamos el numerador y denominador de la fracción:
;
.
Esta es la incertidumbre de la forma. 0/0
.
Intentemos resolver este ejemplo usando el primer límite maravilloso. Dado que el valor de la variable tiende a cero, haremos una sustitución para que la nueva variable tienda no a , sino a cero. Para ello, pasamos de x a una nueva variable t, realizando la sustitución , . Luego a las , .
Primero, transformamos la función más allá del signo de límite multiplicando el numerador y denominador de la fracción por:
.
Sustituyamos y usemos las fórmulas trigonométricas dadas anteriormente.
;
;
.
La función es continua en . Encontramos su límite:
.
Transformemos la segunda fracción y apliquemos el primer límite maravilloso:
.
Hicimos una sustitución en el numerador de la fracción.
Aplicamos la propiedad del límite de un producto de funciones:
.
Ejemplo 4
Encuentra el límite:
.
En , , . Tenemos incertidumbre de la forma. 0/0 .
Transformemos la función bajo el signo de límite. Apliquemos la fórmula:
.
Sustituyamos:
.
Transformemos el denominador:
.
Entonces
.
Desde y para , hacemos la sustitución y aplicamos el teorema sobre el límite de una función compleja y el primer límite notable:
.
Aplicamos las propiedades aritméticas del límite de una función:
.
Ejemplo 5
Encuentra el límite de la función:
.
Es fácil ver que en este ejemplo tenemos una incertidumbre de la forma 0/0
. Para revelarlo aplicamos el resultado del problema anterior, según el cual
.
Introduzcamos la notación:
(A5.1). Entonces
(A5.2) .
De (A5.1) tenemos:
.
Sustituyémoslo en la función original:
,
Dónde ,
,
;
;
;
.
Usamos (A5.2) y la continuidad de la función coseno. Aplicamos las propiedades aritméticas del límite de una función.
,
aquí m es un número distinto de cero;
;
;
.
Ejemplo 6
Encuentra el límite:
.
Cuando el numerador y el denominador de la fracción tienden a 0
. Esta es la incertidumbre de la forma. 0/0
. Para ampliarlo transformamos el numerador de la fracción:
.
Apliquemos la fórmula:
.
Sustituyamos:
;
,
Dónde .
Apliquemos la fórmula:
.
Sustituyamos:
;
,
Dónde .
Numerador de fracción:
.
La función detrás del signo de límite tomará la forma:
.
Encontremos el límite del último factor, teniendo en cuenta su continuidad en:
.
Apliquemos la fórmula trigonométrica:
.
sustituyamos
. Entonces
.
Dividamos el numerador y denominador entre , apliquemos el primer límite destacable y una de sus consecuencias:
.
Finalmente tenemos:
.
Nota 1: También puedes aplicar la fórmula.
.
Entonces .
|
El primer límite destacable. La derivación del primer límite destacable es de interés desde el punto de vista de la aplicación de la teoría de los límites, y por ello os la ofrecemos casi en su totalidad. Consideremos el comportamiento de la función. |
Entonces claramente el área DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
S D MOA = 
SMOA =  =
= S D C O A =
S D C O A = 
Volviendo a la desigualdad mencionada y duplicándola, obtenemos:
pecado X < X < tg X.
Después de la división por el término pecado X:
 o
o 
Porque el  , entonces la variable
, entonces la variable  se concluye entre dos cantidades que tienen el mismo límite, es decir , con base en el teorema del límite de la función intermedia del párrafo anterior, tenemos:
se concluye entre dos cantidades que tienen el mismo límite, es decir , con base en el teorema del límite de la función intermedia del párrafo anterior, tenemos:
-primer límite maravilloso .
Ejemplo. Calcula los límites de las funciones usando el primer límite destacable:





Respuesta. 1) 1, 2) 0, 3)

Ejercicio: Calcula el límite de una función usando el primer límite destacable:

Respuesta: -2.
El segundo límite destacable.
Para derivar el segundo límite destacable, introducimos la definición del número mi:
Definición.
Límite variable  en
en  llamó a un númeromi
:
llamó a un númeromi
:
- El segundo límite maravilloso.
Número mi- numero irracional. Su valor a diez decimales verdaderos generalmente se redondea a un decimal verdadero:
mi= 2,7182818284..."2.7.
Teorema. Función  enX
tendiendo al infinito, tendiendo al límitemi
:
enX
tendiendo al infinito, tendiendo al límitemi
:

Ejemplo. Calcula los límites de las funciones:

Solución.
Según las propiedades de los límites, el límite del grado es igual al grado del límite, es decir:


Además, de manera similar se puede demostrar que 


Respuesta. 1)mi 3 , 2)mi 2 , 3)mi 4 .
Ejercicio. Calcula el límite de la función usando el segundo límite destacable:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ACERCA DE  respuesta:e-5
respuesta:e-5
Continuidad de una función Continuidad de una función en un punto
Definición. FunciónF ( X ), X Î ( a ; b ) X oh Î ( a ; b ), si el límite de la funciónF ( X ) en el puntoX oh existe y es igual al valor de la función en este punto:
 .
.
Según esta definición, la continuidad de la función F(X) en el punto X oh significa que se cumplen las siguientes condiciones:
función F(X) debe definirse en el punto X oh ;
función y F(X) debe haber un límite en el punto X oh ;
límite de una función F(X) en el punto X oh debe coincidir con el valor de la función en este punto.
Ejemplo.
Función F(X)
=
X 2
definido en toda la recta numérica y continuo en un punto X= 1 porque F( 1)
= 1 y 
Continuidad de una función en un conjunto.
Definición. Funciónf(x), se llama continua en el intervalo(a; b), si es continua en todos los puntos de este intervalo.
Si una función es continua en algún punto, entonces este punto se llama punto de continuidad de esta función. En los casos en que el límite de una función en un punto dado no existe o su valor no coincide con el valor de la función en un punto dado, entonces la función se llama discontinua en este punto y el punto en sí se llama discontinuidad. punto de la función f(x).
Propiedades de funciones continuas.
1) La suma de un número finito de funciones continuas en un punto A,
2) Producto de un número finito de funciones continuas en un punto A, hay una función que es continua en este punto.
3) La relación de un número finito de funciones continuas en un punto. A, es una función que es continua en este punto si el valor de la función en el denominador es diferente de cero en el punto A.
Ejemplo.
Función F(X) = X PAG, Dónde norte Î norte, es continua en toda la recta numérica. Este hecho se puede probar usando la propiedad 2 y la continuidad de la función. F(X) = X.
Función F(X) = sX PAG (Con– constante) es continua en toda la recta numérica, según la propiedad 2 y el ejemplo 1.
Teorema 1. Un polinomio es una función continua en toda la recta numérica.
Teorema 2 . Cualquier función racional fraccionaria es continua en cada punto de su dominio de definición..
Ejemplo.

Definición
FunciónF
(
X
)
llamado continuo en un puntox = un
, si en este punto su incremento  tiende a cero cuando el argumento incrementa
tiende a cero cuando el argumento incrementa  tiende a cero, o en otras palabras: funciónF
(X)
llamado continuo en un puntox = un
, si en este punto un incremento infinitesimal del argumento corresponde a un incremento infinitesimal de la función, es decir, si
tiende a cero, o en otras palabras: funciónF
(X)
llamado continuo en un puntox = un
, si en este punto un incremento infinitesimal del argumento corresponde a un incremento infinitesimal de la función, es decir, si 
 en
en  . Para ello, considere un círculo de radio 1; denotemos el ángulo central del MOB por X, donde
. Para ello, considere un círculo de radio 1; denotemos el ángulo central del MOB por X, donde  .
.