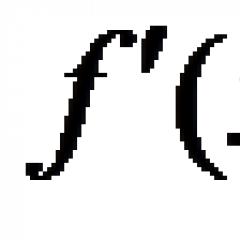Estudio de funciones para monotonicidad y extremo.

Raíz

Extremos y convexidad.

Asíntotas de la gráfica de una función.Definición. Punto crítico funciones = en(F X

) es el punto en el que la derivada es cero o no existe. Teorema. Si en el intervalo (a; b) la derivada

) es el punto en el que la derivada es cero o no existe. positivo/negativo, entonces la función aumenta/disminuye en este intervalo. Si al pasar por el punto crítico la derivada

Asíntotas de la gráfica de una función. cambia de signo de “+” a “-” (de “-” a “+”), entonces − es el punto máximo (mínimo) de la función Función llamado convexo arriba (abajo) en el intervalo (a; b), si en este intervalo los puntos de la gráfica se encuentran debajo (arriba) de las tangentes construidas en estos puntos. Punto de inflexión

es un punto en la gráfica de una función que la divide en partes con diferentes direcciones de convexidad.

Ejemplo 2.3. Explorar función

para monotonía y extremos, convexidad.

1. Examinamos la función en busca de monotonicidad y extremos. Hagamos un dibujo ().

arroz. 2.1

y''

−

asunto abajo

asunto arriba

Arroz. 2.2. Estudio de una función de convexidad.

Calculemos las ordenadas de los puntos de inflexión del gráfico:

Coordenadas de puntos de inflexión: (0; 0), (1; −1).

1) 2) 3)

4) 5) 6)

2.32. Examine la función para determinar monotonicidad y extremos:

1) 2.33. Encuentra los valores más pequeño y más grande de la función:

2) en el intervalo;

3) en el intervalo [-1; 1];

4) en el intervalo [−4; 4];

en el intervalo [−2; 1]. F 2.34. Los costos de producción C (cu) dependen del volumen de producción. F(unidades): Encuentre los costos de producción más altos si F cambios a lo largo del intervalo. encontrar valor

, en el que el beneficio será máximo si los ingresos por la venta de una unidad de producción son iguales a 15 u.m. mi.

2.35. Se requiere asignar un terreno rectangular de 512 m2, cercarlo y dividirlo con una cerca en tres partes iguales paralelas a uno de los lados del sitio. ¿Cuál debe ser el tamaño del sitio para que se utilice la menor cantidad de material para el cercado?

2.36. Dado el perímetro de una ventana rectangular, encuentre sus dimensiones tales que deje pasar la mayor cantidad de luz. F 2.37. Encuentre la ganancia máxima si los ingresos R y los costos C están determinados por las fórmulas: donde

− cantidad de bienes vendidos. 2.38. Dependencia del volumen de producción. W. de los costos de capital A
determinado por la función de los costos de capital Encuentra el intervalo de cambio

, donde aumentar los costos de capital es ineficaz.

2.40. La dependencia del volumen de producción (en unidades monetarias) de los costos de capital está determinada por la función Encuentre el intervalo de valores en el que aumentar los costos de capital es ineficaz.

2.41. Se cree que el aumento de las ventas por costes publicitarios (millones de rublos) está determinado por la relación Los ingresos por la venta de una unidad de producción equivalen a 20 mil rublos. Encuentre el nivel de costos publicitarios en el que la empresa obtendrá el máximo beneficio.

2.42. Los ingresos por la producción de productos utilizando unidades de recursos son iguales a El costo de una unidad de recurso es de 10 den. unidades ¿Qué cantidad de un recurso se debe comprar para que la ganancia sea mayor?

2.43. La función de costo tiene la forma El ingreso por la venta de una unidad de producción es 50. Encuentre la ganancia máxima que puede recibir el fabricante.

2.44. La dependencia de los ingresos del monopolio de la cantidad de producción se define como: La función de costos en este intervalo tiene la forma Encuentre el valor de producción óptimo para el monopolio.

2.45. El precio de los productos de un productor monopolista se fija de acuerdo con la relación identificada como . ¿A qué valor de la producción del producto serán mayores los ingresos por sus ventas?

2.46. La función de costo tiene la siguiente forma en en . Actualmente el nivel de producción ¿Bajo qué condición en el parámetro? pag¿Es rentable para una empresa reducir la producción si el ingreso por la venta de una unidad de producción es 50?

Hipermercado del conocimiento >>Matemáticas >>Matemáticas grado 10 >> Aplicación de la derivada al estudio de funciones de monotonicidad y extremos

§ 35. Aplicación de la derivada al estudio de funciones de monotonicidad y extremos.

1. Estudio de funciones de monotonicidad.

En la Fig. 129 muestra una gráfica de alguna función diferenciable creciente y = f(x). Dibujemos tangentes a gráficos en los puntos x= x 1 y x- x 2. ¿Qué tienen en común las líneas construidas? Lo que tienen en común es que forman un ángulo agudo con el eje x, lo que significa que ambas rectas tienen un coeficiente angular positivo. Pero el coeficiente angular de la tangente es igual al valor de la derivada en la abscisa del punto de tangencia. Así, en el punto x = x 3 la tangente es paralela al eje x, en este punto se cumple la igualdad f"(X 3) = 0. En general, en cualquier punto x del dominio de definición de la función diferenciable creciente la desigualdad se mantiene

En la Fig. 130 muestra una gráfica de algunos diferenciables decrecientes funciones y = f(x). Dibujemos tangentes a la gráfica en los puntos x= x 1 y x= x 2. ¿En las rectas construidas? Lo que tienen en común es que ambas forman un ángulo obtuso con el eje x, lo que significa que ambas líneas rectas tienen una pendiente negativa. Pero el coeficiente angular de la tangente es igual al valor de la derivada en la abscisa del punto de tangencia. Así, en el punto x = x 3 la tangente es paralela al eje x, en este punto se cumple la igualdad f "(x 3) = 0. En general, en cualquier punto x del dominio de definición de la función diferenciable decreciente , la desigualdad
Estas consideraciones muestran que existe una cierta conexión entre la naturaleza de la monotonicidad de una función y el signo de su derivada:

si una función aumenta en un intervalo y tiene una derivada, entonces la derivada no es negativa; Si una función disminuye en un intervalo y tiene una derivada, entonces la derivada no es positiva.
Para la práctica, es mucho más importante que los teoremas inversos también sean verdaderos, lo que muestra cómo se puede utilizar el signo de la derivada para establecer la naturaleza de la monotonicidad de una función en un intervalo. En este caso, para evitar malentendidos, sólo se toman espacios abiertos, es decir. intervalos o vigas abiertas. El caso es que para una función definida en el intervalo [a, b], no es muy correcto plantear la cuestión de la existencia y valor de la derivada en el punto final (en el punto x = a o en el punto x = b), ya que en el punto x = y el incremento del argumento solo puede ser positivo, y en el punto x = b - solo negativo. La definición de derivado no prevé tales restricciones.

Las demostraciones de estos teoremas suelen realizarse en un curso de matemáticas superiores. Nos limitaremos al razonamiento “práctico” realizado anteriormente y, para mayor persuasión, daremos también una interpretación física de los teoremas formulados.

Sea un punto material que se mueva en línea recta, s = s(t) es la ley del movimiento. Si la velocidad es siempre positiva, entonces el punto se aleja constantemente del origen, es decir la función s = s(t) aumenta. Si la velocidad es siempre negativa, entonces el punto se acerca constantemente al origen, es decir la función s = s(t) es decreciente. Si la velocidad del movimiento era positiva, entonces en algún momento particular se volvió cero y luego volvió a ser positiva, entonces el cuerpo en movimiento en el momento especificado parece desacelerarse, pero aún continúa alejándose del punto de partida. punto. Entonces en este caso la función s = s(t) aumenta. ¿Qué es la velocidad? Esta es la derivada del camino con respecto al tiempo. Esto significa que la naturaleza de la monotonicidad de la función (en este caso, la función s = s(t)) depende del signo de la derivada (velocidad). Esto es exactamente lo que dicen ambos teoremas formulados.

Ejemplo 1. Demuestre que la función es creciente en toda la recta numérica.
Solución. Encontremos la derivada de la función dada:

Obviamente, para todo x la desigualdad . Esto significa, según el Teorema 1, que la función aumenta en toda la recta numérica.

Ejemplo 2. a) Demuestre que la función y = 5cos x + 3m4x - 10x disminuye en toda la recta numérica;
b) decidir la ecuacion 5cos x + sen4x - 10x = x 3 + 5.

Solución, a) Encuentra la derivada de la función dada:

La expresión resultante es siempre negativa. De hecho, para todos los valores de x se cumplen las siguientes desigualdades:

Esta desigualdad es válida para todos los valores de x. Esto significa, según el teorema 2, que la función disminuye en toda la recta numérica.

b) Considere la ecuación 5cosx + sin4x - 10x = x 3 + 5. Como se acaba de establecer, y = 5cosx + sin4x-10x es una función decreciente. Al mismo tiempo, y = x 3 +5 es una función creciente. Se cumple la siguiente afirmación: si una de las funciones y = f(x) o y = s(x) aumenta y la otra disminuye, y si la ecuación f(x) = g(x) tiene raíz, entonces sólo una (La Fig. 131 ilustra claramente esta afirmación). No es difícil encontrar la raíz de una ecuación dada: este es el número x = 0 (con este valor, la ecuación se convierte en la igualdad numérica correcta 5 = 5).
Entonces, x = 0 es la única raíz de la ecuación dada.

Ejemplo 3. a) Examinar la monotonicidad de la función y = 2x 3 + 3x 2 -1; b) construye una gráfica de esta función.

Solución, a) Estudiar la monotonicidad de una función significa averiguar en qué intervalos del dominio de definición la función aumenta y en cuáles disminuye. Según los teoremas 1 y 2, esto está relacionado con el signo de la derivada.

Encontremos la derivada de esta función: f"(x)=6x 2 +6x y luego f"(x)=6x(x + 1).

En la Fig. 132 se indican esquemáticamente los signos de la derivada sobre intervalos del dominio de definición: en el rayo (-oo, -1) la derivada es positiva, en el intervalo (-1,0) - negativa, en el rayo (0, + - positivo. Esto significa que en el primero de los intervalos indicados la función aumenta, en el segundo disminuye y en el tercero aumenta.

Normalmente, si una función es continua no sólo en un intervalo abierto, sino también en sus puntos finales, estos puntos finales se incluyen en el intervalo de monotonicidad de la función.

Por tanto, la función dada aumenta en el rayo, aumenta en el rayo y disminuye en el segmento [-1,0].

b) Las gráficas de funciones se construyen “punto por punto”. Para hacer esto, necesitas hacer una tabla de los valores de la función y = 2x3 +3x 2 -1, donde debes incluir los valores de la función en los puntos finales de los intervalos de monotonicidad x = -1 y x = 0 y un par de valores más:

Marquemos estos puntos en el plano de coordenadas. Tengamos en cuenta los intervalos de aumento y disminución de la función encontrados en el inciso a) y también el hecho de que en los puntos x = -1 y x = 0 la derivada de la función es igual a cero, es decir la tangente a la gráfica de la función en los puntos indicados es paralela al eje de abscisas, además, en el punto (-1; 0) incluso coincide con el eje de abscisas. Finalmente, tengamos en cuenta que la función es continua, es decir su gráfica es una línea continua. La gráfica de la función especificada en la condición se muestra en la Fig. 133.

Para concluir nuestra discusión sobre el estudio de funciones de monotonicidad, prestemos atención a una circunstancia. Hemos visto que si la desigualdad f"(x) > 0 se satisface en el intervalo X, entonces la función y-f(x) aumenta en el intervalo X; si la desigualdad f"(x) se satisface en el intervalo X< 0, то функция убывает на этом промежутке. А что будет, если на всем промежутке выполняется тождество (х) =0 ? Видимо, функция не должна ни возрастать, ни убывать. Что же это за функция? Ответ очевиден - это постоянная функция у = С (буква С - первая буква слова соп81ап1а, что означает «постоянная»). Справедлива следующая теорема, формальное доказательство которой мы не приводим, ограничиваясь приведенными выше правдоподобными рассуждениями.

En el futuro usaremos este teorema, es decir podemos estar convencidos de su utilidad para las matemáticas. Y ahora daremos (para los más curiosos) un ejemplo del uso del Teorema 3 (de la categoría de entretenimiento matemático). Presentaremos una nueva forma de demostrar la conocida identidad sen 2 x + cos 2 x= 1.
Considere la función y = f(x), donde f(x) = sin 2 x + cos 2 x. Encontremos su derivada:

Entonces, para todo x se cumple la igualdad f"(x) = 0, lo que significa f(x) = C. Para encontrar el valor de C, basta con calcular el valor de la función en cualquier punto x, por ejemplo, x = 0. Tenemos: f(0) = sen 2 0+cos2 0=0 + 1 = 1.

Por tanto, C = 1, es decir, sen 2 x + cos 2 x = 1

2. Puntos extremos de la función y encontrarlos.

Volvamos a la gráfica de la función y = 2 x 3 + 3x 2 -1 (Fig. 133). Hay dos puntos únicos en el gráfico que determinan su estructura: estos son los puntos (-1; 0) y (0; -1). En estos puntos:

1) hay un cambio en la naturaleza de la monotonicidad de la función (a la izquierda del punto x = -1 la función aumenta, a la derecha, pero solo hasta el punto x = 0, la función disminuye; a la izquierda del punto x = 0 la función disminuye, a la derecha aumenta);

2) la tangente a la gráfica de la función es paralela al eje x, es decir la derivada de la función en cada uno de los puntos indicados es igual a cero;

3) f(-1) - el valor más grande de la función, pero no en todo el dominio de definición, sino en el sentido local, es decir comparado con los valores de la función de una determinada vecindad del punto x = -1. De la misma manera, f(0) es el valor más pequeño de la función, pero no en todo el dominio de definición, sino en el sentido local, es decir comparado con los valores de la función de alguna vecindad del punto x = 0.

Ahora mire la fig. 134, que muestra una gráfica de otra función. ¿No es parecido al gráfico anterior? Tiene los mismos dos puntos únicos, pero una de las tres características anteriores de estos puntos ha cambiado: ahora las tangentes a la gráfica en estos puntos no son paralelas al eje x. En el punto x = -1 la tangente no existe en absoluto, y en el punto x = 0 es perpendicular al eje x (más precisamente, coincide con el eje y).

Ya conoce el curso posterior del razonamiento: si aparece un nuevo modelo matemático o una nueva característica de un modelo matemático, debe estudiarse especialmente, es decir, introducir un nuevo término, nuevas designaciones, formular nuevas propiedades.

Definición 1. Un punto x = x 0 se denomina punto mínimo de la función y = f (x) si este punto tiene una vecindad para la cual todos los puntos (excepto el propio punto x = x 0) satisfacen la siguiente desigualdad:
f(x)>f(x0).

Así, las funciones cuyas gráficas se muestran en la Fig. 133 y 134 tienen un punto mínimo x=0. ¿Por qué? Debido a que este punto tiene una vecindad, por ejemplo, o (-0,2, 0,2), para todos
cuyos puntos, excepto el punto x = 0, se cumple la desigualdad f(x) > f(O). Esto es cierto para ambas funciones.
El valor de la función en el punto mínimo suele denotarse por . No confunda este valor (el más pequeño, pero en un sentido local) con, es decir. con el valor más pequeño de la función en todo el dominio de definición considerado (en el sentido global). Mire nuevamente la Fig. 133 y 134. Ves que ni una ni la otra función tienen un valor mínimo, sino que existen.

Definición 2. Un punto x = x 0 se denomina punto máximo de la función y = f (x) si este punto tiene una vecindad para la cual todos los puntos, excepto el propio punto x = x 0, satisfacen la siguiente desigualdad:
f(x)

Así, las funciones cuyas gráficas se muestran en la Fig. 133 y 134 tienen un punto máximo x = - 1. ¿Por qué? Porque en este punto
hay una vecindad, por ejemplo, para todos los puntos en los cuales, excepto x=-1, se satisface la desigualdad f(x)< f(-1). Это верно для обеих функций.
El valor de la función en el punto máximo suele denotarse por . No confunda este valor (el más grande, pero en sentido local) con ., es decir con el valor más grande de la función en todo el dominio de definición considerado (en el sentido global). Mire nuevamente la Fig. 133 y 134. Ves que ni una ni la otra función tienen el mayor valor, pero existen.

Los puntos mínimo y máximo de una función se combinan mediante un término común: puntos extremos (de la palabra latina extremum - "extremo").

¿Cómo encontrar los puntos extremos de una función? Podemos encontrar la respuesta a esta pregunta analizando una vez más los modelos gráficos presentados en la Fig. 133 y 134.

Tenga en cuenta: para la función cuya gráfica se muestra en la Fig. 133, en ambos puntos extremos la derivada desaparece (las tangentes son paralelas al eje x). Y para la función cuya gráfica se muestra en la Fig. 134, en ambos puntos extremos la derivada no existe. Esto no es accidental, ya que, como se demuestra en el curso del análisis matemático, el siguiente teorema es verdadero.

Teorema 4. Si la función y = f(x) tiene un extremo en el punto x = x 0, entonces en este punto la derivada de la función es cero o no existe.

Por conveniencia, aceptaremos llamar estacionarios a los puntos internos del dominio de definición de una función, en los que la derivada de la función es igual a cero, y a los puntos internos del dominio de definición de la función, en los que la función es continua, pero la derivada de la función no existe, crítica.

Ejemplo 4. Construya una gráfica de la función y = 2x 2 -6x + 3.

Solución. Sabes que la gráfica de una función cuadrática dada es una parábola y las ramas de la parábola están dirigidas hacia arriba, ya que el coeficiente de xr es positivo. Pero en este caso, el vértice de la parábola es el punto mínimo de la función, la tangente a la parábola en su vértice es paralela al eje x, lo que significa que en el vértice de la parábola la condición y"=0 debe quedar satisfecho Tenemos: y"=(2x 2 -6x + 3)"=4x -6.

Igualando la derivada a cero, obtenemos: 4x-6=0; x = 1,5.

Sustituyendo el valor encontrado de x en la ecuación de la parábola, obtenemos:

y = 21,52 - 6-1,5 + 3 = -1,5. Entonces, el vértice de la parábola es el punto (1,5; -1,5) y el eje de la parábola es la recta x = 1,5 (Fig. 135). Como puntos de control conviene tomar el punto (0; 3) y el punto (3; 3) simétrico al mismo con respecto al eje de la parábola. En la Fig. 136 utilizando los tres puntos encontrados, se construye una parábola: una gráfica de una función cuadrática dada.

¿Recuerdas cómo trazamos la función cuadrática y = ax 2 + bx + c en los grados 8 y 9? Casi de la misma manera, solo que el eje de la parábola se encontró no usando una derivada, sino usando una fórmula que debía memorizarse. La solución que se muestra en el ejemplo 4 le libera de tener que recordar esta fórmula. Para encontrar la abscisa del vértice de la parábola y = ax 2 + bx + c o la ecuación de su eje de simetría, basta con igualar la derivada de la función cuadrática a cero.

Ahora volvamos al Teorema 4, que dice que si en el punto x = x 0 la función y = f(x) tiene un extremo, entonces x = x 0 es un punto estacionario o crítico de la función. Surge una pregunta natural: ¿es cierto el teorema inverso, es decir? ¿Es cierto que si x = x 0 es un punto estacionario o crítico, entonces en este punto la función tiene un extremo? Respondemos: no, incorrecto. Mira la figura. 137, que muestra una gráfica de una función creciente que no tiene puntos extremos. Esta función tiene un punto estacionario x = x 1, en el cual la derivada desaparece (en este punto la gráfica de la función tiene una tangente paralela al eje x), pero este no es un punto extremo, sino un punto de inflexión, y allí es un punto crítico x = x 2, en el que la derivada no existe, pero tampoco es un punto extremo, sino un punto de ruptura en el gráfico. Por lo tanto, digamos esto: el Teorema 4 proporciona sólo una condición necesaria para un extremo (el teorema directo es válido), pero no es una condición suficiente (el teorema inverso no es verdadero).

Pero ¿qué pasa con una condición suficiente? ¿Cómo saber si hay un extremo en un punto estacionario o crítico? Para responder a esta pregunta, considere nuevamente las gráficas de funciones presentadas en la Fig. 133, 134, 136 y 137.
Observamos que al pasar por el punto máximo (estamos hablando del punto x = -1 en las Fig. 133 y 134), la naturaleza de la monotonicidad de la función cambia: a la izquierda del punto máximo la función aumenta, a a la derecha disminuye. Los signos de la derivada cambian en consecuencia: a la izquierda del punto máximo la derivada es positiva, a la derecha es negativa.
Observamos que al pasar por el punto mínimo (estamos hablando del punto x = 0 en la Fig. 133 y 134 y del punto x = 1,5 en la Fig. 136), la naturaleza de la monotonicidad de la función también cambia: al A la izquierda del punto mínimo la función disminuye, a la derecha aumenta. Los signos de la derivada cambian en consecuencia: a la izquierda del punto mínimo la derivada es negativa, a la derecha es positiva.

Si tanto a la izquierda como a la derecha del punto estacionario o crítico la derivada tiene el mismo signo, entonces no hay extremo en este punto, este es exactamente el caso de la función cuya gráfica se muestra en la Fig. 137.
Nuestro razonamiento puede servir como confirmación (pero, por supuesto, no como prueba: en el curso del análisis matemático se realizan pruebas rigurosas) de la validez del siguiente teorema.

Teorema 5 (condiciones suficientes para un extremo). Sea la función y=f(x) continua en el intervalo X y tenga un punto estacionario o crítico x = x 0 dentro del intervalo.

a) si este punto tiene una vecindad tal que en él en x<х 0 выполняется неравенство f(x) < 0,а при x >x 0 - desigualdad f"x)>0, entonces x =x 0 - punto mínimo de la función Y=f(x);

b) si este punto tiene una vecindad tal que en él para x< x 0 выполняется неравенство f"(x) >Ah, y para x > x 0 - desigualdad f(x)< О, то x = x 0 - точка максимума функции У=f(х);

c) si este punto tiene una vecindad tal que tanto a la izquierda como a la derecha del punto x 0 los signos de la derivada son iguales, entonces en el punto x = x 0 no hay extremo.

Ejemplo 5. a) Encuentra los puntos extremos de la función.
y = 3x 4 -16x 3 + 24x2 -11; b) construye una gráfica de esta función.

Solución, a) Encuentra la derivada de esta función:

La derivada desaparece en los puntos x = O y x = 2; estos son dos puntos estacionarios de la función dada. En la Fig. 138 muestra esquemáticamente los signos de la derivada en intervalos del dominio de definición: en el intervalo la derivada es negativa, en el intervalo (0, 2) es positiva, en el intervalo es positiva.
Esto significa que x = 0 es el punto mínimo de la función y x = 2 no es el punto extremo. En el primero de los intervalos anteriores la función disminuye, en el segundo y tercero aumenta.

En el punto mínimo x = 0 tenemos f(0) = -11 (sustituimos el valor x = 0 en la especificación analítica de la función), lo que significa = -11.

b) Para construir la gráfica de una función, necesitas conocer los puntos particularmente importantes de la gráfica. Éstas incluyen:
- punto mínimo encontrado (0; -11);

Punto estacionario x = 2; en este punto

Puntos de intersección con ejes de coordenadas; en este ejemplo, este es el punto ya encontrado (0; -11), el punto de intersección del gráfico con el eje y. Y una cosa más: puedes adivinar que f(1)=0, lo que significa que se ha encontrado el punto de intersección de la gráfica con el eje x: este es el punto (1; 0).

Entonces, tenemos un punto mínimo (0; -11), el punto de intersección de la gráfica con el eje x - el punto (1; 0) y un punto estacionario (2; 5). En este punto, la tangente a la gráfica de la función es horizontal, pero este no es un punto extremo, sino un punto de inflexión.

El gráfico de la función se muestra esquemáticamente en la Fig. 139. Tenga en cuenta que hay un punto más de intersección de la gráfica con el eje x, pero no pudimos encontrarlo.

Concluyendo este punto, observamos que en realidad hemos desarrollado

Algoritmo para estudiar la función continua "y = f(x)"sobre monotonicidad y extremos

1. Encuentra la derivada f"(x).
2. Encuentre puntos estacionarios y críticos.
3. Marque los puntos estacionarios y críticos en la recta numérica y determine los signos de la derivada en los intervalos resultantes.
4. Basándose en los teoremas del § 35, saque conclusiones sobre la monotonicidad de la función y sus puntos extremos.
Tenga en cuenta que si una función dada tiene la forma, entonces los polos de la función, es decir, Los puntos en los que el denominador q(x) se vuelve cero también se marcan en la recta numérica, y esto se hace antes de determinar los signos de la derivada. Pero, por supuesto, los polos no pueden ser puntos extremos.
Ejemplo 6. Examine la función en busca de monotonicidad y extremos.
Solución. Tenga en cuenta que la función es continua en todas partes, excepto en el punto x = 0. Usemos el algoritmo anterior.
1) Encuentra la derivada de la función dada:

2) La derivada desaparece en los puntos x = 2 y x = -2; estos son puntos estacionarios. La derivada no existe en el punto x = 0, pero este no es un punto crítico, es un punto de discontinuidad de la función (polo).

3) Marque los puntos -2, 0 y 2 en la recta numérica y coloque los signos de la derivada en los intervalos resultantes (Fig. 140).

4) Sacamos conclusiones: en el rayo (-°°, -2] la función disminuye, en el semiintervalo [-2, 0] la función aumenta, en el semiintervalo (0, 2] la función disminuye, en el rayo la función aumenta, en el intervalo (Fig. 128 ).

1. Considere una función en el intervalo (0, + 00).
sea x1< х 2 . Так как х 1 и х 2 - , то из х 1 < x 2 следует (см. пример 1 из § 33), т. е. f(x 1) >f(x2).

Entonces, de la desigualdad x 1< х 2 следует, что f(x 1) >f(x2). Esto significa que la función disminuye en el rayo abierto (0, + 00) (Fig. 129).

2. Considere una función en el intervalo (-oo, 0). Sea x 1< х 2 , х 1 и х 2 - отрицательные числа. Тогда - х 1 >- x 2, y ambos lados de la última desigualdad son números positivos y, por lo tanto, (utilizamos nuevamente la desigualdad probada en el ejemplo 1 del § 33). A continuación tenemos de dónde venimos.

Entonces, de la desigualdad x 1< х 2 следует, что f(x 1) >f(x 2) es decir la función disminuye en el rayo abierto (- 00 , 0)

Por lo general, los términos "función creciente" y "función decreciente" se combinan bajo el nombre general de función monótona, y el estudio de una función creciente y decreciente se denomina estudio de una función monotónica.

Solución.

1) Tracemos la función y = 2x2 y tomemos la rama de esta parábola en x< 0 (рис. 130).

2) Construir y seleccionar su parte en el segmento (Fig. 131).

Leamos la gráfica de la función y = f(x).

1. El dominio de definición de la función es la recta numérica completa.

2. y = 0 en x = 0; y > 0 para x > 0.

3. La función disminuye en el rayo (-oo, 0], aumenta en el segmento, disminuye en el rayo, es convexa hacia arriba en el segmento, convexa hacia abajo en el rayo, luego la función disminuye. Pero en el intervalo numérico (Fig. 128).

3. Función

1. Considere una función en el intervalo (0, + 00).
sea x1< х 2 . Так как х 1 и х 2 — положительные числа, то из х 1 < x 2 следует (см. пример 1 из § 33), т. е. f(x 1) >f(x2).
Entonces, de la desigualdad x 1< х 2 следует, что f(x 1) >f(x2). Esto significa que la función disminuye en el rayo abierto (0, + 00) (Fig. 129).

2. Considere una función en el intervalo (-oo, 0). Sea x 1< х 2 , х 1 и х 2 — отрицательные числа. Тогда - х 1 >- x 2, y ambas partes de este último son desiguales
las propiedades son números positivos y, por lo tanto, (utilizamos nuevamente la desigualdad probada en el Ejemplo 1 del § 33). A continuación tenemos de dónde venimos.
Entonces, de la desigualdad x 1< х 2 следует, что f(x 1) >f(x 2) es decir la función disminuye en el rayo abierto (- 00 , 0)
Por lo general, los términos "función creciente" y "función decreciente" se combinan bajo el nombre general de función monótona, y el estudio de una función creciente y decreciente se denomina estudio de una función monotónica.

Solución.

1) Tracemos la función y = 2x2 y tomemos la rama de esta parábola en x< 0 (рис. 130).

2) Construyamos una gráfica de la función y resaltemos su parte en el segmento (Fig. 131).

3) Construyamos una hipérbola y seleccionemos su parte en el rayo abierto (4, + 00) (Fig. 132).
4) Representemos las tres "piezas" en un sistema de coordenadas: esta es la gráfica de la función y = f(x) (Fig. 133).
Leamos la gráfica de la función y = f(x).
1. El dominio de definición de la función es la recta numérica completa.

2. y = 0 en x = 0; y > 0 para x > 0.

3. La función disminuye en el rayo (-oo, 0], aumenta en el segmento, disminuye en el rayo, es convexa hacia arriba en el segmento, convexa hacia abajo en el rayo)