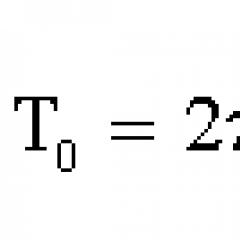Wibracje mechaniczne - Hipermarket Wiedzy. Drgania mechaniczne Wzory na temat fal mechanicznych
Studiując tę sekcję, pamiętaj o tym wahania o różnym charakterze fizycznym są opisane na podstawie powszechnych stanowisk matematycznych. Tutaj konieczne jest jasne zrozumienie takich pojęć, jak oscylacja harmoniczna, faza, różnica faz, amplituda, częstotliwość, okres oscylacji.
Należy pamiętać, że w każdym rzeczywistym układzie oscylacyjnym występuje opór ośrodka, tj. oscylacje zostaną wytłumione. Do scharakteryzowania tłumienia drgań wprowadza się współczynnik tłumienia i logarytmiczny ubytek tłumienia.
Jeżeli oscylacje występują pod wpływem zewnętrznej, okresowo zmieniającej się siły, wówczas takie oscylacje nazywa się wymuszonymi. Będą niezniszczone. Amplituda drgań wymuszonych zależy od częstotliwości siły napędowej. Gdy częstotliwość oscylacji wymuszonych zbliża się do częstotliwości oscylacji naturalnych, amplituda oscylacji wymuszonych gwałtownie wzrasta. Zjawisko to nazywa się rezonansem.
Przechodząc do badania fal elektromagnetycznych, musisz to jasno zrozumiećfala elektromagnetycznajest polem elektromagnetycznym rozchodzącym się w przestrzeni. Najprostszym układem emitującym fale elektromagnetyczne jest dipol elektryczny. Jeśli dipol ulega oscylacjom harmonicznym, wówczas emituje falę monochromatyczną.
Tabela wzorów: oscylacje i fale
|
Prawa fizyczne, wzory, zmienne |
Wzory oscylacyjne i falowe |
||||||
|
Równanie drgań harmonicznych: gdzie x jest przemieszczeniem (odchyleniem) wahającej się wielkości od położenia równowagi; A - amplituda; ω - częstotliwość kołowa (cykliczna); α - faza początkowa; (ωt+α) - faza. |
|||||||
|
Zależność między okresem a częstotliwością kołową: |
|||||||
|
Częstotliwość: |
|||||||
|
Zależność między częstotliwością kołową a częstotliwością: |
|||||||
|
Okresy drgań naturalnych 1) wahadło sprężynowe: gdzie k jest sztywnością sprężyny; 2) wahadło matematyczne: gdzie l jest długością wahadła, g - przyspieszenie swobodnego spadania; 3) obwód oscylacyjny: gdzie L jest indukcyjnością obwodu, C to pojemność kondensatora. |
|
||||||
|
Naturalna frekwencja: |
|||||||
|
Dodanie oscylacji o tej samej częstotliwości i kierunku: 1) amplituda powstałych oscylacji gdzie A 1 i A 2 to amplitudy składowych drgań, α 1 i α 2 – fazy początkowe składowych drgań; 2) początkowa faza powstałej oscylacji |
|
||||||
|
Równanie tłumionych oscylacji: e = 2,71... - podstawa logarytmów naturalnych. |
|
||||||
|
Amplituda tłumionych oscylacji: gdzie A 0 jest amplitudą w początkowym momencie; β - współczynnik tłumienia; |
|
||||||
|
Współczynnik tłumienia: ciało oscylujące gdzie r jest współczynnikiem oporu ośrodka, m - masa ciała; obwód oscylacyjny gdzie R jest aktywnym oporem, L jest indukcyjnością obwodu. |
|||||||
|
Częstotliwość tłumionych oscylacji ω: |
|
||||||
|
Okres drgań tłumionych T: |
|
||||||
|
Logarytmiczny ubytek tłumienia: |
Drgania harmoniczne to drgania wykonywane zgodnie z prawami sinusa i cosinusa. Poniższy rysunek przedstawia wykres zmian współrzędnych punktu w czasie zgodnie z prawem cosinusa.
zdjęcie
Amplituda oscylacji
Amplituda drgań harmonicznych jest największą wartością wychylenia ciała z położenia równowagi. Amplituda może przyjmować różne wartości. Będzie to zależeć od tego, jak bardzo wyprzedzimy ciało w początkowej chwili z położenia równowagi.
Amplituda jest określona przez warunki początkowe, czyli energię przekazaną ciału w początkowej chwili. Ponieważ sinus i cosinus mogą przyjmować wartości z zakresu od -1 do 1, równanie musi zawierać współczynnik Xm, wyrażający amplitudę oscylacji. Równanie ruchu dla drgań harmonicznych:
x = Xm*cos(ω0*t).
Okres oscylacji
Okres drgań to czas potrzebny na wykonanie jednego pełnego drgania. Okres oscylacji jest oznaczony literą T. Jednostki miary okresu odpowiadają jednostkom czasu. Oznacza to, że w SI są to sekundy.
Częstotliwość oscylacji to liczba oscylacji wykonywanych w jednostce czasu. Częstotliwość oscylacji oznaczona jest literą ν. Częstotliwość oscylacji można wyrazić w postaci okresu oscylacji.
ν = 1/T.
Jednostki częstotliwości podano w SI 1/sek. Ta jednostka miary nazywa się Herc. Liczba oscylacji w czasie 2*pi sekund będzie równa:
ω0 = 2*pi* ν = 2*pi/T.
Częstotliwość oscylacji
Wielkość ta nazywana jest cykliczną częstotliwością oscylacji. W niektórych publikacjach pojawia się nazwa częstotliwość kołowa. Częstotliwość drgań własnych układu oscylacyjnego to częstotliwość drgań swobodnych.
Częstotliwość drgań własnych oblicza się ze wzoru:
Częstotliwość drgań własnych zależy od właściwości materiału i masy ładunku. Im większa sztywność sprężyny, tym większa częstotliwość jej drgań własnych. Im większa masa ładunku, tym niższa częstotliwość drgań własnych.
Te dwa wnioski są oczywiste. Im sztywniejsza sprężyna, tym większe przyspieszenie nada ciału, gdy układ utraci równowagę. Im większa masa ciała, tym wolniej będzie się zmieniać prędkość tego ciała.
Okres swobodnej oscylacji:
T = 2*pi/ ω0 = 2*pi*√(m/k)
Warto zauważyć, że przy małych kątach odchylenia okres oscylacji ciała na sprężynie i okres oscylacji wahadła nie będą zależeć od amplitudy oscylacji.
Zapiszmy wzory na okres i częstotliwość drgań swobodnych wahadła matematycznego.
wtedy okres będzie równy
T = 2*pi*√(l/g).
Wzór ten będzie ważny tylko dla małych kątów odchylenia. Ze wzoru widzimy, że okres drgań rośnie wraz ze wzrostem długości gwintu wahadła. Im dłuższa długość, tym wolniej ciało będzie wibrować.
Okres oscylacji w ogóle nie zależy od masy ładunku. Ale to zależy od przyspieszenia swobodnego spadania. W miarę zmniejszania się g okres oscylacji będzie się zwiększał. Właściwość ta jest szeroko stosowana w praktyce. Na przykład, aby zmierzyć dokładną wartość swobodnego przyspieszenia.
Drgania harmoniczne zachodzą zgodnie z prawem:
X = A cos(ω T + φ 0),
Gdzie X– przemieszczenie cząstki z położenia równowagi, A– amplituda oscylacji, ω – częstotliwość kołowa, φ 0 – faza początkowa, T- czas.
Okres oscylacji T = .
Prędkość oscylującej cząstki:
υ
=
 = – Aω grzech(ω T
+ φ 0),
= – Aω grzech(ω T
+ φ 0),
przyśpieszenie A
=
 = –Aω 2 cos (ω T
+ φ 0).
= –Aω 2 cos (ω T
+ φ 0).
Energia kinetyczna cząstki poddanej ruchowi oscylacyjnemu: mi k =  =
= grzech 2 (ω T+ φ 0).
grzech 2 (ω T+ φ 0).
Energia potencjalna:
mi n=  cos 2 (ω T
+ φ 0).
cos 2 (ω T
+ φ 0).
Okresy drgań wahadła
- wiosna T
=
 ,
,
Gdzie M– masa ładunku, k– współczynnik sztywności sprężyny,
– matematyczny T
=
 ,
,
Gdzie l– długość zawieszenia, G- przyśpieszenie grawitacyjne,
– fizyczne T
=
 ,
,
Gdzie I– moment bezwładności wahadła względem osi przechodzącej przez punkt zawieszenia, M– masa wahadła, l– odległość punktu zawieszenia od środka masy.
Skróconą długość wahadła fizycznego wyznacza się z warunku: l np. =  ,
,
Oznaczenia są takie same jak dla wahadła fizycznego.
Po dodaniu dwóch oscylacji harmonicznych o tej samej częstotliwości i jednym kierunku otrzymuje się oscylacje harmoniczne o tej samej częstotliwości i amplitudzie:
A = A 1 2 + A 2 2 + 2A 1 A 2 cos(φ 2 – φ 1)
i faza początkowa: φ = arctan  .
.
Gdzie A 1 , A 2 – amplitudy, φ 1, φ 2 – początkowe fazy drgań złożonych.
Trajektoria powstałego ruchu po dodaniu wzajemnie prostopadłych oscylacji o tej samej częstotliwości:
 +
+
 –
–
 cos (φ 2 – φ 1) = sin 2 (φ 2 – φ 1).
cos (φ 2 – φ 1) = sin 2 (φ 2 – φ 1).
Drgania tłumione występują zgodnie z prawem:
X = A 0 mi - β T cos(ω T + φ 0),
gdzie β jest współczynnikiem tłumienia, znaczenie pozostałych parametrów jest takie samo jak dla oscylacji harmonicznych, A 0 – amplituda początkowa. W pewnym momencie T amplituda drgań:
A = A 0 mi - β T .
Logarytmiczny ubytek tłumienia nazywany jest:
λ = log  = β T,
= β T,
Gdzie T– okres oscylacji: T
=
 .
.
Współczynnik jakości układu oscylacyjnego nazywa się:
Równanie płaskiej fali biegnącej ma postać:
y = y 0 cos ω( T ± ),
Gdzie Na– przemieszczenie wielkości oscylacyjnej z położenia równowagi, Na 0 – amplituda, ω – częstotliwość kątowa, T- czas, X– współrzędna, wzdłuż której rozchodzi się fala, υ – prędkość rozchodzenia się fali.
Znak „+” odpowiada fali rozchodzącej się względem osi X, znak „–” odpowiada fali rozchodzącej się wzdłuż osi X.
Długość fali nazywana jest jej okresem przestrzennym:
λ = υ T,
Gdzie υ – prędkość propagacji fali, T– okres propagacji oscylacji.
Równanie falowe można zapisać:
y = y 0 cos 2π (+).
Falę stojącą opisuje równanie:
y
= (2y 0co  ) cos ω T.
) cos ω T.
Amplituda fali stojącej jest ujęta w nawiasach. Punkty o maksymalnej amplitudzie nazywane są antywęzłami,
X n = N ,
punkty o zerowej amplitudzie – węzły,
X y = ( N + ) .
Przykłady rozwiązywania problemów
Problem 20
Amplituda oscylacji harmonicznych wynosi 50 mm, okres wynosi 4 s, a faza początkowa . a) Zapisz równanie tego drgania; b) znaleźć przemieszczenie punktu oscylacyjnego z położenia równowagi w T=0 i przy T= 1,5 s; c) narysuj wykres tego ruchu.
Rozwiązanie
Równanie oscylacji jest zapisane jako X = A bo( T+ 0).
W zależności od warunku znany jest okres drgań. Dzięki niemu możemy wyrazić częstotliwość kołową =
 .
Pozostałe parametry są znane:
.
Pozostałe parametry są znane:
A) X= 0,05 cos( T + ).
b) Przesunięcie X Na T= 0.
X 1 = 0,05 cos = 0,05
 = 0,0355 m.
= 0,0355 m.
Na T= 1,5 s
X 2 = 0,05 cos( 1,5 + )= 0,05 cos = – 0,05 m.
V  ) wykres funkcji X= 0,05 cos ( T
+
) w następujący sposób:
) wykres funkcji X= 0,05 cos ( T
+
) w następujący sposób:
Określmy położenie kilku punktów. Znany X 1 (0) i X 2 (1,5), a także okres oscylacji. Zatem poprzez T= wartość 4 s X powtarza się, a po T = 2 s zmienia znak. Pomiędzy maksimum i minimum w środku jest 0.
Zadanie 21
Punkt wykonuje oscylację harmoniczną. Okres oscylacji wynosi 2 s, amplituda wynosi 50 mm, faza początkowa wynosi zero. Znajdź prędkość punktu w chwili, gdy jego przemieszczenie z położenia równowagi wynosi 25 mm.
Rozwiązanie
1 sposób. Zapisujemy równanie oscylacji punktu:
X= 0,05 cos T,
ponieważ =
 =.
=.
Znalezienie prędkości w danym momencie T:
υ
=
 = – 0,05
co T.
= – 0,05
co T.
Znajdujemy moment w czasie, w którym przemieszczenie wynosi 0,025 m:
0,025 = 0,05 cos T 1 ,
stąd cos T 1 = , T 1 = . Podstawiamy tę wartość do wyrażenia prędkości:
υ
= – 0,05 grzech
=
– 0,05
 = 0,136 m/s.
= 0,136 m/s.
Metoda 2. Całkowita energia ruchu oscylacyjnego:
mi
=
 ,
,
Gdzie A– amplituda, – częstotliwość kołowa, M – masa cząstek.
W każdym momencie czasu składa się ona z energii potencjalnej i kinetycznej punktu
mi k =
 ,
mi n =
,
mi n =
 , Ale k
= M 2, co oznacza mi n =
, Ale k
= M 2, co oznacza mi n =
 .
.
Zapiszmy prawo zachowania energii:
 =
=
 +
+ ,
,
stąd otrzymujemy: A 2 2 = υ 2 + 2 X 2 ,
υ
=
 =
=
 = 0,136 m/s.
= 0,136 m/s.
Zadanie 22
Amplituda oscylacji harmonicznych punktu materialnego A= 2 cm, energia całkowita mi= 3∙10 -7 J. Przy jakim przemieszczeniu od położenia równowagi na punkt drgań działa siła F = 2,25∙10 -5 N?
Rozwiązanie
Całkowita energia punktu wykonującego drgania harmoniczne jest równa:
mi
=
 .
(13)
.
(13)
Moduł siły sprężystości wyraża się poprzez przemieszczenie punktów z położenia równowagi X w następujący sposób:
F = k x (14)
Wzór (13) uwzględnia masę M i częstotliwości kołowej , a w (14) – współczynnik sztywności k. Ale częstotliwość kołowa jest powiązana z M I k:
2 =
 ,
,
stąd k
= M 2 i F = M 2 X. Wyraziwszy M 2 z zależności (13) otrzymujemy:
M 2 =
 ,
F
=
,
F
=
 X.
X.
Skąd czerpiemy wyrażenie na przemieszczenie X:
X
=
 .
.
Podstawienie wartości liczbowych daje:
X
=
 = 1,5∙10 -2 m = 1,5 cm.
= 1,5∙10 -2 m = 1,5 cm.
Zadanie 23
Punkt uczestniczy w dwóch oscylacjach o tych samych okresach i fazach początkowych. Amplitudy oscylacji A 1 = 3 cm i A 2 = 4 cm Znajdź amplitudę powstałych drgań, jeśli: 1) drgania występują w jednym kierunku; 2) oscylacje są wzajemnie prostopadłe.
Rozwiązanie
Jeżeli oscylacje występują w jednym kierunku, wówczas amplitudę powstałych oscylacji określa się jako:
Gdzie A 1 i A 2 – amplitudy drgań dodanych, 1 i 2 – fazy początkowe. Zgodnie z warunkiem fazy początkowe są takie same, co oznacza 2 – 1 = 0 i cos 0 = 1.
Stąd:
A
=
 =
= =
A 1 +A 2 = 7 cm.
=
A 1 +A 2 = 7 cm.
Jeżeli drgania są wzajemnie prostopadłe, wówczas równanie powstałego ruchu będzie wyglądało następująco:
 cos( 2 – 1) = grzech 2 ( 2 – 1).
cos( 2 – 1) = grzech 2 ( 2 – 1).
Ponieważ według warunku 2 – 1 = 0, cos 0 = 1, sin 0 = 0, równanie zostanie zapisane jako:  =0,
=0,
Lub  =0,
=0,
Lub  .
.

Powstały związek pomiędzy X I Na można przedstawić na wykresie. Z wykresu wynika, że efektem będzie oscylacja punktu na linii prostej MN. Amplituda tych drgań jest określana jako: A
=
 = 5cm.
= 5cm.
Zadanie 24
Okres drgań tłumionych T=4 s, logarytmiczny ubytek tłumienia = 1,6, faza początkowa wynosi zero. Przesunięcie punktu w T = równe 4,5 cm 1) Zapisz równanie tej drgań; 2) Skonstruuj wykres tego ruchu dla dwóch okresów.
Rozwiązanie
Równanie tłumionych oscylacji przy zerowej fazie początkowej ma postać:
X = A 0 mi - T cos2 .
Nie ma wystarczającej liczby początkowych wartości amplitudy, aby zastąpić wartości liczbowe A 0 i współczynnik tłumienia .
Współczynnik tłumienia można wyznaczyć z zależności na logarytmiczny ubytek tłumienia:
= T.
Zatem =
=
 = 0,4 s -1 .
= 0,4 s -1 .
Początkową amplitudę można wyznaczyć zastępując drugi warunek:
4,5 cm = A 0
 co2
co2  =A 0
=A 0
 co = A 0
co = A 0

 .
.
Stąd znajdziemy:
A 0
=
4,5∙
 (cm) = 7,75 cm.
(cm) = 7,75 cm.
Ostateczne równanie ruchu wygląda następująco:
X
= 0,0775
 koszt.
koszt.


Zadanie 25
Jaki jest logarytmiczny ubytek tłumienia wahadła matematycznego, jeśli dla T = 1-minutowa amplituda oscylacji zmniejszyła się o połowę? Długość wahadła l = 1 m.
Rozwiązanie
Logarytmiczny ubytek tłumienia można znaleźć z zależności: = T,
gdzie jest współczynnikiem tłumienia, T– okres oscylacji. Naturalna częstotliwość kołowa wahadła matematycznego:
0
=
 = 3,13 s -1 .
= 3,13 s -1 .
Współczynnik tłumienia drgań można wyznaczyć z warunku: A 0 = A 0 mi - T ,
T= ln2 = 0,693,
=
 = 0,0116c-1.
= 0,0116c-1.
Od << 0 ,
то
в формуле
=
 można pominąć w porównaniu z 0, a okres oscylacji można wyznaczyć ze wzoru:
T
=
można pominąć w porównaniu z 0, a okres oscylacji można wyznaczyć ze wzoru:
T
=
 = 2c.
= 2c.
Zastępujemy i T do wyrażenia na logarytmiczny ubytek tłumienia i otrzymujemy:
= T= 0,0116 s -1 ∙ 2 s = 0,0232.
Zadanie 26
Równanie drgań nietłumionych podane jest w postaci X= 4 sin600 T cm.
Znaleźć przemieszczenie od położenia równowagi punktu położonego w pewnej odległości l= 75 cm od źródła wibracji T= 0,01 s po rozpoczęciu oscylacji. Prędkość propagacji oscylacji υ = 300 m/s.
Rozwiązanie
Zapiszmy równanie fali rozchodzącej się z danego źródła: X= 0,04 grzech 600 ( T– ).
Znajdujemy fazę fali w danym momencie w danym miejscu:
T–
= 0,01 – = 0,0075 ,
= 0,0075 ,
600 ∙ 0,0075 = 4,5,
grzech 4,5 = grzech = 1.
Dlatego przesunięcie punktu X= 0,04 m, tj. na odległość l = 75 cm od źródła w momencie T= 0,01 s maksymalne przemieszczenie punktu.
Bibliografia
Volkenshtein V.S.. Zbiór problemów dla ogólnego przebiegu fizyki. – Petersburg: SpetsLit, 2001.
Savelyev I.V.. Zbiór pytań i problemów z fizyki ogólnej. – M.: Nauka, 1998.
I uzyskać dwie bezpłatne lekcje w szkole języka angielskiego SkyEng!
Sama tam studiuję - jest bardzo fajnie. Jest postęp.
W aplikacji możesz uczyć się słów, ćwiczyć słuchanie i wymowę.
Spróbuj. Dwie lekcje za darmo z mojego linku!
Kliknij
Ruchy oscylacyjne (lub oscylacje) w fizyce i technologii tego typu ruchy (lub zmiany stanów) nazywane są ruchami charakteryzującymi się pewnym stopniem powtarzalności.
Oscylacje zachodzące zgodnie z prawami sinusa lub cosinusa nazywane są harmonicznymi.
Równanie drgań harmonicznych:
gdzie t-czas; wartość x zmieniająca się w czasie (współrzędna, ładunek, prąd, SEM itp.); A - amplituda oscylacji - maksymalne odchylenie wartości oscylacyjnej od wartości średniej (zerowej); - faza oscylacji; - faza początkowa; w - częstotliwość cykliczna (zmiana fazy w jednostce czasu). W tym okresie faza zmienia się na .
Równanie różniczkowe drgań harmonicznych
Równanie postaci:
równanie różniczkowe drgań harmonicznych.
Rodzaje oscylacji okresowych można przedstawić z dowolną dokładnością jako sumę oscylacji harmonicznych, tzw. szereg harmoniczny.
Oscylacje, które wykona ciało, jeśli zostanie wytrącone z równowagi (nieważne w jaki sposób) i pozostawione samemu sobie, nazywane są swobodnymi (naturalnymi) oscylacjami. Jeżeli drgania naturalne spowodowane są obecnością jedynie siły quasi-sprężystej, to będą one harmoniczne.
Drgania ciała spowodowane jednoczesnym działaniem siły quasi-sprężystej i siły tarcia (która jest proporcjonalna do prędkości chwilowej: ) nazywane są drganiami tłumionymi.
Równanie (3) nazywane jest równaniem różniczkowym drgań tłumionych. Oto współczynnik tłumienia.
Rozwiązanie równania różniczkowego drgań
Rozwiązaniem równania różniczkowego drgań tłumionych (3) jest zależność postaci:
Równanie (4) nazywane jest równaniem drgań tłumionych. Z równania (4) wynika, że amplituda drgań tłumionych zależy od czasu. Stałe A są określone przez warunki początkowe. Amplituda oscylacji maleje i ogólnie wyglądają one tak, jak pokazano na rys. 1
 Ryż. 1.
Ryż. 1.
Okres drgań tłumionych oblicza się ze wzoru (5):
Fizyczne znaczenie współczynnika tłumienia jest takie, że współczynnik tłumienia jest odwrotnością czasu relaksacji. A czas relaksacji to czas, w którym amplituda maleje e-krotnie. Jednakże współczynnik tłumienia nie charakteryzuje w pełni tłumienia. Zazwyczaj tłumienie drgań charakteryzuje się spadkiem tłumienia. Ta ostatnia pokazuje, ile razy amplituda oscylacji maleje w czasie równym okresowi oscylacji. Oznacza to, że ubytek tłumienia wyznacza się w następujący sposób:
Logarytm ubytku tłumienia nazywany jest ubytkiem logarytmicznym i jest oczywiście równy:
Jeśli układ oscylacyjny zostanie wystawiony na działanie zewnętrznej siły okresowej, powstają tak zwane oscylacje wymuszone, które nie są tłumione.
Oscylacje wymuszone należy odróżnić od samooscylacji. W przypadku samooscylacji w układzie przyjmuje się specjalny mechanizm, który w czasie własnych oscylacji „dostarcza” do układu niewielkie porcje energii.
Przykłady rozwiązywania problemów
PRZYKŁAD 1
| Ćwiczenia | Znajdź energię drgań swobodnych ładunku zawieszonego na sprężynie. Rozważmy przypadek wahadła fizycznego, wiedząc, że sztywność sprężyny wynosi k, a amplituda drgań wynosi A.
|
| Rozwiązanie | Znajdźmy energię drgań swobodnych. Reprezentowana jest przez dwa rodzaje energii: kinetyczną i potencjalną. Dla piłki zawieszonej na sprężynie: Drgania piłki opisuje równanie drgań: Zapiszmy równanie na oscylacje prędkości piłki, wiedząc, że ruch odbywa się tylko wzdłuż osi X, zatem: Podstawiając (1.2) i (1.3) do (1.1) otrzymujemy: wiedząc, że dla wahadła fizycznego |
| Odpowiedź | Energia drgań swobodnych jest proporcjonalna do kwadratu amplitudy drgań |
§ 6. WIBRACJE MECHANICZNEPodstawowe formuły
Równanie harmoniczne
Gdzie X - przemieszczenie punktu oscylacyjnego z położenia równowagi; T- czas; A,ω, φ - odpowiednio amplituda, częstotliwość kątowa, początkowa faza oscylacji; - faza oscylacji w danej chwili T.
Częstotliwość kątowa
gdzie ν i T są częstotliwością i okresem oscylacji.
Prędkość punktu wykonującego oscylacje harmoniczne wynosi
Przyspieszenie podczas oscylacji harmonicznych
Amplituda A wynikowe oscylacje uzyskane przez dodanie dwóch oscylacji o tych samych częstotliwościach, występujących wzdłuż jednej prostej, określa się ze wzoru
Gdzie A 1 I A 2 - amplitudy składowych drgań; φ 1 i φ 2 to ich fazy początkowe.
Fazę początkową φ powstałych oscylacji można znaleźć ze wzoru
Częstotliwość uderzeń powstających podczas dodawania dwóch oscylacji występujących wzdłuż jednej linii prostej o różnych, ale podobnych częstotliwościach ν 1 i ν 2,
Równanie trajektorii punktu uczestniczącego w dwóch wzajemnie prostopadłych oscylacjach o amplitudach A 1 i A 2 oraz fazach początkowych φ 1 i φ 2,
Jeżeli początkowe fazy φ 1 i φ 2 składowych drgań są takie same, to równanie trajektorii przyjmuje postać
oznacza to, że punkt porusza się po linii prostej.
W przypadku, gdy różnica faz wynosi , równanie przyjmuje postać
oznacza to, że punkt porusza się po elipsie.
Równanie różniczkowe drgań harmonicznych punktu materialnego
Lub gdzie m jest masą punktu; k- współczynnik siły quasi-sprężystej ( k=Tω 2).
Całkowita energia punktu materialnego wykonującego oscylacje harmoniczne wynosi
Okres drgań ciała zawieszonego na sprężynie (wahadło sprężyste)
Gdzie M- masa ciała; k- sztywność sprężyny. Wzór obowiązuje dla drgań sprężystych w granicach, w których spełnione jest prawo Hooke'a (przy małej masie sprężyny w porównaniu z masą ciała).
Okres drgań wahadła matematycznego
Gdzie l- długość wahadła; G- przyśpieszenie grawitacyjne. Okres drgań wahadła fizycznego
Gdzie J- moment bezwładności ciała oscylującego względem osi
wahanie; A- odległość środka masy wahadła od osi drgań;
Zmniejszona długość wahadła fizycznego.
Podane wzory są dokładne dla przypadku nieskończenie małych amplitud. W przypadku skończonych amplitud wzory te dają jedynie przybliżone wyniki. Przy amplitudach nie większych niż błąd wartości okresu nie przekracza 1%.
Okres drgań skrętnych ciała zawieszonego na elastycznej nici wynosi
Gdzie J- moment bezwładności korpusu względem osi pokrywającej się z nicią sprężystą; k- sztywność elastycznej nici, równa stosunkowi momentu sprężystego powstającego, gdy nić jest skręcona, do kąta, pod jakim nić jest skręcona.
Równanie różniczkowe tłumionych oscylacji lub,
Gdzie R- współczynnik oporu; δ - współczynnik tłumienia: ; ω 0 - naturalna częstotliwość kątowa drgań *
Równanie tłumionych oscylacji
Gdzie Na)- amplituda tłumionych oscylacji w danej chwili T;ω jest ich częstotliwością kątową.
Częstotliwość kątowa drgań tłumionych
О Zależność amplitudy drgań tłumionych od czasu
Gdzie A 0 - amplituda oscylacji w danej chwili T=0.
Logarytmiczny dekrement oscylacji
Gdzie Na) I A(t+T)- amplitudy dwóch kolejnych oscylacji oddzielonych w czasie okresem.
Równanie różniczkowe drgań wymuszonych
gdzie jest zewnętrzną siłą okresową działającą na oscylujący punkt materialny i powodującą wymuszone oscylacje; F 0 - jego wartość amplitudy;
Amplituda drgań wymuszonych
Częstotliwość rezonansowa i amplituda rezonansowa oraz
Przykłady rozwiązywania problemów
Przykład 1. Punkt oscyluje zgodnie z prawem x(t)= , Gdzie A=2 patrz Określ fazę początkową φ jeśli
X(0)= cm i X , (0)<0. Построить векторную диаграмму для мо- мента T=0.
Rozwiązanie. Skorzystajmy z równania ruchu i wyraźmy przemieszczenie w tej chwili T=0 przez fazę początkową:
Stąd znajdujemy fazę początkową:
* We wcześniej podanych wzorach na drgania harmoniczne tę samą wielkość oznaczono po prostu ω (bez indeksu 0).
Podstawmy podane wartości do tego wyrażenia X(0) i A:φ= = . Wartość argumentu spełniają dwie wartości kąta:
Aby zdecydować, która z tych wartości kąta φ również spełnia warunek, najpierw znajdujemy:
Podstawienie wartości do tego wyrażenia T=0 i na przemian wartości początkowych faz i , znajdujemy
T  jak zawsze A>0 i ω>0, wówczas warunek spełnia tylko pierwsza wartość fazy początkowej. Zatem pożądana faza początkowa
jak zawsze A>0 i ω>0, wówczas warunek spełnia tylko pierwsza wartość fazy początkowej. Zatem pożądana faza początkowa
Korzystając ze znalezionej wartości φ, konstruujemy diagram wektorowy (ryc. 6.1). Przykład 2. Punkt materialny z masą T=5 g wykonuje oscylacje harmoniczne z częstotliwością ν =0,5 Hz. Amplituda oscylacji A=3 cm. Wyznacz: 1) prędkość υ wskazuje na moment przemieszczenia x== 1,5 cm; 2) maksymalną siłę F max działającą na punkt; 3) Ryc. 6.1 całkowita energia mi punkt oscylacyjny.
i wzór na prędkość otrzymujemy biorąc pierwszą pochodną przemieszczenia po czasie:
Aby wyrazić prędkość poprzez przemieszczenie, należy wykluczyć czas ze wzorów (1) i (2). Aby to zrobić, podnosimy oba równania i dzielimy pierwsze przez A 2 , drugi na A 2 ω 2 i dodaj:
Po rozwiązaniu ostatniego równania dla υ , znajdziemy
Po wykonaniu obliczeń przy użyciu tego wzoru otrzymujemy
Znak plus odpowiada przypadkowi, gdy kierunek prędkości pokrywa się z dodatnim kierunkiem osi X, znak minus - gdy kierunek prędkości pokrywa się z ujemnym kierunkiem osi X.
Przemieszczenie podczas oscylacji harmonicznych, oprócz równania (1), można również wyznaczyć za pomocą równania
Powtarzając to samo rozwiązanie z tym równaniem, otrzymujemy tę samą odpowiedź.
2. Siłę działającą na punkt wyznaczamy, korzystając z drugiego prawa Newtona:
Gdzie A - przyspieszenie punktu, które uzyskujemy biorąc pochodną prędkości od czasu:
Podstawiając wyrażenie przyspieszenia do wzoru (3), otrzymujemy
Stąd maksymalna wartość siły
Podstawiając wartości π, ν do tego równania, T I A, znajdziemy
3. Całkowita energia punktu drgającego jest sumą energii kinetycznej i potencjalnej obliczonej dla dowolnej chwili.
Energię całkowitą najłatwiej obliczyć w momencie, gdy energia kinetyczna osiąga wartość maksymalną. W tym momencie energia potencjalna wynosi zero. Zatem całkowita energia mi punkt oscylacji jest równy maksymalnej energii kinetycznej
Prędkość maksymalną wyznaczamy ze wzoru (2), ustawiając: . Podstawiając wyrażenie prędkości do wzoru (4), znajdujemy
Podstawiając wartości wielkości do tego wzoru i wykonując obliczenia, otrzymujemy
lub µJ.
Przykład 3. Na końcach cienki pręt l= 1 m i masa M 3 = 400 g wzmocnionych kuleczek z masami M 1 = 200 g I M 2 = 300g. Pręt oscyluje wokół osi poziomej, prostopadłej
prostopadle do pręta i przechodząc przez jego środek (punkt O na ryc. 6.2). Zdefiniuj okres T drgania wywoływane przez pręt.
Rozwiązanie. Okres oscylacji wahadła fizycznego, takiego jak pręt z kulkami, jest określony przez zależność
Gdzie J- T - jego masa; l Z - odległość środka masy wahadła od osi.
Moment bezwładności tego wahadła jest równy sumie momentów bezwładności kulek J 1 i J 2 i pręt J 3:
Traktując kule jako punkty materialne, wyrażamy ich momenty bezwładności:
Ponieważ oś przechodzi przez środek pręta, jego moment bezwładności względem tej osi J 3 = = . Podstawianie otrzymanych wyrażeń J 1 , J 2 I J 3 do wzoru (2) wyznaczamy całkowity moment bezwładności wahadła fizycznego:
Po przeprowadzeniu obliczeń przy użyciu tego wzoru znajdujemy
Ryż. 6.2 Masa wahadła składa się z mas kulek i masy pręta:
Dystans l Z Środek masy wahadła od osi oscylacji znajdziemy w oparciu o następujące rozważania. Jeżeli oś X kieruj się wzdłuż pręta i zrównaj początek współrzędnych z punktem O, następnie wymaganą odległość l równa współrzędnej środka masy wahadła, tj.
Zastępowanie wartości ilości M 1 , M 2 , M, l i po dokonaniu obliczeń znajdujemy
Po wykonaniu obliczeń ze wzoru (1) otrzymujemy okres drgań wahadła fizycznego:
Przykład 4. Wahadło fizyczne to pręt o określonej długości l= 1 m i masa 3 T 1 Z przymocowany do jednego z końców obręczą o średnicy i masie T 1 . Pozioma oś Oz
wahadło przechodzi przez środek pręta prostopadle do niego (ryc. 6.3). Zdefiniuj okres T drgania takiego wahadła.
Rozwiązanie. Okres drgań wahadła fizycznego określa się ze wzoru

Gdzie J- moment bezwładności wahadła względem osi drgań; T - jego masa; l C - odległość od środka masy wahadła do osi drgań.
Moment bezwładności wahadła jest równy sumie momentów bezwładności pręta J 1 i obręcz J 2:
Moment bezwładności pręta względem osi prostopadłej do pręta i przechodzącej przez jego środek masy określa wzór. W tym przypadku t= 3T 1 i
Moment bezwładności obręczy wyznaczamy korzystając z twierdzenia Steinera, gdzie J- moment bezwładności względem dowolnej osi; J 0 - moment bezwładności względem osi przechodzącej przez środek masy równoległej do danej osi; A - odległość pomiędzy wskazanymi osiami. Stosując tę formułę do obręczy, otrzymujemy
Zastępowanie wyrażeń J 1 i J 2 do wzoru (2) wyznaczamy moment bezwładności wahadła względem osi obrotu:
Dystans l Z od osi wahadła do środka masy jest równa
Podstawianie wyrażeń do wzoru (1) J, l s i masę wahadła wyznaczamy okres jego oscylacji:
Po obliczeniu za pomocą tego wzoru otrzymamy T=2,17 s.
Przykład 5. Dodaje się dwie oscylacje w tym samym kierunku, wyrażone równaniami; X 2 = =, gdzie A 1 = 1 cm, A 2 =2 cm, s, s, ω = =. 1. Wyznacz fazy początkowe φ 1 i φ 2 składowych oscylacyjnych
Baniya. 2. Znajdź amplitudę A oraz początkowa faza φ powstałej oscylacji. Zapisz równanie powstałych drgań.
Rozwiązanie. 1. Równanie drgań harmonicznych ma postać
Przekształćmy równania podane w opisie problemu do tej samej postaci:

Z porównania wyrażeń (2) z równością (1) znajdujemy początkowe fazy pierwszej i drugiej oscylacji:
Cieszę się i cieszę.
2. Aby określić amplitudę A powstałych oscylacji, wygodnie jest skorzystać ze schematu wektorowego przedstawionego w Ryż. 6.4. Zgodnie z twierdzeniem cosinusa otrzymujemy
gdzie jest różnica faz między składowymi oscylacji. Ponieważ , zastępując znalezione wartości φ 2 i φ 1, otrzymujemy rad.
Zastąpmy wartości A 1 , A 2 i do wzoru (3) i wykonaj obliczenia:
A= 2,65cm.
Wyznaczmy tangens fazy początkowej φ powstałego drgania bezpośrednio z rys. 6.4: ![]() , skąd pochodzi faza początkowa
, skąd pochodzi faza początkowa
![]()
Zastąpmy wartości A 1 , A 2 , φ 1, φ 2 i wykonaj obliczenia:
Ponieważ częstotliwości kątowe dodanych oscylacji są takie same, powstałe oscylacje będą miały tę samą częstotliwość ω. Pozwala nam to zapisać równanie wynikowych oscylacji w postaci , gdzie A=2,65 cm, , rad.
Przykład 6. Punkt materialny uczestniczy jednocześnie w dwóch wzajemnie prostopadłych oscylacjach harmonicznych, których równania wynoszą:
Gdzie A 1 = 1 cm, A 2 = 2 cm, . Znajdź równanie trajektorii punktu. Konstruuj trajektorię zgodnie ze skalą i wskaż kierunek ruchu punktu.
Rozwiązanie. Aby znaleźć równanie trajektorii punktu, eliminujemy czas T z podanych równań (1) i (2). Aby to zrobić, użyj
Skorzystajmy ze wzoru. W tym wypadku zatem
Ponieważ zgodnie ze wzorem (1) , a następnie równanie trajektorii
Wynikowym wyrażeniem jest równanie paraboli, której oś pokrywa się z osią Oh. Z równań (1) i (2) wynika, że przemieszczenie punktu wzdłuż osi współrzędnych jest ograniczone i wynosi od -1 do +1 cm wzdłuż osi Oh i od -2 do +2 cm wzdłuż osi Jednostka organizacyjna.
Aby skonstruować trajektorię, używamy równania (3) w celu znalezienia wartości y, odpowiadający zakresowi wartości X, spełniając warunek cm i utwórz tabelę:
|
X , CM |
||||||

Po narysowaniu osi współrzędnych i wybraniu skali nanosimy ją na płaszczyznę xOj znalezione punkty. Łącząc je gładką krzywą, otrzymujemy trajektorię punktu drgającego zgodnie z równaniami ruchu (1) i (2) (rys. 6.5).
Aby wskazać kierunek ruchu punktu, będziemy monitorować, jak zmienia się jego położenie w czasie. W początkowej chwili T=0 współrzędne punktu są równe X(0)=1 cm i y(0)=2 cm w kolejnym momencie, na przykład kiedy T 1 =l s, współrzędne punktów ulegną zmianie i staną się równe X(1)= -1cm, y( T )=0. Znając położenie punktów w początkowym i kolejnych (bliskich) momentach czasu, można wskazać kierunek ruchu punktu po trajektorii. Na ryc. 6.5 ten kierunek ruchu jest oznaczony strzałką (od pkt A do pochodzenia). Po chwili T 2 = 2 s punkt oscylacyjny osiągnie punkt D, będzie poruszać się w przeciwnym kierunku.
Zadania
Kinematyka drgań harmonicznych
6.1. Równanie drgań punktów ma postać , gdzie ω=π s -1, τ=0,2 s. Zdefiniuj okres T oraz początkowa faza φ oscylacji.
6.2. Zdefiniuj okres T, częstotliwość v i faza początkowa φ drgań, określona równaniem, gdzie ω=2,5π s -1, τ=0,4 s.
6.3. Punkt oscyluje zgodnie z prawem, gdzie A x(0)=2środki masowego przekazu ; 2) x(0) = cm i ; 3) x(0)=2cm i ; 4) x(0)= i . Zbuduj diagram wektorowy dla danej chwili T=0.
6.4. Punkt oscyluje zgodnie z prawem, gdzie A=4 cm Określ fazę początkową φ jeśli: 1) x(0)= 2 środki masowego przekazu ; 2) X(0)= cm i ; 3) X(0)= cm i ; 4) X(0)=cm i . Zbuduj diagram wektorowy dla danej chwili T=0.