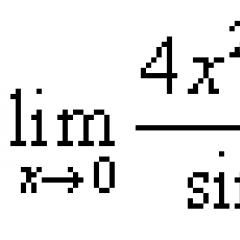Drugi niezwykły limit. Pierwsza niezwykła granica: przykłady znalezienia, problemy i szczegółowe rozwiązania Limit cos 1 x
Istnieje kilka niezwykłych limitów, ale najbardziej znane to pierwszy i drugi niezwykły limit. Niezwykłą cechą tych limitów jest to, że są one szeroko stosowane i przy ich pomocy można znaleźć inne ograniczenia występujące w wielu problemach. Oto, co zrobimy w praktycznej części tej lekcji. Aby rozwiązać problemy, redukując je do pierwszej lub drugiej niezwykłej granicy, nie ma potrzeby ujawniania zawartych w nich niepewności, ponieważ wartości tych granic od dawna dedukują wielcy matematycy.
Pierwsza cudowna granica nazywa się granicą stosunku sinusa nieskończenie małego łuku do tego samego łuku, wyrażoną w radianach:
Przejdźmy do rozwiązywania problemów na pierwszym niezwykłym limicie. Uwaga: jeśli pod znakiem granicy znajduje się funkcja trygonometryczna, jest to prawie pewny znak, że to wyrażenie można sprowadzić do pierwszej niezwykłej granicy.
Przykład 1. Znajdź granicę.
Rozwiązanie. Zamiast tego substytucja X zero prowadzi do niepewności:
![]() .
.
Mianownik jest sinusem, dlatego wyrażenie można doprowadzić do pierwszej niezwykłej granicy. Zacznijmy transformację:
![]() .
.
Mianownik to sinus trzech X, ale licznik ma tylko jeden X, co oznacza, że musisz w liczniku umieścić trzy X. Po co? Aby przedstawić 3 X = A i uzyskaj wyrażenie .
I dochodzimy do odmiany pierwszej niezwykłej granicy:
ponieważ nie ma znaczenia, która litera (zmienna) w tym wzorze stoi zamiast X.
Mnożymy X przez trzy i natychmiast dzielimy:
 .
.
Zgodnie z pierwszą zauważoną niezwykłą granicą zastępujemy wyrażenie ułamkowe:
Teraz możemy w końcu rozwiązać ten limit:
 .
.
Przykład 2. Znajdź granicę.
Rozwiązanie. Bezpośrednie podstawienie ponownie prowadzi do niepewności „zero podzielone przez zero”:
![]() .
.
Aby uzyskać pierwszą niezwykłą granicę, konieczne jest, aby x pod znakiem sinusa w liczniku i tylko x w mianowniku miały ten sam współczynnik. Niech ten współczynnik będzie równy 2. Aby to zrobić, wyobraźmy sobie bieżący współczynnik dla x jak poniżej, wykonując operacje na ułamkach, otrzymujemy:
 .
.
Przykład 3. Znajdź granicę.
Rozwiązanie. Podstawiając ponownie otrzymujemy niepewność „zero podzielone przez zero”:
 .
.
Prawdopodobnie już rozumiesz, że z oryginalnego wyrażenia możesz uzyskać pierwszą cudowną granicę pomnożoną przez pierwszą cudowną granicę. W tym celu rozkładamy kwadraty x w liczniku i sinus w mianowniku na identyczne czynniki, a aby otrzymać takie same współczynniki dla x i sinusa, dzielimy x w liczniku przez 3 i natychmiast mnożymy o 3. Otrzymujemy:
 .
.
Przykład 4. Znajdź granicę.
Rozwiązanie. Po raz kolejny otrzymujemy niepewność „zero podzielone przez zero”:
![]() .
.
Możemy otrzymać stosunek dwóch pierwszych niezwykłych granic. Dzielimy licznik i mianownik przez x. Następnie, aby współczynniki sinusów i xes się pokrywały, mnożymy górny x przez 2 i od razu dzielimy przez 2, a dolny x mnożymy przez 3 i od razu dzielimy przez 3. Otrzymujemy:

Przykład 5. Znajdź granicę.
Rozwiązanie. I znowu niepewność „zera podzielonego przez zero”:
Z trygonometrii pamiętamy, że tangens to stosunek sinusa do cosinusa, a cosinus zera jest równy jeden. Wykonujemy przekształcenia i otrzymujemy:
 .
.
Przykład 6. Znajdź granicę.
Rozwiązanie. Funkcja trygonometryczna pod znakiem granicy ponownie sugeruje użycie pierwszej niezwykłej granicy. Przedstawiamy to jako stosunek sinusa do cosinusa.
Pierwsza niezwykła granica jest często używana do obliczania granic zawierających sinus, arcsinus, tangens, arcus tangens i wynikające z tego niepewności zera podzielone przez zero.
Formuła
Wzór na pierwszą niezwykłą granicę jest następujący: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$
Zauważmy, że dla $ \alpha\to 0 $ otrzymamy $ \sin\alpha \to 0 $, zatem w liczniku i mianowniku mamy zera. Zatem do ujawnienia niepewności $ \frac(0)(0) $ potrzebny jest wzór na pierwszą niezwykłą granicę.
Aby zastosować formułę, muszą zostać spełnione dwa warunki:
- Wyrażenia zawarte w sinusie i mianowniku ułamka są takie same
- Wyrażenia w sinusie i mianowniku ułamka dążą do zera
Uwaga! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Chociaż wyrażenia pod sinusem i w mianowniku są takie same, jednak $ 2x ^2+1 = 1 $, dla $ x\to 0 $. Drugi warunek nie jest spełniony, zatem NIE MOŻNA zastosować formuły!
Konsekwencje
Dość rzadko w zadaniach widać czysty pierwszy cudowny limit, w którym można od razu zapisać odpowiedź. W praktyce wszystko wygląda nieco bardziej skomplikowanie, ale w takich przypadkach przydatne będzie poznanie konsekwencji pierwszego niezwykłego limitu. Dzięki nim szybko obliczysz wymagane limity.
$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$
$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$
$$ \lim_(\alfa\do 0) \frac(tg\alfa)(\alfa) = 1 $$
$$ \lim_(\alfa\do 0) \frac(\arcsin\alfa)(\alfa) = 1 $$
$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$
Przykłady rozwiązań
Rozważmy pierwszą niezwykłą granicę, przykłady jej rozwiązania do obliczania granic zawierających funkcje trygonometryczne i niepewność $ \bigg[\frac(0)(0)\bigg] $
| Przykład 1 |
| Oblicz $ \lim_(x\to 0) \frac(\sin2x)(4x) $ |
| Rozwiązanie |
|
Przyjrzyjmy się granicy i zauważmy, że zawiera ona sinus. Następnie podstawiamy licznik i mianownik $ x = 0 $ i dzielimy niepewność zero przez zero: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)(0 ) $$ Już dwa znaki, że musimy zastosować cudowną granicę, ale jest mały niuans: nie możemy od razu zastosować wzoru, ponieważ wyrażenie pod znakiem sinusa różni się od wyrażenia w mianowniku. I potrzebujemy, żeby były równe. Dlatego korzystając z elementarnych przekształceń licznika zamieniamy go na $2x$. Aby to zrobić, wyjmiemy dwa z mianownika ułamka jako osobny czynnik. Wygląda to tak: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ Proszę zauważ, że na koniec $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ otrzymano zgodnie ze wzorem. Jeśli nie możesz rozwiązać swojego problemu, wyślij go do nas. Dostarczymy szczegółowe rozwiązanie. Będziesz mógł zobaczyć postęp obliczeń i uzyskać informacje. Dzięki temu szybko otrzymasz ocenę od nauczyciela! |
| Odpowiedź |
| $$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$ |
| Przykład 2 |
| Znajdź $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $ |
| Rozwiązanie |
|
Jak zawsze, najpierw musisz poznać rodzaj niepewności. Jeśli jest to zero podzielone przez zero, to zwracamy uwagę na obecność sinusa: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Ta niepewność pozwala nam skorzystać ze wzoru na pierwszą niezwykłą granicę, ale wyrażenie z mianownika nie jest równe argumentowi sinusa? Dlatego formuły nie można zastosować „od razu”. Należy pomnożyć i podzielić ułamek przez argument sinusa: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x -x^4)(x ^3+2x)) = $$ Teraz zapisujemy właściwości granic: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x -x^4)\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Druga granica dokładnie pasuje do wzoru i jest równa do jednego: $$ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x )(2x-x^4) = $$ Podstaw ponownie $ x = 0 $ na ułamek i otrzymamy niepewność $ \frac(0)(0) $. Aby to wyeliminować, wystarczy wyjąć z nawiasu $ x $ i zmniejszyć o: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^ 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2 )(2) = 1 $$ |
| Odpowiedź |
| $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$ |
| Przykład 4 |
| Oblicz $ \lim_(x\to0) \frac(\sin2x)(tg3x) $ |
| Rozwiązanie |
|
Rozpocznijmy obliczenia od podstawienia $ x=0 $. W rezultacie otrzymujemy niepewność $ \frac(0)(0) $. Granica zawiera sinus i tangens, co wskazuje na możliwy rozwój sytuacji przy użyciu wzoru pierwszej niezwykłej granicy. Przekształćmy licznik i mianownik ułamka we wzór i konsekwencję: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Teraz widzimy, że w liczniku i mianowniku znajdują się wyrażenia pasujące do formuły i konsekwencji. Argument sinus i argument tangens są takie same dla odpowiednich mianowników $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$ |
| Odpowiedź |
| $$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$ |
W artykule: „Pierwszy niezwykły limit, przykłady rozwiązań” omówiono przypadki, w których wskazane jest skorzystanie z tej formuły i jej konsekwencje.
Pierwszą niezwykłą granicą jest następująca równość:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Ponieważ dla $\alpha\to(0)$ mamy $\sin\alpha\to(0)$, mówią, że pierwsza niezwykła granica ujawnia niepewność postaci $\frac(0)(0)$. Ogólnie rzecz biorąc, we wzorze (1) zamiast zmiennej $\alfa$ można umieścić dowolne wyrażenie pod znakiem sinusa i w mianowniku, o ile spełnione są dwa warunki:
- Wyrażenia pod znakiem sinusa i w mianowniku jednocześnie dążą do zera, tj. istnieje niepewność postaci $\frac(0)(0)$.
- Wyrażenia pod znakiem sinusa i w mianowniku są takie same.
Często stosuje się również wnioski z pierwszego niezwykłego limitu:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(równanie)
Na tej stronie rozwiązano jedenaście przykładów. Przykład nr 1 poświęcony jest dowodowi wzorów (2)-(4). Przykłady nr 2, nr 3, nr 4 i nr 5 zawierają rozwiązania ze szczegółowymi komentarzami. Przykłady nr 6-10 zawierają rozwiązania praktycznie bez komentarzy, ponieważ szczegółowe wyjaśnienia podano w poprzednich przykładach. Rozwiązanie wykorzystuje kilka wzorów trygonometrycznych, które można znaleźć.
Zauważmy, że obecność funkcji trygonometrycznych w połączeniu z niepewnością $\frac (0) (0)$ nie musi koniecznie oznaczać zastosowania pierwszej niezwykłej granicy. Czasami wystarczą proste przekształcenia trygonometryczne - na przykład patrz.
Przykład nr 1
Udowodnić, że $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alfa)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Ponieważ $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, to:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Ponieważ $\lim_(\alpha\to(0))\cos(0)=1$ i $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , To:
$ $ \ lim_ (\ alfa \ do (0)) \ Frac (\ sin (\ alfa)) (\ alfa \ cos (\ alfa)) = \ Frac (\ Displaystyle \ lim_ (\ alfa \ do (0)) \ Frac (\ sin (\ alfa)) (\ alfa)) (\ Displaystyle \ lim _ (\ alfa \ do (0)) \ cos (\ alfa)) = \ Frac (1) (1) = 1. $$
b) Dokonajmy zmiany $\alpha=\sin(y)$. Ponieważ $\sin(0)=0$, to z warunku $\alpha\to(0)$ mamy $y\to(0)$. Ponadto istnieje otoczenie zera, w którym $\arcsin\alpha=\arcsin(\sin(y))=y$, więc:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\ Frac (1) (\ Displaystyle \ lim_ (y \ do (0)) \ Frac (\ sin (y)) (y)) = \ Frac (1) (1) = 1. $$
Udowodniono równość $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$.
c) Dokonajmy zamiany $\alpha=\tg(y)$. Ponieważ $\tg(0)=0$, to warunki $\alpha\to(0)$ i $y\to(0)$ są równoważne. Dodatkowo istnieje otoczenie zera, w którym $\arctg\alpha=\arctg\tg(y))=y$, zatem bazując na wynikach punktu a), będziemy mieli:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\ Frac (1) (\ Displaystyle \ lim_ (y \ do (0)) \ Frac (\ tg (y)) (y)) = \ Frac (1) (1) = 1. $$
Udowodniono równość $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
Równania a), b), c) są często używane wraz z pierwszą niezwykłą granicą.
Przykład nr 2
Oblicz granicę $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) (x+7))$.
Ponieważ $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ i $\lim_( x \to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, tj. a licznik i mianownik ułamka jednocześnie dążą do zera, wówczas mamy do czynienia z niepewnością postaci $\frac(0)(0)$, czyli zrobione. Ponadto jasne jest, że wyrażenia pod znakiem sinusa i w mianowniku pokrywają się (tj. i są spełnione):
Zatem oba warunki wymienione na początku strony są spełnione. Wynika z tego, że obowiązuje formuła, tj. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7 ))=1$.
Odpowiedź: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Przykład nr 3
Znajdź $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Ponieważ $\lim_(x\to(0))\sin(9x)=0$ i $\lim_(x\to(0))x=0$, to mamy do czynienia z niepewnością postaci $\frac (0 )(0)$, tj. zrobione. Jednak wyrażenia pod znakiem sinusa i w mianowniku nie pokrywają się. Tutaj musisz dostosować wyrażenie w mianowniku do żądanej formy. Potrzebujemy wyrażenia $9x$, aby znaleźć się w mianowniku, wtedy stanie się prawdą. Zasadniczo brakuje nam w mianowniku współczynnika 9 $, co nie jest takie trudne do wprowadzenia — wystarczy pomnożyć wyrażenie w mianowniku przez 9 $. Naturalnie, aby zrekompensować mnożenie przez 9 $, będziesz musiał natychmiast podzielić przez 9 $:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Teraz wyrażenia w mianowniku i pod znakiem sinusa pokrywają się. Obydwa warunki granicy $\lim_(x\to(0))\frac(\sin(9x))(9x)$ są spełnione. Zatem $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. A to oznacza, że:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Odpowiedź: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Przykład nr 4
Znajdź $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Ponieważ $\lim_(x\to(0))\sin(5x)=0$ i $\lim_(x\to(0))\tg(8x)=0$, mamy tu do czynienia z niepewnością formy $\frac(0)(0)$. Jednakże forma pierwszego niezwykłego limitu zostaje naruszona. Licznik zawierający $\sin(5x)$ wymaga mianownika $5x$. W tej sytuacji najłatwiej jest podzielić licznik przez 5x$ i od razu pomnożyć przez 5x$. Dodatkowo wykonamy podobną operację z mianownikiem, mnożąc i dzieląc $\tg(8x)$ przez $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Zmniejszając o $x$ i wychodząc stałą $\frac(5)(8)$ poza znak graniczny, otrzymujemy:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Należy zauważyć, że $\lim_(x\to(0))\frac(\sin(5x))(5x)$ w pełni spełnia wymagania pierwszego niezwykłego limitu. Aby znaleźć $\lim_(x\to(0))\frac(\tg(8x))(8x)$, stosuje się następujący wzór:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) = \ Frac (5) (8) \ cdot \ Frac (\ Displaystyle \ lim_ (x \ do (0)) \ Frac (\ sin (5x)) (5x)) (\ Displaystyle \ lim_ (x \ do (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Odpowiedź: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Przykład nr 5
Znajdź $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Ponieważ $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (pamiętaj, że $\cos(0)=1$) i $\ lim_(x\to(0))x^2=0$, wówczas mamy do czynienia z niepewnością postaci $\frac(0)(0)$. Aby jednak zastosować pierwszą granicę niezwykłą, należy pozbyć się cosinusa w liczniku, przechodząc do sinusów (aby później zastosować wzór) lub stycznych (aby później zastosować wzór). Można tego dokonać za pomocą następującej transformacji:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Wróćmy do limitu:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
Ułamek $\frac(\sin^2(5x))(x^2)$ jest już bliski postaci wymaganej dla pierwszej niezwykłej granicy. Popracujmy trochę z ułamkiem $\frac(\sin^2(5x))(x^2)$, dostosowując go do pierwszej niezwykłej granicy (pamiętaj, że wyrażenia w liczniku i pod sinusem muszą się zgadzać):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Wróćmy do omawianego limitu:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Odpowiedź: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Przykład nr 6
Znajdź granicę $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Ponieważ $\lim_(x\to(0))(1-\cos(6x))=0$ i $\lim_(x\to(0))(1-\cos(2x))=0$, to mamy do czynienia z niepewnością $\frac(0)(0)$. Ujawnijmy to za pomocą pierwszej niezwykłej granicy. Aby to zrobić, przejdźmy od cosinusów do sinusów. Ponieważ $1-\cos(2\alpha)=2\sin^2(\alpha)$, to:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Przechodząc do sinusów w podanej granicy, będziemy mieli:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) = 9 \ cdot \ Frac (\ Displaystyle \ lim_ (x \ do (0)) \ lewo (\ Frac (\ sin (3x)) (3x) \ prawo) ^ 2) (\ Displaystyle \ lim_ (x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Odpowiedź: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Przykład nr 7
Oblicz limit $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ z zastrzeżeniem $\alpha\neq \ beta$.
Szczegółowe wyjaśnienia podano wcześniej, ale tutaj po prostu zauważamy, że znowu istnieje niepewność $\frac(0)(0)$. Przejdźmy od cosinusów do sinusów, korzystając ze wzoru
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Korzystając z tego wzoru, otrzymujemy:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\prawo| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Odpowiedź: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.
Przykład nr 8
Znajdź granicę $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Ponieważ $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (pamiętaj, że $\sin(0)=\tg(0)=0$) i $\ lim_(x\to(0))x^3=0$, wówczas mamy do czynienia z niepewnością postaci $\frac(0)(0)$. Podzielmy to w następujący sposób:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Odpowiedź: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Przykład nr 9
Znajdź granicę $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Ponieważ $\lim_(x\to(3))(1-\cos(x-3))=0$ i $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, to występuje niepewność postaci $\frac(0)(0)$. Przed przystąpieniem do jej rozwinięcia wygodnie jest dokonać zmiany zmiennej w taki sposób, aby nowa zmienna dążyła do zera (należy pamiętać, że we wzorach zmienna $\alpha \to 0$). Najłatwiej jest wprowadzić zmienną $t=x-3$. Jednak dla wygody dalszych przekształceń (korzyść tę widać w trakcie poniższego rozwiązania) warto dokonać następującej zamiany: $t=\frac(x-3)(2)$. Zaznaczam, że w tym przypadku mają zastosowanie oba zamienniki, po prostu drugie zastąpienie pozwoli ci mniej pracować z ułamkami. Ponieważ $x\to(3)$, to $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\prawo| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Odpowiedź: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Przykład nr 10
Znajdź granicę $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^ 2 )$.
Po raz kolejny mamy do czynienia z niepewnością $\frac(0)(0)$. Przed przystąpieniem do jej rozwinięcia wygodnie jest dokonać zmiany zmiennej w taki sposób, aby nowa zmienna dążyła do zera (należy pamiętać, że we wzorach zmienna ma postać $\alpha\to(0)$). Najłatwiej jest wprowadzić zmienną $t=\frac(\pi)(2)-x$. Ponieważ $x\to\frac(\pi)(2)$, to $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\lewo|\frac(0)(0)\prawo| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\do(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\do(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Odpowiedź: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Przykład nr 11
Znajdź granice $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2 \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
W tym przypadku nie musimy korzystać z pierwszego cudownego limitu. Należy pamiętać, że zarówno pierwsza, jak i druga granica zawierają tylko funkcje i liczby trygonometryczne. Często w tego typu przykładach możliwe jest uproszczenie wyrażenia znajdującego się pod znakiem ograniczającym. Co więcej, po wspomnianym uproszczeniu i ograniczeniu niektórych czynników niepewność znika. Podałem ten przykład tylko w jednym celu: pokazać, że obecność funkcji trygonometrycznych pod znakiem granicy nie musi koniecznie oznaczać zastosowania pierwszej niezwykłej granicy.
Ponieważ $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (pamiętaj, że $\sin\frac(\pi)(2)=1$ ) i $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (przypomnę, że $\cos\frac(\pi)(2)=0$), to mamy radzenie sobie z niepewnością w postaci $\frac(0)(0)$. Nie oznacza to jednak, że będziemy musieli skorzystać z pierwszego cudownego limitu. Aby ujawnić niepewność wystarczy wziąć pod uwagę, że $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
Podobne rozwiązanie znajduje się w książce rozwiązań Demidowicza (nr 475). Jeśli chodzi o drugą granicę, podobnie jak w poprzednich przykładach w tej sekcji, mamy niepewność w postaci $\frac(0)(0)$. Dlaczego powstaje? Powstaje, ponieważ $\tg\frac(2\pi)(3)=-\sqrt(3)$ i $2\cos\frac(2\pi)(3)=-1$. Używamy tych wartości do przekształcania wyrażeń w liczniku i mianowniku. Celem naszych działań jest zapisanie sumy w liczniku i mianowniku jako iloczynu. Nawiasem mówiąc, często w ramach podobnego typu wygodnie jest zmienić zmienną, wykonaną w taki sposób, aby nowa zmienna dążyła do zera (patrz np. Przykłady nr 9 lub nr 10 na tej stronie). Jednak w tym przykładzie nie ma sensu zastępować, choć w razie potrzeby zastąpienie zmiennej $t=x-\frac(2\pi)(3)$ nie jest trudne do wdrożenia.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
Jak widać, pierwszego cudownego limitu nie musieliśmy stosować. Oczywiście możesz to zrobić, jeśli chcesz (patrz uwaga poniżej), ale nie jest to konieczne.
Jakie jest rozwiązanie wykorzystujące pierwszą niezwykłą granicę? Pokaż ukryj
Korzystając z pierwszej niezwykłej granicy otrzymujemy:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ po prawej))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Odpowiedź: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
Zebrano wzory, właściwości i twierdzenia stosowane przy rozwiązywaniu problemów, które można rozwiązać przy użyciu pierwszej niezwykłej granicy. Podano szczegółowe rozwiązania przykładów wykorzystujących pierwszą niezwykłą granicę jej konsekwencji.
TreśćZobacz też: Dowód pierwszej niezwykłej granicy i jej konsekwencji
Stosowane wzory, własności i twierdzenia
Tutaj przyjrzymy się przykładom rozwiązań problemów związanych z obliczaniem limitów z wykorzystaniem pierwszego niezwykłego limitu i jego konsekwencjami.
Poniżej wymieniono wzory, właściwości i twierdzenia najczęściej używane w tego typu obliczeniach.
- Pierwsze niezwykłe ograniczenie i jego konsekwencje:
. - Wzory trygonometryczne na sinus, cosinus, tangens i cotangens:
;
;
;
Na , ;
;
;
;
;
;
.
Przykłady rozwiązań
Przykład 1
Dla tego.
1. Oblicz limit.
Ponieważ funkcja jest ciągła dla wszystkich x, łącznie z punktem, to
.
2. Ponieważ funkcja nie jest zdefiniowana (i dlatego nie jest ciągła) dla , musimy upewnić się, że istnieje przebite sąsiedztwo punktu, w którym . W naszym przypadku o godz. Zatem ten warunek jest spełniony.
3. Oblicz limit. W naszym przypadku jest ona równa pierwszej niezwykłej granicy:
.
Zatem,
.
Podobnie granicę funkcji znajdujemy w mianowniku:
;
Na ;
.
Na koniec stosujemy arytmetyczne właściwości granicy funkcji:
.
Aplikujmy.
Na . Z tabeli równoważnych funkcji znajdujemy:
Na ; Na .
Następnie .
Przykład 2
Znajdź granicę:
.
Rozwiązanie wykorzystujące pierwszą niezwykłą granicę
Na , , . To jest niepewność formy 0/0 .
Przekształćmy funkcję poza znak graniczny:
.
Dokonajmy zmiany zmiennej. Od i dla , zatem
.
Podobnie mamy:
.
Zatem funkcja cosinus jest ciągła na całej osi liczbowej
.
Stosujemy własności arytmetyczne granic:
.
Rozwiązanie wykorzystujące równoważne funkcje
Zastosujmy twierdzenie o zastępowaniu funkcji równoważnymi w granicy ilorazu.
Na . Z tabeli równoważnych funkcji znajdujemy:
Na ; Na .
Następnie .
Przykład 3
Znajdź granicę:
.
Podstawiamy licznik i mianownik ułamka:
;
.
To jest niepewność formy 0/0
.
Spróbujmy rozwiązać ten przykład, korzystając z pierwszego cudownego limitu. Ponieważ wartość zmiennej w niej dąży do zera, dokonamy podstawienia tak, aby nowa zmienna dążyła nie do , ale do zera. Aby to zrobić, przechodzimy od x do nowej zmiennej t, dokonując podstawienia , . Następnie o , .
Najpierw przekształcamy funkcję poza znak graniczny, mnożąc licznik i mianownik ułamka przez:
.
Zastąpmy i zastosujmy podane powyżej wzory trygonometryczne.
;
;
.
Funkcja jest ciągła w . Znajdujemy jego granicę:
.
Przekształćmy drugi ułamek i zastosujmy pierwszą cudowną granicę:
.
Dokonaliśmy podstawienia w liczniku ułamka.
Stosujemy własność granicy iloczynu funkcji:
.
Przykład 4
Znajdź granicę:
.
Na , , . Mamy niepewność co do formy 0/0 .
Przekształćmy funkcję pod znakiem granicy. Zastosujmy wzór:
.
Zastąpmy:
.
Przekształćmy mianownik:
.
Następnie
.
Ponieważ i dla , dokonujemy podstawienia i stosujemy twierdzenie o granicy funkcji zespolonej i pierwszej niezwykłej granicy:
.
Stosujemy własności arytmetyczne granicy funkcji:
.
Przykład 5
Znajdź granicę funkcji:
.
Łatwo zauważyć, że w tym przykładzie mamy niepewność formy 0/0
. Aby to ujawnić, stosujemy wynik poprzedniego problemu, zgodnie z którym
.
Wprowadźmy oznaczenie:
(A5.1). Następnie
(A5.2) .
Z (A5.1) mamy:
.
Zastąpmy to oryginalną funkcją:
,
Gdzie ,
,
;
;
;
.
Korzystamy z (A5.2) i ciągłości funkcji cosinus. Stosujemy własności arytmetyczne granicy funkcji.
,
tutaj m jest liczbą niezerową, ;
;
;
.
Przykład 6
Znajdź granicę:
.
Kiedy , licznik i mianownik ułamka mają tendencję do 0
. To jest niepewność formy 0/0
. Aby go rozwinąć, przekształcamy licznik ułamka:
.
Zastosujmy wzór:
.
Zastąpmy:
;
,
Gdzie .
Zastosujmy wzór:
.
Zastąpmy:
;
,
Gdzie .
Licznik ułamka:
.
Funkcja znajdująca się za znakiem ograniczającym będzie miała postać:
.
Znajdźmy granicę ostatniego czynnika, biorąc pod uwagę jego ciągłość w :
.
Zastosujmy wzór trygonometryczny:
.
Zastąpmy
. Następnie
.
Podzielmy licznik i mianownik przez , zastosujmy pierwszą niezwykłą granicę i jedną z jej konsekwencji:
.
Wreszcie mamy:
.
Uwaga 1: Można również zastosować formułę
.
Następnie .
|
Pierwszy niezwykły limit. Wyprowadzenie pierwszej niezwykłej granicy jest interesujące z punktu widzenia zastosowania teorii granic, dlatego proponujemy je Państwu niemal w całości. Rozważmy zachowanie funkcji |
Następnie wyraźnie obszar DMOA< площадь сектора МОА < площадьDСОА (см. рис. 1).
SD MOA = 
S MOA =  =
= S D do OA =
S D do OA = 
Wracając do wspomnianej nierówności i podwajając ją, otrzymujemy:
grzech X < X < tg X.
Po podziale według terminu grzech X:
 Lub
Lub 
Ponieważ  , a następnie zmienna
, a następnie zmienna  zawierana jest pomiędzy dwiema wielkościami, które mają tę samą granicę, tj. , bazując na twierdzeniu o granicy funkcji pośredniej z poprzedniego akapitu, mamy:
zawierana jest pomiędzy dwiema wielkościami, które mają tę samą granicę, tj. , bazując na twierdzeniu o granicy funkcji pośredniej z poprzedniego akapitu, mamy:
-pierwszy wspaniały limit .
Przykład. Oblicz granice funkcji, korzystając z pierwszej niezwykłej granicy:





Odpowiedź. 1) 1, 2) 0, 3)

Ćwiczenia: Oblicz granicę funkcji, korzystając z pierwszej niezwykłej granicy:

Odpowiedź: -2.
Drugi niezwykły limit.
Aby wyprowadzić drugą niezwykłą granicę, wprowadzamy definicję liczby mi:
Definicja.
Zmienny limit  Na
Na  nazywany numeremmi
:
nazywany numeremmi
:
- Drugi wspaniały limit
Numer mi- Liczba niewymierna. Jego wartość do dziesięciu prawdziwych miejsc po przecinku jest zwykle zaokrąglana do jednego prawdziwego miejsca po przecinku:
mi= 2,7182818284…”2.7.
Twierdzenie. Funkcjonować  NaX
dążący do nieskończoności, zmierzający do granicymi
:
NaX
dążący do nieskończoności, zmierzający do granicymi
:

Przykład. Oblicz granice funkcji:

Rozwiązanie.
Zgodnie z właściwościami granic granica stopnia jest równa stopniowi granicy, tj.:


Co więcej, w podobny sposób można to udowodnić 


Odpowiedź. 1)mi 3 , 2)mi 2 , 3)mi 4 .
Ćwiczenia. Oblicz granicę funkcji, korzystając z drugiej niezwykłej granicy:

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
O  odpowiedź: e -5
odpowiedź: e -5
Ciągłość funkcji Ciągłość funkcji w punkcie
Definicja. FunkcjonowaćF ( X ), X Î ( A ; B ) X O Î ( A ; B ), jeśli granica funkcjiF ( X ) w tym punkcieX O istnieje i jest równa wartości funkcji w tym punkcie:
 .
.
Zgodnie z tą definicją ciągłość funkcji F(X) w tym punkcie X O oznacza, że spełnione są następujące warunki:
funkcjonować F(X) należy zdefiniować w punkcie X O ;
funkcja F(X) w tym punkcie musi być granica X O ;
granica funkcji F(X) w tym punkcie X O musi odpowiadać wartości funkcji w tym punkcie.
Przykład.
Funkcjonować F(X)
=
X 2
zdefiniowane na całej osi liczbowej i ciągłe w punkcie X= 1 ponieważ F( 1)
= 1 i 
Ciągłość funkcji na zbiorze
Definicja. Funkcjonowaćf(x), nazywa się ciągłym w przedziale(a; b), jeśli jest ciągła w każdym punkcie tego przedziału.
Jeżeli funkcja jest w pewnym momencie ciągła, to punkt ten nazywa się punktem ciągłości tej funkcji. W przypadku, gdy granica funkcji w danym punkcie nie istnieje lub jej wartość nie pokrywa się z wartością funkcji w danym punkcie, wówczas funkcję w tym punkcie nazywamy nieciągłą, a sam punkt nazywamy nieciągłością punkt funkcji f(x).
Własności funkcji ciągłych.
1) Suma skończonej liczby funkcji ciągłych w punkcie A,
2) Iloczyn skończonej liczby funkcji ciągłych w punkcie A, istnieje funkcja ciągła w tym punkcie.
3) Stosunek skończonej liczby funkcji ciągłych w punkcie A, jest funkcją ciągłą w tym punkcie, jeśli wartość funkcji w mianowniku jest różna od zera w tym punkcie A.
Przykład.
Funkcjonować F(X) = X P, Gdzie N Î N, jest ciągła na całej osi liczbowej. Fakt ten można udowodnić korzystając z własności 2 i ciągłości funkcji F(X) = X.
Funkcjonować F(X) = sX P (Z– stała) jest ciągła na całej osi liczbowej, w oparciu o właściwość 2 i przykład 1.
Twierdzenie 1. Wielomian to funkcja ciągła na całej osi liczbowej.
Twierdzenie 2 . Każda ułamkowa funkcja wymierna jest ciągła w każdym punkcie swojej dziedziny definicji.
Przykład.

Definicja
FunkcjonowaćF
(
X
)
nazywany ciągłym w punkciex = a
, jeśli w tym momencie jego przyrost  dąży do zera, gdy argument wzrasta
dąży do zera, gdy argument wzrasta  dąży do zera, czyli innymi słowy: funkcjaF
(X)
nazywany ciągłym w punkciex = a
, jeśli w tym momencie nieskończenie mały przyrost argumentu odpowiada nieskończenie małemu przyrostowi funkcji, tj. jeśli
dąży do zera, czyli innymi słowy: funkcjaF
(X)
nazywany ciągłym w punkciex = a
, jeśli w tym momencie nieskończenie mały przyrost argumentu odpowiada nieskończenie małemu przyrostowi funkcji, tj. jeśli 
 Na
Na  . Aby to zrobić, rozważ okrąg o promieniu 1; oznaczmy kąt środkowy MOB przez X, w której
. Aby to zrobić, rozważ okrąg o promieniu 1; oznaczmy kąt środkowy MOB przez X, w której  .
.