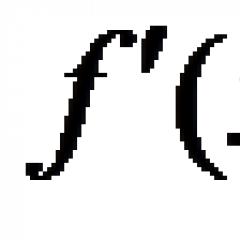Badanie funkcji monotoniczności i ekstremum. Wykres funkcji

Ekstrema i wypukłość.

Asymptoty wykresu funkcji

Definicja.Punkt krytyczny Funkcje Na = F(X) to punkt, w którym pochodna wynosi zero lub nie istnieje.

Twierdzenie. Jeśli w przedziale (a; b) pochodna dodatnia/ujemna, wówczas funkcja rośnie/maleje w tym przedziale.

Twierdzenie. Jeżeli po przejściu przez punkt krytyczny pochodna zmienia znak z „+” na „−” (z „−” na „+”), wówczas − jest maksymalnym (minimalnym) punktem funkcji

Definicja. Funkcjonować zwany wypukły w górę (w dół) w przedziale (a; b), jeżeli w tym przedziale punkty wykresu leżą pod (nad) stycznymi zbudowanymi w tych punktach. Punkt przegięcia jest punktem na wykresie funkcji, który dzieli ją na części o różnych kierunkach wypukłości.

Przykład 2.3.

Przeglądaj funkcję dla monotonii i ekstremów, wypukłość.

1. Badamy funkcję monotoniczności i ekstremów.

Zróbmy rysunek ( Ryż. 2.1).

Ryż. 2.2. Badanie funkcji wypukłości

Obliczmy współrzędne punktów przegięcia wykresu:

Współrzędne punktów przegięcia: (0; 0), (1; −1).

2.32. Zbadaj funkcję pod kątem monotoniczności i ekstremów:

1) 2) 3)

4) 5) 6)

2.33. Znajdź najmniejsze i największe wartości funkcji:

1) w przerwie;

2) na przedziale [-1; 1];

3) na przedziale [-4; 4];

4) na przedziale [−2; 1].

2,34. Koszty produkcji C (cu) zależą od wielkości produkcji X(jednostki): Znajdź najwyższe koszty produkcji, jeśli X zmiany w odstępie czasu. Znajdź wartość X, przy którym zysk będzie maksymalny, jeżeli przychód ze sprzedaży jednostki produkcyjnej będzie równy 15 j.m. mi.

2.35. Wymagane jest wydzielenie prostokątnej działki o powierzchni 512 m2, ogrodzenie jej i podzielenie płotem na trzy równe części równoległe do jednego z boków działki. Jaka powinna być wielkość placu, aby na ogrodzenie zużyć jak najmniej materiału?

2,36. Mając obwód prostokątnego okna, znajdź jego wymiary takie, aby przepuszczało jak najwięcej światła.

2,37. Znajdź maksymalny zysk, jeśli dochód R i koszty C są określone według wzorów: gdzie X− ilość sprzedanego towaru.

2,38. Zależność wielkości produkcji W z kosztów kapitału DO określona przez funkcję
Znajdź interwał wymiany DO, gdzie zwiększanie kosztów kapitału jest nieefektywne.

2,39. Funkcja kosztu ma postać Dochód ze sprzedaży jednostki produkcji jest równy 200. Znajdź optymalną wartość produkcji dla producenta.

2.40. Zależność wielkości produkcji (w jednostkach pieniężnych) od kosztów kapitału określa funkcja Znajdź przedział wartości, przy którym zwiększanie kosztów kapitału jest nieefektywne.

2.41. Uważa się, że wzrost sprzedaży z kosztów reklamy (w milionach rubli) zależy od stosunku Dochód ze sprzedaży jednostki produkcyjnej wynosi 20 tysięcy rubli. Znajdź poziom kosztów reklamy, przy którym firma uzyska maksymalny zysk.

2.42. Dochód z produkcji produktów przy użyciu jednostek zasobów jest równy Koszt jednostki zasobów wynosi 10 den. jednostki Jaką część surowca należy zakupić, aby zysk był jak największy?

2,43. Funkcja kosztu ma postać Dochód ze sprzedaży jednostki produkcyjnej wynosi 50. Znajdź maksymalną wartość zysku, jaką może uzyskać producent.

2,44. Zależność dochodu monopolu od wielkości produkcji definiuje się jako: Funkcja kosztu w tym przedziale ma postać Znajdź optymalną wartość wyjściową dla monopolu.

2,45. Cenę produktów producenta monopolistycznego ustala się według współczynnika określonego jako . Przy jakiej wartości produkcji produktu dochód ze sprzedaży będzie największy?

2,46. Funkcja kosztu ma następującą postać Na Na . Obecnie poziom produkcji Pod jakim warunkiem parametru P Czy opłaca się firmie ograniczać produkcję, jeśli dochód ze sprzedaży jednostki produkcji wynosi 50?

Hipermarket wiedzy >>Matematyka >>Matematyka klasa 10 >> Zastosowanie pochodnej do badania funkcji monotoniczności i ekstremów

§ 35. Zastosowanie pochodnej do badania funkcji monotoniczności i ekstremów

1. Badanie funkcji monotoniczności

Na ryc. 129 pokazuje wykres pewnej rosnącej funkcji różniczkowalnej y = f(x). Narysujmy styczne do grafika w punktach x= x 1 i x- x 2. Co łączy skonstruowane linie? Łączy je to, że tworzą kąt ostry z osią x, co oznacza, że ​​obie proste mają dodatni współczynnik kątowy. Ale współczynnik kątowy stycznej jest równy wartości pochodnej na odciętej punktu styczności. Zatem w punkcie x = x 3 styczna jest równoległa do osi x, w tym momencie zachodzi równość f "(X 3) = 0. Ogólnie rzecz biorąc, w dowolnym punkcie x z dziedziny definicji rosnącej funkcji różniczkowalnej nierówność

Na ryc. 130 pokazuje wykres pewnego malejącego różniczku Funkcje y = f(x). Narysujmy styczne do wykresu w punktach x= x 1 i x= x 2. Na skonstruowanych liniach prostych? Łączy je to, że tworzą kąt rozwarty z osią x, co oznacza, że ​​obie linie proste mają nachylenie ujemne. Ale współczynnik kątowy stycznej jest równy wartości pochodnej w odciętej punktu styczności. Zatem w punkcie x = x 3 styczna jest równoległa do osi x, w tym momencie zachodzi równość f "(x 3) = 0. Ogólnie rzecz biorąc, w dowolnym punkcie x z dziedziny definicji malejącej funkcji różniczkowalnej , nierówność
Rozważania te pokazują, że istnieje pewien związek pomiędzy naturą monotoniczności funkcji a znakiem jej pochodnej:

jeśli funkcja rośnie na pewnym przedziale i ma na niej pochodną, ​​to pochodna jest nieujemna; jeśli funkcja maleje na pewnym przedziale i ma na niej pochodną, ​​to pochodna jest niedodatnia.
Dla praktyki o wiele ważniejsze jest, aby prawdziwe były także twierdzenia odwrotne, pokazujące, w jaki sposób znak pochodnej można wykorzystać do ustalenia natury monotoniczności funkcji na przedziale. W takim przypadku, aby uniknąć nieporozumień, zajmowane są tylko otwarte przestrzenie, tj. odstępy lub otwarte belki. Faktem jest, że dla funkcji określonej na przedziale [a, b] niezbyt trafne jest stawianie pytania o istnienie i wartość pochodnej w punkcie końcowym (w punkcie x = a lub w punkcie x = b), ponieważ w punkcie x = i przyrost argumentu może być tylko dodatni, a w punkcie x = b - tylko ujemny. Definicja instrumentu pochodnego nie przewiduje takich ograniczeń.

Dowody tych twierdzeń przeprowadza się zwykle w ramach zajęć z matematyki wyższej. Ograniczymy się do „praktycznego” rozumowania przeprowadzonego powyżej i dla większej przekonywalności podamy także fizyczną interpretację sformułowanych twierdzeń.

Niech punkt materialny porusza się po linii prostej, s = s(t) jest zasadą ruchu. Jeśli prędkość jest zawsze dodatnia, to punkt stale oddala się od początku, tj. funkcja s = s(t) rośnie. Jeśli prędkość jest zawsze ujemna, to punkt stale zbliża się do początku, tj. funkcja s = s(t) jest malejąca. Jeśli prędkość ruchu była dodatnia, to w pewnym momencie spadła do zera, a następnie ponownie stała się dodatnia, to poruszające się ciało w określonym momencie wydaje się zwalniać, ale nadal oddala się od wartości początkowej punkt. Zatem w tym przypadku funkcja s = s(t) rośnie. Co to jest prędkość? Jest to pochodna ścieżki po czasie. Oznacza to, że charakter monotoniczności funkcji – w tym przypadku funkcji s = s(t) – zależy od znaku pochodnej (prędkości). To właśnie mówią oba sformułowane twierdzenia.

Przykład 1. Udowodnić, że funkcja jest rosnąca na całej osi liczbowej.
Rozwiązanie. Znajdźmy pochodną danej funkcji:

Oczywiście dla wszystkich x nierówność . Oznacza to, zgodnie z Twierdzeniem 1, że funkcja rośnie na całej osi liczbowej.

Przykład 2. a) Udowodnij, że funkcja y = 5cos x + 3m4x - 10x maleje na całej osi liczbowej;
b) zdecydować równanie 5cos x + sin4x - 10x = x 3 + 5.

Rozwiązanie, a) Znajdź pochodną danej funkcji:

Wynikowe wyrażenie jest zawsze ujemne. W rzeczywistości dla wszystkich wartości x obowiązują następujące nierówności:

Ta nierówność dotyczy wszystkich wartości x. Oznacza to, że zgodnie z Twierdzeniem 2 funkcja maleje na całej osi liczbowej.

b) Rozważmy równanie 5cosx + sin4x - 10x = x 3 + 5. Jak właśnie ustalono, y = 5cosx + sin4x-10x jest funkcją malejącą. Jednocześnie y = x 3 +5 jest funkcją rosnącą. Zachodzi następujące stwierdzenie: jeśli jedna z funkcji y = f(x) lub y = s(x) rośnie, a druga maleje i jeśli równanie f(x) = g(x) ma pierwiastek, to tylko jedna (Ryc. 131 wyraźnie ilustruje to stwierdzenie). Znalezienie pierwiastka danego równania nie jest trudne - jest to liczba x = 0 (przy tej wartości równanie zamienia się w poprawną równość liczbową 5 = 5).
Zatem x = 0 jest jedynym pierwiastkiem danego równania.

Przykład 3. a) Zbadaj monotoniczność funkcji y = 2x 3 + 3x 2 -1; b) skonstruuj wykres tej funkcji.

Rozwiązanie, a) Badanie funkcji pod kątem monotoniczności oznacza sprawdzenie, w jakich przedziałach dziedziny definicji funkcja rośnie, a w jakich maleje. Zgodnie z twierdzeniami 1 i 2 ma to związek ze znakiem pochodnej.

Znajdźmy pochodną tej funkcji: f”(x)=6x 2 +6x i dalej f”(x)=6x(x + 1).

Na ryc. 132 przedstawiono schematycznie znaki pochodnej na przedziałach dziedziny definicji: na półprostej (-oo,-1) pochodna jest dodatnia, na przedziale (-1,0) - ujemna, na półprostej (0,-1) + - dodatnie Oznacza to, że w pierwszym ze wskazanych przedziałów funkcja rośnie, w drugim maleje, w trzecim rośnie.

Zwykle, jeśli funkcja jest ciągła nie tylko na przedziale otwartym, ale także w punktach końcowych, te punkty końcowe są uwzględniane w przedziale monotoniczności funkcji.

Zatem dana funkcja rośnie na półprostej, rośnie na półprostej i maleje na odcinku [-1,0].

b) Wykresy funkcji budowane są „punkt po punkcie”. Aby to zrobić, należy sporządzić tabelę wartości funkcji y = 2x3 +3x 2 -1, w której należy uwzględnić wartości funkcji w punktach końcowych przedziałów monotoniczności x = -1 i x = 0 i kilka innych wartości:

Zaznaczmy te punkty na płaszczyźnie współrzędnych. Weźmy pod uwagę przedziały wzrostu i spadku funkcji znalezione w części a), a także fakt, że w punktach x = -1 i x = 0 pochodna funkcji jest równa zeru, tj. styczna do wykresu funkcji we wskazanych punktach jest równoległa do osi odciętych, ponadto w punkcie (-1; 0) pokrywa się nawet z osią odciętych. Na koniec weźmy pod uwagę, że funkcja jest ciągła, tj. jego wykres jest linią ciągłą. Wykres funkcji określonej w warunku pokazano na ryc. 133.

Kończąc naszą dyskusję na temat badania funkcji monotoniczności, zwróćmy uwagę na jedną okoliczność. Widzieliśmy, że jeśli nierówność f”(x) > 0 jest spełniona na przedziale X, to funkcja y-f(x) rośnie w przedziale X; jeżeli nierówność f”(x) jest spełniona na przedziale X< 0, то функция убывает на этом промежутке. А что будет, если на всем промежутке выполняется тождество (х) =0 ? Видимо, функция не должна ни возрастать, ни убывать. Что же это за функция? Ответ очевиден - это постоянная функция у = С (буква С - первая буква слова соп81ап1а, что означает «постоянная»). Справедлива следующая теорема, формальное доказательство которой мы не приводим, ограничиваясь приведенными выше правдоподобными рассуждениями.

W przyszłości będziemy korzystać z tego twierdzenia, tj. możemy być przekonani o jego przydatności dla matematyki. A teraz podamy (dla ciekawszych) przykład zastosowania Twierdzenia 3 (z kategorii rozrywki matematycznej). Zaprezentujemy nowy sposób udowodnienia dobrze znanej tożsamości sin 2 x + cos 2 x= 1.
Rozważmy funkcję y = f(x), gdzie f(x) = sin 2 x + cos 2 x. Znajdźmy jego pochodną:

Zatem dla wszystkich x zachodzi równość f"(x) = 0, co oznacza f(x) = C. Aby znaleźć wartość C, wystarczy obliczyć wartość funkcji w dowolnym punkcie x, np. x = 0. Mamy: f(0) = sin 2 0+cos2 0=0 + 1 = 1.

Zatem C = 1, tj. sin 2 x + cos 2 x = 1

2. Ekstrema funkcji i ich znajdowanie

Wróćmy do wykresu funkcji y = 2 x 3 + 3x 2 -1 (ryc. 133). Na wykresie znajdują się dwa unikalne punkty, które określają jego strukturę - są to punkty (-1; 0) i (0; -1). W tych punktach:

1) następuje zmiana charakteru monotoniczności funkcji (na lewo od punktu x = -1 funkcja rośnie, na prawo od niej, ale tylko do punktu x = 0 funkcja maleje; na lewo od punktu x = 0 funkcja maleje, na prawo od niego rośnie);

2) styczna do wykresu funkcji jest równoległa do osi x, tj. pochodna funkcji w każdym ze wskazanych punktów jest równa zero;

3) f(-1) – największa wartość funkcji, ale nie w całym zakresie definicji, ale w sensie lokalnym, tj. w porównaniu z wartościami funkcji z pewnego otoczenia punktu x = -1. Podobnie f(0) jest najmniejszą wartością funkcji, ale nie w całej dziedzinie definicji, ale w sensie lokalnym, tj. w porównaniu z wartościami funkcji z jakiegoś sąsiedztwa punktu x = 0.

Teraz spójrz na rys. 134, który pokazuje wykres innej funkcji. Czy nie jest podobny do poprzedniego wykresu? Ma te same dwa unikalne punkty, ale jedna z trzech powyższych cech tych punktów uległa zmianie: teraz styczne do wykresu w tych punktach nie są równoległe do osi x. W punkcie x = -1 styczna w ogóle nie istnieje, natomiast w punkcie x = 0 jest prostopadła do osi x (dokładniej pokrywa się z osią y).

Znasz już dalszy tok rozumowania: jeśli pojawi się nowy model matematyczny lub nowa cecha modelu matematycznego, należy go specjalnie przestudiować, tj. wprowadzić nowy termin, nowe oznaczenia, sformułować nowe właściwości.

Definicja 1. Punkt x = x 0 nazywany jest punktem minimalnym funkcji y = f (x), jeśli punkt ten ma otoczenie, dla którego wszystkie punkty (z wyjątkiem samego punktu x = x 0) spełniają następującą nierówność:
f(x)>f(x0).

Zatem funkcje, których wykresy pokazano na ryc. Liczby 133 i 134 mają punkt minimalny x=0. Dlaczego? Ponieważ ten punkt ma na przykład otoczenie lub (-0,2, 0,2) dla wszystkich
punktów, z których poza punktem x = 0 zachodzi nierówność f(x) > f(O). Dotyczy to obu funkcji.
Wartość funkcji w punkcie minimalnym jest zwykle oznaczana przez . Nie należy mylić tej wartości (najmniejszej, ale w sensie lokalnym) z m.in. z najmniejszą wartością funkcji w całym rozpatrywanym obszarze definicji (w sensie globalnym). Spójrz ponownie na rys. 133 i 134. Widzisz, że ani jedna, ani druga funkcja nie ma wartości minimalnej, ale istnieje.

Definicja 2. Punkt x = x 0 nazywany jest punktem maksymalnym funkcji y = f (x), jeśli punkt ten ma otoczenie, dla którego wszystkie punkty, z wyjątkiem samego punktu x = x 0, spełniają następującą nierówność:
k(x)

Zatem funkcje, których wykresy pokazano na ryc. Liczby 133 i 134 mają punkt maksymalny x = - 1. Dlaczego? Ponieważ w tym momencie
istnieje np. otoczenie, w którym dla wszystkich punktów oprócz x=-1 spełniona jest nierówność f(x)< f(-1). Это верно для обеих функций.
Wartość funkcji w punkcie maksymalnym jest zwykle oznaczana przez . Nie należy mylić tej wartości (największej, ale w sensie lokalnym) z ., tj. z największą wartością funkcji w całym rozpatrywanym obszarze definicji (w sensie globalnym). Spójrz ponownie na rys. 133 i 134. Widzisz, że ani jedna, ani druga funkcja nie ma największej wartości, ale istnieje.

Punkty minimalne i maksymalne funkcji łączy wspólny termin - punkty ekstremalne (od łacińskiego słowa ekstremum - „ekstremalne”).

Jak znaleźć ekstrema funkcji? Odpowiedź na to pytanie możemy znaleźć ponownie analizując modele graficzne przedstawione na ryc. 133 i 134.

Uwaga: dla funkcji, której wykres pokazano na ryc. 133, w obu ekstremach pochodna zanika (styczne są równoległe do osi x). Natomiast dla funkcji, której wykres pokazano na ryc. 134, w obu ekstremach pochodna nie istnieje. Nie jest to przypadkowe, gdyż jak udowodniono w toku analizy matematycznej, prawdziwe jest następujące twierdzenie.

Twierdzenie 4. Jeżeli funkcja y = f(x) ma ekstremum w punkcie x = x 0, to w tym punkcie pochodna funkcji albo wynosi zero, albo nie istnieje.

Dla wygody zgodzimy się nazywać punkty wewnętrzne dziedziny definicji funkcji, w których pochodna funkcji jest równa zeru, stacjonarnymi, a punkty wewnętrzne dziedziny definicji funkcji, w których funkcja jest ciągła, ale pochodna funkcji nie istnieje, krytyczna.

Przykład 4. Skonstruuj wykres funkcji y = 2x 2 -6x + 3.

Rozwiązanie. Wiadomo, że wykres danej funkcji kwadratowej jest parabolą, a gałęzie paraboli są skierowane w górę, ponieważ współczynnik xr jest dodatni. Ale w tym przypadku wierzchołek paraboli jest punktem minimalnym funkcji, styczna do paraboli w jej wierzchołku jest równoległa do osi x, co oznacza, że ​​w wierzchołku paraboli musi być spełniony warunek y”=0 być usatysfakcjonowanym. Mamy: y"=(2x 2 -6x + 3)"=4x -6.

Przyrównując pochodną do zera otrzymujemy: 4x-6=0; x = 1,5.

Podstawiając znalezioną wartość x do równania paraboli, otrzymujemy:

y = 21,52 - 6-1,5 + 3 = -1,5. Zatem wierzchołkiem paraboli jest punkt (1,5; -1,5), a osią paraboli jest linia prosta x = 1,5 (ryc. 135). Jako punkty kontrolne wygodnie jest przyjąć punkt (0; 3) i punkt (3; 3) symetrycznie do niego względem osi paraboli. Na ryc. 136, wykorzystując znalezione trzy punkty, konstruuje się parabolę – wykres danej funkcji kwadratowej.

Pamiętacie, jak w klasach 8-9 rysowaliśmy funkcję kwadratową y = ax 2 + bx + c? Niemal w ten sam sposób wyznaczono jedynie oś paraboli nie za pomocą pochodnej, a za pomocą wzoru, który trzeba było zapamiętać. Rozwiązanie pokazane w przykładzie 4 uwalnia Cię od konieczności zapamiętywania tego wzoru. Aby znaleźć odciętą wierzchołek paraboli y = ax 2 + bx + c lub równanie jej osi symetrii, wystarczy przyrównać pochodną funkcji kwadratowej do zera.

Wróćmy teraz do Twierdzenia 4, które mówi, że jeśli w punkcie x = x 0 funkcja y = f(x) ma ekstremum, to x = x 0 jest punktem stacjonarnym lub krytycznym tej funkcji. Naturalnie pojawia się pytanie: czy prawdziwe jest twierdzenie odwrotne, tj. Czy prawdą jest, że jeśli x = x 0 jest punktem stacjonarnym lub krytycznym, to w tym punkcie funkcja ma ekstremum? Odpowiadamy: nie, błędnie. Spójrz na rys. 137, który pokazuje wykres funkcji rosnącej, która nie ma ekstremów. Funkcja ta ma punkt stacjonarny x = x 1, w którym pochodna znika (w tym miejscu wykres funkcji ma styczną równoległą do osi x), ale nie jest to punkt ekstremum, tylko punkt przegięcia i tam to punkt krytyczny x = x 2, w którym pochodna nie istnieje, ale to też nie jest punkt ekstremalny, tylko punkt załamania na wykresie. Zatem powiedzmy tak: Twierdzenie 4 podaje jedynie warunek konieczny ekstremum (twierdzenie bezpośrednie jest ważne), ale nie jest warunkiem wystarczającym (twierdzenie odwrotne nie jest prawdziwe).

Ale co z warunkiem wystarczającym? Jak sprawdzić, czy istnieje ekstremum w punkcie stacjonarnym lub krytycznym? Aby odpowiedzieć na to pytanie, rozważmy ponownie wykresy funkcji przedstawione na ryc. 133, 134, 136 i 137.
Zauważamy, że przy przejściu przez punkt maksymalny (mówimy o punkcie x = -1 na rys. 133 i 134) zmienia się charakter monotoniczności funkcji: na lewo od punktu maksymalnego funkcja rośnie, do w prawo maleje. Znaki pochodnej zmieniają się odpowiednio: na lewo od maksymalnego punktu pochodna jest dodatnia, na prawo ujemna.
Zauważamy, że przy przejściu przez punkt minimalny (mówimy o punkcie x = 0 na ryc. 133 i 134 oraz punkcie x = 1,5 na ryc. 136) zmienia się także charakter monotoniczności funkcji: na na lewo od punktu minimalnego funkcja maleje, na prawo rośnie. Znaki pochodnej zmieniają się odpowiednio: na lewo od punktu minimalnego pochodna jest ujemna, na prawo jest dodatnia.

Jeżeli zarówno na lewo, jak i na prawo od punktu stacjonarnego lub krytycznego pochodna ma ten sam znak, to w tym punkcie nie ma ekstremum, dokładnie tak jest w przypadku funkcji, której wykres pokazano na ryc. 137.
Nasze rozumowanie może służyć jako potwierdzenie (ale oczywiście nie dowód – w toku analizy matematycznej przeprowadza się rygorystyczne dowody) słuszności poniższego twierdzenia.

Twierdzenie 5 (warunki wystarczające na ekstremum). Niech funkcja y=f(x) będzie ciągła na przedziale X i będzie miała stacjonarny lub krytyczny punkt x = x 0 wewnątrz tego przedziału.

a) jeśli ten punkt ma takie otoczenie, że w punkcie x<х 0 выполняется неравенство f(x) < 0,а при x >x 0 - nierówność f"x)>0, wówczas x =x 0 - minimalny punkt funkcji Y=f(x);

b) jeśli ten punkt ma takie otoczenie, że w nim jest dla x< x 0 выполняется неравенство f"(x) >Aha, i dla x > x 0 - nierówność f(x)< О, то x = x 0 - точка максимума функции У=f(х);

c) jeżeli punkt ten ma takie otoczenie, że zarówno na lewo, jak i na prawo od punktu x 0 znaki pochodnej są takie same, to w punkcie x = x 0 nie ma ekstremum.

Przykład 5. a) Znajdź ekstrema funkcji
y = 3x 4 -16x 3 + 24x2 -11; b) skonstruuj wykres tej funkcji.

Rozwiązanie, a) Znajdź pochodną tej funkcji:

Pochodna zanika w punktach x = O i x = 2 - są to dwa stacjonarne punkty danej funkcji. Na ryc. 138 pokazuje schematycznie znaki pochodnej na przedziałach z dziedziny definicji: na przedziale pochodna jest ujemna, na przedziale (0, 2) jest dodatnia, na przedziale jest dodatnia.
Oznacza to, że x = 0 jest punktem minimalnym funkcji, a x = 2 nie jest punktem ekstremalnym. W pierwszym z powyższych przedziałów funkcja maleje, w drugim i trzecim rośnie.

W punkcie minimalnym x = 0 mamy f(0) = -11 (podstawiając wartość x = 0 do analitycznego określenia funkcji), co oznacza = -11.

b) Aby skonstruować wykres funkcji, należy znać szczególnie ważne punkty wykresu. Obejmują one:
- znaleziony punkt minimalny (0; -11);

Punkt stacjonarny x = 2; w tym momencie

Punkty przecięcia z osiami współrzędnych; w tym przykładzie jest to już znaleziony punkt (0; -11) - punkt przecięcia wykresu z osią y. I jeszcze jedno: można się domyślić, że f(1)=0, co oznacza, że ​​znaleziono punkt przecięcia wykresu z osią x - jest to punkt (1; 0).

Mamy więc punkt minimalny (0; -11), punkt przecięcia wykresu z osią x - punkt (1; 0) i punkt stacjonarny (2; 5). W tym momencie styczna do wykresu funkcji jest pozioma, ale nie jest to punkt ekstremalny, ale punkt przegięcia.

Wykres funkcji pokazano schematycznie na ryc. 139. Zauważ, że istnieje jeszcze jeden punkt przecięcia wykresu z osią x, ale nie udało nam się go znaleźć.

Podsumowując ten punkt, zauważamy, że faktycznie się rozwinęliśmy

Algorytm badania funkcji ciągłej ”y = f(x)”o monotoniczności i ekstremach

1. Znajdź pochodną f”(x).
2. Znajdź punkty stacjonarne i krytyczne.
3. Zaznacz na osi liczbowej punkty stacjonarne i krytyczne oraz wyznacz znaki pochodnej na otrzymanych przedziałach.
4. Na podstawie twierdzeń z § 35 wyciągnąć wnioski dotyczące monotoniczności funkcji i jej ekstremów.
Należy pamiętać, że jeśli dana funkcja ma postać, to bieguny funkcji, tj. na osi liczbowej zaznacza się także punkty, w których mianownik q(x) staje się zerem, i robi się to przed wyznaczeniem znaku pochodnej. Ale oczywiście bieguny nie mogą być punktami ekstremalnymi.
Przykład 6. Zbadaj funkcję pod kątem monotoniczności i ekstremów.
Rozwiązanie. Zauważ, że funkcja jest ciągła wszędzie z wyjątkiem punktu x = 0. Skorzystajmy z powyższego algorytmu.
1) Znajdź pochodną danej funkcji:

2) Pochodna zanika w punktach x = 2 i x = -2 - są to punkty stacjonarne. W punkcie x = 0 pochodna nie istnieje, ale nie jest to punkt krytyczny, tylko punkt nieciągłości funkcji (biegun).

3) Zaznacz na osi liczbowej punkty -2, 0 i 2, a na powstałych przedziałach umieść znaki pochodnej (ryc. 140).

4) Wyciągamy wnioski: na półprzedziale (-°°, -2] funkcja maleje, na półprzedziale [-2, 0] funkcja rośnie, na półprzedziale (0, 2] funkcja maleje, na promieniu funkcja rośnie, na przedziale (ryc. 128 ).

1. Rozważmy funkcję na przedziale (0, + 00).
Niech x1< х 2 . Так как х 1 и х 2 - , то из х 1 < x 2 следует (см. пример 1 из § 33), т. е. f(x 1) >f(x 2).

Zatem z nierówności x 1< х 2 следует, что f(x 1) >f(x 2). Oznacza to, że funkcja maleje na półprostej (0, + 00) (ryc. 129).

2. Rozważmy funkcję na przedziale (-oo, 0). Niech x 1< х 2 , х 1 и х 2 - отрицательные числа. Тогда - х 1 >- x 2, a obie strony ostatniej nierówności są liczbami dodatnimi i dlatego (ponownie skorzystaliśmy z nierówności udowodnionej w przykładzie 1 z § 33). Następnie mamy, skąd pochodzimy.

Zatem z nierówności x 1< х 2 следует, что f(x 1) >f(x 2) tj. funkcja maleje na promieniu otwartym (- 00 , 0)

Zwykle terminy „funkcja rosnąca” i „funkcja malejąca” są łączone pod ogólną nazwą funkcja monotoniczna, a badanie funkcji zwiększania i zmniejszania nazywa się badaniem funkcji monotoniczności.

Rozwiązanie.

1) Narysujmy funkcję y = 2x2 i weźmy gałąź tej paraboli w punkcie x< 0 (рис. 130).

2) Zbuduj i wybierz jego część na segmencie (ryc. 131).

3) Skonstruujmy hiperbolę i wybierzmy jej część na półprostej otwartej (4, + 00) (ryc. 132).
4) Przedstawmy wszystkie trzy „części” w jednym układzie współrzędnych – jest to wykres funkcji y = f(x) (ryc. 133).

Przeczytajmy wykres funkcji y = f(x).

1. Dziedziną definicji funkcji jest cała oś liczbowa.

2. y = 0 przy x = 0; y > 0 dla x > 0.

3. Funkcja maleje na półprostej (-oo, 0], rośnie na odcinku, maleje na półprostej, jest wypukła w górę na odcinku, wypukła w dół na półprostej, po czym funkcja maleje. Ale na przedziale liczbowym (ryc. 128).

3. Funkcja y

1. Rozważmy funkcję na przedziale (0, + 00).
Niech x1< х 2 . Так как х 1 и х 2 — положительные числа, то из х 1 < x 2 следует (см. пример 1 из § 33), т. е. f(x 1) >f(x 2).
Zatem z nierówności x 1< х 2 следует, что f(x 1) >f(x 2). Oznacza to, że funkcja maleje na półprostej (0, + 00) (ryc. 129).

2. Rozważmy funkcję na przedziale (-oo, 0). Niech x 1< х 2 , х 1 и х 2 — отрицательные числа. Тогда - х 1 >- x 2, a obie części tego ostatniego są nierówne
właściwości są liczbami dodatnimi i dlatego (ponownie wykorzystaliśmy nierówność udowodnioną w przykładzie 1 z § 33). Następnie mamy, skąd pochodzimy.
Zatem z nierówności x 1< х 2 следует, что f(x 1) >f(x 2) tj. funkcja maleje na promieniu otwartym (- 00 , 0)
Zwykle terminy „funkcja rosnąca” i „funkcja malejąca” są łączone pod ogólną nazwą funkcja monotoniczna, a badanie funkcji zwiększania i zmniejszania nazywa się badaniem funkcji monotoniczności.

Rozwiązanie.

1) Narysujmy funkcję y = 2x2 i weźmy gałąź tej paraboli w punkcie x< 0 (рис. 130).

2) Zbudujmy wykres funkcji i zaznaczmy jej część na odcinku (ryc. 131).

3) Skonstruujmy hiperbolę i wybierzmy jej część na półprostej otwartej (4, + 00) (ryc. 132).
4) Przedstawmy wszystkie trzy „części” w jednym układzie współrzędnych – jest to wykres funkcji y = f(x) (ryc. 133).
Przeczytajmy wykres funkcji y = f(x).
1. Dziedziną definicji funkcji jest cała oś liczbowa.

2. y = 0 przy x = 0; y > 0 dla x > 0.

3. Funkcja maleje na półprostej (-oo, 0], rośnie na odcinku, maleje na półprostej, jest wypukła w górę na odcinku, wypukła w dół na półprostej)