Równania prostej w przestrzeni. Linia prosta

KĄT MIĘDZY PŁASZCZYZNAMI

Rozważmy dwie płaszczyzny α 1 i α 2, określone odpowiednio równaniami:

Pod kąt między dwiema płaszczyznami zrozumiemy jeden z kątów dwuściennych utworzonych przez te płaszczyzny. Oczywiste jest, że kąt między wektorami normalnymi a płaszczyznami α 1 i α 2 jest równy jednemu ze wskazanych sąsiednich kątów dwuściennych lub . Dlatego . Ponieważ I , To

Przykład. Określ kąt między płaszczyznami X+2y-3z+4=0 i 2 X+3y+z+8=0.

Warunek równoległości dwóch płaszczyzn.

Dwie płaszczyzny α 1 i α 2 są równoległe wtedy i tylko wtedy, gdy ich wektory normalne są równoległe, a zatem .

Zatem dwie płaszczyzny są do siebie równoległe wtedy i tylko wtedy, gdy współczynniki odpowiednich współrzędnych są proporcjonalne:

Lub

Warunek prostopadłości płaszczyzn.

Jest oczywiste, że dwie płaszczyzny są prostopadłe wtedy i tylko wtedy, gdy ich wektory normalne są prostopadłe, a zatem, lub .

Zatem, .

Przykłady.

PROSTO W PRZESTRZENI.

RÓWNANIE WEKTOROWE DLA LINII.

PARAMETRYCZNE RÓWNANIA BEZPOŚREDNIE

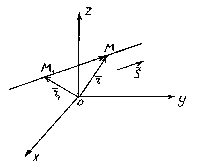
Położenie linii w przestrzeni jest całkowicie określane poprzez określenie dowolnego z jej punktów stałych M 1 i wektor równoległy do tej prostej.

Nazywa się wektor równoległy do prostej przewodniki wektor tej linii.

Więc niech linia prosta l przechodzi przez punkt M 1 (X 1 , y 1 , z 1), leżącego na prostej równoległej do wektora .

Rozważ dowolny punkt M(x,y,z) na linii prostej. Z rysunku wynika, że .

Wektory i są współliniowe, więc istnieje taka liczba T, co , gdzie jest mnożnik T może przyjmować dowolną wartość liczbową w zależności od położenia punktu M na linii prostej. Czynnik T zwany parametrem. Po wyznaczeniu wektorów promieni punktów M 1 i M odpowiednio poprzez i , otrzymujemy . To równanie nazywa się wektor równanie prostej. Pokazuje to dla każdej wartości parametru T odpowiada wektorowi promienia pewnego punktu M, leżąc na linii prostej.

Zapiszmy to równanie w postaci współrzędnych. Zauważ, że , i stąd

Powstałe równania nazywane są parametryczny równania prostej.

Podczas zmiany parametru T współrzędne się zmieniają X, y I z i okres M porusza się po linii prostej.

RÓWNANIA KANONICZNE BEZPOŚREDNIEJ

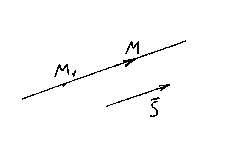
Pozwalać M 1 (X 1 , y 1 , z 1) – punkt leżący na prostej l, I jest jego wektorem kierunkowym. Weźmy jeszcze raz dowolny punkt na prostej M(x,y,z) i rozważ wektor .

Oczywiste jest, że wektory są również współliniowe, więc odpowiadające im współrzędne muszą być proporcjonalne, dlatego

– kanoniczny równania prostej.

Notatka 1. Należy zauważyć, że równania kanoniczne linii można uzyskać z równań parametrycznych poprzez wyeliminowanie parametru T. Rzeczywiście, z równań parametrycznych otrzymujemy Lub .

Przykład. Zapisz równanie prostej w formie parametrycznej.

Oznaczmy , stąd X = 2 + 3T, y = –1 + 2T, z = 1 –T.

Uwaga 2. Niech linia będzie prostopadła do jednej z osi współrzędnych, na przykład osi Wół. Wtedy wektor kierunkowy linii jest prostopadły Wół, stąd, M=0. W konsekwencji równania parametryczne linii prostej przyjmują postać

Eliminacja parametru z równań T, otrzymujemy równania prostej w postaci

Jednak i w tym przypadku zgadzamy się formalnie zapisać równania kanoniczne prostej w postaci . Zatem jeśli mianownik jednego z ułamków wynosi zero, oznacza to, że linia prosta jest prostopadła do odpowiedniej osi współrzędnych.

Podobnie równania kanoniczne odpowiada linii prostej prostopadłej do osi Wół I Oj lub równolegle do osi Oz.

Przykłady.

RÓWNANIA OGÓLNE LINIA PROSTA JAKO LINIA PRZECIĘCIA DWÓCH PŁASZCZYZN

Przez każdą linię prostą w przestrzeni przechodzi niezliczona ilość płaszczyzn. Dowolne dwa z nich, przecinające się, definiują to w przestrzeni. W konsekwencji równania dowolnych dwóch takich płaszczyzn, rozpatrywane łącznie, reprezentują równania tej prostej.

Ogólnie rzecz biorąc, dowolne dwie nierównoległe płaszczyzny określone przez równania ogólne

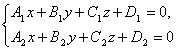
określić linię ich przecięcia. Równania te nazywane są równania ogólne prosty.

Przykłady.

Konstruuj prostą daną za pomocą równań

Aby zbudować prostą, wystarczy znaleźć dowolne dwa jej punkty. Najłatwiej jest wybrać punkty przecięcia prostej z płaszczyznami współrzędnych. Na przykład punkt przecięcia z płaszczyzną xOj otrzymujemy z równań prostej, zakładając z= 0:

Po rozwiązaniu tego systemu znajdujemy sedno M 1 (1;2;0).

Podobnie, zakładając y= 0, otrzymujemy punkt przecięcia prostej z płaszczyzną xOz:

Z ogólnych równań prostej można przejść do jej równań kanonicznych lub parametrycznych. Aby to zrobić, musisz znaleźć jakiś punkt M 1 na linii prostej i wektor kierunkowy linii prostej.

Współrzędne punktu M 1 otrzymujemy z tego układu równań, nadając jednej ze współrzędnych dowolną wartość. Aby znaleźć wektor kierunkowy, należy pamiętać, że wektor ten musi być prostopadły do obu wektorów normalnych I . Dlatego poza wektorem kierunkowym linii prostej l możesz wziąć iloczyn wektorowy normalnych wektorów:

Przykład. Podaj ogólne równania prostej do postaci kanonicznej.

Znajdźmy punkt leżący na prostej. W tym celu wybieramy dowolnie jedną ze współrzędnych, np. y= 0 i rozwiązujemy układ równań:

Wektory normalne płaszczyzn wyznaczających linię mają współrzędne Dlatego wektor kierunku będzie prosty

. Stąd, l: .

KĄT MIĘDZY PROSTYMI

Kąt pomiędzy liniami prostymi w przestrzeni nazwiemy dowolny z sąsiednich kątów utworzonych przez dwie linie proste poprowadzone przez dowolny punkt równoległy do danych.

Niech w przestrzeni zostaną dane dwie proste:

Oczywiście kąt φ między prostymi można przyjąć jako kąt między ich wektorami kierunkowymi i . Ponieważ , to korzystając ze wzoru na cosinus kąta między wektorami otrzymujemy

Spójrzmy na przykładowe rozwiązanie.

Przykład.

Znajdź współrzędne dowolnego punktu na linii określonej w przestrzeni równaniami dwóch przecinających się płaszczyzn .

Rozwiązanie.

Zapiszmy układ równań w następującej postaci

Jako moll bazowy macierzy głównej układu przyjmujemy niezerową mollę drugiego rzędu , to znaczy z jest wolną nieznaną zmienną. Przesuńmy wyrazy zawierające z na prawą stronę równań: .

Przyjmijmy , gdzie jest dowolną liczbą rzeczywistą, a następnie .

Rozwiążmy powstały układ równań:

Zatem ogólne rozwiązanie układu równań ma postać , gdzie .

Jeżeli przyjmiemy konkretną wartość parametru, to otrzymamy konkretne rozwiązanie układu równań, który daje nam pożądane współrzędne punktu leżącego na danej prostej. Weźmy to w takim razie , zatem jest pożądanym punktem linii.

Znalezione współrzędne punktu można sprawdzić podstawiając je do oryginalnych równań dwóch przecinających się płaszczyzn:

Odpowiedź:

Wektor kierunkowy linii, wzdłuż której przecinają się dwie płaszczyzny.

W prostokątnym układzie współrzędnych wektor kierunkowy linii prostej jest nierozerwalnie związany z linią prostą. Gdy prostą a w prostokątnym układzie współrzędnych w przestrzeni trójwymiarowej wyznaczają równania dwóch przecinających się płaszczyzn i , to współrzędne wektora kierującego prostej nie są widoczne. Teraz pokażemy, jak je określić.

Wiemy, że prosta jest prostopadła do płaszczyzny, gdy jest prostopadła do dowolnej prostej leżącej w tej płaszczyźnie. Wtedy wektor normalny płaszczyzny jest prostopadły do dowolnego niezerowego wektora leżącego w tej płaszczyźnie. Wykorzystamy te fakty do znalezienia wektora kierunku linii.

Linia prosta a leży zarówno w płaszczyźnie, jak i w płaszczyźnie. Dlatego wektor kierunkowy linii prostej a jest również prostopadły do wektora normalnego płaszczyzna i wektor normalny samolot Zatem wektor kierunkowy linii prostej a wynosi I :

Zbiór wszystkich wektorów kierunkowych linii prostej i możemy go zdefiniować jako , gdzie jest parametrem, który może przyjmować dowolne wartości rzeczywiste inne niż zero.

Przykład.

Znajdź współrzędne dowolnego wektora kierunkowego prostej, który jest określony w prostokątnym układzie współrzędnych Oxyz w przestrzeni trójwymiarowej za pomocą równań dwóch przecinających się płaszczyzn .

Rozwiązanie.

Wektorami normalnymi płaszczyzn są wektory I odpowiednio. Wektor kierujący linii prostej, będący przecięciem dwóch danych płaszczyzn, jest iloczynem wektorowym wektorów normalnych:

Odpowiedź:

Przejście do równań parametrycznych i kanonicznych prostej w przestrzeni.

Zdarzają się przypadki, w których użycie równań dwóch przecinających się płaszczyzn do opisu linii prostej nie jest do końca wygodne. Niektóre problemy są łatwiejsze do rozwiązania, jeśli znane są równania kanoniczne linii prostej w przestrzeni: lub równania parametryczne linii w przestrzeni postaci , gdzie x 1 , y 1 , z 1 to współrzędne pewnego punktu na linii, a x , a y , a z to współrzędne wektora kierującego linii i jest parametrem przyjmującym dowolne wartości rzeczywiste. Opiszmy proces przejścia od równań liniowych postaci do równań kanonicznych i parametrycznych linii prostej w przestrzeni.

W poprzednich akapitach nauczyliśmy się znajdować współrzędne określonego punktu na linii, a także współrzędne pewnego wektora kierunku linii, które są określone przez równania dwóch przecinających się płaszczyzn. Dane te wystarczą do zapisania równań kanonicznych i parametrycznych tej prostej w prostokątnym układzie współrzędnych w przestrzeni.

Rozważmy rozwiązanie przykładu, a następnie pokażemy inny sposób znalezienia równań kanonicznych i parametrycznych linii w przestrzeni.

Przykład.

Rozwiązanie.

Najpierw obliczmy współrzędne wektora kierującego linii prostej. Aby to zrobić, znajdujemy iloczyn wektorowy wektorów normalnych I samoloty I :

To jest, .

Teraz określmy współrzędne pewnego punktu na danej linii. Aby to zrobić, znajdziemy jedno z rozwiązań układu równań .

Wyznacznik jest różne od zera, przyjmijmy to jako moll bazowy macierzy głównej układu. Wtedy zmienna z jest dowolna, przenosimy z nią wyrazy na prawą stronę równań i nadajemy zmiennej z dowolną wartość:

Powstały układ równań rozwiązujemy metodą Cramera:

Stąd,

Akceptujemy i otrzymujemy współrzędne punktu na prostej: .

Teraz możemy zapisać wymagane równania kanoniczne i parametryczne pierwotnej linii w przestrzeni:

Odpowiedź:

Oto drugi sposób rozwiązania tego problemu.

Znajdując współrzędne określonego punktu na linii, rozwiązujemy układ równań . Generalnie rozwiązania można zapisać w postaci .

I to są dokładnie wymagane równania parametryczne linii prostej w przestrzeni. Jeśli każde z otrzymanych równań zostanie rozwiązane względem parametru, a następnie zrównane zostaną prawe strony równości, wówczas otrzymamy równania kanoniczne prostej w przestrzeni

Pokażmy rozwiązanie poprzedniego problemu za pomocą tej metody.

Przykład.

Linię prostą w przestrzeni trójwymiarowej definiują równania dwóch przecinających się płaszczyzn . Zapisz równania kanoniczne i parametryczne tej prostej.

Rozwiązanie.

Rozwiązujemy ten układ dwóch równań z trzema niewiadomymi (rozwiązanie podano w poprzednim przykładzie, nie będziemy go powtarzać). W tym przypadku otrzymujemy . Są to pożądane równania parametryczne linii prostej w przestrzeni.

Pozostaje otrzymać równania kanoniczne linii prostej w przestrzeni:

Powstałe równania linii prostych różnią się zewnętrznie od równań otrzymanych w poprzednim przykładzie, ale są równoważne, ponieważ definiują ten sam zbiór punktów w przestrzeni trójwymiarowej (a zatem tę samą linię prostą).

Odpowiedź:

Bibliografia.

Bugrov Ya.S., Nikolsky S.M. Wyższa matematyka. Tom pierwszy: Elementy algebry liniowej i geometrii analitycznej.
Ilyin V.A., Poznyak E.G. Geometria analityczna.

W prostokątnym układzie współrzędnych na płaszczyźnie linię prostą można wyznaczyć za pomocą równania kanonicznego linii prostej. W tym artykule najpierw wyprowadzimy, zapiszemy równania kanoniczne prostych na płaszczyźnie, które są równoległe do osi współrzędnych lub pokrywają się z nimi, a także podamy przykłady. Następnie pokażemy związek pomiędzy równaniem kanonicznym prostej na płaszczyźnie a innymi typami równań tej prostej. Podsumowując, szczegółowo rozważymy rozwiązania typowych przykładów i problemów tworzenia równania kanonicznego linii na płaszczyźnie.

Nawigacja strony.

Równanie kanoniczne prostej na płaszczyźnie - opis i przykłady.

Niech Oxy zostanie naprawiony w samolocie. Postawmy sobie zadanie: otrzymać równanie prostej a, jeśli jest to jakiś punkt prostej a i jest wektorem kierunku prostej a.

Niech będzie zmiennoprzecinkowym linii a . Wtedy wektor jest wektorem kierunku linii a i ma współrzędne (w razie potrzeby zobacz artykuł). Oczywiście zbiór wszystkich punktów na płaszczyźnie definiuje prostą przechodzącą przez punkt i mającą wektor kierunkowy wtedy i tylko wtedy, gdy wektory i są współliniowe.

Przykład.

Napisz równanie kanoniczne prostej, która w prostokątnym układzie współrzędnych Oxy na płaszczyźnie przechodzi przez dwa punkty i .

Rozwiązanie.

Korzystając ze znanych współrzędnych punktu początkowego i końcowego, możemy znaleźć współrzędne wektora: . Ten wektor jest wektorem kierunku prostej, której równania szukamy. Równanie kanoniczne linii przechodzącej przez punkt i mającej wektor kierunkowy.

Rozwiązanie.

Normalny wektor liniowy ma współrzędne , a ten wektor jest wektorem kierunku linii, której równania szukamy ze względu na prostopadłość linii. Zatem pożądane równanie kanoniczne linii na płaszczyźnie zostanie zapisane jako .

Odpowiedź:

Bibliografia.

Bugrov Ya.S., Nikolsky S.M. Wyższa matematyka. Tom pierwszy: Elementy algebry liniowej i geometrii analitycznej.
Ilyin V.A., Poznyak E.G. Geometria analityczna.

Pozwalać l- jakaś prosta linia przestrzeni. Podobnie jak w planimetrii, dowolny wektor

A =/= 0, linia współliniowa l, zwany wektor przewodnik tę linię prostą.

Położenie linii w przestrzeni jest całkowicie określone poprzez określenie wektora kierunku i punktu należącego do linii.

Niech będzie prosto l z wektorem prowadzącym A przechodzi przez punkt M 0, a M jest dowolnym punktem w przestrzeni. Oczywiście punkt M (ryc. 197) należy do prostej l wtedy i tylko wtedy, gdy wektor $\overrightarrow(M_0 M)$ jest współliniowy z wektorem A , tj.

$\overrightarrow(M_0 M)$ = T A , T$\W$ R. (1)

Jeżeli punkty M i M 0 są określone przez ich wektory promieni R I R 0 (ryc. 198) względem pewnego punktu O w przestrzeni, wówczas $\overrightarrow(M_0 M)$ = R - R 0 , a równanie (1) przyjmuje postać

R = R 0 + T A , T$\W$ R. (2)

Równania (1) i (2) są wywoływane równania wektorowo-parametryczne linii prostej. Zmienny T w równaniach wektorowo-parametrycznych linia prosta nazywana jest parametr.

Niech punkt M 0 będzie linią prostą l i wektor kierunkowy a są określone przez ich współrzędne:

M 0 ( X 0 ; Na 0 , z 0), A = (A 1 ; A 2 ; A 3).

A następnie, jeśli ( X; y; z) - współrzędne dowolnego punktu M linii prostej l, To

$\overrightarrow(M_0 M) $ = ( x - x 0 ; y - y 0 ; z - z 0)

a równanie wektora (1) jest równoważne trzem następującym równaniom:

x - x 0 = ta 1 , y - y 0 = ta 2 , z - z 0 = ta 3

$$ \begin(przypadki) x = x_0 + ta_1 \\ y = y_0 + ta_2 \\ z = z_0 + ta_3, \;\;t\in R\end(przypadki) (3)$$

Równania (3) są wywoływane równania parametryczne prostej w kosmosie.

Zadanie 1. Napisz równania parametryczne prostej przechodzącej przez punkt

M 0 (-3; 2; 4) i posiadający wektor kierunkowy A = (2; -5; 3).

W tym przypadku X 0 = -3, Na 0 = 2, z 0 = 4; A 1 = 2; A 2 = -5; A 3 = 3. Podstawiając te wartości do wzorów (3), otrzymujemy równania parametryczne tej prostej

$$ \begin(przypadki) x = -3 - 2t \\ y = 2 - 5t \\ z = 4 + 3t, \;\;t\in R\end(przypadki) $$

Wykluczmy parametr T z równań (3). Można to zrobić, ponieważ A =/= 0, a zatem jedna ze współrzędnych wektora A jest oczywiście różne od zera.

Niech najpierw wszystkie współrzędne będą różne od zera. Następnie

$$ t=\frac(x-x_0)(a_1),\;\;t=\frac(y-y_0)(a_2),\;\;t=\frac(z-z_0)(a_3) $$

i dlatego

$$ \frac(x-x_0)(a_1)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3) \;\; (4)$$

Równania te nazywane są równania kanoniczne prostej .

Należy zauważyć, że równania (4) tworzą układ dwóch równań z trzema zmiennymi x, y I z.

Jeżeli w równaniach (3) mamy jedną ze współrzędnych wektora A , Na przykład A 1 jest równe zero, a następnie poprzez wyeliminowanie parametru T, ponownie otrzymujemy układ dwóch równań z trzema zmiennymi x, y I z:

$x=x_0, \;\; \frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)$

Równania te nazywane są także równaniami linii kanonicznych. Dla jednolitości są one również umownie zapisywane w postaci (4)

$\frac(x-x_0)(0)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)$

zakładając, że jeśli mianownik wynosi zero, to odpowiadający mu licznik również wynosi zero. Równania te są równaniami linii przechodzącej przez punkt M 0 ( X 0 ; Na 0 , z 0) równolegle do płaszczyzny współrzędnych yOz, ponieważ jego wektor kierunkowy (0; A 2 ; A 3).

Wreszcie, jeśli w równaniach (3) występują dwie współrzędne wektorowe A , Na przykład A 1 i A 2 są równe zeru, wówczas równania te przyjmują postać

X = X 0 , y = Na 0 , z = z 0 + T A 3 , T$\W$ R.

Są to równania linii przechodzącej przez punkt M 0 ( X 0 ; Na 0 ; z 0) równolegle do osi Oz. Dla takiej linii prostej X = X 0 , y = Na 0, o z- Jakikolwiek numer. I w tym przypadku dla jednolitości równanie prostej można zapisać (z tym samym zastrzeżeniem) w postaci (4)

$\frac(x-x_0)(0)=\frac(y-y_0)(0)=\frac(z-z_0)(a_3)$

Zatem dla dowolnej prostej w przestrzeni można zapisać równania kanoniczne (4) i odwrotnie dowolne równanie postaci (4) pod warunkiem, że co najmniej jeden ze współczynników A 1 , A 2 , A 3 nie jest równe zero, definiuje jakąś linię prostą w przestrzeni.

Zadanie 2. Napisz równania kanoniczne linii przechodzącej przez punkt M 0 (- 1; 1, 7) równolegle do wektora A = (1; 2; 3).

Równania (4) w tym przypadku zapisuje się następująco:

$\frac(x+1)(1)=\frac(y-1)(2)=\frac(z-7)(3)$

Wyprowadźmy równania linii prostej przechodzącej przez dwa dane punkty M 1 ( X 1 ; Na 1 ; z 1) i

M2( X 2 ; Na 2 ; z 2). Oczywiście możemy wziąć wektor A = (X 2 - X 1 ; Na 2 - Na 1 ; z 2 - z 1), a poza punktem M 0, przez który przechodzi linia prosta, na przykład punkt M 1. Następnie równania (4) zostaną zapisane w następujący sposób:

$\frac(x-x_1)(x_2 - x_1)=\frac(y-y_1)(y_2 - y_1)=\frac(z-z_1)(z_2 - z_1)$ (5)

Są to równania linii przechodzącej przez dwa punkty M 1 ( X 1 ; Na 1 ; z 1) i

M2( X 2 ; Na 2 ;z 2).

Zadanie 3. Napisz równania linii prostej przechodzącej przez punkty M 1 (-4; 1; -3) i M 2 (-5; 0; 3).

W tym przypadku X 1 = -4, Na 1 = 1, z 1 = -3, X 2 = -5, Na 2 = 0, z 2 = 3. Podstawiając te wartości do wzorów (5), otrzymujemy

$\frac(x+4)(-1)=\frac(y-1)(-1)=\frac(z+3)(6)$

Zadanie 4. Zapisz równania linii przechodzącej przez punkty M 1 (3; -2; 1) i

M 2 (5; -2; 1/2).

Po podstawieniu współrzędnych punktów M 1 i M 2 do równań (5) otrzymujemy

$\frac(x-3)(2)=\frac(y+2)(0)=\frac(z-1)(-\frac(1)(2))$

Niech Oxyz zostanie unieruchomiony w przestrzeni trójwymiarowej. Zdefiniujmy w nim linię prostą. Wybierzmy następujący sposób określenia prostej w przestrzeni: określ punkt, przez który przechodzi prosta a oraz wektor kierunkowy prostej a. Zakładamy, że punkt leży na prostej a i - wektor kierujący linii prostej a.

Oczywiście zbiór punktów w przestrzeni trójwymiarowej wyznacza linię prostą wtedy i tylko wtedy, gdy wektory i są współliniowe.

Proszę zwrócić uwagę na następujące ważne fakty:

Podajmy kilka przykładów równań kanonicznych linii prostej w przestrzeni:

Tworzenie równań kanonicznych prostej w przestrzeni.

Zatem równania kanoniczne linii prostej w ustalonym prostokątnym układzie współrzędnych Oxyz w trójwymiarowej przestrzeni postaci odpowiadają linii prostej przechodzącej przez punkt , a wektor kierunkowy tej linii prostej jest wektorem . Zatem jeśli znamy postać równań kanonicznych prostej w przestrzeni, to możemy od razu zapisać współrzędne wektora kierującego tej prostej, a jeśli współrzędne wektora kierującego prostej i współrzędne jakiegoś punktu tej prostej, to możemy od razu zapisać jej równania kanoniczne.

Pokażemy rozwiązania takich problemów.

Przykład.

Linię prostą w prostokątnym układzie współrzędnych Oxyz w przestrzeni trójwymiarowej wyznaczają równania kanoniczne prostej postaci . Zapisz współrzędne wszystkich wektorów kierunkowych tej prostej.

Rozwiązanie.

Liczby w mianownikach równań kanonicznych prostej są odpowiadającymi współrzędnymi wektora kierującego tej prostej, to znaczy: - jeden z wektorów kierunkowych pierwotnej linii prostej. Następnie zbiór wszystkich wektorów kierunkowych prostej można określić jako , gdzie jest parametrem, który może przyjmować dowolną wartość rzeczywistą z wyjątkiem zera.

Odpowiedź:

Przykład.

Napisz równania kanoniczne prostej, która w prostokątnym układzie współrzędnych Oxyz w przestrzeni przechodzi przez ten punkt , a wektor kierunkowy linii prostej ma współrzędne .

Rozwiązanie.

Z stanu jaki mamy. Oznacza to, że mamy wszystkie dane, aby zapisać wymagane równania kanoniczne linii prostej w przestrzeni. W naszym przypadku

.

Odpowiedź:

Rozważaliśmy najprostszy problem złożenia równań kanonicznych prostej w zadanym prostokątnym układzie współrzędnych w przestrzeni trójwymiarowej, gdy znane są współrzędne wektora kierującego linii i współrzędne jakiegoś punktu na linii. Jednak znacznie częściej pojawiają się problemy, w których najpierw trzeba znaleźć współrzędne wektora kierującego linii, a dopiero potem zapisać równania kanoniczne linii. Jako przykład można przytoczyć problem znalezienia równań prostej przechodzącej przez dany punkt przestrzeni równoległej do danej prostej oraz problem znalezienia równań prostej przechodzącej przez dany punkt przestrzeni prostopadłej do danej płaszczyzny .

Szczególne przypadki równań kanonicznych prostej w przestrzeni.

Zauważyliśmy już, że jedna lub dwie liczby w równaniach kanonicznych linii w przestrzeni mają postać może być równe zeru. Następnie napisz jest uważane za formalne (ponieważ mianowniki jednego lub dwóch ułamków będą miały zera) i należy je rozumieć jako , Gdzie .

Przyjrzyjmy się bliżej wszystkim tym szczególnym przypadkom równań kanonicznych linii w przestrzeni.

Pozwalać , Lub , Lub , to równania kanoniczne prostych mają postać

Lub

Lub

W takich przypadkach w prostokątnym układzie współrzędnych Oxyz w przestrzeni proste leżą odpowiednio w płaszczyznach , lub , które są równoległe do płaszczyzn współrzędnych odpowiednio Oyz , Oxz lub Oxy (lub pokrywają się z tymi płaszczyznami współrzędnych w , lub ) . Na rysunku pokazano przykłady takich linii.

Na , Lub , Lub równania kanoniczne prostych zostaną zapisane jako

Lub

Lub

odpowiednio.

W takich przypadkach linie są równoległe odpowiednio do osi współrzędnych Oz, Oy lub Ox (lub pokrywają się z tymi osiami w punkcie lub). Rzeczywiście, wektory kierunkowe rozważanych linii mają współrzędne , lub , lub , oczywiste jest, że są one współliniowe z wektorami , lub , lub , odpowiednio, gdzie są wektory kierunkowe linii współrzędnych. Przyjrzyj się ilustracjom tych szczególnych przypadków równań kanonicznych prostej w przestrzeni.

Aby skonsolidować materiał w tym akapicie, pozostaje rozważyć rozwiązania przykładów.

Przykład.

Zapisz równania kanoniczne linii współrzędnych Ox, Oy i Oz.

Rozwiązanie.

Wektory kierunkowe linii współrzędnych Ox, Oy i Oz są wektorami współrzędnych i odpowiednio. Ponadto linie współrzędnych przechodzą przez początek współrzędnych - przez punkt. Teraz możemy zapisać równania kanoniczne linii współrzędnych Ox, Oy i Oz, mają one postać i odpowiednio.

Odpowiedź:

Równania kanoniczne osi współrzędnych Ox, - równania kanoniczne osi rzędnych Oy, - równania kanoniczne osi zastosowania.

Przykład.

Ułóż równania kanoniczne prostej, która w prostokątnym układzie współrzędnych Oxyz w przestrzeni przechodzi przez punkt i równolegle do osi rzędnych Oy.

Rozwiązanie.

Ponieważ linia prosta, której równania kanoniczne musimy ułożyć, jest równoległa do osi współrzędnych Oy, wówczas jej wektor kierunkowy jest wektorem. Wtedy równania kanoniczne tej prostej w przestrzeni mają postać .

Odpowiedź:

Równania kanoniczne prostej przechodzącej przez dwa dane punkty w przestrzeni.

Postawmy sobie zadanie: napisać równania kanoniczne prostej przechodzącej w prostokątnym układzie współrzędnych Oxyz w przestrzeni trójwymiarowej przez dwa rozbieżne punkty i .

Możesz przyjąć wektor jako wektor kierunkowy danej linii prostej (jeśli wektor bardziej Ci się podoba, możesz go przyjąć). Korzystając ze znanych współrzędnych punktów M 1 i M 2, można obliczyć współrzędne wektora: . Teraz możemy zapisać równania kanoniczne linii, ponieważ znamy współrzędne punktu linii (w naszym przypadku nawet współrzędne dwóch punktów M 1 i M 2) i znamy współrzędne jej wektora kierunkowego . Zatem daną linię prostą w prostokątnym układzie współrzędnych Oxyz w przestrzeni trójwymiarowej wyznaczają równania kanoniczne postaci Lub . To jest to, czego szukamy równania kanoniczne prostej przechodzącej przez dwa dane punkty w przestrzeni.

Przykład.

Napisz równania kanoniczne prostej przechodzącej przez dwa punkty w przestrzeni trójwymiarowej I .

Rozwiązanie.

Z stanu jaki mamy. Podstawiamy te dane do równań kanonicznych linii prostej przechodzącej przez dwa punkty :

Jeśli użyjemy kanonicznych równań prostych postaci , wtedy otrzymamy
.

Odpowiedź:

Lub

Przejście od równań kanonicznych prostej w przestrzeni do innych typów równań prostej.

Aby rozwiązać niektóre problemy, równania kanoniczne prostej w przestrzeni może okazać się mniej wygodne niż równania parametryczne prostej w przestrzeni postaci . Czasami lepiej jest zdefiniować linię prostą w prostokątnym układzie współrzędnych Oxyz w przestrzeni poprzez równania dwóch przecinających się płaszczyzn jako . Powstaje zatem zadanie przejścia od równań kanonicznych prostej w przestrzeni do równań parametrycznych prostej lub do równań dwóch przecinających się płaszczyzn.

Łatwo jest przejść od równań prostej w postaci kanonicznej do równań parametrycznych tej prostej. Aby to zrobić, należy wziąć każdy z ułamków w równaniach kanonicznych linii w przestrzeni równy parametrowi i rozwiązać powstałe równania w odniesieniu do zmiennych x, y i z:

W takim przypadku parametr może przyjmować dowolne wartości rzeczywiste (ponieważ zmienne x, y i z mogą przyjmować dowolne wartości rzeczywiste).

Teraz pokażemy, jak to zrobić z równań kanonicznych linii prostej otrzymać równania dwóch przecinających się płaszczyzn, które wyznaczają tę samą linię.

Podwójna równość jest zasadniczo układem trzech równań postaci (przyrównaliśmy ułamki z równań kanonicznych do linii prostej parami). Ponieważ rozumiemy proporcję jako , następnie

Więc mamy
.

Ponieważ liczby a x , a y i a z nie są jednocześnie równe zeru, to główna macierz powstałego układu jest równa dwa, gdyż

i co najmniej jeden z wyznaczników drugiego rzędu

różny od zera.

W związku z tym możliwe jest wykluczenie z układu równania, które nie uczestniczy w tworzeniu podstawy molowej. Zatem równania kanoniczne prostej w przestrzeni będą równoważne układowi dwóch równań liniowych z trzema niewiadomymi, które są równaniami przecinających się płaszczyzn, a linia przecięcia tych płaszczyzn będzie linią prostą wyznaczoną przez równania kanoniczne linii formularza .

Dla przejrzystości podajemy szczegółowe rozwiązanie przykładu, w praktyce wszystko jest prostsze.

Przykład.

Zapisz równania dwóch przecinających się płaszczyzn definiujących prostą określoną w prostokątnym układzie współrzędnych Oxyz w przestrzeni za pomocą równań kanonicznych tej prostej. Zapisz równania dwóch płaszczyzn przecinających się wzdłuż tej prostej.

Rozwiązanie.

Przyrównajmy parami ułamki tworzące równania kanoniczne prostej:

Wyznacznik głównej macierzy wynikowego układu równań liniowych jest równy zeru (w razie potrzeby patrz artykuł), a moll jest drugiego rzędu jest różna od zera, przyjmujemy to jako moll podstawy. Zatem ranga macierzy głównej układu równań jest równe dwa, a trzecie równanie układu nie uczestniczy w tworzeniu podstawowego molla, to znaczy trzecie równanie można wykluczyć z układu. Stąd, . W ten sposób otrzymaliśmy wymagane równania dwóch przecinających się płaszczyzn, które definiują pierwotną linię prostą.

Odpowiedź:

Bibliografia.

Bugrov Ya.S., Nikolsky S.M. Wyższa matematyka. Tom pierwszy: Elementy algebry liniowej i geometrii analitycznej.
Ilyin V.A., Poznyak E.G. Geometria analityczna.