Matris vektör üzerinde çalışır. Matrislerin çarpılması: örnekler, eylemlerin algoritması, ürün özellikleri

Tanım 1.

Matrislerin (C \u003d AB) ürünü, yalnızca matrisin sütunlarının sayısının, matris satırlarının sayısına eşit olduğu için sadece koordineli matrisler için bir işlemdir:

C ⏟ M × n \u003d A ⏟ M × P × B ⏟ P × n

Örnek 1.

Dana Matrix:

A \u003d a (i j) boyutları M × n;
B \u003d B (i J) Boyutları P × n

C matrisi, aşağıdaki formülle hesaplanan öğeler C i J:

c i J \u003d A I 1 × B1 J + A 2 × B2 J +. . . + A i P × B P J, I \u003d 1 ,. . . m, j \u003d 1,. . . M.

Örnek 2.

AV \u003d VA'nın eserlerini hesaplayın:

A \u003d 1 2 1 0 1 2, B \u003d 1 0 0 1 1 1

Matrislerin çarpma kuralını kullanarak çözüm:

Bir ⏟ 2 × 3 × ⏟ 3 × 2 \u003d 1 2 1 0 1 2 × 1 0 0 1 1 1 \u003d 1 × 1 + 2 × 0 + 1 × 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 \u003d 2 3 2 3 ⏟ 2 × 2

⏟ 3 × 2 × A ⏟ 2 × 3 \u003d 1 0 0 1 1 1 × 1 2 1 0 1 2 \u003d 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 \u003d 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3.

B ve B'nin çalışması bulunur, ancak farklı boyutlarda matrislerdir: ve A'ya eşit değildir.

Matrislerin çarpımının özellikleri

Matrislerin çarpımının özellikleri:

(A c) c \u003d a (c) - Matrislerin birleştirici çarpımı;
A (B + C) \u003d A B + A C - çarpımın dağılımı;
(A + C) C \u003d A C + C - çarpımın dağılımı;
λ (a b) \u003d (λ a)

Örnek 1.

1 numaralı mülkü kontrol ediyoruz: (A B) C \u003d A (C'de):

(A × C) × A \u003d 1 2 3 4 × 5 6 7 8 × 1 0 0 0 2 \u003d 19 22 43 50 × 1 0 0 2 \u003d 19 44 43 100,

A (in × c) \u003d 1 2 3 4 × 5 6 7 8 1 0 0 2 \u003d 1 2 3 4 × 5 12 7 16 \u003d 19 44 43 100.

Örnek 2.

2 numaralı mülkü kontrol ediyoruz: a (B + C) \u003d A B + A C:

A × (B + C) \u003d 1 2 3 4 × 5 6 7 8 + 1 0 0 2 \u003d 1 2 3 4 × 6 6 7 10 \u003d 20 26 46 58,

Ve B + ve C \u003d 1 2 3 4 × 5 6 7 8 + 1 2 3 4 × 1 0 0 2 \u003d 19 22 43 50 + 1 4 3 8 \u003d 20 26 46 58.

Üç matris çalışması

Üç matrisin ürünü bir B C, 2 yoldan hesaplanır:

c: (a b) c üzerinde bir içeri ve çarpın;
ya önce C'de bul ve sonra A (C'de) çarp.

Örnek 3.

Matris 2 yolunu çarpın:

4 3 7 5 × - 28 93 38 - 126 × 7 3 2 1

Eylemlerin algoritması:

2 matrisin bir ürününü bulun;
sonra tekrar 2 matrisin ürününü bulun.

bir). A B \u003d 4 3 7 5 × - 28 93 38 - 126 \u003d 4 (- 28) + 3 × 38 4 × 93 + 3 (- 126) 7 (- 28) + 5 × 38 7 × 93 + 5 (- 126) \u003d 2 - 6 - 6 21

2). Ve C \u003d (A C) C \u003d 2 - 6 - 6 21 7 3 2 1 \u003d 2 × 7 - 6 × 2 2 × 3 - 6 × 1 - 6 × 7 + 21 × 2 - 6 × 3 + 21 × 1 \u003d 2 0 0 3.

A'nın formülünü C \u003d (a b) ile kullanıyoruz:

bir). C \u003d - 28 93 38 - 126 7 3 2 1 \u003d - 28 × 7 + 93 × 2 - 28 × 3 + 93 × 1 38 × 7 - 126 × 2 38 × 3 - 126 × 1 \u003d - 10 9 14 - 12

2). Ve C \u003d (A C) C \u003d 7 3 2 1 - 10 9 14 - 12 \u003d 4 (- 10) + 3 × 14 4 × 9 + 3 (- 12) 7 (- 10) + 5 × 14 7 × 9 + 5 (- 12) \u003d 2 0 0 3

Cevap: 4 3 7 5 - 28 93 38 - 126 7 3 2 1 \u003d 2 0 0 3

Matrisin sayıya çarpması

Tanım 2.

Matris A'nın K numaralısının çalışması, ilk çarpımdan belirli bir öğenin belirli bir numarasına elde edilen aynı boyuttaki matris B \u003d A k'dir:

b, j \u003d k × a i, j

Özellikler Matrisin sayı ile çarpılması:

1 × A \u003d a
0 × a \u003d sıfır matris
k (A + B) \u003d K A + K B
(K + N) A \u003d K A + N A
(K × n) × A \u003d K (n × a)

Örnek 4.

Matrisin çalışmasını A \u003d 4 2 9 0 ila 5 bulun.

5 A \u003d 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 \u003d 20 10 45 0

Vektördeki matrisin çarpılması

Tanım 3.

Matrisin ve vektörün çalışmalarını bulmak için, "Sütuna" Kural'a göre çarpmanız gerekir:

matrisini, matrisin vektör kolonuna çarpınsa, matrisdeki sütunların sütun sayısı, vektör sütunundaki satır sayısıyla çakışmalıdır;
vektör kolonunun çarpımının sonucu yalnızca bir vektör sütundur:

A B \u003d A 11 A 12 ⋯ A 1 N A 21 A 22 ⋯ A 2 N ⋯ ⋯ ⋯ ⋯ A m 1 A M 2 ⋯ ⋯ ⋯ A M 1 A M 2 ⋯ A MNB 1 B 2 ⋯ B 1 N \u003d A 11 × B1 + A 12 × B2 + ⋯ + A 1 N × BNA 21 × B 1 + A 22 × 2 + ⋯ + A 2 N × BN ⋯ ⋯ ⋯ ⋯ AM 1 × B1 + AM 2 × B2 + ⋯ + AMN × BN \u003d C 1 C 2 ⋯ C 1 m

matrisini vektör dizesine çarparsanız, çarpma matrisi olağanüstü bir sütun olmalı ve sütunların sayısı vektör hattındaki sütun sayısını eşleştirmesi gerekir:

Ve B \u003d A A ⋯ A BB ⋯ B \u003d A 1 × B 1 A 1 × B2 ⋯ A 1 × BNA 2 × B1 A 2 × B2 ⋯ A 2 × BN ⋯ ⋯ ⋯ ⋯ A × B1 A × × B 2 ⋯ A × BN \u003d C 11 C 12 ⋯ C 1 NC 21 C 22 ⋯ C 2 N ⋯ ⋯ ⋯ CN 1 CN 2 ⋯ CNN

Örnek 5.

Matris A ve vektör sütununun çalışmasını:

A B \u003d 2 4 0 - 2 1 3 - 1 0 1 1 2 - 1 \u003d 2 × 1 + 4 × 2 + 0 × (- 1) - 2 × 1 + 1 × 2 + 3 × (- 1) - 1 × 1 + 0 × 2 + 1 × (- 1) \u003d 2 + 8 + 0 - 2 + 2 - 3 - 1 + 0 - 1 \u003d 10 - 3 - 2

Örnek 6.

Matris a ve vektör hattının çalışmasını buluruz:

A \u003d 3 2 0 - 1, B \u003d - 1 1 0 2

A B \u003d 3 2 0 1 × - 1 1 0 2 \u003d 3 × (- 1) 3 × 1 3 × 0 3 × 2 2 × (- 1) 2 × 1 2 × 0 2 × 2 0 × (- 1) 0 × 1 0 × 0 0 × 2 1 × (- 1) 1 × 1 1 × 0 1 × 2 \u003d - 3 3 0 6 - 2 2 0 4 0 0 0 - 1 1 0 2

Cevap: A B \u003d - 3 3 0 6 - 2 2 0 4 0 0 0 0 - 1 1 0 2

Metinde bir hata görürseniz, lütfen seçin ve Ctrl + Enter tuşuna basın.

Matlab sisteminde matrisler ve vektörlerdeki matematiksel işlemler yeterince gerçekleştirilir. İlk sıradan eklemeleri ve matrislerin ve vektörlerin çoğaltılmasını düşünün. İki versiyonun verilmesine izin verin

a \u003d; % vektör dizisi
b \u003d; % vektör sütunu

sonra bu iki vektörün çarpılması, böylece yazılabilir.

c \u003d a * b; % C \u003d 1 + 2 + 3 + 4 + 5 \u003d 16
d \u003d B * a; % D - MATRIX 5X5 ELEMANLARI

Vektörler üzerindeki işlemlere uygun olarak, vektör dizisinin vektör sütundaki çarpımı bir numara verir ve vektörel kolun vektörelin üzerindeki çarpımı, yukarıdaki örnekteki hesaplamaların sonucu olan iki boyutlu bir matris verir. , yani

İki vektörün eklenmesi ve çıkarılması, böylece yazılmıştır.

a1 \u003d;
a2 \u003d;
c \u003d A1 + A2; % C \u003d;
c \u003d A2-A1; % C \u003d;

Ekleme ve çıkarma işlemlerinin iki sütun vektörü veya iki vektör arasında gerçekleştirilebileceği belirtilmelidir. Aksi takdirde, Matlab bir hata mesajı verecek, çünkü Dart vektörler katlanmamalıdır. Bu, kabul edilemez aritmetik işlemlerle ilgili durumdur: bunları hesaplamamanın imkansızlığı durumunda, MATLAB sistemi bir hata bildirir ve programın yürütülmesi uygun hatta tamamlanacaktır.

Benzer şekilde, çarpma ve matrisler arasındaki ilavelerin operasyonları yapılır:

A \u003d;
B \u003d olanlar (3);
C \u003d A + B; Aynı boyutta iki matrisin% eklenmesi
D \u003d A + 5; matrisin% eklenmesi ve sayı
E \u003d a * b; matrisin% ve üzerinde çoğalması
F \u003d b * a; Birinde matrisin% çoğaltılması
G \u003d 5 * a; Matrisinin% sayısına çarpması

Ters matris hesaplama işlemlerinin yanı sıra transpoza matrisleri ve vektörleri, aşağıdaki gibi yazılmıştır:

a \u003d; % vektör dizisi
b \u003d a '; % vektör sütunu oluştu
% Transpozer vektör dize a.
A \u003d; % matris 3x3 eleman
B \u003d A * a; % B \u003d - Vektör Dize
C \u003d a * b; % C \u003d - vektör sütun
D \u003d a * a * a '; % D \u003d 45 - sayı, e-posta matrisinin toplamı
E \u003d a '; % E - aktarılmış matris a
F \u003d inv (a); % F - Ters Matris A
G \u003d a ^ -1; % G - Ters Matris A

Yukarıdaki örnekten, matrislerin ve vektörlerin transpozisyon çalışmasının, vektör veya matris adından sonra ayarlanan '(kesme) sembolü ile gösterildiği görülmektedir. Ters matrisin hesaplanması, FONKSİYON INV () işlevini arayarak yapılabilir veya matrisi -1'e çıkarın. Her iki durumda da sonuç aynı olacaktır ve çeşitli algoritmaların uygulanmasında kullanım kolaylığı için iki yöntem oluşturulur.

Hesaplama işlemi sırasında, bir vektörün veya matrisin veya matrisin elemanlarını yavaşça çarpmak, bölmek veya dikleştirmek gerekirse, o zaman bunun için operatörler kullanılır:

. * - Elemental Çarpma;
./ ve. \\ - öğe bölümleri;
. ^ - İlköğretim bağı.

Bu operatörlerin işlemini aşağıdaki örnekte düşünün.

a \u003d; % vektör dizisi
b \u003d; % vektör dizisi
c \u003d a. * B; % C \u003d.
A \u003d olanlar (3); Birimlerden oluşan% matris 3x3
B \u003d; % Matris 3x3
C \u003d A. * B; % matris 3x3 oluşan
D \u003d a/b; % matris 3x3 oluşan
E \u003d A. \\ b; % matris 3x3 oluşan
F \u003d A. ^ 2; Matris ve kare unsurlarının% inşası

Bu bölümün sonuçlanmasında, vektörler ve matrislerle çalışırken yararlı olan birkaç işlevi göz önünde bulundurun.

Vektör elemanının maksimum değerini aramak için, elemanın elde edilen maksimum değerini ve konumunu (dizin) döndüren standart maksimum () işlevi kullanılır:

a \u003d;
\u003d maksimum (a); % v \u003d 6, i \u003d 2;

v \u003d maks (a); % v \u003d 6;

Aşağıdaki örnek, Max () işlevini çağırmak için iki farklı yol göstermektedir. İlk durumda, öğenin maksimum değeri ve vektördeki endeksinin değeri belirlenir ve ikincisinde - sadece elemanın maksimum değeri.

Matrisler durumunda, bu özellik Örnekte aşağıda gösterildiği gibi sütunlardaki maksimum değerleri belirler:

A \u003d;
\u003d maksimum (a); % V \u003d, i \u003d
V \u003d maks (a); % V \u003d.

Max () işlevinin tam sözdizimi, komut penceresinde MATLAB komutunu yazarak bulunabilir.

yardım.<название функции>

Benzer şekilde, MIN () işlevi, vektör elemanının veya matrisin minimum değerini veya endeksini belirleyen fonksiyon çalışır.

Matrisler ve vektörlerle çalışmanın bir başka kullanışlı özelliği, matrisin vektörün veya sütunlarının öğelerinin değerlerinin miktarını hesaplayan toplam () işlevidir:

a \u003d;
s \u003d toplam (a); % S \u003d 3 + 5 + 4 + 2 + 1 \u003d 15
A \u003d;
S1 \u003d toplam (a); % S1 \u003d.
S2 \u003d toplam (toplam (a)); % S2 \u003d 39

S2 toplamını hesaplarken, matris elemanlarının değerlerinin toplamı ilk önce sütunlarda hesaplanır ve ardından satırla hesaplanır. Sonuç olarak, S2 değişkeni, Matris A'nın tüm unsurlarının değerlerinin toplamını içerir.

Vektör veya matrisin öğelerinin değerlerini artan veya inen, sıralama () işlevi aşağıdaki gibi kullanılır:

a \u003d;

b1 \u003d Sıralama (a); % B1 \u003d.
b2 \u003d Sıralama (A, 'Descend'); % B2 \u003d.
b3 \u003d sıralama (a, 'ascend'); % B3 \u003d.

matrisler için

A \u003d;
B1 \u003d Sıralama (a); % B1 \u003d.
B2 \u003d Sıralama (A, 'Descend'); % B2 \u003d.

Birçok pratik görevin genellikle bir vektör veya matriste belirli bir öğeyi bulması gerekir. Bu, gerekli elemanların bulunduğu, örneğin, aşağıdaki gibi bir argüman olarak kabul edilen standart Bul () işlevi kullanılarak yapılabilir.

a \u003d;
b1 \u003d Bul (a \u003d\u003d 2); % B1 \u003d 4 - Element indeksi 2
b2 \u003d bulun (a ~ \u003d 2); % B2 \u003d - 2 olmadan endeksler
b3 \u003d Bul (a\u003e 3); % B3 \u003d.

Verilen örnekte, '\u003d\u003d' karakteri, eşitliği kontrol etmek anlamına gelir ve '~ \u003d' karakteri, vektörün elementlerinin değerlerinin eşitsizliğine ilişkin denetimini gerçekleştirir. Bu operatörler hakkında daha fazla ayrıntı koşullu operatörler bölümünde açıklanacaktır.

Vektörler ve matrislerle çalışmanın bir başka kullanışlı özelliği, ortalamayı hesaplamak için ortalama () işlevidir. aritmetik değerHangi aşağıdaki gibi çalışır:

a \u003d;
m \u003d ortalama (a); % m \u003d 3
A \u003d;
M1 \u003d ortalama (a); % M1 \u003d.
M2 \u003d ortalama (ortalama (a)); % M2 \u003d 4.333

Her vektör tek mermi veya tek hatlı bir matris olarak kabul edilebilir. Tek rulo matris, bir vektör sütun ve tek satırlı bir matris - bir vektör dizesi olarak adlandırılır.

M * n'nin A-Matrisi ise, vektör sütunu B'nin bir boyutuna sahiptir ve B vektör dizisi B boyutuna sahiptir.

Böylece, matrisi vektöre çarpmak için, vektörü bir vektör sütun olarak düşünmeniz gerekir. Vektörin matris üzerindeki çarptığında, vektör olarak düşünülmelidir.

Çarpma matrisi

karmaşık vektör üzerinde

Sonucu alıyoruz

Vektörün sürekli boyutuyla görebileceğiniz gibi, iki çözüm olabiliriz.

Dikkatinizi, aynı değerlere rağmen, tamamen farklı (farklı boyutlara sahip) rağmen, birinci ve ikinci düzenlemede matrisin yapıldığına dikkatinizi çekmek istiyorum.

İlk durumda, vektör sütun olarak kabul edilir ve daha sonra gereklidir. matrisi vektör üzerinde çarpmave ikinci durumda, bir vektör dizemiz var ve sonra bir matris üzerinde vektör sanat.

Bu bot, entegre değerleri olan vektör ve matrisler de dahil olmak üzere çarpar. Entegre çevrimiçi değerlerle matrislerin daha eksiksiz bir şekilde çarpılması temelinde oluşturuldu

Vektöre çarpma özellikleri matris

Matris

Vektör sütun

Vektör dize

Keyfi

1. Sütun vektörlerinin toplamı üzerindeki matrisin ürünü, vektörlerin her biri için matrisin çalışmasının miktarına eşittir.

2. Matris üzerindeki satır satırlarının toplamının ürün, matris üzerindeki vektörlerin miktarına eşittir.

3. Ortak vektör çarpan, matris üzerinde vektör / vektör üzerinde matris işinden çıkarılabilir

4. Matrisin çalışmalarında ve kolon vektörünün yapımı, matris ve sütun vektöründeki vektör dizisinin çalışmasının ürününe eşit, kolon vektörünün üretimi.

Bu nedenle, önceki derste, matrislerin eklenmesi ve çıkarılması için kuralları söküyoruz. Bunlar o kadar basit operasyonlar, çoğu öğrencinin kendilerini kelimenin tam anlamıyla anladığı için.

Ancak, erken sevinirsiniz. Freebie bitti - çarpıma gidin. Hemen sizi uyarıyorum: çarpın iki matris, aynı koordinatlara sahip hücrelerdeki sayıları aynı koordinatlarla çarpılmıyor. Her şey burada çok daha eğlenceli. Ve ön tanımlarla başlamak.

Tutarlı matrisler

Matrisin en önemli özelliklerinden biri boyutudur. Biz zaten yüzlerce kez konuştuk: rekor $ a \u003d \\ sol [m \\ right] $, Matris'te tam olarak $ satır ve $ N $ Sütunlar anlamına gelir. Satırları sütunlarla karıştırmayacağımız, zaten tartıştık. Şimdi önemlidir.

Tanım. Formun Matrisleri A \u003d \\ LOFT] $ ve $ B \u003d \\ LOFT] $ ve $ B \u003d \\ Sol [n \\ Tims k \\ right] $, burada ilk matrisdeki sütun sayısının sayıya çakıştığı İkincisinde satırların koordineli olarak adlandırılır.

Bir kez daha: İlk matrisdeki sütun sayısı, saniyedeki satır sayısına eşittir! Buradan bir kerede iki çıkış alıyoruz:

Matrislerin sırası için önemliyiz. Örneğin, matrisler $ a \u003d \\ sol [3 \\ times 2 \\ right] $ ve $ B \u003d \\ Sol [2 \\ Times 5 \\ Right] $ 'a kabul edilir (ilk matriste 2 sütun ve ikincildeki 2 satır) , ancak aksine - Matrisler $ B \u003d \\ Sol [2 \\ Times 5 \\ Right] $ ve $ a \u003d \\ Sol [3 \\ Times 2 \\ Right] $ - Artık kabul edilmiyor (ilk matristeki 5 sütun - değil İkincisinde 3 satır).
Tüm boyutları birbirinden sonra yazıp yazmadığınızı kontrol etmek kolaydır. Önceki paragraf örneğinde: "3 2 2 5" - ortada aynı sayıda, bu yüzden matrisler kabul edilir. Ancak "2 5 3 2" - kararlaştırılmadı, çünkü ortada farklı sayılar var.

Buna ek olarak, kaptan, aynı miktarda $ \\ sola [n \\ tims n \\ right] $ 'ın kare matrislerinin her zaman tutarlı olduğu için belirgindir.

Matematikte, nesneleri aktarma prosedürü önemli olduğunda (örneğin, yukarıdaki tanımda, matrisler için prosedür önemlidir), genellikle sipariş edilen çiftlerden bahseder. Okulda onlarla tanıştık: $ \\ Sol (1; 0 \\ sağ) $ ve $ \\ Sol (0; 1 \\ sağ) $ ve $ \\ Sol (0; 1 \\ sağ) Koordinatlarının düzlemde farklı noktalar belirlediğini düşünüyorum.

Böylece: Koordinatlar ayrıca sayılardan derlenen çiftler de sipariş edilir. Ancak hiçbir şey böyle bir çift matrisleri önler. Sonra söylenebilir: "İlk Matris'deki sütun sayısı ikincinde sıra sayısıyla çakışıyorsa," sipariş edilen $ \\ Sol matris (A; B \\ sağ) $ bir çift tutarlıdır. "

Peki, ne?

Çarpma tanımı

İki tutarlı matris düşünün: $ a \u003d \\ sol [m \\ tims n \\ right] $ ve $ B \u003d \\ Sol [n \\ time k \\ right] $. Ve onlar için bir çarpma işlemi tanımlarız.

Tanım. İki tutarlı matrisin ürünü $ a \u003d \\ sol [m \\ tims n \\ right] $ ve $ b \u003d \\ sol [n \\ tims k \\ right] $ yeni bir matris $ c \u003d \\ sol [m \\ tims k \\ Sağ] $ öğeleri formül tarafından değerlendirilir:

\\ [\\ başlar (hizalama) & ((c) _ (i; j)) \u003d ((a) _ (i; 1)) \\ CDOT ((B) _ (1; j)) + ((a) _ (i; 2)) \\ cdot ((b) _ (2; j)) + \\ ldots + ((a) _ (i; n)) \\ cdot ((b) _ (n; j)) \u003d \\\\ & \u003d \\ sum \\ limits_ (t \u003d 1) ^ (n) (((((a) _ (i; t)) \\ CDOT ((B) _ (t; j))) \\ ucu (hizala) \\]

Standart standarttır: $ c \u003d a \\ cdot b $.

Bu tanımını ilk görenler için, hemen iki soru ortaya çıkıyor:

Sadece oyun için bu nedir?
Neden bu kadar zor?

Peki, sırayla her şey hakkında. İlk soru ile başlayalım. Bütün bu indeksler ne anlama geliyor? Ve gerçek matrislerle çalışırken nasıl hata yapılmaz?

Her şeyden önce, $ ((c) _ (i; j)) $ 'ı hesaplamanın (((C) _ (i; j)) $' ı (özellikle indeksler arasında bir virgülle bir nokta koyduğunu, bu yüzden karışmaz, ancak hiç olmadığı için bir nokta koyduğunu unutmayın. onları koymak için gerekli - ben kendimi tanımındaki formülü incittim) aslında basit bir kurala varıyor:

İlk matriste $ -un bir satır alıyoruz;
İkinci matriste bir $ J $ -A sütunu alıyoruz;
İki sayı dizisini alırız. Bu dizilerin eşyalarını aynı numaralarla değiştirin ve elde edilen çalışmaları katlayın.

Bu işlem resimleri anlamak kolaydır:

İki matrisin çarpma diyagramı

Bir kez daha: İkinci matrisdeki $ J $ sütunu olan $ J $ sütunu olan $ i $ satırını düzeltiyorum, elemanları aynı numaralara dönüştürün ve elde edilen işler katlanır - $ ((c) _ ( ij)) $. Ve böylece tüm 1 \\ le \\ le m $ ve $ 1 \\ le j \\ le k $ için. Şunlar. Böyle bir "sapkınlık" ın toplam m \\ tims k $ olacaktır.

Aslında, biz zaten matrislerin çoğalması ile tanıştık. okul programı, sadece güçlü bir şekilde kesilmiş bir biçimde. Vektöre izin ver:

\\ [\\ başlar (hizalama) \\ vec (a) \u003d \\ sol (((x) _ (a)); (((Y) _ (a)); (((Z) _ (a)) \\ sağda); \\\\ \\ outrightarrow (b) \u003d \\ sol (((x) _ (b)); (((Y) _ (b)); ((z) _ (b)) \\ \u200b\u200bsağ). \\\\ \\ end (hizala) \\]

Sonra skaler çalışmaları çift yönde işlerin miktarı olacaktır:

\\ [\\ outrightarrow (a) \\ tims \\ outrightarrow (b) \u003d ((x) _ (a)) \\ cdot ((x) _ (b)) + ((Y) _ (a)) \\ cdot ((y) ) _ (b)) + ((z) _ (a)) \\ CDOT ((Z) _ (b)) \\]

Aslında, bu uzak yıllarda, ağaçlar yeşil olduğunda ve gökyüzü daha parlak olduğunda, biz sadece $ \\ ostraightarrow (B) $ sütun vektöründe $ \\ ougarrowarrow vektör dizisi ile çarpılır.

Bugün hiçbir şey değişmedi. Şimdi bu satırlar ve sütunlar daha fazla hale geldi.

Ama yeterli teori! Gerçek örneklere bakalım. Ve en basit durumda - kare matrislerden başlayın.

Kare matrislerin çarpılması

Görev 1. Çarpma yapın:

\\ [\\ Sola [\\ başlar (dizi) (* (35) (R)) 1 & 2 \\\\ -3 ve 4 \\\\ \\ ucu (dizi) \\ right] \\ CDOT \\ Sol [\\ BACE (dizi) (* (35) (r)) -2 ve 4 \\\\ 3 ve 1 \\ \\ end (dizi) \\ sağ] \\]

Karar. Böylece, iki matrisimiz var: $ A \u003d \\ Sol [2 \\ Times 2 \\ Right] $ ve $ B \u003d \\ Sol [2 \\ Times 2 \\ Right] $. Kabul edildikleri açıktır (aynı büyüklükteki kare matrisler her zaman tutarlıdır). Bu nedenle, çarpma gerçekleştiriyoruz:

\\ [\\ Başlar (Hizala) & \\ Sol [\\ BACE (Dizi) (* (35) (R)) 1 & 2 \\\\ -3 & 4 \\\\ \\ \\ \\\\ \\ right] \\ CDOT \\ Sol [\\ başlar (Dizi) (* (35) (R)) -2 ve 4 \\\\ 3 ve 1 \\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACAK (dizi) (* (35) (r)) 1 \\ CDOT \\ Sol (-2 \\ sağ) +2 \\ CDOT 3 & 1 \\ CDOT 4 + 2 \\ CDOT 1 \\\\ -3 \\ CDOT \\ Sol (-2 \\ sağ) +4 \\ CDOT 3 & -3 \\ CDOT 4 + 4 \\ CDOT 1 \\\\ \\ ucu (dizi) \\ sağ] \u003d \\\\ & \u003d \\ sol [\\ başlar (dizi) (* (* (35) (r)) 4 & 6 \\\\ 18 & -8 \\\\ \\ ucu ( Dizi) \\ sağ]. \\ Ucu (hizala) \\]

Bu kadar!

Cevap: $ \\ Sol [\\ BACE (dizi) (* (* (35) (r)) 4 & 6 \\\\ 8 & -8 \\\\\\ end (dizi) \\ right] $.

Görev 2. Çarpımı gerçekleştirin:

\\ [\\ Sol [\\ BACAK (MATRIX) 1 & 3 \\\\ 2 & 6 \\ '\\ end (Matrix) \\ Right] \\ CDOT \\ Sol [\\ BACAK (Dizi) (* (35) (R)) 9 & 6 \\\\ -3 & -2 \\\\\\ end (dizi) \\ sağ] \\]

Karar. Yine kararlaştırılan matrisler, böylece eylemler yapın: \\ [\\]

\\ [\\ BACAK (HIGNIGN) \\ Sol [\\ BACE (MATRIX) 1 & 3 \\\\ 2 & 6 \\\\ SON (MATRIX) \\ SAĞLIK] \\ CDOT \\ Sol [\\ BACE (Dizi) (* (* (3) ) 9 & 6 \\\\ -3 & -2 \\\\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACE (dizi) (* (35) (R)) 1 \\ CDOT 9 + 3 \\ CDOT \\ Sol ( -3 \\ sağ) & 1 \\ CDOT 6 + 3 \\ CDOT \\ Sol (-2 \\ sağ) \\\\ 2 \\ CDOT 9 + 6 \\ CDOT \\ Sol (-3 \\ sağ) & 2 \\ CDOT 6 + 6 \\ CDOT \\ Sol (-2 \\ sağ) \\\\ \\ ucu (dizi) \\ sağ] \u003d \\\\ & \u003d \\ sol [\\ BACE (MATRIX) 0 & 0 \\\\ 0 & 0 \\\\ UN (MATRIX) \\ Right]. \\ Ucu (hizala) \\]

Gördüğümüz gibi, Zeros ile dolu matrisin ortaya çıktı.

Cevap: $ \\ Sol [\\ BACE (MATRIX) 0 & 0 \\\\ 0 & 0 \\\\ UN (MATRIX) \\ Right] $.

Yukarıdaki örneklerden, matrislerin çoğalması zor bir işlem olmadığı açıktır. En azından 2 beden 2'nin kare matrisleri için.

Hesaplamalar sürecinde, doğrudan boyandığı bir ara matris oluşturduk, bir veya başka bir hücrede hangi numaralar dahil edildi. Bu görevleri çözerken böyle yapılması gerektiğidir.

Matris çalışmasının ana özellikleri

Kısaca. Matris Çarpımı:

BMUTUTATIVE: $ A \\ CDOT B \\ NE B \\ CDOT Genel durumda bir $. Elbette, eşitliğin $ A \\ CDOT B \u003d B \\ CDOT A $ (örneğin, $ B \u003d E $ tek bir matris olduğunda) olduğu için özel matrisler vardır, ancak çoğu durumda çalışmaz;
İlişkili: $ \\ Sol (A \\ CDOT B \\ Right) \\ CDOT C \u003d A \\ CDOT \\ Sol (B \\ CDOT C \\ Right) $. Burada seçenekler olmadan: Matrislerin yanında durmak, bir sonraki ve bu iki matrisin sağında hayatta kalamaz, hayatta kalamaz.
DAĞITIM: $ A \\ CDOT \\ Sol (B + C \\ Right) \u003d A \\ CDOT B + A \\ CDOT C $ ve $ \\ Sol (A + B \\ Right) \\ CDOT C \u003d A \\ CDOT C + B \\ CDOT C $ (ticari olmayanlık nedeniyle, işin sağa ve sola dağıtımı ayrı olarak reçete etmek zorundadır.

Ve şimdi - hepsi aynı, ancak daha ayrıntılı olarak.

Matrislerin çarpılması, büyük ölçüde klasik sayıların çarpımını hatırlatır. Ancak, en önemlisi olan farklılıklar var. matrislerin çoğalması, genel olarak konuşursak, ticari olmayan.

Görevdeki matrisleri bir kez daha düşünün 1. Doğrudan işlerini zaten biliyoruz:

\\ [\\ Sola [\\ başlar (dizi) (* (35) (R)) 1 & 2 \\\\ -3 ve 4 \\\\ \\ ucu (dizi) \\ right] \\ CDOT \\ Sol [\\ BACE (dizi) (* (35) (r)) -2 ve 4 \\\\ 3 ve 1 \\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACE (Dizi) (* (35) (R)) 4 & 6 \\\\ 18 ve -8 \\\\\\ end (dizi) \\ sağ] \\]

Ancak matrisleri bazı yerlerde değiştirirseniz, tamamen farklı bir sonuç alacağız:

\\ [\\ sol [\\ başlar (dizi) (* (35) (R)) -2 ve 4 \\\\ 3 ve 1 \\ \\ ucu (dizi) \\ sağ] \\ CDOT \\ Sol [\\ BACAK (Dizi) (* ( 35) (r)) 1 & 2 \\\\ -3 ve 4 \\ ucu (dizi) \\ sağ] \u003d \\ sol [\\ başlar (matris) -14 ve 4 \\\\ 0 & 10 \\\\ \\ end (matris) \\ SAĞ] \\]

$ A \\ CDOT B \\ NE B \\ CDOT A $ 'a dönüşür. Ek olarak, çarpma işlemi yalnızca koordineli matrisler için tanımlanır $ a \u003d \\ to \u003d \\ sol [m \\ tims n \\ right] $ ve $ b \u003d \\ sol [n \\ time k \\ right] $, ancak kimse kaldıklarını garanti etmez onları yerlerde değiştirirlerse kabul etti. Örneğin, $ \\ sol matrisler [2 \\ times 3 \\ right] $ ve $ \\ sol [3 \\ times 5 \\ right] $ belirtilen sırada oldukça tutarlıdır, ancak aynı matrisler $ \\ sola [3 \\ times 5 \\ Doğru] $ ve $ \\ sol [2 \\ times 3 \\ right] $ Ters siparişte kaydedilen $ artık kabul edilmez. Üzüntü. :(

Kare matrisler arasında belirtilen boyut $ n $, her zaman doğrudan ve ters sırayla çarptığında da aynı sonucu verir. Tüm benzer matrisler (ve genel olarak ne kadar) ayrı bir ders için konuyla nasıl tarif edilir. Bugün bunun hakkında konuşmayacağız. :)

Bununla birlikte, matrislerin çoğalması ilişkilidir:

\\ [\\ sol) \\ CDOT C \u003d A \\ CDOT \\ Sol (B \\ CDOT C \\ Right) \\]

Bu nedenle, bir kerede bir üst üste birkaç matris çarpmanız gerektiğinde, bir süre boyunca yapmak oldukça gereklidir: Yakındaki bazı matrislerin ilginç bir sonuç vermesi oldukça mümkün. Örneğin, yukarıda tartışılan Görev 2'deki gibi bir sıfır matris.

Gerçek görevlerde, en sık, \\ sol [n \\ times n \\ right] $ 'nın kare matrislerini çarpmak zorundadır. Tüm bu matrislerin seti, $ ((m) ^ (n)) $ tarafından gösterilir (yani, $ a \u003d \\ to to [n \\ right] $ ve \\ aynı şeyi ifade eder) ve gerekli olacaktır. BT MATRIX $ E $, bekar olarak adlandırılır.

Tanım. $ N $ tutarının tek matrisi, herhangi bir kare matris için $ a \u003d \\ \\ sol [n \\ tims n \\ right] $ eşitlik ile gerçekleştirildiği gibi bir $ e matrisidir:

Böyle bir matris her zaman eşit görünüyor: Ana çapraz köşegende birimler var ve diğer tüm hücrelerde - sıfırlar.

\\ [\\ Başlar (Hizala) & A \\ CDOT \\ Sol (B + C \\ Right) \u003d A \\ CDOT B + A \\ CDOT C; \\\\ & \\ sol (A + B \\ sağ) \\ CDOT C \u003d A \\ CDOT C + B \\ CDOT C. \\\\ \\ end (Hizala) \\]

Başka bir deyişle, bir matrisi diğer ikisinin toplamı için çarpmanız gerekirse, bu "iki başkasına" her birine çarpabilir ve ardından sonuçları katlayabilirsiniz. Uygulamada, genellikle bir ters çalışma yapmak için gereklidir: Aynı matrisi fark ettik, braket için taşırız, eklemeyi gerçekleştiriyoruz ve böylece hayatınızı basitleştiriyoruz. :)

Not: Dağıtımı tanımlamak için, iki formül kaydetmek zorunda kaldık: Miktarın ikinci çarpandayken ve birincisinin ilk sırada olduğu yerlerde. Bu, matrislerin çarpımının komutatıcı olmadığı gerçeğinden (ve genel olarak, normal olmayan bir cebirde, sıradan sayılarla çalışırken bile akla gelmez). Ve eğer söyleyelim ki, bu mülkü sınavda yazmanız gerekecek, daha sonra kesinlikle her iki formül yazacaksınız, aksi takdirde öğretmen biraz kızabilir.

Tamam, bütün bunlar kare matrisler hakkında peri masallarıydı. Peki ya dikdörtgen?

Dikdörtgen matrisler durumu

Ve hiçbir şey kare ile aynı değildir.

Görev 3. Çarpımı gerçekleştirin:

\\ [\\ Sol [\\ BACAK (MATRIX) \\ BACE (MATRIX) 5 \\\\ 2 \\\\ 3 \\ \\ end (MATRIX) & \\ BACE (MATRIX) 4 \\\\ 5 \\\\ 1 \\\\\\ UN (MATRIX) \\ \\ \\ Ucu (matris) \\ right] \\ CDOT \\ Sol [\\ BACE (Dizi) (* (35) (R)) -2 & 5 \\\\ 3 ve 4 \\ \\ ucu (dizi) \\ sağ] \\]

Karar. İki matrisimiz var: $ A \u003d \\ Sol [3 \\ Times 2 \\ Right] $ ve $ B \u003d \\ Sol [2 \\ Times 2 \\ Right] $. Bir üst üste boyutları belirten numaraları içtik:

Gördüğünüz gibi, merkezi iki sayı çakışır. Böylece, matrisler kabul edilir ve çoğalabilirler. Ve çıktıda, Matrix $ C \u003d \\ Sol [3 \\ Times 2 \\ Right] $ alıyoruz:

\\ [\\ Başlar (hizalayın) \\ sol [\\ BACE (MATRIX) \\ BACAK (MATRIX) 5 \\\\ 2 \\\\ 3 \\\\ UND (MATRIX) & \\ BAŞLATI (MATRIX) 4 \\\\ 5 \\\\ 1 \\\\ \\ end (Matris) \\\\ \\ ucu (matris) \\ right] \\ CDOT \\ Sol [\\ BACE (Dizi) (* (35) (R)) -2 & 5 \\\\ 3 ve 4 \\\\ End (dizi) \\ sağ] \u003d \\ Sol [\\ BACAK (Dizi) (* (35) (R)) 5 \\ CDOT \\ Sol (-2 \\ sağ) +4 \\ CDOT 3 & 5 \\ CDOT 5 + 4 \\ CDOT 4 \\\\ 2 \\ CDOT \\ Sol (-2 \\ sağ) +5 \\ CDOT 3 & 2 \\ CDOT 5 + 5 \\ CDOT 4 \\\\ 3 \\ CDOT \\ Sol (-2 \\ sağ) +1 \\ CDOT 3 & 3 \\ CDOT 5 + 1 \\ CDOT 4 \\\\ ucu (dizi) \\ right] \u003d \\\\ & \u003d \\ sol [\\ başlar (dizi) (* (* (35) (r)) 2 ve 41 \\\\ 11 ve 30 \\\\ -3 & 19 \\ \\ ucu (Dizi) \\ sağ]. \\ Ucu (hizala) \\]

Her şey açıktır: 3 satırın son matrisinde ve 2 sütununda. Oldukça $ \u003d \\ Sol [3 \\ Times 2 \\ Right] $.

Cevap: $ \\ Sol [\\ BACE (Dizi) (* (35) (R)) \\ BAŞLAT (Dizi) (* (* (35) (r)) 2 \\\\ 11 \\\\ - 3 \\ \\ end (dizi) & \\ BAŞLANGIÇ (MATRIX) 41 \\\\ 30 \\\\ 19 \\\\ end (MATRIX) \\\\ UN (dizi) \\ Right] $.

Şimdi en iyilerinden birini düşünün eğitim Görevleri Sadece matrislerle çalışmaya başlayanlar için. İçinde, sadece iki işareti çoğalmak gerekmez, ancak önce bu çarpmanın izin verilip verilmeyeceğini belirler mi?

Görev 4. Mümkün olan tüm matris çiftlerini bulun:

\\\\]; $ B \u003d \\ Sol [\\ BACE (MATRIX) \\ BACAK (MATRIX) 0 \\\\ 2 \\\\ 0 \\\\ 4 \\\\ UND (MATRIX) \\ BAŞLATMA (MATRIX) 1 \\\\ 0 \\\\ 3 \\\\ 0 \\\\\\ Son (matris) \\ \\ ucu (matris) \\ right] $; $ C \u003d \\ sol [\\ başlar (matris) 0 & 1 \\\\ 1 & 0 \\\\ end (matris) \\ right] $.

Karar. Başlamak için, matrislerin boyutlarını yazın:

\\; \\ B \u003d \\ sol [4 \\ tims 2 \\ sağ]; \\ c \u003d \\ Sol [2 \\ Times 2 \\ Right] \\]

$ A $ Matrix'in sadece bir $ B $ matris ile koordine edilebileceğini, çünkü $ A $ 'deki sütun sayısı 4'tür ve bu tür bir sayıda satır sadece B $' dır. Bu nedenle, bir iş bulabiliriz:

\\\\ CDOT \\ Sol [\\ BACE (Dizi) (* (35) (R)) 0 & 1 \\\\ 2 & 0 \\\\ 0 & 3 \\\\ 4 & 0 \\\\\\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACAK (Dizi) (* (35) (R)) - 10 & 7 \\\\ 10 & 7 \\\\ \\ ucu (dizi) \\ sağ] \\]

Okuyucuyu kendi başınıza yürütmek için ara adımlar öneriyorum. Sadece elde edilen matrisin boyutunun, herhangi bir hesaplamadan önce bile önceden belirlemek için daha iyi olduğunu unutmayın:

\\\\ CDOT \\ Sol [4 \\ Times 2 \\ sağ] \u003d \\ Sol [2 \\ Times 2 \\ Right] \\]

Başka bir deyişle, matrislerin tutarlılığını sağlayan "Transit" katsayılarını kaldırıyoruz.

Başka hangi seçenekler mümkündür? Tabii ki, $ B \\ CDOT A $, çünkü $ B \u003d \\ Sol [4 \\ Times 2 \\ Right] $, $ a \u003d \\ Sol [2 \\ Times 4 \\ Right] $, bu yüzden buharı \\ sol sipariş verdi (b; \\ sağ) $ tutarlıdır ve işin boyutu:

\\\\ CDOT \\ Sol [2 \\ Times 4 \\ Right] \u003d \\ Sol [4 \\ Times 4 \\ Right] \\]

Kısacası, çıktılarda, katsayıların kolayca dikkate alınması gereken bir $ \\ sol matris [4 \\ times 4 \\ right] $ olacaktır:

\\\\ CDOT \\ Sol [\\ BACE (Dizi) (* (* (35) (R)) 1 & -1 ve 2 ve -2 \\\\ 1 ve 1 ve 2 & 2 \\\\ \\ end (dizi) \\ sağ] \u003d \\ Sol [\\ '(Dizi) (* (* (35) (r)) 1 ve 1 ve 2 & 2 \\\\ 2 ve 3 ve 6 ve 6 \\\\ 4 ve -4 ve 6 ve 6 \\\\ 4 ve -4 ve 8 ve 6 -8 \\\\\\ end (dizi) \\ sağ] \\]

Açıkçası, başka bir $ C \\ CDOT A $ ve $ B \\ CDOT C $ - ve bu kadar kabul edebilirsiniz. Bu nedenle, elde edilen eserleri yazarız:

Kolaydı.:)

Cevap: $ ab \u003d \\ sol [\\ başlar (dizi) (* (* (35) (r) -10 ve 7 \\\\ 10 ve 7 \\ \\ ucu (dizi) \\ right] $; $ BA \u003d \\ LOFT [\\ BACAK (Dizi) (* (* (35) (R)) 1 & 1 ve 2 & 2 \\\\ 2 ve 3 ve 4 ve 6 \\\\ 2 ve 3 ve 6 & 6 \\\\ 4 4 ve -4 ve 8 ve -8 \\\\\\ ucu (dizi) \\ right] $; $ Ca \u003d \\ sol [\\ başlar (dizi) (* (* (35) (r) 1 & 1 & 2 & 2 \\\\ 1 & -1 & 2 & -2 \\\\ \\ \\ 1 & -1 & 2 & -2 \\\\ \\ end (dizi) \\ right] $; $ BC \u003d \\ LOFT [\\ BACE (Dizi) (* (* (35) (R)) 1 & 0 \\\\ 0 & 2 \\\\ 3 ve 0 \\\\ 0 ve 4 \\ nidir (dizi) \\ sağ] $.

Genel olarak, bu görevi kendiniz yapmanızı şiddetle tavsiye ederim. Ve içinde olan bir tane daha benzer bir görev ödev. Bu basit düşünme, matrislerin çarpımının tüm temel aşamalarını çözmenize yardımcı olacaktır.

Ancak bu hikayede bitmiyor. Özel çarpma vakalarına gidin. :)

Vektör dizeleri ve vektör sütunları

En yaygın matris işlemlerinden biri, bir satır veya bir sütunun içindeki bir matris üzerinde çarpmadır.

Tanım. Vektör sütunu, $ \\ sola [m \\ times 1 \\ right] $, yani solunumun bir matrisidir. birkaç satırdan ve sadece bir sütundan oluşur.

Vektör dizesi, bir $ \\ sol matrisdir [1 \\ tims n \\ right] $, yani bir satır ve birkaç sütundan oluşur.

Aslında, bu nesnelerle zaten tanıştık. Örneğin, stereometri $ \\ ourightarrow (a) \u003d \\ sol (x; y; z \\ sağ) $ 'ın normal üç boyutlu vektör vektörü bir vektör dizgisinden başka bir şey değildir. Satırlar ve sütunlar arasındaki farkın teorisinin bakış açısına göre neredeyse no. Çevreleyen matris faktörleri ile kararlaştırılmaya özen gösterilmesi gerekir.

Görev 5. Çarpımı gerçekleştirin:

\\ [\\ sola [\\ başlar (dizi) (* (35) (R)) 2 & -1 ve 3 \\\\ 4 ve 2 ve 0 \\\\ -1 ve 1 ve 1 \\ \\ \\ \\ \\ -1 ve 1 ve 1 \\ \\ \\ \\ \\ CDOT \\ Sol [\\ BACE (Dizi) (* (35) (r)) 1 \\\\ 2 \\\\ -1 \\\\\\ end (dizi) \\ right] \\]

Karar. Bizden önce, kararlaştırılan matrislerin çalışması: $ \\ Sol [3 \\ Times 3 \\ Right] \\ CDOT \\ Sol [3 \\ Times 1 \\ Right] \u003d \\ Sol [3 \\ Times 1 \\ Right] $. Bu işi bulun:

\\ [\\ sola [\\ başlar (dizi) (* (35) (R)) 2 & -1 ve 3 \\\\ 4 ve 2 ve 0 \\\\ -1 ve 1 ve 1 \\ \\ \\ \\ \\ -1 ve 1 ve 1 \\ \\ \\ \\ \\ CDOT \\ Sol [\\ BACE (Dizi) (* (35) (R)) 1 \\\\ 2 \\\\ -1 \\\\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACAK (dizi) (* (35) (R)) 2 \\ CDOT 1+ \\ Sol (-1 \\ sağ) \\ CDOT 2 + 3 \\ CDOT \\ Sol (-1 \\ sağ) \\\\ 4 \\ CDOT 1 + 2 \\ CDOT 2 + 0 \\ CDOT 2 \\ \\ -1 \\ CDOT 1 + 1 \\ CDOT 2 + 1 \\ CDOT \\ Sol (-1 \\ sağ) \\\\ \\ ucu (dizi) \\ sağ] \u003d \\ Sol [\\ BACE (dizi) (* (35) (R)) -3 \\\\ 8 \\\\ 0 \\\\ \\ ucu (dizi) \\ sağ] \\]

Cevap: $ \\ Sol [\\ BACE (dizi) (* (* (35) (r)) - 3 \\\\ 8 \\\\ 0 \\\\\\ end (dizi) \\ right] $.

Görev 6. Çarpımı gerçekleştirin:

\\ [\\ Sol [\\ BACAK (dizi) (* (35) (R)) 1 & 2 & -3 \\ \\ ucu (dizi) \\ sağ] \\ CDOT \\ Sol [\\ BACAK (Dizi) (* (35) ( r)) 3 & 1 & -1 \\\\ 4 & 6 & 0 \\\\ \\ \\ \\ \\ \\ \\] \\]

Karar. Yine, her şey tutarlıdır: $ \\ Sol [1 \\ Times 3 \\ Right] \\ CDOT \\ Sol [3 \\ Times 3 \\ Right] \u003d \\ Sol [1 \\ Times 3 \\ Right] $. İşi düşünüyoruz:

\\ [\\ Sol [\\ BACAK (dizi) (* (35) (R)) 1 & 2 & -3 \\ \\ ucu (dizi) \\ sağ] \\ CDOT \\ Sol [\\ BACAK (Dizi) (* (35) ( R)) 3 & 1 & -1 \\\\ 4 & -1 & 3 \\\\ 2 & 6 & 0 \\\\ \\ \\ \\ \\ sol [\\ BACE (dizi) (* (35) (R) ) 5 & -19 & 5 \\\\ \\ ucu (dizi) \\ sağ] \\]

Cevap: $ \\ Sol [\\ BACE (MATRIX) 5 & -19 & 5 \\\\ UND (MATRIX) \\ ROUF] $.

Gördüğünüz gibi, bir vektör dizesini çarptığınızda ve çıkıştaki kare matristeki bir vektör sütunu çoğalttığınızda, her zaman aynı boyutta bir dize veya sütun alırız. Bu gerçeğin birçok uygulaması var - çözmekten lineer denklemler Her türlü koordinat dönüşümünden önce (bu, hangi sonunda, denklem sistemlerini de azaltır, ancak üzücü değil).

Sanırım her şey burada açıktı. Bugünün dersinin son bölümüne gidin.

Matrisin derecesine kadar yapımı

Tüm operasyonlar arasında belirli bir dikkat çarpan, bir dereceye kadar yükseltilir - bu aynı nesneyi kendilerine birkaç kez çarptığımız zamandır. Matrisler istisna değildir, aynı zamanda çeşitli derecelere de dikilebilirler.

Bu tür işler her zaman kabul edilir:

\\\\ cdot \\ sol [n \\ tims n \\ right] \u003d \\ sol [n \\ Times n \\ right] \\]

Ve her zamanki derece ile aynı olduğunu gösterir:

\\ [\\ '(Hizala) ve A \\ CDOT A \u003d ((a) ^ (2)); \\\\ & a \\ cdot a \\ cdot a \u003d ((a) ^ (3)); \\\\ \\ underbrace (a \\ cdot a \\ cdot \\ ldots \\ cdot a) _ (n) \u003d ((a) ^ (n)). \\\\ \\ end (hizala) \\]

İlk bakışta, her şey basit. Nasıl çalıştığını görelim:

Görev 7. Matrisini belirtilen dereceye getirin:

$ (((\\ Sola [\\ başlar (matris) 1 & 1 \\\\ 0 ve 1 \\ ucu (matris) \\ sağ]) ^ (3)) $

Karar. Peki, dikeyelim. İlk önce bir kareden erend:

\\ [\\ Başlar (hizalama) & ((\\ sola [\\ başlar (matris) 1 & 1 \\ \\ 0 & 1 \\\\ ucu (matris) \\ sağ]) ^ (2)) \u003d \\ sol [\\ başlar (matris ) 1 & 1 \\\\ 0 & 1 \\ \\ ucu (matris) \\ sağ] \\ CDOT \\ Sol [\\ BACAK (MATRIX) 1 & 1 \\\\ 0 & 1 \\ ucu (MATRIX) \\ Right] \u003d \\\\ & \u003d \\ Sol [\\ BACAK (Dizi) (* (35) (R)) 1 \\ CDOT 1 + 1 \\ CDOT 0 & 1 \\ CDOT 1 + 1 \\ CDOT 1 \\\\ 0 \\ CDOT 1 + 1 \\ CDOT 0 & 0 \\ CDOT 1 + 1 \\ CDOT 1 \\\\\\ UND (dizi) \\ sağ] \u003d \\\\ & \u003d \\ sol [\\ BACE (Dizi) (* (* (35) (R)) 1 & 2 \\\\ 0 & 1 \\\\ Son (dizi) \\ sağ] \\ ucu (hizala) \\]

\\ [\\ Başlar (hizalama) & ((\\ sol [\\ başlar (matris) 1 & 1 \\\\ 0 & 1 \\ ucu (matris) \\ sağ]) ^ (3)) \u003d ((\\ sol [\\ başlar (Matris) 1 & 1 \\\\ 0 & 1 \\\\ \\ ucu (matris) \\ sağ]) ^ (3)) \\ CDOT \\ Sol [\\ BACE (MATRIX) 1 & 1 \\\\ 0 & 1 \\ ucu (matris ) \\ Sağ] \u003d \\\\ & \u003d \\ sol [\\ BACAK (dizi) (* (35) (R)) 1 & 2 \\\\ 0 & 1 \\\\ \\ end (dizi) \\ right] \\ CDOT \\ Sol [\\ Başla (Matrix) 1 & 1 \\\\ 0 & 1 \\\\ ucu (Matrix) \\ Right] \u003d \\\\ \\ & \u003d \\ Sol [\\ BACE (Dizi) (* (35) (R)) 1 & 3 \\\\ 0 ve 1 \\\\\\ end (dizi) \\ sağ] \\ \\ \\ (hizala) \\]

Bu kadar.:)

Cevap: $ \\ Sol [\\ BACE (MATRIX) 1 & 3 \\\\ 0 & 1 \\\\ UND (MATRIX) \\ Right] $.

Görev 8. Matris'i belirtilen dereceye getirin:

\\ [(((\\ Sola [\\ başlar (matris) 1 & 1 \\\\ 0 ve 1 \\ \\ ucu (matris) \\ sağ]) ^ (10)) \\]

Karar. Ancak "derecenin çok büyük", "dünya adil değil" ve "öğretiler tamamen kaybettiği" gerçeğinde ağlamak gerekli değildir. Aslında, her şey kolaydır:

\\ [\\ Başlar (hizalama) & ((\\ sol [\\ başlar (matris) 1 & 1 \\\\ 0 & 1 \\\\ ucu (matris) \\ sağ]) ^ (10)) \u003d ((\\ sol [\\ başlar (Matris) 1 ve 1 \\\\ 0 & 1 \\\\ \\ ucu (matris) \\ sağ]) ^ (3)) \\ CDOT ((\\ sol [\\ başlar (matris) 1 & 1 \\\\ 0 & 1 \\\\\\ Son (Matrix) \\ sağ]) ^ (3)) \\ CDOT ((\\ sola [\\ başlar (matris) 1 & 1 \\\\ 0 & 1 \\ ucu (matris) \\ sağ]) ^ (3)) \\ CDOT \\ Sola [\\ BACAK (MATRIX) 1 & 1 \\\\ 0 & 1 \\ \\ end (MATRIX) \\ Right] \u003d \\\\ & \u003d \\ Sol (\\ Sol [\\ BACE (MATRIX) 1 & 3 \\\\ 0 & 1 \\ \\\\ UND (MATRIX) \\ Right] \\ CDOT \\ Sol [\\ BACE (MATRIX) 1 & 3 \\\\ 0 & 1 \\ \\ end (MATRIX) \\ Right] \\ Right) \\ CDOT \\ Sol (\\ Sol [\\ Bitti ( Matrix) 1 & 3 \\\\ 0 & 1 \\ \\ ucu (Matrix) \\ Right] \\ CDOT \\ Sol [\\ BACE (MATRIX) 1 & 1 \\\\ 0 & 1 \\ end (MATRIX) \\ Right] \\ Right) \u003d \\\\ & \u003d \\ sol [\\ başlar (matris) 1 & 6 \\\\ 0 & 1 \\ \\ ucu (matris) \\ sağ] \\ CDOT \\ Sol [\\ BACE (MATRIX) 1 & 4 \\\\ 0 & 1 \\\\\\ Son (Matrix) \\ Right] \u003d \\\\ & \u003d \\ Sol [\\ BACE (MATRIX) 1 & 10 \\\\ 0 & 1 \\\\ UN (MATRIX) \\ SAĞLIK] \\ \\ (HIGN) \\]

Not: İkinci satırda, çarpma ilişkisini kullandık. Aslında, önceki görevde kullandık, ama orada dolaylı bir şekilde.

Cevap: $ \\ Sol [\\ BACE (MATRIX) 1 & 10 \\\\ 0 & 1 \\\\ end (MATRIX) \\ Right] $.

Gördüğünüz gibi, matrisin yapımında karmaşık bir şey değil. Son örnek genelleştirilebilir:

\\ [(((\\ sola [\\ başlar (matris) 1 ve 1 \\\\ 0 ve 1 \\ ucu (matris) \\ sağ]) ^ (n)) \u003d \\ sol [\\ BACAK (dizi) (* (35) ( R)) 1 & n \\\\ 0 & 1 \\\\ \\ ucu (dizi) \\ sağ] \\]

Bu gerçeğin matematiksel indüksiyon veya doğrudan çarpma yoluyla kanıtlanması kolaydır. Bununla birlikte, her zaman derece bu tür desenler tarafından yakalanabileceği zaman değildir. Bu nedenle, dikkatli olun: genellikle birkaç matrisin "stroy", bazı düzenli kalıpları aramaktan daha kolay ve daha hızlı olduğu ortaya çıkıyor.

Genel olarak, olmadığı yerde en yüksek anlamı aramayın. Sonuç olarak, daha büyük bir matris yapımını göz önünde bulundurun - alternatif olarak $ \\ Sol [3 \\ Times 3 \\ Right] $.

Görev 9. Matrisini belirtilen dereceye getirin:

\\ [(\\ Sol [\\ başlar (matris) 0 ve 1 ve 1 \\\\ 1 ve 0 ve 1 \\ \\ \\ 1 ve 1 ve 0 \\ \\ \\ \\ \\ \\ \\ \\ \\ sağ]) ^ (3)) \\]

Karar. Düzenlilikleri aramayacak. "Stroy" çalışıyoruz:

\\ [(((\\ sol [\\ başlar (matris) 0 ve 1 ve 1 \\\\ 1 \\ \\ \\ \\ \\ \\ 1 ve 1 ve 0 \\ \\ end (matris) \\ sağ]) ^ (3)) \u003d ((\\ Sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 ve 0 & 1 \\\\ 1 ve 1 ve 0 \\ \\ \\ \\ \\ \\ \\ sağ]) ^ (2)) \\ CDOT \\ Sol [\\ Begin (Matrix) ) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 ve 1 ve 0 \\\\ \\ end (Matrix) \\ Right] \\]

Başlamak için, bu matrisi meydanda dikleyin:

\\ [\\ BACAK (HIGNIGN) & (((\\ Sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\ \\ \\ (MATRIX) \\ ROOGHT]) ^ ( 2)) \u003d \\ sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 ve 0 & 1 \\\\ 1 ve 1 ve 0 \\ \\ end (MATRIX) \\ Right] \\ CDOT \\ Sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 ve 1 ve 0 \\\\\\ end (MATRIX) \\ Right] \u003d \\\\ & \u003d \\ Sol [\\ BACE (Dizi) (* (35) (R) ) 2 & 1 & 1 \\\\ 1 & 2 & 1 \\\\ 1 ve 1 ve 2 \\ \\ ucu (dizi) \\ sağ] \\ ucu (hizalama) \\]

Şimdi küp içine dikildi:

\\ [\\ BACAK (HIGNIGN) & (((\\ Sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\ \\ \\ (MATRIX) \\ ROOGHT]) ^ ( 3)) \u003d \\ sol [\\ başlar (dizi) (* (35) (R)) 2 & 1 ve 1 \\\\ 1 ve 2 ve 1 \\\\ 1 ve 1 ve 2 \\ nin (dizi) \\ sağ] \\ CDOT \\ Sol [\\ BACE (MATRIX) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 ve 1 ve 0 \\\\ \\ end (MATRIX) \\ SAĞ] \u003d \\\\ & \u003d \\ Sol [\\ BACE (Dizi) (* (35) (r)) 2 ve 3 ve 3 \\\\ 3 ve 2 ve 3 \\\\ 3 ve 3 ve 2 \\ \\ \\ \\ \\ \\ \\ \\ sağ] \\ ucu (hizalama) \\]

Bu kadar. Görev çözüldü.

Cevap: $ \\ Sol [\\ BACE (MATRIX) 2 & 3 & 3 \\\\ 3 & 2 & 3 \\\\ 3 ve 3 ve 2 \\ \\ end (MATRIX) \\ Right] $.

Gördüğünüz gibi, hesaplama hacmi daha fazla hale geldi, ancak bunun anlamı bundan değişmedi. :)

Bu derste tamamlanabilir. Bir dahaki sefere ters işletmeye bakacağız: mevcut işlere göre orijinal faktörleri arayacağız.

Muhtemelen tahmin ederken, hakkında olacak ters matris ve konumunun yöntemleri.

Anlatım 6. Bilgisayar matematiğinin tipik problemlerini çözmek için paralel sayısal algoritmalar: Matrislerin çoğaltılması.

Matrisin vektöre çarpması. Mümkün olan maksimum hızı elde edin. Orta seviye paralelliği kullanarak. P \u003d n için paralel hesaplamaların organizasyonu. Sınırlı bir işlemci setinin kullanımı. Matris çarpımı. Problem çözme algoritmalarının makro işlem analizi. Veri ayrılmasına dayanan paralellik organizasyonu.

Vektördeki matrisin çarpılması

Matrisin Vector'a çarpma sorunu oranlarla belirlenir

Böylece, ortaya çıkan sonuç, elde edilen vektör, matris satırlarını ve vektörünü çarpmak için aynı tür işlemlerin tekrarlanmasını içerir. Böyle bir işlemin elde edilmesi, matris ve vektörün dize elemanlarının elemanı çarpmasını ve elde edilen ürünlerin bir sonraki toplamını içerir. Toplam gerekli skaler operasyon sayısı büyüklüğü ile tahmin edilmektedir.

Matris ve vektörün çarpılmasında gerçekleştirilen eylemden aşağıdaki gibi, problemi çözmek için paralel yöntemler paralel toplama algoritmaları temelinde elde edilebilir (bkz. Paragraf 4.1). Bu bölümde, paralelleştirme yöntemlerinin analizi, kullanımı için mevcut işlemcilerin miktarına bağlı olarak paralel hesaplama organizasyonu göz önüne alınarak tamamlanacaktır. Ayrıca, matrisin vektöre çarpma sorunu örneği üzerine, işbirliği yapan etkileşimi organize etmek için maliyetleri azaltmak için bilgisayar sisteminin en uygun topolojisini (işlemciler arasındaki mevcut iletişim kanalları) seçme ihtiyacına dikkat çekilecektir.

Mümkün olan maksimum hız ()

Seçmek için vektördeki matrisin çarpma algoritmasındaki bilgi bağımlılıklarının bir analizini gerçekleştirin. muhtemel yöntemler paralelleştirme. Görülebileceği gibi, vektördeki matrisin bireysel çizgilerinin çarpımını hesaplarken yapılır, bağımsızdır ve paralel olarak yapılabilir;

Her satırın Vector'a çarpılması, bağımsız ayrıntılı çarpma işlemlerini içerir ve ayrıca paralel olarak da gerçekleştirilebilir;

Matris dizesinin her bir çarpma işleminde elde edilen ürünlerin topluluğu, toplam algoritması (seri algoritma, normal ve değiştirilmiş kaskad şemaları) için önceden düşünülen seçeneklerden birine göre yapılabilir.

Böylece, gerekli maksimum sayıda işlemci büyüklüğü ile belirlenir.

Böyle bir sayıda işlemcinin kullanımı aşağıdaki gibi gösterilebilir. Birçok işlemci gruplara ayrılmıştır

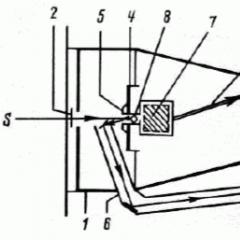
her biri, tek bir matris dizesinin Vector'a çarpma işlemini gerçekleştirmek için ayarlanan bir işlemci temsil eder. Her grup işlemcisi üzerindeki hesaplamaların başında, matris string elemanı ve ilgili vektör öğesi gönderilir. Daha sonra, her işlemci bir çarpma işlemi gerçekleştirir. Daha sonra hesaplamalar, basamaklı bir toplama şemasına göre yapılır. Şekil 2'deki çizim için. 6.1, bir matris boyutuna sahip grup işlemciler için hesaplamalı bir şemayı göstermektedir.

İncir. 6.1. Bilgi işlem diyagramı çoklu multipli matris satır vektör üzerinde

İşlemciler kullanırken paralel algoritmanın yürütme süresi, paralel bir çarpma işleminin yürütülmesi ve bir Cascade şeması yürütme süresi ile belirlenir

Sonuç olarak, algoritmanın performans göstergeleri aşağıdaki oranlarla belirlenir:

Matrisin çarpılması problemi için, en uygun topolojilerin vektöründeki yapılar, sağlanan yapılar hızlı iletim Cascade bir toplama şemasında veri (tek uzunluk yolları) (bkz. Şekil 4.5). Bu tür topolojiler, tam bir bağ sistemine sahip yapıdır ( tam grafik) BEN. hiperkub. Diğer topolojiler, veri transfer yollarının uzaması nedeniyle iletişim süresinde bir artışa yol açar. Yani, işlemcilerin yalnızca sol ve sağdaki en yakın komşularla bir bağlantı sistemi olan bir lineer bir düzenleme ile ( kural veya yüzük) Cascade şeması için, her birinin transmisyon yolunun yineleme üzerindeki kısmi miktarın uzunluğu eşittir. Doğrusal bir yapıya sahip topolojilerdeki uzunluk uzunluğu boyunca veri iletiminin, veri iletim işlemlerinin yürütülmesini gerektirdiğini varsayarsak, toplam paralel işlem sayısı (veri aktarımının toplam süresi) değeri ile belirlenir.

(İlk işlemci önyükleme için veri iletimi hariç).

Bir hesaplama sisteminin bir topoloji ile dikdörtgen şeklinde uygulanması İki boyutlu kafes Boyut, gerçekleştirilen hesaplamanın basit ve görsel bir yorumuna yol açar (ağ yapısı, işlenecek verilerin yapısına karşılık gelir). Böyle bir topoloji için, matris dizesi, kafesin yataylarını yerleştirmek için en uygundur; Bu durumda, vektörün elemanları bilgisayar sisteminin dikeylerine gönderilmelidir. Böyle bir veri yerleşiminde hesaplamaları gerçekleştirmek, kafenin sıralarıyla paralel olarak gerçekleştirilebilir; Sonuç olarak, toplam veri iletimi sayısı cetvelin () için sonuçlarla çakışıyor.

Haberleşme eylemleri, görevin çözülmesi için gerçekleştirilen, MVS işlemcilerinin çiftleri arasında veri iletilmesinde oluşur. Detaylı analiz Bu tür işlemlerin uygulanmasının süresi 3.3. Paragrafta gerçekleştirilmiştir.

4. Paralel bir algoritmanın uygulanması için öneriler. Paralel bir algoritmayı uygularken, kullanılan kaynak işlemcilerin indirilmesinde ilk aşamayı seçmeniz önerilir. En basit bu başlatma, hesaplama sisteminin topolojisi ile formda topolojisi ile sağlanır. tam grafik (Bir paralel veri aktarımı işlemi ile yükleme sağlanır). Formda birçok işlemci düzenlerken hypercuba Merkezi kontrol işlemcisinin matris sıralarının ve vektörün işlemci gruplarının kontrol işlemcilerinin, tamir, matrisin elemanlarını seçtiği, matris satırlarının ve vektörün kontrol işlemcilerine dağıtılmasını sağlayan ilk yükleme işleminin iki seviyeli yönetimi olabilir. aktüatördeki satırlar ve vektör. Formdaki topolojiler için cetveller veya yüzükler Sıralı veri iletim işlemleri, sıralı azalan miktarda verilerden, öğelerinden gönderilen miktarda verilmiştir.

Orta seviye paralellik ()

1. Paralel bir bilgi işlem yöntemi seçmek. Kullanılan mevcut işlemci miktarında (), matris dizelerinin çarpım işlemlerini gerçekleştirirken, geleneksel bir cascade toplama şeması, vektöre uygulanamaz hale gelir. Basitlik için, malzemeyi koyarız ve değiştirilmiş basamaklı şemayı kullanırız. Her işlemcinin ilk yükü bu durumdaki artışlar ve işlemci, matris satırlarının ve vektörün () kısımları yüklenir (). Vektördeki matrisin çarpımının yürütme süresi, değer olarak değerlendirilebilir.

Değiştirilmiş bir kaskad şeması uygulamak için gereken işlemci sayısını kullanırken, yani için Bu ifade, yürütme süresinin bir tahminini verir (ne zaman).

Algoritmanın yürütme süresi olduğu tahmin edildiğinde işlemciler sayısıyla, her bir kademeli toplama yinelemesinin kullanıldığı yeni bir paralel bilgi işlem yürütme düzeni önerilebilir. yapılmayan işlemci setleri. Mevcut sayıda işlemci sayısının böyle bir kampanyasıyla, matris hattının ve vektörün sadece bir çarpma işlemini uygulamak için yeterli olduğu ortaya çıkıyor. Ek olarak, bir sonraki basamaklandırma toplamının bir sonraki yinelemesini yaparken, önceki tüm yinelemelerin yürütülmesinden sorumlu işlemciler ücretsizdir. Bununla birlikte, önerilen bir yaklaşımın bu eksikliği, matrisin aşağıdaki satırlarını işlemek için rölanti işlemcileri kullanılarak saygınlığa ödenebilir. Sonuç olarak, aşağıdaki şema oluşturulabilir. konveyörmatrisin ve vektörün çarpılması gerçekleştirilmesi:

Birçok işlemci döngüsünün olmayan işlemci gruplarına ayrılmıştır.

bu durumda, grup, işlemcilerden oluşur ve kaskad algoritmasının yinelemesini gerçekleştirmek için kullanılır (grup, ilköğretim çarpımını uygulamak için kullanılır); toplam işlemci sayısı;

Hesaplamaların başlatılması, matrisin ve vektörün 1 dizisinin bir grubunun bir grubunun yükleme işlemcilerinden oluşur; İlk yükün ardından, eleman çarpımının paralel çalışması ve geleneksel cascade toplama şemasının uygulanmasının uygulanması;

Hesaplamalar yaparken, işlem tamamlandıktan sonra her seferinde, bir sonraki matrisin bir sonraki satırının grubu grubunun işlemcileri yüklenir ve yeni yüklenen veriler için hesaplama işlemi başlatılır.

Açıklanan algoritmanın uygulanmasının bir sonucu olarak, çok sayıda işlemci, matris dizesinin çarpımını vektöre çarpmasını gerçekleştirmek için konveyörü uygular. Aynı konveyörde, matrisin birkaç ayrı çizgisi farklı işlem aşamalarında bulunabilir. Örneğin, birinci satırın elemanlarının ve vektör işlemcilerinin elemanlarının çarpışmasından sonra, grup işlemciler matrisin ilk dizesi için basamaklı algoritmanın ilk yinelemesini gerçekleştirir ve grup işlemcileri, temel çarpımını yürütecektir. Matrisin ikinci çizgisinin değerleri vb. Şekil 2'deki çizim için. 6.2 Konveyörün 2 yinelemesinden sonra hesaplama işleminin durumu verilir.

İncir. 6.2. 2 yineleme tamamladıktan sonra matris dizesinin çoğalması için konveyör durumu

2. Algoritmanın performansının değerlendirilmesi. İlk satırın vektöre basamak şemasına göre çarpılması, yürütmeden sonra () paralel işlemlerden sonra da tamamlanacaktır. Diğer çizgiler için - bilgi işlem konveyör şemasına göre, her bir sonraki satırın çarpma sonuçlarının ortaya çıkması, konveyörün sonraki bir yinelemesini tamamladıktan sonra ortaya çıkacaktır. Sonuç olarak, matrisin çarpımını vektöre yapmanın toplam süresi telaffuz edilebilir

Bu derecelendirme, önceki paragrafta () açıklanan paralel algoritmanın yürütme süresinden biraz daha fazladır, ancak yeni önerilen yöntem, iletilen verilerin daha küçük bir miktarını gerektirir (vektör sadece bir kez gönderilir). Ek olarak, konveyör şemasının kullanılması, hesaplamaların sonuçlarının bir kısmının daha önceki bir görünümüne (bir dizi veri işleme durumunda yararlı olabilecek) yol açar.

Sonuç olarak, algoritmanın performans göstergeleri aşağıdaki formun ilişkileri ile belirlenir:

3. Bilgi işlem sisteminin topolojisinin seçimi. Bilgi işlem sisteminin uygun topolojisi, bilgi işlem devresi tarafından tamamen belirlenir - bu tamamlandı İkili ağaç yükseklik. Böyle bir ağ topolojisiyle veri iletimlerinin sayısı, konveyör tarafından yapılan toplam yineleme sayısı ile belirlenir, yani.

Hesaplamaların başlatılması ağaç yaprakları ile başlar, toplama sonuçları kök işlemcisinde biriktirilir.

Haberleşme sistemleri için gerçekleştirilen iletişimin karmaşıklığının analizi, diğer işbirliği tonu topolojilerine sahip bilgisayar sistemleri için gerçekleştirilmelidir. kendini beğenme (Ayrıca bkz. Madde 3.4).

Paralel bilgi işlem organizasyonu ne zaman

1. Paralel bir bilgi işlem yöntemi seçmek. Matrisin Vector'a çarpması için işlemciler kullanırken, daha önce halihazırda el kitabında, matris dizelerinin işlemcilere dağıtıldığı ve her işlemcinin bir çarpma işlemini uyguladığı çizgi çarpımının paralel bir algoritması kullanılır. matrisin vektöre ayrı satır. Paralel bilgi işlem organize etmenin bir başka yolu binadan oluşabilir. Çarpma için konveyör şeması Vektör üzerinde dize matrisi çarpma(skaler ürün vektörleri) mevcut tüm işlemcileri doğrusal bir sekans biçiminde bulabilmesi ( cetveller).

Benzer bir hesaplama şeması aşağıdaki gibi tanımlanabilir. Doğrusal bir sekans biçiminde birçok işlemciyi hayal edin (bkz. Şekil 4.7):

her işlemci,,, matris kolonunun ve vektör elemanının elemanlarını çarpmak için kullanılır. Her işlemciye hesaplamalar yapılması, aşağıdakilerden oluşur:

Matrisin sütununun bir sonraki elemanı istenir;

Elemanların çarpılması ve;

Yukarıdaki işlemcinin hesaplanmasının sonucu istenmektedir;

Değerlerin eklenmesi gerçekleştirilir;

Sonuç, aşağıdaki işlemciye gönderilir.

İncir. 6.3. İki yinelemenin yürütülmesinden sonra matris dizesinin çoğalması için doğrusal konveyörün durumu

Açıklanan şemayı başlatırken, bir dizi ek eylemi gerçekleştirmeniz gerekir:

İlk yinelemeyi gerçekleştirirken, her işlemci ayrıca vektör öğesini ister;

Hesaplamaları senkronize etmek için (devrenin bir sonraki yinelemesini yürütürken, önceki işlemcinin hesaplanmasının sonucu) işlemcinin başlatma aşamasında () işlemcinin başlatma aşamasında, () bekleme döngüsünü gerçekleştirir.

Ek olarak, bir önceki işlemciye sahip olmayan birinci işlemci için tarif edilen şemanın homojenliği için, boş bir ekleme işlemi ( ).

Şekil 2'deki çizim için. 6.3, konveyörün ikinci yinelemesinden sonra hesaplama işleminin durumunu göstermektedir.

2. Algoritmanın performansının değerlendirilmesi. İlk satırın vektöre, tarif edilen konveyör şemasına göre çarpılması () paralel işlemlerin yürütülmesinden sonra tamamlanacaktır. Aşağıdaki satırların çarpımının sonucu, konveyörün düzenli bir yinelemesini tamamladıktan sonra ortaya çıkacaktır (hatırlayın, her işlemcinin yinelemesi, çarpma ve ek işlemler gerçekleştirmeyi içerir). Sonuç olarak, matrisin çarpımının vektöre toplam çarpma süresi oranı ile ifade edilebilir:

Bu değerlendirme aynı zamanda minimumdan daha büyüktür. olası zaman Paralel bir algoritma yapmak. Konveyör hesaplama devresinin kullanımının faydası, önceki paragrafta belirtildiği gibi, bulaşan veri sayısını azaltmada ve hesaplama sonuçlarının önceki görünümünde.

Bu hesaplamalı şemanın etkinliğinin göstergeleri ilişkiler tarafından belirlenir:

, ,

3. Bilgi işlem sisteminin topolojisinin seçimi. Açıklanan algoritmayı gerçekleştirmek için hesaplama sisteminin istenen topolojisi, önerilen bilgi işlem şeması tarafından benzersiz bir şekilde belirlenir - bu doğrusal olarak sipariş edilen birden fazla işlemcidir ( kural).

Sınırlı bir işlemci seti ()

1. Paralel bir bilgi işlem yöntemi seçmek. İşlemci sayısında bir azalma ile, matrisin toplu çarpışmanın paralel bilgi işlem şeması, yapım çarpma için algoritmanın uyarlanması sonucu elde edilebilir. Bu durumda, eleman çarpma sonuçlarının basamaklandırma toplama şeması dejenere edilir ve matris dizesinin vektöre çarpması, tek bir işlemciye tamamen gerçekleştirilir. Bu yaklaşımla elde edilen hesaplamalı şema aşağıdaki gibi belirtilebilir:

Mevcut işlemcilerin her biri için, matrisin vektörü ve çizgileri gönderilir;

Matris dizelerinin bir çarpma işleminin gerçekleştirilmesi, vektöre geleneksel bir seri algoritma kullanılarak gerçekleştirilir.

Matrisin boyutunun işlemci sayısının birden çok olmayabileceği ve daha sonra matris dizesinin işlemciler arasında eşit olarak bölünemeyeceği belirtilmelidir. Bu durumlarda, işlemcilerin tek tip yükleme sisteminden geri çekilmesi ve kuralları işlemcilere yerleştirilmesinin yalnızca (yani, bir satırın elemanları) gerçekleştirilmesi için basit bir bilgi işlem şeması elde etmek mümkündür. matrisin birkaç işlemci arasında ayrılamaz). Eşit olmayan sayıda satır, farklı hesaplama yüklerinin işlemcilerine yol açar; Böylece, hesaplamaların tamamlanması (sorun sorununun genel süresi), en yüklenen işlemcinin çalışmaları sırasında belirlenecektir (bireysel işlemciler, hesaplamalar paylarının tükenmesinden dolayı bu toplam sürede durabilir. ). İşlemcinin düzensiz yüklenmesi, MVS kullanmanın verimliliğini ve dikkate alınması sonucu verimliliği azaltır bu örnek Bunu sonlandırabilirsin sorun Dengeleme

3. Bilgi işlem sisteminin topolojisinin seçimi. Önerilen hesaplamalı şemada gerçekleştirilen işbirlikleri etkileşimlerinin doğası gereği, işlemcilerin MVS'nin olası bir topolojisi biçimindeki organizasyonu olabilir yıldızlar (Bkz. Şekil 1.1). Benzer bir topolojinin kontrol işlemcisi, bilgi işlemcilerini kaynak verilerle indirmek ve yapılan hesaplama sonuçlarını almak için kullanılabilir.

Matris Çarpma

Matrisin matrisinin çarpılması sorunu, oranlarla belirlenir.

(Malzemenin basitliği için, değişken matrislerin kare ve sipariş sahip olduğunu varsayacağız).

Bu görevi gerçekleştiren olası paralel yöntemlerin analizi, matrisin çarpım probleminin vektöre çarpma sorunu ile analoji ile gerçekleştirilebilir. Böyle bir analizi bırakmak bağımsız çalışmaMatris çarpımının görevi, karmaşık görevleri çözmek için paralel yollar oluşturmak için çeşitli ortak yaklaşımların kullanımı örneğini göstereceğiz.