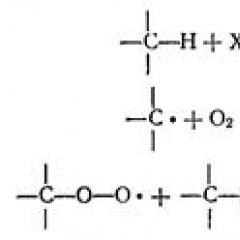
Geom Progression of formula. Geometric progression
Geometric progression, along with arithmetic, is important numerical nextwhich is studied in the school year of algebra in grade 9. In this article, consider the denominator of geometric progression, and how its value affects its properties.
Definition of progression geometric
To begin with, we give the definition of this numeric row. The progress of geometric is called such a number of rational numbers, which is formed by the consistent multiplication of its first element for a constant number, which is called the denominator.
For example, the numbers in a row 3, 6, 12, 24, ... is a geometric progression, because if you multiply 3 (first element) by 2, then we get 6. If 6 multiply by 2, then we get 12, and so on.
The members of the sequence under consideration are customary to signify the AI \u200b\u200bsymbol, where i is an integer indicating the element number in the row.
The above definition of progression can be written in the language of mathematics as follows: An \u003d BN-1 * A1, where b is the denominator. Check out this formula easily: if n \u003d 1, then b1-1 \u003d 1, and we obtain A1 \u003d A1. If n \u003d 2, then An \u003d b * A1, and we again come to the definition of the number of numbers under consideration. Similar arguments can be continued for large values \u200b\u200bof N.
The denominator of the progression of geometric

The number B fully determines which character will be all the numerical series. The denominator B may be positive, negative, and also have a value more than one or less. All listed options lead to different sequences:
- b\u003e 1. There is an increasing number of rational numbers. For example, 1, 2, 4, 8, ... if the element A1 is negative, then the entire sequence will increase only by the module, but to decrease with the sign of the numbers.
- b \u003d 1. Often this case is not called progress, since there is a normal number of identical rational numbers. For example, -4, -4, -4.
Formula for sum
Before moving to consideration specific tasks Using the denominator of the type of progression under consideration, it is necessary to bring an important formula for the amount of its first n elements. The formula has the form: Sn \u003d (Bn - 1) * A1 / (B - 1).
You can get this expression yourself if you consider the recursive sequence of progression members. We also note that in the above formula it is enough to know only the first element and the denominator to find the amount of an arbitrary number of members.
Infinitely decreasing sequence

Above was given an explanation that it represents. Now, knowing the formula for SN, we apply it to this numerical row. Since any number, the module of which does not exceed 1, when erected in high degrees tends to zero, that is, b∞ \u003d\u003e 0, if -1
Since the difference (1 - b) will always be positive, regardless of the values \u200b\u200bof the denominator, the sign of the amount of decreasing infinitely progression of geometric S∞ is uniquely determined by the sign of its first element A1.
Now consider several tasks where we show how to apply the knowledge gained on specific numbers.
Task number 1. Calculation of unknown elements of progression and amount
The progression of the geometric, denominator of the progression 2, and its first element 3 is equal to its 7th and 10th members, and what is the sum of its seven initial elements?
The condition of the problem is quite simple and implies the direct use of the above formulas. So, to calculate the element with the number N, we use the expression AN \u003d BN-1 * A1. For the 7th element, we have: A7 \u003d B6 * A1, substituting the known data, we obtain: A7 \u003d 26 * 3 \u003d 192. The same way is done for the 10th member: a10 \u003d 29 * 3 \u003d 1536.
We use the well-known formula for the amount and determine this value for the 7th first elements of the series. We have: S7 \u003d (27 - 1) * 3 / (2 - 1) \u003d 381.
Task number 2. Determination of the amount of arbitrary elements of progression
Let -2 be equal to an denominator of progression in the geometric progression of BN-1 * 4, where N is an integer. It is necessary to determine the amount from the 5th to the 10th element of this series inclusive.
The problem may not be solved directly using the known formulas. It can be solved by 2 different methods. For the completeness of the presentation of the topic, we bring both.
Method 1. The idea of \u200b\u200bit is simple: you need to calculate the two relevant sums of the first members, and then deduct from one other. Calculate a smaller amount: S10 \u003d ((-2) 10 - 1) * 4 / (-2 - 1) \u003d -1364. Now we calculate a large amount: S4 \u003d ((-2) 4 - 1) * 4 / (-2 - 1) \u003d -20. Note that in the latter expression only 4 terms were summed up, since the 5th is already included in the amount that you want to calculate under the problem of the problem. Finally, we take the difference: S510 \u003d S10 - S4 \u003d -1364 - (-20) \u003d -1344.
Method 2. Before substituting the numbers and count, it is possible to obtain a formula for the amount between members M and N of the series under consideration. We do absolutely the same as in Method 1, only we work first with the symbol presentation of the amount. We have: SNM \u003d (BN - 1) * A1 / (B - 1) - (BM-1 - 1) * A1 / (B - 1) \u003d A1 * (BN - BM-1) / (B - 1). In the resulting expression, you can substitute known numbers and calculate the final result: S105 \u003d 4 * ((-2) 10 - (-2) 4) / (-2 - 1) \u003d -1344.
Task # 3. What is the denominator?

Let A1 \u003d 2, find the denominator of the progression of geometric, provided that its infinite amount is 3, and it is known that this is a decreasing number of numbers.
By the condition of the task it is not difficult to guess which formula should be used to solve it. Of course, for the sum of the progression of infinitely decreasing. We have: S∞ \u003d A1 / (1 - b). Where express the denominator: B \u003d 1 - A1 / S∞. It remains to substitute the known values \u200b\u200band obtain the desired number: B \u003d 1 - 2/3 \u003d -1 / 3 or -0.333 (3). You can qualitatively check this result if you remember that for this type of sequence, the module b should not go beyond 1. As can be seen, | -1 / 3 |
Task number 4. Restoration of a number of numbers
Let 2 elements of the numerical series, for example, the 5th equal to the 30th and 10th equal to 60. It is necessary to restore the whole range according to these data, knowing that it satisfies the properties of the progression of geometric.
To solve the task, it is necessary to start a corresponding expression for each well-known member. We have: A5 \u003d B4 * A1 and A10 \u003d B9 * A1. Now we divide the second expression on the first, we obtain: A10 / A5 \u003d B9 * A1 / (B4 * A1) \u003d B5. From here, we determine the denominator, taking the root of the fifth degree from the relationship known from the terms of the task of the members, B \u003d 1,148698. The resulting number is substituted into one of the expressions for the known element, we obtain: A1 \u003d A5 / B4 \u003d 30 / (1,148698) 4 \u003d 17,2304966.
Thus, we found, which is equal to the denominator of the progression of BN, and the geometrical progression of BN-1 * 17,2304966 \u003d an, where B \u003d 1,148698.
Where are the progression of geometric?

If it were not for the use of this numerical series in practice, his study would be reduced to purely theoretical interest. But this application exists.

The following are the 3 most famous examples:
- The paradox of Zeno, in which the dexterous Achilles cannot catch up with a slow turtle, is solved using the concept of decreasing infinitely sequences of numbers.
- If there is wheat grains on each cell of the chessboard, so that on the 1st cell put 1 grain, on the 2nd - 2, on the 3rd - 3 and so on, then to fill all the cells of the board will be needed 18446744073709551615 grains!
- In the game "Hanoi Tower" to rearrange the discs from one rod to another, it is necessary to perform 2n - 1 operations, that is, their number increases in the geometric progression on the number of disks used.
Kyiv Street, 16 0016 Armenia, Yerevan +374 11 233 255
Geometric progression is the new kind The numeric sequence with which we have to meet. For a successful acquaintance does not prevent at least know and understand. Then there will be no problems with geometric progress.)
What geometric progression? The concept of geometric progression.
We begin the excursion, as usual, from the elementary. I am writing an unfinished sequence of numbers:
1, 10, 100, 1000, 10000, …
Can you catch pattern and say what numbers will go further? Pepper is clear, then the numbers are 100,000, 10,000,000 and so on. Even without much mental tension, everything is clear, really because?)
Okay. Another example. I am writing this sequence:
1, 2, 4, 8, 16, …
Will be able to say what numbers will go further, following the number 16 and call eighth Sequence member? If you realized that it will be the number 128, it is very good. So, half the way in understanding meaning and key moments Geometric progression has already been done. You can grow further.)
And now again go from sensations to strict mathematics.
Key points of geometric progression.
Key point number 1.
Geometric progression is sequence of numbers. Like progression. Nothing cunning. Only this sequence is arranged differently.Hence, naturally, and another name wears, yes ...
Key point number 2.
With the second key point, the question of the stylming will be. Let's come back a little back and remember the key property of arithmetic progression. Here it is: each member differs from the previous on the same magnitude.
Is it possible to formulate a similar key property for geometric progression? Think a little ... Take a look at the examples given. Guess? Yes! In the geometric progression (any!) Everyone is different from the previous at the same number of times.Always!
In the first example, this is a dozen. What a member of the sequence neither take it more than the previous one ten times.
In the second example, this is a twice: each member more than the previous one twice.
It is this key to the geometric progression and differs from arithmetic. In arithmetic progression, every next member is obtained addness The same magnitude to the previous member. And here - multiplying The previous member for the same magnitude. That's the whole difference.)
Key point number 3.
This key point is completely identical to such for arithmetic progression. Namely: each member of the geometric progression is in its place.All exactly in-point as in arithmetic progression and comments, I think unnecessary. There is a first member, there is a hundred first, etc. Rearrange at least two members - regularity (and together with it and geometric progression) will disappear. There will be simply a sequence of numbers without any logic.
That's all. That's the whole point of geometric progression.
Terms and designations.
But now, having understood with the meaning and key moments of geometric progression, it is possible to proceed to the theory. And otherwise what theory without understanding the meaning is true?
How to denote geometric progression?
How geometric progression is recorded in general? No problem! Each member of the progression is also written in the form of the letter. Only for arithmetic progression, usually used letter "but"for geometric - beak "B". Member number, as usual, is indicated the index on the right below. Progression members themselves simply list through the comma or point with a comma.
Like this:
b 1,b. 2 , b. 3 , b. 4 , b. 5 , b. 6 , …
Briefly, this progression is recorded like this: (b N.) .
Or so, for the final progressions:
B 1, B 2, B 3, B 4, B 5, B 6.
B 1, b 2, ..., b 29, b 30.
Or, in a brief record:
(b N.), n.=30 .
Here, in fact, all the symbols. All the same, only the letter is different, yes.) And now go directly to the definition.
Determination of geometric progression.
Geometric progression is number sequence, the first member of which is different from zero, and each subsequent member is equal to the previous member multiplied by the same non-zero number.
That's all definition. Most words and phrases are understandable and familiar to you. If, of course, you understand the meaning of the geometric progression "on the fingers" and in general. But there are several new phrases for which I would like to pay special attention.
First, words: "The first member of which distracted from zero".
This restriction for the first term was not introduced by chance. What do you think will happen if the first member b. 1 Will it turn out to be zero? What will be the second member, if each member is more than the previous one in the same number of times? Suppose three times? Let's see ... We multiply the first term (i.e. 0) for 3 and get ... zero! And the third dick? Also zero! And the fourth dick is also zero! Etc…
We get just a bag of rebounds The zeros sequence:
0, 0, 0, 0, …
Of course, such a sequence has the right to life, but it does not represent any practical interest. Everything is clear. Anyone her dick is zero. The amount of any number of members is also zero ... What can I do with her interesting? Nothing…
Next keywords: "Multiplied to the same non-zero number."
This is the same number too wears your special name - denominator geometric progression. We start acquaintance.)
Denominator geometric progression.
Everything is easier than simple.
An denominator of geometric progression is a non-zero number (or value), showinghow many times Each member of progression more than the previous one.
Again, by analogy with arithmetic progress, the key word to pay attention to this definition is the word "more". It means that each member of the geometric progression is obtained multiplyingon this most denominator previous member.
I explain.
To calculate, let's say second Member, you need to take first Member I. multiply His denominator. For calculation tenth Member, you need to take ninth Member I. multiply His denominator.
The denominator itself of geometric progression can at the same time to be any. Anyone! Whole, fractional, positive, negative, irrational - every way. In addition to zero. This is about this and tells us the word "non-zero" in the definition. Why this word is needed here - about this below.
Denominator geometric progression denotes, most often, beak q..
How to find it q. ? No problem! Need to take any member of the progression and share. Division is fraction. Hence the name - "denominator of progression." The denominator, it is usually in the fraraty sitting, yes ...) Although, in logic, the magnitude q. should be called private geometric progression, by analogy with difference For arithmetic progression. But agreed to call denominator. And we will not be inventing the bike either.)
We define, for example, the value q. For such geometric progression:
2, 6, 18, 54, …
All elementary. Take anyone The number of sequences. What we want, so take. In addition to the first. For example, 18. And divide on previous number. That is, by 6.
We get:
Q. = 18/6 = 3
That's all. This is the right answer. For this geometric progression, the denominator is three.
Find now the denominator q. For other geometric progression. For example, this is:
1, -2, 4, -8, 16, …
All the same. Whatever signs are from the members themselves, we still take anyone The number of sequences (for example, 16) and divide on previous number (i.e. -8).
We get:
d. = 16/(-8) = -2
And all the things.) This time, the denominator of the progression was negative. Minus two. It happens.)
Take now this is the progression:
1, 1/3, 1/9, 1/27, …
And again, regardless of the type of numbers facing the sequence (at least, at least fractional, even negative, although irrational), take any number (for example, 1/9) and divide the previous number (1/3). According to the rules of action with fractions, naturally.
We get:
And that's all.) Here the denominator turned out to be fractional: q. = 1/3.
But this is "progression" as you?
3, 3, 3, 3, 3, …
Obviously here q. = 1 . Formally, this is also a geometric progression, only with identical members.) But such progressions for studying and practical application not interesting. Just like progression with solid zeros. Therefore, we will consider them and will not.
As you can see, the denominator of progression can be any - whole, fractional, positive, negative - every way! Can not be just zero. Didn't guess why?
Well, let's see what a specific example, what will happen if you take as a denominator q. Nolik.) Let us, for example, will b. 1 = 2 , but q. = 0 . What will the second term be equal then?
We consider:
B. 2 = b. 1 · q. \u003d 2 · 0 \u003d 0
And the third dick?
B. 3 = b. 2 · q. \u003d 0 · 0 \u003d 0
Types and behavior of geometric progressions.
With everything was more or less clear: if the difference in progression d. Positive, then progression increases. If the difference is negative, then the progression decreases. Only two options. There is no third.)
But with the behavior of geometric progression, everything will be more interesting and more diverse!)
As soon as members behave here: and increase, and decrease, and they are unlimited approach to zero, and even change the signs, alternately rushing in the "plus", then in "minus"! And in all this variety, you need to be able to understand well, yes ...
We understand?) We start from the simplest case.
The denominator is positive ( q. >0)
With a positive denominator, firstly, members of geometric progression can go into plus infinity (i.e. increase indefinitely) and can go into minus Infinity(i.e., unlimited decrease). We have already picked up for such behavior of progress.
For example:
(b N.): 1, 2, 4, 8, 16, …
Everything is simple here. Every member of the progression is obtained more than previous. And every member is obtained multiplying Previous member on positive number +2 (i.e. q. = 2 ). The behavior of such a progression is obvious: all members of the progression is growing indefinitely, going into space. In plus infinity ...
And now this is the progression:
(b N.): -1, -2, -4, -8, -16, …
Here, too, every member of the progression is obtained multiplying Previous member on positive number +2. But the behavior of such a progression is already the opposite: each member of the progression is obtained less than previous, And all its members will unlimited decreasing, leaving the minus infinity.
And now let's think: what about these two progressions? That's right, denominator! Here and there q. = +2 . Positive.Two. And here behavior These two progressions are fundamentally different! Didn't guess why? Yes! All business B. first member!It is he, as they say, and orders music.) See ourselves.
In the first case, the first term of progression positive (+1) And, it became, all subsequent members obtained by multiplying positivedenominator q. = +2 will also be positive.
But in the second case, the first member negative (-one). Therefore, all subsequent members of the progression obtained by multiplying positive q. = +2 will also get negative. For "minus" on the "plus" always gives "minus", yes.)
As you can see, in contrast to arithmetic progression, geometric progression can behave completely differently not only depending from the denominatorq.but also depending from the first term, Yes.)
We remember: the behavior of geometric progression is uniquely determined by its first member b. 1 and denominatorq. .
And now we begin the analysis of less familiar, but but much more interesting cases!
Take, for example, this is the sequence:
(b N.): 1, 1/2, 1/4, 1/8, 1/16, …
This sequence is also a geometric progression! Each member of this progression is also obtained multiplying previous member, at the same number. Only the number is - fractional: q. = +1/2 . Or +0,5 . And (important!) Number, little units:q. = 1/2<1.
What is interesting this geometric progression? Where are her members seek? Let's see:
1/2 = 0,5;
1/4 = 0,25;
1/8 = 0,125;
1/16 = 0,0625;
…….
What interesting here can be noticed? First, immediately striking the decrease of members of the progression: each her member less Previous Rivne 2 times. Or, in accordance with the definition of geometric progression, each member moreprevious at 1/2 timesbecause denominator progression q. = 1/2 . And from multiplication on positive, less united, the result usually decreases, yes ...
what yet Can you notice in the behavior of this progression? Does her members decrease unlimitedgoing into minus infinity? Not! They decrease in a special way. First, quite quickly decrease, and then everything is slower and slower. And staying all the time positive. Let and very, very small. And why do they like themselves? Did you guessed? Yes! They strive for zero!) And pay attention to the very zero members of our progression never reach!Only infinitely close to it are approaching. It is very important.)
A similar situation will be in such a progression:
(b N.): -1, -1/2, -1/4, -1/8, -1/16, …
Here b. 1 = -1 , but q. = 1/2 . All the same, just to zero now the members will approach the other side below. All the time remaining negative.)
Such geometric progression, whose members unlimited approach zero (no matter, with a positive or negative side), in mathematics wears a special name - infinitely decreasing geometric progression. This progression is so interesting and unusual that it will even be about her separate lesson .)
So, we looked at all possible positive Dannels - and large units and smaller units. We do not consider the unit itself as a denominator for the reasons set out above (remember an example with a sequence of triples ...)
Let's summarize:
positive and more units (q.\u003e 1), then members of the progression:
a.) indefinitely increase (ifb. 1 >0);
b) unlimited decrease (ifb. 1 <0).
If the denominator of geometric progression positive and less one (0< q.<1), то члены прогрессии:
a) infinitely close to zero from above (if ab. 1 >0);
b) infinitely close to zero below (if ab. 1 <0).
It remains now to consider the case negative denominator.
Denominator negative ( q. <0)
For example, we will not go far. What, actually, shame the grandmother?!) Let, for example, the first term of the progression will be b. 1 = 1 , and the denominator will take q \u003d -2..
We get this sequence:
(b N.): 1, -2, 4, -8, 16, …
And so on.) Every member of the progression is obtained multiplying Previous member on a negative number -2. At the same time, all members standing at odd places (first, third, fifth, etc.) will be positive, and on even places (second, fourth, etc.) - negative. Signs strictly alternate. Plus-minus plus-minus ... such geometric progression is called - increasingly aligning.
Where are her members seek? And nowhere.) Yes, in absolute value (i.e. module) The members of our progression increasingly increase (hence the name "increasing"). But at the same time, each member of the progression is alternately thrown into the heat, then in the cold. Then in the "plus", then in "minus". Our progression fluctuates ... And the scope of oscillations with each step is growing rapidly, yes.) It became, the striving of members of the progression somewhere specifically here not.Neither plus infinity, nor to minus infinity, nor to zero - nowhere.
We now consider some fractional denominator between zero and minus one.
For example, let it be b. 1 = 1 , but q \u003d -1/2..
Then we get the progression:
(b N.): 1, -1/2, 1/4, -1/8, 1/16, …
And again we have alternation of signs! But, unlike the previous example, there is already a clear tendency to approach the members to zero.) Only this time, our members approach zero is not strictly from above or bottom, but again hesitation. Alternately accepting that positive, then negative values. But at the same time they are modules get closer and closer to the cherished tongue.)
Such geometric progression is called infinitely decreasing aligning.
What are the interesting these two examples? So that in both cases takes place alternating signs! This chip is characteristic only for progress with a negative denominator, yes.) It became if in some task you will see a geometric progression with alkaline member, then you will be firmly known that its denominator is 100% negative and not mistaken in the sign.)
By the way, in the case of a negative denominator, the sign of the first member does not affect the behavior of the progression itself. With any way, the first member of the progression is, in any case, the alignment of members will be observed. The whole question is only in which places (Even or odd) will stand members with specific signs.
Remember:
If the denominator of geometric progression negative , then signs of progression of progression alternate.
At the same time, the members themselves:
a) indefinitely increaseby module, if aq.<-1;
b) endlessly approach zero if -1< q.<0 (прогрессия бесконечно убывающая).
That's all. All sample cases are disassembled.)
In the process of dismissing a variety of examples of geometric progressions, I periodically used the words: "She strives for zero", "She strives for the plus infinity", "She strives for minus infinity"... anything terrible.) These speech turnover (and specific examples) - just an initial acquaintance with behavior Value numerical sequences. On the example of geometric progression.
Why do we generally need to know the behavior of the progression? What is the difference where she seeks? To zero whether, to plus infinity, to minus infinity ... We are something from this?
The point is that already in the university, in the course of the highest mathematics, you will need the ability to work with the most different numeric sequences (with any, and not only the progression!) And the ability to represent exactly how this or that sequence behaves - whether she increases It is unlimited, whether it decreases whether she strives to a specific number (and not necessarily to zero) or even does not seek to go to anything ... This topic is a whole section - this topic is in the course of Matanalya. theory of limits. A little more specifically - the concept the limit of the numeric sequence.Very interesting topic! It makes sense to go to the institute and deal.)
Some examples from this section (sequences having a limit) and in particular, infinitely decreasing geometric progression Start getting up to school. Get used to.)
Moreover, the ability to well explore the behavior of sequences in the future will play a hand and very useful in study of functions. A variety of. But the skill competently work with the functions (calculate the derivatives, to investigate them in the full program, build their graphs) already sharply increases your mathematical level! Doubt? Do not. Still remember my words.)
Let's look at the geometric progression in life?
In the surrounding life with geometric progress, we face very and very often. Even without suspecting.)
For example, various microorganisms that surround us everywhere in huge quantities and which we do not even see without a microscope, multiply precisely in geometric progression.
Let's say one bacterium is multiplied by the division in half, giving offspring in 2 bacteria. In turn, each of them, multiplying, is also divided into half, giving general offspring in 4 bacteria. The next generation already will give 8 bacteria, then 16 bacteria, 32, 64, and so on. With each next generation, the number of bacteria doubles. Typical example of geometric progression.)
Also in geometric progression, some insects are breeding, flies. And rabbits sometimes, by the way, too.)
Another example of geometric progression, closer to everyday life, is the so-called compound interest. Such an interesting phenomenon is often found in bank deposits and is called capitalization of interest. What it is?
You yourself are still, of course, young. In school, learn, do not appeal in banks. But your parents are already adults and independent people. Go to work, the money on bread is earned, and part of the money put into the bank, making savings.)
Let's say, your dad wants to podnapolize a certain amount of money for family holidays in Turkey and put on a bank 50,000 rubles under 10% per annum for a period of three years with the annual capitalization of interest. And during the whole of this period, nothing can be done with the contribution. It is impossible to replenish the contribution nor to take money from the account. What profit will he get through these three years?
Well, firstly, it is necessary to figure out what is 10% per annum. It means that in a year At the initial amount of the deposit by the Bank will be accrued 10%. From what? Of course, from initial deposit amount.
We consider the size of the account in a year. If the initial amount of the contribution was 50,000 rubles (that is, 100%), then in a year there will be how many percent? Right, 110%! From 50,000 rubles.
Here we consider 110% of 50,000 rubles:
50000 · 1.1 \u003d 55000 rubles.
I hope you understand that you find 110% of the value means multiplying this amount by number 1.1? If you do not understand why this is exactly the case, remember the fifth and sixth grades. Namely - Communication of interest with fractions and parts.)
Thus, the increase in the first year will be 5,000 rubles.
And how much money will be in the account in two years? 60000 rubles? Unfortunately (or rather, fortunately), everything is not so simple. The entire percent capitalization focus is that with every new interest accrual, these most interest will be considered already from the new amount!From the one that already Lies on the account at the moment.And the interest accrued for the previous period is added to the initial deposit amount and, thus, they themselves participate in the accrual of new percent! That is, they become a full part of the shared account. Or in common capital.Hence the name - capitalization of interest.
This is in the economy. And in mathematics such interest are called complex percent.Or percent percent.) Their chip lies in the fact that with a consistent calculation interest each time they are considered from a new value.And not from the initial ...
Became to calculate the amount through two yearswe need to calculate 110% of the amount that will be in the account in a year. That is, already from 55,000 rubles.
We consider 110% of 55,000 rubles:
55000 · 1.1 \u003d 60500 rubles.
So, the percentage gain for the second year will be already 5,500 rubles, and in two years - 10,500 rubles.
Now it is already possible to guess that after three years the amount in the account will be 110% of 60,500 rubles. That is, 110% again from the previous one (last year)amounts.
So we think:
60500 · 1.1 \u003d 66550 rubles.
And now we build our money amounts by year in the sequence:
50000;
55000 \u003d 50,000 · 1.1;
60500 \u003d 55000 · 1.1 \u003d (50,000 · 1,1) · 1.1;
66550 \u003d 60500 · 1.1 \u003d ((50000 · 1,1) · 1,1) · 1,1
So how? What is not geometric progression? First Member b. 1 = 50000 , and the denominator q. = 1,1 . Each member is more than the previous one strictly 1.1 times. Everything is in strict accordance with the definition.)
And how many additional interest bonuses "swears" to your dad, while it was 500 rubles for three years in a bank account?
We consider:
66550 - 50000 \u003d 16550 rubles
Nehuto, of course. But this is if the initial deposit amount is small. And if more? Say, not 50, and 200 thousand rubles? Then the increase for three years will be already 66,200 rubles (if calculating). What is already very good.) And if the contribution is even more? That's what it is ...
Conclusion: The higher the initial contribution, the more profitable the capitalization of interest becomes. That is why deposits with capitalization of interest are provided by banks for long terms. Let's say for five years.
Also in geometric progression, all non-torrential diseases of the type of influenza, measles and even more terrible diseases (the same atypical pneumonia in the early 2000s or plague in the Middle Ages) are likely to spread. From here and such scales of epidemics, yes ...) And all due to the fact that the geometric progression with a whole positive denominator (q.>1) - The thing that is growing very quickly! Remember the reproduction of bacteria: two from one bacterium are obtained, out of two - four, out of four - eight and so on ... with the distribution of any infection all the same.)
The simplest tasks for geometric progression.
Let's start, as always, with a simple task. Purely understanding meaning.
1. It is known that the second member of the geometric progression is 6, and the denominator is -0.5. Find the first, third and fourth members.
So, we are given infinite geometric progression, and known second member This progression:
B 2 \u003d 6
In addition, we are still known denominator progression:
Q \u003d -0.5
And you need to find first, thirdand fourthmembers of this progression.
So act. Record sequence by the condition of the task. Right in general, where the second member is Sixer:
b 1, 6,b. 3 , b. 4 , …
And now proceed to the search. We start, as always, from the simplest. You can count, for example, the third dick b 3.? Can! We already know with you (right in the meaning of geometric progression) that the third dick (B 3) More than second (b. 2 ) in "q" time!
We write:
b 3 \u003d.b. 2 · q.
We substitute in this expression six instead b 2.and -0.5 instead q. And believe. And do not ignore the minus, of course ...
b 3 \u003d 6 · (-0,5) \u003d -3
Like this. The third member was minus. No wonder: our denominator q. - Negative. And plus multiply by minus, it will be known, minus.)
We now consider the next, fourth term of progression:
b 4 \u003d.b. 3 · q.
B 4 \u003d -3 · (-0,5) \u003d 1.5
Fourth dick - again with a plus. The fifth member will be with a minus, the sixth - with a plus and so on. Signs - alternate!
So, the third and fourth members found. It turned out this sequence:
b 1; 6; -3; 1.5; ...
It remains now to find the first member. b 1. According to a well-known second. To do this, walk in the other side, left. This means that in this case the second member of the progression we need to not multiply the denominator, and divide
We divide and get:
![]()
That's all.) The answer to the task will be like this:
-12; 6; -3; 1,5; …
As you can see, the principle of solving the same as in. Know any Member I. denominator Geometric progression - we can find any other member. What we want, such and squeeze.) With the only difference that addition / subtraction is replaced by multiplication / division.
We remember: if we are known for at least one member and denominator of geometric progression, then we can always find any other member of this progression.
Next task, according to tradition, from the real OGE version:
2.
...; 150; x; 6; 1.2; ...
So how? This time there is no first member nor a denominator q., just the sequence of numbers is set ... something familiar is already true? Yes! A similar task has already disassembled in arithmetic progression!
So do not be afraid. All the same. Turn on your head and remember the elementary meaning of geometric progression. We look carefully on our sequence and we think that the parameters of the geometric progression of the three main (first member, denominator, member number) are hidden in it.
Members numbers? No member numbers, yes ... but there are four consistent numbers. What does this word mean, it makes no sense to explain at this stage.) Do you have two in this sequence adjacent known numbers?There is! It is 6 and 1.2. So we can find the denominator of progression.Here and take the number 1.2 and divide on the previous number. On the sixth.
We get:
We get:
x. \u003d 150 · 0.2 \u003d 30
Answer: x. = 30 .
As you see, everything is quite simple. The main difficulty consists only in calculations. Especially hard happens in the case of negative and fractional denominators. So those who have problems, repeat the arithmetic! How to work with fractions, how to work with negative numbers and so on ... otherwise here you will slow down mercilessly.
And now a little modified a task. Now it will be interesting! Remove in it the last number 1.2. Here is such a task now by resolving:
3. Several successive members of the geometric progression are written:
...; 150; x; 6; ...
Find a member of the progression indicated by the letter x.
All the same, only two neighboring famous We have no progression of progression. This is the main problem. Because the amount q. through two neighboring member we are so easy to determine we can not. Do we have a chance to cope with the task? Sure!
Cut the unknown member x."Directly in the meaning of geometric progression! In general.
Yes Yes! Right with an unknown denominator!
On the one hand, for the IKSA, we can record this ratio:
X. \u003d 150 ·q.
On the other hand, the same XE, we have the full right to paint and through following Member, through the Six! Sharing the six to the denominator.
Like this:
X. = 6/ q.
Obviously, now you can equate both of these relationships. Since we express the same magnitude (X), but two different ways.
We obtain the equation:
Multiplying all by q.Simplifying, cutting, we obtain equation:
q 2 \u003d 1/25
We decide and get:
q \u003d ± 1/5 \u003d ± 0.2
Oops! The denominator turned out to be double! +0.2 and -0.2. And which one to choose? Dead end?
Tranquility! Yes, the task really has two solutions!Nothing wrong with that. It happens.) You are not surprised when, for example, get two roots, solving the usual? Here is the same story.)
For q \u003d +0.2 we'll get:
X \u003d 150 · 0.2 \u003d 30
And for q. = -0,2 will be:
X \u003d 150 · (-0.2) \u003d -30
We get a dual answer: x. = 30; x. = -30.
What does this interesting fact mean? And what exists two progressionsatisfying the task condition!
Like these ones:
…; 150; 30; 6; …
…; 150; -30; 6; …
Both are suitable.) What do you think, because of what we have a split response? Once due to the elimination of a particular member of the progression (1.2), coming after the six. And knowing only the previous one (n-1) -th and subsequent (n + 1) -th member of the geometric progression, we can no longer say anything about the N-th member standing between them. Two options are possible - with a plus and with a minus.
But not trouble. As a rule, in the tasks for geometric progression there is additional information that gives a unambiguous answer. Say, words: "Alignmenting Progression"or "Progression with a positive denominator" And so on ... it is these words and should serve as a hook, what a sign, plus or minus, should be selected when the final response is made. If there is no such information, then - yes, the task will have two solutions.)
And now we solve yourself.
4. Determine whether the number 20 will be a member of geometric progression:
4 ; 6; 9; …
5. Announced geometric progression:
…; 5; x. ; 45; …
Find a progression member marked x. .
6. Find the fourth positive member of the geometric progression:
625; -250; 100; …
7. The second member of the geometric progression is -360, and its fifth member is equal to 23.04. Find the first member of this progression.
Answers (in disorder): -15; 900; not; 2.56.
Congratulations, if everything happened!
Something is not joined? Somewhere the answer double turned out? We read carefully the condition of the task!
The last task does not come out? There's nothing complicated there.) We work directly in the meaning of geometric progression. Well, the picture can be drawn. It helps.)
As you can see, everything is elementary. If the progression is short. And if long? Or the number of the desired member is very big? I would like, by analogy with arithmetic progress, somehow get a convenient formula that allows you to easily find any member of any geometric progression by his number. Not multiplying many, many times on q.. And there is such a formula!) Details - in the next lesson.
The formula of the N-th member of the geometric progression is the thing is very simple. As in meaning and by the general mind. But the tasks on the formula of the N-th member are found all sorts of - from very primitive to quite serious. And in the process of our acquaintance we will also consider both those and others. Well, get acquainted?)
So, for the beginning itself itself formulan.
Here she is:
b N. = b. 1 · q N. -1
Formula as a formula, nothing supernatural. It looks even easier and more compact than a similar formula for. The meaning of the formula is also simple as the boots.
This formula allows you to find any member of the geometric progression by its number " n.".
As you see, in the sense, a complete analogy with arithmetic progress. We know the number N - we can count and a member under this number. What we want. Not multiplying sequentially on "Q" many, many times. That's the whole point.)
I understand that at this level of work with the progression of all incoming in the formula of the magnitude, you should already be understood, but I consider it my debt to decipher each. Just in case.
So let's go:
B. 1 – first a member of geometric progression;
Q. – ;
N. - Member number;
B N. – enhancingn.-y) Member of geometric progression.
This formula binds the four main parameters of any geometric progression - b. N., b. 1 , q. and n.. And around these four key figures and all-all progression tasks are spinning.
"And how is it displayed?" - I hear a curious question ... elementary! Look!
What is equal second Member of progression? No problem! Directly writing:
b 2 \u003d B 1 · Q
And the third dick? Also not a problem! The second member is pushing once again onq..
Like this:
B 3 \u003d B 2 · Q
Recall now that the second term, in turn, is equal to B 1 · Q and substitute this expression in our equality:
B 3 \u003d B 2 · Q \u003d (B 1 · Q) · Q \u003d B 1 · Q · Q \u003d B 1 · Q 2
We get:
B. 3 \u003d B 1 · q 2
Now read our record in Russian: the third The member is equal to the first term multiplied by Q in second degree. Catch? Not yet? Good, one more step.
What is the fourth dick? All the same! Multiply previous (i.e. the third dick) on Q:
B 4 \u003d B 3 · Q \u003d (B 1 · Q 2) · Q \u003d B 1 · Q 2 · Q \u003d B 1 · Q 3
TOTAL:
B. 4 \u003d B 1 · q 3
And again translate into Russian: fourth The member is equal to the first term multiplied by Q in third degree.
Etc. So how? Caught regularity? Yes! For any member with any number, the number of identical factor Q (i.e. the degree of denominator) will always be per unit less than the number of the desired membern..
Therefore, our formula will, without options:
b n \u003db. 1 · q N. -1
That's all the things.)
Well, they cut the challenges, probably?)
Solving tasks on the formulan.-Ho member of geometric progression.
Let's start, as usual, with direct use of the formula. Here is a typical problem:
In geometric progression it is known that b. 1 \u003d 512 I. q. \u003d -1/2. Find the tenth progression member.
Of course, this problem can generally solve this problem. Directly in the sense of geometric progression. But we have to warm up with the formula of N-th member, right? So breathe.
Our data for the application of the formula is as follows.
Known first term. This is 512.
B. 1 = 512.
Also known denominator of progression: q. = -1/2.
It only remains to figure out what is equal to the number of n. No problem! Are we interested in the tenth member? So we substitute in the general formula of the top ten instead of n.
And carefully consider arithmetic:
Answer: -1.
As you can see, the tenth progression member was minus. Nothing amazing: the denominator of progression from us -1/2, i.e. negative number. And this tells us that the signs of our progression alternate, yes.)
Everything is simple here. And here is a similar task, but a little more complicated in terms of calculations.
In geometric progression, it is known that:
B. 1 = 3
Find the thirteenth progression member.
All the same, only this time the denominator of the progression - irrational. Root from two. Well, nothing terrible. Formula is a universal thing, with any numbers copes.
We work directly by the formula:
The formula, of course, worked as it should, but ... here are some and hang. What to do next to the root? How to build a root on the twelfth degree?
As-like ... It is necessary to understand that any formula, of course, is good, but the knowledge of the whole of the previous mathematics is not canceled! How to build? Yes, the properties of degrees remember! Turn the root B. fractionaland - by the formula of the exercise degree.
Like this:
Answer: 192.
And all things.)
What is the main difficulty with the direct use of the N-th member formula? Yes! The main difficulty is work with degrees! Namely, the construction of negative numbers, fractions, roots and the like designs. So those who have problems with this, the urgent request to repeat the degree and their properties! Otherwise, in this topic you will slow down, yes ...)
And now we cut the typical tasks for the search. one of the elements of the formulaIf all others are given. To successfully solve such tasks, the recipe is one and simple to horror - we write formulan.-Ho member in general!Right in the notebook next to the condition. And then out of the condition we think that we are given and what is missing. And express from the formula the desired magnitude. Everything!
For example, such a harmless task.
The fifth member of the geometric progression with denominator 3 is 567. Find the first member of this progression.
Nothing difficult. We work directly by spell.
We write the formula of the N-th member!
b N. = b. 1 · q N. -1
What is given to us? First, a denominator of progression is given: q. = 3.
In addition, we are given fifth dick: b. 5 = 567 .
Everything? Not! We have given a number n! This is the five: n \u003d 5.
I hope you already understand that in the record b. 5 = 567 Two parameters are hidden at once - this is the fifth dick itself (567) and its number (5). In a similar lesson, I have already spoken about this, but I also consider not superfluous to remind.)
Now we substitute our data in the formula:
567 = b. 1 · 3 5-1
We consider arithmetic, we simplify and get a simple linear equation:
81 b. 1 = 567
We decide and get:
B. 1 = 7
As you see, with the search for the first member of any problems. But when searching for denominator q. and numbers n. Surprises may also meet. And to them (to surprises), too, you need to be prepared, yes.)
For example, such a task:
The fifth member of the geometric progression with a positive denominator is equal to 162, and the first term of this progression is 2. Find the denominator of the progression.
This time we are given the first and fifth members, and they ask for a denominator of progression. Here and proceed.
We write formulan.-Ho member!
b N. = b. 1 · q N. -1
Our source data will be as follows:
B. 5 = 162
B. 1 = 2
N. = 5
Not enough meaning q.. No problem! Now we will find.) We substitute in the formula everything we know.
We get:
162 \u003d 2 ·q. 5-1
2 q. 4 = 162
Q. 4 = 81
A simple equation of the fourth degree. But now - carefully! At this stage of solutions, many students immediately relieve the root (fourth degree) and receive an answer. q.=3 .
Like this:
Q 4 \u003d 81
Q. = 3
But actually, this is an unfinished answer. More precisely, incomplete. Why? The fact is that the answer q. = -3 also suitable: (-3) 4 will also be 81!
All due to the fact that the power equation x N. = a. always has two opposite roots for readyn. . With a plus and with a minus:
Both are suitable.
For example, solving (i.e. second degree)
x 2 \u003d 9
For some reason you are not surprised by the appearance two roots x \u003d ± 3? So here is the same. And with any other thought The degree (fourth, sixth, tenth, etc.) will also be the same. Details - in the subject of pro
Therefore, the right decision will be like this:
Q. 4 = 81
Q. \u003d ± 3.
Well, with signs figured out. What are the correct - plus or minus? Well, we read once again the condition of the task in search additional information.It, of course, may not be, but in this problem such information available.We in the condition direct text says that the progression of positive denominator.
Therefore, the answer is obvious:
Q. = 3
Everything is simple here. And what do you think it would be if the wording of the task would be like this:
The fifth member of the geometric progression is 162, and the first term of this progression is 2. Find the denominator of the progression.
What is the difference? Yes! In condition nothing Not said about the sign of the denominator. Neither straight nor indirectly. And here the task would have already had two solutions!
Q. = 3 and q. = -3
Yes Yes! And plus and with a minus.) Mathematically this fact would mean that there are two progressionthat are suitable under the condition of the task. And for each - your denominator. For the sake of interest, practice and write down the first five members of each of them.)
And now the member number is practicing. This task is the most difficult, yes. But but more creative.)
Dana Geometric Progression:
3; 6; 12; 24; …
What is the number 768 in this progression?
The first step is still the same: we write formulan.-Ho member!
b N. = b. 1 · q N. -1
And now, as usual, we substitute the data known to us. GM ... not substituted! Where is the first member, where is the denominator, where is everything else?!
Where-where ... and the eyes why do we need? Eyelashes clapping? This time the progression is given to us directly as sequences. First member see? We see! This is a triple (B 1 \u003d 3). And the denominator? We do not yet see, but it is very easily considered. If, of course, understand.
So we think. Directly within the meaning of geometric progression: take anyone (except the first) and divide to the previous one.
At least like this:
Q. = 24/12 = 2
What else do we know? We are still known some member of this progression, equal to 768. under some number N:
B N. = 768
The number it is unknown to us, but our task is just that it is to find it.) So we are looking for. All the necessary data for substitution in the formula we already downloaded. Unnoticed for yourself.)
So we substitute:
768 \u003d 3 · 2 N. -1
We make elementary - we divide both parts on the top three and rewrite the equation in the usual form: the unknown left, known - right.
We get:
2 N. -1 = 256
Here is such an interesting equation. It is necessary to find "n". What is unusual? Yes, I do not argue. Actually, this is the simplest. It is so called due to the fact that the unknown (in this case it is a number n.) Worth in indicator degree.
At the stage of acquaintance with geometric progression (this is the ninth grade), the exponential equations are not taught, yes ... this is the subject of high school. But there is nothing terrible. Even if you do not know how such equations are solved, let's try to find our n., guided by simple logic and common sense.
We begin to reason. On the left we have a two to some extent. We do not yet know what it is specifically for the degree, but it is not scary. But we firmly know that this degree is 256! So I remember, in what extent deucend gives us 256. Remember? Yes! IN eighth Degree!
256 = 2 8
If they did not remember or with the recognition of the degrees of the problem, it is also nothing terrible: just consistently erect a twice in the square, in the cube, in the fourth degree, fifth, and so on. Selection, in fact, but at this level - quite rolling.
Anyway, we will get:
2 N. -1 = 2 8
N.-1 = 8
N. = 9
So, 768 is ninth Member of our progression. Everything, the task is solved.)
Answer: 9.
What? Boring? Tired of an elementary? I agree. Me too. Stepping to the next level.)
More complex tasks.
And now we solve the tasks more abruptly. Not so much superconded, but over which they have to work a little to get to the answer.
For example, such.
Find the second member of the geometric progression if its fourth member is equal to -24, and the seventh member is 192.
This is a classic genre. There are some two different members of the progression, and it is necessary to find some more member. And all the members are not neighboring. What confuses at first, yes ...
As in, to solve such tasks, we consider two ways. The first method is universal. Algebraic. It works safely and with any source data. Therefore, it is from him and start.)
We describe each member by the formula n.-Ho member!
All exactly in-point as with arithmetic progress. Only this time we work with other general formula. That's all.) But the essence is the same: take and alternately We substitute our source data in the N-th formula. For each member - their own.
For the fourth member, write:
B. 4 = b. 1 · q. 3
-24 = b. 1 · q. 3
There is. One equation is ready.
For the seventh member we write:
B. 7 = b. 1 · q. 6
192 = b. 1 · q. 6
Total received two equations for same progression .
We collect the system:

Despite its formidable view, the system is quite simple. The most obvious solution is the usual substitution. Express b. 1 From the upper equation and substitute to the bottom:

Looking a bit with the lower equation (reducing degrees and dividing on -24), we get:
q. 3 = -8
To the same equation, by the way, you can come and easier way! What? Now I will demonstrate you another secret, but the very beautiful, powerful and useful way to solve such systems. Such systems in the equations of which are sitting only works.At least in one. Called method of the Millen Detectionone equation to another.
So, in front of us system:
In both equations on the left - compositionand right - just a number. This is a very good sign.) Let's take it and ... divide, let's say, the lower equation to the top! What means, did you share one equation to another? Very simple. Take left part one equation (lower) and delim. Her on left part another equation (top). With the right side similarly: right part one equation delim. on the right part Other.
The whole division process looks like this:

Now, reducing everything that is reduced, we get:
Q. 3 = -8
What is good this way? In the fact that in the process of such a division, everything is not good and inconvenient can safely reduce and remain quite harmless equation! That is why it is so important only multiplications At least in one of the system equations. There is no multiplication - there is nothing to cut, yes ...
In general, this method (like many other non-trivial ways of solving systems) even deserves a separate lesson. Be sure to figure it out in more detail. Someday…
However, it doesn't matter how exactly you solve the system, in any case, now we need to solve the resulting equation:
Q. 3 = -8
No problem: Remove the root (cubic) and - ready!
![]()
Please note that here when extracting it is not necessary to put plus / minus. The inventive (third) degree is root. And the answer is also alone, yes.)
So, the denominator of the progression is found. Minus two. Excellent! The process goes.)
For the first member (let's say, from the upper equation) we will get:
![]()
Excellent! We know the first member, know the denominator. And now we have the opportunity to find any member of the progression. Including the second.)
For the second member, everything is completely simple:
b. 2 = b. 1 · q. \u003d 3 · (-2) \u003d -6
Answer: -6.
So, the algebraic way to solve the problem, we laid out on the shelves. Complicated? Not very, I agree. Long and tedious? Yes, of course. But sometimes you can significantly reduce the amount of work. For this is graphic method.Good old and familiar by us.)
Draw a task!
Yes! Exactly. We again depict our progression on the numeric axis. Not necessarily on Lineber, it is not necessary to withstand equal intervals between members (which, by the way, will not be the same, because Progression is geometric!), But simply schematic We draw our sequence.
I got like this:

And now we look at the picture and we think. How many identical multipliers "q" share fourth and seventh Members? True, three!
Therefore, we have the full right to write:
-24 ·q. 3 = 192
From here is now easily searched by Q:
q. 3 = -8
q. = -2
That's fine, the denominator is already in his pocket. And now we look at the picture again: how many such denominants sits between second and fourth members? Two! Therefore, to record the connection between these members, the denominator will erect in square.
Here we write:
b. 2 · q. 2 = -24 From! b. 2 = -24/ q. 2
We substitute our found denominator in the expression for B 2, we believe and get:
![]()
Answer: -6.
As you can see, everything is much easier and faster than through the system. Moreover, here we all did not even need to consider the first dick! At all.)
Here is such a simple and visual way-Light. But he has a serious disadvantage. Guess? Yes! It is only suitable for very short pieces of progression. Such, where the distances between the members of interest are not very large. But in all other cases, the picture is already difficult to draw, yes ... then we solve the problem analytically, through the system.) And the system is universal. With any numbers copes.
Another epic problem:
The second member of the geometric progression is 10 more than the first, and the third member is 30 more than the second. Find a denominator of progression.
What is cool? Not at all! All the same. Again we translate the condition of the task in the pure algebra.
1) describe each member by formula n.-Ho member!
Second term: B 2 \u003d B 1 · Q
Third member: B 3 \u003d B 1 · Q 2
2) write a link between members from the condition of the problem.
Read the condition: "The second member of the geometric progression is 10 more than the first." Stop, it is valuable!
We write:
B. 2 = b. 1 +10
And this phrase is translated into clean mathematics:
B. 3 = b. 2 +30
Received two equations. We combine them into the system:
![]()
The system is simple. But something many different indexes at the beaks. Substitute instead of the second and third members of their expression through the first member and the denominator! In vain, what did we paint them?
We get:
![]()
But this system is no longer a gift, yes ... how to solve? Unfortunately, a universal secret spell on solving complex nonlinear There are no systems in mathematics and can not be. It is fantastic! But the first thing that should come to mind when trying to spryy like a strong nuthek - it is estimate, doesn't one of the system equations be reduced to a beautiful view that allows, for example, it is easy to express one of the variables through the other?
So I estimate. The first equation of the system is clearly easier for the second. It is subjected to torture.) And do not try from the first equation something express something? Since we want to find a denominator q., it would be more profitable for us to express b. 1 through q..
So we will try to do this procedure with the first equation, applying the old good:
b 1 Q \u003d B 1 +10
B 1 Q - B 1 \u003d 10
B 1 (Q-1) \u003d 10
Everything! So we expressed unnecessary us variable (B 1) through necessary (q). Yes, not the easiest expression received. The fraction is some ... But the system we have a decent level, yes.)
![]()
Typical. What to do - know.
We write ... (required!) :
q ≠ 1.
We multiply everything to the denominator (Q-1) and reduce all the fractions:
10 q. 2 = 10 q. + 30(q.-1)
We divide everything for the top ten, reveal the brackets, collect everything on the left:
q. 2 – 4 q. + 3 = 0
We solve the resulting and get two roots:
q. 1 = 1
q. 2 = 3
The final answer is one: q. = 3 .
Answer: 3.
As you can see, the path of solving most tasks on the formula of the N-th member of geometric progression is always one: read carefully The condition of the task and using the N-th member formula we translate all useful information into a clean algebra.
Namely:
1) We describe separately each given in the task member by the formulan.-Ho member.
2) From the terms of the task, we translate the link between members in a mathematical form. Make an equation or system of equations.
3) solve the obtained equation or system of equations, we find unknown progression parameters.
4) In the case of an ambiguous response, we read carefully the condition of the problem in search of additional information (if there is such). Also, we are aspiring the resulting response with the ODZ (if any).
And now we list the main problems most often leading to errors in the process of solving problems of geometric progression.
1. Elementary arithmetic. Actions with fractions and negative numbers.
2. If at least one of these three points of the problem, you will inevitably be mistaken in this topic. Unfortunately ... so do not be lazy and repeat what is mentioned above. And on the links - go. Sometimes helps.)
Modified and recurrent formulas.
And now consider a couple of typical examination tasks with a less familiar flow of condition. Yes, yes, you guess! it modified and recurrent Formulas N-th member. With such formulas, we already faced and worked in the arithmetic progression. Here everything is similar. The essence is the same.
For example, such a task from OGE:
Geometric progression is set by the formula b N. \u003d 3 · 2 N. . Find the sum of the first and fourth of its members.
This time, the progression is not quite familiar to us. In the form of some formula. So what? This formula - also formulan.-Ho member! We know with you that the formula of the N-th member can be written both in the general form, through the letters and for specific progression. FROM specific First member and denominator.
In our case, we actually asked the formula of a general member for geometric progression here with such parameters:
b. 1 = 6
Q. = 2
Check?) We write the formula of the N-th member in general and substitute in it b. 1 and q.. We get:
B N. = b. 1 · q N. -1
B N. \u003d 6 · 2 N. -1
We simplify using the decomposition of multipliers and the properties of degrees, and we get:
b N. \u003d 6 · 2 N. -1 \u003d 3 · 2 · 2 N. -1 \u003d 3 · 2 N. -1+1 \u003d 3 · 2 N.
As you can see, everything is honest. But our goal with you is not to demonstrate the conclusion of a specific formula. This is so, lyric retreat. Purely for understanding.) Our goal is to solve the task for the formula, which is given to us in the condition. Capture?) So we work with a modified formula directly.
We consider the first term. Substitute n.=1 In general formula:
b. 1 = 3 · 2 1 \u003d 3 · 2 \u003d 6
Like this. By the way, I do not fit and pay your attention to the typical lap with the calculation of the first member. Do not, looking at the formula b N. \u003d 3 · 2 N., Immediately rush to write that the first member is Troika! It is a gross mistake, yes ...)
We continue. Substitute n.=4 and we consider the fourth dick:
B. 4 = 3 · 2 4 \u003d 3 · 16 \u003d 48
Well, finally, we consider the required amount:
B. 1 + b. 4 = 6+48 = 54
Answer: 54.
More task.
Geometric progression is asked:
B. 1 = -7;
B N. +1 = 3 b N.
Find the fourth term of progression.
Here the progression is set by the recurrent formula. Well, okay.) How to work with such a formula - We also know.
So act. Steps.
1) We consider two consistent Member of Progression.
The first member is already set. Minus seven. But the next, second member can easily calculate on the recurrent formula. If you understand the principle of its work, of course.)
Here we consider the second member according to the famous first:
B. 2 = 3 b. 1 \u003d 3 · (-7) \u003d -21
2) We consider the denominator of progression
Also no problems. Straight, Delim. second Member of first.
We get:
Q. = -21/(-7) = 3
3) write formulan.-Ho member in the usual form and consider the desired member.
So, the first member know, denominator - too. Here we write:
B N. \u003d -7 · 3 N. -1
B. 4 \u003d -7 · 3 3 = -7 · 27 \u003d -189
Answer: -189
As you can see, working with such formulas for geometric progression is no other of its essence from that for the progression of arithmetic. It is only important to understand the general essence and meaning of these formulas. Well, the meaning of geometric progression also needs to be understood, yes.) And then there will be no stupid errors.
Well, fuck yourself?)
Complete elementary tasks, for warm-up:
1. Dana geometric progression in which b. 1 \u003d 243, and q. \u003d -2/3. Find the sixth member of the progression.
2. The overall member of the geometric progression is set by the formula b N. = 5∙2 N. +1 . Find the number of the last three-digit member of this progression.
3. Geometric progression is set by the terms:
B. 1 = -3;
B N. +1 = 6 b N.
Find the fifth member of the progression.
A little more complicated:
4. Dana Geometric Progression:
B. 1 =2048; q. =-0,5
What is the sixth negative member?
What does it seem superer? Not at all. Save the logic and understanding of the meaning of geometric progression. Well, the formula of the N-th member, of course.
5. The third member of the geometric progression is -14, and the eighth member is 112. Find the denominator of the progression.
6. The sum of the first and second member of the geometric progression is 75, and the sum of the second and third members is 150. Find the sixth member of the progression.
Answers (in disorder): 6; -3888; -one; 800; -32; 448.
That's almost everything. It remains only to learn to consider us the sum of the first members of the geometric progression Yes, discover infinitely decreasing geometric progression and its sum. Very interesting and unusual thing, by the way! About it - in the following lessons.)
Mathematics is that, wherebypeople control nature and by themselves.
Soviet mathematician, academician A.N. Kolmogorov
Geometric progression.
Along with the tasks for arithmetic progression, the problems associated with the concept of geometric progression are common on the entrance tests in mathematics. To successfully solve such tasks, it is necessary to know the properties of geometric progression and have good use skills.
This article is devoted to the presentation of the main properties of geometric progression. Here are examples of solutions of typical tasks., Borrowed from the tasks of entrance tests in mathematics.
Previously note the basic properties of geometric progression and remind the most important formulas and approval, associated with this concept.
Definition. The numerical sequence is called geometric progress if each of its number starting from the second equal to the previous one multiplied by the same number. The number is called denominator of geometric progression.
For geometric progressionformulas are valid
, (1)
where. Formula (1) is called the formula of a general member of the geometrical progression, and formula (2) is the main property of geometric progression: each member of the progression coincides with the average geometric of its neighboring members and.
Note What exactly because of this property, the progression under consideration is called "geometric".
The above formulas (1) and (2) are generalized as follows:
, (3)
To calculate the sum First Members of geometric progression The formula is applied
If you designate, then
where. Since, formula (6) is a generalization of formula (5).
In the case when and geometric progression is infinitely decreasing. To calculate the sumall members of infinitely decreasing geometric progression is used formula
. (7)
For example , With the help of formula (7) you can show, what
where. These equalities are obtained from formula (7), provided that, (first equality) and, (second equality).
Theorem. If, then
Evidence. If, then
Theorem is proved.
Let us turn to the consideration of examples of solving problems on the topic "Geometric Progression".
Example 1. Dano:, and. To find .
Decision. If apply formula (5), then
Answer:.
Example 2.Let it be. To find .
Decision. Since, we use the formulas (5), (6) and we obtain the system of equations
If the second system equation (9) is divided into the first, then or. Hence the I. . Consider two cases.
1. If, then from the first equation of system (9) we have.
2. If, then.
Example 3.Let, and. To find .
Decision. From formula (2) it follows that or. Since, then or.
By condition . However, therefore. Since then here have a system of equations
If the second equation of the system is divided into the first, then or.
Since, the equation has the only suitable root. In this case, from the first equation of the system flows.
Taking into account the formula (7), we get.
Answer:.
Example 4.Danar: and. To find .
Decision. Since, then.
Since, then or
According to the formula (2) we have. In this regard, from equality (10) we get or.
However, by condition, therefore.
Example 5. It is known that . To find .
Decision. According to the theorem we have two equalities
Since, then or. Since, then.
Answer:.
Example 6. Danar: and. To find .
Decision. Taking into account the formula (5), we get
Since, then. Since, and, then.
Example 7. Let it be. To find .
Decision. According to the formula (1) you can record
Therefore, we have or. It is known that therefore.
Answer:.
Example 8. Find a denominator of infinite decreasing geometric progression if
and.
Decision. From formula (7) follows and . From here and from the terms of the task we obtain a system of equations
If the first equation of the system is to build a square, and then the obtained equation is divided into second equation, I get
Or .
Answer:.
Example 9. Find all values \u200b\u200bin which the sequence is geometric progress.
Decision. Let, and. According to formula (2), which sets the basic property of geometric progression, can be recorded or.
From here we get a square equation, The roots of which are and.
Perform check: if, then; If, then, and.
In the first case we have And, and in the second - and.
Answer: ,.
Example 10.Solve equation
, (11)
where and.
Decision. The left part of equation (11) is the sum of infinite decreasing geometric progression, in which, provided: and.
From formula (7) follows, what . In this regard, equation (11) takes or . Suitable root the square equation is
Answer:.
Example 11.P treaty of positive numbers Forms arithmetic progression, but - Geometric progression, what does it have to do with . To find .
Decision.As arithmetic sequenceT. (The main property of arithmetic progression). Insofar as, then or. This implies , that geometric progression has the form. According to Formula (2), then write down that.
As it is . In this case, the expression takes a view or. By condition , Therefore, from the equation We get the only solution to the problem under consideration. .
Answer:.
Example 12.Calculate the sum
. (12)
Decision. Multiply on 5 both parts of equality (12) and get
If subdued from the resulting expression (12)T.
or .
For the calculation, we substitute in the formula (7) of the values, and we get. Since, then.
Answer:.
The examples of solving solutions given here will be useful to applicants when preparing for introductory tests. For a deeper study of problem solving methods, associated with geometric progress, You can use textbooks from the list of recommended literature.
1. Collection of problems in mathematics for incoming in the soil / ed. M.I. Schanavi. - M.: World and Education, 2013. - 608 p.
2. Suprun V.P. Mathematics for high school students: Additional sections of the school program. - M.: Lenand / URSS, 2014. - 216 p.
3. Medical M.M. Full course of elementary mathematics in tasks and exercises. Book 2: Numeric sequences and progression. - M.: Oditus, 2015. - 208 p.
Have questions?
To get a tutor help - register.
the site, with full or partial copying of the material reference to the original source is required.
Arithmetic and geometric progression
Theoretical information
Theoretical information
Arithmetic progression |
Geometric progression |
|
Definition |
Arithmetic progression a N. The sequence is called, each member of which, starting from the second, is equal to the previous member, folded with the same number d. (d. - progression difference) |
Geometric progression b N. The sequence of non-zero numbers is called, each member of which, starting from the second, is the previous member, multiplied by the same number q. (q. - denominator of progression) |
Recurrent formula |
For any natural n. |
For any natural n. |
NO Formula |
a n \u003d a 1 + d (n - 1) |
b n \u003d b 1 ∙ q n - 1, b n ≠ 0 |
| Characteristic property |  |
|
| N-first members |  |
 |
Examples of tasks with comments
Exercise 1
In arithmetic progression ( a N.) a 1. = -6, a 2.
According to the formula of the NO member:
a 22. = a 1. + d (22 - 1) \u003d a 1. + 21 D.
By condition:
a 1. \u003d -6, then a 22. \u003d -6 + 21 d.
It is necessary to find the difference in progression:
d \u003d a 2 - A 1 = -8 – (-6) = -2
a 22. = -6 + 21 ∙ (-2) = - 48.
Answer: a 22. = -48.
Task 2.
Find the fifth member of the geometric progression: -3; 6; ....
1st method (using the N formula)
According to the formula of the NO member of the geometric progression:
b 5 \u003d B 1 ∙ Q 5 - 1 = b 1 ∙ Q 4.
As b 1. = -3,
2nd method (using a recurrent formula)
Since the progression denominator is -2 (Q \u003d -2), then:
b 3. = 6 ∙ (-2) = -12;
b 4. = -12 ∙ (-2) = 24;
b 5. = 24 ∙ (-2) = -48.
Answer: b 5. = -48.
Task 3.
In arithmetic progression ( a n) a 74 = 34; a 76. \u003d 156. Find a seventy-fifth member of this progression.
For arithmetic progression, the characteristic property has the form ![]() .
.
Therefore:
![]() .
.
Substitute data in the formula:
![]()
Answer: 95.
Task 4.
In arithmetic progression ( a n) a n \u003d 3N - 4. Find the sum of seventeen first members.
To find the sum of the N first members of arithmetic progression, two formulas are used:
![]() .
.
What of them are more convenient to apply?
Under the condition is known for the formula of the N-WHO member of the initial progression ( a N.) a N. \u003d 3n - 4 can be found immediately and a 1., I. a 16. without finding d. Therefore, we use the first formula.

Answer: 368.
Task 5.
In arithmetic progression ( a N.) a 1. = -6; a 2. \u003d -8. Find a twenty-second progression member.
According to the formula of the NO member:
a 22 \u003d A 1 + D (22 – 1) = a 1. + 21d.
Under the condition if a 1. \u003d -6 then a 22. \u003d -6 + 21d. It is necessary to find the difference in progression:
d \u003d a 2 - A 1 = -8 – (-6) = -2
a 22. = -6 + 21 ∙ (-2) = -48.
Answer: a 22. = -48.
Task 6.
Several consecutive members of the geometric progression are recorded:
![]()
Find a member of the progression indicated by the letter x.
When solving, we use the formula of the N-th member b n \u003d b 1 ∙ q n - 1 For geometric progressions. The first member of the progression. To find a denominator of the progression of Q, you must take any of the data of the progression of progression and divide into the previous one. In our example, you can take and divide on. We obtain that Q \u003d 3. Instead of N in the formula, we substitute 3, since it is necessary to find a third term given by geometric progression.
Substitting the found values \u200b\u200bin the formula, we get:
![]() .
.
Answer:.
Task 7.
From the arithmetic progress given to the formula of the N-th member, select the one for which the condition is performed a 27. > 9:
Since the specified condition should be performed for the 27th member of the progression, we will substitute 27 instead of n into each of the four progressions. In the 4th progression we get:
![]() .
.
Answer: 4.
Task 8.
In arithmetic progression a 1. \u003d 3, d \u003d -1.5. Specify the highest value of n for which inequality is performed a N. > -6.