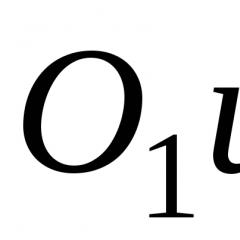Appendix 1. METHODS OF STATISTICAL ANALYSIS AND FORECASTING IN BUSINESS

2. Mathematical models as a necessary tool for statistical analysis and forecasting in business

Let's start with a simple example demonstrating the differences purely statistical, purely probabilistic And probabilistic-statistical approaches to developing a predictive solution. At the same time, this example clearly shows the role of mathematical models in the technology of forming a predictive solution.

Statistical method of decision making. Let the reader imagine himself as a businessman watching his two businessman friends play ( A And IN) into bones. The game follows the following rules. Four consecutive dice are thrown. Player A receives one monetary unit from the player IN, if as a result of these four throws six points are thrown at least once (let's call this outcome “six”), and pays one monetary unit to the player IN otherwise (let's call this outcome “not six”). After one hundred rounds, the reader must change one of the players, and he has the right to choose the situation on which he will bet his monetary unit in the next series of rounds: for the appearance of at least one “six” or against. The correct implementation of this choice is determined, naturally, by the quality of his forecast regarding the outcome of the game when betting on the outcome “six”: if the probability of this outcome is correctly estimated to be greater than half, then the player must bet on this outcome. So, the observer’s task is to make a reliable forecast.

Statistical method The solution to this problem is dictated by ordinary common sense and is as follows. Having observed one hundred rounds of play by previous partners and calculating the relative frequencies of their winnings, it would seem natural to bet on the situation that arose more often during the game. For example, it was recorded that in 52 games out of 100 the player won IN, i.e. in 52 rounds out of 100, the “six” never came up when the dice were thrown four times (accordingly, in the remaining 48 games out of a hundred, the outcome “six” was achieved). Consequently, the reader who has applied the statistical method of reasoning concludes that it is more profitable to bet on the outcome “not six”, i.e. on that outcome, the relative frequency of occurrence of which is 0.52 (more than half).

Probability-theoretic solution method . This method is based on a certain mathematical model the phenomenon being studied: assuming the dice to be regular (i.e., symmetrical), and therefore, taking the chances of any side of the dice falling out in one throw to be equal to each other (in other words, the relative frequency, or probability, of getting a “one” is equal to the relative frequency of getting a “two” , “threes”, etc. and is equal to 1/6), you can calculate the probability P(“not six”) of the implementation of the “not six” situation, i.e. the probability of the event that during four consecutive throws of the dice a “six” will never appear. This calculation is based on the following facts arising from the model assumptions we have accepted. Probability don't throw it away six at one throw The dice is made up of the chances of one, two, three, four and five appearing as a result of one throw and therefore amounts to (in accordance with the definition of the probability of any event) the value of 5/6. Then we use the rule of probability multiplication, according to which the probability of the occurrence of several independent events is equal to the product of the probabilities of these events. In our case, we consider the occurrence of four independent events, each of which consists of not getting a “six” in one throw and has a probability of occurrence equal to 5/6. That's why

As you can see, the probability of the “not six” situation turned out to be less than half, therefore, the chances of the “six” situation are preferable (the corresponding probability is: 1-0.482 = 0.518). This means that a reader who has used a probability-theoretic method of reasoning will come to a solution that is diametrically opposite compared to a reader with a statistical way of thinking and will bet “six” on the situation in the game.

Probabilistic-statistical (or mathematical-statistical) method of decision making. This method, as it were, synthesizes the tools of the two previous ones, since when developing the final conclusion with its help, those accumulated as a result of observing the game are also used. raw statistics(in the form of relative frequencies of occurrence of situations “six” and “not six”, which, as we remember, were equal to 0.48 and 0.52, respectively), and probability-theoretic model considerations. However, the model adopted in this case is less rigid, less limited, it is, as it were, adjusts to reality using for this purpose, accumulated statistical information. In particular, this model no longer postulates the correctness of the dice used, allowing that the center of gravity of the die can be shifted in some special way. The nature of this bias (if it exists) should somehow appear in the initial statistical data that we have. However, the reader who knows the probabilistic-statistical way of thinking should be aware that the values ​​​​of the relative frequencies of the outcomes “six” and “not six” obtained from these data give only some approximate estimates the true (theoretical) chances of one and the other situation: after all, by tossing, say, 10 times even a perfectly symmetrical coin, we can accidentally get seven “coats of arms”; accordingly, the relative frequency of the “coat of arms” falling out, calculated from these test results, will be equal to 0.7; but this does not mean that the true (theoretical) chances (probabilities) of the appearance of the “coat of arms” and the other side of the coin are estimated at 0.7 and 0.3, respectively - these probabilities, as we know, are equal to 0.5. In the same way, the relative frequency of the “not six” outcome (equal to 0.52) that we established in a series of one hundred game rounds may differ from the true (theoretical) probability of the same event and, therefore, may not be a sufficient basis for choosing this situation in the game !

It turns out that the whole question is how much the observed data can differ (as a result of implementing n tests) the relative frequency of the event of interest to us from the true probability of the occurrence of this event, and how this difference, i.e., the error, depends on the number of observations at our disposal (intuitively it is clear that the longer we watched the game, i.e., the more The greater the total number of observations we used, the more trustworthy are the empirical relative frequencies we calculated, i.e., the smaller their difference from the true probability values ​​unknown to us). The answer to this question can be obtained in our case if we use a number of additional model considerations: a) assume that the result of each round does not depend in any way on the results of previous rounds, and the unknown probability of the “not six” situation occurring remains the same throughout all rounds of the game; b) use the fact that the behavior of a randomly changing (as the experiment is repeated) error is approximately described law of normal probability distributions with a mean value equal to zero and a variance equal to (see, paragraph 3.1.5).

These considerations, in particular, make it possible to estimate the absolute value of error , replacing the unknown probability value of the event of interest to us (in our case, the “not six” outcome) with the relative frequency of this event recorded in a series of tests (in our case, a ). If we were able to numerically estimate the absolute value of the possible error, then it is natural to apply the following decision-making rule: if the relative frequency of occurrence of the “not six” outcome is more than half and continues to exceed 0.5 after subtracting the possible error from it, then it is more profitable to bet on “not six” "; if the relative frequency is less than half and continues to be less than 0.5 after adding a possible error to it, then it is more profitable to bet on “six”; in other cases, the observer has no basis for a statistical conclusion about the advantages of a particular choice of bet in the game (i.e., one must either continue to observe or participate in the game with an arbitrary choice of bet, expecting that this cannot lead to any tangible winning or losing).

An approximate calculation of the maximum possible value of this error, based on model consideration b) (i.e., the Moivre-Laplace theorem, see also section 4.3), gives in the example under consideration that with practical certainty, namely with a probability of 0.95, inequality is true

Squaring this inequality and solving the resulting quadratic inequality for the unknown parameter gives

or, with an accuracy up to values ​​of the order of smallness higher than ,

In this case (for and ) we get:

Hence,

Thus, observations of the outcomes of one hundred games give us reason only to conclude that the unknown value of the probability of the “not six” outcome that interests us can actually be any number from the segment , i.e., it can be either a value less than 0.5 (and then you need to bet in the game on the situation “six”), and with a value greater than 0.5 (and then you need to bet in the game on the situation “not six”).

In other words, the reader, using the probabilistic-statistical method of solving the problem and the above model premises, should come to the following “cautious” conclusion: One hundred games as initial statistical material was not enough to make a reliable conclusion about which of the game outcomes is more likely. Hence the decision: either continue the role of “spectator” until the range of possible values ​​for probability , obtained from estimates of the form (4), turns out to lie entirely to the left or right of 0.5, or to enter into the game, assessing it as close to “ harmless”, i.e. one in which you will practically remain “within your own” during a long series of tours.

The given example illustrates the role and purpose of theoretical-probabilistic and mathematical-statistical methods, their relationships. If probability theory provides the researcher with a set of mathematical models, intended to describe patterns in the behavior of real phenomena or systems, the functioning of which occurs under the influence of a large number of interacting random factors, then mathematical statistics tools make it possible to select among a variety of possible probability-theoretic models the one which in a certain sense best corresponds to the statistical data available to the researcher, characterizing the actual behavior of the specific system under study.

Mathematical model . A mathematical model is a certain mathematical construction that represents an abstraction of the real world: in the model, the relationships between real elements of interest to the researcher are replaced by suitable relationships between the elements of the mathematical construction (mathematical categories). These relationships are usually presented in the form of equations and (or) inequalities between indicators (variables) characterizing the functioning of the simulated real system. The art of constructing a mathematical model is to combine as much brevity as possible in its mathematical description with sufficient accuracy of the model reproduction of exactly those aspects of the analyzed reality that are of interest to the researcher.

Above, when analyzing the relationships between purely statistical, purely theoretical-probabilistic and mixed - probabilistic-statistical methods of reasoning, we, in fact, used the simplest models, namely:

statistical frequency model the random event of interest to us, which is that as a result of four consecutive throws of the dice, a “six” will never come up; based on background relative frequency this events and taking it as the probability of the occurrence of this event in a future series of tests, we, thereby, use the model of a random experiment with a known probability of its outcome (see also section 1.1.3);

theoretical probabilistic model of Bernoulli test sequence(see also clause 3.1.1), which has nothing to do with the use of observational results (i.e., with statistics); To calculate the probability of the event we are interested in, it is enough to accept the hypothetical assumption that the dice used are perfectly symmetrical. Then, in accordance with the model of a series of independent tests and the probability multiplication theorem, valid within the framework of this model, the probability of interest to us is calculated using the formula;

probabilistic-statistical model, which interprets the relative frequency estimated in a purely statistical approach as a kind of random variable (see also Section 2.1), the behavior of which obeys the rules defined by the so-called Moivre–Laplace theorem; When constructing this model, both probability-theoretic concepts and rules and statistical techniques based on observational results were used.

To summarize this example, we can say that:

probabilistic model – this is a mathematical model that simulates the functioning mechanism hypothetical(not specific) real phenomenon (or system) of stochastic nature; in our example, hypotheticality referred to the properties of the die: it had to be perfectly symmetrical;

probabilistic-statistical model– uh then a probabilistic model, the values ​​of individual characteristics (parameters) of which are estimated based on the results of observations (initial statistical data) characterizing the functioning of the modeled specific(rather than a hypothetical) phenomenon (or system).

A probabilistic-statistical model that describes the functioning mechanism of an economic or socio-economic system is called econometric.

Predictive and management models in business . Let us return to the tasks of statistical analysis of the functioning mechanism of an enterprise (firm) and related forecasts. Reconsidering " phase space” of these problems, it is not difficult to describe the general logical structure of the models necessary to solve them. This structure follows directly from the definition formulated above business strategies.

In order to formalize (i.e. write in terms of a mathematical model) the problems of optimal control and forecasting in business, we introduce the following notation:

– column vector of resulting indicators (sales volume, etc.);

– column vector of “behavioural” (controlled) variables (investments in the development of fixed assets, in marketing services, etc.);

– column vector of so-called “status” variables, i.e. indicators characterizing the state of the company (number of employees, fixed assets, age of the company, etc.);

– vector-column of geo-socio-economic-demographic characteristics of the external environment (indicators of the general economic situation, characteristics of clients and suppliers, etc.);

– column vector of random regression residuals (more about them below).

Then the system of equations on the basis of which can be carried out optimal enterprise management And performing the necessary forecast calculations, in the most general form can be represented in the form:

, (5)

where is some vector-valued ( -dimensional) function of , the structure (parameter values) of which, generally speaking, depends on the levels at which the values ​​of the variables of the “state” of the company and the “external environment” are recorded.

Then basic problem statistical analysis and forecasting in business consists of constructing the best (in a certain sense) estimate for an unknown function using the initial statistical information of the form available to the researcher

where are the values ​​of respectively behavioral, “status”, external and resulting variables characterizing the th time step (or measured at the th statistically surveyed enterprise), . Accordingly, the parameter ( sample size) is interpreted as total observation duration for the values ​​of the analyzed variables at the enterprise under study, if observations were recorded in time, And How the total number of statistically surveyed enterprises of the same type, if observations were recorded in space(i.e., moving from one enterprise to another). In this case, the description of the function must be accompanied by the calculation method guaranteed approximation errors(forecast errors), i.e. such vector (-dimensional) values ​​and that for any given values ​​and would guarantee the fulfillment of inequalities (with a probability no less than , where is a predetermined positive value sufficiently close to unity), i.e. . respectively, behavioral (controlled), “status” and environmental variables for the time point of the classical regression model, the value is identically equal to zero (cm).

For some general information about the mathematical tools for solving problems (9) and (10), see below, in paragraph 4.

Previous

From the book: Plavinsky S.L. Biostatistics. Planning, processing and presentation of the results of biomedical research using the systemS.A.S. St. Petersburg: Publishing house St. Petersburg MAPO. - 2005

When conducting any scientific research, the reliability of the conclusions is threatened by three main reasons:

1. Systematic errors

2. Random errors

3. The influence of third variables (confounding)

The impact of systematic errors is minimized at the stage of choosing a research design, statistical processing aimed at testing statistical hypotheses attempts to eliminate the influence of random errors (minimization of random errors - appropriate sample size), but an attempt to describe the influence of third variables is often the reason for working with statistical models.

Statistical models are built on the fact that first an assumption is made about the nature of the relationships between the analyzed variables, then the compliance of the data with the model is checked and, depending on the degree of this correspondence, certain conclusions are drawn.

The simplest form of statistical model is linear regression. When using it, the assumption is made that two indicators are linearly related to each other and it is this hypothesis that is tested (in addition, the assumption is made that one variable depends on the other). Thus, statistical models are based on two types of assumptions - like statistical hypothesis testing methods, they assume that the data is distributed in a certain way (most often according to a normal distribution), and in addition to this, an assumption is made about the nature of the relationship. Therefore, it is twice as easy to make a mistake when using statistical models and they are usually considered as tools that require additional training in statistics.

Just as in the case of hypothesis testing, for ease of understanding we should consider separately models for qualitative and quantitative variables. Although medical researchers now work more frequently with qualitative measures, statistical models are better developed for quantitative variables.

In principle, the following options are possible in which we may want to use statistical models:

1. The dependent variable is quantitative, independent variables are also quantitative - the main type of model is multiple (linear) regression

2. The dependent variable is quantitative, the independent variables are qualitative - the main type of model is multivariate analysis of variance

3. The dependent variable is quantitative, independent variables are both quantitative and qualitative - the main type of model is the general linear model

4. The dependent variable is qualitative, the independent variables are also qualitative - the main type of model is loglinear analysis

5. The dependent variable is qualitative, the independent variables are quantitative - the main type of model is discriminant analysis

6. The dependent variable is qualitative, independent variables are both qualitative and quantitative - the main type of model is logistic regression.

As you can see from the list above, in general there are two most common procedures - general linear model for dependent quantitative variables and logistic regression for dependent qualitative variables, and all other models are special cases of these two.

For some applications, such as the analysis of patient survival in a prospective study, the techniques described above are not sufficiently appropriate because in this case there is more than one dependent variable (one - what happened to the patient, the second - when it happened). Therefore, special forms of statistical models have been developed for survival analysis, the most well-known of which are parametric regression methods (Weibull) and nonparametric regression models (Cox model).

There are also special forms of statistical models that try to find hidden relationships between the variables included in the analysis and observations. These techniques came to biostatistics from psychometry and include:

1. Factor analysis - a technique for detecting directly unobservable factors responsible for the relationships between quantitative variables

2. Cluster analysis - a technique for combining observations or variables into groups based on the “sameness” of measured quantitative characteristics

3. Correspondence analysis - an analogue of factor analysis for multidimensional tables

4. Multidimensional scaling - a technique that tries to arrange variables relative to each other in a lower-dimensional space (to create an analogue of a geographical map)

Recently, due to the transition in data storage to computer media and, in connection with this, a sharp increase in routinely collected data, new statistical models have emerged aimed at identifying patterns in large and poorly structured databases. These include:

1. Tree modeling (regression trees) - a technique for segmenting data, finding points that best divide observations into groups depending on the value of the final variable (for example, determining the risk group for hospital mortality depending on a large set of biochemical parameters measured during hospitalization)

2. Neural network modeling is a technique for determining relationships between a set of input parameters and a dependent variable that does not make assumptions about the true form of these relationships (such as linear regression). For statisticians, neural network modeling is multiple nonlinear regression. Neural network modeling programs form a structure that, working on the “black box” principle, can quite accurately predict output parameters based on a set of input values.

It should be noted that these techniques, especially neural network modeling, have found widespread use in technical applications. Machine vision systems, optical character recognition, biometric security systems, almost all of them use neural network modeling algorithms. However, the use of these methods in medical research, after a short period of fascination, has not become widespread. The reason for this is the need to have huge amounts of data if there is a desire to get a real, working model. Typically, neural network and tree models require thousands of observations, and the observations must be fairly homogeneous. In the case of small groups, the so-called Fitting a model to data (overfitting), when the model perfectly describes a given set of results, but is absolutely inapplicable to any other set of data.

It's very easy to imagine why this happens. Neural network modeling is based on an attempt to divide data into groups given the presence of a large number of input parameters. Let's say we want to teach a computer to distinguish men from women, and we present it with a group consisting of a biostatistics professor and three graduate students. Then, after analyzing the data, the computer can easily find a rule that differentiates men and women: if someone is a teacher, then he is a man. In this group, the separation will be better than in any other parameters, such as voice timbre, waist and hip circumference, hair length, etc. However, will such a result be generalizable?

It is precisely because of the dependence on a large number of observations that neural network and tree modeling methods are not widely used in medical science, and given the sad fact that domestic science has recently generally preferred to work with small samples, they can still wait quite a long time before they are widely used (This may change with the widespread introduction of computerized disease registries, such as cancer registries).

Statistical Modeling

Statistical and econometric modeling- research of objects of knowledge on their statistical models; construction and study of models of real-life objects, processes or phenomena (for example: economic processes in econometrics) in order to obtain explanations of these phenomena, as well as to predict phenomena or indicators of interest to the researcher.

The parameters of such models are estimated using statistical methods. For example: maximum likelihood method, least squares method, method of moments.

Y = b_1 + b_2×X

where Y - expenses, X - income, b_1 and b_2 - parameters of the equation (parameters), u - stochastic error (disturbance, error term).

Types of statistical and econometric models

Linear regression (OLS) Regression on binary variables Autoregressive model System of simultaneous equations (SEM) Linear probability model (LPM) Logit model (Logit) Probit model (Probit), etc.

Wikimedia Foundation. 2010.

See what “Statistical Modeling” is in other dictionaries:

Statistical Modeling- a way to study the processes of behavior of probabilistic systems in conditions where the internal interactions in these systems are unknown. It consists in machine imitation of the process being studied, which is, as it were, copied onto... ... Economic and mathematical dictionary

A method of applied and computational mathematics, consisting of the implementation on a computer of specially developed stochastics. models of the phenomena or objects being studied. The expansion of the scope of application of S. m. is associated with the rapid development of technology and especially... ... Mathematical Encyclopedia

A numerical method for solving mathematical problems, in which the required quantities are represented by the probabilistic characteristics of some random phenomenon, this phenomenon is modeled, after which the necessary characteristics are approximately determined... ... Great Soviet Encyclopedia

Modeling situations using statistical patterns inherent in the phenomenon under consideration. Dictionary of business terms. Akademik.ru. 2001... Dictionary of business terms

Modeling is the study of objects of knowledge on their models; building and studying models of real-life objects, processes or phenomena in order to obtain explanations of these phenomena, as well as to predict phenomena of interest... ... Wikipedia

SIMULATION MODELING in sociology- a type of mathematical modeling that consists of reproducing a social process or the functioning of a social system on a computer. Almost always involves the reproduction of random factors influencing the phenomenon being studied, and, as a consequence,... ... Sociology: Encyclopedia

MODELING, STATISTICAL- development of various models that reflect the statistical patterns of the described object, phenomenon. A common specific feature of these models is the consideration of random disturbances or deviations. Objects S.m. are different... ... Large economic dictionary

STATISTICAL MODELING- representation or description of a certain phenomenon or system of relationships between phenomena through a set of variables (indicators, characteristics) and statistical relationships between them. The goal of M.S. (like any other modeling) imagine... ... Sociology: Encyclopedia

To improve this article, it is advisable?: Correct the article according to the stylistic rules of Wikipedia. Simulation modeling (situational... Wikipedia

SIMULATION MODELING- (...from the French modele sample) a method of studying any phenomena and processes using statistical tests (Monte Carlo method) using a computer. The method is based on drawing (simulating) the influence of random factors on the phenomenon being studied or... ... Encyclopedic Dictionary of Psychology and Pedagogy

Books

• Statistical modeling. Monte Carlo methods. Textbook for bachelor's and master's degrees, Mikhailov G.A.. The textbook is devoted to the features of modeling random variables, processes and fields. Particular attention is paid to numerical integration, in particular the Monte Carlo method. A solution is given...

The assumptions embodied in statistical modeling describe a set of probability distributions, some of which are assumed to adequately approximate the distribution. From the definition, a specific data set is selected. The probability distributions inherent in statistical modeling are what distinguish statistical models from other, non-statistical, mathematical models.

Connection with mathematics

This scientific method is rooted primarily in mathematics. Statistical modeling of systems is usually specified by mathematical equations that relate one or more random variables and possibly other non-random variables. Thus, a statistical model is “a formal representation of a theory” (Herman Ader, citing Kenneth Bollen).

All statistical hypothesis tests and all statistical estimates are derived from statistical models. More generally, statistical models are part of the basis of statistical inference.

Statistical modeling methods

Informally, a statistical model can be thought of as a statistical assumption (or set of statistical assumptions) with a certain property: this assumption allows us to calculate the probability of any event. As an example, consider a pair of regular six-sided dice. We will study two different statistical assumptions about dice.

The first statistical assumption constitutes a statistical model because with only one assumption we can calculate the probability of any event. An alternative statistical assumption does not constitute a statistical model because with only one assumption we cannot calculate the probability of each event.

In the example above, with the first assumption, calculating the probability of an event is easy. However, in some other examples, the calculation may be difficult or even impractical (for example, it may require millions of years of calculations). For the assumption that makes up the statistical model, this difficulty is acceptable: performing the calculation does not have to be practical, just theoretically possible.

Examples of models

Let's assume that we have a population of schoolchildren with children evenly distributed by age. A child's height will be stochastically related to age: for example, when we know a child is 7 years old, this affects the probability that the child will be 5 feet tall (roughly 152 cm). We could formalize this relationship in a linear regression model, for example: height = b0 + b1agei + εi, where b0 is the intercept, b1 is the parameter by which age is multiplied to obtain the height prediction, εi is the error term. This implies that height is predicted by age with some error.

A valid model must fit all data points. So a straight line (heighti = b0 + b1agei) cannot be an equation for a data model - unless it fits all data points exactly, that is, all data points lie perfectly on the line. The error term εi must be included in the equation for the model to fit all data points.

To make statistical inference, we first need to assume some probability distributions for εi. For example, we can assume that the distributions of εi are Gaussian, with zero mean. In this case, the model will have 3 parameters: b0, b1 and the variance of the Gaussian distribution.

general description

This is a special class of mathematical model. What makes a statistical model different from other mathematical models is that it is non-deterministic. It is used to model statistical data. Thus, in a statistical model defined by mathematical equations, some variables do not have specific values, but instead have probability distributions; that is, some variables are stochastic. In the example above, ε is a stochastic variable; without this variable the model would be deterministic.

Statistical models are often used in statistical analysis and modeling, even when the physical process being modeled is deterministic. For example, coin tossing is in principle a deterministic process; yet it is usually modeled as stochastic (via the Bernoulli process).

Parametric models

They are the most commonly used statistical models. Regarding semi-parametric and non-parametric models, Sir David Cox said: "They generally include fewer assumptions about the structure and shape of the distribution, but usually contain strong assumptions about independence." Like all other mentioned models, they are also often used in the statistical method of mathematical modeling.

Multi-level models

Multilevel models (also known as hierarchical linear models, nested data models, mixed models, random coefficients, random effects models, random parameter models, or partitioned models) are statistical models of parameters that vary across more than one level. An example would be a student performance model that contains measures for individual students as well as measures for the classrooms in which students are grouped. These models can be thought of as generalizations of linear models (in particular linear regression), although they can also extend to nonlinear models. These models became much more popular once sufficient computing power and software became available.

Multilevel models are especially suitable for research projects where data for participants is organized at more than one level (that is, nested data). The units of analysis are typically individuals (at a lower level) that are nested within contextual/aggregate units (at a higher level). While the lowest level of data in multilevel models is typically individual, repeated measures of individuals can also be considered. Thus, multilevel models provide an alternative type of analysis for univariate or multivariate repeated measures analyses. Individual differences in growth curves may be considered. Additionally, multilevel models can be used as an alternative to ANCOVA, where scores on the dependent variable are adjusted for covariates (eg, individual differences) before testing for treatment differences. Multilevel models are able to analyze these experiments without the assumption of homogeneity of regression slopes, which is required by ANCOVA.

Multilevel models can be used for data with many levels, although two-level models are the most common, and the rest of this article focuses only on these. The dependent variable should be examined at the lowest level of analysis.

Model selection

Model selection is the task of selecting from a set of candidate models given data, carried out within the framework of statistical modeling. In the simplest cases, an already existing data set is considered. However, the task may also involve designing experiments so that the collected data are well suited to the model selection task. Given candidate models with similar predictive or explanatory power, the simplest model is likely to be the best choice (Occam's razor).

Konishi & Kitagawa states, “Most statistical inference problems can be considered statistical modeling problems.” Likewise, Cox said, “How the problem at hand is translated into a statistical model is often the most important part of the analysis.”

Model selection may also refer to the problem of selecting a few representative models from a large set of computational models for the purpose of decision making or optimization under uncertainty.

Graphic models

A graphical model, or probabilistic graphical model (PGM) or structured probability model, is a probabilistic model for which the graph expresses the structure of the conditional relationship between random variables. They are commonly used in probability theory, statistics (especially Bayesian statistics), and machine learning.

Econometric models

Econometric models are statistical models used in econometrics. An econometric model defines the statistical relationships that are believed to exist between various economic quantities related to a particular economic phenomenon. An econometric model can be derived from a deterministic economic model that accounts for uncertainty, or from an economic model that is itself stochastic. However, it is also possible to use econometric models that are not tied to any particular economic theory.

Statistical modeling is a numerical method for solving mathematical problems, in which the desired quantities are represented by the probabilistic characteristics of some random phenomenon. This phenomenon is modeled, after which the required characteristics are approximately determined by statistical processing of the “observations” of the model.

The development of such models consists of choosing a method of statistical analysis, planning the process of obtaining data, assembling data about the ecological system, algorithmizing and computer calculation of statistical relationships. Changing the patterns of development of the environmental situation requires repeating the described procedure, but in a new capacity.

Statistical finding of a mathematical model includes choosing the type of model and determining its parameters. Moreover, the desired function can be either a function of one independent variable (single-factor) or many variables (multi-factor). The task of choosing the type of model is an informal task, since the same dependence can be described with the same error by a variety of analytical expressions (regression equations). A rational choice of the type of model can be justified by taking into account a number of criteria: compactness (for example, described by a monomial or polynomial), interpretability (the ability to give meaningful meaning to the coefficient of the model), etc. The task of calculating the parameters of the selected model is often purely formal and is carried out on a computer.

When forming a statistical hypothesis about a certain ecological system, it is necessary to have an array of diverse data (database), which can be unreasonably large. An adequate understanding of the system is associated in this case with the separation of unimportant information. Both the list (type) of data and the amount of data can be reduced. One of the methods for carrying out such a compression of environmental information (without a priori assumptions about the structure and dynamics of the observed ecosystem) can be factor analysis. Data reduction is carried out by the method of least squares, principal components and other multivariate statistical methods using in the future, for example, cluster analysis.

Note that primary environmental information has more-less the following features:

– multidimensionality of data;

– nonlinearity and ambiguity of relationships in the system under study;

– measurement error;

– the influence of unaccounted factors;

– spatiotemporal dynamics.

When solving the first problem of choosing the type of model, it is assumed that m input (x 1, x 2, ..., x m and n output (y 1, y 2, ..., y) data are known. In this case, it is possible, in in particular, the following two models in matrix notation:

where X and Y are known input (output) and output (input) parameters of an environmental object ("black box") in vector notation form; A and B are the desired matrices of constant model coefficients (model parameters).

Along with the indicated models a more general form of statistical modeling is considered:

where F is the vector of hidden influencing factors; C and D are the required coefficient matrices.

When solving environmental problems It is advisable to use both linear and nonlinear mathematical models, since many environmental patterns have been little studied. As a result, the multidimensionality and nonlinearity of the modeled relationships will be taken into account.

Based on a generalized model it is possible to identify internal hidden factors of the environmental processes being studied that are not known to the environmental engineer, but their manifestation is reflected in the components of the vectors X and Y. This procedure is most appropriate in the case where there is no strict cause-and-effect relationship between the values ​​of X and Y. A generalized model taking into account the influence of hidden factors eliminates a certain contradiction between two models with matrices A and B, when in fact two different models could be used to describe the same ecological process. This contradiction is caused by the opposite meaning of the cause-and-effect relationship between quantities A and Y (in one case, X is the input, and Y is the output, and in the other, vice versa). A generalized model, taking into account the value F, describes a more complex system from which both values ​​X and Y are output, and hidden factors F act on the input.

It is important in statistical modeling to use a priori data, when during the decision process some regularities of the models can be established and their potential number can be narrowed.

Suppose it is necessary to create a model with the help of which the fertility of a certain type of soil can be numerically determined in 24 hours, taking into account its temperature T and humidity W. Neither wheat nor an apple tree can produce a crop in 24 hours. But for test sowing, you can use bacteria with a short life cycle, and use the amount of P released CO 2 per unit time as a quantitative criterion for the intensity of their vital activity. Then the mathematical model of the process under study is the expression

where P 0 is a numerical indicator of soil quality.

It seems that we do not have any data on the form of the function f(T, W) because the systems engineer does not have the necessary agronomic knowledge. But it is not so. Who doesn’t know that at T≈0°C water freezes and, therefore, CO 2 cannot be released, and at 80°C pasteurization occurs, i.e. most bacteria die. A priori data are already sufficient to state that the desired function is quasi-parabolic in nature, close to zero at T = 0 and 80°C and has an extremum within this temperature range. Similar reasoning regarding humidity leads to the fact that the maximum extremum of the desired function is recorded at W=20% and its approach to zero at W=0 and 40%. Thus, the form of the approximate mathematical model has been determined a priori, and the task of the experiment is only to clarify the nature of the function f(T, W) at T = 20 ... 30 and 50 ... 60 ° C, as well as for W = 10 ... 15 and 25 ... 30% and more accurate determination of the coordinates of the extremum (which reduces the amount of experimental work, i.e., the amount of statistical data).