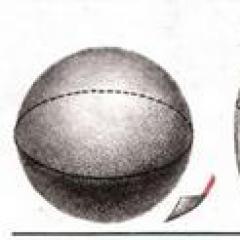
Girando la esfera del revés. Para los que no les gustan las matemáticas
El gran matemático David Hilbert dijo una vez que una teoría matemática puede considerarse perfecta solo cuando puede presentarse a la primera persona que conoce. Los seguidores de Hilbert están completamente desesperados tratando de vivir con esta receta. Las matemáticas se están volviendo cada vez más especializadas, y ahora un científico matemático a veces necesita mucho trabajo, incluso a sus colegas, para explicar la esencia de los problemas que está resolviendo. Sin embargo, de vez en cuando, la investigación en las ramas principales y aparentemente inaccesibles de esta ciencia conduce a un descubrimiento que es interesante para el profano y, al mismo tiempo, puede explicarse sin simplificar demasiado. Un ejemplo sorprendente de esto es el teorema de Stephen Smale sobre los llamados mapeos regulares de la esfera, publicado en 1959.
El campo en el que trabajaba Smale, la topología diferencial, era una de las ramas más abstractas de las matemáticas modernas. Es aún más sorprendente que, sin embargo, fuera posible encontrar una explicación visual de una de las consecuencias más llamativas del teorema de Smale. Es decir, puede demostrar cómo darle la vuelta a la esfera.
En el sentido habitual, esto es, por supuesto, imposible: la esfera tendría que romperse. Pero en la topología diferencial se permite - mentalmente, por supuesto - arrastrar una superficie a través de sí misma - estas son las "reglas del juego" en esta ciencia. Pero luego una solución simple llama la atención de inmediato.

Es necesario apretar los lados opuestos hacia el centro hasta que se atraviesen (I). La superficie interior pintada (II) sobresale de dos bordes opuestos. Continuemos este proceso de "estirar" la superficie interior hasta que el anillo formado por la parte restante de la superficie exterior (II) desaparezca por completo. Desafortunadamente, durante este proceso, el anillo forma un lazo apretado (III), que debe apretarse. El resultado es una cicatriz (IV), y esto no satisface a los topólogos diferenciales, porque consideran solo las llamadas "superficies lisas", que no tienen esquinas ni torceduras.
Entonces, la tarea es darle la vuelta a la esfera de tal manera que, al deshacerse del rizo, no quede una cicatriz. Y aquí la intuición sugiere nuevamente que el problema es insoluble. Cuando Smale anunció por primera vez que podía probar la existencia de una solución, nadie le creyó. Pero la intuición estaba equivocada: no había un solo error lógico en la demostración de Smale. Los matemáticos se convencieron de que teóricamente era posible seguir la demostración paso a paso y encontrar una descripción explícita de la deformación que evertía la esfera. Pero era tan difícil que parecía una causa perdida. Durante algún tiempo después del descubrimiento de Smale, se supo que, en principio, era posible darle la vuelta a una esfera sin cicatriz, pero nadie tenía la menor idea de cómo hacerlo.
Pero, al final, los matemáticos hicieron frente a esta tarea. Cómo: lo entenderá mirando las imágenes. Son entretenidos.
Aunque la prueba de Smale no consistió solo en dibujos. Es curioso que en su obra no haya ninguno, esas figuras que están implícitamente contenidas en su aparato analítico abstracto son demasiado complejas. El artista más inventivo no habría podido retratarlos; la imaginación de los matemáticos es asombrosa. Pero quizás aún más llamativa sea su capacidad para transmitirse las ideas más complejas entre sí sin recurrir a los dibujos. La historia con el giro de la esfera es una clara evidencia de esto. Se dio a conocer al gran público gracias al topólogo francés Rene Thom, quien lo supo de su colega Bernard Moren, quien a su vez, del estadounidense Arnold Shapiro, inventor de esta "inversión". Esto es especialmente curioso si se tiene en cuenta que Bernard Morin es ciego.

Estas imágenes muestran cómo se puede dar la vuelta a una esfera sin violar los requisitos de la topología diferencial. Primero, debe acercar los lados opuestos de la esfera gris (A), empujándolos entre sí. Luego, la superficie pintada (B) aparece en ambos lados. Luego es necesario estirar una de las piezas coloreadas (C) de tal manera que se obtenga una superficie que se asemeje a una silla de montar sobre dos "patas" (O). Estas dos patas se tuercen en sentido antihorario para obtener la superficie E. Se muestra nuevamente (P) “en sección” con cintas, que, como en la “esfera marcada”, representan secciones transversales en diez niveles diferentes.
Entonces no tiene sentido representar las superficies resultantes en cada etapa, son demasiado complejas. Pero puede, si lo desea, considerar las cintas en los 10 niveles y terminar mentalmente de dibujar. No obstante, decidimos mostrar una etapa (H2), solo para que uno pudiera imaginar cuál es el tipo de las figuras resultantes. La superficie G aparece después de que el asiento de la superficie P se comprime y se gira 90 °.
Unos cuantos pasos más. A saber: entre las etapas I y J, dos patas de la misma forma se atraviesan. Cada sección de superficie en forma de cinta en la etapa J tiene dos lados grises uno frente al otro. Entre las etapas J y K, la capa interna se expande y la externa se contrae; se obtiene la superficie K, exactamente igual que J, pero solo los colores han cambiado de lugar.
Luego, todas las acciones se llevan a cabo en "orden inverso". Puedes hacerte una idea mirando las imágenes I, H, C, etc. Solo necesitas intercambiar los colores de las cintas en cada imagen. Presentamos el final de esta segunda fila de imágenes. La superficie L corresponde a la superficie F, L2 a E, etc.
La esfera coloreada (superficie P) corresponde a la esfera gris (superficie A). Entonces, la deformación está hecha y no hay cicatriz. La posibilidad misma de este truco fue probada por primera vez por S. Smale. Y todas las etapas sucesivas de deformación fueron inventadas por A. Shapiro ...
P. S. ¿De qué más están hablando los científicos británicos? Que el mecanismo de darle la vuelta a la esfera a veces no es más filosófico que, digamos, un programa PDF creado por algún programador talentoso.
En el espacio tridimensional, puedes darle la vuelta en una clase de buceo, es decir, con posibles auto-intersecciones, pero sin torceduras. En otras palabras, la imagen de la esfera en cada momento de deformación debe permanecer suave, es decir, diferenciable.
La torsión de la esfera no es en absoluto una paradoja lógica, es un teorema, solo uno muy contradictorio. Con más precisión:
Es difícil imaginar un ejemplo concreto de una familia de inmersiones así, aunque hay muchas ilustraciones y películas. Por otro lado, es mucho más fácil demostrar que existe tal familia, y esto es exactamente lo que hizo Smale.
Historia
Esta paradoja fue descubierta por Smale en 1958. Según la leyenda, cuando Smale intentó publicar este teorema, recibió una respuesta diciendo que la afirmación es obviamente incorrecta, ya que en el proceso de tal "eversión" se debe preservar el grado del mapa gaussiano. [ ] De hecho, el grado del mapa de Gauss debe preservarse; en particular, esto muestra que el círculo no se puede "girar" en el plano, pero los grados de los mapas de Gauss y y en v ambos son iguales a 1. Además, el grado de incrustación es igual a 1.
Variaciones y generalizaciones
Escriba una reseña sobre el artículo "Revertir la esfera"
Literatura
- Smale, Stephen Una clasificación de inmersiones de las dos esferas. Trans. Amer. Matemáticas. Soc. 90 1958 281-290.
- Francis, J. Moscú: Mir, 1991. Capítulo 6. Volviendo la esfera del revés.
Notas (editar)
Extracto de la inversión de la esfera
—Una vez más, coronel —dijo el general—, no puedo, sin embargo, dejar a la mitad de la gente en el bosque. Les pido, les pido ”, repitió,“ que tomen posición y se preparen para el ataque.- Y le pido que no se entrometa en otros asuntos que no sean los suyos - respondió con ardor el coronel. - Si fueras un soldado de caballería ...
"No soy un soldado de caballería, coronel, pero soy un general ruso, y si no lo sabe ..."
"Es muy conocido, Su Excelencia", gritó de repente el coronel, tocando el caballo y poniéndose rojo carmesí. “No querrás estar encadenado y verás que este puesto no es inútil en ninguna parte. No quiero exterminar mi estante para tu placer.
Se olvida de sí mismo, coronel. No estoy observando mi placer y no permitiré que se diga esto.
El general, aceptando la invitación del coronel al torneo de la valentía, enderezando el pecho y frunciendo el ceño, cabalgó con él hacia la cadena, como si todas sus discordias se resolvieran allí, encadenado, bajo las balas. Llegaron encadenados, varias balas volaron sobre ellos y se detuvieron en silencio. No había nada que mirar en la cadena, ya que incluso desde el lugar donde habían estado anteriormente, estaba claro que era imposible moverse entre los matorrales y barrancos de la caballería, y que los franceses pasaban por alto el ala izquierda. El general y el coronel se miraron severamente y significativamente, como dos gallos preparándose para la batalla, el uno al otro, esperando en vano signos de cobardía. Ambos aprobaron el examen. Como no había nada que decir, y ni uno ni el otro querían darle al otro una razón para decir que él fue el primero en salir de las balas, se habrían quedado allí durante mucho tiempo, experimentando mutuamente el coraje, si en esa vez en el bosque, casi detrás de ellos, escucharon el crepitar de los rifles y un grito sordo y fundido. Los franceses atacaron a los soldados que se encontraban en el bosque con leña. Los húsares ya no podían retirarse con la infantería. Fueron cortados del camino de retirada a la izquierda por la cadena francesa. Ahora, por más incómodo que fuera el terreno, era necesario atacar para abrirse camino.
El escuadrón donde sirvió Rostov, que acababa de subirse a los caballos, se detuvo frente al enemigo. Una vez más, como en el puente de Ensk, no había nadie entre el escuadrón y el enemigo, y entre ellos, dividiéndolos, se extendía la misma línea terrible de incertidumbre y miedo, como una línea que separa a los vivos de los muertos. Todas las personas sintieron esta línea, y la pregunta de si cruzarían o no y cómo cruzarían la línea les preocupó.
Imagina que la esfera bidimensional "ordinaria" S 2 está fabricado con material elástico que puede atravesarse por sí mismo. ¿Es posible darle la vuelta a la esfera en el espacio tridimensional habitual $$ \ mathbb (R) ^ 3 $$ sin torceduras ni roturas, pero con posible auto-intersección (es decir, en la clase de inmersión)?
En 2000, Smale recopiló una lista de 18 tareas que, en su opinión, deben resolverse en el siglo XXI. Esta lista se compila en el espíritu de los problemas de Hilbert y, al igual que los problemas del milenio compilados más tarde, incluye la hipótesis de Riemann, la cuestión de la igualdad de las clases P y NP, el problema de resolver las ecuaciones de Navier-Stokes y también la Conjetura de Poincaré, ahora probada por Perelman. Smale compiló su lista a instancias de Arnold, entonces presidente de la Unión Matemática Internacional, quien probablemente tomó la idea de la lista de la lista de problemas de Hilbert.
Y finalmente, la pregunta: ¿es posible "convertir" un círculo en un plano, es decir, encontrar una familia continua de inmersiones, como arriba?
Comentarios (1)
Curioso. Me viene a la mente lo siguiente. Imaginemos una esfera en forma de proyección estereográfica: un plano con infinito. Luego, girar la esfera de adentro hacia afuera parece como hacer girar el avión en la otra dirección, es decir, con una orientación diferente. Hay un agujero en el razonamiento en alguna parte, ¿verdad?
Pues bien, la proyección estereográfica implica la selección de un punto en una esfera, que no corresponde a nada en el plano, y eso cambia las reglas del juego, porque según las condiciones, la esfera no se puede romper, y el punto no se puede perforar exactamente.
Bueno, en principio, sospechaba que había un punto débil con un punto infinitamente distante. Solo quería conocer una opinión independiente;).
Misha, me gustaría saber si las superficies K3 ocurren en la teoría de cuerdas, y si es así, ¿cómo surgen exactamente allí?
Sí, a veces las hay. En el contexto de la compactación. K3 tiene el grupo de holonomía $$ SU (2) \ subset SU (2) \ times SU (2) $$ y por lo tanto retiene la mitad de las supersimetrías. Fenomenológicamente, estos modelos no son muy interesantes, pero la gente los considera de todos modos.
Giro la esfera sin torceduras incluso más fácil que en la película. Debe pegar parte de la superficie de la esfera hacia adentro con el dedo. Gire esta parte interior de la esfera 180 grados, mientras el agujero se cierra sin torceduras. Los meridianos de la esfera, que eran círculos, se convertirán en "ochos" con una cabeza más pequeña dentro de otra más grande. A continuación, inflamos la casi bola interior hasta que gotee. Naturalmente, su apariencia resultará invertida. Sigue siendo lo que era en su mayor parte, y ahora que se ha vuelto más pequeño en comparación con lo hinchado, para desplegarse 180 grados. El orificio apretado se abrirá, enderezará la abolladura y se logrará el objetivo.
Aquí resulta que un punto se convierte en infinito y el infinito se convierte en un punto. O, "la igualdad del universo": lo que está adentro, lo que está afuera.
Por lo tanto, surge un paradigma: el microcosmos se puede estudiar utilizando el macrocosmos y viceversa.
La pregunta está en el límite de radio =] h / 2; 2 / h [. Aquí h se usa como el límite métrico de precisión de medición, es decir, el mismo épsilon dividido por dos.
Además, la existencia física de dicha esfera puede probarse o refutarse en varios casos.
¿O me equivoco?