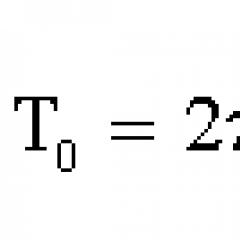Vibraciones mecánicas - Hipermercado del Conocimiento. Vibraciones mecánicas Fórmulas sobre el tema ondas mecánicas.
Al estudiar esta sección, tenga en cuenta que fluctuaciones de diferente naturaleza física se describen desde posiciones matemáticas comunes. Aquí es necesario comprender claramente conceptos tales como oscilación armónica, fase, diferencia de fase, amplitud, frecuencia y período de oscilación.
Hay que tener en cuenta que en cualquier sistema oscilatorio real existe una resistencia del medio, es decir las oscilaciones serán amortiguadas. Para caracterizar la amortiguación de las oscilaciones, se introducen un coeficiente de amortiguación y una disminución de la amortiguación logarítmica.
Si las oscilaciones ocurren bajo la influencia de una fuerza externa que cambia periódicamente, entonces dichas oscilaciones se denominan forzadas. No estarán amortiguados. La amplitud de las oscilaciones forzadas depende de la frecuencia de la fuerza impulsora. A medida que la frecuencia de las oscilaciones forzadas se acerca a la frecuencia de las oscilaciones naturales, la amplitud de las oscilaciones forzadas aumenta drásticamente. Este fenómeno se llama resonancia.
Al pasar al estudio de las ondas electromagnéticas, es necesario comprender claramente queonda electromagnéticaEs un campo electromagnético que se propaga en el espacio. El sistema más simple que emite ondas electromagnéticas es un dipolo eléctrico. Si un dipolo sufre oscilaciones armónicas, emite una onda monocromática.
Tabla de fórmulas: oscilaciones y ondas.
|
Leyes físicas, fórmulas, variables. |
Fórmulas de oscilación y onda. |
||||||
|
Ecuación de vibración armónica: donde x es el desplazamiento (desviación) de la cantidad fluctuante desde la posición de equilibrio; A - amplitud; ω - frecuencia circular (cíclica); α - fase inicial; (ωt+α) - fase. |
|||||||
|
Relación entre período y frecuencia circular: |
|||||||
|
Frecuencia: |
|||||||
|
Relación entre frecuencia circular y frecuencia: |
|||||||
|
Períodos de oscilaciones naturales. 1) péndulo de resorte: donde k es la rigidez del resorte; 2) péndulo matemático: donde l es la longitud del péndulo, g - aceleración de caída libre; 3) circuito oscilatorio: donde L es la inductancia del circuito, C es la capacitancia del capacitor. |
|
||||||
|
Frecuencia natural: |
|||||||
|
Suma de oscilaciones de la misma frecuencia y dirección: 1) amplitud de la oscilación resultante donde A 1 y A 2 son las amplitudes de los componentes de vibración, α 1 y α 2 - fases iniciales de los componentes de vibración; 2) la fase inicial de la oscilación resultante |
|
||||||
|
Ecuación de oscilaciones amortiguadas: e = 2,71... - la base de los logaritmos naturales. |
|
||||||
|
Amplitud de oscilaciones amortiguadas: donde A 0 es la amplitud en el momento inicial; β - coeficiente de atenuación; |
|
||||||
|
Coeficiente de atenuación: cuerpo oscilante donde r es el coeficiente de resistencia del medio, metro - peso corporal; circuito oscilatorio donde R es la resistencia activa, L es la inductancia del circuito. |
|||||||
|
Frecuencia de oscilaciones amortiguadas ω: |
|
||||||
|
Período de oscilaciones amortiguadas T: |
|
||||||
|
Decremento de amortiguación logarítmica: |
Las oscilaciones armónicas son oscilaciones realizadas según las leyes del seno y el coseno. La siguiente figura muestra una gráfica de los cambios en las coordenadas de un punto a lo largo del tiempo según la ley del coseno.
imagen
amplitud de oscilación
La amplitud de una vibración armónica es el mayor valor del desplazamiento de un cuerpo desde su posición de equilibrio. La amplitud puede adoptar diferentes valores. Dependerá de cuánto desplacemos el cuerpo en el momento inicial de la posición de equilibrio.
La amplitud está determinada por las condiciones iniciales, es decir, la energía impartida al cuerpo en el momento inicial. Dado que el seno y el coseno pueden tomar valores en el rango de -1 a 1, la ecuación debe contener un factor Xm, que exprese la amplitud de las oscilaciones. Ecuación de movimiento para vibraciones armónicas:
x = Xm*cos(ω0*t).
Periodo de oscilación
El período de oscilación es el tiempo que lleva completar una oscilación completa. El período de oscilación se designa con la letra T. Las unidades de medida del período corresponden a las unidades de tiempo. Es decir, en SI son segundos.
La frecuencia de oscilación es el número de oscilaciones realizadas por unidad de tiempo. La frecuencia de oscilación se designa con la letra ν. La frecuencia de oscilación se puede expresar en términos del período de oscilación.
ν = 1/T.
Las unidades de frecuencia están en SI 1/seg. Esta unidad de medida se llama Hercios. El número de oscilaciones en un tiempo de 2*pi segundos será igual a:
ω0 = 2*pi* ν = 2*pi/T.
Frecuencia de oscilación
Esta cantidad se llama frecuencia cíclica de oscilaciones. En alguna literatura aparece el nombre de frecuencia circular. La frecuencia natural de un sistema oscilatorio es la frecuencia de oscilaciones libres.
La frecuencia de las oscilaciones naturales se calcula mediante la fórmula:
La frecuencia de las vibraciones naturales depende de las propiedades del material y de la masa de la carga. Cuanto mayor es la rigidez del resorte, mayor es la frecuencia de sus propias vibraciones. Cuanto mayor es la masa de la carga, menor es la frecuencia de las oscilaciones naturales.
Estas dos conclusiones son obvias. Cuanto más rígido sea el resorte, mayor será la aceleración que impartirá al cuerpo cuando el sistema pierda el equilibrio. Cuanto mayor sea la masa de un cuerpo, más lentamente cambiará su velocidad.
Periodo de oscilación libre:
T = 2*pi/ ω0 = 2*pi*√(m/k)
Es de destacar que en ángulos de desviación pequeños, el período de oscilación del cuerpo sobre el resorte y el período de oscilación del péndulo no dependerán de la amplitud de las oscilaciones.
Anotemos las fórmulas para el período y la frecuencia de oscilaciones libres de un péndulo matemático.
entonces el periodo será igual
T = 2*pi*√(l/g).
Esta fórmula será válida sólo para ángulos de desviación pequeños. De la fórmula vemos que el período de oscilación aumenta al aumentar la longitud del hilo del péndulo. Cuanto mayor sea la longitud, más lento vibrará el cuerpo.
El período de oscilación no depende en absoluto de la masa de la carga. Pero depende de la aceleración de la caída libre. A medida que g disminuye, el período de oscilación aumentará. Esta propiedad se utiliza ampliamente en la práctica. Por ejemplo, para medir el valor exacto de la aceleración libre.
Las oscilaciones armónicas ocurren según la ley:
X = A porque(ω t + φ 0),
Dónde X– desplazamiento de la partícula desde la posición de equilibrio, A– amplitud de oscilaciones, ω – frecuencia circular, φ 0 – fase inicial, t- tiempo.
Periodo de oscilación t = .
Velocidad de partícula oscilante:
υ
=
 = – Aω pecado(ω t
+ φ 0),
= – Aω pecado(ω t
+ φ 0),
aceleración a
=
 = –Aω 2 porque (ω t
+ φ 0).
= –Aω 2 porque (ω t
+ φ 0).
Energía cinética de una partícula en movimiento oscilatorio: mi k =  =
= pecado 2 (ω t+ φ 0).
pecado 2 (ω t+ φ 0).
Energía potencial:
mi norte=  porque 2 (ω t
+ φ 0).
porque 2 (ω t
+ φ 0).
Períodos de oscilaciones del péndulo.
- primavera t
=
 ,
,
Dónde metro– masa de carga, k– coeficiente de rigidez del resorte,
– matemático t
=
 ,
,
Dónde yo– longitud de la suspensión, gramo- aceleración de la gravedad,
- físico t
=
 ,
,
Dónde I– momento de inercia del péndulo con respecto al eje que pasa por el punto de suspensión, metro– masa del péndulo, yo– distancia desde el punto de suspensión al centro de masa.
La longitud reducida de un péndulo físico se encuentra a partir de la condición: yo np =  ,
,
Las designaciones son las mismas que las de un péndulo físico.
Cuando se suman dos oscilaciones armónicas de la misma frecuencia y una dirección, se obtiene una oscilación armónica de la misma frecuencia con amplitud:
A = A 1 2 + A 2 2 + 2A 1 A 2 porque(φ 2 – φ 1)
y fase inicial: φ = arctan  .
.
Dónde A 1 , A 2 – amplitudes, φ 1, φ 2 – fases iniciales de oscilaciones plegadas.
La trayectoria del movimiento resultante cuando se suman oscilaciones mutuamente perpendiculares de la misma frecuencia:
 +
+
 –
–
 cos (φ 2 – φ 1) = pecado 2 (φ 2 – φ 1).
cos (φ 2 – φ 1) = pecado 2 (φ 2 – φ 1).
Las oscilaciones amortiguadas se producen según la ley:
X = A 0 mi - β t porque(ω t + φ 0),
donde β es el coeficiente de amortiguación, el significado de los parámetros restantes es el mismo que para las oscilaciones armónicas, A 0 – amplitud inicial. En un momento en el tiempo t amplitud de vibración:
A = A 0 mi - β t .
El decremento logarítmico de la amortiguación se llama:
λ = registro  = β t,
= β t,
Dónde t– período de oscilación: t
=
 .
.
El factor de calidad de un sistema oscilatorio se llama:
La ecuación de una onda viajera plana tiene la forma:
y = y 0 porque ω( t ± ),
Dónde en– desplazamiento de la cantidad oscilante desde la posición de equilibrio, en 0 – amplitud, ω – frecuencia angular, t- tiempo, X– coordenada a lo largo de la cual se propaga la onda, υ – velocidad de propagación de las ondas.
El signo “+” corresponde a una onda que se propaga contra el eje X, el signo “-” corresponde a una onda que se propaga a lo largo del eje X.
La longitud de onda se llama período espacial:
λ = υ t,
Dónde υ – velocidad de propagación de la onda, t– período de propagación de oscilaciones.
La ecuación de onda se puede escribir:
y = y 0 porque 2π (+).
Una onda estacionaria se describe mediante la ecuación:
y
= (2y 0cos  ) porque ω t.
) porque ω t.
La amplitud de la onda estacionaria está entre paréntesis. Los puntos con máxima amplitud se llaman antinodos,
X norte = norte ,
puntos con amplitud cero - nodos,
X y = ( norte + ) .
Ejemplos de resolución de problemas
Problema 20
La amplitud de las oscilaciones armónicas es de 50 mm, el período es de 4 s y la fase inicial . a) Escriba la ecuación de esta oscilación; b) encuentre el desplazamiento del punto oscilante desde la posición de equilibrio en t=0 y en t= 1,5 s; c) dibuja una gráfica de este movimiento.
Solución
La ecuación de oscilación se escribe como X = a porque( t+ 0).
Según la condición, se conoce el período de oscilación. A través de él podemos expresar la frecuencia circular =
 .
Se conocen los parámetros restantes:
.
Se conocen los parámetros restantes:
A) X= 0,05cos( t + ).
b) compensación X en t= 0.
X 1 = 0,05 porque = 0,05
 = 0,0355m.
= 0,0355m.
En t= 1,5 s
X 2 = 0,05 cos( 1,5 + )= 0,05 cos = – 0,05 m.
V  ) gráfica de una función X=0,05cos ( t
+
) como sigue:
) gráfica de una función X=0,05cos ( t
+
) como sigue:
Determinemos la posición de varios puntos. Conocido X 1 (0) y X 2 (1,5), así como el período de oscilación. Entonces, a través de t= valor de 4 s X se repite, y después t = 2 s cambia de signo. Entre el máximo y el mínimo en el medio es 0.
Problema 21
El punto sufre una oscilación armónica. El período de oscilación es de 2 s, la amplitud es de 50 mm y la fase inicial es cero. Encuentre la velocidad del punto en el momento en que su desplazamiento desde la posición de equilibrio es de 25 mm.
Solución
1 vía. Anotamos la ecuación de oscilación puntual:
X= 0,05 cos t,
porque =
 =.
=.
Encontrar la velocidad en el momento del tiempo. t:
υ
=
 = – 0,05
porque t.
= – 0,05
porque t.
Encontramos el momento en el tiempo en el que el desplazamiento es de 0,025 m:
0,025 = 0,05 cos t 1 ,
por lo tanto cos t 1 = , t 1 = . Sustituimos este valor en la expresión de velocidad:
υ
= – 0,05 sen
=
– 0,05
 = 0,136 m/s.
= 0,136 m/s.
Método 2. Energía total del movimiento oscilatorio:
mi
=
 ,
,
Dónde A– amplitud, – frecuencia circular, metro – masa de partículas.
En cada momento del tiempo se compone de la energía potencial y cinética del punto.
mi k =
 ,
mi norte =
,
mi norte =
 , Pero k
= metro 2, lo que significa mi norte =
, Pero k
= metro 2, lo que significa mi norte =
 .
.
Anotemos la ley de conservación de la energía:
 =
=
 +
+ ,
,
de aquí obtenemos: a 2 2 = υ 2 + 2 X 2 ,
υ
=
 =
=
 = 0,136 m/s.
= 0,136 m/s.
Problema 22
Amplitud de oscilaciones armónicas de un punto material. A= 2 cm, energía total mi= 3∙10 -7 J. ¿A qué desplazamiento desde la posición de equilibrio actúa la fuerza sobre el punto oscilante? F = 2,25∙10-5N?
Solución
La energía total de un punto que realiza oscilaciones armónicas es igual a:
mi
=
 .
(13)
.
(13)
El módulo de fuerza elástica se expresa mediante el desplazamiento de puntos desde la posición de equilibrio. X de la siguiente manera:
F = k x (14)
La fórmula (13) incluye la masa. metro y frecuencia circular , y en (14) – el coeficiente de rigidez k. Pero la frecuencia circular está relacionada con metro Y k:
2 =
 ,
,
de aquí k
= metro 2 y F = metro 2 X. Habiendo expresado metro 2 de la relación (13) obtenemos:
metro 2 =
 ,
F
=
,
F
=
 X.
X.
De donde obtenemos la expresión para el desplazamiento. X:
X
=
 .
.
Sustituyendo los valores numéricos se obtiene:
X
=
 = 1,5∙10 -2m = 1,5cm.
= 1,5∙10 -2m = 1,5cm.
Problema 23
El punto participa en dos oscilaciones con los mismos períodos y fases iniciales. amplitudes de oscilación A 1 = 3 cm y A 2 = 4 cm Encuentre la amplitud de la vibración resultante si: 1) las vibraciones ocurren en una dirección; 2) las oscilaciones son mutuamente perpendiculares.
Solución
Si las oscilaciones ocurren en una dirección, entonces la amplitud de la oscilación resultante se determina como:
Dónde A 1 y A 2 – amplitudes de oscilaciones agregadas, 1 y 2 – fases iniciales. Según la condición, las fases iniciales son las mismas, lo que significa 2 – 1 = 0, y cos 0 = 1.
Por eso:
A
=
 =
= =
A 1 +A 2 = 7 cm.
=
A 1 +A 2 = 7 cm.
Si las oscilaciones son mutuamente perpendiculares, entonces la ecuación del movimiento resultante será:
 cos( 2 – 1) = sen 2 ( 2 – 1).
cos( 2 – 1) = sen 2 ( 2 – 1).
Dado que por condición 2 – 1 = 0, cos 0 = 1, sen 0 = 0, la ecuación se escribirá como:  =0,
=0,
o  =0,
=0,
o  .
.

La relación resultante entre X Y en se puede representar en un gráfico. El gráfico muestra que el resultado será una oscilación de un punto en una línea recta. Minnesota. La amplitud de esta oscilación se determina como: A
=
 = 5 cm.
= 5 cm.
Problema 24
Período de oscilaciones amortiguadas. t=4 s, decremento de amortiguación logarítmico = 1,6, la fase inicial es cero. Desplazamiento puntual en t = igual a 4,5 cm 1) Escribe la ecuación de esta vibración; 2) Construya una gráfica de este movimiento para dos períodos.
Solución
La ecuación de oscilaciones amortiguadas con fase inicial cero tiene la forma:
X = A 0 mi - t cos2 .
No hay suficientes valores de amplitud inicial para sustituir valores numéricos A 0 y coeficiente de atenuación .
El coeficiente de atenuación se puede determinar a partir de la relación del decremento de atenuación logarítmico:
= t.
Así =
=
 = 0,4s-1.
= 0,4s-1.
La amplitud inicial se puede determinar sustituyendo la segunda condición:
4,5 centímetros = A 0
 porque 2
porque 2  = Un 0
= Un 0
 porque = A 0
porque = A 0

 .
.
Desde aquí encontramos:
A 0
=
4,5∙
 (cm) = 7,75cm.
(cm) = 7,75cm.
La ecuación final de movimiento es:
X
= 0,0775
 costo.
costo.


Problema 25
¿Cuál es el decremento logarítmico del amortiguamiento de un péndulo matemático, si por t = 1 min ¿la amplitud de las oscilaciones se redujo a la mitad? Longitud del péndulo yo = 1m.
Solución
El decremento logarítmico de la amortiguación se puede encontrar a partir de la relación: = t,
donde es el coeficiente de atenuación, t– período de oscilación. Frecuencia circular natural de un péndulo matemático:
0
=
 = 3,13s-1.
= 3,13s-1.
El coeficiente de amortiguación de oscilaciones se puede determinar a partir de la condición: A 0 = A 0 mi - t ,
t= ln2 = 0,693,
=
 = 0,0116c -1 .
= 0,0116c -1 .
Desde << 0 ,
то
в формуле
=
 se puede despreciar en comparación con 0 y el período de oscilación se puede determinar mediante la fórmula:
t
=
se puede despreciar en comparación con 0 y el período de oscilación se puede determinar mediante la fórmula:
t
=
 = 2c.
= 2c.
Sustituimos y t en la expresión para el decremento de amortiguación logarítmico y obtenemos:
= t= 0,0116 s -1 ∙ 2 s = 0,0232.
Problema 26
La ecuación de oscilaciones no amortiguadas se da en la forma X= 4 sen600 t cm.
Encuentre el desplazamiento desde la posición de equilibrio de un punto ubicado a una distancia yo= 75 cm desde la fuente de vibración, a través t= 0,01 s después del inicio de la oscilación. Velocidad de propagación de la oscilación υ = 300m/s.
Solución
Escribamos la ecuación de una onda que se propaga desde una fuente determinada: X= 0,04 sen 600 ( t– ).
Encontramos la fase de la onda en un momento dado en un lugar determinado:
t–
= 0,01 – = 0,0075 ,
= 0,0075 ,
600 ∙ 0,0075 = 4,5,
pecado 4,5 = pecado = 1.
Por lo tanto, el desplazamiento del punto X= 0,04 m, es decir en la distancia yo = 75 cm desde la fuente en el momento t= 0,01 s de desplazamiento máximo del punto.
Bibliografía
Volkenshtein V.S.. Colección de problemas para el curso general de física. – San Petersburgo: SpetsLit, 2001.
Savelyev I.V.. Colección de preguntas y problemas de física general. – M.: Nauka, 1998.
Y obtén dos lecciones gratis¡En la escuela de inglés SkyEng!
Yo mismo estudio allí, es genial. Hay progreso.
En la aplicación podrás aprender palabras, entrenar la escucha y la pronunciación.
Darle una oportunidad. ¡Dos lecciones gratis usando mi enlace!
Hacer clic
Movimientos oscilatorios (u oscilaciones) en física y tecnología se denomina a este tipo de movimientos (o cambios de estado) que tienen cierto grado de repetibilidad.
Las oscilaciones que se producen según las leyes del seno o el coseno se denominan armónicas.
Ecuación de vibración armónica:
donde t-tiempo; el valor de x cambia con el tiempo (coordenada, carga, corriente, fem, etc.); A - amplitud de oscilaciones - la desviación máxima del valor de oscilación del valor promedio (cero); - fase de oscilación; - fase inicial; w - frecuencia cíclica (cambio de fase por unidad de tiempo). Durante el período la fase cambia a .
Ecuación diferencial de vibraciones armónicas.
Ecuación de la forma:
Ecuación diferencial de vibraciones armónicas.
Los tipos de oscilaciones periódicas se pueden representar con cualquier grado de precisión como una suma de oscilaciones armónicas, las llamadas series armónicas.
Las oscilaciones que hará un cuerpo si se lo saca del equilibrio (no importa cómo) y se lo deja solo se llaman oscilaciones libres (naturales). Si las vibraciones naturales son causadas por la presencia únicamente de una fuerza cuasi elástica, entonces serán armónicas.
Las oscilaciones del cuerpo causadas por la acción simultánea de una fuerza cuasi elástica y una fuerza de fricción (que es proporcional a la velocidad instantánea: ) se denominan oscilaciones amortiguadas.
La ecuación (3) se denomina ecuación diferencial de oscilaciones amortiguadas. Aquí está el coeficiente de atenuación.
Solución de la ecuación diferencial de oscilaciones.
La solución a la ecuación diferencial de oscilaciones amortiguadas (3) es una relación de la forma:
La ecuación (4) se llama ecuación de oscilaciones amortiguadas. La ecuación (4) muestra que la amplitud de las oscilaciones amortiguadas depende del tiempo. Las constantes A están determinadas por las condiciones iniciales. La amplitud de las oscilaciones disminuye y generalmente se ven como se muestra en la Fig. 1
 arroz. 1.
arroz. 1.
El período de oscilaciones amortiguadas se calcula mediante la fórmula (5):
El significado físico del coeficiente de amortiguación es que el coeficiente de amortiguación es el recíproco del tiempo de relajación. Y el tiempo de relajación es el tiempo durante el cual la amplitud disminuye e veces. Sin embargo, el coeficiente de atenuación no caracteriza completamente la atenuación. Normalmente, la amortiguación de las oscilaciones se caracteriza por una disminución de la amortiguación. Este último muestra cuántas veces disminuye la amplitud de la oscilación durante un tiempo igual al período de oscilación. Es decir, la disminución de la amortiguación se determina de la siguiente manera:
El logaritmo de la disminución de la amortiguación se llama disminución logarítmica y obviamente es igual a:
Si el sistema oscilatorio está expuesto a una fuerza periódica externa, se producen las llamadas oscilaciones forzadas, que no están amortiguadas.
Las oscilaciones forzadas deben distinguirse de las autooscilaciones. En el caso de las autooscilaciones del sistema, se supone que existe un mecanismo especial que, junto con sus propias oscilaciones, "suministra" pequeñas porciones de energía al sistema.
Ejemplos de resolución de problemas
EJEMPLO 1
| Ejercicio | Encuentre la energía de las oscilaciones libres de una carga suspendida sobre un resorte. Considere el caso de un péndulo físico, sabiendo que la rigidez del resorte es k y la amplitud de las oscilaciones es A.
|
| Solución | Encontremos la energía de las vibraciones libres. Está representado por dos tipos de energía: cinética y potencial. Para una bola suspendida de un resorte: Las oscilaciones de la pelota se describen mediante la ecuación de oscilación: Escribamos la ecuación para las oscilaciones de la velocidad de la pelota, sabiendo que el movimiento se produce solo a lo largo del eje X, por lo tanto: Sustituyendo (1.2) y (1.3) en (1.1), obtenemos: sabiendo que para un péndulo físico |
| Respuesta | La energía de las vibraciones libres es proporcional al cuadrado de la amplitud de la vibración. |
§ 6. VIBRACIONES MECÁNICASFórmulas básicas
Ecuación armónica
Dónde X - desplazamiento del punto oscilante desde la posición de equilibrio; t- tiempo; A,ω, φ - amplitud, frecuencia angular, fase inicial de oscilaciones, respectivamente; - fase de oscilaciones en el momento t.
Frecuencia angular
donde ν y T son la frecuencia y el período de las oscilaciones.
La velocidad de un punto que realiza oscilaciones armónicas es
Aceleración durante la oscilación armónica.
Amplitud A la oscilación resultante obtenida sumando dos oscilaciones con las mismas frecuencias, que ocurren a lo largo de una línea recta, está determinada por la fórmula
Dónde a 1 Y A 2 - amplitudes de componentes de vibración; φ 1 y φ 2 son sus fases iniciales.
La fase inicial φ de la oscilación resultante se puede encontrar a partir de la fórmula
La frecuencia de los latidos que surgen al sumar dos oscilaciones que ocurren a lo largo de una línea recta con frecuencias diferentes pero similares ν 1 y ν 2,
Ecuación de la trayectoria de un punto que participa en dos oscilaciones mutuamente perpendiculares con amplitudes A 1 y A 2 y fases iniciales φ 1 y φ 2,
Si las fases iniciales φ 1 y φ 2 de los componentes de la oscilación son las mismas, entonces la ecuación de la trayectoria toma la forma
es decir, el punto se mueve en línea recta.
En el caso de que la diferencia de fase sea , la ecuación toma la forma
es decir, el punto se mueve a lo largo de una elipse.
Ecuación diferencial de oscilaciones armónicas de un punto material.
O donde m es la masa del punto; k- coeficiente de fuerza cuasi elástica ( k=tω2).
La energía total de un punto material que realiza oscilaciones armónicas es
El período de oscilación de un cuerpo suspendido de un resorte (péndulo de resorte)
Dónde metro- masa corporal; k- rigidez del resorte. La fórmula es válida para vibraciones elásticas dentro de los límites en los que se cumple la ley de Hooke (con una masa de resorte pequeña en comparación con la masa corporal).
Período de oscilación de un péndulo matemático.
Dónde yo- longitud del péndulo; gramo- aceleración de la gravedad. Período de oscilación de un péndulo físico.
Dónde j- momento de inercia del cuerpo oscilante con respecto al eje
vacilación; A- la distancia del centro de masa del péndulo al eje de oscilación;
Longitud reducida de un péndulo físico.
Las fórmulas dadas son precisas para el caso de amplitudes infinitesimales. Para amplitudes finitas, estas fórmulas sólo dan resultados aproximados. En amplitudes no superiores a, el error en el valor del período no supera el 1%.
El período de vibraciones de torsión de un cuerpo suspendido de un hilo elástico es
Dónde j- momento de inercia del cuerpo con respecto al eje coincidente con el hilo elástico; k- la rigidez de un hilo elástico, igual a la relación entre el momento elástico que surge cuando se retuerce el hilo y el ángulo en el que se retuerce el hilo.
Ecuación diferencial de oscilaciones amortiguadas, o,
Dónde r- coeficiente de resistencia; δ - coeficiente de atenuación: ; ω 0 - frecuencia angular natural de las oscilaciones *
Ecuación de oscilación amortiguada
Dónde En)- amplitud de las oscilaciones amortiguadas en el momento t;ω es su frecuencia angular.
Frecuencia angular de oscilaciones amortiguadas.
О Dependencia de la amplitud de las oscilaciones amortiguadas con el tiempo
Dónde A 0 - amplitud de oscilaciones en el momento t=0.
Decremento de la oscilación logarítmica
Dónde En) Y A(t+T)- amplitudes de dos oscilaciones sucesivas separadas en el tiempo por un período.
Ecuación diferencial de oscilaciones forzadas.
¿Dónde está la fuerza periódica externa que actúa sobre un punto material oscilante y provoca oscilaciones forzadas? F 0 - su valor de amplitud;
Amplitud de oscilaciones forzadas.
Frecuencia resonante y amplitud resonante y
Ejemplos de resolución de problemas
Ejemplo 1. El punto oscila según la ley. x(t)= , Dónde A=2 ver Determinar la fase inicial φ si
X(0)= centímetros y X , (0)<0. Построить векторную диаграмму для мо- мента t=0.
Solución. Usemos la ecuación de movimiento y expresemos el desplazamiento en el momento. t=0 a través de la fase inicial:
A partir de aquí nos encontramos con la fase inicial:
* En las fórmulas dadas anteriormente para vibraciones armónicas, la misma cantidad se designó simplemente ω (sin el índice 0).
Sustituyamos los valores dados en esta expresión. X(0) y A:φ= = . El valor del argumento se satisface con dos valores de ángulo:
Para decidir cuál de estos valores del ángulo φ también satisface la condición, primero encontramos:
Sustituyendo el valor en esta expresión t=0 y alternativamente los valores de las fases iniciales y , encontramos
t  como siempre A>0 y ω>0, entonces sólo el primer valor de la fase inicial satisface la condición. Así, la deseada fase inicial
como siempre A>0 y ω>0, entonces sólo el primer valor de la fase inicial satisface la condición. Así, la deseada fase inicial
Usando el valor encontrado de φ, construimos un diagrama vectorial (Fig. 6.1). Ejemplo 2. Punto material con masa t=5 g realiza oscilaciones armónicas con frecuencia ν = 0,5 Hz. amplitud de oscilación A=3 cm Determinar: 1) velocidad υ. puntos en el momento en que el desplazamiento x== 1,5 cm; 2) la fuerza máxima F max que actúa sobre el punto; 3) figura. 6.1 energía total mi punto oscilante.
y obtenemos la fórmula de la velocidad tomando la primera derivada del desplazamiento:
Para expresar la velocidad mediante el desplazamiento, es necesario excluir el tiempo de las fórmulas (1) y (2). Para hacer esto, elevamos ambas ecuaciones al cuadrado y dividimos la primera entre A 2 , el segundo sobre A 2 ω 2 y sumar:
Habiendo resuelto la última ecuación para υ , lo encontraremos
Habiendo realizado cálculos usando esta fórmula, obtenemos
El signo más corresponde al caso en que la dirección de la velocidad coincide con la dirección positiva del eje. X, signo menos: cuando la dirección de la velocidad coincide con la dirección negativa del eje X.
El desplazamiento durante la oscilación armónica, además de la ecuación (1), también se puede determinar mediante la ecuación
Repitiendo la misma solución con esta ecuación, obtenemos la misma respuesta.
2. Hallamos la fuerza que actúa sobre un punto usando la segunda ley de Newton:
Dónde A - aceleración del punto, que obtenemos tomando la derivada del tiempo de la velocidad:
Sustituyendo la expresión de aceleración en la fórmula (3), obtenemos
De ahí el valor máximo de la fuerza.
Sustituyendo los valores de π, ν en esta ecuación, t Y A, lo encontraremos
3. La energía total de un punto oscilante es la suma de las energías cinética y potencial calculadas para cualquier momento en el tiempo.
La forma más sencilla de calcular la energía total es en el momento en que la energía cinética alcanza su valor máximo. En este momento la energía potencial es cero. Por lo tanto la energía total mi El punto de oscilación es igual a la energía cinética máxima.
Determinamos la velocidad máxima a partir de la fórmula (2), estableciendo: . Sustituyendo la expresión de velocidad en la fórmula (4), encontramos
Sustituyendo los valores de las cantidades en esta fórmula y haciendo cálculos, obtenemos
o µJ.
Ejemplo 3. En los extremos de una varilla delgada yo= 1 m y masa metro 3 =400 g bolitas reforzadas con masas metro 1 = 200 gramos Y metro 2 = 300 g. La varilla oscila alrededor de un eje horizontal, perpendicular
dicular a la varilla y pasando por su centro (punto O en la Fig. 6.2). Definir periodo t oscilaciones realizadas por la varilla.
Solución. El período de oscilación de un péndulo físico, como una varilla con bolas, está determinado por la relación
Dónde j- T- su masa; yo CON - la distancia desde el centro de masa del péndulo al eje.
El momento de inercia de este péndulo es igual a la suma de los momentos de inercia de las bolas. j 1 y j 2 y varilla j 3:
Tomando las bolas como puntos materiales, expresamos sus momentos de inercia:
Dado que el eje pasa por el centro de la varilla, su momento de inercia con respecto a este eje j 3 = = . Sustituyendo las expresiones resultantes. j 1 , j 2 Y j 3 en la fórmula (2), encontramos el momento de inercia total del péndulo físico:
Habiendo realizado cálculos usando esta fórmula, encontramos
Arroz. 6.2 La masa del péndulo se compone de las masas de las bolas y la masa de la varilla:
Distancia yo CON Encontraremos el centro de masa del péndulo a partir del eje de oscilación basándonos en las siguientes consideraciones. si el eje X Dirija a lo largo de la varilla y alinee el origen de coordenadas con el punto. ACERCA DE, entonces la distancia requerida yo igual a la coordenada del centro de masa del péndulo, es decir
Sustituyendo los valores de las cantidades. metro 1 , metro 2 , metro, yo y después de hacer cálculos encontramos
Habiendo realizado cálculos utilizando la fórmula (1), obtenemos el período de oscilación de un péndulo físico:
Ejemplo 4. Un péndulo físico es una varilla de longitud. yo= 1 m y masa 3 t 1 Con unido a uno de sus extremos con un aro de diámetro y masa t 1 . Eje horizontal Onz
el péndulo pasa por el centro de la varilla perpendicular a él (figura 6.3). Definir periodo t oscilaciones de tal péndulo.
Solución. El período de oscilación de un péndulo físico está determinado por la fórmula

Dónde j- momento de inercia del péndulo con respecto al eje de oscilación; T- su masa; yo C - la distancia desde el centro de masa del péndulo al eje de oscilación.
El momento de inercia del péndulo es igual a la suma de los momentos de inercia de la varilla. j 1 y aro j 2:
El momento de inercia de la varilla con respecto al eje perpendicular a la varilla y que pasa por su centro de masa está determinado por la fórmula. En este caso t= 3t 1 y
Encontramos el momento de inercia del aro usando el teorema de Steiner, donde j- momento de inercia alrededor de un eje arbitrario; j 0 - momento de inercia alrededor de un eje que pasa por el centro de masa paralelo a un eje dado; A - la distancia entre los ejes indicados. Aplicando esta fórmula al aro, obtenemos
Sustituyendo expresiones j 1 y j 2 en la fórmula (2), encontramos el momento de inercia del péndulo con respecto al eje de rotación:
Distancia yo CON desde el eje del péndulo hasta su centro de masa es igual a
Sustituyendo las expresiones en la fórmula (1) j, yo s y la masa del péndulo, encontramos el período de sus oscilaciones:
Después de calcular usando esta fórmula obtenemos t= 2,17 s.
Ejemplo 5. Se suman dos oscilaciones de la misma dirección, expresadas por las ecuaciones; X 2 = =, donde A 1 = 1 cm, A 2 =2 cm, s, s, ω = =. 1. Determine las fases iniciales φ 1 y φ 2 de los componentes oscilatorios.
Bania. 2. Encuentra la amplitud A y la fase inicial φ de la oscilación resultante. Escribe la ecuación para la vibración resultante.
Solución. 1. La ecuación de vibración armónica tiene la forma.
Transformemos las ecuaciones especificadas en el enunciado del problema a la misma forma:

Al comparar las expresiones (2) con la igualdad (1), encontramos las fases iniciales de la primera y segunda oscilaciones:
Contento y contento.
2. Para determinar la amplitud. A de la oscilación resultante, es conveniente utilizar el diagrama vectorial presentado en arroz. 6.4. Según el teorema del coseno, obtenemos
¿Dónde está la diferencia de fase entre los componentes de las oscilaciones? Desde entonces, sustituyendo los valores encontrados de φ 2 y φ 1 obtenemos rad.
sustituyamos los valores A 1 , A 2 y en la fórmula (3) y realizar los cálculos:
A= 2,65 cm.
Determinemos la tangente de la fase inicial φ de la oscilación resultante directamente de la Fig. 6.4: ![]() , de donde proviene la fase inicial
, de donde proviene la fase inicial
![]()
sustituyamos los valores A 1 , A 2 , φ 1, φ 2 y realizar los cálculos:
Dado que las frecuencias angulares de las oscilaciones sumadas son las mismas, la oscilación resultante tendrá la misma frecuencia ω. Esto nos permite escribir la ecuación de la oscilación resultante en la forma , donde A=2,65 cm, rad.
Ejemplo 6. Un punto material participa simultáneamente en dos oscilaciones armónicas mutuamente perpendiculares, cuyas ecuaciones son
Dónde a 1 = 1 cm, A 2 = 2 cm, . Encuentra la ecuación de la trayectoria del punto. Construir una trayectoria respetando la escala e indicar la dirección de movimiento del punto.
Solución. Para encontrar la ecuación de la trayectoria de un punto, eliminamos el tiempo. t de las ecuaciones dadas (1) y (2). Para hacer esto, use
Usemos la fórmula. En este caso, por lo tanto
Dado que según la fórmula (1) , entonces la ecuación de trayectoria
La expresión resultante es la ecuación de una parábola cuyo eje coincide con el eje Oh. De las ecuaciones (1) y (2) se deduce que el desplazamiento de un punto a lo largo de los ejes de coordenadas es limitado y varía de -1 a +1 cm a lo largo del eje. Oh y de -2 a +2 cm a lo largo del eje UNED.
Para construir la trayectoria, usamos la ecuación (3) para encontrar los valores y, correspondiente a un rango de valores X, satisfaciendo la condición cm, y crea una tabla:
|
X , CM |
||||||

Habiendo dibujado los ejes de coordenadas y elegido la escala, la trazamos en el plano. xoy puntos encontrados. Al conectarlos con una curva suave, obtenemos la trayectoria de un punto que oscila de acuerdo con las ecuaciones de movimiento (1) y (2) (figura 6.5).
Para indicar la dirección del movimiento de un punto, seguiremos cómo cambia su posición a lo largo del tiempo. En el momento inicial t=0 las coordenadas de los puntos son iguales X(0)=1 cm y y(0)=2 cm. En un momento posterior, por ejemplo cuando t 1 =l s, las coordenadas de los puntos cambiarán y se volverán iguales X(1)= -1cm, y( t )=0. Conociendo las posiciones de los puntos en los momentos de tiempo inicial y posterior (cercano), es posible indicar la dirección de movimiento del punto a lo largo de la trayectoria. En la Fig. 6.5 esta dirección de movimiento está indicada por una flecha (desde el punto A al origen). despues del momento t 2 = 2 s el punto oscilante llegará al punto D, se moverá en la dirección opuesta.
Tareas
Cinemática de oscilaciones armónicas.
6.1. La ecuación de oscilaciones puntuales tiene la forma , donde ω=π s -1, τ=0,2 s. Definir periodo t y la fase inicial φ de oscilaciones.
6.2. Definir periodo T, frecuencia v y fase inicial φ de oscilaciones, dada por la ecuación, donde ω=2.5π s -1, τ=0.4 s.
6.3. El punto oscila según la ley, donde A x(0)=2 medios de comunicación en masa ; 2) x(0) = cm y ; 3) x(0)=2cm y ; 4) x(0)= y . Construya un diagrama vectorial por el momento. t=0.
6.4. El punto oscila según la ley, donde A=4 cm. Determine la fase inicial φ si: 1) x(0)= 2 medios de comunicación en masa ; 2) X(0)= cm y ; 3) X(0)= cm y ; 4) X(0)=cm y . Construya un diagrama vectorial por el momento. t=0.