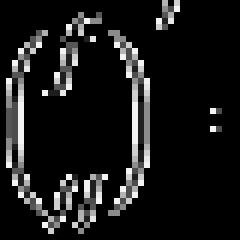Y tgx jest nieskończenie dużą funkcją w. Definicja nieskończenie dużego ciągu

Rachunek nieskończenie małych i dużych

Nieskończenie mały rachunek różniczkowy- obliczenia wykonywane na wielkościach nieskończenie małych, w których otrzymany wynik traktuje się jako nieskończoną sumę nieskończenie małych. Rachunek nieskończenie małych jest ogólną koncepcją rachunku różniczkowego i całkowego, która stanowi podstawę współczesnej matematyki wyższej. Pojęcie nieskończenie małej ilości jest ściśle powiązane z pojęciem granicy.

Nieskończenie mały

Podciąg A N zwany nieskończenie mały, Jeśli . Na przykład ciąg liczb jest nieskończenie mały.

Funkcja nazywa się nieskończenie małe w pobliżu punktu X 0 jeśli .

Funkcja nazywa się nieskończenie małe w nieskończoności, Jeśli Lub .

Nieskończenie mała jest także funkcja będąca różnicą między funkcją a jej granicą, to znaczy jeśli , To F(X) − A = α( X) , .

Nieskończenie duża ilość

Podciąg A N zwany nieskończenie duży, Jeśli .

Funkcja nazywa się nieskończenie duża w pobliżu punktu X 0 jeśli .

Funkcja nazywa się nieskończenie duży w nieskończoności, Jeśli Lub .

We wszystkich przypadkach zakłada się, że nieskończoność po prawej stronie równości ma określony znak (albo „plus”, albo „minus”). To jest na przykład funkcja X grzech X nie jest nieskończenie duży w .

Własności nieskończenie małe i nieskończenie duże

Porównanie wielkości nieskończenie małych

Jak porównać nieskończenie małe ilości?
Stosunek wielkości nieskończenie małych tworzy tzw. niepewność.

Definicje

Załóżmy, że mamy nieskończenie małe wartości α( X) i β( X) (lub, co nie jest istotne dla definicji, ciągi nieskończenie małe).

Aby obliczyć takie granice, wygodnie jest skorzystać z reguły L'Hopitala.

Przykłady porównawcze

Za pomocą O-symbolika, uzyskane wyniki można zapisać w następującej formie X 5 = o(X 3). W tym przypadku prawdziwe są następujące wpisy: 2X 2 + 6X = O(X) I X = O(2X 2 + 6X).

Równoważne wartości

Definicja

Jeśli , to nazywa się nieskończenie małe wielkości α i β równowartość ().
Jest oczywiste, że ilości równoważne są szczególnym przypadkiem nieskończenie małych ilości tego samego rzędu małości.

Gdy obowiązują następujące relacje równoważności: , , .

Twierdzenie

Granica ilorazu (stosunku) dwóch nieskończenie małych wielkości nie ulegnie zmianie, jeśli jedną z nich (lub obie) zastąpimy wielkością równoważną.

Twierdzenie to ma praktyczne znaczenie przy znajdowaniu granic (patrz przykład).

Przykład użycia

Wymiana SIN 2X wartość równoważna 2 X, otrzymujemy

Szkic historyczny

Pojęcie „nieskończenie małego” było omawiane już w starożytności w powiązaniu z koncepcją niepodzielnych atomów, ale nie było uwzględniane w matematyce klasycznej. Odrodziła się ponownie wraz z pojawieniem się w XVI wieku „metody niepodzielności” – podziału badanej figury na nieskończenie małe sekcje.

W XVII wieku miała miejsce algebraizacja rachunku nieskończenie małego. Zaczęto je definiować jako wielkości liczbowe, które są mniejsze od dowolnej ilości skończonej (niezerowej), a jednocześnie nie są równe zeru. Sztuka analizy polegała na sporządzeniu relacji zawierającej nieskończenie małe (różniczki) i następnie jej całkowaniu.

Matematycy ze starej szkoły wystawili tę koncepcję na próbę nieskończenie mały ostra krytyka. Michel Rolle napisał, że nowy rachunek różniczkowy jest „ zestaw genialnych błędów"; Voltaire zjadliwie zauważył, że rachunek różniczkowy to sztuka obliczania i dokładnego mierzenia rzeczy, których istnienia nie można udowodnić. Nawet Huygens przyznał, że nie rozumiał znaczenia różniczek wyższych rzędów.

Za ironię losu można uznać pojawienie się w połowie stulecia niestandardowych analiz, które dowiodły, że pierwotny punkt widzenia – rzeczywiste nieskończenie małe – również był spójny i mógł stanowić podstawę analiz.

Zobacz też

Fundacja Wikimedia. 2010.

Zobacz, co oznacza „nieskończenie duży” w innych słownikach:

Zmienna ilość Y jest odwrotnością nieskończenie małej wielkości X, czyli Y = 1/X... Wielki słownik encyklopedyczny

Zmienna y jest odwrotnością nieskończenie małego x, to znaczy y = 1/x. * * * NIESKOŃCZONE DUŻE NIESKOŃCZONE DUŻE, zmienna ilość Y, odwrotna do nieskończenie małej wielkości X, czyli Y = 1/X... słownik encyklopedyczny

W matematyce zmienna wielkość, która w danym procesie zmian staje się i pozostaje większa pod względem wartości bezwzględnej niż jakakolwiek z góry określona liczba. Studium B.b. ilości można sprowadzić do badania nieskończenie małych (patrz... ... Wielka encyklopedia radziecka

Funkcje nieskończenie małe

Wywoływana jest funkcja %%f(x)%%. nieskończenie mały(b.m.) z %%x \to a \in \overline(\mathbb(R))%%, jeśli przy tej tendencji argumentu granica funkcji jest równa zeru.

Koncepcja b.m. Funkcja jest nierozerwalnie powiązana z instrukcjami zmiany jej argumentu. Możemy porozmawiać o b.m. działa przy %%a \to a + 0%% i %%a \to a - 0%%. Zwykle b.m. funkcje są oznaczone pierwszymi literami alfabetu greckiego %%\alpha, \beta, \gamma, \ldots%%

Przykłady

1. Funkcja %%f(x) = x%% to b.m. przy %%x \to 0%%, ponieważ jego granica w punkcie %%a = 0%% wynosi zero. Zgodnie z twierdzeniem o związku granicy dwustronnej z granicą jednostronną funkcja ta ma postać b.m. zarówno z %%x \to +0%%, jak i %%x \to -0%%.
2. Funkcja %%f(x) = 1/(x^2)%% - b.m. przy %%x \to \infty%% (jak również przy %%x \to +\infty%% i %%x \to -\infty%%).

Stała liczba różna od zera, niezależnie od tego, jak mała jest jej wartość bezwzględna, nie jest b.m. funkcjonować. W przypadku liczb stałych jedynym wyjątkiem jest zero, ponieważ funkcja %%f(x) \equiv 0%% ma granicę zera.

Twierdzenie

Funkcja %%f(x)%% ma w punkcie %%a \in \overline(\mathbb(R))%% rozszerzonej osi liczbowej końcową granicę równą liczbie %%b%% wtedy i tylko jeśli ta funkcja jest równa sumie tej liczby %%b%% i b.m. funkcje %%\alpha(x)%% z %%x \to a%% lub $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$

Własności funkcji nieskończenie małych

Zgodnie z regułami przejścia do granicy z %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, następują następujące stwierdzenia:

1. Suma końcowej liczby b.m. funkcje dla %%x \to a%% to b.m. w %%x \do a%%.
2. Iloczyn dowolnej liczby b.m. funkcje dla %%x \to a%% to b.m. w %%x \do a%%.

Produkt b.m. funkcji w %%x \to a%% i funkcją ograniczoną w pewnym przebitym sąsiedztwie %%\stackrel(\circ)(\text(U))(a)%% punktu a, jest b.m. w %%x \do funkcji%%.

Jasne jest, że iloczyn funkcji stałej i b.m. w %%x \to a%% jest b.m. funkcja w %%x \to a%%.

Równoważne funkcje nieskończenie małe

Wywoływane są nieskończenie małe funkcje %%\alpha(x), \beta(x)%% dla %%x \to a%% równowartość i napisz %%\alpha(x) \sim \beta(x)%%, if

$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alfa(x))) = 1. $$

Twierdzenie o podstawieniu b.m. funkcje równoważne

Niech %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% będzie b.m. funkcje dla %%x \to a%%, gdzie %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, następnie $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limity_(x \do a)(\frac(\alpha_1(x))(\beta_1(x))). $$

Odpowiednik b.m. Funkcje.

Niech %%\alpha(x)%% będzie b.m. wówczas funkcja w %%x \to a%%.

1. %%\sin(\alfa(x)) \sim \alfa(x)%%
2. %%\displaystyle 1 - \cos(\alfa (x)) \sim \frac(\alfa ^2(x))(2)%%
3. %%\tan \alfa(x) \sim \alfa(x)%%
4. %%\arcsin\alfa(x) \sim \alfa(x)%%
5. %%\arctan\alfa(x) \sim \alfa(x)%%
6. %%\ln(1 + \alfa(x)) \sim \alfa(x)%%
7. %%\displaystyle\sqrt[n](1 + \alfa(x)) - 1 \sim \frac(\alfa(x))(n)%%
8. %%\displaystyle a^(\alfa(x)) - 1 \sim \alfa(x) \ln(a)%%

Przykład

$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(tablica) $$

Nieskończenie duże funkcje

Wywoływana jest funkcja %%f(x)%%. nieskończenie duży(b.b.) z %%x \to a \in \overline(\mathbb(R))%%, jeśli przy tej tendencji argumentu funkcja ma nieskończoną granicę.

Podobny do b.m. koncepcja funkcji b.b. Funkcja jest nierozerwalnie powiązana z instrukcjami zmiany jej argumentu. Możemy porozmawiać o b.b. funkcje dla %%x \to a + 0%% i %%x \to a - 0%%. Określenie „nieskończenie duża” nie mówi o wartości bezwzględnej funkcji, ale o charakterze jej zmiany w pobliżu rozpatrywanego punktu. Żadna stała liczba, niezależnie od tego, jak duża jest jej wartość bezwzględna, nie jest nieskończenie duża.

Przykłady

1. Funkcja %%f(x) = 1/x%% - b.b. przy %%x \do 0%%.
2. Funkcja %%f(x) = x%% - b.b. w %%x \to \infty%%.

Jeżeli warunki definicji $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(tablica) $$

potem o tym rozmawiają pozytywny Lub negatywny nocleg ze śniadaniem. przy funkcji %%a%%.

Przykład

Funkcja %%1/(x^2)%% - dodatni t.b. przy %%x \do 0%%.

Związek pomiędzy b.b. i b.m. Funkcje

Jeśli %%f(x)%% to b.b. z funkcją %%x \to a%%, następnie %%1/f(x)%% - b.m.

w %%x \do a%%. Jeśli %%\alpha(x)%% - b.m. dla %%x \to a%% jest niezerową funkcją w pewnym przebitym sąsiedztwie punktu %%a%%, wówczas %%1/\alpha(x)%% jest b.b. w %%x \do a%%.

Własności nieskończenie dużych funkcji

Przedstawmy kilka właściwości bb. Funkcje. Właściwości te wynikają bezpośrednio z definicji b.b. funkcje i własności funkcji mających skończone granice, a także z twierdzenia o związku pomiędzy b.b. i b.m. Funkcje.

1. Iloczyn skończonej liczby b.b. funkcje dla %%x \to a%% to b.b. funkcja w %%x \to a%%. Rzeczywiście, jeśli %%f_k(x), k = \overline(1, n)%% - b.b. funkcjonuje w %%x \to a%%, następnie w pewnym przebitym sąsiedztwie punktu %%a%% %%f_k(x) \ne 0%%, oraz na podstawie twierdzenia o połączeniu b.b. i b.m. funkcje %%1/f_k(x)%% - b.m. funkcja w %%x \to a%%. Okazuje się, że %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m funkcja dla %%x \to a%% i %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funkcja w %%x \to a%%.
2. Produkt b.b. funkcje dla %%x \to a%%, a funkcja, która w pewnym przebitym sąsiedztwie punktu %%a%% w wartości bezwzględnej jest większa od stałej dodatniej, to b.b. funkcja w %%x \to a%%. W szczególności produkt b.b. funkcja z %%x \to a%% i funkcja, która ma skończoną niezerową granicę w punkcie %%a%% będzie b.b. funkcja w %%x \to a%%.

Suma funkcji ograniczonej w pewnym przebitym sąsiedztwie punktu %%a%% i b.b. funkcje z %%x \to a%% to b.b. funkcja w %%x \to a%%.

Na przykład funkcje %%x - \sin x%% i %%x + \cos x%% to b.b. w %%x \to \infty%%.

3. Suma dwóch b.b. działa w %%x \to a%% występuje niepewność. W zależności od znaku wyrazów charakter zmiany takiej sumy może być bardzo różny.

   Przykład

   Niech zostaną podane funkcje %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. działa w %%x \to \infty%%. Następnie:

   • %%f(x) + g(x) = 3x%% - b.b. funkcja w %%x \to \infty%%;
   • %%f(x) + h(x) = 0%% - b.m. funkcja w %%x \to \infty%%;
   • %%h(x) + v(x) = \sin x%% nie ma ograniczenia w %%x \to \infty%%.

Podano definicję nieskończenie dużego ciągu. Rozważane są koncepcje sąsiedztwa punktów w nieskończoności. Podano uniwersalną definicję granicy ciągu, która ma zastosowanie zarówno do granic skończonych, jak i nieskończonych. Rozważane są przykłady zastosowania definicji nieskończenie dużego ciągu.

Treść

Zobacz też: Wyznaczanie limitu sekwencji

Definicja

Podciąg (βn) nazywamy ciągiem nieskończenie dużym, jeśli dla dowolnej liczby M, niezależnie od jej wielkości, istnieje liczba naturalna N M zależna od M taka, że ​​dla wszystkich liczb naturalnych n > N M nierówność zachodzi
|β n | >M.
W tym przypadku piszą
.
Lub o godz.
Mówią, że dąży do nieskończoności, czyli zbiega się do nieskończoności.

Jeśli zaczynając od jakiejś liczby N 0 , To
( zbiega się do plus nieskończoności).
Jeśli następnie
( zbiega się do minus nieskończoności).

Zapiszmy te definicje posługując się logicznymi symbolami istnienia i powszechności:
(1) .
(2) .
(3) .

Ciągi z granicami (2) i (3) są szczególnymi przypadkami nieskończenie dużego ciągu (1). Z definicji tych wynika, że ​​jeśli granica ciągu jest równa plus minus nieskończoność, to jest ona również równa nieskończoności:
.
Sytuacja odwrotna nie jest oczywiście prawdą. Członkowie sekwencji mogą mieć znaki naprzemienne. W tym przypadku granica może być równa nieskończoności, ale bez określonego znaku.

Należy również zauważyć, że jeśli jakaś właściwość obowiązuje dla dowolnego ciągu o granicy równej nieskończoności, to ta sama właściwość obowiązuje dla ciągu, którego granica jest równa plus lub minus nieskończoności.

W wielu podręcznikach rachunku różniczkowego definicja nieskończenie dużego ciągu stwierdza, że ​​liczba M jest dodatnia: M > 0 . Jednakże ten wymóg jest niepotrzebny. Jeśli zostanie anulowany, nie pojawią się żadne sprzeczności. Po prostu małe lub ujemne wartości nas nie interesują. Interesuje nas zachowanie ciągu dla dowolnie dużych dodatnich wartości M. Zatem jeśli zajdzie taka potrzeba, wówczas M można ograniczyć od dołu dowolną z góry ustaloną liczbą a, czyli możemy założyć, że M > a.

Gdy zdefiniowaliśmy ε – sąsiedztwo punktu końcowego, wówczas wymaganie ε > 0 jest ważne. Dla wartości ujemnych nierówność w ogóle nie może zostać spełniona.

Sąsiedztwa punktów w nieskończoności

Rozważając granice skończone, wprowadziliśmy pojęcie sąsiedztwa punktu. Przypomnijmy, że otoczenie punktu końcowego jest przedziałem otwartym zawierającym ten punkt. Możemy także wprowadzić pojęcie sąsiedztwa punktów w nieskończoności.

Niech M będzie dowolną liczbą.
Sąsiedztwo punktu „nieskończoność”, , nazywa się zbiorem.
Sąsiedztwo punktu „plus nieskończoność”, , nazywa się zbiorem.
W pobliżu punktu „minus nieskończoność”, , nazywa się zbiorem.

Ściśle mówiąc, otoczenie punktu „nieskończoności” to zbiór
(4) ,
gdzie M 1 oraz m 2 - dowolne liczby dodatnie. Będziemy używać pierwszej definicji, ponieważ jest prostsza. Chociaż wszystko, co powiedziano poniżej, jest również prawdą w przypadku korzystania z definicji (4).

Możemy teraz podać ujednoliconą definicję granicy ciągu, która ma zastosowanie zarówno do granic skończonych, jak i nieskończonych.

Uniwersalna definicja granicy ciągu.
Punkt a (skończony lub w nieskończoności) jest granicą ciągu, jeśli dla dowolnego otoczenia tego punktu istnieje liczba naturalna N taka, że ​​wszystkie elementy ciągu o liczbach należą do tego sąsiedztwa.

Zatem jeśli istnieje granica, to poza otoczeniem punktu a może znajdować się tylko skończona liczba elementów ciągu, czyli zbiór pusty. Warunek ten jest konieczny i wystarczający. Dowód tej własności jest dokładnie taki sam, jak dla granic skończonych.

Własność sąsiedztwa ciągu zbieżnego
Aby punkt a (skończony lub w nieskończoności) był granicą ciągu, konieczne i wystarczające jest, aby poza jakimkolwiek otoczeniem tego punktu znajdowała się skończona liczba wyrazów ciągu lub zbiór pusty.
Dowód .

Czasami wprowadza się także pojęcia ε – sąsiedztwa punktów w nieskończoności.
Przypomnijmy, że ε-sąsiedztwo skończonego punktu a jest zbiorem .
Wprowadźmy następującą notację. Niech ε oznacza sąsiedztwo punktu a. Następnie dla punktu końcowego
.
Dla punktów w nieskończoności:
;
;
.
Korzystając z koncepcji sąsiedztw ε, możemy podać inną uniwersalną definicję granicy ciągu:

Punkt a (skończony lub w nieskończoności) jest granicą ciągu, jeśli dla dowolnej liczby dodatniej ε > 0 istnieje liczba naturalna N ε zależna od ε taka, że ​​dla wszystkich liczb n > N ε wyrazy x n należą do ε-sąsiedztwa punktu a:
.

Używając logicznych symboli istnienia i uniwersalności, definicję tę można zapisać w następujący sposób:
.

Przykłady nieskończenie dużych ciągów

Przykład 1

.

.
Zapiszmy definicję nieskończenie dużego ciągu:
(1) .
W naszym przypadku
.

Wprowadzamy liczby i , łącząc je z nierównościami:
.
Zgodnie z właściwościami nierówności, jeśli i , to
.
Zauważ, że ta nierówność zachodzi dla dowolnego n. Dlatego możesz wybrać w ten sposób:
Na ;
Na .

Zatem dla każdego możemy znaleźć liczbę naturalną spełniającą nierówność. Wtedy dla wszystkich
.
To znaczy, że . Oznacza to, że ciąg jest nieskończenie duży.

Przykład 2

Korzystając z definicji nieskończenie dużego ciągu, pokaż to
.

(2) .
Ogólny wyraz danego ciągu ma postać:
.

Wpisz liczby i:
.
.

Wtedy dla każdego można znaleźć liczbę naturalną spełniającą nierówność, więc dla wszystkich ,
.
To znaczy, że .

.

Przykład 3

Korzystając z definicji nieskończenie dużego ciągu, pokaż to
.

Zapiszmy definicję granicy ciągu równego minus nieskończoność:
(3) .
Ogólny wyraz danego ciągu ma postać:
.

Wpisz liczby i:
.
Z tego jasno wynika, że ​​jeśli i , to
.

Skoro dla każdego można znaleźć liczbę naturalną spełniającą nierówność, to zatem
.

Biorąc pod uwagę , jako N możemy przyjąć dowolną liczbę naturalną spełniającą następującą nierówność:
.

Przykład 4

Korzystając z definicji nieskończenie dużego ciągu, pokaż to
.

Zapiszmy wyraz ogólny ciągu:
.
Zapiszmy definicję granicy ciągu równego plus nieskończoność:
(2) .

Ponieważ n jest liczbą naturalną, n = 1, 2, 3, ... , To
;
;
.

Wprowadzamy liczby i M, łącząc je z nierównościami:
.
Z tego jasno wynika, że ​​jeśli i , to
.

Zatem dla dowolnej liczby M możemy znaleźć liczbę naturalną spełniającą nierówność. Wtedy dla wszystkich
.
To znaczy, że .

Bibliografia:
L.D. Kudryavtsev. Kurs analizy matematycznej. Tom 1. Moskwa, 2003.
CM. Nikolski. Kurs analizy matematycznej. Tom 1. Moskwa, 1983.

Zobacz też:

def: Funkcja nazywa się nieskończenie mały o, jeśli .

W zapisie „ ” założymy, że x 0 może przyjąć jako wartość końcową: x 0= Konst i nieskończony: x 0= ∞.

Własności funkcji nieskończenie małych:

1) Suma algebraiczna skończonej liczby nieskończenie małych funkcji jest nieskończenie małą sumą funkcji.

2) Iloczyn skończonej liczby nieskończenie małych funkcji jest funkcją nieskończenie małą.

3) Iloczyn funkcji ograniczonej i funkcji nieskończenie małej jest funkcją nieskończenie małą.

4) Iloraz dzielenia funkcji nieskończenie małej przez funkcję, której granica jest różna od zera, jest funkcją nieskończenie małą.

Przykład: Funkcjonować y = 2 + X jest nieskończenie małe w , ponieważ .

def: Funkcja nazywa się nieskończenie duży o, jeśli .

Własności nieskończenie dużych funkcji:

1) Suma nieskończenie dużych funkcji jest funkcją nieskończenie dużą.

2) Iloczyn nieskończenie dużej funkcji i funkcji, której granica jest różna od zera, jest funkcją nieskończenie dużą.

3) Suma nieskończenie dużej funkcji i funkcji ograniczonej jest funkcją nieskończenie dużą.

4) Iloraz dzielenia nieskończenie dużej funkcji przez funkcję mającą skończoną granicę jest funkcją nieskończenie dużą.

Przykład: Funkcjonować y= jest nieskończenie duży w , ponieważ .

Twierdzenie.Zależność między nieskończenie małymi i nieskończenie dużymi ilościami. Jeśli funkcja jest nieskończenie mała w , to jest nieskończenie duża w . I odwrotnie, jeśli funkcja jest nieskończenie duża w , to funkcja jest nieskończenie mała w .

Stosunek dwóch nieskończenie małych jest zwykle oznaczony symbolem, a dwóch nieskończenie dużych – symbolem. Obie relacje są nieokreślone w tym sensie, że ich granica może istnieć lub nie, być równa określonej liczbie lub być nieskończona, w zależności od rodzaju konkretnych funkcji zawartych w wyrażeniach nieokreślonych.

Oprócz niepewności rodzaju i niepewności, następujące wyrażenia to:

Różnica nieskończenie dużych tego samego znaku;

Iloczyn nieskończenie małego i nieskończenie dużego;

Funkcja wykładnicza, której podstawa dąży do 1, a wykładnik do ;

Funkcja wykładnicza, której podstawa jest nieskończenie mała i której wykładnik jest nieskończenie duży;

Funkcja wykładnicza, której podstawa i wykładnik są nieskończenie małe;

Funkcja wykładnicza, której podstawa jest nieskończenie duża, a wykładnik nieskończenie mały.

Mówi się, że istnieje niepewność odpowiedniego typu. W takich przypadkach wywoływane jest obliczenie limitu ujawniając niepewność. Aby ujawnić niepewność, wyrażenie pod znakiem granicy jest konwertowane do postaci niezawierającej niepewności.

Przy obliczaniu granic wykorzystuje się właściwości granic, a także właściwości funkcji nieskończenie małych i nieskończenie dużych.

Spójrzmy na przykłady obliczeń różnych limitów.

1) . 2) .

4) , ponieważ iloczyn nieskończenie małej funkcji i funkcji ograniczonej jest nieskończenie małe.

5) . 6) .

7) = =

. W tym przypadku wystąpiła niepewność typu, która została ujawniona poprzez rozłożenie wielomianów na czynniki i sprowadzenie ich do wspólnego współczynnika.

= .

W tym przypadku wystąpiła niepewność typu , którą rozwiązano mnożąc licznik i mianownik przez wyrażenie, korzystając ze wzoru, a następnie zmniejszając ułamek przez (+1).

9)
. W tym przykładzie niepewność typu ujawniono poprzez podzielenie licznika i mianownika ułamka przez potęgę wiodącą.

Cudowne Granice

Pierwsza cudowna granica : .

Dowód. Rozważmy okrąg jednostkowy (ryc. 3).

Ryc.3. Okrąg jednostkowy

Pozwalać X– radialna miara kąta środkowego MOA(), Następnie OA = R= 1, MK= grzech X, NA= tg X. Porównywanie pól trójkątów OMA, OTA i sektory OMA, otrzymujemy:

,

.

Ostatnią nierówność podziel przez grzech X, otrzymujemy:

.

Ponieważ w , następnie według właściwości 5) granic

Stąd pochodzi wartość odwrotna i to należało udowodnić.

Komentarz: Jeśli funkcja jest nieskończenie mała w , tj. , wówczas pierwsza niezwykła granica ma postać:

.

Przyjrzyjmy się przykładom obliczeń limitów przy użyciu pierwszego niezwykłego limitu.

Obliczając tę ​​granicę, skorzystaliśmy ze wzoru trygonometrycznego: .

.

Przyjrzyjmy się przykładom obliczeń limitów przy użyciu drugiego niezwykłego limitu.

2) .

3) . Istnieje niepewność typu. W takim razie dokonajmy zamiany; Na .

Funkcjonować y=f(x) zwany nieskończenie mały Na x → a albo kiedy X→∞, jeśli lub , tj. funkcja nieskończenie mała to funkcja, której granica w danym punkcie wynosi zero.

Przykłady.

1. Funkcja k(x)=(X-1) 2 jest nieskończenie małe w X→1, ponieważ (patrz rysunek).

2. Funkcja k(x)= tg X– nieskończenie przy X→0.

3. k(x)= log(1+ X) – nieskończenie przy X→0.

4. k(x) = 1/X– nieskończenie przy X→∞.

Ustalmy następującą ważną zależność:

Twierdzenie. Jeśli funkcja y=f(x) reprezentowalny z x → a jako suma liczby stałej B i nieskończenie mała wielkość α(x): f (x)=b+ α(x) To .

I odwrotnie, jeśli , to fa (x)=b+α(x), Gdzie topór)– nieskończenie przy x → a.

Dowód.

1. Udowodnimy pierwszą część twierdzenia. Od równości f(x)=b+α(x) powinien |f(x) – b|=| α|. Lecz odkąd topór) jest nieskończenie mała, to dla dowolnego ε istnieje δ – otoczenie punktu A, przed wszystkimi X z czego, wartości topór) zaspokoić relację |α(x)|< ε. Następnie |f(x) – b|< ε. A to oznacza, że.

2. Jeśli , to dla dowolnego ε >0 dla wszystkich X od pewnego δ – sąsiedztwo punktu A będzie |f(x) – b|< ε. Ale jeśli oznaczymy f(x) – b= α, To |α(x)|< ε, co oznacza, że A– nieskończenie małe.

Rozważmy podstawowe właściwości funkcji nieskończenie małych.

Twierdzenie 1. Suma algebraiczna dwóch, trzech i ogólnie dowolnej skończonej liczby nieskończenie małych jest funkcją nieskończenie małą.

Dowód. Przedstawmy dowód dla dwóch wyrazów. Pozwalać f(x)=α(x)+β(x), gdzie i . Musimy udowodnić, że dla dowolnie małego ε > Znaleziono 0 δ> 0, tak że dla X, spełniając nierówność |x – a|<δ , wykonane |f(x)|< ε.

Ustalmy więc dowolną liczbę ε > 0. Ponieważ zgodnie z warunkami twierdzenia α(x) jest funkcją nieskończenie małą, to istnieje takie δ 1 > 0, czyli |x – a|< δ1 mamy |α(x)|< ε / 2. Podobnie od β(x) jest nieskończenie małe, to istnieje takie δ 2 > 0, czyli |x – a|< δ2 mamy | β(x)|< ε / 2.

Weźmy δ=min(δ 1 , δ2 } .Następnie w sąsiedztwie punktu A promień δ każda z nierówności będzie spełniona |α(x)|< ε / 2 i | β(x)|< ε / 2. Dlatego w tej okolicy nie będzie

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

te. |f(x)|< ε, co należało udowodnić.

Twierdzenie 2. Iloczyn funkcji nieskończenie małej topór) dla ograniczonej funkcji k(x) Na x → a(albo kiedy x → ∞) jest funkcją nieskończenie małą.

Dowód. Ponieważ funkcja k(x) jest ograniczona, to jest liczba M tak, że dla wszystkich wartości X z jakiegoś sąsiedztwa punktu a|f(x)|≤M. Co więcej, od topór) jest nieskończenie małą funkcją w x → a, następnie dla dowolnego ε > 0 istnieje sąsiedztwo punktu A, w którym nierówność będzie zachowana |α(x)|< ε /M. Następnie w mniejszej z tych dzielnic, które mamy | αf|< ε /M= ε. A to oznacza, że af– nieskończenie małe. Z okazji x → ∞ dowód przeprowadza się analogicznie.

Z udowodnionego twierdzenia wynika:

Wniosek 1. Jeśli i wtedy.

Konsekwencja 2. Jeśli c= stała, następnie .

Twierdzenie 3. Stosunek funkcji nieskończenie małej α(x) na funkcję k(x), którego granica jest różna od zera, jest funkcją nieskończenie małą.

Dowód. Pozwalać . Następnie 1 /f(x) istnieje ograniczona funkcja. Dlatego ułamek jest iloczynem nieskończenie małej funkcji i ograniczonej funkcji, tj. funkcja jest nieskończenie mała.