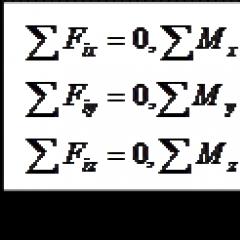Условия за равновесие на система от сили в пространството. Теоретична механика

Условие за равновесие на пространствена система от събиращи се сили: алгебричната сума на проекциите на всички сили върху три взаимно перпендикулярни координатни оси трябва да бъде равна на нула, т.е.

Да се намери моментът на силата спрямо оста z,трябва да проектирате силата до самолета нперпендикулярно на оста z(фиг. 12), след това намерете момента на проекцията F nспрямо точка O, която е пресечната точка на равнината нсмучат z.Момент на проекция F nи ще бъде момент на сила спрямо оста z:

Пространствена система от произволно разположени силие система от сили, чиито линии на действие не лежат в една и съща равнина и не се пресичат в една точка. Резултатът от такава система от сили също е равен на геометричната сума на тези сили, но се изобразява чрез диагонал на сложни обемни фигури (тетраедър, октаедър и др.).

Условие за равновесие за пространствена система от произволно разположени сили:алгебричната сума на проекциите на всички сили върху три взаимно перпендикулярни координатни оси трябва да бъде равна на нула, а алгебричната сума на моментите на всички сили спрямо същите координатни оси трябва да бъде равна на нула, т.е.

Триене

Триененаречено съпротивление на движението на тялото. Силата, с която тялото се съпротивлява на движението, се нарича сила на триене.

Силата на триене винаги е насочена в посока, обратна на движението. Силата на триене зависи от материала на триещите се тела, чистотата на обработката и наличието на смазка и не зависи от размера на триещите се повърхности.

Триенето се случва: сух, полутечен, течен.

Разграничете триенето почивка, движение, плъзганеИ валцуване.Силата на статично триене е по-голяма от силата на триене при движение.

Силата на триене е равна на произведението на силата на нормалното налягане и коефициента на триене при плъзгане (фиг. 14):

F tr =R n ƒ,

Където Rn = mg cos a - нормална сила на натиск;

ƒ - коефициент на триене при плъзгане.

Коефициент на триене при плъзганеСъотношението на силата на триене към силата на нормалното налягане се нарича:

Наричат се материали, които имат много малко триене антифрикционни(бабит, бронз, графит) Използва се за производство на лагери и др.

Материалите с високо триене се наричат фрикционен(специални пластмаси, използващи азбест и мед). Използва се за накладки на спирачни накладки и накладки на дискове на съединителя.

Когато плъзгащата се повърхност е смазана, тялото започва да се движи с по-малко триене.

Нека разложим силата на гравитацията G на компоненти G ’ и G " (фиг. 15)

Нека създадем уравнение на равновесие:

Където ч-разстояние от повърхността до линията на действие на силата;

к-коефициент на триене при търкаляне. Той е равен на сегмента OS (виж фиг. 16)

F dv = F tr,

F tr =R p k/h

Ако h = d,

F tr =R p k/d

ако h = g,

F tr =R p k/d

Ние комбинираме началото на координатите с точката на пресичане на линиите на действие на силите на системата. Проектираме всички сили върху координатните оси и сумираме съответните проекции (фиг. 7.4). Получаваме проекциите на резултата върху координатните оси:

Модулът на резултантната система от събиращи се сили се определя по формулата

Посоката на резултантния вектор се определя от ъглите

Произволна пространствена система от сили

Привеждане на произволна пространствена система от сили в центъра на О.

Дадена е пространствена система от сили (фиг. 7.5, а). Нека го пренесем в центъра О.

Силите трябва да се движат успоредно и се образува система от двойки сили. Моментът на всяка от тези двойки е равен на произведението на модула на силата и разстоянието до центъра на редукция.

В центъра на редукция възниква лъч от сили, който може да бъде заменен от общата сила (главен вектор) F GL (фиг. 7.5, б).

Моментите на двойки сили могат да се добавят, получавайки общия момент на системата M ch (основен момент).

Така произволна пространствена система от сили се свежда до главния вектор и главния момент.

Основният вектор обикновено се разлага на три компонента, насочени по координатните оси (фиг. 7.5, c).

Обикновено общият момент се разлага на компоненти: три момента спрямо координатните оси.

Абсолютната стойност на главния вектор (фиг. 7.5b) е равна на

Абсолютната стойност на главния момент се определя по формулата.

Уравнения на равновесие за пространствена система от сили

В равновесие Егл = 0; М гл = 0. Получаваме шест уравнения на равновесие:

Шестте равновесни уравнения на пространствената система от сили съответстват на шест независими възможни движения на тялото в пространството: три движения по координатните оси и три завъртания около тези оси.

Примери за решаване на проблеми

Пример 1.Върху кубовидно тяло с ръб А= 10 cm действат три сили (фиг. 7.6). Определете моментите на силите спрямо координатните оси, съвпадащи с ръбовете на куба.

Решение

1. Моменти на силите около оста О:

2. Моменти на силите около оста OU.

Пример 2.Две колела са фиксирани на хоризонтален вал, g 1 = 0,4 m; g 2 = 0,8 м. Други размери са на фиг. 7.7. Към колело 1 се прилага сила F 1,към колело 2 - мощност Е 2= 12 kN, Е 3= 4kN.

Определете силата F 1и реакции в пантите АИ INв състояние на баланс.

Нека ви напомним:

1. В равновесие са изпълнени шест равновесни уравнения.

Моментните уравнения трябва да бъдат написани спрямо опорите А и Б.

2. Правомощия Е 2 \\О х; Е 2\\Oy;Е 3\\Ой.

Моментите на тези сили спрямо съответните оси са равни на нула.

3. Изчислението трябва да бъде завършено чрез проверка с помощта на допълнителни уравнения за равновесие.

Решение

1. Определете силата F\,съставяйки уравнението на моментите на силите спрямо оста Oz:

2. Определете реакциите в подкрепа А.Има два реакционни компонента, действащи върху опората ( У А ; X А ).

Съставяме уравнението на моментите на силите около оста О"(в подкрепа IN).

Въртене около ос О"няма да се случи:

Знакът минус означава, че реакцията е насочена в обратна посока.

Въртене около ос OU"не се случи, съставяме уравнение за моментите на силите спрямо оста OU"(в подкрепа IN):

3. Определете реакциите в опора B. Два компонента на реакцията действат върху опората ( X Б , Y B ). Съставяме уравнението на моментите на силите около оста о(поддържа А):

Съставяме уравнението на моментите около оста OU(поддържа А):

4.Проверете. Използваме проекционни уравнения:

Изчислението е направено правилно.

Пример 3.Определете числената стойност на силата П 1 , при което вал слънце(фиг. 1.21, а)ще бъде в равновесие. При намерената стойност на силата П 1 определяне на реакциите на подкрепа.

Сили, действащи върху зъбни колела Р И П 1 насочена тангенциално към началните кръгове на колелата; сила T И Т 1 - според радиусите на колелата; сила A 1успоредно на оста на вала. T = 0.36P, 7T 1 = P 1; A 1 = 0,12P 1.

Решение

Опорите на вала, показани на фиг. 1.21, а, трябва да се разглеждат като пространствени шарнирни опори, които предотвратяват линейни движения в посоките на осите ИИ v(избраната координатна система е показана на фиг. 1.21, b).

Освобождаваме вала от връзките и заменяме тяхното действие с реакции V V, N V, V C, N C (фиг. 1.21, b). Получихме пространствена система от сили, за която съставяме уравнения на равновесие, използвайки избраната координатна система (фиг. 1.21.6):

Където A 1*1.25D/2 - момент около оста Исила A 1,приложен към дясната предавка.

Моменти около оста Исила Т 1И A 1(приложено към средната предавка), P 1 (приложено към дясната предавка) и P са равни на нула, тъй като силите P, T 1, P 1 са успоредни на оста И,и сила A 1 пресича оста И.

където V C = 0.37P;

където V B =0.37P.

оттук и реакциите V БИ V Cопределени правилно;

Където A 1* 1.25D/2- момент около оста vсила A 1,приложен към средната предавка.

Моменти около оста vсили T, P 1 (приложени към средната предавка), A 1И Т 1(приложени към дясната предавка) са равни на нула, тъй като силите T, R 1, T 1успоредна на оста v,сила A 1пресича оста v.

откъдето H C = 0.81P;

от където H C = 1.274P

Нека създадем уравнение за проверка:

оттук и реакциите N VИ Н Сопределени правилно.

В заключение отбелязваме, че реакциите на подкрепа се оказаха със знак плюс. Това показва, че избраните направления V B, N B, V C И Н С съвпадат с действителните посоки на реакциите на свързване.

Пример 4.Силата на натиск на мотовилката на парния двигател P = 25 kN се предава към средата на шийката на коляновия вал в точката дпод ъгъл α = 30° спрямо хоризонталата с вертикални бузи на коляното (фиг. 1.22). На края на вала е монтирана ремъчна шайба. Напрежението на задвижващия клон на ремъка е два пъти по-голямо от това на задвижвания клон, т.е. S 1 = 2S 2 . Сила на тежестта на маховика G = 10 kN.

Определете напрежението на клоновете на задвижването на ремъка и реакциите на лагерите АИ IN,пренебрегвайки масата на вала.

Решение

Разглеждаме равновесието на хоризонтален колянов вал с шайба. Ние прилагаме посочените сили в съответствие с условията на проблема P, S 1, S 2 И Ж . Освобождаваме вала от опорните крепежни елементи и заменяме тяхното действие с реакции V A, N A, V BИ N V.Избираме координатните оси, както е показано на фиг. 1.22. На панти АИ INне възникват реакции по оста w,тъй като напрежението на клоните на колана и всички други сили действат в равнини, перпендикулярни на тази ос.

Нека създадем уравнения на равновесие:

Освен това, според условията на задачата, имаме още едно уравнение

Така че тук има шест неизвестни сили S 1, S 2, N A, V A, N B И V Б и шест уравнения, които ги свързват.

Уравнение на проекциите върху ос wв разглеждания пример се превръща в идентичността 0 = 0, тъй като всички сили лежат в равнини, перпендикулярни на оста w.

Замествайки S 1 =2S 2 в уравненията на равновесието и решавайки ги, намираме:

Стойност на реакцията N VОказа се със знак минус. Това означава, че в действителност неговата посока е противоположна на тази, приета на фиг. 1.22.

Тестови въпроси и задачи

1. Запишете формулите за изчисляване на главния вектор на пространствена система от сближаващи се сили.

2. Запишете формулата за изчисляване на главния вектор на пространствена система от произволно разположени сили.

3. Запишете формулата за изчисляване на главния момент на пространствена система от сили.

4. Напишете системата от уравнения за равновесие на пространствената система от сили.

5. Кое уравнение на равновесието трябва да се използва за определяне на реакцията на пръта R 1 (фиг. 7.8)?

6. Определете основния момент на силовата система (фиг. 7.9). Референтната точка е началото на координатите. Координатните оси съвпадат с ръбовете на куба, ръбът на куба е 20 cm; Е 1 - 20kN; Е 2 - 30kN.

7. Определете реакцията Xb (фиг. 7.10). Вертикалната ос с макарата се натоварва от две хоризонтални сили. правомощия F 1 И Е 2 успоредна на оста о AO = 0,3 м; ОВ= 0,5 m; F 1 = 2kN; F 2 = 3,5 kN.

Препоръка. Създайте уравнение за моменти около оста OU" в точката А.

8. Отговорете на въпросите от теста.

Условия на векторно равновесие за произволна система от сили: за равновесието на система от сили, приложени към твърдо тяло, е необходимо и достатъчно главният вектор на системата от сили да е равен на нула и главният момент на системата от сили спрямо всеки център на редукция също да е равен на нула. В противен случай: за да има ~0, следните условия са необходими и достатъчни:

,
или
,
. (19)

Условия за равновесие на пространствена система от сили в аналитичен вид

За равновесието на пространствена система от сили, приложени към твърдо тяло, е необходимо и достатъчно трите суми на проекциите на всички сили върху декартовите координатни оси да са равни на нула, а трите суми на моментите на всички сили относителни към трите координатни оси също са равни на нула.

. (20)

Условия за равновесие на пространствена система от събиращи се сили

За равновесието на пространствена система от събиращи се сили, приложени към твърдо тяло, е необходимо и достатъчно сумите на проекциите на силите върху всяка от трите правоъгълни координатни оси да бъдат равни на нула:

;
;
, (21)

В случай на плоска система от събиращи се сили, една от координатните оси, обикновено
, се избира перпендикулярно на силите, а другите две оси се избират съответно в равнината на силите. д За равновесието на плоска система от събиращи се сили, действащи върху твърдо тяло, е необходимо и достатъчно сумите от проекциите на тези сили върху всяка от двете правоъгълни координатни оси, лежащи в равнината на силите, да са равни на нула:

;
, (22)

Условия на равновесие за пространствена система от успоредни сили

Нека насочим оста
успоредно на силите: за равновесието на пространствена система от успоредни сили, приложени към твърдо тяло, е необходимо и достатъчно алгебричната сума на тези сили да бъде равна на нула и сумата от моментите на силите спрямо две координатни оси, перпендикулярни на силите, да е също равно на нула:

Условия на равновесие за плоска система от сили

Нека позиционираме осите
И
в равнината на действие на силите.

Условия на равновесие за плоска система от сили в първата форма: за равновесието на плоска система от сили, действащи върху твърдо тяло, е необходимо и достатъчно сумите от проекциите на тези сили върху всяка от двете правоъгълни координатни оси, разположени в равнината на действие на силите, да са равни на нула и сумата от алгебричните моменти на силите спрямо всяка точка, разположена в равнината на силите на действие, също беше нула:

(24)

За равновесието на плоска система от успоредни сили, приложени към твърдо тяло, е необходимо и достатъчно алгебричната сума на силите да бъде равна на нула, а сумата от алгебричните моменти на силите спрямо всяка точка, разположена в равнината на силите също е равно на нула:

(25)

Теорема за трите момента (втора форма на условията на равновесие): за равновесието на плоска система от сили, приложени към твърдо тяло, е необходимо и достатъчно сумите от алгебричните моменти на силите на системата спрямо всеки три точки, разположени в равнината на действие на силите и не лежащи на една и съща права линия са равни на нула:

Трета форма на равновесни условия: за равновесието на плоска система от сили, приложени към твърдо тяло, е необходимо и достатъчно сумите на алгебричните моменти на силите спрямо всеки две точки, лежащи в равнината на действие на силите, да са равни на нула и алгебричните сумата от проекциите на тези сили върху всяка ос на равнината, която не е перпендикулярна на правата линия, минаваща през две моментни точки, също беше равна на нула, т.е.

Че., за равновесието на произволна пространствена система от сили е необходимо и достатъчно алгебричната сума на проекциите на всички тези сили върху всяка от трите произволно избрани координатни оси да е равна на нула и алгебричната сума на техните моменти спрямо всяка от тези оси също е равна на нула.

Извикват се условия (1.33). условия на равновесие на произволна пространствена система от сили в аналитична форма.

Условия на равновесие за пространствена система от успоредни сили.Ако линиите на действие на всички сили на дадена система от сили са разположени в различни равнини и са успоредни една на друга, тогава такава система от сили се нарича пространствена система от успоредни сили.

Използвайки условията на равновесие (1.33) на произволна пространствена система от сили, могат да се намерят условията на равновесие на пространствена система от успоредни сили. (Условията за равновесие, които по-рано изведехме за равнинни и пространствени системи от сближаващи се сили, произволна равнинна система от сили и равнинна система от успоредни сили, също могат да бъдат получени с помощта на условията за равновесие (1.33) на произволна пространствена система от сили).

Нека върху твърдо тяло действа пространствена система от успоредни сили (Фигура 1.26). Тъй като изборът на координатни оси е произволен, е възможно да изберете координатни оси така, че оста zбеше успореден на силите. При този избор на координатни оси проекциите на всяка от силите върху оста хИ прии техните моменти около оста zще бъдат равни на нула и следователно равенствата , и са изпълнени независимо от това дали дадена система от сили е в равновесие или не, и следователно престават да бъдат условия на равновесие. Следователно системата (1.33) ще даде само три условия на равновесие:

следователно за равновесието на пространствена система от успоредни сили е необходимо и достатъчно алгебричната сума на проекциите на всички сили върху оста, успоредна на тези сили, да е равна на нула и алгебричната сума на техните моменти спрямо всяка от двете координати оси, перпендикулярни на тези сили, също е равно на нула.

1. Изберете тяло (или точка), чието равновесие трябва да се вземе предвид в тази задача.

2. Освободете избраното тяло от връзки и изобразете (подредете) всички активни сили и сили на реакция на изхвърлени връзки, действащи върху това тяло (и само върху това тяло). Отделно трябва да се изобрази тяло, освободено от връзки, към което е прикрепена система от активни и противодействащи сили.

3. Напишете уравнения за равновесие. За да съставите уравнения на равновесие, първо трябва да изберете координатните оси. Този избор може да бъде направен произволно, но получените уравнения на равновесието ще бъдат решени по-лесно, ако една от осите е насочена перпендикулярно на линията на действие на някаква неизвестна сила на реакция. Решаването на получените уравнения на равновесие по правило трябва да се извърши до края в обща форма (алгебрично). След това за необходимите количества ще бъдат получени формули, които позволяват да се анализират намерените резултати; числените стойности на намерените количества се заместват само в крайните формули. Уравненията на равновесието се съставят с помощта на аналитичния метод за решаване на задачи за равновесието на система от сближаващи се сили. Въпреки това, ако броят на събиращите се сили, чието равновесие се разглежда, е три, тогава е удобно да се приложи геометричният метод за решаване на тези проблеми. Решението в този случай се свежда до факта, че вместо уравненията на равновесието на всички действащи сили (активни и реакционни връзки) се построява силов триъгълник, който въз основа на геометричното условие на равновесие трябва да бъде затворен (конструкцията на този триъгълник трябва да започва с дадена сила). Чрез решаване на триъгълника на силата намираме търсените количества.

Динамика

За да разберете раздела за динамиката, трябва да знаете следната информация. От математиката - скаларното произведение на два вектора, диференциални уравнения. От физиката – законите за запазване на енергията и импулса. Теория на трептенията. Препоръчително е да прегледате тези теми.

Както беше изяснено в § 4.4, необходимите и достатъчни условия за равновесие на пространствена система от сили, приложени към твърдо тяло, могат да бъдат записани под формата на три проекционни уравнения (4.16) и три момента (4.17):

, , . (7.14)

Ако тялото е напълно фиксирано, тогава силите, действащи върху него, са в равновесие и уравненията (7.13) и (7.14) служат за определяне на опорните реакции. Разбира се, може да има случаи, когато тези уравнения не са достатъчни за определяне на опорните реакции; Ние няма да разглеждаме такива статично неопределени системи.

За пространствена система от успоредни сили уравненията на равновесието приемат формата (§ 4.4 [‡]):

, , . (7.15)

Нека сега разгледаме случаите, когато тялото е само частично фиксирано, т.е. връзките, които се налагат на тялото, не гарантират баланса на тялото. Могат да бъдат посочени четири специални случая.

1. Твърдото тяло има една фиксирана точка. С други думи, той е прикрепен към фиксирана точка с помощта на перфектна сферична връзка.

Нека поставим началото на фиксираната координатна система в тази точка. Действие на свързване в точка АНека го заменим с реакция; тъй като е неизвестен по големина и посока, ще го представим под формата на три неизвестни компонента , , , насочени съответно по осите , , .

Уравненията на равновесието (7.13) и (7.14) в този случай ще бъдат записани във формата:

1) ,

2) ,

3) ,

4) ,

5) ,

Последните три уравнения не съдържат компоненти на реакцията, тъй като линията на действие на тази сила минава през точката А. Следователно тези уравнения установяват връзките между активните сили, необходими за равновесието на тялото, и първите три уравнения могат да се използват за определяне на компонентите на реакцията.

По този начин, условието за равновесие на твърдо тяло, което има една фиксирана точка, е равенството на нула на всяка от алгебричните суми на моментите на всички активни сили на системата спрямо три оси, пресичащи се в фиксирана точка на тялото .

2. Тялото има две фиксирани точки. Такъв ще бъде например случаят, ако е прикрепен към две фиксирани точки с помощта на панти.

Нека изберем началото на координатите в точката Аи насочете оста по линията, минаваща през точките АИ IN. Нека заменим действието на връзките с реакции, насочвайки компонентите на реакцията по координатните оси. Нека обозначим разстоянието между точките АИ INпрез А; тогава уравненията на равновесието (7.13) и (7.14) ще бъдат записани в следната форма:

1) ,

2) ,

3) ,

4) ,

5) ,

Последното уравнение не съдържа сили на реакция и установява връзката между активните сили, необходими за равновесието на тялото. следователно условието за равновесие на твърдо тяло, което има две фиксирани точки, е равенството на нула на алгебричната сума на моментите на всички активни сили, приложени към тялото спрямо оста, минаваща през фиксираните точки . Първите пет уравнения се използват за определяне на неизвестните компоненти на реакциите , , , , , .

Имайте предвид, че компонентите и не могат да бъдат определени поотделно. От третото уравнение се определя само сумата + и следователно проблемът по отношение на всяко от тези неизвестни за твърдо тяло е статически неопределен. Въпреки това, ако в точката INАко има не сферичен, а цилиндричен шарнир (т.е. лагер), който не пречи на надлъжното плъзгане на тялото по оста на въртене, тогава проблемът става статично определим.

Тялото има фиксирана ос на въртене, по която може да се плъзга без триене.Това означава, че в точки АИ INима цилиндрични панти (лагери), а компонентите на техните реакции по оста на въртене са равни на нула. Следователно уравненията на равновесието ще приемат формата:

1) ,

2) ,

4) ,

5) ,

Две от уравненията (7.18), а именно третото и шестото, налагат ограничения върху системата от активни сили, а останалите уравнения служат за определяне на реакциите.

Тялото лежи в три точки върху гладка повърхност, като опорните точки не лежат на една и съща права линия. Нека обозначим тези точки с А, INИ СЪСи е съвместим със самолета ABCкоординатна равнина Аху. Заменяйки действието на връзките с вертикални реакции , и , записваме условията на равновесие (7.14) в следната форма:

3) ,

4) ,

5) ,

Третото - петото уравнения могат да служат за определяне на неизвестни реакции, а първото, второто и шестото уравнения представляват условията, свързващи активните сили и необходими за равновесието на тялото. Разбира се, за да се балансира тялото, трябва да са изпълнени следните условия: , , тъй като в опорните точки могат да възникнат само реакции от приетата по-горе посока.

Ако тялото лежи върху хоризонтална равнина в повече от три точки, тогава проблемът става статично неопределим, тъй като в този случай ще има толкова реакции, колкото са точките, и ще останат само три уравнения за определяне на реакциите.

Задача 7.3.Намерете главния вектор и главния момент на системата от сили, показана на фиг. Силите се прилагат към върховете на куба и са насочени по ръбовете му, и , . Дължината на ръба на куба е А.