The angles of a triangle are always. Scientific electronic library

Theorem. The sum of the interior angles of a triangle is equal to two right angles.

Take some ABC triangle (Fig. 208). Let us denote its interior angles by numbers 1, 2, and 3. Let us prove that

∠1 + ∠2 + ∠3 = 180 °.

Let's draw through some vertex of the triangle, for example B, a straight line МN parallel to АС.

At vertex B, we got three angles: ∠4, ∠2 and ∠5. Their sum is the unfolded angle, therefore, it is equal to 180 °:

∠4 + ∠2 + ∠5 = 180 °.

But ∠4 = ∠1 are internal cross-lying angles at parallel lines МN and АС and secant AB.

∠5 = ∠3 are the internal cross-lying angles at parallel straight lines МN and АС and secant ВС.

Hence, ∠4 and ∠5 can be replaced by the equal ∠1 and ∠3.

Therefore, ∠1 + ∠2 + ∠3 = 180 °. The theorem is proved.

2. Property of the outer corner of a triangle.

Indeed, in triangle ABC (Fig. 209) ∠1 + ∠2 = 180 ° - ∠3, but also ∠BCD, the outer angle of this triangle, not adjacent to ∠1 and ∠2, is also equal to 180 ° - ∠3 ...

Thus:

∠1 + ∠2 = 180 ° - ∠3;

∠BCD = 180 ° - ∠3.

Therefore, ∠1 + ∠2 = ∠BCD.

The derived property of the external angle of a triangle clarifies the content of the previously proved theorem on the external angle of a triangle, in which it was stated only that the external angle of a triangle is greater than each internal angle of a triangle that is not adjacent to it; now it is established that the external angle is equal to the sum of both internal angles that are not adjacent to it.

3. Property of a right-angled triangle with an angle of 30 °.

Let the angle B in a right-angled triangle ACB be equal to 30 ° (Fig. 210). Then its other acute angle will be equal to 60 °.

Let us prove that the AC leg is equal to half of the AB hypotenuse. Let us extend the leg AC beyond the vertex of the right angle C and set aside the segment CM equal to the segment AC. We connect point M with point B. The resulting triangle BCM equal to triangle ASV. We see that each angle of the triangle ABM is 60 °, therefore, this triangle is equilateral.

The AC leg is equal to half of AM, and since AM is equal to AB, the AC leg will be equal to half of the hypotenuse of AB.

Targets and goals:

Educational:

• repeat and generalize knowledge about the triangle;
• prove the theorem on the sum of the angles of a triangle;
• practically verify the correctness of the statement of the theorem;
• learn to apply the knowledge gained in solving problems.

Developing:

• develop geometric thinking, interest in the subject, cognitive and creative activities of students, mathematical speech, the ability to independently acquire knowledge.

Educational:

• develop personal qualities students, such as dedication, perseverance, accuracy, the ability to work in a team.

Equipment: multimedia projector, colored paper triangles, "Living Mathematics" educational complex, computer, screen.

Preparatory stage: the teacher instructs the student to prepare historical background on the theorem "The sum of the angles of a triangle".

Lesson type: learning new material.

During the classes

I. Organizational moment

Greetings. The psychological attitude of students to work.

II. Warm up

We got acquainted with the geometric shape "triangle" in the previous lessons. Let's reiterate what we know about the triangle?

Students work in groups. They are given the opportunity to communicate with each other, each to independently build the process of cognition.

What happened? Each group makes their suggestions, the teacher writes them down on the board. Results are discussed:

Picture 1

III. We formulate the task of the lesson

So, we already know a lot about the triangle. But not all. Each of you has triangles and protractors on your desk. What task do you think we can formulate?

Pupils formulate the task of the lesson - find the sum of the angles of a triangle.

IV. Explanation of the new material

Practical part(contributes to the updating of knowledge and self-knowledge skills) Take measurements of the angles using a protractor and find their sum. Write the results in a notebook (listen to the answers received). We find out that the sum of the angles is different for everyone (this can happen because the protractor was inaccurately attached, the calculation was careless, etc.).

Bend along the dotted lines and find out what else the sum of the angles of the triangle is equal to:

a)
Picture 2

b)
Figure 3

v)
Figure 4

G)
Figure 5

e)
Figure 6

After completing the practical work, the students formulate the answer: The sum of the angles of the triangle is equal to the degree measure of the unfolded angle, i.e. 180 °.

Teacher: In mathematics practical work makes it possible only to make some statement, but it needs to be proved. A statement, the validity of which is established by proof, is called a theorem. What theorem can we formulate and prove?

Students: The angles of a triangle add up to 180 degrees.

Historical reference: The property of the sum of the angles of a triangle was established back in Ancient egypt... The proof set out in modern textbooks, is contained in the commentaries of Proclus to Euclid's Beginnings. Proclus claims that this proof (Fig. 8) was discovered by the Pythagoreans (5th century BC). In the first book of the Elements, Euclid sets out another proof of the theorem on the sum of the angles of a triangle, which is easy to understand with the help of the drawing (Fig. 7):

Figure 7

Figure 8

Drawings are displayed on the screen through a projector.

The teacher suggests using drawings to prove the theorem.

Then the proof is carried out using the CMK "Living Mathematics"... The teacher projects the proof of the theorem on the computer.

The theorem on the sum of the angles of a triangle: "The sum of the angles of a triangle is 180 °"

Figure 9

Proof:

a)

Figure 10

b)

Figure 11

v)

Figure 12

Students in a notebook makes a short note of the proof of the theorem:

Theorem: The angles of a triangle add up to 180 °.

Figure 13

Given:Δ ABC

Prove: A + B + C = 180 °.

Proof:

What was required to be proved.

V. Phys. a minute.

Vi. Explanation of the new material (continued)

The corollary from the theorem on the sum of the angles of a triangle is deduced by students independently, this contributes to the development of the ability to formulate their own point of view, express and argue for it:

In any triangle, either all corners are acute, or two acute angles, and the third is obtuse or straight.

If all angles in a triangle are sharp, then it is called acute-angled.

If one of the corners of the triangle is obtuse, then it is called obtuse.

If one of the angles of a triangle is a straight line, then it is called rectangular.

The triangle sum theorem allows you to classify triangles not only by sides, but also by angles. (In the course of introducing the types of triangles, students fill out the table)

Table 1

Triangle view	Isosceles	Equilateral	Versatile
Rectangular
Obtuse
Acute-angled

Vii. Consolidation of the studied material.

1. Solve problems orally:

(Drawings are displayed on the screen through a projector)

(supporting synopsis)

Visual geometry grade 7. Support note number 4 The sum of the angles of the triangle.

Great French scientist of the 17th century Blaise Pascal in childhood he liked to mess with geometric shapes... He was familiar with the protractor and knew how to measure angles. The young researcher noticed that all triangles have the same sum of three angles - 180 °. “How can we prove this? thought Pascal. "After all, you can't check the sum of the angles of all triangles - there are an infinite number of them." Then he cut off two corners of the triangle with scissors and attached them to the third corner. The resulting angle is 180 °, as you know. This was his first own discovery. Further destiny the boy was already predetermined.

In this topic, you will learn five signs of equality for right triangles and perhaps the most popular property of a right triangle with an angle of 30 °. It sounds like this: the leg, lying opposite an angle of 30 °, is equal to half the hypotenuse. Dividing an equilateral triangle by its height, we immediately obtain a proof of this property.

THEOREM. The angles of a triangle add up to 180 °. For the proof, draw a straight line through the vertex, parallel to the base. The dark corners are equal and the gray corners are equal as they lie across parallel lines. The dark corner, the gray corner, and the apex angle form a flat angle, and their sum is 180 °. It follows from the theorem that the angles equilateral triangle are equal to 60 ° and that the sum of the acute angles of a right-angled triangle is 90 °.

Outside corner of a triangle is called the angle adjacent to the angle of the triangle. Therefore, sometimes the angles of the triangle itself are called interior angles.

THEOREM on the external angle of a triangle... The outer corner of a triangle is equal to the sum of two inner ones that are not adjacent to it. Indeed, the outer corner and two inner ones that are not adjacent to it complement the shaded corner up to 180 °. It follows from the theorem that the external angle is greater than any internal angle not adjacent to it.

THEOREM on the relations between the sides and angles of a triangle... In a triangle, the larger side is opposite the larger side, and the larger side is opposite the larger side. Hence follows: 1) The leg is less than the hypotenuse. 2) The perpendicular is less inclined.

Distance from point to line ... Since the perpendicular is less than any oblique drawn from the same point, its length is taken as the distance from the point to the straight line.

Triangle inequality ... The length of any side of a triangle is less than the sum of its other two sides, i.e. a< b + с , b< а + с , with< а + b . Consequence... The length of the polyline is greater than the line segment connecting its ends.

SIGNS OF EQUALITY
RECTANGULAR TRIANGLES

On two legs... If two legs of one right-angled triangle are respectively equal to two legs of another triangle, then such triangles are equal.

Along the leg and adjacent acute corner... If the leg and the adjacent acute angle of one right-angled triangle are respectively equal to the leg and the adjacent acute angle of the other triangle, then such triangles are equal.

Along the leg and the opposite sharp corner... If the leg and the acute angle opposite to it of one right-angled triangle are respectively equal to the leg and the acute angle opposite to it of the other triangle, then such triangles are equal.

By hypotenuse and acute angle... If the hypotenuse and acute angle of one right-angled triangle are respectively equal to the hypotenuse and acute angle of another triangle, then such triangles are equal.

The proof of these signs immediately comes down to one of the criteria for the equality of triangles.

On the leg and hypotenuse... If the leg and hypotenuse of one right triangle are respectively equal to the leg and hypotenuse of another right triangle, then such triangles are equal.

Proof. We attach the triangles with equal legs. We get an isosceles triangle. Its height, drawn from the top, will also be the median. Then the second legs of the triangles are equal, and the triangles are equal on three sides.

THEOREM on the property of the leg lying opposite an angle of 30 °... The leg, lying opposite an angle of 30 °, is equal to half the hypotenuse. This is proved by extending the triangle to an equilateral one.

THEOREM on the property of points of the bisector of an angle... Any point of the bisector of an angle is equidistant from its sides. If the point is equidistant from the sides of the angle, then it lies on the bisector of the angle. This is proved by drawing two perpendiculars to the sides of the corner and considering right-angled triangles.

Second great point ... The bisectors of a triangle intersect at one point.

Distance between parallel lines. THEOREM... All points of each of the two parallel lines are equidistant from the other line. The theorem implies the definition of the distance between parallel lines.

Definition... The distance between two parallel straight lines is the distance from any point of one of the parallel straight lines to another straight line.

Detailed theorem proofs

This is the pivotal lecture number 4 on geometry in the 7th grade. Choose further actions:

Triangle . Acute-angled, obtuse-angled and right-angled triangles.

Legs and hypotenuse. Isosceles and equilateral triangle.

The sum of the angles of a triangle.

The outer corner of the triangle. Signs of equality of triangles.

Wonderful lines and points in the triangle: heights, medians,

bisectors, median e perpendiculars, orthocenter,

center of gravity, center of an inscribed circle, center of an inscribed circle.

Pythagorean theorem. Aspect ratio in an arbitrary triangle.

Triangle Is a polygon with three sides (or three corners). The sides of a triangle are often denoted by small letters that correspond to in capital letters indicating opposite vertices.

If all three corners are sharp (Fig. 20), then this is acute-angled triangle ... If one of the corners is straight(C, fig. 21), that is right triangle; partiesa, bforming a right angle are called legs; sidecopposite to the right angle is called hypotenuse... If one of obtuse angles (B, fig. 22), that is obtuse triangle.


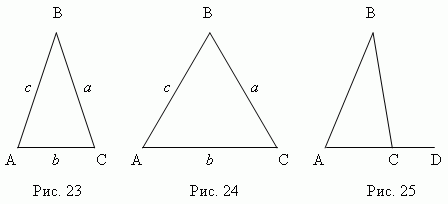
Triangle ABC (fig. 23) - isosceles, if two its sides are equal (a= c); these equal sides are called lateral, the third party is called basis triangle. Triangle ABC (fig. 24) - equilateral, if all its sides are equal (a = b = c). In general ( a ≠ b ≠ c) we have scalene triangle .

Basic properties of triangles. In any triangle:

1. There is a larger angle against the larger side, and vice versa.

2. Against equal sides lie equal angles, and vice versa.

In particular, all angles in equilateral triangle are equal.

3. The angles of a triangle add up to 180 º .

From the last two properties it follows that each angle in an equilateral

triangle is 60 º.

4. Continuing one of the sides of the triangle (AC, fig. 25), we get external

angle BCD . The outer angle of the triangle is equal to the sum of the inner angles,

not adjacent to him : BCD = A + B.

5. Any side of a triangle is less than the sum of the other two sides and more

their differences (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Signs of equality of triangles.

Triangles are equal if they are respectively equal:

a ) two sides and the angle between them;

b ) two corners and the side adjacent to them;

c) three sides.

Signs of equality of right-angled triangles.

Two rectangular triangles are equal if one of the following conditions is true:

1) their legs are equal;

2) the leg and hypotenuse of one triangle are equal to the leg and hypotenuse of the other;

3) the hypotenuse and acute angle of one triangle are equal to the hypotenuse and acute angle of the other;

4) the leg and the adjacent acute angle of one triangle are equal to the leg and the adjacent acute angle of the other;

5) the leg and the opposite acute angle of one triangle are equal to the leg and the opposite sharp corner of the other.

Wonderful lines and points in the triangle.

Height triangle isperpendicular,dropped from any vertex to the opposite side ( or its continuation). This side is calledbase of triangle . Three heights of a triangle always intersectat one pointcalled orthocenter triangle. Orthocenter of an acute-angled triangle (point O , fig. 26) is located inside the triangle, andthe orthocenter of an obtuse triangle (point O , fig. 27) – outside; the orthocenter of a right-angled triangle coincides with the vertex of the right angle.

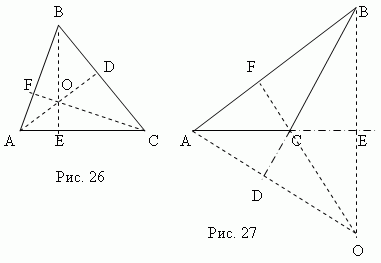
Median - this is section connecting any vertex of the triangle to the midpoint of the opposite side. Three medians of a triangle (AD, BE, CF, fig. 28) intersect at one point O always lying inside the triangle and being his center of gravity. This point divides each median by a 2: 1 ratio from the top.

Bisector - this is bisector segment corner from apex to a point intersection with the opposite side. Three bisectors of a triangle (AD, BE, CF, fig. 29) intersect at one point Oh always lying inside a triangle and being the center of the inscribed circle(see the section "Inscribedand the described polygons ").

The bisector divides the opposite side into parts proportional to the adjacent sides ; for example, in fig. 29 AE: CE = AB: BC.

Median perpendicular Is a perpendicular drawn from the middle segment points (sides). Three median perpendiculars of triangle ABC(KO, MO, NO, fig. 30 ) intersect at one point O, which is center the circumscribed circle (points K, M, N - the midpoints of the sides of the triangle ABC).

In an acute-angled triangle, this point lies inside the triangle; in obtuse - outside; in rectangular - in the middle of the hypotenuse. Orthocenter, center of gravity, center of circumscribed and center of inscribed circle coincide only in an equilateral triangle.

Pythagorean theorem. In a right triangle, the square of lengththe hypotenuse is equal to the sum of the squares of the lengths of the legs.

The proof of the Pythagorean theorem clearly follows from Fig. 31. Consider a right triangle ABC with legs a, b and hypotenuse c.

Let's build a square AKMB using the hypotenuse AB as a side. Thenextend the sides of the right triangle ABC so to get a square CDEF whose side is equal toa + b.It is now clear that the area of ​​a square CDEF is ( a + b) 2 ... On the other hand, this area is equal to the sum squares four right triangles and square AKMB, that is

c 2 + 4 (ab / 2) = c 2 + 2 ab,

from here,

c 2 + 2 ab= (a + b) 2 ,

and finally we have:

c 2 =a 2 + b 2 .

Aspect ratio in an arbitrary triangle.

In the general case (for an arbitrary triangle) we have:

c 2 =a 2 + b 2 – 2ab· cos C,

where C - the angle between the sidesa and b .

>> Geometry: The sum of the angles of a triangle. Complete lessons

LESSON TOPIC: The sum of the angles of a triangle.

Lesson objectives:

• Consolidation and testing of students' knowledge on the topic: "The sum of the angles of a triangle";
• Proof of the property of the angles of a triangle;
• The use of this property in solving the simplest problems;
• Using historical material for development cognitive activity students;
• Instilling the skill of accuracy when building drawings.

Lesson Objectives:

• Test the students' ability to solve problems.

Lesson plan:

1. Triangle;
2. The theorem on the sum of the angles of a triangle;
3. Sample tasks.

Triangle.

File: O.gif Triangle- the simplest polygon with 3 vertices (corners) and 3 sides; part of the plane bounded by three points and three line segments connecting these points in pairs.
Three points of space that do not lie on one straight line correspond to one and only one plane.
Any polygon can be divided into triangles - this process is called triangulation.
There is a section of mathematics entirely devoted to the study of the laws of triangles - Trigonometry.

The theorem on the sum of the angles of a triangle.

File: T.gif The theorem on the sum of the angles of a triangle is a classical theorem of Euclidean geometry, which states that the sum of the angles of a triangle is 180 °.

Proof" :

Let Δ ABC be given. Draw a line parallel to (AC) through vertex B and mark point D on it so that points A and D lie on opposite sides of line BC. Then the angle (DBC) and the angle (ACB) are equal as internal criss-crossing lines with parallel lines BD and AC and secant (BC). Then the sum of the angles of the triangle at the vertices B and C is equal to the angle (ABD). But the angle (ABD) and angle (BAC) at the vertex A of triangle ABC are internal one-sided with parallel lines BD and AC and secant (AB), and their sum is 180 °. Therefore, the sum of the angles of the triangle is 180 °. The theorem is proved.

Consequences.

The outer angle of a triangle is equal to the sum of the two angles of the triangle that are not adjacent to it.

Proof:

Let Δ ABC be given. Point D lies on line AC so that A lies between C and D. Then BAD is external to the corner of the triangle at the vertex A and A + BAD = 180 °. But A + B + C = 180 °, and therefore B + C = 180 ° - A. Hence BAD = B + C. The corollary is proved.

Consequences.

The outer corner of a triangle is greater than any corner of the triangle that is not adjacent to it.

Task.

The outer corner of a triangle is the angle adjacent to any corner of this triangle. Prove that the outer angle of a triangle is equal to the sum of two angles of a triangle that are not adjacent to it.
(Fig. 1)

Solution:

Let in Δ ABC ∠DAC - external (Fig. 1). Then ∠DAC = 180 ° -∠BAC (by the property of adjacent angles), by the theorem on the sum of the angles of a triangle ∠B + ∠C = 180 ° -∠BAC. From these equalities we obtain ∠DАС = ∠В + ∠С

Interesting fact:

The sum of the angles of a triangle " :

In Lobachevsky's geometry, the sum of the angles of a triangle is always less than 180. In Euclid's geometry, it is always equal to 180. In Riemannian geometry, the sum of the angles of a triangle is always greater than 180.

From the history of mathematics:

Euclid (III century BC) in his work "Beginnings" gives the following definition: "Parallel are straight lines that are in the same plane and, being continued in both directions indefinitely, do not meet each other on either side" ...
Posidonius (I century BC) "Two straight lines lying in the same plane, equidistant from each other"
The ancient Greek scientist Pappus (III century BC) introduced the symbol of parallel straight lines - the = sign. Subsequently English economist Ricardo (1720-1823) used this symbol as an equal sign.
Only in the 18th century began to use the symbol of parallelism of straight lines - the || sign.
The living connection between generations is not interrupted for a moment, every day we assimilate the experience accumulated by our ancestors. The ancient Greeks, on the basis of observations and from practical experience, drew conclusions, expressed hypotheses, and then, at meetings of scientists - symposia (literally "feast") - they tried to substantiate and prove these hypotheses. At that time, the statement was formed: "In a dispute, truth is born."

Questions:

1. What is a triangle?
2. What does the triangle sum theorem say?
3. What is the outer angle of the triangle?