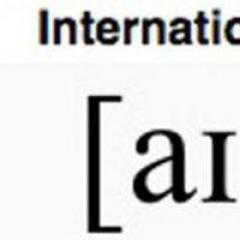El concepto de función. Funciones limitadas

1) Dominio de función y rango de función.

El dominio de una función es el conjunto de todos los valores válidos de los argumentos válidos. X(variable X), para lo cual la función y = f(x) determinado. El rango de una función es el conjunto de todos los valores reales. y, que la función acepta.

En matemáticas elementales, las funciones se estudian únicamente en el conjunto de los números reales.

2) Función ceros.

La función cero es el valor del argumento en el que el valor de la función es igual a cero.

3) Intervalos de signo constante de una función.

Los intervalos de signo constante de una función son conjuntos de valores de argumentos en los que los valores de la función son solo positivos o solo negativos.

4) Monotonicidad de la función..

Una función creciente (en un intervalo determinado) es una función en la que un valor mayor del argumento de este intervalo corresponde a un valor mayor de la función.

Una función decreciente (en un intervalo determinado) es una función en la que un valor mayor del argumento de este intervalo corresponde a un valor menor de la función.

5) Función par (impar).

Una función par es una función cuyo dominio de definición es simétrico con respecto al origen y para cualquier X desde el dominio de la definición la igualdad f(-x) = f(x).

La gráfica de una función par es simétrica con respecto a la ordenada. X Una función impar es una función cuyo dominio de definición es simétrico con respecto al origen y para cualquier desde el dominio de la definición la igualdad es verdadera f(-x) = -f(x)

)..

La gráfica de una función impar es simétrica con respecto al origen.

6) Funciones limitadas e ilimitadas.

Una función se dice acotada si existe un número positivo M tal que |f(x)| ≤ M para todos los valores de x. Si tal número no existe, entonces la función es ilimitada.

7) Periodicidad de la función

Una función f(x) es periódica si existe un número T distinto de cero tal que para cualquier x del dominio de definición de la función se cumple lo siguiente: f(x+T) = f(x). Este número más pequeño se llama período de la función. Todas las funciones trigonométricas son periódicas. (Fórmulas trigonométricas).

19. Funciones elementales básicas, sus propiedades y gráficas. Aplicación de funciones en economía.

Funciones elementales básicas. Sus propiedades y gráficas. se llama función de la forma , donde x es una variable, a y b son números reales.

Número A llamada pendiente de la recta, es igual a la tangente del ángulo de inclinación de esta recta a la dirección positiva del eje x. La gráfica de una función lineal es una línea recta. Está definido por dos puntos.

Propiedades de una función lineal

1. Dominio de definición: el conjunto de todos los números reales: D(y)=R

2. El conjunto de valores es el conjunto de todos los números reales: E(y)=R

3. La función toma un valor cero cuando o.

4. La función aumenta (disminuye) en todo el dominio de definición.

5. Una función lineal es continua en todo el dominio de definición, diferenciable y .

2. Función cuadrática.

Una función de la forma, donde x es una variable y los coeficientes a, b, c son números reales, se llama cuadrático.

Impares a B C determinar la ubicación del gráfico en el plano de coordenadas

El coeficiente a determina la dirección de las ramas. La gráfica de una función cuadrática es una parábola. Las coordenadas del vértice de la parábola se encuentran mediante las fórmulas:

Propiedades de la función:

2. Un conjunto de valores para uno de los intervalos: o.

3. La función toma valores cero cuando , donde el discriminante se calcula mediante la fórmula :.

4. La función es continua en todo el dominio de definición y la derivada de la función es igual a.

Lección y presentación sobre el tema: "Propiedades de una función. Funciones crecientes y decrecientes"

Materiales adicionales
Estimados usuarios, ¡no olviden dejar sus comentarios, reseñas, deseos! Todos los materiales han sido revisados por un programa antivirus.

Ayudas educativas y simuladores en la tienda online de Integral para 9º grado
Libro de texto interactivo para noveno grado "Reglas y ejercicios de geometría"
Libro de texto electrónico "Geometría comprensible" para los grados 7-9

Chicos, seguimos estudiando funciones numéricas. Hoy nos centraremos en un tema como las propiedades de las funciones. Las funciones tienen muchas propiedades. Recuerda qué propiedades estudiamos recientemente. Así es, el dominio de la definición y el dominio de los valores son una de las propiedades clave. Nunca te olvides de ellos y recuerda que una función siempre tiene estas propiedades.

En esta sección, definiremos algunas propiedades de las funciones. Recomiendo seguir el orden en el que los determinaremos a la hora de resolver problemas.

Función creciente y decreciente.

La primera propiedad que definiremos es la función creciente y decreciente.

Se dice que una función es creciente en el conjunto X⊂D(f) si para cualquier x1 y x2 tal que x1< x2 - выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.
Se dice que una función es decreciente en el conjunto X⊂D(f) si para cualquier x1 y x2 tal que x1< x2 - выполняется неравенство f(x1)>f(x2). Es decir, un valor mayor del argumento corresponde a un valor menor de la función.

Los conceptos de "creciente" y "decreciente" de una función son muy fáciles de entender si observas detenidamente las gráficas de la función. Para una función creciente: parece que estamos subiendo una colina, para una función decreciente, estamos bajando en consecuencia. La vista general de funciones crecientes y decrecientes se presenta en los siguientes gráficos.

Las funciones crecientes y decrecientes generalmente se denominan monotonicidad. Es decir, nuestra tarea es encontrar los intervalos de disminución y aumento de la función. En el caso general, esto se formula de la siguiente manera: encuentre intervalos de monotonicidad o examine la monotonicidad de una función.

Examina la monotonicidad de la función $y=3x+2$.
Solución: verifiquemos la función para cualquier x1 y x2 y dejemos que x1< x2.
$f(x1)=3x1+2$
$f(x2)=3x2+2$
Desde, x1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.

Función limitada

Se dice que una función $y=f(x)$ está acotada desde abajo en el conjunto X⊂D(f) si existe un número a tal que para cualquier хϵХ se cumpla la desigualdad f(x)< a.

Se dice que una función $y=f(x)$ está acotada desde arriba en el conjunto X⊂D(f) si existe un número a tal que para cualquier хϵХ se cumple la desigualdad f(x)< a.

Si no se especifica el intervalo X, entonces se considera que la función está limitada a todo el dominio de definición. Una función que está acotada tanto por arriba como por abajo se llama acotada.

La limitación de la función es fácil de leer en el gráfico. Es posible trazar una línea recta.
$у=а$, y si la función es superior a esta línea, entonces está limitada desde abajo. Si está debajo, entonces arriba en consecuencia. A continuación se muestra una gráfica de una función acotada a continuación. Chicos, intenten dibujar ustedes mismos la gráfica de una función limitada.

Examina la acotación de la función $y=\sqrt(16-x^2)$.
Solución: La raíz cuadrada de un determinado número es mayor o igual a cero. Obviamente, nuestra función también es mayor o igual a cero, es decir, acotada desde abajo.
Solo podemos extraer la raíz cuadrada de un número no negativo, entonces $16-x^2≥0$.
La solución a nuestra desigualdad será el intervalo [-4;4]. En este segmento $16-x^2≤16$ o $\sqrt(16-x^2)≤4$, pero esto significa acotado desde arriba.
Respuesta: nuestra función está limitada a dos rectas $y=0$ y $y=4$.

Valor más alto y más bajo

El valor más pequeño de la función y= f(x) en el conjunto X⊂D(f) es algún número m tal que:

b) Para cualquier хϵХ, se cumple $f(x)≥f(x0)$.

El valor más grande de la función y=f(x) en el conjunto X⊂D(f) es algún número m tal que:
a) Existe algún x0 tal que $f(x0)=m$.
b) Para cualquier хϵХ, se cumple $f(x)≤f(x0)$.

Los valores más grandes y más pequeños generalmente se indican con y max. y tu nombre .

Los conceptos de acotación y el valor más grande con el más pequeño de una función están estrechamente relacionados. Las siguientes afirmaciones son ciertas:
a) Si hay un valor mínimo para una función, entonces está acotado por debajo.
b) Si una función tiene el mayor valor, entonces está acotada por arriba.
c) Si la función no está acotada arriba, entonces el valor mayor no existe.
d) Si la función no está acotada por debajo, entonces el valor más pequeño no existe.

Encuentra el valor más grande y más pequeño de la función $y=\sqrt(9-4x^2+16x)$.
Solución: $f(x)=y=\sqrt(9-4x^2+16x)=\sqrt(9-(x-4)^2+16)=\sqrt(25-(x-4)^2 )≤5$.
Para $х=4$ $f(4)=5$, para todos los demás valores la función toma valores más pequeños o no existe, es decir, este es el valor más grande de la función.
Por definición: $9-4x^2+16x≥0$. Encontremos las raíces del trinomio cuadrático $(2x+1)(2x-9)≥0$. En $x=-0.5$ y $x=4.5$ la función desaparece; en todos los demás puntos es mayor que cero. Entonces, por definición, el valor más pequeño de la función es igual a cero.
Respuesta: y máx. =5 y y nombre. =0.

Chicos, también hemos estudiado el concepto de convexidad de una función. Al resolver algunos problemas, es posible que necesitemos esta propiedad. Esta propiedad también se determina fácilmente mediante gráficos.

Una función es convexa hacia abajo si dos puntos cualesquiera de la gráfica de la función original están conectados y la gráfica de la función está debajo de la línea que conecta los puntos.

Una función es convexa hacia arriba si dos puntos cualesquiera de la gráfica de la función original están conectados y la gráfica de la función está por encima de la línea que conecta los puntos.

Una función es continua si la gráfica de nuestra función no tiene interrupciones, por ejemplo, como la gráfica de la función anterior.

Si necesita encontrar las propiedades de una función, la secuencia de búsqueda de las propiedades es la siguiente:
a) Dominio de definición.
b) Monotonía.
c) Limitación.
d) El valor mayor y menor.
d) Continuidad.
e) Rango de valores.

Encuentra las propiedades de la función $y=-2x+5$.
Solución.
a) Dominio de definición D(y)=(-∞;+∞).
b) Monotonía. Comprobemos los valores x1 y x2 y dejemos que x1< x2.
$f(x1)=-2x1+2$.
$f(x2)=-2x2+2$.
Desde x1< x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
c) Limitación. Obviamente la función no está limitada.
d) El valor mayor y menor. Como la función no está acotada, no existe un valor máximo ni mínimo.
d) Continuidad. La gráfica de nuestra función no tiene cortes, entonces la función es continua.
e) Rango de valores. mi(y)=(-∞;+∞).

Problemas sobre las propiedades de una función para solución independiente.

Encuentra propiedades de función:
a) $y=2x+7$,
b) $y=3x^2$,
c) $y=\frac(4)(x)$.

Teorema sobre el límite de una función monótona. Se proporciona una demostración del teorema utilizando dos métodos. También se dan definiciones de funciones estrictamente crecientes, no decrecientes, estrictamente decrecientes y no crecientes. Definición de función monótona.

Contenido

La función no está limitada desde arriba.

1.1. Sea finito el número b: .
1.1.2. Deje que la función no esté acotada arriba.

en .

Denotemos.
en .
Entonces para cualquiera lo hay, entonces

Esto significa que el límite a la izquierda en el punto b es (ver "Definiciones de límites infinitos unilaterales de una función en un punto final").

b temprano más infinito

La función está limitada desde arriba.
1. Deje que la función no disminuya en el intervalo.
1.2.1. Sea la función acotada arriba por el número M: para .

Demostremos que en este caso hay un límite.
.
Como la función está acotada arriba, hay un supremo finito
;
Según la definición de límite superior exacto, se cumplen las siguientes condiciones:
.

Para cualquier positivo hay un argumento para el cual
en .

Dado que la función no disminuye, entonces cuando .
en .
Luego a las .

La función no está limitada desde arriba.

La función está limitada desde arriba.
O
Entonces encontramos que para cualquier persona hay un número, entonces
1.2.1. Sea la función acotada arriba por el número M: para .

"Definiciones de límites unilaterales en el infinito").
.

1.2. Sea el número b igual a más infinito: .

1.2.2. Deje que la función no esté acotada arriba.
en .
Dado que la función no está acotada arriba, entonces para cualquier número M existe un argumento para el cual

Dado que la función no disminuye, entonces cuando .

Luego a las .

Entonces, para cualquiera hay un número, entonces
.
Esto significa que el límite en es igual a (ver "Definiciones de límites infinitos unilaterales en el infinito").
;
La función no es creciente.
.
Consideremos ahora el caso en el que la función no aumenta. Puede, como se indicó anteriormente, considerar cada opción por separado. Pero los cubriremos de inmediato. Para esto utilizamos . Demostremos que en este caso hay un límite.

Considere el mínimo finito del conjunto de valores de la función:
en .
Aquí B puede ser un número finito o un punto en el infinito.
en .
Según la definición de límite inferior exacto, se cumplen las siguientes condiciones:

para cualquier vecindad del punto B existe un argumento para el cual
en .
Según las condiciones del teorema, .

Es por eso .

Dado que la función no aumenta, entonces cuando .

Ahora demostraremos que existe un límite en el punto a y encontraremos su valor.

Consideremos la función. -1 Según las condiciones del teorema, la función es monótona para .

Reemplacemos la variable x con - x (o hagamos una sustitución y luego reemplacemos la variable t con x ). Entonces la función es monótona para .
.
Multiplicar desigualdades por
.

y cambiando su orden llegamos a la conclusión de que la función es monótona para .
.

De manera similar, es fácil demostrar que si no disminuye, entonces no aumenta. Entonces, según lo demostrado anteriormente, existe un límite
(1) .
Si no aumenta, no disminuye. En este caso hay un límite
.
Ahora queda demostrar que si hay un límite de una función en , entonces hay un límite de la función en , y estos límites son iguales:
en .

Introduzcamos la notación:
en .
Expresemos f en términos de g:
en .
Tomemos un número positivo arbitrario.
en .

Sea una vecindad épsilon del punto A.
La vecindad épsilon se define para valores finitos e infinitos de A (ver "Vecindad de un punto"). Dado que existe un límite (1), entonces, de acuerdo con la definición de límite, para cualquiera existe tal que
La vecindad épsilon se define para valores finitos e infinitos de A (ver "Vecindad de un punto"). Dado que existe un límite (1), entonces, de acuerdo con la definición de límite, para cualquiera existe tal que
La vecindad épsilon se define para valores finitos e infinitos de A (ver "Vecindad de un punto"). Dado que existe un límite (1), entonces, de acuerdo con la definición de límite, para cualquiera existe tal que
en .

Sea a un número finito. Expresemos la vecindad perforada por la izquierda del punto -a usando las desigualdades:
en .
Reemplacemos x por -x y tengamos en cuenta que:
.

Las dos últimas desigualdades definen la vecindad derecha perforada del punto a.

Entonces

Sea a un número infinito, .

Repetimos el razonamiento.

en ; Entonces, encontramos que para cualquier persona existe tal que Esto significa que El teorema ha sido demostrado. Ver también: El concepto de función. Funciones limitadas. Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función.(Funciones limitadas e ilimitadas.) | La función se llama limitado , si existe un número tan positivo METRO qué |.

METRO para todos los valores X. Si tal número no existe, entonces la función es ilimitado(- X) = Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función. (X EJEMPLOS. Funciones pares, impares, monótonas. Funciones pares e impares. Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función.(- X) = - Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función. (X EJEMPLOS. Si por cualquier x desde el dominio de definición de la función se cumple lo siguiente: F ), entonces la función se llama incluso; si sucede:

extraño. Gráfica de una función par X simétrico respecto al eje Y X(Fig.5), una gráfica de una función impar X 2 >Funciones limitadas e ilimitadas. simétrico sobre Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función.(Funciones limitadas e ilimitadas. 2 ) >ilimitado(Funciones limitadas e ilimitadas. origen ilimitado(Funciones limitadas e ilimitadas.) (Figura 6). Función monótona. Si para dos valores cualesquiera del argumento X simétrico respecto al eje Y X(Fig.5), una gráfica de una función impar X 2 >Funciones limitadas e ilimitadas. simétrico sobre Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función.(Funciones limitadas e ilimitadas. 2 ) <ilimitado(Funciones limitadas e ilimitadas. 1 1 y Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función.(Funciones limitadas e ilimitadas. 2 de la condición 1 sigue. Una función que solo aumenta o solo disminuye se llama monótono.

3. Secuencias numéricas. Definición y ejemplos.

Diremos que la variable X Hay variable ordenada, si se conoce el área de su cambio, y para cada uno de dos de sus valores se puede decir cuál es el anterior y cuál es el siguiente. Un caso especial de cantidad variable ordenada es una cantidad variable cuyos valores forman secuencia numérica x 1 ,x 2 ,…,x n ,… Para tales valores en i< j, i, j Î N , significado xyo se considera antecedente, y xj– posterior independientemente de cuál de estos valores sea mayor. Por tanto, una secuencia numérica es una variable cuyos valores sucesivos pueden renumerarse. Denotaremos una secuencia numérica por . Los números individuales en una secuencia se llaman sus elementos.

Por ejemplo, la secuencia numérica está formada por las siguientes cantidades:

3. , donde a, d– números constantes.

Límite de secuencia numérica.

Número a llamado límite secuencias X = {xn), si para un número positivo arbitrariamente predeterminado arbitrariamente pequeño ε existe tal número natural norte que delante de todos norte>norte la desigualdad |x n - a|< ε.

si el numero a hay un límite de secuencia X = {xn), entonces dicen que xn se esfuerza por a, y escribe.

Para formular esta definición en términos geométricos, introducimos el siguiente concepto. Barrio del punto x 0 se llama intervalo arbitrario ( a, b), que contiene este punto dentro de sí mismo. La vecindad de un punto a menudo se considera x0, para cual x0 es el medio, entonces x0 llamado centro barrio, y el valor ( b–a)/2 – radio vecindario.

Entonces, descubramos qué significa geométricamente el concepto de límite de una secuencia numérica. Para hacer esto, escribimos la última desigualdad de la definición como Esta desigualdad significa que todos los elementos de la secuencia con números norte>norte debe estar en el intervalo (a – ε; a + ε).

Por lo tanto, un número constante a hay un límite para la secuencia numérica ( xn), si para cualquier vecindario pequeño centrado en el punto a radio ε (ε es la vecindad del punto a) existe tal elemento de la secuencia con número norte que todos los elementos siguientes estén numerados norte>norte se ubicará dentro de esta vecindad.

Ejemplos.

1. Sea la variable X toma valores secuencialmente

Demostremos que el límite de esta secuencia numérica es igual a 1. Tomemos un número positivo arbitrario ε. Necesitamos encontrar un número tan natural. norte que delante de todos norte>norte se mantiene la desigualdad | xn - 1| < ε. Действительно, т.к.

entonces para satisfacer la relación |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве norte cualquier número natural que satisfaga la desigualdad, obtenemos lo que necesitamos. Entonces, si tomamos, por ejemplo, entonces, poniendo norte= 6, para todos norte>6 tendremos.

2. Utilizando la definición del límite de una secuencia numérica, demuestre que .

Tomemos un ε > 0 arbitrario. Consideremos entonces, si o, es decir, . Por tanto, elegimos cualquier número natural que satisfaga la desigualdad.

Ejemplos.

3. Consideremos. En x→1 el numerador de la fracción tiende a 1 y el denominador tiende a 0. Pero desde entonces, es decir es una función infinitesimal en x→ 1, entonces

Teorema 4. Sean tres funciones f(x), u(x) Y v(x), satisfaciendo las desigualdades u (x)≤f(x)≤v(x). Si las funciones tu(x) Y v(x) tener el mismo límite en x→a(o x→∞), entonces la función f(x) tiende al mismo límite, es decir Si

Teorema 5. Estoy gordo x→a(o x→∞) función y=f(x) acepta valores no negativos y≥0 y al mismo tiempo tiende al límite b, entonces este límite no puede ser negativo: b≥0.

Prueba. Realizaremos la prueba por contradicción. pretendamos que b<0 , Entonces |y – b|≥|b| y, por lo tanto, el módulo de diferencia no tiende a cero cuando x→a. Pero entonces y no llega al limite b en x→a, lo que contradice las condiciones del teorema.

Teorema 6. Si dos funciones f(x) Y gramo(x) para todos los valores del argumento X satisfacer la desigualdad f(x)≥ g(x) y tienen límites, entonces la desigualdad se cumple b≥c.

Prueba. Según las condiciones del teorema. f(x)-g(x) ≥0, por lo tanto, por el Teorema 5, o .

6. Revelación de incertidumbre (0/0), ∞ -∞

I. Incertidumbre.

Al factorizar el numerador, usamos la regla de dividir un polinomio por un polinomio por un "ángulo". Desde el número X=1 es la raíz del polinomio x3 – 6x2 + 11X– 6, entonces al dividir obtenemos

7. Límite de secuencia . El concepto de logaritmo natural.

EL SEGUNDO LÍMITE NOTABLE

Ejemplos:

Logaritmo a base mi (mi- un número trascendental aproximadamente igual a 2,718281828...) se llama logaritmo natural. Logaritmo natural de un número X denotado en X. Los logaritmos naturales se utilizan ampliamente en cálculos matemáticos, físicos y de ingeniería.

Los logaritmos se utilizan ampliamente.

base, llamada natural. Los logaritmos naturales se indican con el símbolo

El concepto de límite de una función.

El concepto de continuidad de una función está directamente relacionado con el concepto de límite de una función.

Un número A se llama límite de una función f en un punto a, límite de un conjunto E, si para cualquier vecindad V(A) del punto A, existe una vecindad perforada del punto a tal que su imagen bajo el mapeo f es un subconjunto de la vecindad dada V(A) del punto A.

El límite de una función f en un punto a, límite para el conjunto E, se denota como sigue: o, si se puede omitir la mención del conjunto E.

Dado que cada vecindad puede asociarse con su propia vecindad regular (simétrica), la definición del límite se puede formular en el lenguaje -δ como es habitual en el análisis matemático:

El límite de una función en un punto f en un punto a, el límite del conjunto E, está directamente relacionado con el límite de la secuencia.

Consideraremos todas las posibles secuencias de puntos del conjunto E que tienen el punto a como límite, y las correspondientes secuencias de valores de funciones en los puntos de la secuencia. Si existe un límite de una función f en el punto a, entonces este límite será el límite de cada secuencia.

Lo contrario también es cierto: si todas las secuencias convergen al mismo valor, entonces la función tiene un límite igual a ese valor.

EL PRIMER LÍMITE DESTACABLE

Función no definida cuando X=0, ya que el numerador y denominador de la fracción se vuelven cero. La gráfica de la función se muestra en la figura.

Sin embargo, es posible encontrar el límite de esta función cuando X→0.

Demos una prueba de la fórmula escrita. Considere un círculo de radio 1 y suponga que el ángulo α, expresado en radianes, está contenido dentro de 0< α < π/2. (Так как четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α >0.) De la figura queda claro que

SΔOAC .

Dado que las áreas indicadas son respectivamente iguales

SΔOAC=0,5∙JEFE.∙O.A.∙pecado α= 0,5 senα, Secta S. OAC = 0,5∙JEFE. 2 ∙α=0.5α, SΔOBC=0,5∙JEFE.∙antes de Cristo= 0,5tgα.

Por eso,

pecado α< α < tg α.

Dividamos todos los términos de la desigualdad por sen α > 0: .

Pero . Por lo tanto, basándonos en el Teorema 4 sobre límites, concluimos que la fórmula derivada se denomina primer límite destacable.

Así, el primer límite destacable sirve para revelar incertidumbre. Tenga en cuenta que la fórmula resultante no debe confundirse con los límites Ejemplos.

11.Límite y sus límites asociados.

EL SEGUNDO LÍMITE NOTABLE

El segundo límite notable sirve para revelar la incertidumbre de 1 ∞ y se ve así:

Prestemos atención a que en la fórmula del segundo límite notable, el exponente debe contener una expresión inversa a la que se suma a la unidad en la base (ya que en este caso es posible introducir un cambio de variables y reducir el límite buscado al segundo límite destacable)

Ejemplos.

1. Función f(x)=(X-1) 2 es infinitesimal en X→1, ya que (ver figura).

2. Función f(x)= tg X– infinitesimal en X→0.

3. f(x)= iniciar sesión(1+ X) – infinitesimal en X→0.

4. f(x) = 1/X– infinitesimal en X→∞.

Establezcamos la siguiente relación importante:

Teorema. Si la función y=f(x) representable con x→a como suma de un número constante b y magnitud infinitesimal α(x): f (x)=b+ α(x) Eso .

Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a.

Prueba.

1. Probemos la primera parte del enunciado. Desde la igualdad f(x)=b+a(x) debería |f(x) – b|=| α|. Pero desde hacha) es infinitesimal, entonces para ε arbitrario hay δ – una vecindad del punto a, en frente de todos X de donde, valores hacha) satisfacer la relación |α(x)|< ε. Entonces |f(x) – b|< ε. Y esto significa que.

2. Si , entonces para cualquier ε >0 para todos X desde algún δ - vecindad de un punto a voluntad |f(x) – b|< ε. Pero si denotamos f(x) – b= α, Eso |α(x)|< ε, lo que significa que a– infinitesimal.

Consideremos las propiedades básicas de las funciones infinitesimales.

Teorema 1. La suma algebraica de dos, tres y en general cualquier número finito de infinitesimales es una función infinitesimal.

Prueba. Demos una prueba para dos términos. Dejar f(x)=α(x)+β(x), dónde y . Necesitamos demostrar que para ε arbitrariamente pequeño > 0 encontrado δ> 0, tal que para X, satisfaciendo la desigualdad |x – un |<δ , realizado |f(x)|< ε.

Entonces, arreglemos un número arbitrario ε > 0. Dado que según las condiciones del teorema a(x) es una función infinitesimal, entonces existe tal δ 1 > 0, que es |x – a|< δ 1 tenemos |α(x)|< ε / 2. Asimismo, desde β(x) es infinitesimal, entonces existe tal δ 2 > 0, que es |x – a|< δ 2 tenemos | β(x)|< ε / 2.

Echemos δ=mín(δ 1 , δ2 } .Luego en las proximidades del punto a radio δ cada una de las desigualdades será satisfecha |α(x)|< ε / 2 y | β(x)|< ε / 2. Por lo tanto, en este barrio habrá

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

aquellos. |f(x)|< ε, que es lo que había que demostrar.

Teorema 2. Producto de una función infinitesimal hacha) para una función limitada f(x) en x→a(o cuando x→∞) es una función infinitesimal.

Prueba. Desde la función f(x) es limitado, entonces hay un número METRO tal que para todos los valores X desde algún barrio de un punto a|f(x)|≤M. Es más, desde hacha) es una función infinitesimal en x→a, entonces para un ε arbitrario > 0 hay una vecindad del punto a, en el que la desigualdad se mantendrá |α(x)|< ε /METRO. Luego, en el más pequeño de estos barrios tenemos | αf|< ε /METRO= ε. Y esto significa que af– infinitesimal. Para la ocasión x→∞ la prueba se realiza de manera similar.

Del teorema probado se sigue:

Corolario 1. Si y , entonces

Corolario 2. Si c= constante, entonces.

Teorema 3. Razón de una función infinitesimal a(x) por función f(x), cuyo límite es distinto de cero, es una función infinitesimal.

Prueba. Dejar . Entonces 1 /f(x) hay una función limitada. Por tanto, una fracción es el producto de una función infinitesimal y una función limitada, es decir la función es infinitesimal.

Ejemplos.

1. Está claro que cuando x→+∞ función y=x 2 + 1 es infinitamente grande. Pero entonces, según el teorema formulado anteriormente, la función es infinitesimal en x→+∞, es decir. .

También se puede demostrar el teorema inverso.

Teorema 2. Si la función f(x)- infinitesimal en x→a(o x→∞) y no desaparece, entonces y= 1/f(x) es una función infinitamente grande.

Realice usted mismo la prueba del teorema.

Ejemplos.

3. , ya que las funciones y son infinitesimales en x→+∞, entonces, como la suma de funciones infinitesimales es una función infinitesimal. Una función es la suma de un número constante y una función infinitesimal. En consecuencia, por el Teorema 1 para funciones infinitesimales obtenemos la igualdad requerida.

Por tanto, las propiedades más simples de funciones infinitesimales e infinitamente grandes se pueden escribir utilizando las siguientes relaciones condicionales: A≠ 0

13. Funciones infinitesimales del mismo orden, infinitesimales equivalentes.

Funciones infinitesimales y se llaman infinitesimales del mismo orden de pequeñez si , denota . Y finalmente, si no existe, entonces las funciones infinitesimales son incomparables.

EJEMPLO 2. Comparación de funciones infinitesimales

Funciones infinitesimales equivalentes.

Si , entonces se llaman funciones infinitesimales equivalente, denota ~ .

Funciones localmente equivalentes:

Cuando si

Algunas equivalencias(en ):

Límites unilaterales.

Hasta ahora hemos considerado determinar el límite de una función cuando x→a de manera arbitraria, es decir el límite de la función no dependía de cómo se ubicara X hacia a, a la izquierda o a la derecha de a. Sin embargo, es bastante común encontrar funciones que no tienen límite bajo esta condición, pero sí tienen límite si x→a, quedando a un lado de A, izquierda o derecha (ver figura). Por tanto, se introducen los conceptos de límites unilaterales.

Si f(x) tiende al límite b en X tendiendo a un cierto número a Entonces X acepta solo valores menores que a, luego escriben y llaman blímite de la función f(x) en el punto a de la izquierda.

entonces el numero b llamado límite de la función y=f(x) en x→a a la izquierda, si sea cual sea el número positivo ε, existe tal número δ (menor a

Asimismo, si x→a y adquiere grandes valores a, luego escriben y llaman b límite de la función en el punto A a la derecha. Aquellos. número b llamado límite de la función y=f(x) como x→a a la derecha, si sea cual sea el número positivo ε, existe tal número δ (mayor A) que la desigualdad es válida para todos.

Tenga en cuenta que si los límites a la izquierda y a la derecha en el punto a para función f(x) no coinciden, entonces la función no tiene límite (bilateral) en el punto A.

Ejemplos.

1. Considere la función y=f(x), definido en el segmento de la siguiente manera

Encontremos los límites de la función. f(x) en x→ 3. Obviamente, y

En otras palabras, para cualquier número arbitrariamente pequeño de épsilon, existe un número delta que depende de épsilon tal que del hecho de que para cualquier x que satisfaga la desigualdad se deduce que las diferencias en los valores de la función en estos puntos serán arbitrariamente pequeño.

Criterio para la continuidad de una función en un punto.:

Función voluntad continuo en el punto A si y solo si es continuo en el punto A tanto por la derecha como por la izquierda, es decir, de modo que en el punto A hay dos límites unilaterales, son iguales entre sí e iguales al valor de la función en el punto A.

Definición 2: La función es continua. en un conjunto si es continuo en todos los puntos de este conjunto.

Derivada de una función en un punto

Dejemos que dana se defina en un vecindario. Consideremos

Si este límite existe, entonces se llama derivada de la función f en el punto .

Derivada de una función– el límite de la relación entre el incremento de la función y el incremento del argumento, cuando se incrementa el argumento.

La operación de calcular o encontrar la derivada en un punto se llama diferenciación .

Reglas de diferenciación.

Derivado funciones f(x) en el punto x=x 0 Se llama relación entre el incremento de una función en este punto y el incremento del argumento, ya que este último tiende a cero. Se llama encontrar la derivada. diferenciación. La derivada de una función se calcula según la regla general de derivación: denotemos f(x) = u, g(x) = v- funciones diferenciables en un punto X. Reglas básicas de diferenciación. 1) (la derivada de una suma es igual a la suma de sus derivadas) 2) (de aquí, en particular, se sigue que la derivada del producto de una función y una constante es igual al producto de la derivada de esta función y la constante) 3) Derivada de un cociente: , si g  0 4) Derivada de una función compleja: 5) Si la función se especifica paramétricamente: , entonces

Ejemplos.

1. y = X a es una función potencia con un exponente arbitrario.

Función implícita

Si una función está dada por la ecuación y=ƒ(x), resuelta con respecto a y, entonces la función está dada en forma explícita (función explícita).

Bajo tarea implícita Las funciones entienden la definición de una función en forma de ecuación F(x;y)=0, no resuelta con respecto a y.

Cualquier función dada explícitamente y=ƒ (x) puede escribirse como dada implícitamente por la ecuación ƒ(x)-y=0, pero no al revés.

No siempre es fácil, y a veces imposible, resolver una ecuación para y (por ejemplo, y+2x+cozy-1=0 o 2 y -x+y=0).

Si la función implícita viene dada por la ecuación F(x; y) = 0, entonces para encontrar la derivada de y con respecto a x no es necesario resolver la ecuación con respecto a y: basta con derivar esta ecuación con respecto a x, considerando y en función de x, y luego resuelve la ecuación resultante para y."

La derivada de una función implícita se expresa en términos del argumento x y la función y.

Ejemplo:

Encuentra la derivada de la función y, dada por la ecuación x 3 + y 3 -3xy = 0.

Solución: La función y se especifica implícitamente. Derivamos respecto de x la igualdad x 3 +y 3 -3xy=0. De la relación resultante

3x 2 +3y 2 y"-3(1 y+x y")=0

se deduce que y 2 y"-xy"=y-x 2, es decir, y"=(y-x 2)/(y 2 -x).

Derivados de orden superior

Está claro que la derivada

funciones y=f(x) También hay una función de X:

y" =f "(x)

Si la función f"(x) es diferenciable, entonces su derivada se denota con el símbolo y"" =f "" (x)x dos veces.
La derivada de la segunda derivada, es decir funciones y""=f""(x), llamado tercera derivada de la función y=f(x) o derivada de la función f(x) de tercer orden y está indicado por los símbolos

En absoluto norte-i derivada o derivada norte función de orden y=f(x) indicado por símbolos

Phil Leibniz:

Supongamos que las funciones y son diferenciables junto con sus derivadas hasta el enésimo orden inclusive. Aplicando la regla para derivar el producto de dos funciones, obtenemos

Comparemos estas expresiones con las potencias del binomio:

La regla de correspondencia es sorprendente: para obtener una fórmula para la derivada de primer, segundo o tercer orden del producto de funciones y , es necesario reemplazar las potencias y en la expresión para (donde norte= 1,2,3) derivadas de las órdenes correspondientes. Además, las potencias cero de las cantidades y deben sustituirse por derivadas de orden cero, es decir, las funciones y:

Generalizando esta regla al caso de derivadas de orden arbitrario norte, obtenemos La fórmula de Leibniz,

donde están los coeficientes binomiales:

Teorema de Rolle.

Este teorema permite encontrar puntos críticos y luego, utilizando condiciones suficientes, examinar la función en busca de extremos.

Sea 1) f(x) definida y continua en algún intervalo cerrado; 2) existe una derivada finita, al menos en el intervalo abierto (a;b); 3) en los extremos del intervalo f-i toma valores iguales f(a) = f(b). Entonces entre los puntos a y b hay un punto c tal que la derivada en este punto será = 0.

Según el teorema sobre la propiedad de funciones continuas en un intervalo, la función f(x) toma sus valores máximo y mínimo en este intervalo.

f(x 1) = M – máximo, f(x 2) = m – mínimo; x 1 ;x 2 О

1) Sea M = m, es decir m £ f(x) £ M

Þ f(x) tomará valores constantes en el intervalo de aby, y Þ su derivada será igual a cero. f’(x)=0

2) Sea M>m

Porque según las condiciones del teorema, f(a) = f(b) Þ tomará su valor más pequeño o más grande no en los extremos del segmento, sino que Þ tomará M o m en el punto interior de este segmento. Entonces, según el teorema de Fermat, f’(c)=0.

Teorema de Lagrange.

Fórmula de incremento finito o Teorema del valor medio de Lagrange afirma que si una función Definición de función: Si cada número x del conjunto de números D está asociado con un solo número y, entonces se dice que se da una función f en el conjunto D y se escribe y= f(x), donde x se llama variable independiente o argumento de esta función, y el conjunto D es el dominio de definición de esta función. es continua en el intervalo [ a;b] y diferenciable en el intervalo ( a;b), entonces hay un punto tal que

El teorema de Cauchy.

Si las funciones f(x) y g(x) son continuas en el intervalo y derivables en el intervalo (a, b) y g¢(x) ¹ 0 en el intervalo (a, b), entonces hay al menos una punto e, un< e < b, такая, что

Aquellos. la relación de incrementos de funciones en un segmento dado es igual a la relación de derivadas en el punto e. Ejemplos de cursos de conferencias sobre resolución de problemas Cálculo del volumen de un cuerpo a partir de áreas conocidas de sus secciones paralelas Cálculo integral

Ejemplos de trabajos de curso Ingenieria Eléctrica

Para demostrar este teorema, a primera vista es muy conveniente utilizar el teorema de Lagrange. Escribe una fórmula en diferencias finitas para cada función y luego divídelas entre sí. Sin embargo, esta idea es errónea, porque El punto e para cada función es generalmente diferente. Por supuesto, en algunos casos especiales este punto del intervalo puede resultar el mismo para ambas funciones, pero esto es una coincidencia muy rara, no una regla, y por lo tanto no puede usarse para probar el teorema.

Prueba. Considere la función auxiliar

Como x→x 0, el valor de c también tiende a x 0; Vayamos al límite en la igualdad anterior:

Porque , Eso .

Es por eso

(el límite de la razón de dos infinitesimales es igual al límite de la razón de sus derivadas, si esta última existe)

Regla de L'Hopital, en ∞/∞.

Tenga en cuenta: todas las definiciones involucran un conjunto numérico X, que es parte del dominio de la función: X con D(f). En la práctica, la mayoría de las veces hay casos en los que X es un intervalo numérico (segmento, intervalo, rayo, etc.).
Definición 1.
Se dice que una función y = f(x) es creciente en un conjunto X con D(f) si para dos puntos cualesquiera x 1 y x 2 del conjunto X tales que x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).
Definición 2.
Se dice que una función y = f(x) es decreciente en un conjunto X con D(f) si para dos puntos cualesquiera x 1 y x 2 del conjunto X tales que x 1< х 2 , функции выполняется неравенство f(x 1) >f(x2).
En la práctica, es más conveniente utilizar las siguientes formulaciones: una función aumenta si un valor mayor del argumento corresponde a un valor mayor de la función; una función disminuye si un valor mayor del argumento corresponde a un valor menor de la función.
En los grados 7 y 8 utilizamos la siguiente interpretación geométrica de los conceptos de aumento o disminución de una función: moviéndonos a lo largo de la gráfica de una función creciente de izquierda a derecha, parece que estamos subiendo una colina (Fig. 55); Moviéndonos a lo largo de la gráfica de una función decreciente de izquierda a derecha, es como si bajáramos una colina (Fig. 56).
Por lo general, los términos "función creciente" y "función decreciente" se combinan bajo el nombre general de función monótona, y el estudio de una función creciente o decreciente se denomina estudio de una función monotónica.
Observemos una circunstancia más: si una función aumenta (o disminuye) en su dominio natural de definición, generalmente decimos que la función aumenta (o disminuye), sin indicar el conjunto numérico X.
Ejemplo 1.
Examine la función para determinar la monotonicidad:
A) y = x 3 + 2; b) y = 5 - 2x.
Solución:
a) Tome valores arbitrarios del argumento x 1 y x 2 y sea x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

La última desigualdad significa que f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).
Entonces de x 1< х 2 следует f(х 1) >f(x 2), lo que significa que la función dada es decreciente (en toda la recta numérica).
Definición 3.
Se dice que una función y - f(x) está acotada desde abajo en un conjunto X con D(f) si todos los valores de la función en el conjunto X son mayores que un cierto número (en otras palabras, si hay un número m tal que para cualquier valor x є X la desigualdad f( x) >m).
Definición 4.
Se dice que una función y = f(x) está acotada desde arriba a un conjunto X con D(f) si todos los valores de la función son menores que un cierto número (en otras palabras, si hay un número M tal que para cualquier valor x є X se cumple la desigualdad f(x)< М).
Si no se especifica el conjunto X, entonces se entiende que estamos hablando de que la función está acotada desde abajo o desde arriba en todo el dominio de definición.
Si una función está acotada tanto por debajo como por arriba, entonces se llama acotada.
La acotación de una función se lee fácilmente en su gráfica: si una función está acotada desde abajo, entonces su gráfica está completamente ubicada por encima de una determinada línea horizontal y = m (Fig. 57); si una función está acotada desde arriba, entonces su gráfica está completamente ubicada debajo de alguna línea horizontal y = M (Fig. 58).

Ejemplo 2. Examinar la acotación de una función.
Solución. Por un lado, la desigualdad es bastante obvia (según la definición de raíz cuadrada, esto significa que la función está acotada por debajo. Por otro lado, tenemos y por lo tanto
Esto significa que la función tiene un límite superior. Ahora mire la gráfica de la función dada (Fig. 52 del párrafo anterior). La limitación de la función tanto arriba como abajo se puede leer con bastante facilidad en el gráfico.
Definición 5.
El número m se denomina valor más pequeño de la función y = f(x) en el conjunto X C D(f) si:
1) en X hay un punto x 0 tal que f(x 0) = m;
2) para todo x de X se cumple la desigualdad m>f(x 0).
Definición 6.
El número M se llama el valor más grande de la función y = f(x) en el conjunto X C D(f), si:
1) en X hay un punto x 0 tal que f(x 0) = M;
2) para todo x de X la desigualdad
Denotamos el valor más pequeño de una función tanto en el séptimo como en el octavo grado con el símbolo y, y el más grande con el símbolo y.
Si no se especifica el conjunto X, se supone que estamos hablando de encontrar el valor más pequeño o más grande de la función en todo el dominio de definición.
Las siguientes declaraciones útiles son bastante obvias:
1) Si una función tiene Y, entonces está acotada por debajo.
2) Si una función tiene Y, entonces está acotada arriba.
3) Si la función no está acotada por debajo, entonces Y no existe.
4) Si la función no está acotada arriba, entonces Y no existe.
Ejemplo 3.
Encuentra los valores más pequeño y más grande de una función.
Solución.
Es bastante obvio, especialmente si usa la gráfica de funciones (Fig. 52), que = 0 (la función alcanza este valor en los puntos x = -3 y x = 3), a = 3 (la función alcanza este valor en x = 0.
En séptimo y octavo grado mencionamos dos propiedades más de las funciones. La primera se llamó propiedad de convexidad de una función. Se considera que una función es convexa hacia abajo en un intervalo X si, conectando dos puntos cualesquiera de su gráfica (con abscisas de X) con un segmento de recta, encontramos que la parte correspondiente de la gráfica se encuentra debajo del segmento dibujado (Fig. 59). continuidad Una función es convexa hacia arriba en un intervalo X si, al conectar dos puntos cualesquiera de su gráfica (con abscisas de X) de la función con un segmento de recta, encontramos que la parte correspondiente de la gráfica se encuentra encima del segmento dibujado ( Figura 60).

La segunda propiedad, la continuidad de una función en el intervalo X, significa que la gráfica de la función en el intervalo X es continua, es decir No tiene pinchazos ni saltos.
Comentario.
De hecho, en matemáticas todo es, como dicen, “exactamente al revés”: la gráfica de una función se representa como una línea continua (sin pinchazos ni saltos) sólo cuando se demuestra la continuidad de la función. Pero aún no está a nuestro alcance una definición formal de la continuidad de una función, que es bastante compleja y sutil. Lo mismo puede decirse de la convexidad de una función. Cuando analicemos estas dos propiedades de las funciones, seguiremos confiando en conceptos visuales e intuitivos.
Ahora revisemos nuestro conocimiento. Recordando las funciones que estudiamos en 7º y 8º grado, aclaremos cómo son sus gráficas y enumeremos las propiedades de la función, siguiendo un orden determinado, por ejemplo este: dominio de definición; monótono; limitación; , ; continuidad; rango; convexo.
Posteriormente, aparecerán nuevas propiedades de funciones y la lista de propiedades cambiará en consecuencia.
1. Función constante y = C
La gráfica de la función y = C se muestra en la Fig. 61 - línea recta, paralela al eje x. Esta es una característica tan poco interesante que no tiene sentido enumerar sus propiedades.

La gráfica de la función y = kx + m es una línea recta (Fig. 62, 63).

Propiedades de la función y = kx + m:
1)
2) aumenta si k > 0 (Fig. 62), disminuye si k< 0 (рис. 63);

4) no existe ni el valor mayor ni el menor;
5) la función es continua;
6)
7) no tiene sentido hablar de convexidad.

La gráfica de la función y = kx 2 es una parábola con un vértice en el origen y con ramas dirigidas hacia arriba si k > O (Fig. 64), y hacia abajo si k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.
Propiedades de la función y - kx 2:
Para el caso k> 0 (Fig.64):
1) D(f) = (-oo,+oo);

4) = no existe;
5) continuo;
6) E(f) = la función disminuye, y en el intervalo, disminuye en el rayo;
7) convexo hacia arriba.
La gráfica de la función y = f(x) se traza punto por punto; Cuantos más puntos de la forma (x; f(x)) tomemos, más precisa será la idea de la gráfica que obtendremos. Si toma muchos de estos puntos, obtendrá una imagen más completa del gráfico. Es en este caso que la intuición nos dice que la gráfica debe representarse como una línea continua (en este caso, en forma de parábola). Y luego, leyendo el gráfico, sacamos conclusiones sobre la continuidad de la función, sobre su convexidad hacia abajo o hacia arriba, sobre el rango de valores de la función. Debe comprender que de las siete propiedades enumeradas, solo las propiedades 1), 2), 3), 4) son "legítimas" - "legítimas" en el sentido de que podemos justificarlas refiriéndonos a definiciones precisas. Sobre las propiedades restantes sólo tenemos ideas visuales e intuitivas. Por cierto, esto no tiene nada de malo. De la historia del desarrollo de las matemáticas se sabe que la humanidad utilizó a menudo y durante mucho tiempo diversas propiedades de ciertos objetos, sin conocer las definiciones exactas. Luego, cuando se pudieron formular tales definiciones, todo encajó.

La gráfica de la función es una hipérbola, los ejes de coordenadas sirven como asíntotas de la hipérbola (Fig. 66, 67).
1) D(f) = (-00,0)1U (0,+oo);
2) si k > 0, entonces la función disminuye en el rayo abierto (-oo, 0) y en el rayo abierto (0, +oo) (Fig. 66); si a< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) no está limitado ni desde abajo ni desde arriba;
4) no existe ni el valor más pequeño ni el más grande;
5) la función es continua en el rayo abierto (-oo, 0) y en el rayo abierto (0, +oo);
6) E(f) = (-oo,0) U (0,+oo);
7) si k > 0, entonces la función es convexa hacia arriba en x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, es decir en la viga abierta (0, +oo) (Fig. 66). Si a< 0, то функция выпукла вверх при х >O y convexo hacia abajo en x< О (рис. 67).
La gráfica de la función es una rama de una parábola (Fig. 68). Propiedades de la función:
1) D(f) = , aumenta en el rayo )