Wpisany okrąg. Okrąg wokół trójkąta Trójkąt wokół koła

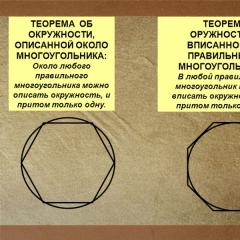
TWIERDZENIE O KRĘGU OPISANO O WIELOKANIE: W pobliżu dowolnego wielokąta foremnego okrąg może być opisany, a co więcej, tylko jeden. TWIERDZENIE O BRONI WSTAWIONEJ W REGULARNY WIELOKĄT: W dowolny regularny wielokąt można wpisać okrąg, a co więcej, tylko jeden.

SPa4a4 rRN Obliczanie powierzchni wielokąta foremnego, jego boku oraz promienia okręgu wpisanego i promienia okręgu wpisanego

Pola wielokątów foremnych Pola wielokątów foremnych NAZWY I OBSZARY WIELOKĄTÓW Liczba boków Nazwa wielokąta Pole wielokąta foremnego 3 Trójkąt0.433a 2 4 Czworokąt 1.000a 2 5Pentagon1.720a 2 6Sześciokąt2.598a 2 7Ośmiokąt 2.7a2.8a3 0,634 kwadrat

0 wpisanych narożników. Hipokrates z Chios Dowód we współczesnych podręcznikach, że wpisany kąt jest mierzony przez połowę łuku, na którym się on opiera, podany jest w Elementach Euklidesa. Jednak Hipokrates z Chios (V wiek pne) odwołuje się do tej propozycji w swojej pracy o „dziurach”. Z dzieł Hipokratesa wynika, że ​​już w drugiej połowie V wieku. pne mi. Znana była duża liczba twierdzeń przedstawionych w „Zasadach” Euklidesa, a geometria osiągnęła wysoki poziom rozwoju. To, że wpisany kąt opiera się na średnicy, Babilończycy znali 4000 lat temu. Pierwszy tego dowód przypisuje się Pamfilii, pisarzowi rzymskiemu z czasów Nerona, Talesowi z Miletu.

0 regularne wielokąty Regularne czworokąty, sześciokąty i ośmiokąty występują w starożytnych egipskich i babilońskich zabytkach w postaci obrazów na ścianach i ornamentów wykutych w kamieniu. Starożytni greccy naukowcy zaczęli wykazywać duże zainteresowanie prawidłowymi liczbami od czasów Pitagorasa. Podział koła na kilka równych części w celu zbudowania regularnych wielokątów był ważny dla pitagorejczyków, którzy twierdzili, że liczby są podstawą wszystkich zjawisk na świecie. Doktryna regularnych wielokątów, zapoczątkowana w szkole Pitagorasa, była kontynuowana i rozwijana w VI wieku. pne e., został usystematyzowany przez Euklidesa i zamieszczony w IV księdze „Początków”. Oprócz skonstruowania regularnego trójkąta, czworokąta, pięciokąta i sześciokąta, Euclid rozwiązuje również problem skonstruowania regularnego piętnastokąta przy użyciu jedynie cyrkla i linijki. Ta figura przyciągnęła uwagę starożytnych, ponieważ zauważono, że łuk kąta nachylenia ekliptyki do równika reprezentuje całe koło, to znaczy jest ściągnięty bokiem regularnej piętnastki.

ABC O1 O2 O1 - środek okręgu opisanego, O2 - środek okręgu wpisanego Konieczność: Dość: D AB + CD = BC + AD a więc AB = CD = BAD = ADC, ale BAD + ABC = 180 Stąd ADC + ABC = 180 , a wokół trapezu ABCD można opisać okrąg. Dodatkowo AB + CD = BC + AD, a zatem okrąg można wpisać w ABCD. Konieczne i wystarczające jest, aby trapez był równoboczny, a bok był równy połowie sumy podstaw.

Definicja 2

Wielokąt spełniający warunek z Definicji 1 nazywany jest opisanym wokół okręgu.

Rysunek 1. Wpisany okrąg

Twierdzenie 1 (na okręgu wpisanym w trójkąt)

Twierdzenie 1

W dowolnym trójkącie możesz wpisać okrąg, a ponadto tylko jeden.

Dowód.

Rozważ trójkąt $ ABC $. Narysujmy w nim dwusieczne, które przecinają się w punkcie $O $ i narysujmy z niego prostopadłe do boków trójkąta (ryc. 2)

Rysunek 2. Ilustracja twierdzenia 1

Istnienie: Narysuj okrąg o środku w punkcie $ O $ i promieniu $ OK \ $ Ponieważ punkt $ O $ leży na trzech dwusiecznych, jest w równej odległości od boków trójkąta $ ABC $. Oznacza to, że $ OM = OK = OL $. Dlatego skonstruowany okrąg przechodzi również przez punkty $ M \ i \ L $. Ponieważ $ OM, OK \ i \ OL $ są prostopadłe do boków trójkąta, to zgodnie z twierdzeniem o stycznej do okręgu skonstruowany okrąg dotyka wszystkich trzech boków trójkąta. Dlatego ze względu na arbitralność trójkąta okrąg można wpisać w dowolny trójkąt.

Niepowtarzalność: Załóżmy, że jeszcze jeden okrąg można wpisać w trójkąt $ABC $ o środku w punkcie $O "$. Jego środek jest równoodległy od boków trójkąta, a zatem pokrywa się z punktem $O $ i ma promień równy długości $ OK $ Ale wtedy ten okrąg będzie się pokrywał z pierwszym.

Twierdzenie jest udowodnione.

Wniosek 1: Środek koła wpisanego w trójkąt leży w miejscu przecięcia jego dwusiecznych.

Oto kilka innych faktów związanych z koncepcją okręgu wpisanego:

Nie każdy czworokąt można wpisać w okrąg.

W każdym opisanym czworoboku sumy przeciwległych boków są równe.

Jeśli sumy przeciwległych boków czworoboku wypukłego są równe, można w niego wpisać okrąg.

Definicja 3

Jeśli wszystkie wierzchołki wielokąta leżą na okręgu, wówczas okrąg nazywa się opisany wielokątem (ryc. 3).

Definicja 4

Wielokąt spełniający warunek Definicji 2 nazywamy wpisanym w okrąg.

Rysunek 3. Zakreślony okrąg

Twierdzenie 2 (na kole opisanym wokół trójkąta)

Twierdzenie 2

Wokół dowolnego trójkąta możesz opisać okrąg, a ponadto tylko jeden.

Dowód.

Rozważ trójkąt $ ABC $. Rysujemy w nim prostopadłe przecinające się w punkcie $ O $ i łączymy je z wierzchołkami trójkąta (ryc. 4)

Rysunek 4. Ilustracja twierdzenia 2

Istnienie: Skonstruuj okrąg o środku $ O $ i promieniu $ OC $. Punkt $ O $ jest w równej odległości od wierzchołków trójkąta, czyli $ OA = OB = OC $. Dlatego skonstruowany okrąg przechodzi przez wszystkie wierzchołki tego trójkąta, co oznacza, że ​​jest opisany wokół tego trójkąta.

Wyjątkowość: Załóżmy, że wokół trójkąta $ABC $ można opisać jeszcze jeden okrąg ze środkiem w punkcie $O "$. Jego środek jest równoodległy od wierzchołków trójkąta, a zatem pokrywa się z punktem $O $ i ma promień równy długości $ OC $ Ale wtedy ten okrąg będzie się pokrywał z pierwszym.

Twierdzenie jest udowodnione.

Wniosek 1: Środek okręgu opisanego wokół trójkąta pokrywa się z punktem przecięcia jego pionów środkowych.

Oto kilka innych faktów związanych z koncepcją koła ograniczonego:

Nie zawsze można opisać okrąg wokół czworoboku.

W każdym czworoboku wpisanym suma kątów przeciwnych wynosi $ (180) ^ 0 $.

Jeżeli suma przeciwnych kątów czworokąta wynosi $ (180) ^ 0 $, to wokół niego można opisać okrąg.

Przykład problemu z pojęciami koła wpisanego i opisanego

Przykład 1

W trójkącie równoramiennym podstawa ma 8 cm, bok boczny 5 cm Znajdź promień wpisanego koła.

Rozwiązanie.

Rozważ trójkąt $ ABC $. Z wniosku 1 wiemy, że środek okręgu wpisanego leży na przecięciu dwusiecznych. Narysujmy dwusieczne $AK $ i $BM $, które przecinają się w punkcie $O $. Narysuj prostopadłą $ OH $ od punktu $ O $ do boku $ BC $. Narysujmy obrazek:

Rysunek 5.

Ponieważ trójkąt jest równoramienny, to $BM $ jest zarówno medianą, jak i wysokością. Według twierdzenia Pitagorasa $ (BM) ^ 2 = (BC) ^ 2- (MC) ^ 2, \ BM = \ sqrt ((BC) ^ 2- \ frac ((AC) ^ 2) (4)) = \ sqrt (25-16) = \ sqrt (9) = 3 $. $ OM = OH = r $ - wymagany promień okręgu wpisanego. Ponieważ $ MC $ i $ CH $ są odcinkami przecinających się stycznych, to z twierdzenia o przecinającej się stycznej mamy $ CH = MC = 4 \ cm $. Dlatego $ BH = 5-4 = 1 \ cm $. $ BO = 3-r $. Z trójkąta $ OHB $, przez twierdzenie Pitagorasa, otrzymujemy:

\ [((3-r)) ^ 2 = r ^ 2 + 1 \] \ \ \

Odpowiedź:$ \ frac (4) (3) $.

W tej lekcji przypomnimy podstawy, na których opiera się teoria okręgów wpisanych i opisanych, przypomnimy znaki czworokątów wpisanych i wpisanych. Ponadto wyprowadzimy wzory na znalezienie promieni okręgów opisanych i wpisanych w różnych przypadkach.

Motyw: koło

Lekcja: Wpisane i zakreślone koła

Przede wszystkim mówimy o okręgach wpisanych i opisanych względem trójkąta. Jesteśmy przygotowani na ten temat, ponieważ badaliśmy właściwości dwusiecznych i prostopadłych trójkąta.

Okrąg można wpisać w dowolny trójkąt (patrz rys. 1).

Ryż. jeden

Dowód:

Wiemy, że wszystkie dwusieczne trójkąta przecinają się w jednym punkcie - niech w punkcie O. Narysuj dwusieczne AO, BO, CO. Punkt ich przecięcia O jest równoodległy od boków trójkąta. Jest w równej odległości od boków kąta - AC i AB, ponieważ należy do dwusiecznej tego kąta. Podobnie jest w równej odległości od boków rogów, a więc od trzech boków trójkąta.

Opuśćmy prostopadłe z punktu O na boki trójkąta - OM na stronę AC, OL na BC, OK na AB. Te prostopadłe będą odległościami od punktu O do boków trójkąta i są równe:

.

Oznaczmy odległość od punktu O do boków trójkąta jako r i rozważmy okrąg o środku w punkcie O i promieniu r.

Okrąg dotyka linii AB, ponieważ ma z nim wspólny punkt K, a promień OK narysowany do tego punktu jest prostopadły do ​​prostej AB. Podobnie okrąg dotyka linii AC i BC. W ten sposób okrąg dotyka wszystkich boków trójkąta, co oznacza, że ​​jest wpisany w trójkąt.

Tak więc trzy dwusieczne trójkąta przecinają się w punkcie, który jest środkiem wpisanego koła.

Rozważ jeszcze jedno twierdzenie, dotyczy ono punktu przecięcia środkowych prostopadłych trójkąta. Wiemy, że przecinają się one w jednym punkcie, a ten punkt pokrywa się ze środkiem okręgu opisanego wokół trójkąta.

Okrąg można opisać wokół dowolnego trójkąta.

Tak więc podany jest trójkąt. Narysujmy punkt środkowy prostopadle p 1 do boku trójkąta BC, p 2 - do boku AB, p 3 - do boku AC (patrz rys. 2).

Zgodnie z twierdzeniem o własnościach pionów środkowych, punkt należący do pionu środkowego do odcinka znajduje się w równej odległości od końców odcinka. Stąd, ponieważ punkt Q należy do punktu środkowego prostopadłego do odcinka AC. Podobnie i. Zatem punkt Q jest w równej odległości od wierzchołków trójkąta. Stąd QA, QB, QC są promieniami

Ryż. 2

okrąg opisany wokół trójkąta. Oznaczmy promień przez R. Punkt O przecięcia pionów środkowych jest środkiem okręgu opisanego.

Rozważ okrąg wpisany w pewien czworokąt i właściwości tego czworokąta (patrz ryc. 3).

Przypomnijmy własności punktu leżącego na dwusiecznej kąta.

Podano kąt, jego dwusieczna jest AL, punkt M leży na dwusiecznej.

Jeżeli punkt M leży na dwusiecznej kąta, to jest w równej odległości od boków kąta, to znaczy odległości od punktu M do AC i BC boków kąta są równe.

Ryż. 3

Odległość od punktu do linii prostej to długość prostopadłej. Narysujmy z punktu M prostopadłe MK do strony AB i MP do strony AC.

Rozważ trójkąty i. Są to trójkąty prostokątne i są równe, ponieważ mają wspólną przeciwprostokątną AM, a kąty i są równe, ponieważ AL jest dwusieczną kąta. Zatem trójkąty prostokątne są równe w przeciwprostokątnej i kącie ostrym, z czego wynika, zgodnie z wymaganiami. Zatem punkt na dwusiecznej kąta jest równoodległy od boków tego kąta.

Dodatkowo nogawki. Zatem odcinki stycznych narysowanych do okręgu z jednego punktu są równe.

Wróćmy więc do czworoboku. Pierwszą czynnością jest narysowanie w nim dwusiecznych.

Wszystkie dwusieczne czworokąta przecinają się w jednym punkcie - punkcie O, środku wpisanego koła.

Od punktu O obniżamy prostopadłe do boków czworokąta do punktów K, L, M, N i wyznaczamy punkty styczności (patrz rys. 3).

Styczne narysowane do okręgu z jednego punktu są sobie równe, a zatem z każdego wierzchołka wyłania się para równych stycznych: ,,,.

Ryż. 3

Jeśli okrąg można wpisać w czworobok, to sumy jego przeciwległych boków są równe. Łatwo to udowodnić:

Rozwińmy nawiasy:

W ten sposób udowodniliśmy proste, ale ważne twierdzenie.

Jeśli okrąg można wpisać w czworobok, to sumy jego przeciwległych boków są równe.

Twierdzenie odwrotne jest prawdziwe.

Jeśli w czworoboku sumy przeciwległych boków są równe, to można w niego wpisać okrąg.

Rozważ okrąg wokół czworokąta.

Podano okrąg o środku O i dowolny czworokąt ABCD. Rozważ właściwości tego czworokąta. Wszystkie cztery środkowe prostopadłe tego czworoboku przecinają się w jednym punkcie: ten punkt jest środkiem opisanego okręgu.

Udowodnienie, że wszystkie cztery prostopadłe przecinają się w jednym punkcie, byłoby żmudne. Jest jeszcze jeden znak. Rozważmy kąt ے A, jest to wpisany kąt koła, opiera się na łuku i jest mierzony przez połowę miary tego łuku (patrz rys. 4). Wyznaczmy kąt ے А dla, a następnie łuk. Podobnie oznaczamy kąt przeciwny ے С, ponieważ jest on wpisany w okrąg i spoczywa na łuku. Stąd łuk.

Ryż. 4

Łuki i tworzą pełne koło. W związku z tym:

,

Podziel otrzymane wyrażenie przez dwa, otrzymamy:

Tak więc udowodniliśmy bezpośrednie twierdzenie.

Twierdzenie

Jeśli okrąg jest opisany wokół czworoboku, suma jego przeciwnych kątów jest równa.

Jest to konieczne i wystarczające kryterium, czyli twierdzenie odwrotne jest prawdziwe.

Jeśli suma przeciwnych kątów czworokąta jest równa, wokół tego czworokąta można opisać okrąg.

Na podstawie tych twierdzeń zauważamy, że nie można opisać okręgu wokół równoległoboku, ponieważ jego przeciwne kąty są równe, a ich suma nie jest równa (patrz ryc. 5).

Ryż. 5

Okrąg można opisać wokół równoległoboku, jeśli jego przeciwne kąty byłyby równe 90 °, to znaczy, gdyby był prostokątem, w ten sposób można opisać okrąg wokół prostokąta (patrz ryc. 6).

Ryż. 6

Nie da się też opisać okręgu wokół rombu, ale można go wpisać, ponieważ wszystkie boki rombu są równe, a zatem sumy przeciwległych boków rombu są równe.

Ponadto w przypadku rombu każda przekątna jest dwusieczną, punkt przecięcia dwusiecznych jest równoodległy od wszystkich stron rombu (patrz ryc. 7).

Ryż. 7

Udowodniliśmy więc, że okrąg można wpisać w dowolny trójkąt, a środek tego okręgu pokrywa się z punktem przecięcia dwusiecznych trójkąta. Udowodniliśmy również, że okrąg można opisać wokół dowolnego trójkąta, a jego środek pokrywa się z punktem przecięcia środkowych prostopadłych. Ponadto widzieliśmy, że w niektóre czworokąty można wpisać okrąg, a do tego konieczne jest, aby sumy przeciwległych boków czworokąta były równe. Pokazaliśmy również, że okrąg można opisać wokół niektórych czworokątów, a warunkiem koniecznym i wystarczającym do tego jest równość sumy przeciwnych kątów.

Bibliografia

1. Aleksandrow n.e. i inne Geometria, klasa 8. - M .: Edukacja, 2006.
2. Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Geometria, klasa 8. - M .: Edukacja, 2011.
3. Merzlyak A.G., Polonskiy V.B., Yakir S.M. Geometria, klasa 8. - M .: VENTANA-GRAF, 2009.

1. Uztest.ru ().
2. Mschool.kubsu.ru ().
3. Ege-study.ru ().

Praca domowa

Definicja 2

Wielokąt spełniający warunek z Definicji 1 nazywany jest opisanym wokół okręgu.

Rysunek 1. Wpisany okrąg

Twierdzenie 1 (na okręgu wpisanym w trójkąt)

Twierdzenie 1

W dowolnym trójkącie możesz wpisać okrąg, a ponadto tylko jeden.

Dowód.

Rozważ trójkąt $ ABC $. Narysujmy w nim dwusieczne, które przecinają się w punkcie $O $ i narysujmy z niego prostopadłe do boków trójkąta (ryc. 2)

Rysunek 2. Ilustracja twierdzenia 1

Istnienie: Narysuj okrąg o środku w punkcie $ O $ i promieniu $ OK \ $ Ponieważ punkt $ O $ leży na trzech dwusiecznych, jest w równej odległości od boków trójkąta $ ABC $. Oznacza to, że $ OM = OK = OL $. Dlatego skonstruowany okrąg przechodzi również przez punkty $ M \ i \ L $. Ponieważ $ OM, OK \ i \ OL $ są prostopadłe do boków trójkąta, to zgodnie z twierdzeniem o stycznej do okręgu skonstruowany okrąg dotyka wszystkich trzech boków trójkąta. Dlatego ze względu na arbitralność trójkąta okrąg można wpisać w dowolny trójkąt.

Niepowtarzalność: Załóżmy, że jeszcze jeden okrąg można wpisać w trójkąt $ABC $ o środku w punkcie $O "$. Jego środek jest równoodległy od boków trójkąta, a zatem pokrywa się z punktem $O $ i ma promień równy długości $ OK $ Ale wtedy ten okrąg będzie się pokrywał z pierwszym.

Twierdzenie jest udowodnione.

Wniosek 1: Środek koła wpisanego w trójkąt leży w miejscu przecięcia jego dwusiecznych.

Oto kilka innych faktów związanych z koncepcją okręgu wpisanego:

Nie każdy czworokąt można wpisać w okrąg.

W każdym opisanym czworoboku sumy przeciwległych boków są równe.

Jeśli sumy przeciwległych boków czworoboku wypukłego są równe, można w niego wpisać okrąg.

Definicja 3

Jeśli wszystkie wierzchołki wielokąta leżą na okręgu, wówczas okrąg nazywa się opisany wielokątem (ryc. 3).

Definicja 4

Wielokąt spełniający warunek Definicji 2 nazywamy wpisanym w okrąg.

Rysunek 3. Zakreślony okrąg

Twierdzenie 2 (na kole opisanym wokół trójkąta)

Twierdzenie 2

Wokół dowolnego trójkąta możesz opisać okrąg, a ponadto tylko jeden.

Dowód.

Rozważ trójkąt $ ABC $. Rysujemy w nim prostopadłe przecinające się w punkcie $ O $ i łączymy je z wierzchołkami trójkąta (ryc. 4)

Rysunek 4. Ilustracja twierdzenia 2

Istnienie: Skonstruuj okrąg o środku $ O $ i promieniu $ OC $. Punkt $ O $ jest w równej odległości od wierzchołków trójkąta, czyli $ OA = OB = OC $. Dlatego skonstruowany okrąg przechodzi przez wszystkie wierzchołki tego trójkąta, co oznacza, że ​​jest opisany wokół tego trójkąta.

Wyjątkowość: Załóżmy, że wokół trójkąta $ABC $ można opisać jeszcze jeden okrąg ze środkiem w punkcie $O "$. Jego środek jest równoodległy od wierzchołków trójkąta, a zatem pokrywa się z punktem $O $ i ma promień równy długości $ OC $ Ale wtedy ten okrąg będzie się pokrywał z pierwszym.

Twierdzenie jest udowodnione.

Wniosek 1: Środek okręgu opisanego wokół trójkąta pokrywa się z punktem przecięcia jego pionów środkowych.

Oto kilka innych faktów związanych z koncepcją koła ograniczonego:

Nie zawsze można opisać okrąg wokół czworoboku.

W każdym czworoboku wpisanym suma kątów przeciwnych wynosi $ (180) ^ 0 $.

Jeżeli suma przeciwnych kątów czworokąta wynosi $ (180) ^ 0 $, to wokół niego można opisać okrąg.

Przykład problemu z pojęciami koła wpisanego i opisanego

Przykład 1

W trójkącie równoramiennym podstawa ma 8 cm, bok boczny 5 cm Znajdź promień wpisanego koła.

Rozwiązanie.

Rozważ trójkąt $ ABC $. Z wniosku 1 wiemy, że środek okręgu wpisanego leży na przecięciu dwusiecznych. Narysujmy dwusieczne $AK $ i $BM $, które przecinają się w punkcie $O $. Narysuj prostopadłą $ OH $ od punktu $ O $ do boku $ BC $. Narysujmy obrazek:

Rysunek 5.

Ponieważ trójkąt jest równoramienny, to $BM $ jest zarówno medianą, jak i wysokością. Według twierdzenia Pitagorasa $ (BM) ^ 2 = (BC) ^ 2- (MC) ^ 2, \ BM = \ sqrt ((BC) ^ 2- \ frac ((AC) ^ 2) (4)) = \ sqrt (25-16) = \ sqrt (9) = 3 $. $ OM = OH = r $ - wymagany promień okręgu wpisanego. Ponieważ $ MC $ i $ CH $ są odcinkami przecinających się stycznych, to z twierdzenia o przecinającej się stycznej mamy $ CH = MC = 4 \ cm $. Dlatego $ BH = 5-4 = 1 \ cm $. $ BO = 3-r $. Z trójkąta $ OHB $, przez twierdzenie Pitagorasa, otrzymujemy:

\ [((3-r)) ^ 2 = r ^ 2 + 1 \] \ \ \

Odpowiedź:$ \ frac (4) (3) $.

I dotyczy wszystkich jego stron.

Kolegium YouTube

• 1 / 5

  Wpisane właściwości okręgu:

  r = (- a + b + c) (a - b + c) (a + b - c) 4 (a + b + c); (\ displaystyle r = (\ sqrt (\ frac ((-a + b + c) (a-b + c) (a + b-c)) (4 (a + b + c))));) 1 r = 1 ha + 1 hb + 1 hc (\ displaystyle (\ frac (1) (r)) = (\ frac (1) (h_ (a))) + (\ frac (1) (h_ (b)) )) + (\ frac (1) (h_ (c))))

  gdzie a, b, c (\ styl wyświetlania a, b, c)- boki trójkąta, h a, h b, h c (\ styl wyświetlania h_ (a), h_ (b), h_ (c))- wysokości narysowane na odpowiednie boki;

  r = S p = (p - a) (p - b) (p - c) p (\ displaystyle r = (\ frac (S) (p)) = (\ sqrt (\ frac ((pa) (pb)) (szt.)) (p))))

  Gdzie S (\ styl wyświetlania S) to pole trójkąta, a p (\ styl wyświetlania p) jest jego półobwodem.

  • Jeśli A B (\ styl wyświetlania AB)- podstawa trójkąta równoramiennego, następnie okrąg styczny do boków kąta ∠ A C B (\ styl wyświetlania \ kąt ACB) w punktach A (\ styl wyświetlania A) oraz B (\ styl wyświetlania B), przechodzi przez środek okręgu wpisanego w trójkąt △ A B C (\ styl wyświetlania \ trójkąt ABC).
  • Twierdzenie Eulera: R 2 - 2 R r = | O ja | 2 (\ styl wyświetlania R ^ (2) -2Rr = | OI | ^ (2)), gdzie R (\ styl wyświetlania R)- promień okręgu opisanego wokół trójkąta, r (\ styl wyświetlania r)- promień okręgu wpisanego, O (\ styl wyświetlania O)- środek koła opisanego, I (\ styl wyświetlania I) jest środkiem wpisanego koła.
  • Jeżeli linia przechodząca przez punkt I równolegle do boku AB przecina boki BC i CA w punktach A 1 i B 1, to A 1 B 1 = A 1 B + A B 1 (\ styl wyświetlania A_ (1) B_ (1) = A_ (1) B + AB_ (1)).
  • Jeśli punkty styczności wpisanego w trójkąt T (\ styl wyświetlania T)łączymy okręgi segmentami, to otrzymujemy trójkąt T 1 o właściwościach:
    • Dwusieczne z T to średnie prostopadłe do T 1
    • Niech T 2 będzie ortotrójkątem T 1. Wtedy jego boki są równoległe do boków pierwotnego trójkąta T.
    • Niech T 3 będzie środkowym trójkątem T 1. Wtedy dwusieczne T są wysokościami T 3.
    • Niech T 4 będzie ortotrójkątem z T 3, wtedy dwusieczne z T będą dwusiecznymi z T 4.
  • Promień okręgu wpisanego w trójkąt prostokątny z odnogami a, b i przeciwprostokątną c jest równy a + b - c 2 (\ styl wyświetlania (\ frac (a + b-c) (2))).
  • Odległość od wierzchołka C trójkąta do punktu, w którym wpisany okrąg styka się z bokiem, jest równa d = a + b - c 2 = p - c (\ displaystyle d = (\ frac (a + b-c) (2)) = p-c).
  • Odległość od wierzchołka C do środka okręgu wpisanego wynosi l c = r grzech ⁡ (γ 2) (\ displaystyle l_ (c) = (\ frac (r) (\ grzech ((\ frac (\ gamma) (2)))))), gdzie r jest promieniem okręgu wpisanego, a γ jest kątem wierzchołka C.
  • Odległość od wierzchołka C do środka okręgu wpisanego można również znaleźć za pomocą wzorów l c = (p - c) 2 + r 2 (\ displaystyle l_ (c) = (\ sqrt ((p-c) ^ (2) + r ^ (2)))) oraz l c = a b - 4 R r (\ displaystyle l_ (c) = (\ sqrt (ab-4Rr)))
  • Twierdzenie trójząb lub twierdzenie o koniczynie: Jeśli D- punkt przecięcia dwusiecznej kąta A z opisanym trójkątem ABC, i oraz J- odpowiednio środki okręgu i ekskoła stykają się z bokiem pne, następnie | D ja | = | DB | = | D C | = | DJ | (\ styl wyświetlania | DI | = | DB | = | DC | = | DJ |).
  • Lemat Verriera: niech okrąg V (\ styl wyświetlania V) dotyczy stron A B (\ styl wyświetlania AB), A C (\ Displaystyle AC) i łuki B C (\ styl wyświetlania BC) ograniczone koło trójkąta. Następnie punkty styczności okręgu V (\ styl wyświetlania V) z bokami i środkiem okręgu wpisanego w trójkąt A B C (\ styl wyświetlania ABC) leżeć na jednej linii prostej.
  • twierdzenie Feuerbacha... Okrąg składający się z dziewięciu punktów dotyka wszystkich trzech dawne kręgi, jak również wpisany okrąg... Punkt dotknięcia krąg Eulera oraz wpisany okrąg znany jako punkt Feuerbacha.

  Koło wpisane do koła opisanego

  R R = 4 S 2 p a b c = cos ⁡ α + cos ⁡ β + cos ⁡ γ - 1; (\ displaystyle (\ frac (r) (R)) = (\ frac (4S ^ (2)) (pabc)) = \ cos \ alpha + \ cos \ beta + \ cos \ gamma -1;)