Znajdź długość boku ab online. Równanie prostej ze spadkiem
Liczbowo równy tangensowi kąta (stanowiącego najmniejszy obrót od osi Ox do osi Oy) pomiędzy dodatnim kierunkiem osi odciętych a daną prostą.
Tangens kąta można obliczyć jako stosunek strony przeciwnej do strony sąsiedniej. k jest zawsze równa , czyli pochodnej równania prostej względem X.
Dla dodatnich wartości nachylenia k i zerowy współczynnik przesunięcia B linia prosta będzie leżeć w pierwszej i trzeciej ćwiartce (w której X I y zarówno pozytywne, jak i negatywne). Jednocześnie duże wartości współczynnika kątowego k bardziej stroma linia prosta będzie odpowiadać, a bardziej płaska będzie odpowiadać mniejszym.
Proste i prostopadłe jeśli , i równoległe jeśli .
Notatki
Fundacja Wikimedia. 2010.
- Ifit (król Elidy)
- Wykaz zarządzeń Prezydenta Federacji Rosyjskiej „W sprawie przyznania odznaczeń państwowych” za rok 2001
Zobacz, co „Współczynnik kątowy linii prostej” znajduje się w innych słownikach:
nachylenie (bezpośrednie)- - Tematy: przemysł naftowy i gazowy EN nachylenie... Przewodnik tłumacza technicznego
Współczynnik nachylenia- liczba (matematyczna) k w równaniu prostej na płaszczyźnie y = kx+b (patrz Geometria analityczna), charakteryzująca nachylenie prostej względem osi x. W prostokątnym układzie współrzędnych U. k. = tan φ, gdzie φ jest kątem pomiędzy ... ... Wielka encyklopedia radziecka
Równania prostej
GEOMETRIA ANALITYCZNA- dział geometrii zajmujący się badaniem najprostszych obiektów geometrycznych za pomocą elementarnej algebry opartej na metodzie współrzędnych. Powstanie geometrii analitycznej przypisuje się zwykle R. Kartezjuszowi, który w ostatnim rozdziale swojej pracy nakreślił jej podstawy... ... Encyklopedia Colliera
Czas reakcji- Pomiar czasu reakcji (RT) jest prawdopodobnie najbardziej szanowanym przedmiotem psychologii empirycznej. Jej początki sięgają 1823 roku, kiedy to astronomia mierzyła indywidualne różnice w szybkości postrzegania gwiazdy przechodzącej przez linię teleskopu. Te … Encyklopedia psychologiczna
ANALIZA MATEMATYCZNA- dział matematyki dostarczający metod ilościowych badań różnych procesów zmian; zajmuje się badaniem szybkości zmian (rachunek różniczkowy) oraz wyznaczaniem długości krzywych, pól i objętości figur ograniczonych zakrzywionymi konturami i... Encyklopedia Colliera
Prosty- Ten termin ma inne znaczenia, patrz Bezpośredni (znaczenia). Linia prosta jest jednym z podstawowych pojęć geometrii, to znaczy nie ma dokładnej, uniwersalnej definicji. W systematycznej prezentacji geometrii linia prosta jest zwykle traktowana jako... ... Wikipedia
Linia prosta- Obraz linii prostych w prostokątnym układzie współrzędnych Linia prosta jest jednym z podstawowych pojęć geometrii. W systematycznym przedstawianiu geometrii linia prosta jest zwykle traktowana jako jedno z pojęć początkowych, które jest definiowane jedynie pośrednio... ... Wikipedia
Bezpośredni- Obraz linii prostych w prostokątnym układzie współrzędnych Linia prosta jest jednym z podstawowych pojęć geometrii. W systematycznym przedstawianiu geometrii linia prosta jest zwykle traktowana jako jedno z pojęć początkowych, które jest definiowane jedynie pośrednio... ... Wikipedia
Drobny wał- Nie mylić z terminem „elipsa”. Elipsa i jej ogniska Elipsa (starożytny grecki ἔλλειψις, w sensie braku mimośrodu do 1) miejsce punktów M płaszczyzny euklidesowej, dla których suma odległości od dwóch danych punktów wynosi F1... ... Wikipedia
Niech na płaszczyźnie, w której znajduje się prostokątny kartezjański układ współrzędnych, linia prosta l przechodzi przez punkt M 0 równolegle do wektora kierunku A (ryc. 96).
Jeśli prosto l przecina oś O X(w punkcie N), następnie pod kątem prostej l z osią O X zrozumiemy kąt α, o który należy obrócić oś O X wokół punktu N w kierunku przeciwnym do obrotu zgodnie z ruchem wskazówek zegara, tak aby oś O X pokrywała się z linią prostą l. (Odnosi się to do kąta mniejszego niż 180°.)
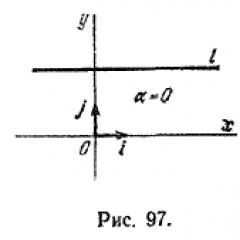
Kąt ten nazywa się kąt nachylenia prosty. Jeśli prosto l równolegle do osi O X, wówczas przyjmuje się, że kąt nachylenia wynosi zero (ryc. 97).
Nazywa się tangensem kąta nachylenia prostej nachylenie linii prostej i jest zwykle oznaczony literą k:
tan α = k. (1)
Jeżeli α = 0, to k= 0; oznacza to, że linia jest równoległa do osi O X a jego nachylenie wynosi zero.
Jeżeli α = 90°, to k= tan α nie ma sensu: oznacza to linię prostą prostopadłą do osi O X(tj. równolegle do osi O Na), nie ma nachylenia.
Nachylenie linii można obliczyć, jeśli znane są współrzędne dowolnych dwóch punktów na tej linii. Niech zostaną dane dwa punkty na prostej: M 1 ( X 1 ; Na 1) i M 2 ( X 2 ; Na 2) i niech na przykład 0< α < 90°, а X 2 > X 1 , Na 2 > Na 1 (ryc. 98).
Następnie z prawego trójkąta M 1 PM 2 znajdujemy
$$ k=tga = \frac(|M_2 P|)(|M_1 P|) = \frac(y_2 - y_1)(x_2 - x_1) $$
$$ k=\frac(y_2 - y_1)(x_2 - x_1) \;\; (2)$$
Podobnie udowodniono, że wzór (2) jest prawdziwy także w przypadku 90°< α < 180°.
Formuła (2) staje się bez znaczenia, jeśli X 2 - X 1 = 0, tj. jeśli jest prosty l równolegle do osi O Na. Dla takich linii prostych nie ma współczynnika nachylenia.
Zadanie 1. Wyznacz współczynnik kątowy prim przechodzący przez punkty
M 1 (3; -5) i M 2 (5; -7).
Podstawiając współrzędne punktów M 1 i M 2 do wzoru (2) otrzymujemy
\(k=\frac(-7-(-5))(5-3)\) lub k = -1
Zadanie 2. Określ nachylenie linii prostej przechodzącej przez punkty M 1 (3; 5) i M 2 (3; -2).
Ponieważ X 2 - X 1 = 0, wówczas równość (2) traci sens. Ta linia prosta nie ma nachylenia. Linia prosta M 1 M 2 jest równoległa do osi O Na.
Zadanie 3. Określ nachylenie prostej przechodzącej przez początek i punkt M 1 (3; -5)
W tym przypadku punkt M 2 pokrywa się z początkiem. Stosując wzór (2) otrzymujemy
$$ k=\frac(y_2 - y_1)(x_2 - x_1)=\frac(0-(-5))(0-3)= -\frac(5)(3); \;\; k= -\frac(5)(3) $$
Utwórzmy równanie prostej ze współczynnikiem kąta k, przechodząc przez punkt
M 1 ( X 1 ; Na 1). Zgodnie ze wzorem (2) współczynnik kątowy prostej wyznacza się ze współrzędnych jej dwóch punktów. W naszym przypadku dany jest punkt M 1, a jako drugi punkt możemy przyjąć dowolny punkt M( X; Na) żądaną linię prostą.
Jeżeli punkt M leży na prostej przechodzącej przez punkt M 1 i ma współczynnik kątowy k, to na mocy wzoru (2) mamy
$$ \frac(y-y_1)(x-x_1)=k \;\; (3) $$
Jeżeli punkt M nie leży na prostej, to równość (3) nie zachodzi. W konsekwencji równość (3) jest równaniem linii przechodzącej przez punkt M 1 ( X 1 ; Na 1) ze spadkiem k; to równanie jest zwykle zapisywane jako
y- y 1 = k(X - X 1). (4)
Jeśli linia prosta przecina oś O Na w pewnym momencie (0; B), wówczas równanie (4) przyjmuje postać
Na - B = k (X- 0),
y = kx + b. (5)
To równanie nazywa się równanie prostej o nachyleniu k i rzędnej początkowej b.
Zadanie 4. Znajdź kąt nachylenia prostej √3 x + 3Na - 7 = 0.
Sprowadźmy to równanie do postaci
$$ y= =\frac(1)(\sqrt3)x + \frac(7)(3) $$
Stąd, k= tan α = - 1 / √ 3, skąd α = 150°
Zadanie 5. Napisz równanie prostej przechodzącej przez punkt P(3; -4) ze współczynnikiem kątowym k = 2 / 5
Zastępowanie k = 2 / 5 , X 1 = 3, y 1 = - 4 do równania (4), otrzymujemy
Na - (- 4) = 2 / 5 (X- 3) lub 2 X - 5Na - 26 = 0.
Zadanie 6. Napisz równanie prostej przechodzącej przez punkt Q (-3; 4) i składową o dodatnim kierunku osi O X kąt 30°.
Jeżeli α = 30°, to k= tan 30° = √ 3 / 3 . Podstawiając do równania (4) wartości X 1 , y 1 i k, otrzymujemy
Na -4 = √ 3 / 3 (X+ 3) lub √3 X-3y + 12 + 3√3 = 0.
W matematyce jednym z parametrów opisujących położenie prostej na kartezjańskiej płaszczyźnie współrzędnych jest współczynnik kątowy tej prostej. Parametr ten charakteryzuje nachylenie prostej do osi odciętej. Aby zrozumieć, jak znaleźć nachylenie, najpierw przypomnij sobie ogólną postać równania linii prostej w układzie współrzędnych XY.
Ogólnie rzecz biorąc, dowolną linię można przedstawić za pomocą wyrażenia ax+by=c, gdzie a, b i c są dowolnymi liczbami rzeczywistymi, ale a 2 + b 2 ≠ 0.
Za pomocą prostych przekształceń równanie takie można sprowadzić do postaci y=kx+d, gdzie k i d są liczbami rzeczywistymi. Liczba k jest nachyleniem, a równanie prostej tego typu nazywa się równaniem z nachyleniem. Okazuje się, że aby znaleźć nachylenie, wystarczy zredukować pierwotne równanie do postaci wskazanej powyżej. Aby uzyskać pełniejsze zrozumienie, rozważ konkretny przykład:
Zadanie: Znajdź nachylenie prostej podanej równaniem 36x - 18y = 108
Rozwiązanie: Przekształćmy pierwotne równanie.
Odpowiedź: Wymagane nachylenie tej linii wynosi 2.
Jeśli podczas transformacji równania otrzymaliśmy wyrażenie typu x = const i w rezultacie nie możemy przedstawić y jako funkcji x, to mamy do czynienia z prostą równoległą do osi X. Współczynnik kątowy takiego linia prosta jest równa nieskończoności.
W przypadku linii wyrażonych równaniem takim jak y = const nachylenie wynosi zero. Jest to typowe dla linii prostych równoległych do osi odciętych. Na przykład:
Zadanie: Znajdź nachylenie prostej podanej równaniem 24x + 12y - 4(3y + 7) = 4
Rozwiązanie: Doprowadźmy pierwotne równanie do jego ogólnej postaci
24x + 12 lat - 12 lat + 28 = 4
Z powstałego wyrażenia nie można wyrazić y, dlatego współczynnik kątowy tej linii jest równy nieskończoności, a sama linia będzie równoległa do osi Y.
Znaczenie geometryczne
Dla lepszego zrozumienia spójrzmy na zdjęcie:
Na rysunku widzimy wykres funkcji takiej jak y = kx. Dla uproszczenia przyjmijmy współczynnik c = 0. W trójkącie OAB stosunek boku BA do AO będzie równy współczynnikowi kątowemu k. Jednocześnie stosunek BA/AO jest tangensem kąta ostrego α w trójkącie prostokątnym OAB. Okazuje się, że współczynnik kątowy prostej jest równy tangensowi kąta, jaki ta prosta tworzy z osią odciętych siatki współrzędnych.
Rozwiązując problem znalezienia współczynnika kątowego linii prostej, znajdujemy tangens kąta między nią a osią X siatki współrzędnych. Przypadki graniczne, gdy rozpatrywana linia jest równoległa do osi współrzędnych, potwierdzają powyższe. Rzeczywiście, dla prostej opisanej równaniem y=const, kąt pomiędzy nią a osią odciętych wynosi zero. Tangens kąta zerowego również wynosi zero i nachylenie również wynosi zero.
Dla prostych prostopadłych do osi x i opisanych równaniem x=const, kąt między nimi a osią X wynosi 90 stopni. Tangens kąta prostego jest równy nieskończoności, a współczynnik kątowy podobnych prostych jest również równy nieskończoności, co potwierdza to, co napisano powyżej.
Styczne nachylenie
Częstym zadaniem często spotykanym w praktyce jest również znalezienie nachylenia stycznej do wykresu funkcji w pewnym punkcie. Styczna jest linią prostą, dlatego też można do niej zastosować pojęcie nachylenia.
Aby dowiedzieć się, jak znaleźć nachylenie stycznej, będziemy musieli przypomnieć sobie pojęcie pochodnej. Pochodną dowolnej funkcji w pewnym punkcie jest stała liczbowo równa tangensowi kąta utworzonego pomiędzy styczną w określonym punkcie do wykresu tej funkcji a osią odciętych. Okazuje się, że aby wyznaczyć współczynnik kątowy stycznej w punkcie x 0, musimy obliczyć wartość pochodnej funkcji pierwotnej w tym punkcie k = f”(x 0). Spójrzmy na przykład:
Zadanie: Znajdź nachylenie prostej stycznej do funkcji y = 12x 2 + 2xe x przy x = 0,1.
Rozwiązanie: Znajdź pochodną funkcji pierwotnej w postaci ogólnej
y"(0,1) = 24,0,1 + 2,0,1, e 0,1 + 2, e 0,1
Odpowiedź: Wymagane nachylenie w punkcie x = 0,1 wynosi 4,831
Rysunek przedstawia kąt nachylenia prostej oraz wskazuje wartość współczynnika kątowego dla różnych opcji położenia prostej względem prostokątnego układu współrzędnych.
Znalezienie nachylenia prostej o znanym kącie nachylenia do osi Wołu nie nastręcza żadnych trudności. Aby to zrobić, wystarczy przypomnieć sobie definicję współczynnika kątowego i obliczyć tangens kąta nachylenia.
Przykład.
Znajdź nachylenie prostej, jeśli jej kąt nachylenia do osi odciętej jest równy .
Rozwiązanie.
Według warunku. Następnie, z definicji nachylenia linii prostej, obliczamy 
.
Odpowiedź:
Zadanie znalezienia kąta nachylenia prostej do osi x przy znanym nachyleniu jest nieco bardziej skomplikowane. Tutaj należy wziąć pod uwagę znak nachylenia. Kiedy kąt nachylenia linii prostej jest ostry i można go znaleźć jako . Gdy kąt nachylenia linii prostej jest rozwarty i można go określić za pomocą wzoru 
.
Przykład.
Wyznacz kąt nachylenia prostej do osi odciętej, jeśli jej nachylenie jest równe 3.
Rozwiązanie.
Ponieważ pod warunkiem współczynnik kątowy jest dodatni, kąt nachylenia linii prostej do osi Wołu jest ostry. Obliczamy to za pomocą wzoru.
Odpowiedź:
Przykład.
Nachylenie prostej wynosi . Określ kąt nachylenia prostej do osi Wołu.
Rozwiązanie.
Oznaczmy k jest współczynnikiem kątowym linii prostej, - kątem nachylenia tej prostej do dodatniego kierunku osi Ox. Ponieważ 
, następnie korzystamy ze wzoru na obliczenie kąta nachylenia prostej w następującej postaci . Podstawiamy do niego dane z warunku: .
Odpowiedź:
Równanie prostej ze współczynnikiem kątowym.
Równanie prostej ze spadkiem ma postać , gdzie k jest nachyleniem prostej, b jest liczbą rzeczywistą. Korzystając z równania prostej ze współczynnikiem kątowym, można określić dowolną linię prostą, która nie jest równoległa do osi Oy (dla prostej równoległej do osi rzędnych współczynnik kątowy nie jest definiowany).
Rozumiemy znaczenie wyrażenia: „linię prostą na płaszczyźnie w ustalonym układzie współrzędnych podaje równanie ze współczynnikiem kątowym postaci „.” Oznacza to, że równanie jest spełnione przez współrzędne dowolnego punktu na prostej i nie jest spełnione przez współrzędne żadnego innego punktu na płaszczyźnie. Zatem, jeżeli podstawiając współrzędne punktu uzyskamy poprawną równość, to przez ten punkt przechodzi prosta. W przeciwnym razie punkt nie leży na prostej.
Przykład.
Linię prostą wyznacza się za pomocą równania o nachyleniu. Czy punkty również należą do tej prostej?
Rozwiązanie.
Podstawmy współrzędne punktu do pierwotnego równania prostej z nachyleniem: 
. Otrzymaliśmy poprawną równość, dlatego punkt M 1 leży na prostej.
Podstawiając współrzędne punktu, otrzymujemy niepoprawną równość: 
. Zatem punkt M 2 nie leży na prostej.
Odpowiedź:
Kropka M 1 należy do prostej, M 2 nie.
Należy zauważyć, że przez punkt przechodzi prosta określona równaniem prostej ze współczynnikiem kątowym, gdyż podstawiając jej współrzędne do równania otrzymujemy poprawną równość: .
Zatem równanie prostej ze współczynnikiem kątowym definiuje na płaszczyźnie linię prostą przechodzącą przez punkt i tworzącą kąt z dodatnim kierunkiem osi odciętych, oraz .
Jako przykład zobrazujmy linię prostą określoną przez równanie prostej ze współczynnikiem kątowym postaci . Linia ta przechodzi przez punkt i ma nachylenie 
radianów (60 stopni) w kierunku dodatnim osi Wół. Jego nachylenie jest równe .
Równanie prostej z nachyleniem przechodzącej przez dany punkt.
Teraz rozwiążemy bardzo ważny problem: otrzymamy równanie prostej o zadanym nachyleniu k i przechodzącej przez punkt .
Ponieważ prosta przechodzi przez punkt, równość jest prawdziwa 
. Nie znamy liczby b. Aby się tego pozbyć, od lewej i prawej strony równania prostej ze współczynnikiem nachylenia odejmujemy lewą i prawą stronę ostatniej równości. W tym przypadku otrzymujemy 
. Ta równość jest równanie prostej o zadanym nachyleniu k, która przechodzi przez dany punkt.
Spójrzmy na przykład.
Przykład.
Zapisz równanie prostej przechodzącej przez punkt, której nachylenie wynosi -2.
Rozwiązanie.
Od stanu jaki mamy 
. Wtedy równanie prostej ze współczynnikiem kątowym przyjmie postać .
Odpowiedź:
Przykład.
Napisz równanie prostej, jeśli wiadomo, że przechodzi ona przez punkt, a kąt nachylenia do dodatniego kierunku osi Ox jest równy .
Rozwiązanie.
Najpierw obliczmy nachylenie prostej, której równania szukamy (rozwiązaliśmy ten problem w poprzednim akapicie tego artykułu). A-przeorat 
. Mamy teraz wszystkie dane do zapisania równania prostej ze współczynnikiem kąta:
Odpowiedź:
Przykład.
Zapisz równanie prostej ze współczynnikiem kątowym przechodzącym przez punkt równoległy do tej prostej.
Rozwiązanie.
Oczywiście kąty nachylenia linii równoległych do osi Wółu pokrywają się (w razie potrzeby zobacz artykuł Równoległość linii), dlatego współczynniki kątowe linii równoległych są równe. Następnie nachylenie prostej, której równanie musimy uzyskać, jest równe 2, ponieważ nachylenie prostej jest równe 2. Teraz możemy utworzyć wymagane równanie prostej o nachyleniu:
Odpowiedź:
Przejście od równania prostej ze współczynnikiem kąta do innych typów równań prostej i odwrotnie.
Pomimo całej znajomości równanie linii prostej ze współczynnikiem kątowym nie zawsze jest wygodne w użyciu przy rozwiązywaniu problemów. W niektórych przypadkach problemy łatwiej jest rozwiązać, gdy równanie prostej przedstawi się w innej formie. Na przykład równanie linii prostej ze współczynnikiem kątowym nie pozwala od razu zapisać współrzędnych wektora kierującego linii prostej lub współrzędnych wektora normalnego linii prostej. Dlatego należy nauczyć się przechodzić od równania prostej ze współczynnikiem kąta do innych typów równań tej prostej.
Z równania prostej ze współczynnikiem kątowym łatwo otrzymać równanie kanoniczne prostej na płaszczyźnie postaci 
. Aby to zrobić, przesuwamy wyraz b z prawej strony równania na lewą stronę z przeciwnym znakiem, a następnie dzielimy obie strony powstałej równości przez nachylenie k: . Działania te prowadzą nas od równania prostej ze współczynnikiem kąta do równania kanonicznego prostej.
Przykład.
Podaj równanie prostej ze współczynnikiem kąta 
do postaci kanonicznej.
Rozwiązanie.
Dokonajmy niezbędnych przekształceń: .
Odpowiedź:
Przykład.
Linię prostą wyznacza się poprzez równanie linii prostej ze współczynnikiem kątowym. Czy wektor jest wektorem normalnym tej prostej?
Rozwiązanie.
Aby rozwiązać ten problem, przejdźmy od równania prostej ze współczynnikiem kąta do ogólnego równania tej prostej: 
. Wiemy, że współczynniki zmiennych x i y w ogólnym równaniu prostej są odpowiadającymi współrzędnymi wektora normalnego tej prostej, czyli wektora normalnego prostej 
. Oczywiste jest, że wektor jest współliniowy z wektorem, ponieważ relacja jest ważna (jeśli to konieczne, zobacz artykuł). Zatem pierwotny wektor jest również normalnym wektorem liniowym , a zatem jest wektorem normalnym i pierwotną linią.
Odpowiedź:
Tak to jest.
A teraz rozwiążemy problem odwrotny - problem redukcji równania prostej na płaszczyźnie do równania prostej ze współczynnikiem kąta.
Z ogólnego równania prostej postaci 
, w którym bardzo łatwo dojść do równania ze współczynnikiem nachylenia. Aby to zrobić, musisz rozwiązać ogólne równanie prostej względem y. W tym przypadku otrzymujemy. Otrzymana równość jest równaniem linii prostej o współczynniku kątowym równym .
Zadania ze znalezieniem pochodnej tangensa wchodzą w skład Jednolitego Egzaminu Państwowego z matematyki i pojawiają się tam co roku. Jednocześnie statystyki z ostatnich lat pokazują, że tego typu zadania sprawiają absolwentom pewne trudności. Jeśli więc student spodziewa się uzyskać przyzwoite wyniki po zdaniu egzaminu Unified State Exam, to zdecydowanie powinien nauczyć się radzić sobie z problemami z rozdziału „Współczynnik kąta stycznej jako wartość pochodnej w punkcie styczności”, przygotowanego przez specjalistów portalu edukacyjnego Shkolkovo. Po zrozumieniu algorytmu ich rozwiązywania student będzie w stanie pomyślnie przejść test certyfikacyjny.
Podstawowe momenty
Rozpoczynając rozwiązywanie problemów USE na ten temat, należy pamiętać o podstawowej definicji: pochodna funkcji w punkcie jest równa nachyleniu stycznej do wykresu funkcji w tym punkcie. To jest geometryczne znaczenie pochodnej.
Istnieje jeszcze jedna ważna definicja, którą należy odświeżyć. Brzmi to tak: współczynnik kątowy jest równy tangensowi kąta nachylenia stycznej do osi odciętej.
Na jakie jeszcze ważne punkty warto zwrócić uwagę w tym temacie? Rozwiązując problemy ze znalezieniem pochodnej w Unified State Examination, należy pamiętać, że kąt utworzony przez styczną może być mniejszy, większy niż 90 stopni lub równy zero.
Jak przygotować się do egzaminu?
Aby mieć pewność, że zadania w ramach Unified State Examination na temat „Współczynnik kątowy stycznej jako wartość pochodnej w punkcie styczności” są dość łatwe, przygotowując się do egzaminu końcowego, skorzystaj z informacji na ten temat sekcja na portalu edukacyjnym Shkolkovo. Znajdziesz tutaj niezbędny materiał teoretyczny, zebrany i przejrzyście przedstawiony przez naszych specjalistów, a także będziesz mógł przećwiczyć wykonywanie ćwiczeń.
Dla każdego zadania, na przykład problemów na temat „Współczynnik kątowy stycznej jako tangens kąta nachylenia”, zapisaliśmy poprawną odpowiedź i algorytm rozwiązania. Jednocześnie uczniowie mogą wykonywać ćwiczenia o różnym stopniu trudności online. W razie potrzeby zadanie można zapisać w sekcji „Ulubione”, aby później móc omówić jego rozwiązanie z nauczycielem.
Ładowanie...