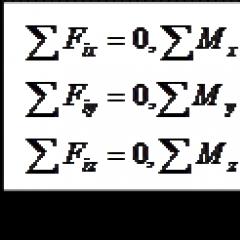Warunki równowagi układu sił w przestrzeni. Mechanika teoretyczna

Warunek równowagi przestrzennego układu sił zbiegających się: suma algebraiczna rzutów wszystkich sił na trzy wzajemnie prostopadłe osie współrzędnych musi być równa zeru, tj.

Aby znaleźć moment siły względem osi z, trzeba zaprojektować siłę do samolotu N prostopadle do osi z(ryc. 12), a następnie znajdź moment projekcji F n względem punktu O, który jest punktem przecięcia płaszczyzny N ssać z. Moment projekcji F n i będzie chwilą siły względem osi z:

Przestrzenny układ sił dowolnie rozmieszczonych to układ sił, których linie działania nie leżą w tej samej płaszczyźnie i nie przecinają się w jednym punkcie. Wypadkowa takiego układu sił jest również równa sumie geometrycznej tych sił, ale jest przedstawiana jako przekątna złożonych figur objętościowych (czworościan, ośmiościan itp.).

Warunek równowagi dla przestrzennego układu sił dowolnie rozmieszczonych: suma algebraiczna rzutów wszystkich sił na trzy wzajemnie prostopadłe osie współrzędnych musi być równa zeru, a suma algebraiczna momentów wszystkich sił względem tych samych osi współrzędnych musi być równa zeru, tj.

Tarcie

Tarcie zwany oporem wobec ruchu ciała. Nazywa się siłę, z jaką ciało opiera się ruchowi siła tarcia.

Siła tarcia jest zawsze skierowana w kierunku przeciwnym do ruchu. Siła tarcia zależy od materiału ciał trących, czystości obróbki i obecności smaru i nie zależy od wielkości powierzchni trących.

Tarcie ma miejsce: suchy, półpłynny, płynny.

Rozróżnij tarcie odpoczynek, ruch, ślizganie się I walcowanie. Siła tarcia statycznego jest większa niż siła tarcia ruchomego.

Siła tarcia jest równa iloczynowi normalnej siły nacisku i współczynnika tarcia ślizgowego (ryc. 14):

F tr =R n ƒ,

Gdzie Rn = mg cos a - normalna siła nacisku;

ƒ - współczynnik tarcia ślizgowego.

Współczynnik tarcia ślizgowego Stosunek siły tarcia do normalnej siły nacisku nazywa się:

Materiały o bardzo małym tarciu nazywane są przeciw tarciu(babbitt, brąz, grafit) Stosowany do produkcji łożysk itp.

Nazywa się materiały o dużym tarciu cierny(specjalne tworzywa sztuczne zawierające azbest i miedź). Stosowany do okładzin klocków hamulcowych i okładzin tarcz sprzęgła.

Po nasmarowaniu powierzchni ślizgowej korpus zaczyna poruszać się z mniejszym tarciem.

Rozłóżmy siłę grawitacji G na składowe G ’ i G ” (ryc. 15)

Stwórzmy równanie równowagi:

Gdzie H- odległość od powierzchni do linii działania siły;

k- współczynnik tarcia tocznego. Jest równy segmentowi OS (patrz ryc. 16)

F dv = F tr,

F tr =R p k/h

Jeśli h = d,

F tr =R p k/d

jeśli h = g,

F tr =R p k/d

Łączymy początek współrzędnych z punktem przecięcia linii działania sił układu. Wszystkie siły rzutujemy na osie współrzędnych i sumujemy odpowiednie rzuty (ryc. 7.4). Otrzymujemy rzuty wypadkowej na osie współrzędnych:

Moduł wypadkowego układu zbieżnych sił określa wzór

Kierunek wynikowego wektora jest określony przez kąty

Dowolny przestrzenny układ sił

Sprowadzenie dowolnego przestrzennego układu sił do środka O.

Podano przestrzenny układ sił (ryc. 7.5, a). Przenieśmy to do centrum O.

Siły muszą być przesuwane równolegle i powstaje układ par sił. Moment każdej z tych par jest równy iloczynowi modułu siły i odległości do środka redukcji.

W środku redukcji powstaje wiązka sił, którą można zastąpić siłą całkowitą (wektor główny) FGL (ryc. 7.5, B).

Momenty par sił można dodać, uzyskując całkowity moment układu M ch (moment główny).

W ten sposób dowolny przestrzenny układ sił sprowadza się do wektora głównego i momentu głównego.

Główny wektor jest zwykle rozkładany na trzy składowe skierowane wzdłuż osi współrzędnych (ryc. 7.5, c).

Zwykle całkowity moment rozkłada się na składowe: trzy momenty względem osi współrzędnych.

Wartość bezwzględna wektora głównego (ryc. 7.5b) jest równa

Wartość bezwzględną momentu głównego określa wzór.

Równania równowagi przestrzennego układu sił

W równowadze F rozdz = 0; M rozdz = 0. Otrzymujemy sześć równań równowagi:

Sześć równań równowagi przestrzennego układu sił odpowiada sześciu niezależnym możliwym ruchom ciała w przestrzeni: trzem ruchom wzdłuż osi współrzędnych i trzem obrotom wokół tych osi.

Przykłady rozwiązywania problemów

Przykład 1. Na korpusie w kształcie sześcianu z krawędzią A= 10 cm działają trzy siły (ryc. 7.6). Wyznaczyć momenty sił względem osi współrzędnych pokrywających się z krawędziami sześcianu.

Rozwiązanie

1. Momenty sił względem osi Oh:

2. Momenty sił względem osi Jednostka organizacyjna.

Przykład 2. Dwa koła są zamocowane na poziomym wale, g 1 = 0,4 m; g 2 = 0,8 m. Pozostałe wymiary znajdują się na ryc. 7.7. Siła jest przykładana do koła 1 F 1, do koła 2 - moc F 2= 12 kN, F 3= 4 kN.

Zdefiniuj siłę F 1 i reakcje w zawiasach A I W w stanie równowagi.

Przypomnijmy:

1. W równowadze spełnionych jest sześć równań równowagi.

Równania momentów należy zapisywać względem podpór A i B.

2. Uprawnienia F 2 \\O X; F 2\\Oj;F 3\\Oj.

Momenty tych sił względem odpowiednich osi są równe zeru.

3. Obliczenia należy uzupełnić poprzez weryfikację za pomocą dodatkowych równań równowagi.

Rozwiązanie

1. Określ siłę F\, po ułożeniu równania momentów sił względem osi Oz:

2. Wyznacz reakcje wspierające A. Na nośnik działają dwa składniki reakcji ( TAK ; XA ).

Układamy równanie momentów sił względem osi Oh"(We wsparciu W).

Obrót wokół osi Oh" nie dzieje się:

Znak minus oznacza, że reakcja jest skierowana w przeciwnym kierunku.

Obrót wokół osi Jednostka organizacyjna” tak się nie dzieje, sporządzamy równanie na momenty sił względem osi Jednostka organizacyjna”(We wsparciu W):

3. Określ reakcje w nośniku B. Na nośnik działają dwa składniki reakcji ( X B , Y B ). Układamy równanie momentów sił względem osi Oh(wsparcie A):

Układamy równanie momentów wokół osi Jednostka organizacyjna(wsparcie A):

4.Sprawdź. Używamy równań rzutowania:

Kalkulacja została wykonana prawidłowo.

Przykład 3. Określ wartość liczbową siły P 1 , przy którym wał Słońce(ryc. 1.21, A) będzie w równowadze. Przy znalezionej wartości siły P 1 określić reakcje podporowe.

Siły działające na koła zębate R I P 1 skierowany stycznie do początkowych okręgów kół; wytrzymałość T I T 1 - zgodnie z promieniami kół; wytrzymałość 1 równolegle do osi wału. T = 0,36 P, 7 T 1 = P 1; A 1 = 0,12 P 1.

Rozwiązanie

Podpory wału pokazane na rys. 1.21, a, należy traktować jako przestrzenne podpory przegubowe, które zapobiegają ruchom liniowym w kierunkach osi I I w(wybrany układ współrzędnych pokazano na rys. 1.21, B).

Uwalniamy wał z połączeń i zastępujemy ich działanie reakcjami V V, N V, V C, N C (ryc. 1.21, B). Otrzymaliśmy przestrzenny układ sił, dla którego układamy równania równowagi wykorzystując wybrany układ współrzędnych (rys. 1.21.6):

Gdzie 1*1.25D/2 - moment względem osi I wytrzymałość 1, włączony na prawy bieg.

Momenty wokół osi I wytrzymałość T 1 I 1(przyłożony do środkowego biegu), P 1 (przyłożony do prawego biegu) i P są równe zeru, ponieważ siły P, T 1, P 1 są równoległe do osi I, i siła A 1 przecina oś I.

Gdzie VC = 0,37P;

Gdzie V B = 0,37 P.

stąd te reakcje V B I V C zdefiniowany poprawnie;

Gdzie 1* 1.25D/2- moment wokół osi w wytrzymałość 1, zastosowany do środkowego biegu.

Momenty wokół osi w siły T, P 1 (przyłożone do biegu środkowego), 1 I T 1(przyłożony do prawego biegu) są równe zeru, ponieważ siły T, R1, T1 równolegle do osi v, siła 1 przecina oś w.

skąd H.C = 0,81P;

skąd H.C = 1,274P

Utwórzmy równanie weryfikacyjne:

stąd te reakcje N.V I N.S zdefiniowane poprawnie.

Podsumowując, zauważamy, że reakcje wsparcia okazały się mieć znak plus. Oznacza to, że wybrane kierunki V B, N B, V C I N.S pokrywają się z rzeczywistymi kierunkami reakcji wiązań.

Przykład 4. Siła nacisku korbowodu silnika parowego P = 25 kN przekazywana jest na środek czopa wału korbowego w miejscu D pod kątem α = 30° do poziomu z policzkami kolan ustawionymi pionowo (ryc. 1.22). Na końcu wału zamontowane jest koło pasowe napędu pasowego. Napięcie gałęzi napędowej paska jest dwukrotnie większe niż gałęzi napędzanej, tj. S 1 = 2 S 2 . Siła ciężkości koła zamachowego G = 10 kN.

Określić napięcie gałęzi napędu pasowego i reakcje łożysk A I W, pomijając masę wału.

Rozwiązanie

Rozważamy równowagę poziomego wału korbowego z kołem pasowym. Przykładamy określone siły zgodnie z warunkami problemu P, S 1, S 2 I G . Uwalniamy wał z łączników wsporczych i zastępujemy ich działanie reakcjami V A, N A, V B I N.V. Wybieramy osie współrzędnych, jak pokazano na ryc. 1,22. Zawiasowe A I W wzdłuż osi nie zachodzą żadne reakcje w, ponieważ napięcie gałęzi pasa i wszystkie inne siły działają w płaszczyznach prostopadłych do tej osi.

Utwórzmy równania równowagi:

Ponadto, zgodnie z warunkami problemu, mamy inne równanie

Zatem istnieje tutaj sześć nieznanych sił S 1, S 2, N A, V A, N B I V B i sześć równań je łączących.

Równanie rzutów na oś w w rozważanym przykładzie zamienia się w tożsamość 0 = 0, ponieważ wszystkie siły leżą w płaszczyznach prostopadłych do osi w.

Podstawiając S 1 =2S 2 do równań równowagi i rozwiązując je, znajdujemy:

Wartość reakcji N.V Okazało się, że jest ze znakiem minus. Oznacza to, że w rzeczywistości jego kierunek jest odwrotny do założonego na ryc. 1,22.

Pytania testowe i zadania

1. Zapisz wzory na obliczenie wektora głównego przestrzennego układu sił zbieżnych.

2. Zapisz wzór na obliczenie wektora głównego układu przestrzennego sił arbitralnie rozmieszczonych.

3. Zapisz wzór na obliczenie momentu głównego przestrzennego układu sił.

4. Zapisz układ równań równowagi przestrzennego układu sił.

5. Które równanie równowagi należy zastosować do określenia reakcji pręta R 1 (rys. 7.8)?

6. Wyznacz moment główny układu sił (ryc. 7.9). Punkt odniesienia jest początkiem współrzędnych. Osie współrzędnych pokrywają się z krawędziami sześcianu, krawędź sześcianu wynosi 20 cm; F 1 - 20 kN; F 2 - 30 kN.

7. Wyznacz reakcję Xb (ryc. 7.10). Oś pionowa z kołem obciążona jest dwoma siłami poziomymi. Uprawnienie F 1 I F 2 równolegle do osi Oh. AO = 0,3 m; OB= 0,5 m; F 1 = 2kN; F 2 = 3,5 kN.

Rekomendacje. Utwórz równanie momentów wokół osi Jednostka organizacyjna” w tym punkcie A.

8. Odpowiedz na pytania testowe.

Warunki równowagi wektorowej dla dowolnego układu sił: dla równowagi układu sił przyłożonych do ciała sztywnego konieczne i wystarczające jest, aby wektor główny układu sił był równy zeru i główny moment układu sił względem dowolnego środka redukcji był również równy zeru. W przeciwnym razie: aby ~0 były konieczne i wystarczające następujące warunki:

,
Lub
,
. (19)

Warunki równowagi przestrzennego układu sił w postaci analitycznej

Dla równowagi przestrzennego układu sił przyłożonych do ciała stałego konieczne i wystarczające jest, aby trzy sumy rzutów wszystkich sił na osie współrzędnych kartezjańskich były równe zero, a trzy sumy momentów wszystkich sił względnych do trzech osi współrzędnych są również równe zeru.

. (20)

Warunki równowagi dla przestrzennego układu sił zbiegających się

Dla równowagi przestrzennego układu zbieżnych sił przyłożonych do ciała stałego konieczne i wystarczające jest, aby sumy rzutów sił na każdą z trzech prostokątnych osi współrzędnych były równe zeru:

;
;
, (21)

W przypadku płaskiego układu zbieżnych sił, zwykle jedna z osi współrzędnych
, wybiera się prostopadle do sił, a pozostałe dwie osie wybiera się odpowiednio w płaszczyźnie sił. D Dla równowagi płaskiego układu zbieżnych sił działających na ciało stałe konieczne i wystarczające jest, aby sumy rzutów tych sił na każdą z dwóch prostokątnych osi współrzędnych leżących w płaszczyźnie sił były równe zeru:

;
, (22)

Warunki równowagi dla przestrzennego układu sił równoległych

Skierujmy oś
równolegle do sił: dla równowagi przestrzennego układu równoległych sił działających na ciało stałe konieczne i wystarczające jest, aby suma algebraiczna tych sił była równa zero, a suma momentów sił względem dwóch osi współrzędnych prostopadłych do tych sił wynosiła również równa zeru:

Warunki równowagi dla płaskiego układu sił

Ustawmy osie
I
w płaszczyźnie działania sił.

Warunki równowagi dla płaskiego układu sił w pierwszej postaci: dla równowagi płaskiego układu sił działających na ciało stałe konieczne i wystarczające jest, aby sumy rzutów tych sił na każdą z dwóch prostokątnych osi współrzędnych znajdujących się w płaszczyźnie działania sił były równe zeru a suma momentów algebraicznych sił względem dowolnego punktu znajdującego się na płaszczyźnie sił również wynosiła zero:

(24)

Dla równowagi płaskiego układu sił równoległych działających na ciało stałe konieczne i wystarczające jest, aby suma algebraiczna sił była równa zero, a suma momentów algebraicznych sił względem dowolnego punktu znajdującego się na płaszczyźnie sił jest również równa zeru:

(25)

Twierdzenie o trzech momentach (druga postać warunków równowagi): dla równowagi płaskiego układu sił przyłożonych do ciała sztywnego konieczne i wystarczające jest, aby sumy momentów algebraicznych sił układu względem dowolnych trzech punktów znajdujących się w płaszczyźnie działania sił, a nie leżących na tej samej linii prostej są równe zeru:

Trzecia postać warunków równowagi: dla równowagi płaskiego układu sił przyłożonych do ciała stałego konieczne i wystarczające jest, aby sumy algebraicznych momentów sił względem dowolnych dwóch punktów leżących na płaszczyźnie działania sił były równe zero, a algebraiczna suma rzutów tych sił na dowolną oś płaszczyzny nieprostopadłą do prostej przechodzącej przez dwa punkty momentowe również była równa zeru, tj.

To., dla równowagi dowolnego przestrzennego układu sił konieczne i wystarczające jest, aby suma algebraiczna rzutów wszystkich tych sił na każdą z trzech dowolnie wybranych osi współrzędnych była równa zeru oraz aby suma algebraiczna ich momentów względem każda z tych osi jest również równa zeru.

Nazywa się warunki (1.33). warunki równowagi dowolnego przestrzennego układu sił w postaci analitycznej.

Warunki równowagi dla przestrzennego układu sił równoległych. Jeżeli linie działania wszystkich sił danego układu sił znajdują się w różnych płaszczyznach i są do siebie równoległe, wówczas taki układ sił nazywa się przestrzenny układ sił równoległych.

Wykorzystując warunki równowagi (1.33) dowolnego przestrzennego układu sił, można znaleźć warunki równowagi przestrzennego układu sił równoległych. (Warunki równowagi, które wcześniej wyprowadziliśmy dla płaskich i przestrzennych układów zbieżnych sił, dowolnego płaskiego układu sił i płaskiego układu sił równoległych, można również otrzymać, korzystając z warunków równowagi (1.33) dowolnego przestrzennego układu sił).

Niech na ciało stałe działa przestrzenny układ sił równoległych (rysunek 1.26). Ponieważ wybór osi współrzędnych jest dowolny, istnieje możliwość takiego doboru osi współrzędnych, aby oś z był równoległy do sił. Przy takim wyborze osi współrzędnych rzuty każdej z sił na oś X I Na i ich momenty względem osi z będą równe zeru, a co za tym idzie równości , i są spełnione niezależnie od tego, czy dany układ sił znajduje się w równowadze, czy nie, a zatem przestają być warunkami równowagi. Zatem układ (1.33) da tylko trzy warunki równowagi:

Stąd, dla równowagi przestrzennego układu sił równoległych konieczne i wystarczające jest, aby suma algebraiczna rzutów wszystkich sił na oś równoległą do tych sił była równa zero oraz aby suma algebraiczna ich momentów względem każdej z dwóch współrzędnych osie prostopadłe do tych sił również są równe zeru.

1. Wybierz ciało (lub punkt), którego równowagę należy uwzględnić w tym zadaniu.

2. Uwolnij wybrane ciało z wiązań i zobrazuj (uporządkuj) wszystkie siły czynne i siły reakcji odrzuconych wiązań działających na to ciało (i tylko na to ciało). Odrębnie należy przedstawić ciało wolne od połączeń, z przyłączonym do niego układem sił czynnych i reakcji.

3. Napisz równania równowagi. Aby sporządzić równania równowagi, należy najpierw wybrać osie współrzędnych. Wyboru tego można dokonać dowolnie, jednak powstałe równania równowagi będą łatwiej rozwiązane, jeśli jedna z osi będzie skierowana prostopadle do linii działania jakiejś nieznanej siły reakcji. Rozwiązanie powstałych równań równowagi należy z reguły przeprowadzić do końca w postaci ogólnej (algebraicznej). Następnie dla wymaganych wielkości otrzymane zostaną wzory, które pozwolą na analizę znalezionych wyników; wartości liczbowe znalezionych wielkości są podstawiane tylko do wzorów końcowych. Równania równowagi sporządza się stosując analityczną metodę rozwiązywania problemów równowagi układu zbieżnych sił. Jeśli jednak liczba zbiegających się sił, których równowaga jest brana pod uwagę, wynosi trzy, wówczas do rozwiązania tych problemów wygodnie jest zastosować metodę geometryczną. Rozwiązanie w tym przypadku sprowadza się do tego, że zamiast równań równowagi wszystkich działających sił (wiązania czynnego i reakcji) konstruowany jest trójkąt sił, który na podstawie geometrycznego warunku równowagi musi zostać domknięty (konstrukcja trójkąt ten powinien zaczynać się od danej siły). Rozwiązując trójkąt sił, znajdujemy wymagane ilości.

Dynamika

Aby zrozumieć sekcję dynamiki, musisz znać następujące informacje. Z matematyki - iloczyn skalarny dwóch wektorów, równania różniczkowe. Z fizyki – prawa zachowania energii i pędu. Teoria oscylacji. Zalecane jest zapoznanie się z tymi tematami.

Jak wyjaśniono w § 4.4, warunki konieczne i wystarczające równowagi przestrzennego układu sił przyłożonych do ciała sztywnego można zapisać w postaci trzech równań rzutowania (4.16) i trzech momentów (4.17):

, , . (7.14)

Jeżeli ciało jest całkowicie nieruchome, wówczas działające na nie siły są w równowadze, a równania (7.13) i (7.14) służą do określenia reakcji podporowych. Oczywiście mogą zaistnieć przypadki, w których równania te nie wystarczą do określenia reakcji podporowych; Nie będziemy rozważać takich układów statycznie niewyznaczalnych.

Dla przestrzennego układu sił równoległych równania równowagi przyjmują postać (§ 4.4[‡]):

, , . (7.15)

Rozważmy teraz przypadki, gdy ciało jest tylko częściowo unieruchomione, tj. połączenia nałożone na ciało nie gwarantują równowagi ciała. Można wskazać cztery szczególne przypadki.

1. Ciało stałe ma jeden punkt stały. Innymi słowy, jest on przymocowany do stałego punktu za pomocą doskonałego złącza kulistego.

Umieśćmy początek ustalonego układu współrzędnych w tym punkcie. Działanie połączenia w punkcie A Zastąpmy to reakcją; ponieważ nie jest znana wielkość i kierunek, przedstawimy go w postaci trzech nieznanych składowych , , , skierowanych odpowiednio wzdłuż osi , , .

Równania równowagi (7.13) i (7.14) w tym przypadku zostaną zapisane w postaci:

1) ,

2) ,

3) ,

4) ,

5) ,

Ostatnie trzy równania nie zawierają składników reakcji, ponieważ linia działania tej siły przechodzi przez punkt A. W konsekwencji równania te ustalają zależności między siłami czynnymi niezbędnymi do zachowania równowagi ciała, a pierwsze trzy równania można wykorzystać do określenia składników reakcji.

Zatem, warunkiem równowagi ciała sztywnego mającego jeden punkt stały jest równość do zera każdej z sum algebraicznych momentów wszystkich sił czynnych układu względem trzech osi przecinających się w ustalonym punkcie ciała .

2. Ciało ma dwa stałe punkty. Będzie tak na przykład w przypadku zamocowania go w dwóch stałych punktach za pomocą zawiasów.

Wybierzmy początek współrzędnych w punkcie A i skieruj oś wzdłuż linii przechodzącej przez punkty A I W. Zastąpmy działanie wiązań reakcjami, kierując składniki reakcji wzdłuż osi współrzędnych. Oznaczmy odległość między punktami A I W Poprzez A; wówczas równania równowagi (7.13) i (7.14) zostaną zapisane w postaci:

1) ,

2) ,

3) ,

4) ,

5) ,

Ostatnie równanie nie zawiera sił reakcji i ustala związek pomiędzy siłami czynnymi niezbędnymi do zachowania równowagi ciała. Stąd, warunkiem równowagi ciała sztywnego, które ma dwa punkty stałe, jest równość do zera algebraicznej sumy momentów wszystkich sił czynnych przyłożonych do ciała względem osi przechodzącej przez punkty stałe . Pierwsze pięć równań służy do wyznaczania nieznanych składników reakcji , , , , .

Należy pamiętać, że składniki i nie mogą być określane oddzielnie. Z trzeciego równania wyznaczana jest tylko suma + i dlatego problem dotyczący każdej z tych niewiadomych dla ciała sztywnego jest statycznie niewyznaczalny. Jeśli jednak w tym momencie W Jeśli nie ma przegubu kulistego, lecz cylindryczny (czyli łożysko), który nie przeszkadza w wzdłużnym przesuwaniu się korpusu wzdłuż osi obrotu, to problem staje się definiowalny statycznie.

Korpus ma stałą oś obrotu, wzdłuż której może się przesuwać bez tarcia. Oznacza to, że w punktach A I W istnieją przeguby cylindryczne (łożyska), a składowe ich reakcji wzdłuż osi obrotu są równe zeru. W rezultacie równania równowagi przyjmą postać:

1) ,

2) ,

4) ,

5) ,

Dwa z równań (7.18), mianowicie trzecie i szóste, nakładają ograniczenia na układ sił czynnych, a pozostałe równania służą do określenia reakcji.

Ciało spoczywa w trzech punktach na gładkiej powierzchni, a punkty podparcia nie leżą na tej samej linii prostej. Oznaczmy te punkty przez A, W I Z i kompatybilny z samolotem ABC płaszczyzna współrzędnych Acha. Zastępując działanie połączeń reakcjami pionowymi , i , warunki równowagi (7.14) zapisujemy w następującej postaci:

3) ,

4) ,

5) ,

Równania trzecie - piąte mogą służyć do wyznaczania nieznanych reakcji, a równania pierwsze, drugie i szóste przedstawiają warunki łączące siły czynne i niezbędne dla równowagi ciała. Oczywiście, aby organizm mógł zachować równowagę muszą zostać spełnione następujące warunki: , , gdyż w punktach podparcia mogą wystąpić jedynie reakcje o wyżej przyjętym kierunku.

Jeśli ciało spoczywa na płaszczyźnie poziomej w więcej niż trzech punktach, wówczas problem staje się statycznie niewyznaczalny, ponieważ w tym przypadku będzie tyle reakcji, ile jest punktów i pozostaną tylko trzy równania do określenia reakcji.

Zadanie 7.3. Znajdź wektor główny i moment główny układu sił pokazanego na ryc. Siły przykładane są do wierzchołków sześcianu i kierowane wzdłuż jego krawędzi, oraz , . Długość krawędzi sześcianu wynosi A.