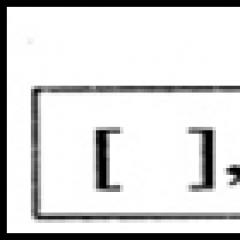
Jak otwierać nawiasy w wyrażeniach i równaniach. Zasady matematyki

Nawiasy służą do wskazania kolejności wykonywania czynności w wyrażeniach numerycznych i alfabetycznych, a także w wyrażeniach ze zmiennymi. Wygodnie jest przejść z wyrażenia z nawiasami do identycznie równego wyrażenia bez nawiasów. Ta technika nazywa się otwieraniem nawiasów.

Rozszerzenie nawiasów oznacza pozbycie się ekspresji tych nawiasów.

Na szczególną uwagę zasługuje inny punkt, który dotyczy specyfiki pisania rozwiązań przy otwieraniu nawiasów. Wyrażenie początkowe możemy zapisać w nawiasach, a wynik uzyskany po otwarciu nawiasów jako równość. Na przykład po otwarciu nawiasów zamiast wyrażenia
3−(5−7) otrzymujemy wyrażenie 3−5+7. Oba te wyrażenia możemy zapisać jako równość 3−(5−7)=3−5+7.

I jeszcze jeden ważny punkt. W matematyce, aby zredukować wpisy, zwyczajowo nie pisze się znaku plus, jeśli jest on pierwszy w wyrażeniu lub w nawiasach. Na przykład, jeśli dodamy dwie liczby dodatnie, na przykład siedem i trzy, to piszemy nie +7 + 3, ale po prostu 7 + 3, mimo że siedem jest również liczbą dodatnią. Podobnie, jeśli widzisz na przykład wyrażenie (5 + x) - wiedz, że przed nawiasem kwadratowym jest plus, którego nie ma, a przed znakiem jest plus + (+5 + x). pięć.

Reguła rozszerzania wspornika do dodawania

Podczas otwierania nawiasów, jeśli przed nawiasami jest plus, to ten plus jest pomijany wraz z nawiasami.

Przykład. Otwórz nawiasy w wyrażeniu 2 + (7 + 3) Przed nawiasami plus, znaki przed liczbami w nawiasach nie zmieniają się.

2 + (7 + 3) = 2 + 7 + 3

Zasada rozwijania nawiasów przy odejmowaniu

Jeśli przed nawiasami jest minus, to ten minus jest pomijany wraz z nawiasami, ale wyrazy, które były w nawiasach, zmieniają swój znak na przeciwny. Brak znaku przed pierwszym terminem w nawiasie oznacza znak +.

Przykład. Nawiasy otwarte w wyrażeniu 2 − (7 + 3)

Przed nawiasami jest minus, więc musisz zmienić znaki przed liczbami z nawiasów. Nie ma znaku w nawiasach przed liczbą 7, co oznacza, że siódemka jest dodatnia, uważa się, że znak + jest przed nią.

2 − (7 + 3) = 2 − (+ 7 + 3)

Przy otwieraniu nawiasów usuwamy z przykładu minus, który był przed nawiasami, oraz same nawiasy 2 − (+ 7 + 3) i zmieniamy znaki, które były w nawiasach na przeciwne.

2 − (+ 7 + 3) = 2 − 7 − 3

Rozwijanie nawiasów podczas mnożenia

Jeśli przed nawiasami znajduje się znak mnożenia, każda liczba w nawiasie jest mnożona przez czynnik przed nawiasami. Jednocześnie pomnożenie minusa przez minus daje plus, a pomnożenie minusa przez plus, jak pomnożenie plusa przez minus, daje minus.

W ten sposób nawiasy w iloczynach są rozszerzane zgodnie z rozdzielczą własnością mnożenia.

Przykład. 2 (9 - 7) = 2 9 - 2 7

Podczas mnożenia nawiasu przez nawias każdy wyraz pierwszego nawiasu jest mnożony przez każdy wyraz drugiego nawiasu.

(2 + 3) (4 + 5) = 2 4 + 2 5 + 3 4 + 3 5

Tak naprawdę nie ma potrzeby zapamiętywać wszystkich reguł, wystarczy pamiętać tylko jedną, tę c(a−b)=ca−cb. Czemu? Ponieważ jeśli podstawimy jedynkę zamiast c, otrzymamy regułę (a-b)=a-b. A jeśli podstawimy minus jeden, otrzymamy regułę −(a−b)=−a+b. Cóż, jeśli zastąpisz c inny nawias kwadratowy, uzyskasz ostatnią regułę.

Rozwiń nawiasy podczas dzielenia

Jeśli po nawiasach znajduje się znak dzielenia, to każda liczba w nawiasie jest podzielna przez dzielnik po nawiasach i odwrotnie.

Przykład. (9 + 6) : 3=9: 3 + 6: 3

Jak rozwinąć nawiasy zagnieżdżone

Jeśli wyrażenie zawiera nawiasy zagnieżdżone, są one rozwijane w kolejności, zaczynając od zewnętrznego lub wewnętrznego.

Jednocześnie przy otwieraniu jednego z nawiasów ważne jest, aby nie dotykać pozostałych nawiasów, tylko przepisać je tak, jak są.

Przykład. 12 - (a + (6 - b) - 3) = 12 - a - (6 - b) + 3 = 12 - a - 6 + b + 3 = 9 - a + b

Równania liniowe. Rozwiązanie, przykłady.

Uwaga!
Są dodatkowe
materiał w sekcji specjalnej 555.
Dla tych, którzy zdecydowanie „nie bardzo…”
I dla tych, którzy "bardzo...")

Równania liniowe.

Równania liniowe nie są najtrudniejszym tematem w matematyce szkolnej. Ale jest tam kilka sztuczek, które mogą zagadać nawet wyszkolonego ucznia. Możemy to rozgryźć?)

Równanie liniowe jest zwykle definiowane jako równanie o postaci:

topór + b = 0 gdzie a i b- dowolne liczby.

2x + 7 = 0. Tutaj a=2, b=7

0,1x - 2,3 = 0 Tutaj a=0,1, b=-2,3

12x + 1/2 = 0 Tutaj a=12, b=1/2

Nic skomplikowanego, prawda? Zwłaszcza jeśli nie zauważasz słów: „gdzie a i b są liczbami”... A jeśli zauważysz, ale niedbale o tym pomyśl?) W końcu, jeśli a=0, b=0(możliwe są jakieś liczby?), wtedy otrzymujemy zabawne wyrażenie:

Ale to nie wszystko! Jeśli powiedzmy a=0, a b=5, okazuje się, że jest to coś całkiem absurdalnego:

Co nadweręża i podkopuje zaufanie do matematyki, tak...) Zwłaszcza na egzaminach. Ale z tych dziwnych wyrażeń musisz także znaleźć X! Który w ogóle nie istnieje. I, co zaskakujące, ten X jest bardzo łatwy do znalezienia. Dowiemy się, jak to zrobić. W tej lekcji.

Jak rozpoznać wygląd równania liniowego? To zależy od tego, jaki wygląd.) Sztuczka polega na tym, że równania liniowe są nazywane nie tylko równaniami postaci topór + b = 0 , ale także wszelkie równania, które do tej postaci sprowadza się poprzez przekształcenia i uproszczenia. A kto wie, czy jest zmniejszony, czy nie?)

W niektórych przypadkach można wyraźnie rozpoznać równanie liniowe. Powiedzmy, że jeśli mamy równanie, w którym są tylko niewiadome pierwszego stopnia, tak liczby. A równanie nie ułamki podzielone przez nieznany , to jest ważne! I podział przez numer, lub ułamek liczbowy - to wszystko! Na przykład:

To jest równanie liniowe. Są tu ułamki, ale nie ma x w kwadracie, sześcianie itd., i nie ma x w mianownikach, tj. Nie dzielenie przez x. A oto równanie

nie można nazwać liniowym. Tutaj wszystkie x są w pierwszym stopniu, ale jest dzielenie przez wyrażenie z x. Po uproszczeniach i przekształceniach możesz otrzymać równanie liniowe, kwadratowe i cokolwiek chcesz.

Okazuje się, że niemożliwe jest znalezienie równania liniowego w jakimś skomplikowanym przykładzie, dopóki prawie go nie rozwiążesz. To denerwujące. Ale w zadaniach z reguły nie pytają o formę równania, prawda? W zadaniach równania są uporządkowane rozwiązywać. To sprawia, że jestem szczęśliwy.)

Rozwiązywanie równań liniowych. Przykłady.

Całe rozwiązanie równań liniowych składa się z identycznych przekształceń równań. Nawiasem mówiąc, te przekształcenia (aż dwie!) leżą u podstaw rozwiązań wszystkie równania matematyczne. Innymi słowy, decyzja każdy Równanie zaczyna się od tych samych przekształceń. W przypadku równań liniowych to (rozwiązanie) na tych przekształceniach kończy się pełną odpowiedzią. Warto skorzystać z linku, prawda?) Ponadto istnieją również przykłady rozwiązywania równań liniowych.

Zacznijmy od najprostszego przykładu. Bez pułapek. Powiedzmy, że musimy rozwiązać następujące równanie.

x - 3 = 2 - 4x

To jest równanie liniowe. Wszystkie X są do pierwszej potęgi, nie ma dzielenia przez X. Ale tak naprawdę nie obchodzi nas, jakie to równanie. Musimy to rozwiązać. Schemat tutaj jest prosty. Zbierz wszystko, co ma x po lewej stronie równania, wszystko bez x (liczby) po prawej.

Aby to zrobić, musisz przenieść - 4x w lewo, oczywiście ze zmianą znaku, ale - 3 - w prawo. Nawiasem mówiąc, to jest pierwsza identyczna transformacja równań. Zdziwiony? Więc nie poszli za linkiem, ale na próżno ...) Otrzymujemy:

x + 4x = 2 + 3

Podajemy podobne, uważamy:

Czego potrzebujemy, aby być całkowicie szczęśliwym? Tak, aby po lewej stronie był czysty X! Pięć przeszkadza. Pozbądź się piątki za pomocą druga identyczna transformacja równań. Mianowicie dzielimy obie części równania przez 5. Otrzymujemy gotową odpowiedź:

Oczywiście elementarny przykład. To na rozgrzewkę.) Nie jest jasne, dlaczego przywołałem tutaj identyczne przekształcenia? OK. Bierzemy byka za rogi.) Zdecydujmy się na coś bardziej imponującego.

Na przykład, oto to równanie:

Gdzie zaczynamy? Z X - w lewo, bez X - w prawo? Może tak być. Małe kroki wzdłuż długiej drogi. I możesz natychmiast, w uniwersalny i potężny sposób. O ile oczywiście w twoim arsenale nie ma identycznych przekształceń równań.

Zadaję Ci kluczowe pytanie: Czego najbardziej nie lubisz w tym równaniu?

95 osób na 100 odpowie: ułamki ! Odpowiedź jest prawidłowa. Więc pozbądźmy się ich. Więc zaczynamy od razu druga identyczna transformacja. Przez co należy pomnożyć ułamek po lewej stronie, aby mianownik został całkowicie zmniejszony? Zgadza się, 3. A po prawej? Przez 4. Ale matematyka pozwala nam pomnożyć obie strony przez ten sam numer. Jak się wydostaniemy? Pomnóżmy obie strony przez 12! Tych. do wspólnego mianownika. Wtedy trzy zostaną zredukowane, a cztery. Nie zapominaj, że musisz pomnożyć każdą część całkowicie. Oto jak wygląda pierwszy krok:

Rozwijanie nawiasów:

Notatka! Licznik ułamka (x+2) Wziąłem w nawiasy! Dzieje się tak, ponieważ mnożąc ułamki, licznik mnoży się przez całość, całkowicie! A teraz możesz redukować ułamki i redukować:

Otwarcie pozostałych nawiasów:

Nie przykład, ale czysta przyjemność!) Teraz przypominamy sobie zaklęcie z niższych klas: z x - w lewo, bez x - w prawo! I zastosuj tę transformację:

Oto niektóre z nich:

I obie części dzielimy przez 25, tj. zastosuj ponownie drugą transformację:

To wszystko. Odpowiedź: x=0,16

Uwaga: aby sprowadzić oryginalne mylące równanie do przyjemnej postaci, użyliśmy dwóch (tylko dwóch!) identyczne przekształcenia- tłumaczenie lewo-prawo ze zmianą znaku i mnożeniem - dzieleniem równania przez tę samą liczbę. To jest uniwersalny sposób! Tak będziemy pracować każdy równania! Absolutnie dowolny. Dlatego cały czas powtarzam te same przekształcenia.)

Jak widać, zasada rozwiązywania równań liniowych jest prosta. Bierzemy równanie i upraszczamy je za pomocą identycznych przekształceń, aż otrzymamy odpowiedź. Główne problemy są tutaj w obliczeniach, a nie w zasadzie rozwiązania.

Ale… Są takie niespodzianki w procesie rozwiązywania najbardziej elementarnych równań liniowych, że potrafią doprowadzić do silnego odrętwienia…) Na szczęście takie niespodzianki mogą być tylko dwie. Nazwijmy je szczególnymi przypadkami.

Szczególne przypadki rozwiązywania równań liniowych.

Najpierw niespodzianka.

Załóżmy, że natkniesz się na równanie elementarne, coś takiego:

2x+3=5x+5 - 3x - 2

Nieco znudzony przenosimy z X w lewo, bez X - w prawo... Ze zmianą znaku wszystko jest podbródkowo-chinarowe... Otrzymujemy:

2x-5x+3x=5-2-3

Wierzymy i… o mój! Otrzymujemy:

Ta równość sama w sobie nie budzi zastrzeżeń. Zero to naprawdę zero. Ale X zniknął! I musimy napisać w odpowiedzi, ile x jest równe. W przeciwnym razie rozwiązanie się nie liczy, tak...) Ślepy zaułek?

Spokój! W takich wątpliwych przypadkach zachowują najogólniejsze zasady. Jak rozwiązywać równania? Co to znaczy rozwiązać równanie? To znaczy, znajdź wszystkie wartości x, które po wstawieniu do oryginalnego równania dadzą nam poprawną równość.

Ale mamy poprawną równość już stało się! 0=0, gdzie tak naprawdę?! Pozostaje dowiedzieć się, przy jakim x jest to uzyskane. W jakie wartości x można podstawić? oryginał równanie jeśli te x's nadal kurczyć się do zera? Pospiesz się?)

Tak!!! Xs można podstawić każdy! Co chcesz. Co najmniej 5, co najmniej 0,05, co najmniej -220. Nadal będą się kurczyć. Jeśli mi nie wierzysz, możesz to sprawdzić.) Zastąp dowolne wartości x w oryginał równanie i obliczenia. Cały czas będzie uzyskiwana czysta prawda: 0=0, 2=2, -7,1=-7,1 i tak dalej.

Oto twoja odpowiedź: x jest dowolną liczbą.

Odpowiedź można zapisać różnymi symbolami matematycznymi, istota się nie zmienia. To jest całkowicie poprawna i kompletna odpowiedź.

Niespodzianka druga.

Weźmy to samo elementarne równanie liniowe i zmieńmy w nim tylko jedną liczbę. Tak zdecydujemy:

2x+1=5x+5 - 3x - 2

Po tych samych identycznych przekształceniach otrzymujemy coś intrygującego:

Lubię to. Rozwiązał równanie liniowe, uzyskał dziwną równość. Mówiąc matematycznie, mamy zła równość. Mówiąc prościej, to nieprawda. Zachwycać się. Niemniej jednak ten nonsens jest całkiem dobrym powodem prawidłowego rozwiązania równania.)

Ponownie myślimy w oparciu o ogólne zasady. Co da nam x po wstawieniu do pierwotnego równania? prawidłowy równość? Tak, żaden! Nie ma takich xów. Cokolwiek zastąpisz, wszystko zostanie zredukowane, bzdury pozostaną.)

Oto twoja odpowiedź: nie ma rozwiązań.

To również jest całkowicie słuszna odpowiedź. W matematyce takie odpowiedzi często się zdarzają.

Lubię to. Teraz mam nadzieję, że utrata X w procesie rozwiązywania dowolnego (nie tylko liniowego) równania w ogóle Ci nie przeszkadza. Sprawa jest znajoma.)

Teraz, gdy uporaliśmy się ze wszystkimi pułapkami w równaniach liniowych, rozwiązanie ich ma sens.

Jeśli podoba Ci się ta strona...

Nawiasem mówiąc, mam dla Ciebie kilka innych interesujących stron.)

Możesz ćwiczyć rozwiązywanie przykładów i sprawdzać swój poziom. Testowanie z natychmiastową weryfikacją. Nauka - z zainteresowaniem!)

możesz zapoznać się z funkcjami i pochodnymi.

Nie wszystkie równania zawierające nawiasy są rozwiązywane w ten sam sposób. Oczywiście najczęściej muszą otworzyć nawiasy i podać podobne terminy (jednak sposoby otwierania nawiasów są różne). Ale czasami nie trzeba otwierać nawiasów. Rozważmy wszystkie te przypadki na konkretnych przykładach:

5x - (3x - 7) = 9 + (-4x + 16).
2x - 3(x + 5) = -12.
(x + 1) (7x - 21) = 0.

Rozwiązywanie równań przez otwarcie wspornika

Ta metoda rozwiązywania równań jest najczęstsza, ale nawet przy całej swojej pozornej uniwersalności dzieli się na podgatunki w zależności od sposobu otwierania nawiasów.

1) Rozwiązanie równania 5x - (3x - 7) = 9 + (-4x + 16).

W tym równaniu przed nawiasami znajdują się znaki minus i plus. Aby otworzyć nawiasy w pierwszym przypadku, w którym są poprzedzone znakiem minus, wszystkie znaki w nawiasach należy odwrócić. Druga para nawiasów poprzedzona jest znakiem plus, który nie ma wpływu na znaki w nawiasach, więc można je po prostu pominąć. Otrzymujemy:

5x - 3x + 7 = 9 - 4x + 16.

Wyrazy z x zostaną przeniesione na lewą stronę równania, a reszta na prawą (znaki przenoszonych wyrazów zmienią się na przeciwne):

5x - 3x + 4x = 9 + 16 - 7.

Oto podobne terminy:

Aby znaleźć nieznany czynnik x, podziel iloczyn 18 przez znany czynnik 6:

x \u003d 18/6 \u003d 3.

2) Rozwiązanie równania 2x - 3(x + 5) = -12.

W tym równaniu najpierw musisz otworzyć nawiasy, ale stosując właściwość rozdzielności: aby pomnożyć -3 przez sumę (x + 5), należy pomnożyć -3 przez każdy wyraz w nawiasie i dodać otrzymane iloczyny:

2x - 3x - 15 = -12

x = 3 / (-1) = 3.

Rozwiązywanie równań bez otwierania nawiasów

Trzecie równanie (x + 1) (7x - 21) \u003d 0 można również rozwiązać, otwierając nawiasy, ale w takich przypadkach znacznie łatwiej jest użyć właściwości mnożenia: iloczyn wynosi zero, gdy jeden z czynników wynosi zero . Znaczy:

x + 1 = 0 lub 7x - 21 = 0.

Jedna z najważniejszych umiejętności w wstęp do 5 klasy to umiejętność rozwiązywania prostych równań. Ponieważ klasa 5 nie jest tak daleko od szkoły podstawowej, nie ma tak wielu rodzajów równań, które uczeń może rozwiązać. Przedstawimy Ci wszystkie główne typy równań, które musisz rozwiązać, jeśli chcesz zapisać się do szkoły fizyki i matematyki.

1 typ: "bulwiasty"
Są to równania, z którymi prawie na pewno się spotkasz, kiedy wstęp do dowolnej szkoły lub koło piątej klasy jako osobne zadanie. Łatwo je odróżnić od innych: zawierają zmienną tylko raz. Na przykład lub.
Rozwiązuje się je bardzo prosto: wystarczy „dostać się” w nieznane, stopniowo „usuwając” wszystko, co zbędne, co go otacza - jak obieranie cebuli - stąd nazwa. Aby go rozwiązać wystarczy zapamiętać kilka zasad z drugiej klasy. Wymieńmy je wszystkie:

Dodatek

termin1 + termin2 = suma
term1 = suma - term2
term2 = suma - term1

Odejmowanie

odjemna - odjemna = różnica
odjemna = odjemna + różnica
subtrahend = minuta - różnica

Mnożenie

mnożnik1 * mnożnik2 = iloczyn
mnożnik1 = iloczyn: mnożnik2
mnożnik2 = iloczyn: mnożnik1

Dział

dywidenda: dzielnik = iloraz
dywidenda = dzielnik * iloraz
dzielnik = dywidenda: iloraz

Spójrzmy na przykład, jak zastosować te zasady.

Zwróć uwagę, że się dzielimy dalej i otrzymujemy . W tej sytuacji znamy dzielnik i iloraz. Aby obliczyć dywidendę, należy pomnożyć dzielnik przez iloraz:

Zbliżyliśmy się trochę do siebie. Teraz widzimy, że… dodane i otrzymane. Tak więc, aby znaleźć jeden z terminów, musisz odjąć znany termin od sumy:

I jeszcze jedna „warstwa” zostaje usunięta z nieznanego! Teraz widzimy sytuację ze znaną wartością iloczynu () i jednym znanym mnożnikiem ().

Teraz sytuacja jest "zmniejszona - odjęta = różnica"

A ostatni krok to znany iloczyn () i jeden z czynników ()

Typ 2: równania z nawiasami
Równania tego typu najczęściej występują w zadaniach - 90% wszystkich zadań dla wstęp do klasy 5. w odróżnieniu „równania cebuli” zmienna tutaj może wystąpić kilka razy, więc nie da się jej rozwiązać metodami z poprzedniego akapitu. Typowe równania: lub
Główną trudnością jest prawidłowe otwarcie nawiasów. Po tym, jak udało nam się to zrobić poprawnie, powinniśmy przynieść podobne terminy (liczby do liczb, zmienne do zmiennych), a po tym otrzymujemy najprostsze „równanie cebuli” które możemy rozwiązać. Ale najpierw najważniejsze.

Rozszerzenie wspornika. Podamy kilka zasad, które należy zastosować w tym przypadku. Ale, jak pokazuje praktyka, uczeń zaczyna poprawnie otwierać nawiasy dopiero po 70-80 rozwiązanych problemach. Podstawowa zasada jest taka: każdy czynnik poza nawiasami musi być pomnożony przez każdy wyraz w nawiasie. A minus przed nawiasem zmienia znak wszystkich wyrażeń, które są w środku. A więc podstawowe zasady ujawniania informacji:

Przynosząc podobne. Tutaj wszystko jest o wiele prostsze: przenosząc wyrazy przez znak równości, musisz upewnić się, że z jednej strony są tylko wyrazy z nieznanym, az drugiej - tylko liczby. Podstawowa zasada jest taka: każdy przenoszony termin zmienia swój znak - jeśli był z, to stanie się z i na odwrót. Po udanym przeniesieniu należy policzyć całkowitą liczbę niewiadomych, ostateczną liczbę po drugiej stronie równości niż zmienne i rozwiązać prosty „równanie cebuli”.

Równanie z jedną niewiadomą, które po otwarciu nawiasów i redukcji wyrazów podobnych przyjmuje postać

topór + b = 0, gdzie a i b są liczbami arbitralnymi, nazywamy równanie liniowe z jedną niewiadomą. Dzisiaj dowiemy się, jak rozwiązać te równania liniowe.

Na przykład wszystkie równania:

2x + 3 \u003d 7 - 0,5x; 0,3x = 0; x / 2 + 3 \u003d 1/2 (x - 2) - liniowy.

Wartość niewiadomej, która zamienia równanie w prawdziwą równość, nazywa się decyzja lub pierwiastek równania .

Na przykład, jeśli w równaniu 3x + 7 \u003d 13 podstawimy liczbę 2 zamiast nieznanego x, to otrzymamy prawidłową równość 3 2 + 7 \u003d 13. Stąd wartość x \u003d 2 jest rozwiązaniem lub pierwiastek równania.

A wartość x \u003d 3 nie zamienia równania 3x + 7 \u003d 13 w prawdziwą równość, ponieważ 3 2 + 7 ≠ 13. Dlatego wartość x \u003d 3 nie jest rozwiązaniem ani pierwiastkiem równania.

Rozwiązanie dowolnych równań liniowych sprowadza się do rozwiązania równań postaci

topór + b = 0.

Przenosimy wyraz wolny z lewej strony równania na prawo, zmieniając znak przed b na przeciwny, otrzymujemy

Jeśli a 0, to x = – b/a .

Przykład 1 Rozwiąż równanie 3x + 2 =11.

Przenosimy 2 z lewej strony równania w prawo, zmieniając znak przed 2 na przeciwny, otrzymujemy
3x \u003d 11 - 2.

Zróbmy więc odejmowanie
3x = 9.

Aby znaleźć x, musisz podzielić iloczyn przez znany czynnik, czyli
x = 9:3.

Zatem wartość x = 3 jest rozwiązaniem lub pierwiastkiem równania.

Odpowiedź: x = 3.

Jeśli a = 0 i b = 0, otrzymujemy równanie 0x \u003d 0. To równanie ma nieskończenie wiele rozwiązań, ponieważ mnożąc dowolną liczbę przez 0, otrzymujemy 0, ale b wynosi również 0. Rozwiązaniem tego równania jest dowolna liczba.

Przykład 2 Rozwiąż równanie 5(x - 3) + 2 = 3 (x - 4) + 2x - 1.

Rozwińmy nawiasy:
5x - 15 + 2 \u003d 3x - 12 + 2x - 1.

5x - 3x - 2x \u003d - 12 - 1 + 15 - 2.

Oto podobni członkowie:
0x = 0.

Odpowiedź: x to dowolna liczba.

Jeśli a = 0 i b ≠ 0, to otrzymujemy równanie 0x = - b. To równanie nie ma rozwiązań, ponieważ mnożąc dowolną liczbę przez 0, otrzymujemy 0, ale b ≠ 0.

Przykład 3 Rozwiąż równanie x + 8 = x + 5.

Pogrupujmy terminy zawierające niewiadome po lewej stronie i terminy wolne po prawej stronie:
x - x \u003d 5 - 8.

Oto podobni członkowie:
0x = - 3.

Odpowiedź: brak rozwiązań.

Na rysunek 1 pokazano schemat rozwiązywania równania liniowego

Skomponujmy ogólny schemat rozwiązywania równań z jedną zmienną. Rozważ rozwiązanie z przykładu 4.

Przykład 4 Rozwiążmy równanie

1) Pomnóż wszystkie wyrazy równania przez najmniejszą wspólną wielokrotność mianowników, równą 12.

2) Po redukcji otrzymujemy
4 (x - 4) + 3 2 (x + 1) - 12 = 6 5 (x - 3) + 24x - 2 (11x + 43)

3) Aby oddzielić członków zawierających członków nieznanych i wolnych, otwórz nawiasy:
4x - 16 + 6x + 6 - 12 \u003d 30x - 90 + 24x - 22x - 86.

4) Grupujemy w jednej części terminy zawierające niewiadome, a w drugiej - terminy wolne:
4x + 6x - 30x - 24x + 22x \u003d - 90 - 86 + 16 - 6 + 12.

5) Oto podobni członkowie:
- 22x = - 154.

6) Podziel przez - 22 , Otrzymujemy
x = 7.

Jak widać, pierwiastek równania to siedem.

W ogóle takie równania można rozwiązać w następujący sposób:

a) sprowadzić równanie do postaci całkowitej;

b) otwarte nawiasy;

c) zgrupuj wyrazy zawierające niewiadomą w jednej części równania, a wyrazy wolne w drugiej;

d) sprowadzać podobnych członków;

e) rozwiązać równanie postaci aх = b, które uzyskano po doprowadzeniu wyrazów podobnych.

Jednak ten schemat nie jest wymagany dla każdego równania. Rozwiązując wiele prostszych równań, trzeba zacząć nie od pierwszego, ale od drugiego ( Przykład. 2), trzeci ( Przykład. trzynaście), a nawet z piątego etapu, jak w przykładzie 5.

Przykład 5 Rozwiąż równanie 2x = 1/4.

Znajdujemy nieznane x \u003d 1/4: 2,
x = 1/8 .

Rozważ rozwiązanie niektórych równań liniowych napotkanych podczas głównego egzaminu państwowego.

Przykład 6 Rozwiąż równanie 2 (x + 3) = 5 - 6x.

2x + 6 = 5 - 6x

2x + 6x = 5 - 6

Odpowiedź: - 0,125

Przykład 7 Rozwiąż równanie - 6 (5 - 3x) \u003d 8x - 7.

– 30 + 18x = 8x – 7

18x - 8x = - 7 +30

Odpowiedź: 2,3

Przykład 8 Rozwiązać równanie

3(3x - 4) = 4 7x + 24

9x - 12 = 28x + 24

9x - 28x = 24 + 12

Przykład 9 Znajdź f(6), jeśli f (x + 2) = 3 7's

Rozwiązanie

Ponieważ musimy znaleźć f(6), a znamy f (x + 2),
wtedy x + 2 = 6.

Rozwiązujemy równanie liniowe x + 2 = 6,
otrzymujemy x \u003d 6 - 2, x \u003d 4.

Jeśli x = 4 to
f(6) = 3 7-4 = 3 3 = 27

Odpowiedź: 27.

Jeśli nadal masz pytania, istnieje chęć dokładniejszego rozwiązania równań. Chętnie Ci pomogę!

TutorOnline zaleca również obejrzenie nowego samouczka wideo naszej nauczycielki Olgi Aleksandrownej, który pomoże Ci zrozumieć zarówno równania liniowe, jak i inne.

blog.site, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.