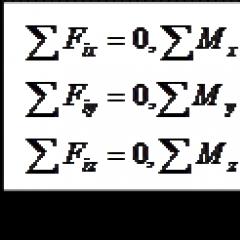Condiciones para el equilibrio de un sistema de fuerzas en el espacio. Mecánica teórica

Condición de equilibrio para un sistema espacial de fuerzas convergentes.: la suma algebraica de las proyecciones de todas las fuerzas sobre tres ejes de coordenadas mutuamente perpendiculares debe ser igual a cero, es decir

Para encontrar el momento de fuerza. relativo al eje z, necesidad de diseñar la fuerza al avión norte perpendicular al eje z(Fig.12), luego encuentre el momento de proyección. f norte relativo al punto O, que es el punto de intersección del plano norte chupar z. Momento de proyección f norte y será un momento de fuerza relativo al eje z:

Sistema espacial de fuerzas ubicadas arbitrariamente. es un sistema de fuerzas cuyas líneas de acción no se encuentran en el mismo plano y no se cruzan en un punto. La resultante de tal sistema de fuerzas también es igual a la suma geométrica de estas fuerzas, pero se representa mediante la diagonal de figuras volumétricas complejas (tetraedro, octaedro, etc.).

Condición de equilibrio para un sistema espacial de fuerzas ubicadas arbitrariamente: la suma algebraica de las proyecciones de todas las fuerzas sobre tres ejes de coordenadas mutuamente perpendiculares debe ser igual a cero y la suma algebraica de los momentos de todas las fuerzas con respecto a los mismos ejes de coordenadas debe ser igual a cero, es decir

Fricción

Fricción llamado resistencia al movimiento del cuerpo. La fuerza con la que un cuerpo resiste el movimiento se llama fuerza de fricción.

La fuerza de fricción siempre se dirige en dirección opuesta al movimiento. La fuerza de fricción depende del material de los cuerpos de fricción, de la limpieza del procesamiento y de la presencia de lubricante y no depende del tamaño de las superficies de fricción.

La fricción ocurre: seco, semilíquido, líquido.

Distinguir entre fricción reposo, movimiento, deslizamiento Y laminación. La fuerza de fricción estática es mayor que la fuerza de fricción en movimiento.

La fuerza de fricción es igual al producto de la fuerza de presión normal y el coeficiente de fricción por deslizamiento (Fig.14):

F tr =R norte ƒ,

Dónde Rn = mg cos a - fuerza de presión normal;

ƒ - coeficiente de fricción por deslizamiento.

Coeficiente de fricción por deslizamiento La relación entre la fuerza de fricción y la fuerza de presión normal se denomina:

Los materiales que tienen muy poca fricción se llaman anti fricción(babbitt, bronce, grafito).Se utilizan para la fabricación de rodamientos, etc.

Los materiales con alta fricción se llaman friccional(plásticos especiales que utilizan amianto y cobre). Se utiliza para forros de pastillas de freno y forros de discos de embrague.

Cuando se lubrica la superficie de deslizamiento, el cuerpo comienza a moverse con menos fricción.

Descompongamos la fuerza de gravedad G en componentes G ’ y G " (Fig.15)

Creemos una ecuación de equilibrio:

Dónde h- distancia desde la superficie a la línea de acción de la fuerza;

k- coeficiente de fricción de rodadura. Es igual al segmento OS (ver Fig. 16)

Fdv = Ftr,

F tr =R p k/h

Si h = re,

F tr =R p k/d

si h = g,

F tr =R p k/d

Combinamos el origen de coordenadas con el punto de intersección de las líneas de acción de las fuerzas del sistema. Proyectamos todas las fuerzas sobre los ejes de coordenadas y sumamos las proyecciones correspondientes (Fig. 7.4). Obtenemos las proyecciones de la resultante sobre los ejes de coordenadas:

El módulo del sistema resultante de fuerzas convergentes está determinado por la fórmula

La dirección del vector resultante está determinada por los ángulos.

Sistema espacial arbitrario de fuerzas.

Llevar un sistema espacial arbitrario de fuerzas al centro de O.

Se da un sistema espacial de fuerzas (figura 7.5, a). Llevémoslo al centro O.

Las fuerzas deben moverse en paralelo y se forma un sistema de pares de fuerzas. El momento de cada uno de estos pares es igual al producto del módulo de fuerza por la distancia al centro de reducción.

En el centro de reducción surge un haz de fuerzas que puede ser reemplazado por la fuerza total (vector principal) F GL (Figura 7.5, b).

Se pueden sumar los momentos de pares de fuerzas, obteniendo el momento total del sistema M ch (momento principal).

Así, un sistema espacial arbitrario de fuerzas se reduce al vector principal y al momento principal.

El vector principal generalmente se descompone en tres componentes dirigidos a lo largo de los ejes de coordenadas (Fig. 7.5, c).

Por lo general, el momento total se descompone en componentes: tres momentos con respecto a los ejes de coordenadas.

El valor absoluto del vector principal (figura 7.5b) es igual a

El valor absoluto del momento principal está determinado por la fórmula.

Ecuaciones de equilibrio para un sistema espacial de fuerzas.

En equilibrio F ch = 0; mch = 0. Obtenemos seis ecuaciones de equilibrio:

Las seis ecuaciones de equilibrio del sistema espacial de fuerzas corresponden a seis posibles movimientos independientes del cuerpo en el espacio: tres movimientos a lo largo de los ejes de coordenadas y tres rotaciones alrededor de estos ejes.

Ejemplos de resolución de problemas

Ejemplo 1. Sobre un cuerpo en forma de cubo con un borde. A= 10 cm actúan tres fuerzas (Fig. 7.6). Determine los momentos de fuerzas relativas a los ejes de coordenadas que coinciden con las aristas del cubo.

Solución

1. Momentos de fuerzas con respecto al eje. Oh:

2. Momentos de fuerzas con respecto al eje. UNED.

Ejemplo 2. Se fijan dos ruedas sobre un eje horizontal, g 1 = 0,4 m; g 2 = 0,8 m Otras dimensiones se muestran en la Fig. 7.7. Se aplica fuerza a la rueda 1. F 1, a la rueda 2 - potencia F 2= 12kN, F 3= 4kN.

Definir fuerza F 1 y reacciones en las bisagras A Y EN en un estado de equilibrio.

Te recordamos:

1. En equilibrio, se satisfacen seis ecuaciones de equilibrio.

Las ecuaciones de momentos deben escribirse en relación con los soportes. A y B.

2. Poderes F 2 \\O X; F 2\\Oy;F 3\\Oye.

Los momentos de estas fuerzas con respecto a los ejes correspondientes son iguales a cero.

3. El cálculo debe completarse mediante verificación utilizando ecuaciones de equilibrio adicionales.

Solución

1. Determinar la fuerza F\, habiendo compuesto la ecuación de momentos de fuerzas con respecto al eje Oz:

2. Determinar reacciones de apoyo. A. Hay dos componentes de reacción que actúan sobre el soporte ( Y A ; XA ).

Redactamos la ecuación de momentos de fuerzas sobre el eje. Oh"(en apoyo EN).

Rotación alrededor de un eje. Oh" no esta pasando:

El signo menos significa que la reacción se dirige en la dirección opuesta.

Rotación alrededor de un eje. UNED" no sucede, elaboramos una ecuación para los momentos de fuerzas con respecto al eje UNED"(en apoyo EN):

3. Determine las reacciones en el soporte B. Dos componentes de la reacción actúan sobre el soporte ( XB , YB ). Redactamos la ecuación de momentos de fuerzas sobre el eje. Oh(apoyo A):

Componemos la ecuación de momentos sobre el eje. UNED(apoyo A):

4.Compruebe. Usamos ecuaciones de proyección:

El cálculo se realizó correctamente.

Ejemplo 3. Determinar el valor numérico de la fuerza. P 1 , en el que el eje Sol(Figura 1.21, A) estará en equilibrio. En el valor de fuerza encontrado P 1 determinar las reacciones de apoyo.

Fuerzas que actúan sobre los engranajes. R Y P 1 dirigido tangencialmente a los círculos iniciales de las ruedas; fortaleza t Y T 1 - según los radios de las ruedas; fortaleza un 1 paralelo al eje del eje. T = 0,36P, 7T1 = P1; Un 1 = 0,12P 1.

Solución

Los soportes del eje que se muestran en la Fig. 1.21, a, deben considerarse soportes de bisagra espaciales que evitan movimientos lineales en las direcciones de los ejes. Y Y v(el sistema de coordenadas seleccionado se muestra en la Fig. 1.21, b).

Liberamos el eje de las conexiones y reemplazamos su acción por reacciones. V V, N V, VC, NORTE C (Figura 1.21, b). Hemos obtenido un sistema espacial de fuerzas, para el cual elaboramos ecuaciones de equilibrio utilizando el sistema de coordenadas seleccionado (Fig. 1.21.6):

Dónde un 1*1.25D/2 - momento respecto al eje Y fortaleza Un 1, aplicado al engranaje correcto.

Momentos respecto al eje Y fortaleza T 1 Y un 1(aplicado al engranaje medio), P 1 (aplicado al engranaje derecho) y P son iguales a cero, ya que las fuerzas P, T 1, P 1 son paralelas al eje Y, y la fuerza A 1 cruza el eje Y.

dónde VC = 0,37P;

dónde VB = 0,37P.

de ahí las reacciones VB Y VC definido correctamente;

Dónde Un 1* 1.25D/2- momento respecto al eje v fortaleza Un 1, aplicado al engranaje medio.

Momentos respecto al eje v fuerzas T, P 1 (aplicadas al engranaje medio), un 1 Y T 1(aplicadas al engranaje derecho) son iguales a cero, ya que las fuerzas T, R 1, T 1 paralelo al eje v, fuerza un 1 cruza el eje v.

de donde HC = 0,81P;

de donde HC = 1.274P

Creemos una ecuación de verificación:

de ahí las reacciones n.v. Y NS definido correctamente.

En conclusión, observamos que las reacciones de apoyo resultaron tener un signo más. Esto indica que las direcciones seleccionadas V B, N B, V C Y NS coinciden con las direcciones reales de las reacciones de enlace.

Ejemplo 4. La fuerza de presión de la biela de la máquina de vapor P = 25 kN se transmite al centro del muñón del cigüeñal en el punto D en un angulo α = 30° con respecto a la horizontal con las mejillas de la rodilla verticales (Fig. 1.22). Una polea de transmisión por correa está montada en el extremo del eje. La tensión del ramal motriz de la correa es dos veces mayor que la del ramal conducido, es decir S 1 = 2S 2 . Fuerza de gravedad del volante G = 10 kN.

Determinar la tensión de las ramas de transmisión por correa y las reacciones de los cojinetes. A Y EN, despreciando la masa del eje.

Solución

Consideremos el equilibrio de un cigüeñal horizontal con una polea. Aplicamos las fuerzas especificadas de acuerdo con las condiciones del problema. P, S 1, S 2 Y GRAMO . Liberamos el eje de los sujetadores de soporte y reemplazamos su acción con reacciones. V A, N A, V B Y nv. Seleccionamos los ejes de coordenadas como se muestra en la Fig. 1.22. Con bisagras A Y EN No se producen reacciones a lo largo del eje. w, ya que la tensión de las ramas del cinturón y todas las demás fuerzas actúan en planos perpendiculares a este eje.

Creemos ecuaciones de equilibrio:

Además, según las condiciones del problema, tenemos otra ecuación

Entonces hay seis fuerzas desconocidas aquí. S 1, S 2, N A, V A, N B Y VB y seis ecuaciones que los conectan.

Ecuación de proyecciones sobre un eje. w en el ejemplo considerado se convierte en la identidad 0 = 0, ya que todas las fuerzas se encuentran en planos perpendiculares al eje w.

Sustituyendo S 1 =2S 2 en las ecuaciones de equilibrio y resolviéndolas, encontramos:

Valor de reacción n.v. Resultó con un signo menos. Esto significa que en realidad su dirección es opuesta a la supuesta en la Fig. 1.22.

Preguntas y tareas de prueba

1. Escriba las fórmulas para calcular el vector principal de un sistema espacial de fuerzas convergentes.

2. Escriba la fórmula para calcular el vector principal de un sistema espacial de fuerzas ubicadas arbitrariamente.

3. Escriba la fórmula para calcular el momento principal de un sistema espacial de fuerzas.

4. Escriba el sistema de ecuaciones de equilibrio para el sistema espacial de fuerzas.

5. ¿Qué ecuación de equilibrio se debe utilizar para determinar la reacción de la varilla R 1 (figura 7.8)?

6. Determine el momento principal del sistema de fuerzas (figura 7.9). El punto de referencia es el origen de coordenadas. Los ejes de coordenadas coinciden con las aristas del cubo, la arista del cubo mide 20 cm; F 1 - 20kN; F 2 - 30 kN.

7. Determine la reacción Xb (figura 7.10). El eje vertical con la polea está cargado por dos fuerzas horizontales. Potestades F 1 Y F 2 paralelo al eje Oh. AO = 0,3 m; transmisión exterior= 0,5 m; F 1 = 2kN; F 2 = 3,5 kN.

Recomendación. Crea una ecuación para momentos con respecto al eje. UNED" en el punto A.

8. Responda las preguntas del examen.

Condiciones de equilibrio vectorial para un sistema arbitrario de fuerzas: Para el equilibrio de un sistema de fuerzas aplicadas a un cuerpo rígido, es necesario y suficiente que el vector principal del sistema de fuerzas sea igual a cero y el momento principal del sistema de fuerzas con respecto a cualquier centro de reducción también sea igual a cero.. De lo contrario: para ~0, las siguientes condiciones son necesarias y suficientes:

,
o
,
. (19)

Condiciones de equilibrio para un sistema espacial de fuerzas en forma analítica.

Para el equilibrio de un sistema espacial de fuerzas aplicadas a un cuerpo sólido, es necesario y suficiente que las tres sumas de las proyecciones de todas las fuerzas sobre los ejes de coordenadas cartesianos sean iguales a cero y las tres sumas de los momentos de todas las fuerzas relativas a los tres ejes de coordenadas también son iguales a cero.

. (20)

Condiciones de equilibrio para un sistema espacial de fuerzas convergentes.

Para el equilibrio de un sistema espacial de fuerzas convergentes aplicadas a un cuerpo sólido, es necesario y suficiente que las sumas de las proyecciones de fuerzas en cada uno de los tres ejes de coordenadas rectangulares sean iguales a cero.:

;
;
, (21)

En el caso de un sistema plano de fuerzas convergentes, uno de los ejes de coordenadas, generalmente
, se elige perpendicular a las fuerzas, y los otros dos ejes se eligen, respectivamente, en el plano de las fuerzas. D Para el equilibrio de un sistema plano de fuerzas convergentes que actúan sobre un cuerpo sólido, es necesario y suficiente que las sumas de las proyecciones de estas fuerzas sobre cada uno de los dos ejes de coordenadas rectangulares que se encuentran en el plano de las fuerzas sean iguales a cero:

;
, (22)

Condiciones de equilibrio para un sistema espacial de fuerzas paralelas.

Dirigamos el eje
paralela a las fuerzas: Para el equilibrio de un sistema espacial de fuerzas paralelas aplicadas a un cuerpo sólido, es necesario y suficiente que la suma algebraica de estas fuerzas sea igual a cero y la suma de los momentos de las fuerzas con respecto a dos ejes de coordenadas perpendiculares a las fuerzas sean también igual a cero:

Condiciones de equilibrio para un sistema plano de fuerzas.

Posicionemos los ejes.
Y
en el plano de acción de las fuerzas.

Condiciones de equilibrio para un sistema plano de fuerzas en la primera forma: Para el equilibrio de un sistema plano de fuerzas que actúan sobre un cuerpo sólido, es necesario y suficiente que las sumas de las proyecciones de estas fuerzas sobre cada uno de los dos ejes de coordenadas rectangulares ubicados en el plano de acción de las fuerzas sean iguales a cero. y la suma de los momentos algebraicos de las fuerzas relativas a cualquier punto ubicado en el plano de acción de las fuerzas también fue cero:

(24)

Para el equilibrio de un sistema plano de fuerzas paralelas aplicadas a un cuerpo sólido, es necesario y suficiente que la suma algebraica de las fuerzas sea igual a cero y la suma de los momentos algebraicos de las fuerzas con respecto a cualquier punto ubicado en el plano. de las fuerzas también es igual a cero:

(25)

Teorema de los tres momentos (segunda forma de condiciones de equilibrio): para el equilibrio de un sistema plano de fuerzas aplicadas a un cuerpo rígido, es necesario y suficiente que las sumas de los momentos algebraicos de las fuerzas del sistema con respecto a tres puntos cualesquiera ubicados en el plano de acción de las fuerzas y que no se encuentran en la misma recta son iguales a cero:

Tercera forma de condiciones de equilibrio: para el equilibrio de un sistema plano de fuerzas aplicadas a un cuerpo sólido, es necesario y suficiente que las sumas de los momentos algebraicos de las fuerzas con respecto a dos puntos cualesquiera que se encuentran en el plano de acción de las fuerzas sean iguales a cero y el algebraico La suma de las proyecciones de estas fuerzas sobre cualquier eje del plano que no sea perpendicular a la recta que pasa por dos puntos de momento también era igual a cero., es decir.

Eso., Para el equilibrio de un sistema espacial arbitrario de fuerzas, es necesario y suficiente que la suma algebraica de las proyecciones de todas estas fuerzas sobre cada uno de los tres ejes de coordenadas elegidos arbitrariamente sea igual a cero y que la suma algebraica de sus momentos con respecto a cada uno de estos ejes también es igual a cero.

Las condiciones (1.33) se llaman Condiciones de equilibrio de un sistema espacial arbitrario de fuerzas en forma analítica..

Condiciones de equilibrio para un sistema espacial de fuerzas paralelas. Si las líneas de acción de todas las fuerzas de un sistema de fuerzas dado están ubicadas en diferentes planos y son paralelas entre sí, entonces dicho sistema de fuerzas se llama sistema espacial de fuerzas paralelas.

Utilizando las condiciones de equilibrio (1.33) de un sistema espacial arbitrario de fuerzas, se pueden encontrar las condiciones de equilibrio de un sistema espacial de fuerzas paralelas. (Las condiciones de equilibrio que dedujimos anteriormente para sistemas planos y espaciales de fuerzas convergentes, un sistema plano arbitrario de fuerzas y un sistema plano de fuerzas paralelas también podrían obtenerse utilizando las condiciones de equilibrio (1.33) de un sistema espacial arbitrario de fuerzas).

Sea un sistema espacial de fuerzas paralelas que actúa sobre un cuerpo sólido (Figura 1.26). Dado que la elección de los ejes de coordenadas es arbitraria, es posible elegir ejes de coordenadas de modo que el eje z era paralelo a las fuerzas. Con esta elección de ejes de coordenadas, las proyecciones de cada una de las fuerzas sobre el eje X Y en y sus momentos respecto al eje z será igual a cero, y, por tanto, las igualdades, y se satisfacen independientemente de si un determinado sistema de fuerzas está en equilibrio o no, y por tanto dejan de ser condiciones de equilibrio. Por lo tanto, el sistema (1.33) dará sólo tres condiciones de equilibrio:

Por eso, Para el equilibrio de un sistema espacial de fuerzas paralelas, es necesario y suficiente que la suma algebraica de las proyecciones de todas las fuerzas sobre el eje paralelo a estas fuerzas sea igual a cero y que la suma algebraica de sus momentos con respecto a cada una de las dos coordenadas. Los ejes perpendiculares a estas fuerzas también son iguales a cero..

1. Seleccione un cuerpo (o punto) cuyo equilibrio deba considerarse en este problema.

2. Liberar el cuerpo seleccionado de los enlaces y representar (organizar) todas las fuerzas activas y de reacción de los enlaces descartados que actúan sobre este cuerpo (y solo sobre este cuerpo). Un cuerpo libre de conexiones, con un sistema de fuerzas activas y de reacción adjunto, debe representarse por separado.

3. Escribe ecuaciones de equilibrio.. Para elaborar ecuaciones de equilibrio, primero debe seleccionar los ejes de coordenadas. Esta elección se puede hacer arbitrariamente, pero las ecuaciones de equilibrio resultantes se resolverán más fácilmente si uno de los ejes se dirige perpendicular a la línea de acción de alguna fuerza de reacción desconocida. La solución de las ecuaciones de equilibrio resultantes debe, por regla general, llevarse a cabo hasta el final en forma general (algebraicamente). Luego, para las cantidades requeridas se obtendrán fórmulas que permitan analizar los resultados encontrados; Los valores numéricos de las cantidades encontradas se sustituyen solo en las fórmulas finales. Las ecuaciones de equilibrio se compilan utilizando el método analítico para resolver problemas de equilibrio de un sistema de fuerzas convergentes. Sin embargo, si el número de fuerzas convergentes cuyo equilibrio se considera es tres, entonces es conveniente aplicar el método geométrico para resolver estos problemas. La solución en este caso se reduce al hecho de que en lugar de las ecuaciones de equilibrio de todas las fuerzas actuantes (enlaces activos y de reacción), se construye un triángulo de fuerzas que, según la condición geométrica de equilibrio, debe ser cerrado (la construcción de este triángulo debe comenzar con una fuerza dada). Resolviendo el triángulo de fuerzas, encontramos las cantidades requeridas.

Dinámica

Para comprender la sección de dinámica, es necesario conocer la siguiente información. De las matemáticas: el producto escalar de dos vectores, ecuaciones diferenciales. De la física: las leyes de conservación de la energía y del momento. Teoría de la oscilación. Se recomienda revisar estos temas.

Como se aclaró en el § 4.4, las condiciones necesarias y suficientes para el equilibrio de un sistema espacial de fuerzas aplicadas a un cuerpo rígido se pueden escribir en forma de tres ecuaciones de proyección (4.16) y tres momentos (4.17):

, , . (7.14)

Si el cuerpo está completamente fijo, entonces las fuerzas que actúan sobre él están en equilibrio y las ecuaciones (7.13) y (7.14) sirven para determinar las reacciones en los apoyos. Por supuesto, puede haber casos en los que estas ecuaciones no sean suficientes para determinar las reacciones en los apoyos; No consideraremos sistemas tan estáticamente indeterminados.

Para un sistema espacial de fuerzas paralelas, las ecuaciones de equilibrio toman la forma (§ 4.4[‡]):

, , . (7.15)

Consideremos ahora los casos en los que el cuerpo está sólo parcialmente fijo, es decir, las conexiones que se imponen al cuerpo no garantizan el equilibrio del mismo. Se pueden señalar cuatro casos especiales.

1. Un cuerpo sólido tiene un punto fijo. Es decir, se fija a un punto fijo mediante una junta esférica perfecta.

Situemos el origen del sistema de coordenadas fijo en este punto. Acción de conexión en un punto. A Reemplacémoslo con una reacción; dado que se desconoce su magnitud y dirección, lo presentaremos en forma de tres componentes desconocidas , , , dirigidas respectivamente a lo largo de los ejes , , .

Las ecuaciones de equilibrio (7.13) y (7.14) en este caso se escribirán en la forma:

1) ,

2) ,

3) ,

4) ,

5) ,

Las últimas tres ecuaciones no contienen componentes de reacción, ya que la línea de acción de esta fuerza pasa por el punto A. En consecuencia, estas ecuaciones establecen las relaciones entre las fuerzas activas necesarias para el equilibrio del cuerpo, y las primeras tres ecuaciones pueden usarse para determinar los componentes de la reacción.

De este modo, La condición para el equilibrio de un cuerpo rígido que tiene un punto fijo es la igualdad a cero de cada una de las sumas algebraicas de los momentos de todas las fuerzas activas del sistema con respecto a tres ejes que se cruzan en un punto fijo del cuerpo. .

2. El cuerpo tiene dos puntos fijos. Este será el caso, por ejemplo, si se fija a dos puntos fijos mediante bisagras.

Elijamos el origen de coordenadas en el punto A y dirigir el eje a lo largo de la línea que pasa por los puntos A Y EN. Reemplacemos la acción de los enlaces con reacciones, dirigiendo los componentes de la reacción a lo largo de los ejes de coordenadas. Denotemos la distancia entre puntos. A Y EN a través de A; entonces las ecuaciones de equilibrio (7.13) y (7.14) se escribirán de la siguiente forma:

1) ,

2) ,

3) ,

4) ,

5) ,

La última ecuación no contiene fuerzas de reacción y establece la conexión entre las fuerzas activas necesarias para el equilibrio del cuerpo. Por eso, La condición para el equilibrio de un cuerpo rígido que tiene dos puntos fijos es la igualdad a cero de la suma algebraica de los momentos de todas las fuerzas activas aplicadas al cuerpo con respecto al eje que pasa por los puntos fijos. . Las primeras cinco ecuaciones se utilizan para determinar las componentes desconocidas de las reacciones , , , , .

Tenga en cuenta que los componentes y no se pueden determinar por separado. A partir de la tercera ecuación sólo se determina la suma + y, por tanto, el problema con respecto a cada una de estas incógnitas para un cuerpo rígido es estáticamente indeterminado. Sin embargo, si en el momento EN Si no hay una bisagra esférica, sino cilíndrica (es decir, un cojinete), que no interfiere con el deslizamiento longitudinal del cuerpo a lo largo del eje de rotación, entonces el problema se vuelve estáticamente definible.

El cuerpo tiene un eje de rotación fijo a lo largo del cual puede deslizarse sin fricción. Esto significa que en puntos A Y EN hay bisagras cilíndricas (cojinetes) y las componentes de sus reacciones a lo largo del eje de rotación son iguales a cero. En consecuencia, las ecuaciones de equilibrio tomarán la forma:

1) ,

2) ,

4) ,

5) ,

Dos de las ecuaciones (7.18), a saber, la tercera y la sexta, imponen restricciones al sistema de fuerzas activas y las ecuaciones restantes sirven para determinar las reacciones.

El cuerpo descansa en tres puntos sobre una superficie lisa y los puntos de apoyo no se encuentran en la misma línea recta. Denotemos estos puntos por A, EN Y CON y compatible con el avión A B C Plano coordinado Ahu. Reemplazando la acción de las conexiones con reacciones verticales , y , escribimos las condiciones de equilibrio (7.14) de la siguiente forma:

3) ,

4) ,

5) ,

Las ecuaciones tercera a quinta pueden servir para determinar reacciones desconocidas, y las ecuaciones primera, segunda y sexta representan las condiciones que conectan las fuerzas activas y son necesarias para el equilibrio del cuerpo. Por supuesto, para que el cuerpo se equilibre se deben cumplir las siguientes condiciones: , , ya que en los puntos de apoyo sólo pueden ocurrir reacciones de la dirección aceptada anteriormente.

Si el cuerpo reposa sobre un plano horizontal en más de tres puntos, entonces el problema se vuelve estáticamente indeterminable, ya que en este caso habrá tantas reacciones como puntos, y solo quedarán tres ecuaciones para determinar las reacciones.

Problema 7.3. Encuentre el vector principal y el momento principal del sistema de fuerzas que se muestra en la Fig. Las fuerzas se aplican a los vértices del cubo y se dirigen a lo largo de sus aristas, y , . La longitud de la arista del cubo es A.