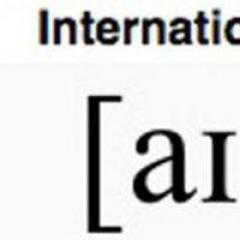Pojęcie funkcji. Ograniczone funkcje
1) Dziedzina funkcji i zakres funkcji.
Dziedziną funkcji jest zbiór wszystkich prawidłowych wartości argumentów X(zmienny X), dla której funkcja y = f(x) określony. Zakres funkcji to zbiór wszystkich wartości rzeczywistych y, co funkcja akceptuje.
W matematyce elementarnej funkcje bada się tylko na zbiorze liczb rzeczywistych.
2) Zera funkcji.
Funkcja zero to wartość argumentu, przy której wartość funkcji jest równa zero.
3) Przedziały stałego znaku funkcji.
Przedziały stałego znaku funkcji to zbiory wartości argumentów, w których wartości funkcji są tylko dodatnie lub tylko ujemne.
4) Monotoniczność funkcji.
Funkcja rosnąca (w pewnym przedziale) to funkcja, w której większej wartości argumentu z tego przedziału odpowiada większa wartość funkcji.
Funkcja malejąca (w pewnym przedziale) to funkcja, w której większa wartość argumentu z tego przedziału odpowiada mniejszej wartości funkcji.
5) Funkcja parzysta (nieparzysta)..
Funkcja parzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego X z dziedziny definicji równość f(-x) = f(x).
Wykres funkcji parzystej jest symetryczny względem rzędnej. X Funkcja nieparzysta to funkcja, której dziedzina definicji jest symetryczna względem początku i dla dowolnego z dziedziny definicji równość jest prawdziwa f(-x) = - f(x
)..
Wykres funkcji nieparzystej jest symetryczny względem początku.
6) Ograniczone i nieograniczone funkcje.
Funkcję nazywamy ograniczoną, jeśli istnieje liczba dodatnia M taka, że |f(x)| ≤ M dla wszystkich wartości x. Jeżeli taka liczba nie istnieje, to funkcja jest nieograniczona.
7) Okresowość funkcji
Funkcja f(x) jest okresowa, jeśli istnieje niezerowa liczba T taka, że dla dowolnego x z dziedziny definicji funkcji zachodzi: f(x+T) = f(x). Ta najmniejsza liczba nazywana jest okresem funkcji. Wszystkie funkcje trygonometryczne są okresowe. (Wzory trygonometryczne).
19. Podstawowe funkcje elementarne, ich własności i wykresy. Zastosowanie funkcji w ekonomii.
Podstawowe funkcje elementarne. Ich właściwości i wykresy nazywa się funkcją postaci , gdzie x jest zmienną, a i b są liczbami rzeczywistymi.
Numer A zwane nachyleniem linii, jest ono równe tangensowi kąta nachylenia tej linii do dodatniego kierunku osi odciętej. Wykres funkcji liniowej jest linią prostą. Jest ona określona przez dwa punkty.
Własności funkcji liniowej
1. Dziedzina definicji - zbiór wszystkich liczb rzeczywistych: D(y)=R
2. Zbiór wartości to zbiór wszystkich liczb rzeczywistych: E(y)=R
3. Funkcja przyjmuje wartość zerową, gdy lub.
4. Funkcja rośnie (maleje) w całym obszarze definicji.
5. Funkcja liniowa jest ciągła w całym zakresie definicji, różniczkowalna i .
2. Funkcja kwadratowa.
Nazywa się funkcję postaci, w której x jest zmienną, a współczynniki a, b, c są liczbami rzeczywistymi kwadratowy
Szanse a, b, c określić położenie wykresu na płaszczyźnie współrzędnych
Współczynnik a określa kierunek gałęzi. Wykres funkcji kwadratowej jest parabolą. Współrzędne wierzchołka paraboli wyznacza się za pomocą wzorów:
Właściwości funkcji:
2. Zbiór wartości dla jednego z przedziałów: lub.
3. Funkcja przyjmuje wartości zerowe, gdy ![]() , gdzie dyskryminator oblicza się ze wzoru:.
, gdzie dyskryminator oblicza się ze wzoru:.
4. Funkcja jest ciągła w całym obszarze definicji, a pochodna funkcji jest równa .
Lekcja i prezentacja na temat: „Właściwości funkcji. Funkcje rosnące i malejące”
Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.
Pomoce dydaktyczne i symulatory w sklepie internetowym Integral dla klasy 9
Interaktywny podręcznik dla klasy 9 „Zasady i ćwiczenia z geometrii”
Podręcznik elektroniczny „Zrozumiała Geometria” dla klas 7-9
Chłopaki, nadal badamy funkcje numeryczne. Dzisiaj skupimy się na takim temacie jak właściwości funkcji. Funkcje mają wiele właściwości. Pamiętaj, jakie właściwości ostatnio badaliśmy. Zgadza się, dziedzina definicji i dziedzina wartości, to jedna z kluczowych właściwości. Nigdy o nich nie zapominaj i pamiętaj, że funkcja zawsze ma te właściwości.
W tej sekcji zdefiniujemy niektóre właściwości funkcji. Zalecam zachowanie kolejności, w jakiej będziemy je ustalać przy rozwiązywaniu problemów.
Funkcja rosnąca i malejąca
Pierwszą właściwością, którą zdefiniujemy, jest funkcja rosnąca i malejąca.
Mówi się, że funkcja rośnie na zbiorze X⊂D(f), jeśli dla dowolnego x1 i x2 takiego, że x1< x2 - выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.Mówi się, że funkcja maleje na zbiorze X⊂D(f), jeśli dla dowolnego x1 i x2 takiego, że x1< x2 - выполняется неравенство f(x1)>f(x2). Oznacza to, że większa wartość argumentu odpowiada mniejszej wartości funkcji.
Pojęcia „zwiększania” i „zmniejszania” funkcji są bardzo łatwe do zrozumienia, jeśli uważnie przyjrzysz się wykresom funkcji. Dla funkcji rosnącej: wydaje nam się, że wspinamy się w górę, dla funkcji malejącej odpowiednio schodzimy w dół. Ogólny pogląd na funkcje rosnące i malejące przedstawiają poniższe wykresy.

Funkcje rosnące i malejące nazywane są ogólnie monotonicznością. Oznacza to, że naszym zadaniem jest znalezienie przedziałów spadku i wzrostu funkcji. W ogólnym przypadku formułuje się to w następujący sposób: znajdź przedziały monotoniczności lub zbadaj funkcję monotoniczności.
Zbadaj monotoniczność funkcji $y=3x+2$.
Rozwiązanie: Sprawdźmy funkcję dla dowolnego x1 i x2 i niech x1< x2.
$f(x1)=3x1+2$
$f(x2)=3x2+2$
Ponieważ x1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.
Ograniczona funkcja
Mówi się, że funkcja $y=f(x)$ jest ograniczona od dołu na zbiorze X⊂D(f) jeśli istnieje taka liczba a, że dla dowolnego хϵХ zachodzi nierówność f(x)< a.
Mówi się, że funkcja $y=f(x)$ jest ograniczona z góry na zbiorze X⊂D(f) jeśli istnieje liczba a taka, że dla dowolnego хϵХ zachodzi nierówność f(x)< a.
Jeżeli nie określono przedziału X, wówczas funkcję uważa się za ograniczoną w całej dziedzinie definicji. Funkcję ograniczoną zarówno od góry, jak i od dołu nazywamy funkcją ograniczoną.
Ograniczenie funkcji można łatwo odczytać z wykresu. Można narysować prostą linię
$у=а$, a jeśli funkcja jest wyższa od tej prostej, to jest ograniczona od dołu. Jeśli poniżej, to odpowiednio powyżej. Poniżej znajduje się wykres funkcji ograniczonej poniżej. Chłopaki, spróbujcie sami narysować wykres ograniczonej funkcji.

Zbadaj granicę funkcji $y=\sqrt(16-x^2)$.
Rozwiązanie: Pierwiastek kwadratowy z określonej liczby jest większy lub równy zero. Jest oczywiste, że nasza funkcja jest również większa lub równa zeru, czyli ograniczona od dołu.
Możemy wyodrębnić pierwiastek kwadratowy tylko z liczby nieujemnej, a następnie $16-x^2≥0$.
Rozwiązaniem naszej nierówności będzie przedział [-4;4]. W tym segmencie $16-x^2≤16$ lub $\sqrt(16-x^2)≤4$, ale to oznacza ograniczone z góry.
Odpowiedź: nasza funkcja ogranicza się do dwóch prostych $y=0$ i $y=4$.
Najwyższa i najniższa wartość
Najmniejszą wartością funkcji y= f(x) na zbiorze X⊂D(f) jest pewna liczba m taka, że:
b) Dla dowolnego хϵХ obowiązuje $f(x)≥f(x0)$.
Największą wartością funkcji y=f(x) na zbiorze X⊂D(f) jest pewna liczba m taka, że:
a) Istnieje takie x0, że $f(x0)=m$.
b) Dla dowolnego хϵХ, $f(x)≤f(x0)$ trzyma.
Największe i najmniejsze wartości są zwykle oznaczane przez y max. i twoje imię .
Pojęcia ograniczenia i największej z najmniejszą wartością funkcji są ze sobą ściśle powiązane. Następujące stwierdzenia są prawdziwe:
a) Jeżeli funkcja ma wartość minimalną, to jest ona ograniczona poniżej.
b) Jeżeli funkcja ma największą wartość, to jest ograniczona powyżej.
c) Jeżeli funkcja nie jest ograniczona powyżej, to największa wartość nie istnieje.
d) Jeżeli funkcja nie jest ograniczona poniżej, to najmniejsza wartość nie istnieje.
Znajdź największą i najmniejszą wartość funkcji $y=\sqrt(9-4x^2+16x)$.
Rozwiązanie: $f(x)=y=\sqrt(9-4x^2+16x)=\sqrt(9-(x-4)^2+16)=\sqrt(25-(x-4)^2 )≤5$.
Dla $х=4$ $f(4)=5$, dla wszystkich pozostałych wartości funkcja przyjmuje mniejsze wartości lub nie istnieje, czyli jest to największa wartość funkcji.
Z definicji: $9-4x^2+16x≥0$. Znajdźmy pierwiastki trójmianu kwadratowego $(2x+1)(2x-9)≥0$. Przy $x=-0,5$ i $x=4,5$ funkcja znika; we wszystkich pozostałych punktach jest większa od zera. Wtedy z definicji najmniejsza wartość funkcji jest równa zeru.
Odpowiedź: y maks. =5 i y imię. =0.
Chłopaki, przestudiowaliśmy także koncepcję wypukłości funkcji. Przy rozwiązywaniu niektórych problemów możemy potrzebować tej właściwości. Właściwość tę można również łatwo określić za pomocą wykresów.
Funkcja jest wypukła w dół, jeśli dowolne dwa punkty na wykresie funkcji pierwotnej są połączone, a wykres funkcji znajduje się poniżej linii łączącej te punkty.
Funkcja jest wypukła w górę, jeśli dowolne dwa punkty na wykresie funkcji pierwotnej są połączone, a wykres funkcji znajduje się powyżej linii łączącej te punkty.

Funkcja jest ciągła, jeśli wykres naszej funkcji nie ma przerw, jak na przykład wykres funkcji powyżej.
Jeśli chcesz znaleźć właściwości funkcji, kolejność wyszukiwania właściwości jest następująca:
a) Dziedzina definicji.
b) Monotonia.
c) Ograniczenie.
d) Największa i najmniejsza wartość.
d) Ciągłość.
e) Zakres wartości.
Znajdź właściwości funkcji $y=-2x+5$.
Rozwiązanie.
a) Dziedzina definicji D(y)=(-∞;+∞).
b) Monotonia. Sprawdźmy dowolne wartości x1 i x2 i niech x1< x2.
$f(x1)=-2x1+2$.
$f(x2)=-2x2+2$.
Od x1< x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
c) Ograniczenie. Oczywiście funkcjonalność nie jest ograniczona.
d) Największa i najmniejsza wartość. Ponieważ funkcja jest nieograniczona, nie ma wartości maksymalnej ani minimalnej.
d) Ciągłość. Wykres naszej funkcji nie ma przerw, wówczas funkcja jest ciągła.
e) Zakres wartości. E(y)=(-∞;+∞).
Zagadnienia własności funkcji do samodzielnego rozwiązania
Znajdź właściwości funkcji:a) $y=2x+7$,
b) $y=3x^2$,
c) $y=\frac(4)(x)$.
Twierdzenie o granicy funkcji monotonicznej. Dowód twierdzenia przedstawiono dwiema metodami. Podano także definicje funkcji ściśle rosnących, niemalejących, ściśle malejących i nierosnących. Definicja funkcji monotonicznej.
TreśćFunkcja nie jest ograniczona od góry
1.1. Niech liczba b będzie skończona: .
1.1.2. Niech funkcja nie będzie ograniczona powyżej.
.
Na .
Oznaczmy .
Na .
Zatem dla każdego, tak jest
Oznacza to, że granica po lewej stronie w punkcie b wynosi (patrz „Definicje jednostronnych nieskończonych granic funkcji w punkcie końcowym”).
b wcześnie plus nieskończoność
Funkcja jest ograniczona od góry
1. Niech funkcja nie maleje na przedziale.
1.2.1. Niech funkcja będzie ograniczona od góry przez liczbę M: dla .
Udowodnimy, że w tym przypadku istnieje granica.
.
Ponieważ funkcja jest ograniczona powyżej, istnieje skończone supremum
;
Zgodnie z definicją dokładnej górnej granicy spełnione są następujące warunki:
.
za każdym pozytywem istnieje argument
Na .
Ponieważ funkcja nie maleje, to kiedy .
Na .
Następnie o godz.
Funkcja nie jest ograniczona od góry
Funkcja jest ograniczona od góry
Lub
Odkryliśmy więc, że dla każdego istnieje liczba, więc
1.2.1. Niech funkcja będzie ograniczona od góry przez liczbę M: dla .
„Definicje jednostronnych granic w nieskończoności”).
.
1.2. Niech liczba b będzie równa plus nieskończoność: .
1.2.2. Niech funkcja nie będzie ograniczona powyżej.
Na .
Ponieważ funkcja nie jest ograniczona powyżej, to dla dowolnej liczby M istnieje argument, dla którego
Ponieważ funkcja nie maleje, to kiedy .
Następnie o godz.
Zatem dla każdego istnieje liczba , więc
.
Oznacza to, że granica w jest równa (patrz „Definicje jednostronnych nieskończonych granic w nieskończoności”).
;
Funkcja nie jest rosnąca
.
Rozważmy teraz przypadek, gdy funkcja nie rośnie. Możesz, jak wyżej, rozważyć każdą opcję osobno. Ale od razu je omówimy. W tym celu używamy . Udowodnimy, że w tym przypadku istnieje granica.
Rozważ skończoną infimum zbioru wartości funkcji:
Na .
Tutaj B może być liczbą skończoną lub punktem w nieskończoności.
Na .
Zgodnie z definicją dokładnej dolnej granicy spełnione są następujące warunki:
dla dowolnego sąsiedztwa punktu B istnieje argument za tym
Na .
Zgodnie z warunkami twierdzenia, .
Dlatego .
Ponieważ funkcja nie rośnie, to kiedy .
Teraz pokażemy, że w punkcie a istnieje granica i znajdziemy jej wartość.
Rozważmy funkcję. -1 Zgodnie z warunkami twierdzenia funkcja jest monotoniczna dla .
Zamieńmy zmienną x na -x (lub dokonajmy podstawienia i następnie zamieńmy zmienną t na x). Wtedy funkcja jest monotoniczna dla .
.
Mnożenie nierówności przez
.
i zmieniając ich kolejność dochodzimy do wniosku, że funkcja jest monotoniczna dla .
.
W podobny sposób łatwo pokazać, że jeśli nie maleje, to nie rośnie. Zatem, zgodnie z tym, co zostało udowodnione powyżej, istnieje granica
(1)
.
Jeśli nie rośnie, to nie maleje. W tym przypadku istnieje granica
.
Pozostaje teraz pokazać, że jeśli istnieje granica funkcji w , to istnieje granica funkcji w , a granice te są równe:
Na .
Wprowadźmy oznaczenie:
Na .
Wyraźmy f w kategoriach g:
Na .
Weźmy dowolną liczbę dodatnią.
Na .
Niech będzie sąsiedztwo epsilon punktu A.
Sąsiedztwo epsilon definiuje się zarówno dla skończonych, jak i nieskończonych wartości A (patrz „Sąsiedztwo punktu”). Skoro istnieje granica (1), to zgodnie z definicją granicy dla każdej istnieje taka, że
Sąsiedztwo epsilon definiuje się zarówno dla skończonych, jak i nieskończonych wartości A (patrz „Sąsiedztwo punktu”). Skoro istnieje granica (1), to zgodnie z definicją granicy dla każdej istnieje taka, że
Sąsiedztwo epsilon definiuje się zarówno dla skończonych, jak i nieskończonych wartości A (patrz „Sąsiedztwo punktu”). Skoro istnieje granica (1), to zgodnie z definicją granicy dla każdej istnieje taka, że
Na .
Niech a będzie liczbą skończoną. Wyraźmy lewe przebite sąsiedztwo punktu -a za pomocą nierówności:
Na .
Zamieńmy x na -x i weźmy pod uwagę, że:
.
Dwie ostatnie nierówności definiują przebite prawe sąsiedztwo punktu a.
NastępnieNiech a będzie liczbą nieskończoną, .
Powtarzamy uzasadnienie.
Na ; Odkryliśmy więc, że dla każdego istnieje coś takiego To znaczy, że Twierdzenie zostało udowodnione. Zobacz też: Pojęcie funkcji. Ograniczone funkcje. Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji.(Ograniczone i nieograniczone funkcje.) | Funkcja nazywa się ograniczony , jeśli istnieje taka liczba dodatnia M co |.
F
X
M dla wszystkich wartości X. Jeśli taka liczba nie istnieje, to funkcja jest Nieograniczony(- X) = Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji. (X PRZYKŁADY. Funkcje parzyste, nieparzyste, monotoniczne. Funkcje parzyste i nieparzyste. Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji.(- X) = - Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji. (X PRZYKŁADY. Jeśli za dowolny x z dziedziny definicji funkcji zachodzi: F ), to wywoływana jest funkcja nawet; Jeśli to się zdarzy:
dziwne. Wykres funkcji parzystej X symetrycznie względem osi Y X(Rys. 5), wykres funkcji nieparzystej X 2 >Ograniczone i nieograniczone funkcje. symetryczny w przybliżeniu Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji.(Ograniczone i nieograniczone funkcje. 2 ) >Nieograniczony(Ograniczone i nieograniczone funkcje. pochodzenie Nieograniczony(Ograniczone i nieograniczone funkcje.) (ryc. 6). Funkcja monotoniczna. Jeśli dla dowolnych dwóch wartości argumentu X symetrycznie względem osi Y X(Rys. 5), wykres funkcji nieparzystej X 2 >Ograniczone i nieograniczone funkcje. symetryczny w przybliżeniu Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji.(Ograniczone i nieograniczone funkcje. 2 ) <Nieograniczony(Ograniczone i nieograniczone funkcje. 1 1 i Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji.(Ograniczone i nieograniczone funkcje. 2 warunku 1 następuje. Nazywa się funkcję, która tylko rośnie lub tylko maleje monotonny.
3. Ciągi liczbowe. Definicja i przykłady.
Powiemy, że zmienna X Jest uporządkowana zmienna, jeśli znany jest obszar jego zmiany i dla każdej z dowolnych dwóch jego wartości można powiedzieć, która jest poprzednia, a która następna. Szczególnym przypadkiem zamówionej ilości zmiennej jest ilość zmienna, której wartości się tworzą sekwencja liczb x 1 ,x 2 ,…,x n ,… Dla takich wartości przy I< j, i, j Î N , oznaczający x ja uważa się za wcześniejsze, oraz x j– kolejne niezależnie od tego, która z tych wartości jest większa. Zatem ciąg liczb jest zmienną, której kolejne wartości można przenumerować. Będziemy oznaczać ciąg liczbowy przez . Poszczególne liczby w sekwencji nazywane są jego elementy.
Na przykład ciąg liczbowy tworzą następujące wielkości:
3. , gdzie a, d– liczby stałe.
Limit sekwencji numerów.
Numer A zwany limit sekwencje X = {x rz), jeśli dla dowolnej, określonej z góry, dowolnie małej liczby dodatniej ε istnieje taka liczba naturalna Nże na oczach wszystkich n>N nierówność |x n - a|< ε.
Jeśli numer A istnieje ograniczenie sekwencji X = {x rz), to tak mówią x rz dąży do A, i napisz.
Aby sformułować tę definicję w kategoriach geometrycznych, wprowadzamy następującą koncepcję. Sąsiedztwo punktu x 0 nazywa się dowolnym przedziałem ( a, b), zawierający ten punkt w sobie. Często bierze się pod uwagę sąsiedztwo punktu x 0, dla którego x 0 jest zatem środkiem x 0 zwany Centrum sąsiedztwo i wartość ( B–A)/2 – promień sąsiedztwo.
Dowiedzmy się zatem, co geometrycznie oznacza pojęcie granicy ciągu liczbowego. W tym celu ostatnią nierówność z definicji zapisujemy w postaci Nierówność ta oznacza, że wszystkie elementy ciągu z liczbami n>N musi leżeć w przedziale (a – ε; a + ε).
Dlatego stała liczba A istnieje ograniczenie sekwencji liczb ( x rz), jeśli dla dowolnego małego sąsiedztwa skupionego w punkcie A promień ε (ε jest otoczeniem punktu A) istnieje taki element ciągu z liczbą N aby wszystkie kolejne elementy były ponumerowane n>N będą zlokalizowane w tej okolicy.
Przykłady.
1. Niech zmienna będzie X przyjmuje wartości sekwencyjnie
Udowodnijmy, że granica tego ciągu liczbowego jest równa 1. Weźmy dowolną liczbę dodatnią ε. Musimy znaleźć taką liczbę naturalną Nże na oczach wszystkich n>N nierówność zachodzi | x rz - 1| < ε. Действительно, т.к.
następnie spełnić relację |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве N dowolna liczba naturalna spełniająca nierówność, otrzymujemy to, czego potrzebujemy. Jeśli więc weźmiemy na przykład umieszczenie N= 6, dla wszystkich N> 6 będziemy mieli.
2. Korzystając z definicji granicy ciągu liczbowego udowodnij, że .
Weźmy dowolne ε > 0. Rozważmy następnie , jeśli lub , tj. . Wybieramy zatem dowolną liczbę naturalną spełniającą nierówność.
Przykłady.
3. Zastanówmy się. Na x → 1 licznik ułamka dąży do 1, a mianownik dąży do 0. Ale ponieważ, tj. jest nieskończenie małą funkcją w x → 1, zatem
Twierdzenie 4. Niech będą dane trzy funkcje f(x), u(x) I v(x), spełniając nierówności u (x)≤f(x)≤ v(x). Jeśli funkcje ty(x) I v(x) mają ten sam limit w x → a(Lub x → ∞), a następnie funkcja k(x) zmierza do tej samej granicy, tj. Jeśli
Twierdzenie 5. Jestem gruby x → a(Lub x → ∞) funkcja y=f(x) akceptuje wartości nieujemne y≥0 a jednocześnie dąży do granicy B, to granica ta nie może być ujemna: b≥0.
Dowód. Dowód przeprowadzimy przez sprzeczność. Udawajmy, że B<0 , Następnie |y – b|≥|b| i dlatego moduł różnicowy nie dąży do zera, gdy x → a. Ale wtedy y nie osiąga limitu B Na x → a, co jest sprzeczne z warunkami twierdzenia.
Twierdzenie 6. Jeśli dwie funkcje k(x) I g(x) dla wszystkich wartości argumentu X spełniają nierówność f(x) ≥ g(x) i mają granice, to nierówność jest spełniona b≥c.
Dowód. Zgodnie z warunkami twierdzenia f(x)-g(x) ≥0, zatem przez Twierdzenie 5, lub .
6. Ujawnienie niepewności (0/0), ∞ -∞
I. Niepewność.
Rozkładając licznik na czynniki, zastosowaliśmy zasadę dzielenia wielomianu przez wielomian przez „kąt”. Od numeru X=1 jest pierwiastkiem wielomianu x 3 – 6x 2 + 11X– 6, to dzieląc otrzymamy
7. Limit sekwencji . Pojęcie logarytmu naturalnego.
DRUGI NIEZWYKŁY LIMIT
Przykłady:
Logarytm do podstawy mi (mi- nazywa się liczbę przestępną równą w przybliżeniu 2,718281828...). naturalny logarytm. Logarytm naturalny liczby X oznaczony ln X. Logarytmy naturalne są szeroko stosowane w matematyce, fizyce i obliczeniach inżynierskich.
Logarytmy są szeroko stosowane
baza, zwana naturalną. Logarytmy naturalne są oznaczone symbolem
Pojęcie granicy funkcji.
Pojęcie ciągłości funkcji jest bezpośrednio powiązane z pojęciem granicy funkcji.
Liczbę A nazywamy granicą funkcji f w punkcie a, granicą zbioru E, jeśli dla dowolnego otoczenia V(A) punktu A istnieje przebite sąsiedztwo punktu a takie, że jego obraz pod odwzorowanie f jest podzbiorem danego sąsiedztwa V(A) punktu A.
Granicę funkcji f w punkcie a, granicę zbioru E, oznaczamy następująco: lub, jeśli można pominąć zbiór E.
Ponieważ każde sąsiedztwo można powiązać ze swoim własnym regularnym (symetrycznym) sąsiedztwem, definicję granicy można sformułować w języku -δ, jak to jest zwyczajowo stosowane w analizie matematycznej:
Granica funkcji w punkcie f w punkcie a, granica zbioru E, jest bezpośrednio powiązana z granicą ciągu.
Rozważymy wszystkie możliwe ciągi punktów zbioru E, które mają punkt a jako granicę, oraz odpowiadające im ciągi wartości funkcji w punktach ciągu. Jeżeli istnieje granica funkcji f w punkcie a, to granica ta będzie granicą każdego ciągu.
Jest też odwrotnie: jeśli wszystkie ciągi zbiegają się do tej samej wartości, to funkcja ma granicę równą tej wartości.
PIERWSZY NIEZWYKŁY LIMIT
Funkcja nie zdefiniowana kiedy X=0, ponieważ licznik i mianownik ułamka wynoszą zero. Wykres funkcji pokazano na rysunku.
Można jednak znaleźć granicę tej funkcji przy X→0.
Przedstawmy dowód zapisanej formuły. Rozważ okrąg o promieniu 1 i załóż, że kąt α wyrażony w radianach mieści się w zakresie 0< α < π/2. (Так как четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α >0.) Z rysunku jasno wynika, że
SΔOAC .
Ponieważ wskazane obszary są odpowiednio równe
SΔOAC=0,5∙OC∙O.A.∙ grzech α= 0,5 sinα, S sekta. OAK = 0,5∙OC 2 ∙α=0,5α, SΔOBC=0,5∙OC∙BC= 0,5 tgα.
Stąd,
grzech α< α < tg α.
Podzielmy wszystkie wyrazy nierówności przez sin α > 0: .
Ale . Dlatego na podstawie Twierdzenia 4 o granicach dochodzimy do wniosku, że otrzymany wzór nazywamy pierwszą niezwykłą granicą.
Zatem pierwsza niezwykła granica służy ujawnieniu niepewności. Należy pamiętać, że otrzymanego wzoru nie należy mylić z granicami Przykłady.
11.Ograniczenie i związane z nim ograniczenia.
DRUGI NIEZWYKŁY LIMIT
Druga niezwykła granica służy do ujawnienia niepewności 1 ∞ i wygląda następująco:
Zwróćmy uwagę, że we wzorze na drugą granicę niezwykłą wykładnik musi zawierać wyrażenie odwrotne do tego, które dodaje się do jednostki u podstawy (ponieważ w tym przypadku istnieje możliwość wprowadzenia zmiany zmiennych i zmniejszyć poszukiwaną granicę do drugiej niezwykłej granicy)
Przykłady.
1. Funkcja k(x)=(X-1) 2 jest nieskończenie małe w X→1, ponieważ (patrz rysunek).
2. Funkcja k(x)= tg X– nieskończenie przy X→0.
3. k(x)= log(1+ X) – nieskończenie przy X→0.
4. k(x) = 1/X– nieskończenie przy X→∞.
Ustalmy następującą ważną zależność:
Twierdzenie. Jeśli funkcja y=f(x) reprezentowalny z x → a jako suma liczby stałej B i nieskończenie mała wielkość α(x): f (x)=b+ α(x) To .
I odwrotnie, jeśli , to fa (x)=b+α(x), Gdzie topór)– nieskończenie przy x → a.
Dowód.
1. Udowodnimy pierwszą część twierdzenia. Od równości f(x)=b+α(x) powinien |f(x) – b|=| α|. Lecz odkąd topór) jest nieskończenie małe, to dla dowolnego ε istnieje δ – otoczenie punktu A, przed wszystkimi X z czego, wartości topór) zaspokoić relację |α(x)|< ε. Następnie |f(x) – b|< ε. A to oznacza, że.
2. Jeśli , to dla dowolnego ε >0 dla wszystkich X od pewnego δ – sąsiedztwo punktu A będzie |f(x) – b|< ε. Ale jeśli oznaczymy f(x) – b= α, To |α(x)|< ε, co oznacza, że A– nieskończenie małe.
Rozważmy podstawowe właściwości funkcji nieskończenie małych.
Twierdzenie 1. Suma algebraiczna dwóch, trzech i ogólnie dowolnej skończonej liczby nieskończenie małych jest funkcją nieskończenie małą.
Dowód. Przedstawmy dowód dla dwóch wyrazów. Pozwalać f(x)=α(x)+β(x), gdzie i . Musimy to udowodnić dla dowolnego dowolnego małego ε > Znaleziono 0 δ> 0, tak że dla X, spełniając nierówność |x – a|<δ , wykonane |f(x)|< ε.
Ustalmy więc dowolną liczbę ε > 0. Ponieważ zgodnie z warunkami twierdzenia α(x) jest funkcją nieskończenie małą, to istnieje takie δ 1 > 0, czyli |x – a|< δ1 mamy |α(x)|< ε / 2. Podobnie od β(x) jest nieskończenie małe, to istnieje takie δ 2 > 0, czyli |x – a|< δ2 mamy | β(x)|< ε / 2.
Weźmy δ=min(δ 1 , δ2 } .Następnie w pobliżu punktu A promień δ każda z nierówności będzie spełniona |α(x)|< ε / 2 i | β(x)|< ε / 2. Dlatego w tej okolicy nie będzie
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
te. |f(x)|< ε, co należało udowodnić.
Twierdzenie 2. Iloczyn funkcji nieskończenie małej topór) dla ograniczonej funkcji k(x) Na x → a(albo kiedy x → ∞) jest funkcją nieskończenie małą.
Dowód. Ponieważ funkcja k(x) jest ograniczona, to jest liczba M tak, że dla wszystkich wartości X z jakiegoś sąsiedztwa punktu a|f(x)|≤M. Co więcej, od topór) jest nieskończenie małą funkcją w x → a, następnie dla dowolnego ε > 0 istnieje sąsiedztwo punktu A, w którym nierówność będzie zachowana |α(x)|< ε /M. Następnie w mniejszej z tych dzielnic, które mamy | αf|< ε /M= ε. A to oznacza, że af– nieskończenie małe. Z okazji x → ∞ dowód przeprowadza się analogicznie.
Z udowodnionego twierdzenia wynika:
Wniosek 1. Jeśli i , to
Konsekwencja 2. Jeśli c= stała, następnie .
Twierdzenie 3. Stosunek funkcji nieskończenie małej α(x) na funkcję k(x), którego granica jest różna od zera, jest funkcją nieskończenie małą.
Dowód. Pozwalać . Następnie 1 /f(x) istnieje ograniczona funkcja. Dlatego ułamek jest iloczynem nieskończenie małej funkcji i ograniczonej funkcji, tj. funkcja jest nieskończenie mała.
Przykłady.
1. Jasne jest, że kiedy x → + ∞ funkcjonować y=x 2 + 1 jest nieskończenie duże. Ale wtedy, zgodnie z twierdzeniem sformułowanym powyżej, funkcja jest nieskończenie mała w x → + ∞, tj. .
Można także udowodnić twierdzenie odwrotne.
Twierdzenie 2. Jeśli funkcja k(x)- nieskończenie mały przy x → a(Lub x → ∞) i wtedy nie znika y= 1/f(x) jest nieskończenie dużą funkcją.
Przeprowadź dowód twierdzenia samodzielnie.
Przykłady.
3. , ponieważ funkcje i są nieskończenie małe w x → + ∞, wówczas suma funkcji nieskończenie małych jest funkcją nieskończenie małą. Funkcja jest sumą stałej liczby i nieskończenie małej funkcji. W konsekwencji z Twierdzenia 1 dla funkcji nieskończenie małych otrzymujemy wymaganą równość.
Zatem najprostsze właściwości nieskończenie dużych i nieskończenie dużych funkcji można zapisać za pomocą następujących relacji warunkowych: A≠ 0
13. Nieskończenie małe funkcje tego samego rzędu, równoważne nieskończenie małe.
Funkcje nieskończenie małe i nazywane są nieskończenie małymi tego samego rzędu małości, jeśli , oznaczają . I wreszcie, jeśli nie istnieje, to nieskończenie małe funkcje są nieporównywalne.
PRZYKŁAD 2. Porównanie funkcji nieskończenie małych
Równoważne funkcje nieskończenie małe.
Jeśli , to wywoływane są funkcje nieskończenie małe równowartość, oznacz ~ .
Funkcje lokalnie równoważne:
Kiedy Jeśli
Niektóre równoważności(Na ):
Granice jednostronne.
Do tej pory rozważaliśmy określenie granicy funkcji, gdy x → a w sposób dowolny, tj. granica funkcji nie zależała od sposobu jej umiejscowienia X w kierunku A, po lewej lub prawej stronie A. Jednak dość często spotyka się funkcje, które w tym warunku nie mają ograniczenia, ale mają granicę jeśli x → a, pozostając po jednej stronie A, w lewo lub w prawo (patrz rysunek). Dlatego wprowadzono pojęcia granic jednostronnych.
Jeśli k(x) zmierza do granicy B Na X zmierzający do określonej liczby A Więc X akceptuje tylko wartości mniejsze niż A, potem piszą i dzwonią blimit funkcji f(x) w punkcie a po lewej stronie.
Więc numer B nazywamy granicą funkcji y=f(x) Na x → a po lewej stronie, jeśli jakakolwiek liczba dodatnia ε jest, istnieje taka liczba δ (mniejsza A
Podobnie, jeśli x → a i przyjmuje duże wartości A, potem piszą i dzwonią B granica funkcji w punkcie A po prawej. Te. numer B zwany granica funkcji y=f(x) jako x → a po prawej stronie, jeśli jakakolwiek liczba dodatnia ε jest, istnieje taka liczba δ (większa A), że nierówność dotyczy wszystkich.
Należy pamiętać, że jeśli granice po lewej i prawej stronie w punkcie A dla funkcji k(x) nie pokrywają się, to funkcja nie ma granicy (dwustronnej) w punkcie A.
Przykłady.
1. Rozważ funkcję y=f(x), zdefiniowane w segmencie w następujący sposób
Znajdźmy granice funkcji k(x) Na x → 3. Oczywiście i
Innymi słowy, dla dowolnej dowolnie małej liczby epsilon istnieje liczba delta zależna od epsilon taka, że z faktu, że dla dowolnego x spełniającego nierówność wynika, że różnice wartości funkcji w tych punktach będą wynosić dowolnie małe.
Kryterium ciągłości funkcji w punkcie:
Funkcjonować będzie ciągły w punkcie A wtedy i tylko wtedy, gdy w punkcie A jest ciągła zarówno po prawej, jak i po lewej stronie, to znaczy tak, że w punkcie A istnieją dwie jednostronne granice, są one sobie równe i równe wartości funkcja w punkcie A.
Definicja 2: Funkcja jest ciągła na zbiorze, jeśli jest on ciągły we wszystkich punktach tego zbioru.
Pochodna funkcji w punkcie
Niech dana zostanie zdefiniowana w sąsiedztwie. Rozważmy
Jeśli ta granica istnieje, nazywa się ją pochodna funkcji f w punkcie .
Pochodna funkcji– granica stosunku przyrostu funkcji do przyrostu argumentu, gdy argument jest zwiększany.
Nazywa się operację obliczania lub znajdowania pochodnej w punkcie różnicowanie .
Zasady różnicowania.
Pochodna Funkcje k(x) w tym punkcie x=x 0 nazywa się stosunkiem przyrostu funkcji w tym punkcie do przyrostu argumentu, ponieważ ten ostatni dąży do zera różnicowanie. Pochodną funkcji obliczamy według ogólnej zasady różniczkowania: Oznaczmy f(x) = u, g(x) = v- funkcje różniczkowalne w punkcie X. Podstawowe zasady różniczkowania 1) (pochodna sumy jest równa sumie jej pochodnych) 2) (w szczególności stąd wynika, że pochodna iloczynu funkcji i stałej jest równa iloczynowi pochodnej tej funkcja i stała) 3) Pochodna ilorazu: , jeśli g 0 4) Pochodna funkcji zespolonej: 5) Jeżeli funkcja jest określona parametrycznie: , to
Przykłady.
1. y = X a jest funkcją potęgową z dowolnym wykładnikiem.
Funkcja niejawna
Jeżeli funkcję dana jest równaniem y=ƒ(x), rozwiązanym względem y, to funkcja ta jest dana w formie jawnej (funkcja jawna).
Pod ukryte zadanie funkcje rozumieją definicję funkcji w postaci równania F(x;y)=0, nierozwiązanego ze względu na y.
Dowolną jawnie daną funkcję y=ƒ (x) można zapisać jako daną w sposób dorozumiany równaniem ƒ(x)-y=0, ale nie odwrotnie.
Rozwiązanie równania dla y nie zawsze jest łatwe, a czasami niemożliwe (na przykład y+2x+cozy-1=0 lub 2 y -x+y=0).
Jeśli ukryta funkcja jest dana równaniem F(x; y) = 0, to aby znaleźć pochodną y po x, nie ma potrzeby rozwiązywania równania po y: wystarczy zróżnicować to równanie ze względu na x, rozważając y jako funkcję x, a następnie rozwiąż powstałe równanie dla y.”
Pochodną funkcji ukrytej wyraża się za pomocą argumentu x i funkcji y.
Przykład:
Znajdź pochodną funkcji y, daną równaniem x 3 + y 3 -3xy = 0.
Rozwiązanie: Funkcja y jest określona niejawnie. Różniczkujemy ze względu na x równość x 3 +y 3 -3xy=0. Z powstałej relacji
3x 2 +3y 2 y"-3(1 y+x y")=0
wynika z tego, że y 2 y"-xy"=y-x 2, tj. y"=(y-x 2)/(y 2 -x).
Instrumenty pochodne wyższego rzędu
Jest oczywiste, że pochodna
Funkcje y=f(x) istnieje również funkcja z X:
y" = f " (x)
Jeśli funkcja f” (x) jest różniczkowalna, to jej pochodną oznaczamy symbolem y"" =f "" (x) x dwa razy.
Pochodna drugiej pochodnej, tj. Funkcje y""=f""(x), zwany trzecia pochodna funkcji y=f(x) Lub pochodna funkcji f(x) trzeciego rzędu i jest oznaczony symbolami
W ogóle N-i pochodna lub pochodna N funkcja trzeciego rzędu y=f(x) oznaczone symbolami
Phil Leibniz:
Załóżmy, że funkcje i są różniczkowalne wraz z ich pochodnymi aż do n-tego rzędu włącznie. Stosując regułę różniczkowania iloczynu dwóch funkcji, otrzymujemy
Porównajmy te wyrażenia z potęgami dwumianu:
Zasada korespondencji jest uderzająca: aby otrzymać wzór na pochodną pierwszego, drugiego lub trzeciego rzędu iloczynu funkcji i , należy zastąpić potęgi i w wyrażeniu na (gdzie N= 1,2,3) pochodne odpowiednich rzędów. Dodatkowo potęgi zerowe wielkości i należy zastąpić pochodnymi rzędu zerowego, czyli funkcjami i:
Uogólnienie tej reguły na przypadek pochodnych dowolnego rzędu N, otrzymujemy Wzór Leibniza,
gdzie są współczynniki dwumianu:
Twierdzenie Rolle'a.
Twierdzenie to umożliwia znalezienie punktów krytycznych, a następnie przy zastosowaniu warunków wystarczających zbadanie funkcji pod kątem ekstremów.
Niech 1) f(x) będzie określone i ciągłe na pewnym przedziale domkniętym; 2) istnieje skończona pochodna, przynajmniej w przedziale otwartym (a;b); 3) na końcach przedziału f-i przyjmuje równe wartości f(a) = f(b). Następnie pomiędzy punktami a i b znajduje się punkt c taki, że pochodna w tym punkcie będzie wynosić = 0.
Zgodnie z twierdzeniem o własności funkcji ciągłych na pewnym przedziale, funkcja f(x) przyjmuje na tym przedziale swoje wartości maksymalne i minimalne.
f(x 1) = M – max, f(x 2) = m – min; x 1 ;x 2 O
1) Niech M = m, tj. m £ f(x) £ M
Þ f(x) będzie przyjmować wartości stałe w przedziale od a do b, a Þ jej pochodna będzie równa zeru. f’(x)=0
2) Niech M>m
Ponieważ zgodnie z warunkami twierdzenia, f(a) = f(b) Þ przyjmie swoją najmniejszą lub największą wartość nie na końcach odcinka, ale Þ przyjmie M lub m w wewnętrznym punkcie tego odcinka. Następnie, zgodnie z twierdzeniem Fermata, f’(c)=0.
Twierdzenie Lagrange'a.
Formuła skończonego przyrostu Lub Twierdzenie Lagrange'a o wartości średniej stwierdza, że jeśli jest to funkcja Definicja funkcji: Jeżeli każdej liczbie x ze zbioru liczb D przyporządkowana jest pojedyncza liczba y, to mówią, że na zbiorze D dana jest funkcja f i piszą y= f(x), gdzie x nazywa się niezależna zmienna lub argument tej funkcji, a zbiór D jest dziedziną definicji tej funkcji. jest ciągła na przedziale [ A;B] i różniczkowalna w przedziale ( A;B), to jest taki punkt, że
Twierdzenie Cauchy'ego.
Jeżeli funkcje f(x) i g(x) są ciągłe na przedziale i różniczkowalne na przedziale (a, b) oraz g¢(x) ¹ 0 na przedziale (a, b), to istnieje co najmniej jeden punkt e, a< e < b, такая, что
Te. stosunek przyrostów funkcji na danym odcinku jest równy stosunkowi pochodnych w punkcie e. Przykłady rozwiązywania problemów przebieg wykładów Obliczanie objętości ciała ze znanych pól jego przekrojów równoległych Rachunek całkowy
Przykłady zajęć Inżynieria elektryczna
Aby udowodnić to twierdzenie, na pierwszy rzut oka bardzo wygodnie jest skorzystać z twierdzenia Lagrange'a. Zapisz wzór na różnicę skończoną dla każdej funkcji, a następnie podziel je przez siebie. Jednak pomysł ten jest błędny, ponieważ punkt e dla każdej funkcji jest generalnie inny. Oczywiście w niektórych szczególnych przypadkach ten punkt przedziału może okazać się taki sam dla obu funkcji, ale jest to bardzo rzadki zbieg okoliczności, a nie reguła i dlatego nie można go wykorzystać do udowodnienia twierdzenia.
Dowód. Rozważmy funkcję pomocniczą
Ponieważ x → x 0, wartość c również dąży do x 0; Przejdźmy do granicy z poprzedniej równości:
Ponieważ , To .
Dlatego
(granica stosunku dwóch nieskończenie małych jest równa granicy stosunku ich pochodnych, jeśli ta ostatnia istnieje)
Reguła L'Hopitala, przy ∞/∞.
Uwaga: wszystkie definicje dotyczą zbioru liczbowego X, który jest częścią dziedziny funkcji: X z D(f). W praktyce najczęściej zdarzają się przypadki, gdy X jest przedziałem liczbowym (odcinek, przedział, półprosta itp.).
Definicja 1.
Mówi się, że funkcja y = f(x) rośnie na zbiorze X z D(f), jeśli dla dowolnych dwóch punktów x 1 i x 2 zbioru X takich, że x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).
Definicja 2.
Mówi się, że funkcja y = f(x) maleje na zbiorze X z D(f), jeśli dla dowolnych dwóch punktów x 1 i x 2 zbioru X takich, że x 1< х 2 , функции выполняется неравенство f(x 1) >f(x 2).
W praktyce wygodniej jest stosować następujące sformułowania: funkcja wzrasta, jeśli większej wartości argumentu odpowiada większa wartość funkcji; funkcja maleje, jeśli większa wartość argumentu odpowiada mniejszej wartości funkcji.
W klasach 7. i 8. stosowaliśmy następującą interpretację geometryczną pojęć zwiększania lub zmniejszania funkcji: poruszając się po wykresie funkcji rosnącej od lewej do prawej, mamy wrażenie, że wspinamy się na wzgórze (ryc. 55); poruszając się po wykresie funkcji malejącej od lewej do prawej, mamy wrażenie, jakbyśmy schodzili po zboczu (ryc. 56).
Zwykle terminy „funkcja rosnąca”, „funkcja malejąca” są łączone pod ogólną nazwą funkcja monotoniczna, a badanie funkcji zwiększającej lub zmniejszającej nazywa się badaniem funkcji monotoniczności.
Zwróćmy uwagę na jeszcze jedną okoliczność: jeśli funkcja rośnie (lub maleje) w swojej naturalnej dziedzinie definicji, to zwykle mówimy, że funkcja jest rosnąca (lub malejąca) - bez podawania zbioru liczbowego X.
Przykład 1.
Zbadaj funkcję pod kątem monotoniczności:
A) y = x 3 + 2; b) y = 5 - 2x.
Rozwiązanie:
a) Weź dowolne wartości argumentu x 1 i x 2 i niech x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

Ostatnia nierówność oznacza, że f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).
Zatem od x1< х 2 следует f(х 1) >f(x 2), co oznacza, że dana funkcja jest malejąca (na całej osi liczbowej).
Definicja 3.
Mówi się, że funkcja y - f(x) jest ograniczona od dołu na zbiorze X przez D(f), jeśli wszystkie wartości funkcji na zbiorze X są większe od pewnej liczby (innymi słowy, jeśli istnieje liczbę m taką, że dla dowolnej wartości x є X nierówność f( x) >m).
Definicja 4.
Mówi się, że funkcja y = f(x) jest ograniczona z góry na zbiorze X przez D(f), jeśli wszystkie wartości funkcji są mniejsze od pewnej liczby (innymi słowy, jeśli istnieje liczba M taka że dla dowolnej wartości x є X zachodzi nierówność f(x).< М).
Jeżeli zbiór X nie jest określony, to rozumie się, że mówimy o funkcji ograniczonej od dołu lub od góry w całym obszarze definicji.
Jeśli funkcja jest ograniczona zarówno od dołu, jak i od góry, nazywa się ją ograniczoną.
Ograniczenie funkcji łatwo odczytać z jej wykresu: jeśli funkcja jest ograniczona od dołu, to jej wykres w całości znajduje się powyżej pewnej poziomej linii y = m (ryc. 57); jeśli funkcja jest ograniczona z góry, to jej wykres w całości znajduje się poniżej jakiejś poziomej linii y = M (ryc. 58).

Przykład 2. Zbadaj ograniczenie funkcji
Rozwiązanie. Z jednej strony nierówność jest dość oczywista (z definicji pierwiastka kwadratowego wynika, że funkcja jest ograniczona od dołu. Z drugiej strony mamy, a zatem
Oznacza to, że funkcja jest ograniczona górnie. Spójrzmy teraz na wykres danej funkcji (ryc. 52 z poprzedniego akapitu). Ograniczenie funkcji zarówno powyżej, jak i poniżej można dość łatwo odczytać z wykresu.
Definicja 5.
Liczbę m nazywamy najmniejszą wartością funkcji y = f(x) na zbiorze X C D(f) jeżeli:
1) w X jest taki punkt x 0, że f(x 0) = m;
2) dla wszystkich x z X zachodzi nierówność m>f(x 0).
Definicja 6.
Liczbę M nazywamy największą wartością funkcji y = f(x) na zbiorze X C D(f), jeżeli:
1) w X jest taki punkt x 0, że f(x 0) = M;
2) dla wszystkich x z X nierówność
Najmniejszą wartość funkcji zarówno w klasie VII, jak i VIII oznaczyliśmy symbolem y, a największą symbolem y.
Jeżeli zbiór X nie jest określony, to przyjmuje się, że mówimy o znalezieniu najmniejszej lub największej wartości funkcji w całym obszarze definicji.
Poniższe przydatne stwierdzenia są dość oczywiste:
1) Jeśli funkcja ma Y, to jest ona ograniczona poniżej.
2) Jeśli funkcja ma Y, to jest ograniczona powyżej.
3) Jeśli funkcja nie jest ograniczona poniżej, to Y nie istnieje.
4) Jeżeli funkcja nie jest ograniczona powyżej, to Y nie istnieje.
Przykład 3.
Znajdź najmniejszą i największą wartość funkcji
Rozwiązanie.
Jest to dość oczywiste, zwłaszcza jeśli skorzystamy z wykresu funkcji (rys. 52), że = 0 (funkcja osiąga tę wartość w punktach x = -3 i x = 3), a = 3 (funkcja osiąga tę wartość w x = 0.
W klasach 7 i 8 wspomnieliśmy jeszcze o dwóch własnościach funkcji. Pierwszą z nich nazwano właściwością wypukłości funkcji. Funkcję uważa się za wypukłą w dół na przedziale X, jeśli łącząc dowolne dwa punkty jej wykresu (z odciętymi z X) odcinkiem prostym stwierdzimy, że odpowiadająca jej część wykresu leży poniżej narysowanego odcinka (ryc. 59). ciągłość Funkcja jest wypukła w górę na przedziale X, jeśli łącząc dowolne dwa punkty jej wykresu (z odciętymi z X) funkcji z odcinkiem prostym stwierdzimy, że odpowiadająca jej część wykresu leży nad narysowanym odcinkiem ( Ryc. 60).

Druga właściwość – ciągłość funkcji na przedziale X – oznacza, że wykres funkcji na przedziale X jest ciągły, tj. nie ma żadnych przebić ani skoków.
Komentarz.
W rzeczywistości w matematyce wszystko jest, jak mówią, „dokładnie odwrotnie”: wykres funkcji przedstawia się jako linię ciągłą (bez przebić i przeskoków) tylko wtedy, gdy udowodniona zostanie ciągłość funkcji. Jednak formalna definicja ciągłości funkcji, która jest dość złożona i subtelna, nie leży jeszcze w naszych możliwościach. To samo można powiedzieć o wypukłości funkcji. Omawiając te dwie właściwości funkcji, nadal będziemy opierać się na koncepcjach wizualnych i intuicyjnych.
Teraz przeanalizujmy naszą wiedzę. Pamiętając funkcje, które badaliśmy w 7. i 8. klasie, wyjaśnijmy, jak wyglądają ich wykresy i wypiszmy własności funkcji, zachowując pewien porządek, np. ten: dziedzina definicji; monotonia; ograniczenie; ,; ciągłość; zakres; wypukły.
Następnie pojawią się nowe właściwości funkcji i odpowiednio zmieni się lista właściwości.
1. Funkcja stała y = C
Wykres funkcji y = C pokazano na ryc. 61 - linia prosta, równoległa do osi x. Jest to na tyle nieciekawa cecha, że nie ma sensu wymieniać jej właściwości.

Wykres funkcji y = kx + m jest linią prostą (ryc. 62, 63).

Własności funkcji y = kx + m:
1) ![]()
2) wzrasta, jeśli k > 0 (ryc. 62), maleje, jeśli k< 0 (рис. 63);
4) nie ma ani największej, ani najmniejszej wartości;
5) funkcja jest ciągła;
6) ![]()
7) nie ma sensu mówić o wypukłości.
Wykres funkcji y = kx 2 jest parabolą z wierzchołkiem w początku i gałęziami skierowanymi w górę, jeśli k > O (rys. 64), i w dół, jeśli k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Własności funkcji y - kx 2:
Dla przypadku k > 0 (rys. 64):
1) D(f) = (-oo,+oo);
4) = nie istnieje;
5) ciągły;
6) E(f) = funkcja maleje, a na przedziale maleje na półprostej;
7) wypukły ku górze.
Wykres funkcji y = f(x) wykreślono punkt po punkcie; Im więcej punktów postaci (x; f(x)) weźmiemy, tym dokładniejsze wyobrażenie o wykresie otrzymamy. Jeśli weźmiesz dużo tych punktów, otrzymasz pełniejszy obraz wykresu. To właśnie w tym przypadku intuicja podpowiada nam, że wykres należy przedstawić w postaci linii ciągłej (w tym przypadku w postaci paraboli). A następnie czytając wykres wyciągamy wnioski na temat ciągłości funkcji, jej wypukłości w dół lub w górę, na temat zakresu wartości funkcji. Trzeba zrozumieć, że z wymienionych siedmiu właściwości jedynie właściwości 1), 2), 3), 4) są „uprawnione” – „uprawnione” w tym sensie, że jesteśmy w stanie je uzasadnić, odwołując się do precyzyjnych definicji. Na pozostałe właściwości mamy jedynie wizualne i intuicyjne wyobrażenia. Swoją drogą, nie ma w tym nic złego. Z historii rozwoju matematyki wiadomo, że ludzkość często i przez długi czas posługiwała się różnymi właściwościami pewnych obiektów, nie znając dokładnych definicji. Potem, gdy udało się sformułować takie definicje, wszystko się ułożyło. ![]()
Wykres funkcji jest hiperbolą, osie współrzędnych służą jako asymptoty hiperboli (ryc. 66, 67).

1) D(f) = (-00,0)1U (0,+oo);
2) jeśli k > 0, to funkcja maleje na półprostej otwartej (-oo, 0) i na półprostej otwartej (0, +oo) (ryc. 66); jeśli< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) nie jest ograniczona ani od dołu, ani od góry;
4) nie ma ani najmniejszej, ani największej wartości;
5) funkcja jest ciągła na półprostej otwartej (-oo, 0) i na półprostej otwartej (0, +oo);
6) E(f) = (-oo,0) U (0,+oo);
7) jeśli k > 0, to funkcja jest wypukła w górę w punkcie x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, tj. na otwartej belce (0, +oo) (ryc. 66). Jeśli< 0, то функция выпукла вверх при х >O i wypukły w dół w punkcie x< О (рис. 67).
Wykres funkcji jest gałęzią paraboli (ryc. 68). Właściwości funkcji:
1) D(f) = , zwiększa się na promieniu )