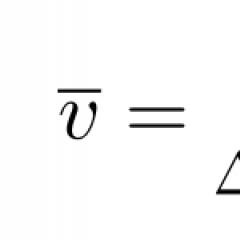Wykres s w funkcji t. Ruch jednostajnie przyspieszony: wzory, przykłady

Rysunek 1. Wykresy ruchu jednostajnego. Avtor24 - internetowa wymiana prac studenckich

Najprostszym rodzajem ruchu jest ruch jednostajny. Można to ustalić, gdy przyspieszenie ciała w dowolnym momencie jest równe zero. Innymi słowy, ruch jednostajny jest reprezentowany w postaci pewnego idealnego położenia ciała, gdy jego prędkość będzie w dowolnym momencie taka sama. Kiedy ciało pokonuje równe odległości w równych odstępach czasu, ruch nabiera cech ruchu jednostajnie prostoliniowego. W prawdziwym życiu takie cechy praktycznie nigdy nie występują.

Definicja 1

Ścieżka to długość trajektorii, po której poruszało się określone ciało w określonym przedziale czasu.

Definicja 2

Przemieszczenie to odległość pomiędzy punktem początkowym i końcowym trajektorii ciała.

Ścieżka i przemieszczenie to różne pojęcia, ponieważ ścieżka jest wielkością skalarną, a przemieszczenie jest wielkością wektorową. W tym przypadku wielkość wektora przemieszczenia jest równa odcinku łączącemu punkt początkowy i końcowy trajektorii ciała.

Jednolita prędkość

Definicja 3

Prędkość ruchu jednostajnego nazywana jest wielkością wektora, którą oblicza się za pomocą określonego wzoru. Mówi, że wektor będzie równy stosunkowi drogi przebytej przez ciało do czasu jego przejścia.

Przy ruchu jednostajnym kierunek wektora prędkości pokrywa się z kierunkiem ruchu. Zasadę tę należy uwzględnić przy konstruowaniu wykresu ruchu jednostajnego. Przemieszczenie i droga takiego ruchu będą miały te same wartości.

Ruch jednostajny obejmuje także stan spoczynku. W tym przypadku ciało pokonuje równe odległości w równych odstępach czasu. W spoczynku wszystkie wartości będą wynosić zero. Przy równomiernym ruchu przebyta odległość składa się z następujących wskaźników złożonych:

współrzędna początkowa;
iloczyn prędkości ciała i czasu ruchu.

Jednolite wykresy ruchu

Konstruując wykres ruchu jednostajnego ze zmianą prędkości w czasie, otrzymasz linię prostą, która będzie biegła równolegle do linii osi X. Pole powstałego prostokąta jest równe długości drogi przebytej przez ciało w określonym czasie. Oznacza to, że powierzchnia prostokąta będzie równa iloczynowi wszystkich jego boków.

Po wykreśleniu zależności przebytej drogi od czasu obliczana jest prędkość, z jaką poruszało się ciało. W tym przypadku wykres ma linię prostą poprowadzoną od początku. Wymaganą wartością modułu wektora prędkości będzie tangens kąta nachylenia prostej względem osi odciętej. Podczas tworzenia wykresu ruchu jednostajnego oś x jest osią czasu. Silne nachylenie wykresu wskazuje, że prędkość ciała jest duża.

W fizyce stosuje się następujące oznaczenia ruchu jednostajnego:

Pokazuje niezmienność prędkości, która jest wyrażona jako stała.

Ruch jednostajny przechodzi:

krzywoliniowa trajektoria;
trajektoria prostoliniowa.

Ruch jednostajny opisuje wzór:

We wzorze tym $s$ to droga, jaką przebyło ciało od początkowego punktu odniesienia, $t$ to czas, w jakim przebywa ciało, a $s_0$ to wartość ścieżki w początkowym momencie.

Ruch po linii prostej

Notatka 1

Ruch nazywamy prostoliniowym, jeśli zachodzi po linii prostej.

Trajektoria ruchu prostoliniowego jest linią prostą. Przy prędkości ruchu jednostajnego nie ma zależności od czasu, ponieważ w dowolnym punkcie trajektorii jest on skierowany w taki sam sposób, jak ruch ciała. Innymi słowy, wektor przemieszczenia pokrywa się w kierunku z wektorem prędkości. Prędkość średnia w dowolnym okresie czasu jest równa prędkości chwilowej.

Prędkość jednostajnego ruchu prostoliniowego pokazuje wartość ruchu punktu materialnego w jednostce czasu.

Przy takim ruchu całkowite przyspieszenie wyraża się wzorem:

W międzynarodowym systemie miar jednostką przyspieszenia jest przyspieszenie, przy którym prędkość ciała zmienia się o 1 metr na sekundę.

Równie zmienny ruch

Szczególnym przypadkiem nierównomiernego ruchu ciała jest ruch jednostajnie prostoliniowy.

Ruch jednostajnie zmienny to ruch, w którym prędkość punktu materialnego zmienia się jednakowo w równych odstępach czasu. Przyspieszenie ciała w ruchu jednostajnym pozostaje niezmienione pod względem kierunku i wielkości.

Ruch jednostajny można podzielić na dwa rodzaje: równomiernie przyspieszany i równomiernie zwalniany.

Ruch ciała lub punktu materialnego z dodatnim przyspieszeniem uważa się za równomiernie przyspieszony. Dzięki takiemu sposobowi poruszania się może przyspieszać z przyspieszeniem na stałym poziomie.

Ruch ciała o ujemnym przyspieszeniu nazywamy ruchem jednostajnie powolnym. Przy tego typu ruchu ciało zwalnia na równym poziomie.

Średnią prędkość ruchu naprzemiennego można wyznaczyć dzieląc ruch ciała przez czas, w którym ten ruch nastąpił. Jednostką średniej prędkości jest m/s.

Chwilowa prędkość i przyspieszenie

Szybkość ciała lub punktu materialnego nazywa się chwilową, jeżeli występuje w określonym momencie lub w danym punkcie trajektorii ruchu. Wartość tę nazywa się wartością graniczną, ponieważ średnia prędkość ciała zmierza do niej w miarę nieskończonego zmniejszania się okresu czasu. Jest oznaczony jako $Δt$.

Prędkość chwilową wyraża się za pomocą następującego wzoru:

Wielkość określającą zmiany prędkości ciała nazywa się przyspieszeniem. Są to wartości graniczne wielkości i zmiana prędkości zmierza do niej z nieskończonym zmniejszaniem się przedziału czasu $Δt$.

Przemieszczenie podczas jednostajnego ruchu liniowego oblicza się ze wzoru:

Wartość $υx$ jest rzutem prędkości na oś X.

Wynika z tego, że prawo ruchu jednostajnego prostoliniowego ma następującą postać:

W początkowej chwili czasu $xo = 0$, zatem pozostałe wartości przyjmują postać.

3. Rozważ rysunek 4.6.
a) W jakich punktach wykresu kąt nachylenia stycznej jest największy?

Szybkość natychmiastowa i średnia

najmniej?

2. Średnia prędkość

waw = l/t. (1)

5. Znajdź:

c) Średnia prędkość Sashy.

6. Znajdź:

b) Średnia prędkość Sashy.

Analiza testu przygotowującego do Internetowej Olimpiady Fizycznej 2008/2009

Klasa 11. Kinematyka

Pytanie nr 1

Korzystając z wykresu przedstawionego na rysunku, określ prędkość rowerzysty po trzech sekundach od rozpoczęcia ruchu.

Rozwiązanie.

Rysunek przedstawia wykres ścieżki w funkcji czasu. Wykres jest linią prostą, co oznacza, że rowerzysta poruszał się równomiernie. Wyznaczmy z wykresu drogę przebytą przez rowerzystę w ustalonym okresie czasu. Na przykład w ciągu 3 s rowerzysta przejechał 9 m, a prędkość rowerzysty wynosi V = L / t = 9/3 = 3 m/s.

Pytanie nr 2

Pieszy i rowerzysta zaczęli jednocześnie zbliżać się do siebie. Ich prędkości są równe odpowiednio V1 = i V2 = . Wyznacz czas ruchu do spotkania, jeśli początkowa odległość między nimi wynosi L = .

Rozwiązanie.

Wyznaczmy prędkość rowerzysty w układzie odniesienia pieszego V12 = V1 + V2 = 6 + 30 = 36 km/h = 10 m/s. Zatem pieszy i rowerzysta zbliżają się do siebie z prędkością 10 m/s, wówczas czas ich przejazdu do spotkania wynosi t = L / V12 = 700/10 = 70 s.

Pytanie nr 3

Samochód jechał z prędkością 15 m/s przez 5 s. Jaką odległość przebył w tym czasie?

Rozwiązanie.

Samochód poruszał się ruchem jednostajnym, zatem przebyta droga wynosi L = Vt = 155 = 75 m.

Pytanie nr 4

Piłka rzucona pionowo w górę powraca do swojego pierwotnego położenia. Rysunek przedstawia wykres jego prędkości w funkcji czasu. W jakim momencie piłka osiągnęła maksymalną wysokość?

Rozwiązanie.

W chwili, gdy piłka osiągnie maksymalną wysokość, jej prędkość wynosi zero. Zgodnie z wykresem przedstawionym na rysunku wyznaczamy, że prędkość piłki wynosi zero w chwili t = 2 s.

Pytanie nr 5

Które z powyższych wielkości są wielkościami wektorowymi?

(Zaznacz wszystkie wielkości wektorowe)

Rozwiązanie.

Spośród wymienionych wielkości prędkość, przyspieszenie i przemieszczenie są wielkościami wektorowymi. Ścieżka jest wielkością skalarną.

Pytanie nr 6

Zawodnik przebiegł dystans 400 m po torze stadionu i wrócił do punktu startu. Wyznacz drogę L przebytą przez sportowca i moduł jego ruchu S.

Rozwiązanie.

Droga przebyta przez zawodnika wynosi L = 400 m. Moduł przemieszczenia wynosi S = 0, ponieważ zawodnik powrócił do punktu, z którego zaczął się poruszać.

Pytanie nr 7

Prędkość ciała poruszającego się prostoliniowo i z jednostajnym przyspieszeniem zmieniała się podczas przemieszczania się z punktu 1 do punktu 2, jak pokazano na rysunku. Jaki kierunek ma wektor przyspieszenia na tym odcinku ścieżki?

Rozwiązanie.

Z rysunku widać, że moduł prędkości ciała maleje w miarę jego ruchu, co oznacza, że wektor przyspieszenia jest skierowany w stronę ruchu, czyli w lewo.

Pytanie nr 8

Korzystając z wykresu modułu prędkości w funkcji czasu, wyznacz przyspieszenie ciała poruszającego się prostoliniowo w chwili t = 2 s.

Rozwiązanie.

Za pomocą wykresu wyznaczamy zmianę prędkości ciała w ustalonym momencie. Przykładowo, w ciągu pierwszych dwóch sekund prędkość ciała zmieniła się o 6 m/s (z V0 = 3 m/s do Vt = 9 m/s). Przyspieszenie a = (Vt – V0) / t = 6/2 = 3 m/s2.

Pytanie nr 9

Gdy samochód porusza się ze stałym przyspieszeniem przez pięć sekund, jego prędkość wzrasta z 10 do 15 m/s. Jaki jest moduł przyspieszenia samochodu?

Rozwiązanie.

Przyspieszenie samochodu a = (Vt – V0) / t= (15 – 10)/5 = 5/5 = 1 m/s2.

Pytanie nr 10

Samochód rusza z miejsca ze stałym przyspieszeniem a = 1 m/s2. Jaką drogę przejedzie samochód w ciągu pierwszych dziesięciu sekund ruchu?

Rozwiązanie.

Samochód porusza się ze stałym przyspieszeniem bez prędkości początkowej - przebyta droga wynosi L = at2/2 = 1102/2 = 50 m.

Pytanie nr 11

Tratwa płynie równomiernie po rzece z prędkością 3 km/h. Krokiew porusza się po tratwie z prędkością 4 km/h. Jaka jest prędkość krokwi w układzie odniesienia związanym z brzegiem?

Rozwiązanie.

Prędkość krokwi w układzie odniesienia związanym z brzegiem

Pytanie nr 12

Helikopter wznosi się pionowo ze stałą prędkością. Jaka jest trajektoria punktu na końcu łopaty wirnika helikoptera w układzie odniesienia skojarzonym z korpusem helikoptera?

Rozwiązanie.

Wyobraź sobie, że jesteś w kokpicie helikoptera, czyli jesteś nieruchomy względem korpusu helikoptera. W tym przypadku widać, że dowolny punkt na wirniku helikoptera opisuje okrąg.

Pytanie nr 13

Ciało porusza się wzdłuż osi X zgodnie z prawem przedstawionym na rysunku, gdzie x to współrzędna w metrach, t to czas w sekundach. Wyznacz moduł przyspieszenia ciała.

Rozwiązanie.

Równanie zależności współrzędnej od czasu dla ruchu prostoliniowego jednostajnie przyspieszonego ma postać ogólną X(t) = X0 + V0хt + akht2/2, gdzie X0 jest współrzędną początkową, a V0х i akh są rzutami prędkość początkowa i przyspieszenie na osi X.

Porównując wyrazy zawierające t2, otrzymujemy akht2/2 = –4,5t2. Skąd bierze się rzut przyspieszenia aх = –9 m/s2 i moduł przyspieszenia a= 9 m/s2.

Pytanie nr 14

Rysunek przedstawia wykresy modułu prędkości w funkcji czasu dla czterech ciał. Które z tych ciał (lub które ciała) przebyło najdalszą podróż?

Rozwiązanie.

Rysunek przedstawia wykresy prędkości poruszających się ciał w funkcji czasu. Jak wiadomo, droga przebyta przez ciało to obszar leżący pod wykresem prędkości. Z rysunku widać, że pod wykresem ciała 4 znajduje się liczba maksymalnej powierzchni. Oznacza to, że w okresie od 0 do t0 ciało 4 przebyło największą drogę.

Pytanie nr 15

Ciało porusza się po linii prostej. Rysunek przedstawia wykres prędkości ciała w funkcji czasu. W jakim przedziale czasu prognoza przyspieszenia jest ujemna?

Rozwiązanie.

Przeanalizujmy wykres:

1. w czasie od 0 do 1 s prędkość ciała jest stała, zatem ax = 0;

2. w czasie od 1 s do 2 s prędkość ciała maleje, więc rzut przyspieszenia wynosi ah< 0;

3. w przedziale czasu od 2s do 3s ciało znajduje się w spoczynku, zatem ax = 0;

4. w przedziale czasu od 3 s do 4 s prędkość ciała wzrasta, zatem rzut osi przyspieszenia > 0.

Zatem prognoza przyspieszenia jest ujemna w przedziale czasu od 1 s do 2 s.

Pytanie nr 16

Samochód poruszający się z prędkością początkową 20 m/s przyspiesza ze stałym przyspieszeniem a = 2 m/s2 przez 5 s. Jaką odległość przebył w tym czasie?

Rozwiązanie.

Aby obliczyć ścieżkę, możesz skorzystać ze wzoru L = V0t + at2/2 = 205 + 252/2 = .

Jak znaleźć średnią prędkość z wykresu

1. Prędkość chwilowa

W tej części rozważymy ruch nierówny. Jednak w tym przypadku będziemy potrzebować wiedzy o prostoliniowym ruchu jednostajnym.

Rysunek 4.1 przedstawia położenie przyspieszającego samochodu na prostej autostradzie w odstępie czasu wynoszącym 1 s. Strzałka wskazuje lusterko wsteczne, którego położenie rozważymy bardziej szczegółowo.

Widzimy, że w równych odstępach czasu samochód pokonuje różne tory, czyli porusza się nierównomiernie.

Skróćmy teraz kolejne odstępy czasowe 20-krotnie – do 0,05 s – i monitorujmy zmianę położenia samochodu przez pół sekundy (nie jest to trudne do zrobienia np. za pomocą nagrania wideo).

Aby nie zaśmiecać rysunku 4.2, pokazano tylko dwa położenia samochodu w odstępie czasu 0,5 s. Kolejne pozycje pojazdu w odstępach 0,05 s są oznaczone położeniem jego lusterka wstecznego (zaznaczone na czerwono).

Widzimy, że gdy kolejne równe odstępy czasu są wystarczająco małe, to drogi pokonywane przez samochód w tych odstępach czasu są praktycznie takie same. Oznacza to, że ruch samochodu w tak krótkich okresach czasu można z dobrą dokładnością uznać za prostoliniowy i równomierny.

Okazuje się, że każdy ruch (nawet krzywoliniowy) ma tę niezwykłą właściwość: jeśli rozpatrzymy go w wystarczająco krótkim czasie Δt, jest on bardzo podobny do prostoliniowego ruchu jednostajnego! Co więcej, im krótszy okres czasu, tym większe podobieństwo.

Prędkość ciała w dostatecznie krótkim czasie nazywa się jego prędkością w danym momencie czasu t, jeżeli ten moment mieści się w przedziale Δt. A jego dokładniejsza nazwa to prędkość chwilowa.

Jak krótki musi być odstęp czasu Δt, aby w tym czasie ruch ciała można było uznać za prostoliniowy i równomierny, zależy od charakteru ruchu ciała.

W przypadku przyspieszania samochodu jest to ułamek sekundy. I na przykład ruch Ziemi wokół Słońca można z dużą dokładnością uznać za prostoliniowy i równomierny nawet w ciągu dnia, chociaż Ziemia w tym czasie przelatuje w przestrzeni ponad dwa i pół miliona kilometrów!

1. Korzystając z rysunku 4.2, wyznacz chwilową prędkość samochodu. Przyjmij, że długość samochodu wynosi 5 m.

Wartość chwilowej prędkości samochodu pokazuje prędkościomierz (rys. 4.3).

Jak znaleźć prędkość chwilową na podstawie wykresu współrzędnych w funkcji czasu

Rysunek 4.4 przedstawia wykres współrzędnych w funkcji czasu dla samochodu poruszającego się po prostej autostradzie.

Widzimy, że porusza się nierównomiernie, ponieważ wykres jego współrzędnych w funkcji czasu jest krzywą, a nie odcinkiem linii prostej.

Pokażmy, jak z tego wykresu wyznaczyć chwilową prędkość samochodu w dowolnym momencie – powiedzmy w chwili t = 3 s (punkt na wykresie).

Aby to zrobić, należy wziąć pod uwagę ruch samochodu w tak krótkim czasie, w którym jego ruch można uznać za liniowy i równomierny.

Rysunek 4.5 pokazuje interesujący nas fragment wykresu z dziesięciokrotnym wzrostem (patrz np. skala czasu).

Widzimy, że tej części wykresu praktycznie nie można odróżnić od odcinka linii prostej (odcinka czerwonego). W kolejnych równych odstępach czasu wynoszących 0,1 s samochód pokonuje niemal identyczne odległości - po 1 m każda.

2. Jaka jest prędkość chwilowa samochodu w chwili t = 3 s?

Wracając do poprzedniej skali rysunku, zobaczymy, że czerwona linia prosta, z którą praktycznie pokrywa się niewielki fragment wykresu, jest styczna do wykresu zależności współrzędnej od czasu w danym momencie (ryc. 4.6).

Zatem chwilową prędkość ciała można ocenić na podstawie współczynnika kątowego stycznej do wykresu współrzędnych w funkcji czasu: im większy współczynnik kątowy stycznej, tym większa prędkość ciała. (Opisany sposób wyznaczania prędkości chwilowej za pomocą stycznej do wykresu zależności współrzędnej od czasu związany jest z pojęciem pochodnej funkcji. Pojęcie to poznasz na kursie „Algebra i początki aialis. ”) A w tych punktach wykresu, w których kąt nachylenia stycznej wynosi zero, wówczas istnieje styczna równoległa do osi czasu t, chwilowa prędkość ciała wynosi zero.

3. Rozważ rysunek 4.6.
b) Znajdź maksymalną i minimalną prędkość chwilową samochodu w ciągu pierwszych 6 sekund jego ruchu.

2. Średnia prędkość

W wielu zadaniach wykorzystuje się średnią prędkość związaną z przebytą drogą:

waw = l/t. (1)

Zdefiniowana w ten sposób średnia prędkość jest wielkością skalarną, ponieważ droga jest wielkością skalarną. (Czasami, aby uniknąć nieporozumień, nazywa się to średnią prędkością względem ziemi.)

Przykładowo, jeśli samochód przejechał po mieście 120 km w ciągu trzech godzin (w tym czasie mógł przyspieszać, hamować i zatrzymywać się na skrzyżowaniach), to jego średnia prędkość wynosiła 40 km/h.

4. O ile zmniejszy się średnia prędkość wspomnianego samochodu, jeżeli łączny czas jazdy wydłuży się o 1 godzinę ze względu na postoje w ruchu?

Średnia prędkość na dwóch odcinkach ruchu

W wielu zagadnieniach ruch ciała rozpatrywany jest w dwóch obszarach, w każdym z których ruch można uznać za jednolity. W tym przypadku zgodnie z definicją prędkości średniej (1) możemy napisać:

wav = (l1 + l2)/(t1 + t2), (2)

gdzie l1 i t1 to droga i czas dla pierwszej sekcji, a l2 i t2 dla drugiej. Spójrzmy na przykłady.
Sasza opuścił wieś na rowerze z prędkością 15 km/h i jechał przez godzinę. A potem zepsuł się rower i Sasza szedł przez kolejną godzinę z prędkością 5 km/h.

5. Znajdź:
a) drogę przebytą przez Saszę podczas całego ruchu;
b) całkowity czas ruchu Sashy;
c) Średnia prędkość Sashy.

W rozpatrywanym przypadku średnia prędkość okazała się równa średniej arytmetycznej prędkości, z jaką Sasza jechał i chodził. Czy to zawsze jest sprawiedliwe? Rozważ następujący przykład.
Pozwól Saszy jeździć na rowerze przez godzinę z prędkością 15 km/h, a następnie tę samą odległość przejść pieszo z prędkością 5 km/h.

6. Znajdź:
a) ścieżka, którą Sasha szła pieszo;
b) drogę przebytą przez Saszę podczas całego ruchu;
c) całkowity czas ruchu Sashy;
b) Średnia prędkość Sashy.

Patrząc na ten przypadek, zobaczysz, że tym razem średnia prędkość nie jest równa średniej arytmetycznej prędkości jazdy i chodzenia. A jeśli przyjrzysz się jeszcze uważniej, zauważysz, że w drugim przypadku średnia prędkość jest mniejsza niż w pierwszym. Dlaczego?

7. Porównaj okresy, w których Sasza jeździł i chodził w pierwszym i drugim przypadku.

Podsumujmy omówione powyżej sytuacje.

Rozważmy najpierw przypadek, gdy ciało poruszało się z różnymi prędkościami przez równe okresy czasu.

Niech ciało porusza się z prędkością v1 przez pierwszą połowę całego czasu ruchu, a przez drugą połowę z prędkością v2. Czy można wyznaczyć średnią prędkość ruchu na całym odcinku, jeśli nie jest znany ani całkowity czas ruchu, ani droga przebyta przez ciało podczas całego ruchu?

Można: w tym celu wprowadzamy oznaczenia wszystkich potrzebnych nam wielkości, niezależnie od tego, czy są one znane, czy nieznane. Jest to powszechna technika rozwiązywania wielu problemów.

Oznaczmy cały czas ruchu przez t, całą drogę przez l, a drogę przebytą w pierwszej i drugiej połowie czasu ruchu odpowiednio przez l1 i l2.

8. Wyraź w kategoriach v1, v2 i t:
a) l1 i l2; b) l; c) średnia prędkość.

Po znalezieniu odpowiedzi na te pytania dowiesz się, czy w ogólnym przypadku prawdziwe jest stwierdzenie: jeśli ciało poruszało się w dwóch odcinkach z różnymi prędkościami przez równe okresy czasu, to jego średnia prędkość na całej drodze jest równa średnia arytmetyczna prędkości w obu sekcjach.

Rozważmy teraz przypadek, gdy ciało poruszało się z różnymi prędkościami przez pierwszą i drugą połowę drogi.

Teraz pozwól ciału poruszać się przez pierwszą połowę całej drogi z prędkością v1, a przez drugą połowę z prędkością v2. Oznaczmy ponownie cały czas ruchu przez t, całą drogę przez l, a przedziały czasu, w których ciało poruszało się w pierwszym i drugim odcinku, będą oznaczone odpowiednio przez t1 i t2.

9. Wyraź w kategoriach v1, v2 i l:
a) t1 i t2; b) t; c) średnia prędkość.

Odpowiadając na te pytania, dowiesz się, czy w ogólnym przypadku prawdziwe jest stwierdzenie: jeśli ciało poruszało się po dwóch odcinkach o równej długości z różnymi prędkościami, to jego średnia prędkość na całej drodze nie jest równa średniej arytmetycznej tych prędkości.

10. Udowodnić, że średnia prędkość ciała, które poruszało się na dwóch odcinkach o tej samej długości z różnymi prędkościami, jest mniejsza, niż gdyby ciało poruszało się na dwóch odcinkach z tą samą prędkością przez jednakowe okresy czasu.
Wskazówka. Dla każdego z dwóch przypadków wyraź średnią prędkość w postaci prędkości w pierwszej i drugiej sekcji i porównaj otrzymane wyrażenia.

11. Na pierwszym odcinku toru ciało poruszało się z prędkością v1, a na drugim – z prędkością v2. Jaki jest stosunek długości tych odcinków, jeśli średnia prędkość ruchu okaże się równa średniej arytmetycznej v1 i v2?

Dodatkowe pytania i zadania

12. Przez jedną trzecią całego czasu pociąg jechał z prędkością v1, a przez pozostały czas z prędkością v2.
a) Wyraź drogę przebytą przez pociąg w postaci v1, v2 i całkowitego czasu podróży t.
b) Wyraź średnią prędkość pociągu w postaci v1 i v2.
c) Znajdź wartość liczbową średniej prędkości przy v1 = 60 km/h, v2 = 90 km/h.

13. Trzy czwarte całej trasy samochód przebył z prędkością v1, a pozostałą część trasy z prędkością v2.
a) Wyraź cały czas ruchu samochodu w postaci v1, v2 oraz całą przebytą drogę l.
b) Wyraź średnią prędkość samochodu w postaci v1 i v2.
c) Znajdź wartość liczbową średniej prędkości przy v1 = 80 km/h, v2 = 100 km/h.

14. Samochód jechał przez 2 godziny z prędkością 60 km/h. Jak długo potem musi jechać z prędkością 80 km/h, aby jego średnia prędkość na całej trasie wyniosła 66,7 km/h?

15. Przenieś do swojego notatnika (komórkami) wykres zależności współrzędnych samochodu od czasu, pokazany na rysunku 4.4. Załóżmy, że samochód porusza się wzdłuż osi x.
a) Wyznacz graficznie średnią prędkość w ciągu 6 s.
b) Korzystając ze stycznej, określ, w jakich przybliżonych momentach prędkość chwilowa samochodu była równa jego prędkości średniej w ciągu 6 s.

16. Ciało porusza się wzdłuż osi x. Zależność współrzędnych ciała od czasu wyraża się wzorem x = 0,2 * t2.
a) Wybierz dogodną skalę i wykreśl x(t) dla pierwszych 6 s.
b) Korzystając z tego wykresu, znajdź moment, w którym chwilowa prędkość ciała była równa prędkości średniej w całym czasie ruchu.

§ 12. Wykresy drogi w funkcji czasu.

Jeśli znana jest trajektoria ruchu punktu, to zależność drogi, jaką przebył punkt od czasu, jaki upłynął, daje pełny opis tego ruchu. Widzieliśmy, że dla ruchu jednostajnego taką zależność można zapisać w postaci wzoru (9.2). Zależność pomiędzy i dla poszczególnych punktów w czasie można także określić w formie tabeli zawierającej odpowiadające im wartości okresu czasu i przebytej drogi. Załóżmy, że prędkość pewnego ruchu jednostajnego wynosi 2 m/s. Wzór (9.2) w tym przypadku ma postać . Zróbmy tabelę ścieżki i czasu takiego ruchu:

Zależność jednej wielkości od drugiej często wygodnie jest przedstawić nie za pomocą wzorów czy tabel, ale wykresów, które wyraźniej pokazują obraz zmian zmiennych wielkości i mogą ułatwić obliczenia. Narysujmy zależność przebytej drogi od czasu dla danego ruchu. Aby to zrobić, weź dwie wzajemnie prostopadłe linie proste - osie współrzędnych; Jedną z nich (oś odciętych) nazwiemy osią czasu, a drugą (oś rzędnych) osią ścieżki. Wybierzmy skalę do zobrazowania przedziałów czasowych i ścieżek i przyjmijmy punkt przecięcia osi jako moment początkowy i punkt początkowy trajektorii. Narysujmy na osiach wartości czasu i przebytej drogi dla rozpatrywanego ruchu (ryc. 18). Aby „powiązać” wartości przebytej drogi z momentami w czasie, rysujemy prostopadłe do osi z odpowiednich punktów na osiach (na przykład punkty 3 s i 6 m). Punkt przecięcia prostopadłych odpowiada jednocześnie obu wielkościom: drodze i momentowi, w ten sposób osiąga się „wiązanie”. Tę samą konstrukcję można wykonać dla dowolnych innych punktów w czasie i odpowiadających im ścieżek, uzyskując dla każdej takiej pary czasu - wartości ścieżki jednego punktu na wykresie. Na ryc.

Wyznacz na podstawie wykresu średnią prędkość ciała w okresach czasu

18 wykonuje się taką konstrukcję, zastępując oba rzędy tabeli jednym rzędem punktów. Gdyby taką konstrukcję przeprowadzić dla wszystkich punktów w czasie, to zamiast poszczególnych punktów otrzymalibyśmy linię ciągłą (również pokazaną na rysunku). Linia ta nazywana jest wykresem ścieżki w funkcji czasu lub w skrócie wykresem ścieżki.

Ryż. 18. Wykres toru ruchu jednostajnego z prędkością 2 m/s

Ryż. 19. Do ćwiczenia 12.1

W naszym przypadku wykres ścieżki okazał się linią prostą. Można wykazać, że wykres toru ruchu jednostajnego jest zawsze linią prostą; i odwrotnie: jeśli wykres drogi w funkcji czasu jest linią prostą, to ruch jest jednostajny.

Powtarzając konstrukcję dla innej prędkości, stwierdzamy, że punkty wykresu dla wyższych prędkości leżą wyżej niż odpowiadające im punkty wykresu dla niższych prędkości (rys. 20). Zatem im większa jest prędkość ruchu jednostajnego, tym bardziej stromy jest wykres ścieżki prostoliniowej, tj. im większy kąt tworzy on z osią czasu.

Ryż. 20. Wykresy toru ruchu jednostajnego przy prędkościach 2 i 3 m/s

Ryż. 21. Wykres tego samego ruchu jak na ryc. 18, narysowany w innej skali

Nachylenie wykresu zależy oczywiście nie tylko od wartości liczbowej prędkości, ale także od wyboru skali czasu i długości. Przykładowo wykres pokazany na ryc. 21 przedstawia ścieżkę w funkcji czasu dla tego samego ruchu, co wykres na ryc. 18, chociaż ma inne nachylenie. Stąd jasno wynika, że możliwe jest porównywanie ruchów według nachylenia wykresów tylko wtedy, gdy są one narysowane w tej samej skali.

Korzystając z wykresów ścieżki, można łatwo rozwiązać różne problemy związane z ruchem. Na przykład na ryc. 18 liniami przerywanymi przedstawia konstrukcje niezbędne do rozwiązania następujących problemów dla danego ruchu: a) znaleźć drogę przebytą w czasie 3,5 s; b) oblicz czas potrzebny na przebycie 9 m. Na rysunku odpowiedzi przedstawiono graficznie (linie przerywane): a) 7 m; b) 4,5 s.

Na wykresach opisujących jednostajny ruch prostoliniowy współrzędne poruszającego się punktu można wykreślić wzdłuż osi rzędnych zamiast po ścieżce. Ten opis otwiera ogromne możliwości. W szczególności umożliwia rozróżnienie kierunku ruchu względem osi. Ponadto, przyjmując początek czasu za zero, można pokazać ruch punktu we wcześniejszych chwilach czasu, co należy uznać za ujemne.

Ryż. 22. Wykresy ruchów z tą samą prędkością, ale w różnych położeniach początkowych poruszającego się punktu

Ryż. 23. Wykresy kilku ruchów z prędkościami ujemnymi

Na przykład na ryc. 22 prosta I to wykres ruchu zachodzącego przy prędkości dodatniej 4 m/s (tj. w kierunku osi), przy czym w chwili początkowej punkt ruchu znajdował się w punkcie o współrzędnej m rysunek przedstawia wykres ruchu zachodzącego z tą samą prędkością, ale przy którym w chwili początkowej punkt ruchu znajduje się w punkcie o współrzędnej (linia II). Prosty. III odpowiada przypadkowi, gdy w tej chwili punkt ruchomy znajdował się w punkcie o współrzędnej m. Wreszcie prosta IV opisuje ruch w przypadku, gdy punkt ruchomy miał w chwili c współrzędną.

Widzimy, że nachylenie wszystkich czterech wykresów jest takie samo: nachylenie zależy tylko od prędkości poruszającego się punktu, a nie od jego położenia początkowego. Przy zmianie położenia początkowego cały wykres jest po prostu przesuwany równolegle do siebie wzdłuż osi w górę lub w dół w odpowiedniej odległości.

Wykresy ruchów zachodzących przy prędkościach ujemnych (czyli w kierunku przeciwnym do kierunku osi) przedstawiono na rys. 23. Są proste, opadające w dół. W przypadku takich ruchów współrzędna punktu maleje z czasem.

12.3. Wykres ścieżki punktu poruszającego się z prędkością odcina odcinek na osi współrzędnych. Jak odległość od punktu początkowego zależy od czasu? Napisz wzór tej zależności.

12.4. Punkt poruszający się z dużą prędkością znajduje się w danej chwili w pewnej odległości od punktu początkowego.

Jak odległość zależy od czasu?

12.5. Punkt poruszający się ruchem jednostajnym po osi miał współrzędne m i m odpowiednio w momentach czasu s i s. Znajdź graficznie, w którym momencie punkt przeszedł przez początek współrzędnych i jaka była współrzędna w momencie początkowym. Znajdź rzut prędkości na oś.

12.6. Korzystając z wykresu drogi, znajdź kiedy i w jakiej odległości od punktu A samochód wyjeżdżający z punktu A zostanie wyprzedzony przez drugi samochód wyjeżdżający z tego samego punktu 20 minut po pierwszym, jeśli pierwszy samochód będzie jechał z prędkością 40 km/h , a drugi porusza się z prędkością 40 km/h z prędkością 60 km/h.

12.7. Korzystając z wykresu znajdź, gdzie i kiedy pojazdy się spotkają, odjeżdżając jednocześnie z prędkością 40 i 60 km/h z punktów A i B, oddalonych od siebie o 100 km.

Wykresy ścieżki można także konstruować dla przypadków, w których ciało porusza się jednostajnie przez pewien okres czasu, następnie porusza się równomiernie, ale z inną prędkością przez kolejny okres czasu, a następnie ponownie zmienia prędkość itp. Na przykład na rys. 26 przedstawia wykres ruchu, na którym ciało poruszało się przez pierwszą godzinę z prędkością 20 km/h, przez drugą godzinę z prędkością 40 km/h, a przez trzecią godzinę z prędkością 15 km/h.

Ćwiczenia:12.8. Skonstruuj wykres drogi ruchu, po której w kolejnych odstępach godzinowych ciało osiągało prędkości 10, -5, 0, 2, -7 km/h. Jakie jest całkowite przemieszczenie ciała?

1. Znalezienie ścieżki za pomocą wykresu prędkości w funkcji czasu

Pokażmy, jak znaleźć drogę przebytą przez ciało, korzystając z wykresu prędkości w funkcji czasu.

Zacznijmy od najprostszego przypadku – ruchu jednostajnego. Rysunek 6.1 przedstawia wykres v(t) – prędkość w funkcji czasu. Jest to odcinek linii prostej równoległy do podstawy czasu, gdyż przy ruchu jednostajnym prędkość jest stała.

Figura zawarta pod tym wykresem jest prostokątem (na rysunku jest zacieniona). Jego powierzchnia jest liczbowo równa iloczynowi prędkości v i czasu ruchu t. Z drugiej strony iloczyn vt jest równy drodze l, którą przebyło ciało. A więc ruchem jednostajnym

ścieżka jest liczbowo równa powierzchni figury zawartej pod wykresem prędkości w funkcji czasu.

Pokażmy teraz, że ruch nierówny ma również tę niezwykłą właściwość.

Niech na przykład wykres prędkości w funkcji czasu będzie wyglądał jak krzywa pokazana na rysunku 6.2.

Podzielmy w myślach cały czas ruchu na tak małe odcinki, aby podczas każdego z nich ruch ciała można uznać za niemal równomierny (podział ten pokazano liniami przerywanymi na rysunku 6.2).

Następnie droga przebyta w każdym takim przedziale jest liczbowo równa powierzchni figury pod odpowiednią bryłą wykresu. Dlatego cała ścieżka jest równa powierzchni figur zawartych pod całym wykresem. (Technika, którą zastosowaliśmy, jest podstawą rachunku całkowego, którego podstawy poznasz na kursie „Początki analizy matematycznej”).

2. Tor i przemieszczenie podczas ruchu prostoliniowego jednostajnie przyspieszonego

Zastosujmy teraz opisaną powyżej metodę do znalezienia ścieżki ruchu prostoliniowego jednostajnie przyspieszonego.

Początkowa prędkość ciała wynosi zero

Skierujmy oś x w kierunku przyspieszenia ciała. Wtedy ax = a, vx = v. Stąd,

Rysunek 6.3 przedstawia wykres v(t).

1. Korzystając z rysunku 6.3 wykazać, że w przypadku ruchu prostoliniowego, jednostajnie przyspieszonego bez prędkości początkowej, tor l wyraża się modułem przyspieszenia a oraz czasem ruchu t wzorem

Główny wniosek:

W przypadku ruchu prostoliniowego, równomiernie przyspieszonego bez prędkości początkowej, droga przebyta przez ciało jest proporcjonalna do kwadratu czasu ruchu.

W ten sposób ruch jednostajnie przyspieszony różni się znacznie od ruchu jednostajnego.

Rysunek 6.4 przedstawia wykresy drogi w funkcji czasu dla dwóch ciał, z których jedno porusza się jednostajnie, a drugie równomiernie przyspiesza bez prędkości początkowej.

2. Spójrz na rysunek 6.4 i odpowiedz na pytania.
a) Jakiego koloru jest wykres ciała poruszającego się ze stałym przyspieszeniem?
b) Jakie jest przyspieszenie tego ciała?
c) Jakie są prędkości ciał w chwili, gdy przebyły tę samą drogę?
d) W którym momencie prędkości ciał są równe?

3. Po ruszeniu samochód w ciągu pierwszych 4 s przebył drogę 20 m. Załóżmy, że samochód porusza się po linii prostej i ma jednostajne przyspieszenie. Nie obliczając przyspieszenia samochodu, określ jaką odległość przejedzie samochód:
a) za 8 s? b) za 16 s? c) za 2 s?

Znajdźmy teraz zależność rzutu przemieszczenia sx na czas. W tym przypadku rzut przyspieszenia na oś x jest dodatni, zatem sx = l, ax = a. Zatem ze wzoru (2) wynika:

sx = axt2/2. (3)

Wzory (2) i (3) są bardzo podobne, co czasami prowadzi do błędów przy rozwiązywaniu prostych problemów. Faktem jest, że wartość prognozy przemieszczenia może być ujemna. Stanie się tak, jeśli oś x będzie skierowana przeciwnie do przemieszczenia: wtedy sx< 0. А путь отрицательным быть не может!

4. Rysunek 6.5 przedstawia wykresy czasu podróży i rzutu przemieszczenia dla określonego ciała. Jakiego koloru jest wykres projekcji przemieszczenia?

Początkowa prędkość ciała nie jest równa zeru

Przypomnijmy, że w tym przypadku zależność rzutu prędkości od czasu wyraża wzór

vx = v0x + axt, (4)

gdzie v0x jest rzutem prędkości początkowej na oś x.

Rozważymy dalej przypadek, gdy v0x > 0, ax > 0. W tym przypadku możemy ponownie skorzystać z faktu, że ścieżka jest liczbowo równa powierzchni figury pod wykresem prędkości w funkcji czasu. (Sami rozważcie inne kombinacje znaków do rzutowania prędkości początkowej i przyspieszenia: wynikiem będzie ten sam ogólny wzór (5).

Rysunek 6.6 przedstawia wykres vx(t) dla v0x > 0, ax > 0.

5. Korzystając z rysunku 6.6 wykazać, że w przypadku ruchu prostoliniowego, jednostajnie przyspieszonego z prędkością początkową, rzut przemieszczenia

sx = v0x + axt2/2.

Ta formuła pozwala znaleźć zależność współrzędnej x ciała od czasu. Przypomnijmy (patrz wzór (6), § 2), że współrzędna x ciała jest powiązana z rzutem jego przemieszczenia sx przez zależność

gdzie x0 jest początkową współrzędną ciała. Stąd,

x = x0 + sx, (6)

Ze wzorów (5), (6) otrzymujemy:

x = x0 + v0xt + axt2/2. (7)

6. Zależność współrzędnej od czasu dla pewnego ciała poruszającego się po osi x wyraża się w jednostkach SI wzorem x = 6 – 5t + t2.
a) Jaka jest początkowa współrzędna ciała?
b) Jaki jest rzut prędkości początkowej na oś x?
c) Jaki jest rzut przyspieszenia na oś x?
d) Narysuj wykres współrzędnej x w funkcji czasu.
e) Narysuj wykres przewidywanej prędkości w funkcji czasu.
f) W którym momencie prędkość ciała jest równa zeru?
g) Czy ciało powróci do punktu wyjścia? Jeśli tak, to w jakim momencie?
h) Czy ciało przejdzie przez początek? Jeśli tak, to w jakim momencie?
i) Narysuj wykres projekcji przemieszczenia w funkcji czasu.
j) Narysuj wykres odległości w funkcji czasu.

3. Zależność drogi od prędkości

Podczas rozwiązywania problemów często wykorzystuje się zależności pomiędzy ścieżką, przyspieszeniem i prędkością (początkową v0, końcową v lub obie). Wyprowadźmy te zależności. Zacznijmy od ruchu bez prędkości początkowej. Ze wzoru (1) otrzymujemy na czas ruchu:

Zastąpmy to wyrażenie wzorem (2) ścieżki:

l = at2/2 = a/2(v/a)2 = v2/2a. (9)

Główny wniosek:

w ruchu prostoliniowym równomiernie przyspieszonym bez prędkości początkowej droga przebyta przez ciało jest proporcjonalna do kwadratu prędkości końcowej.

7. Po ruszeniu samochód nabrał prędkości 10 m/s na dystansie 40 m. Przyjmijmy, że ruch samochodu jest liniowy i ma jednostajne przyspieszenie. Nie obliczając przyspieszenia samochodu, określ, jaką odległość od początku ruchu przebył samochód, gdy jego prędkość była równa: a) 20 m/s? b) 40 m/s? c) 5 m/s?

Zależność (9) można również uzyskać pamiętając, że droga jest liczbowo równa polu figury zawartej pod wykresem prędkości w funkcji czasu (ryc. 6.7).

Ta uwaga pomoże ci łatwo poradzić sobie z kolejnym zadaniem.

8. Korzystając z rysunku 6.8 wykazać, że podczas hamowania ze stałym przyspieszeniem ciało pokonuje drogę lт = v02/2a do całkowitego zatrzymania, gdzie v0 jest prędkością początkową ciała, a a jest modułem przyspieszenia.

W przypadku hamowania pojazdu (samochodu, pociągu) droga przebyta do całkowitego zatrzymania nazywana jest drogą hamowania. Uwaga: droga hamowania przy prędkości początkowej v0 i droga przebyta podczas przyspieszania od zatrzymania do prędkości v0 przy tym samym przyspieszeniu a są takie same.

9. Podczas awaryjnego hamowania na suchym asfalcie przyspieszenie samochodu wynosi w wartości bezwzględnej 5 m/s2. Jaka jest droga hamowania samochodu przy prędkości początkowej: a) 60 km/h (maksymalna dozwolona prędkość w mieście); b) 120 km/h? Znajdź drogę hamowania przy wskazanych prędkościach na oblodzonej nawierzchni, gdy moduł przyspieszenia wynosi 2 m/s2. Porównaj znalezione wartości drogi hamowania z długością klasy.

10. Korzystając z rysunku 6.9 i wzoru wyrażającego pole trapezu poprzez jego wysokość i połowę sumy podstaw, udowodnij, że dla ruchu prostoliniowego jednostajnie przyspieszonego:
a) l = (v2 – v02)/2a, jeśli prędkość ciała wzrasta;
b) l = (v02 – v2)/2a, jeśli prędkość ciała maleje.

11. Udowodnić, że rzuty przemieszczenia, prędkości początkowej i końcowej oraz przyspieszenia są powiązane zależnością

sx = (vx2 – v0x2)/2ax (10)

12. Samochód na trasie 200 m przyspieszył od prędkości 10 m/s do 30 m/s.
a) Z jaką prędkością jechał samochód?
b) W jakim czasie samochód przebył wskazaną drogę?
c) Jaka jest średnia prędkość samochodu?

Dodatkowe pytania i zadania

13. Ostatni wagon odłącza się od jadącego pociągu, po czym pociąg porusza się równomiernie, a wagon jedzie ze stałym przyspieszeniem aż do całkowitego zatrzymania.
a) Narysuj na jednym rysunku wykresy zależności prędkości pociągu i wagonu od czasu.
b) Ile razy droga przebyta przez wagon do przystanku jest mniejsza od drogi przebytej przez pociąg w tym samym czasie?

14. Po opuszczeniu stacji pociąg przez pewien czas jechał ze stałym przyspieszeniem, następnie przez 1 minutę ze stałą prędkością 60 km/h i ponownie ze stałym przyspieszeniem, aż do zatrzymania się na kolejnej stacji. Moduły przyspieszenia podczas przyspieszania i hamowania były różne. Pociąg pokonał odległość między stacjami w ciągu 2 minut.
a) Narysuj schematyczny wykres rzutowania prędkości pociągu w funkcji czasu.
b) Korzystając z tego wykresu, znajdź odległość pomiędzy stacjami.
c) Jaką drogę przejechałby pociąg, gdyby na pierwszym odcinku trasy przyspieszał, a na drugim zwalniał? Jaka byłaby jego maksymalna prędkość?

15. Ciało porusza się ze stałym przyspieszeniem wzdłuż osi x. W chwili początkowej znajdował się w punkcie początkowym współrzędnych, a rzut jego prędkości wynosił 8 m/s. Po 2 s współrzędna ciała wynosiła 12 m.
a) Jaki jest rzut przyspieszenia ciała?
b) Narysuj wykres vx(t).
c) Napisz wzór wyrażający zależność x(t) w jednostkach SI.
d) Czy prędkość ciała będzie wynosić zero? Jeśli tak, to w jakim momencie?
e) Czy ciało dotrze drugi raz do punktu o współrzędnych 12 m? Jeśli tak, to w jakim momencie?
f) Czy ciało powróci do punktu wyjścia? Jeśli tak, to w jakim momencie i jaka będzie przebyta odległość?

16. Po pchnięciu piłka toczy się po pochyłej płaszczyźnie, po czym wraca do punktu wyjścia. Po pchnięciu piłka dwukrotnie znajdowała się w odległości b od punktu początkowego w odstępach czasu t1 i t2. Piłka poruszała się w górę i w dół po pochyłej płaszczyźnie z tym samym przyspieszeniem.
a) Skieruj oś x w górę wzdłuż pochyłej płaszczyzny, wybierz początek w punkcie początkowego położenia kuli i napisz wzór wyrażający zależność x(t), która zawiera moduł prędkości początkowej piłki v0 oraz moduł przyspieszenia piłki a.
b) Korzystając z tego wzoru oraz faktu, że piłka znajdowała się w odległości b od punktu startu w momentach t1 i t2, utwórz układ dwóch równań z dwiema niewiadomymi v0 i a.
c) Po rozwiązaniu tego układu równań wyraź v0 i a w postaci b, t1 i t2.
d) Wyraź całą drogę l przebytą przez piłkę w postaci b, t1 i t2.
e) Znajdź wartości liczbowe v0, a i l dla b = 30 cm, t1 = 1s, t2 = 2s.
f) Wykreśl wykresy vx(t), sx(t), l(t).
g) Korzystając z wykresu sx(t), wyznacz moment, w którym moduł przemieszczenia piłki osiągnął maksimum.

1. Prędkość chwilowa

W tej części rozważymy ruch nierówny. Jednak w tym przypadku będziemy potrzebować wiedzy o prostoliniowym ruchu jednostajnym.

Widzimy, że w równych odstępach czasu samochód pokonuje różne tory, czyli porusza się nierównomiernie.

Skróćmy teraz kolejne odstępy czasowe 20-krotnie – do 0,05 s – i monitorujmy zmianę położenia samochodu przez pół sekundy (nie jest to trudne do zrobienia np. za pomocą nagrania wideo).

Jak krótki musi być odstęp czasu Δt, aby w tym czasie ruch ciała można było uznać za prostoliniowy i równomierny, zależy od charakteru ruchu ciała.

1. Korzystając z rysunku 4.2, wyznacz chwilową prędkość samochodu. Przyjmij, że długość samochodu wynosi 5 m.

Wartość chwilowej prędkości samochodu pokazuje prędkościomierz (rys. 4.3).

Jak znaleźć prędkość chwilową na podstawie wykresu współrzędnych w funkcji czasu

Rysunek 4.4 przedstawia wykres współrzędnych w funkcji czasu dla samochodu poruszającego się po prostej autostradzie.

Widzimy, że porusza się nierównomiernie, ponieważ wykres jego współrzędnych w funkcji czasu jest krzywą, a nie odcinkiem linii prostej.

Pokażmy, jak z tego wykresu wyznaczyć chwilową prędkość samochodu w dowolnym momencie – powiedzmy w chwili t = 3 s (punkt na wykresie).

Aby to zrobić, należy wziąć pod uwagę ruch samochodu w tak krótkim czasie, w którym jego ruch można uznać za liniowy i równomierny.

Rysunek 4.5 pokazuje interesujący nas fragment wykresu z dziesięciokrotnym wzrostem (patrz np. skala czasu).

2. Jaka jest prędkość chwilowa samochodu w chwili t = 3 s?

3. Rozważ rysunek 4.6.
a) W jakich punktach wykresu kąt nachylenia stycznej jest największy? najmniej?
b) Znajdź maksymalną i minimalną prędkość chwilową samochodu w ciągu pierwszych 6 sekund jego ruchu.

2. Średnia prędkość

W wielu zadaniach wykorzystuje się średnią prędkość związaną z przebytą drogą:

waw = l/t. (1)

4. O ile zmniejszy się średnia prędkość wspomnianego samochodu, jeżeli łączny czas jazdy wydłuży się o 1 godzinę ze względu na postoje w ruchu?

Średnia prędkość na dwóch odcinkach ruchu

wav = (l1 + l2)/(t1 + t2), (2)

5. Znajdź:
a) drogę przebytą przez Saszę podczas całego ruchu;
b) całkowity czas ruchu Sashy;
c) Średnia prędkość Sashy.

6. Znajdź:
a) ścieżka, którą Sasha szła pieszo;
b) drogę przebytą przez Saszę podczas całego ruchu;
c) całkowity czas ruchu Sashy;
b) Średnia prędkość Sashy.

7. Porównaj okresy, w których Sasza jeździł i chodził w pierwszym i drugim przypadku.

Podsumujmy omówione powyżej sytuacje.

Rozważmy najpierw przypadek, gdy ciało poruszało się z różnymi prędkościami przez równe okresy czasu.

Można: w tym celu wprowadzamy oznaczenia wszystkich potrzebnych nam wielkości, niezależnie od tego, czy są one znane, czy nieznane. Jest to powszechna technika rozwiązywania wielu problemów.

Oznaczmy cały czas ruchu przez t, całą drogę przez l, a drogę przebytą w pierwszej i drugiej połowie czasu ruchu odpowiednio przez l1 i l2.

8. Wyraź w kategoriach v1, v2 i t:
a) l1 i l2; b) l; c) średnia prędkość.

Rozważmy teraz przypadek, gdy ciało poruszało się z różnymi prędkościami przez pierwszą i drugą połowę drogi.

9. Wyraź w kategoriach v1, v2 i l:
a) t1 i t2; b) t; c) średnia prędkość.

Dodatkowe pytania i zadania

Samochód trzy czwarte całej trasy przebył z prędkością v1, a pozostałą część trasy z prędkością v2.
a) Wyraź cały czas ruchu samochodu w postaci v1, v2 oraz całą przebytą drogę l.
b) Wyraź średnią prędkość samochodu w postaci v1 i v2.
c) Znajdź wartość liczbową średniej prędkości przy v1 = 80 km/h, v2 = 100 km/h.

14. Samochód jechał przez 2 godziny z prędkością 60 km/h. Jak długo potem musi jechać z prędkością 80 km/h, aby jego średnia prędkość na całej trasie wyniosła 66,7 km/h?

Graficzne przedstawienie jednolitego ruchu liniowego

Ruch mechaniczny jest przedstawiony graficznie. Zależność wielkości fizycznych wyraża się za pomocą funkcji. Wyznaczyć:

V (t) - zmiana prędkości w czasie

a(t) - zmiana przyspieszenia w czasie

Za przyspieszenie w funkcji czasu. Ponieważ w ruchu jednostajnym przyspieszenie wynosi zero, zależność a(t) jest linią prostą leżącą na osi czasu.

Zależność prędkości od czasu. Ponieważ ciało porusza się prostoliniowo i równomiernie (v = const), tj. prędkość nie zmienia się w czasie, wówczas wykres zależności prędkości od czasu v(t) jest linią prostą równoległą do osi czasu.

Rzut ruchu ciała jest liczbowo równy polu prostokąta AOBC pod wykresem, ponieważ wielkość wektora ruchu jest równa iloczynowi wektora prędkości i czasu, w którym ruch został wykonany.

Zasada wyznaczania ścieżki za pomocą wykresu v(t): w przypadku prostoliniowego ruchu jednostajnego wielkość wektora przemieszczenia jest równa polu prostokąta pod wykresem prędkości.

Zależność przemieszczenia od czasu. Wykres s(t) - linia nachylona :

Z wykresu wynika, że rzut prędkości jest równy:

Po rozważeniu tego wzoru można stwierdzić, że im większy kąt, tym szybciej ciało się porusza i pokonuje większą odległość w krótszym czasie.

Zasada wyznaczania prędkości z wykresu s(t): Tangens kąta nachylenia wykresu do osi czasu jest równa prędkości ruchu.

Nierówny, prosty ruch.

Ruch jednostajny to ruch ze stałą prędkością. Jeśli prędkość ciała się zmienia, mówimy, że porusza się ono nierównomiernie.

Nazywa się ruch, podczas którego ciało wykonuje nierówne ruchy w równych odstępach czasu nierówny Lub zmienny ruch.

Aby scharakteryzować ruch nierówny, wprowadzono pojęcie prędkości średniej.

Średnia prędkość jazdy równy stosunkowi całej drogi przebytej przez punkt materialny do okresu czasu, w którym tę drogę przebył.

W fizyce największym zainteresowaniem nie jest średnia, ale chwilowa prędkość , który definiuje się jako granicę, do której dąży średnia prędkość w nieskończenie małym okresie czasu Δ T:

Natychmiastowa prędkośćruch zmienny to prędkość ciała w danym momencie lub w danym punkcie trajektorii.

Chwilowa prędkość ciała w dowolnym punkcie krzywoliniowej trajektorii jest skierowana stycznie do trajektorii w tym punkcie.

Na rysunku pokazano różnicę między prędkością średnią i chwilową.

Nazywa się ruch ciała, w którym jego prędkość zmienia się jednakowo w równych odstępach czasu równomiernie przyspieszony Lub ruch jednostajnie zmienny.

Przyspieszenie -jest to wektorowa wielkość fizyczna charakteryzująca szybkość zmiany prędkości, liczbowo równa stosunkowi zmiany prędkości do okresu czasu, w którym ta zmiana nastąpiła.

Jeżeli prędkość zmienia się równomiernie w całym ruchu, to przyspieszenie można obliczyć ze wzoru:

Oznaczenia:

V x - Prędkość ciała w ruchu jednostajnie przyspieszonym po linii prostej

V x o - Prędkość początkowa ciała

a x - Przyspieszenie ciała

t - Czas ruchu ciała

Przyspieszenie pokazuje, jak szybko zmienia się prędkość ciała. Jeśli przyspieszenie jest dodatnie, wówczas prędkość ciała wzrasta, ruch jest przyspieszany. Jeśli przyspieszenie jest ujemne, oznacza to, że prędkość maleje, a ruch jest powolny.

Jednostką przyspieszenia w układzie SI jest [m/s2].

Mierzone jest przyspieszenie akcelerometr

Równanie prędkości dla ruchu jednostajnie przyspieszonego: v x = v xo + a x t

Równanie ruchu prostoliniowego jednostajnie przyspieszonego(ruch podczas ruchu jednostajnie przyspieszonego):

Oznaczenia:

S x - Przemieszczenie ciała podczas ruchu jednostajnie przyspieszonego po linii prostej

V x o - Prędkość początkowa ciała

V x - Prędkość ciała w ruchu jednostajnie przyspieszonym po linii prostej

a x - Przyspieszenie ciała

t - Czas ruchu ciała

Więcej wzorów na znalezienie przemieszczenia podczas ruchu liniowego równomiernie przyspieszonego, które można wykorzystać przy rozwiązywaniu problemów:

Jeśli znana jest prędkość początkowa i końcowa oraz przyspieszenie.

Jeżeli znana jest prędkość początkowa i końcowa ruchu oraz czas całego ruchu

Graficzne przedstawienie nierównego ruchu liniowego

Ruch mechaniczny jest przedstawiony graficznie. Zależność wielkości fizycznych wyraża się za pomocą funkcji. Wyznaczyć:

V(t) – zmiana prędkości w czasie

S(t) - zmiana przemieszczenia (ścieżki) w czasie

1) Metoda analityczna.

Uważamy, że autostrada jest prosta. Zapiszmy równanie ruchu rowerzysty. Ponieważ rowerzysta poruszał się ruchem jednostajnym, jego równanie ruchu ma postać:

(początek współrzędnych umieszczamy w punkcie startu, zatem współrzędna początkowa rowerzysty wynosi zero).

Motocyklista jechał ze stałym przyspieszeniem. Zaczął także poruszać się od punktu startu, zatem jego współrzędna początkowa wynosi zero, prędkość początkowa motocyklisty również wynosi zero (motocyklista zaczął ruszać ze stanu spoczynku).

Biorąc pod uwagę, że motocyklista zaczął poruszać się później, równanie ruchu motocyklisty wygląda następująco:

W tym przypadku prędkość motocyklisty zmieniła się zgodnie z prawem:

W chwili, gdy motocyklista dogonił rowerzystę, ich współrzędne są równe, tj. Lub:

Rozwiązując to równanie dla , znajdujemy czas spotkania:

To jest równanie kwadratowe. Definiujemy dyskryminator:

Określanie korzeni:

Podstawiamy wartości liczbowe do wzorów i obliczamy:

Drugi pierwiastek odrzucamy jako nie odpowiadający fizycznym warunkom problemu: motocyklista nie był w stanie dogonić rowerzysty 0,37 s po tym, jak rowerzysta ruszył, ponieważ sam opuścił punkt startu zaledwie 2 s po ruszeniu przez rowerzystę.

Zatem czas dogonienia motocyklisty z rowerzystą:

Podstawmy tę wartość czasu do wzoru na prawo zmiany prędkości motocyklisty i znajdźmy wartość jego prędkości w tym momencie:

2) Metoda graficzna.

Na tej samej płaszczyźnie współrzędnych budujemy wykresy zmian w czasie współrzędnych rowerzysty i motocyklisty (wykres dla rowerzysty jest na czerwono, dla motocyklisty – na zielono). Można zauważyć, że zależność współrzędnej od czasu dla rowerzysty jest funkcją liniową, a wykres tej funkcji jest linią prostą (przypadek ruchu jednostajnego prostoliniowego). Motocyklista poruszał się ze jednostajnym przyspieszeniem, zatem zależność współrzędnych motocyklisty od czasu jest funkcją kwadratową, której wykresem jest parabola.