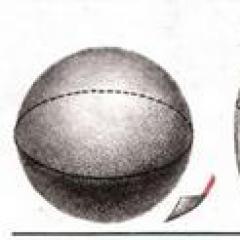
Вивертання сфери навиворіт. Для тих, хто не любить математику
Великий математик Давид Гільберт сказав якось, що математичну теорію можна вважати досконалою лише тоді, коли її вдається викласти першому зустрічному. Послідовники Гільберта приходять у повний відчай, намагаючись жити за цим рецептом. Математика дедалі більше спеціалізується, і нині вченому математику часом варто великої праці навіть своїм колегам пояснити суть розв'язуваних ним завдань. Однак іноді дослідження у провідних і, здавалося б, недоступних розумінню галузях цієї науки призводять до відкриття, яке цікаве для непрофесіонала і в той же час може бути пояснено без надмірного спрощення. Вражаючий приклад цього - теорема Стефена Смейла про так звані регулярні відображення сфери, опублікована в 1959 р.
Область, у якій тоді працював Смейл, – диференціальна топологія – одна з найабстрактніших галузей сучасної математики. Тим дивніше, що таки вдалося вигадати наочне пояснення одному з найдивовижніших наслідків з теореми Смейла. Зокрема, можна продемонструвати, як треба вивертати сферу навиворіт.
У звичайному сенсі це, звісно, неможливо: сферу неодмінно довелося б розірвати. Але в диференціальній топології дозволяється - подумки, зрозуміло, - протягувати поверхню крізь себе - такі «правила гри» у цій науці. Але тоді одразу впадає у вічі просте рішення.

Треба стискати протилежні сторони до центру, доки вони не пройдуть один через один (I). Внутрішня пофарбована поверхня (II) проступає з двох протилежних країв. Продовжимо цей процес «витягування» внутрішньої поверхні доти, поки кільце, утворене частиною зовнішньої поверхні (II), що залишилася, зовсім не зникне. На жаль, при цьому процесі кільце утворює тугу петлю (III), яку доводиться затягнути. В результаті виходить рубець (IV), а це не задовольняє диференціальних топологів, тому що вони розглядають лише так звані «гладкі поверхні», які не мають жодних кутів і зламів.
Отже, завдання полягає в тому, щоб вивернути назовні сферу таким чином, щоб, позбавляючись від кільця, не отримати рубця. І тут інтуїція знову підказує, що завдання не вирішене. Коли Смейл вперше оголосив, що може довести існування рішення, йому ніхто не повірив. Але інтуїція була неправа: у доказі Смейла не знайшлося жодної логічної помилки. Математики переконалися, що теоретично можна простежити підтвердження крок за кроком і знайти явний опис деформації, що вивертає сферу. Але це було так складно, що здавалося безнадійною справою. Протягом деякого часу після відкриття Смейла було відомо, що в принципі можна вивернути назовні сферу без рубця, але ніхто не мав жодного уявлення, як це здійснити.
Але, зрештою, математики з цим завданням впоралися. Як зрозумієте, розглянувши малюнки. Вони цікаві.
Хоча доказ Смейла не складався з одних малюнків. Цікаво, що в його роботі їх взагалі немає - надто вже складні ті постаті, які у неявному вигляді містяться в його абстрактному аналітичному апараті. Їх не вдалося б зобразити найвигадливішому художнику - фантазія математиків разюча. Але, мабуть, ще більш вражаюча їхня здатність передавати один одному найскладніші ідеї, не вдаючись до малюнків. Історія з вивертанням сфери - яскраве тому свідчення. Вона стала відомою широкому загалу завдяки французькому топологу Рене Тома, який дізнався про неї від свого колеги Бернара Морена, а той, у свою чергу, - від американця Арнольда Шапіро, винахідника цієї «вивертки». Це особливо цікаво, якщо врахувати, що Бернар Морен сліпий.

На цих картинках показано, як можна вивернути сферу навиворіт, і при цьому не порушити вимог диференціальної топології. Спочатку треба зблизити протилежні сторони сірої сфери (А), продавлюючи їх один крізь одного. Тоді з обох боків проступає пофарбована поверхня (В). Потім треба розтягнути один із забарвлених шматків (С) таким чином, щоб отримати поверхню, що нагадує сідло на двох «ногах» (О). Ці дві ноги перекручують проти годинникової стрілки та отримують поверхню Е. Вона ж показана знову (Р) «в розрізі» за допомогою стрічок, які, як і в «сфері з рубцем», зображують поперечні перерізи на десяти різних рівнях.
Далі немає сенсу зображати виходять на кожному етапі поверхні - аж надто вони складні. Але можна, якщо завгодно, розглянути стрічки на всіх 10 рівнях і подумки домалювати. Один етап (H2) ми все-таки вирішили показати - просто, щоб можна було собі уявити, який тип фігур, що виходять. Поверхня G з'являється після стиснення та обертання на 90° сідла поверхні Р.
Ще кілька кроків. А саме: між етапами I і J дві однакові формою ноги проходять один крізь одного. У кожного стрічкового перерізу поверхні на етапі J є дві сірі сторони, звернені один до одного. Між етапами J та К внутрішній шар розширюється, а зовнішній стискається; виходить поверхня К - абсолютно така сама, як J, але тільки кольори помінялися місцями.
Далі всі дії йдуть у «зворотному порядку». Ви можете скласти про них уявлення, розглядаючи картинки I, Н, С і т. д. Потрібно лише міняти місцями кольори стрічок на кожній картинці. Закінчення цього другого ряду картинок ми наводимо. Поверхня L відповідає поверхні F, L2 - Е, тощо.
Забарвлена сфера (поверхня Р) відповідає сірій сфері (поверхні А). Отже, деформація виконана і рубця немає. Сама можливість цього трюку була вперше доведена С. Смейлом. А всі послідовні етапи деформації вигадав А. Шапіро…
PS Про що ще говорять британські вчені: про те, що механізм вивертання сфери навиворіт часом не більш філософський, ніж, скажімо, програма для PDF, створена якимось талановитим програмістом.
У тривимірному просторі можна вивернути навиворіт у класі занурень, тобто з можливими самоперетинами, але без перегинів. Іншими словами, образ сфери у кожний момент деформації має залишатися гладким, тобто диференційованим.
Вивертання сфери - це зовсім не логічний парадокс, це теорема, лише дуже контрінтуїтивна. Більш точно:
Досить важко уявити конкретний приклад такого сімейства занурень, хоча існує безліч ілюстрацій та фільмів. З іншого боку, набагато простіше довести, що таке сімейство існує, і це саме зробив Смейл.
Історія
Цей парадокс був відкритий Смейлом у 1958 році. Згідно з легендою, коли Смейл спробував опублікувати цю теорему, він отримав відгук, який говорив, що твердження очевидно неправильне, тому що в процесі такого вивертання ступінь відображення Гауса повинна зберігатися. [ ] Дійсно, ступінь відображення Гауса повинна зберігатися, зокрема це показує, що коло не можна «вивернути» у площині, але ступеня відображення Гауса у і у в обидві рівні 1. Більше того, ступінь будь-якого вкладення дорівнює 1.
Варіації та узагальнення
Напишіть відгук про статтю "Вивертання сфери"
Література
- Smale, Stephen Classification of immersions of the 2-sphere. Trans. Амер. Math. Soc. 90 1958 281-290.
- Франсіс, Дж. Москва: Мир, 1991. Глава 6. Вивертання сфери навиворіт.
Примітки
Уривок, що характеризує Вивертання сфери
— Знову ж таки, полковнику, — говорив генерал, — не можу я залишити половину людей у лісі. Я вас прошу, я вас прошу, повторив він, зайняти позицію і приготуватися до атаки.— А вас прошу не мішуватись не своя справа, — відповів полковник. - Коли б ви був кавалерист...
- Я не кавалерист, полковник, але я російський генерал, і якщо вам це невідомо.
- Дуже відомо, ваше превосходительство, - раптом скрикнув, чіпаючи коня, полковник, і роблячись червоно-червоним. - Чи не завгодно завітати в ланцюги, і ви подивитеся, що цей позиція нікуди непридатний. Я не хочу винищити свою полицю для вашого задоволення.
— Ви забуваєте, полковнику. Я не задоволення свого дотримуюсь і говорити цього не дозволю.
Генерал, приймаючи запрошення полковника на турнір хоробрості, випроставши груди і насупившись, поїхав з ним разом у напрямку до ланцюга, ніби вся їхня розбіжність мала вирішитися там, у ланцюгу, під кулями. Вони приїхали в коло, кілька куль пролетіло над ними, і вони мовчки зупинилися. Дивитися в ланцюзі нічого було, так як і з того місця, на якому вони стояли, ясно було, що по кущах і ярах кавалерії діяти неможливо, і що французи обходять ліве крило. Генерал і полковник строго і значно дивилися, як два півні, що готуються до бою, один на одного, даремно вичікуючи ознак боягузтва. Обидва витримали іспит. Так як говорити було нічого, і ні тому, ні іншому не хотілося дати привід іншому сказати, що він перший виїхав з-під куль, вони довго простояли б там, взаємно відчуваючи хоробрість, якби в цей час у лісі, майже ззаду їх, не почулися тріскотня рушниць і глухий крик, що зливався. Французи напали на солдатів, які перебували у лісі з дровами. Гусарам уже не можна було відступати разом із піхотою. Вони були відрізані від шляху відступу ліворуч французьким ланцюгом. Тепер, як ні незручна була місцевість, необхідно було атакувати, щоб прокласти собі дорогу.
Ескадрон, де служив Ростов, що тільки-но встиг сісти на коней, був зупинений обличчям до ворога. Знову, як і на Енському мосту, між ескадроном і ворогом нікого не було, і між ними, розділяючи їх, лежала та ж страшна риса невідомості та страху, наче риса, що відокремлює живих від мертвих. Всі люди відчували цю межу, і питання про те, чи перейдуть чи ні і як перейдуть вони межу, хвилювало їх.
Уявімо, що «звичайна» двовимірна сфера S 2 зроблена з еластичного матеріалу, який може проходити крізь себе. Чи можна вивернути сферу навиворіт у звичайному тривимірному просторі $$\mathbb(R)^3$$ без зламів та розривів, але з можливим самоперетином (тобто в класі занурень)?
У 2000 році Смейл склав список з 18 завдань, які, на його думку, мають бути вирішені у XXI столітті. Цей список складений у дусі проблем Гільберта, і, як і складені пізніше завдання тисячоліття, включає гіпотезу Рімана, питання про рівність класів P і NP, проблему вирішення рівнянь Навье - Стокса, а також нині доведену Перельманом гіпотезу Пуанкаре. Смейл склав свій список на прохання Арнольда, який займав тоді пост президента міжнародного математичного союзу, який, швидше за все, взяв ідею цього списку зі списку проблем Гільберта.
І, нарешті, питання: чи можна «вивернути» коло в площині, тобто знайти безперервне сімейство занурень, як вище?
Коментарі
Цікаво. Приходить на думку наступна річ. Уявімо сферу у вигляді стереографічної проекції - площину з нескінченністю. Тоді вивертання сфери навиворіт виглядає просто як «згортання» площини на інший бік, тобто. з іншою орієнтацією. Тут десь дірка у міркуваннях, так?
Ну справа в тому, що стереографічна проекція має на увазі виділення точки на сфері, якій не відповідає нічого на площині, а це змінює правила гри, адже за умовами сферу не можна розривати, точно й точку виколювати не можна.
Ну в принципі я підозрював, що там слабке місце з нескінченно віддаленою точкою. Хотів просто знати незалежну думку;).
Мишко, хотілося б почути, чи зустрічаються K3 поверхні теорії струн, і якщо так, то як саме вони там виникають?
Так, трапляються іноді. У контексті компактифікації. K3 має групу голономій $$SU(2)\subset SU(2)\times SU(2)$$ і тому зберігає половину суперсиметрій. Феноменологічно такі моделі не дуже цікаві, але люди все одно їх розглядають.
Я вивертаю сферу без зламів ще простіше, ніж фільм. Треба встромити пальцем частину поверхні сфери всередину. Цю внутрішню частину сфери повернути на 180 градусів, отвір закриється без перегинів. Меридіани сфери, що були колами, перетворяться на «вісімки» з меншою головкою всередині більшої. Далі роздмухуємо внутрішню майже кульку доти, поки не просочиться назовні. Звичайно вид його виявиться вивернутим. Залишається те, що було більшою частиною, а тепер меншою порівняно з роздутою, розгорнути на 180 градусів. Затягнутий отвір розкриється, вм'ятину розпрямляємо, і ціль досягнута!
Тут виходить точка стає нескінченністю, а нескінченність точкою. Або, «однакість всесвіту»: що всередину, що назовні.
Тому виникає парадигма – мікрокосм можна вивчати за допомогою макрокосмосу та навпаки.
Питання межі радіуса =]h/2;2/h[. Тут h використовується як метрична межа точності вимірювань, тобто та сама епсилон поділена на два.
Також фізичне існування такої сфери можна довести чи спростувати для різних випадків.
Чи я не правий?