Miejsce punktów. Twierdzenie o położeniu punktów równoodległych od dwóch danych punktów, w postaci geometrycznej i analitycznej

Miejsce punktów na płaszczyźnie to figura składająca się ze wszystkich punktów na płaszczyźnie, które mają określoną właściwość.

T.1.29. Locus punktów równoodległych od dwóch danych punktów jest punktem środkowym prostopadłym do odcinka linii łączącej te punkty.

Na rysunku 71 środkowy prostopadły CC jest narysowany do segmentu. T.1.29 stwierdza, że: a) każdy punkt prostej jest w równej odległości od A i B; b) każdy punkt płaszczyzny równoodległy od A i B leży na linii prostej

Poniżej wymieniono kilka geometrycznych lokalizacji punktów na płaszczyźnie.

1. Locus punktów znajdujących się w danej odległości od danego punktu to okrąg o środku w tym punkcie i promieniu równym podanej odległości.

2. Locus punktów znajdujących się w określonej odległości od danej prostej składa się z dwóch prostych, z których każda jest równoległa do danej i znajduje się w określonej odległości od niej.

3. Miejsce punktów równoodległych od dwóch przecinających się linii prostych składa się z dwóch linii prostych, na których leżą dwusieczne wszystkich kątów uzyskanych na przecięciu tych linii prostych.

4. Miejscem położenia punktów, z których odcinek jest widoczny pod danym kątem a i leżących po jednej stronie prostej A B, jest łuk kołowy z końcami w punktach A i B.

Metoda miejsc geometrycznych stosowana w rozwiązywaniu problemów konstrukcyjnych opiera się na następującym.

Załóżmy, że musimy skonstruować punkt X spełniający dwa warunki. Zbiór punktów spełniających pierwszy warunek to figura to zbiór punktów spełniających drugi warunek, istnieje figura. Poszukiwany punkt X należy do, czyli jest ich punktem wspólnym.

Przykład 1. Konstruuj wzdłuż obwodu pod kątem B równym i wysokości opadającej z wierzchołka A.

Rozwiązanie. Niech problem zostanie rozwiązany i zbudowany (ryc. 72). Układając odcinki na linii prostej otrzymujemy trójkąty równoramienne

W oparciu o powyższe rozumowanie, budowę można przeprowadzić w następującej kolejności:

1) Narysuj linię prostą i połóż na niej odcinek

2) W pewnej odległości od linii prostej narysuj linię prostą równoległą

3) Mając wierzchołek w punkcie D, budujemy kąt równy Point

A - jeden z wierzchołków pożądanego trójkąta.

4) Prostopadłe środkowe rysujemy do odcinków punktów B i C przecięcia tych pionów środkowych linią prostą - pozostałe dwa wierzchołki pożądanego trójkąta.

Dowód na to, że pożądany jest wykonywany w następujący sposób: wysokość tego trójkąta jest równa konstrukcyjnie, równoramienny, - kąt zewnętrzny tego trójkąta, patrz T. 1. 22), konstrukcyjnie.

Posiadanie jakiejś własności.

Przykłady [ | ]

Formalna definicja[ | ]

W ogólnym przypadku miejsce punktów jest formułowane przez predykat, którego argumentem jest punkt w danej przestrzeni liniowej. Parametry predykatu mogą być różnych typów. Predykat nazywa się wyznacznik umiejscowienie punktów. Parametry predykatu są nazywane różnice umiejscowienie punktów (nie mylić z różnicowaniem w analizie).

Rola różnic w wprowadzaniu różnic gatunkowych do figury. Liczba różnic może być dowolna; różnice mogą w ogóle nie istnieć.

Jeżeli podano wyznacznik, gdzie M (\ styl wyświetlania M)- punkt, - dyferencjały, następnie wymagana liczba A (\ styl wyświetlania A) zestaw w postaci: " A (\ styl wyświetlania A)- umiejscowienie punktów M (\ styl wyświetlania M) takie, że P (M, a, b, c,…) (\ styl wyświetlania P (M, \; a, \; b, \; c, \; \ ldots))”. Dalej, zwykle wskazuje się rolę różnic, nada się im nazwy w odniesieniu do tej konkretnej postaci. Sama figura jest rozumiana jako zbiór (zbiór) punktów M (\ styl wyświetlania M) dla których dla każdego określonego zestawu wartości a, b, c,… (\ styl wyświetlania a, \; b, \; c, \; \ ldots) wypowiedź P (M, a, b, c,…) (\ styl wyświetlania P (M, \; a, \; b, \; c, \; \ ldots)) zamienia się w tożsamość. Każdy konkretny zestaw wartości różnicowych definiuje osobną liczbę, z których każda i wszystkie w agregacie nazywa się nazwą liczby, która jest określona przez GMT.

W sformułowaniu słownym wypowiedź orzecznikowa jest dźwięczna literacko, to znaczy z udziałem różnego rodzaju zwrotów itp. w celu eufonii. Czasami w przypadku prostych wyznaczników generalnie rezygnuje się z oznaczeń literowych.

Przykład: parabola jest zdefiniowana jako zbiór wszystkich takich punktów M (\ styl wyświetlania M) ta odległość od M (\ styl wyświetlania M) do momentu F (\ styl wyświetlania F) jest równa odległości od M (\ styl wyświetlania M) prosto l (\ styl wyświetlania l)... Następnie różnice paraboli - F (\ styl wyświetlania F) oraz l (\ styl wyświetlania l); wyznacznik - predykat P (M, F, l) = (ρ (M, F) = ρ l (M, l)) (\ styl wyświetlania P (M, \; F, \; l) = (\ rho (M, \; F ) = \ rho _ (l) (M, \; l))), gdzie ρ (\ styl wyświetlania \ rho)- odległość między dwoma punktami (metryczna), ρ l (\ styl wyświetlania \ rho _ (l))- odległość od punktu do linii prostej. I mówią: „Parabola to geometryczne miejsce punktów M (\ styl wyświetlania M) w równej odległości od punktu F (\ styl wyświetlania F) i prosto l (\ styl wyświetlania l)... Punkt F (\ styl wyświetlania F) zwany ogniskiem paraboli i linią prostą l (\ styl wyświetlania l)- dyrektorka ”.

Cele Lekcji:

Edukacyjne: pokazać nową metodę rozwiązywania problemów konstruowania geometrycznego miejsca punktów; Nauczyć, jak go używać w rozwiązywaniu problemów.
Rozwijanie: rozwój myślenia wizualno-figuratywnego; zainteresowanie poznawcze.
Wychowanie: rozwijanie umiejętności planowania pracy, poszukiwania racjonalnych sposobów jej realizacji, umiejętności rozsądnej obrony własnego zdania, krytycznej oceny wyniku.

Cele Lekcji:

Nauka nowego materiału.
Sprawdź umiejętność rozwiązywania problemów przez uczniów.

Plan lekcji:

Definicje.
Przykład 1.
Przykład 2.
Przykład 3.
Część teoretyczna.
Pojęcia ogólne.

Wstęp.

Starożytną kulturę egipską i babilońską w dziedzinie matematyki kontynuowali Grecy. Nie tylko przyswoili sobie całe doświadczenie swojej geometrii, ale także poszli znacznie dalej. Naukowcy starożytna Grecja udało się wprowadzić zgromadzoną wiedzę geometryczną do systemu, a tym samym położyć podwaliny geometrii jako nauki dedukcyjnej.

Kupcy greccy poznali matematykę Wschodu, torując szlaki handlowe. Ale mieszkańcy Wschodu nie mieli prawie żadnej teorii, a Grecy szybko to odkryli. Zadawali pytania: dlaczego w trójkącie równoramiennym dwa kąty u podstawy są równe; dlaczego pole trójkąta jest równe połowie pola prostokąta o tych samych podstawach i wysokościach?

Niestety nie zachowały się żadne pierwotne źródła opisujące wczesny okres rozwój matematyki greckiej. Dopiero dzięki odrestaurowanym tekstom z IV wieku p.n.e. oraz pracom uczonych arabskich, bogatych w przekłady pism autorów starożytnej Grecji, mamy edycje Euklidesa, Archimedesa, Apoloniusza i innych. wspaniali ludzie... Ale w tych pracach jest już przedstawiona w pełni rozwinięta nauka matematyczna.

Matematyka grecka przeszła długą i trudną drogę rozwoju, począwszy od VI wieku p.n.e. i do VI wieku. Historycy nauki zgodnie z naturą wiedzy wyróżniają trzy okresy jej rozwoju:

Nagromadzenie jednostek fakty matematyczne i problemy (6 - 5B.B. p.n.e.).
Systematyzacja zdobytej wiedzy (4 - 3 wieki p.n.e.).
Okres matematyki obliczeniowej (III wpne - VI w.).

Locus of points (GMT).

Definicje.

Miejsce geometryczne- termin używany w dawnej literaturze z zakresu geometrii i jest nadal używany w literaturze edukacyjnej na oznaczenie zbiór punktów spełniających określony warunek, z reguły o charakterze geometrycznym. Na przykład: położenie punktów równoodległych od dwóch danych punktów A i B jest punktem środkowym prostopadłym do odcinka AB. Czasami mówią o geometrycznym miejscu linii prostych i innych figur.

Nazwa nawiązuje do idei linii jako „miejsca”, w którym znajdują się punkty.

W geometrii trajektoria pewnego punktu poruszającego się zgodnie z zadanym wzorem lub warunkiem. Na przykład okrąg jest miejscem umieszczenia punktu, który porusza się na płaszczyźnie tak, że odległość od jego położenia do środka pozostaje niezmieniona.

Miejsce punktów (GMT) to zbiór punktów, który obejmuje wszystkie punkty spełniające określony warunek i tylko one.

Miejsce punktów (GMT)- figura retoryczna w matematyce, używana do określenia kształt geometryczny jako zbiór punktów o pewnej własności.

Przykłady.

Punkt środkowy prostopadły do segmentu jest umiejscowieniem punktów równoodległych od końców segmentu.
Okrąg to zbiór punktów równoodległych od danego punktu, zwany środkiem okręgu.
Parabola to zbiór punktów równoodległych od punktu (nazywanego ogniskiem) i linii prostej (nazywanej kierownicą).

Przykład 1.

Prostopadła środkowa dowolnego segmentu to zbiór punktów (tj. zbiór wszystkich punktów) równoodległych od końców tego segmentu. Niech PO będzie prostopadłe do AB i AO = OB:

Wtedy odległości od dowolnego punktu P leżącego na środkowej prostopadłej PO do końców A i B odcinka AB są takie same i równe d.

Tak więc każdy punkt środkowej prostopadłej odcinka ma następującą właściwość: jest równoodległy od końców odcinka.

Przykład 2.

Dwusieczna kąta to zbiór punktów równoodległych od jego boków.

Przykład 3.

Okrąg to zbiór punktów (czyli zbiór wszystkich punktów) równoodległych od jego środka (na rysunku pokazano jeden z tych punktów - A).

Akord przejście przez środek koła (na przykład BC, rysunek 1) nazywa się średnicą i jest oznaczone d lub D. Średnica Jest największym cięciwem równym dwóm promieniom (d = 2 r).

Tangens... Załóżmy, że sieczna PQ (ryc. 2) przechodzi przez punkty K i M okręgu. Załóżmy również, że punkt M porusza się po okręgu, zbliżając się do punktu K. Wtedy sieczna PQ zmieni swoje położenie, obracając się wokół punktu K. Gdy punkt M zbliża się do punktu K, sieczna PQ będzie miała tendencję do pewnego ograniczenia pozycja AB. Prostą AB nazywamy styczną do okręgu w punkcie K. Punkt K nazywamy punktem styczności. Linia styczna i okrąg mają tylko jeden wspólny punkt - punkt styczności.

Właściwości styczne.

Styczna do okręgu jest prostopadła do promienia narysowanego do punktu stycznej (AB prostopadle do OK, rys. 2).
Z punktu poza okręgiem możesz narysować dwie styczne do tego samego okręgu; ich segmenty są równe AB = AC (rys. 3).

Człon Czy część okręgu jest ograniczona łukiem ACB i odpowiadającą cięciwą AB (rys. 4). Długość prostopadłej CD, poprowadzonej od środka cięciwy AB do przecięcia z łukiem ACB, nazywana jest wysokością segmentu.

Narożniki w kole.

Kąt środkowy to kąt utworzony przez dwa promienie (∠AOB, rys. 5). Kąt wpisany - kąt utworzony przez dwa cięciwy AB i AC wyprowadzone z jednego z nich wspólny punkt(∠BAC, rys. 4). Opisany kąt to kąt utworzony przez dwie styczne AB i AC poprowadzone z jednego wspólnego punktu (∠BAC, rys. 3).

Relacje między elementami koła.

Wpisany narożnik(∠ABC, ryc. 7) jest równy połowie kąta środkowego spoczywającego na tym samym łuku AmC (∠AOC, ryc. 7). Dlatego wszystkie kąty wpisane (rys. 7) oparte na tym samym łuku (AmC, rys. 7) są równe. A ponieważ kąt środkowy zawiera tyle samo stopni co jego łuk (AmC, rys. 7), to każdy kąt wpisany jest mierzony przez połowę łuku, na którym się opiera (w naszym przypadku AmC).

Wszystkie kąty wpisane oparte na półokręgu (∠APB, ∠AQB,…, rys. 8) są proste.

Zastrzyk(∠AOD, Rys. 9), utworzony przez dwa cięciwy (AB i CD), jest mierzony przez połówkową sumę łuków między jego bokami: (AnD + CmB) / 2.

Kąt (∠AOD, rys. 10) utworzony przez dwie sieczne (AO i OD) jest mierzony przez połowę różnicy łuków między jego bokami: (AnD - BmC) / 2.

Kąt (∠DCB, rys. 11) utworzony przez styczną i cięciwę (AB i CD) jest mierzony przez połowę łuku w nim zawartego: CmD / 2.

Kąt (∠BOC, rys. 12) utworzony przez styczną i sieczną (CO i BO) jest mierzony przez połowę różnicy łuków między jego bokami: (BmC - CnD) / 2.

Opisany kąt (∠AOC, rys. 12), utworzony przez dwie styczne (CO i AO), jest mierzony przez połowę różnicy łuków zamkniętych między jego bokami: (ABC - CDA) / 2.

Iloczyny odcinków cięciw (AB i CD, ryc. 13 lub ryc. 14), na które są podzielone przez punkt przecięcia, są równe: AO · BO = CO · DO.

Kwadrat stycznej jest równy iloczynowi siecznej i jej części zewnętrznej (rys. 12): OA 2 = OB · OD. Tę właściwość można uznać za szczególny przypadek z ryc. 14.

Akord(AB , rys. 15) prostopadle do średnicy( PŁYTA CD) , O w połowie: AO = OB.

Ryż. 15

Interesujący fakt:

Gratulacje dla P-Razdnika.

Z naukowego punktu widzenia pi to stosunek obwodu koła do jego średnicy. Wydaje się, że to prosta sprawa, ale od czasów starożytnych niepokoi umysły matematyków. I nadal ekscytuje. Do tego stopnia, że naukowcy - 20 lat temu - zgodzili się obchodzić święta w tym dniu. I wezwali całą postępową społeczność do przyłączenia się do obchodów. Dołącza się: zjada okrągłe Pi-rogi, ty-PI-vayet, koniecznie Pi-vo i wydaje dźwięki Pi, kiedy się spotykają.

Fani będą rywalizować, pamiętając znaki pi. I spróbują pobić rekord 24-letniego chińskiego studenta Liu Chao, który bezbłędnie nazwał 68890 znaków z pamięci. Zajęło mu to 24 godziny i 4 minuty.

Wyjazd obchodów wyznaczono na 14 marca – datę, która w pisowni amerykańskiej wygląda na 3,14 – czyli pierwsze trzy cyfry Pi.
Według legendy kapłani babilońscy wiedzieli o liczbie „Pi”. Używany w budownictwie Wieża Babel... Ale nie mogli dokładnie obliczyć jego wartości i dlatego nie poradzili sobie z projektem. Sam symbol liczby „Pi” został po raz pierwszy użyty w jego pismach w 1706 r. przez matematyka Williama Johna (William Jones). Ale w rzeczywistości zakorzenił się po 1737 roku dzięki wysiłkom szwedzkiego matematyka Leonharda Eulera.

Amerykański fizyk Larry Shaw wpadł na pomysł uczczenia święta.
Nie ma dokładnej odpowiedzi na pytanie, ile cyfr w liczbie „Pi” po przecinku. Najprawdopodobniej jest ich nieskończenie wiele. A główna cecha jest to, że sekwencja tych znaków się nie powtarza. Dziś znanych jest 12 411 bilionów. Przebadanych 500 miliardów. I nie znaleziono żadnych powtórzeń.

Według niektórych wybitnych fizyków i matematyków, na przykład Davida Baileya, Petera Borwina i Simona Plouffe'a (David Bailey, Peter Borewin, Simon Plouffe), nikt ich - powtórzeń - nigdy nie znajdzie. Przynajmniej napisz cały Wszechświat znakami. Tak, przynajmniej ile Wszechświatów ... I w tym naukowcy widzą rodzaj ukrytego mistycyzmu. Uważa się, że liczba „Pi” zakodowała nieskończony pierwotny chaos, który później stał się harmonią. Albo jakieś tajemnicze informacje.

Pytania:

Jaka jest definicja koła i koła?
Jakie nowe koncepcje spotkałeś?
Co nazywa się miejscem punktów?
Jaka jest różnica między średnicą a promieniem?
Jak znaleźć promień okręgu opisanego wokół trójkąta?

Lista wykorzystanych źródeł:

Lekcja na temat „Geometria wizualna”
AP Savin Metoda geometrycznego miejsca / Przedmiot do wyboru z matematyki: Instruktaż dla klas 7-9 Liceum... Opracowany przez I.L. Nikolskiej. - M.: Edukacja, s. 74.
Smirnova I.M., Smirnov V.A. Geometria: podręcznik dla klas 7-9 instytucje edukacyjne... - M .: Mnemosina, 2005, s. 84.
Sharygin I.F. Geometria. Klasy 7-9: Podręcznik do kształcenia ogólnego instytucje edukacyjne... - M .: Drop, s. 76.
K. Mazur „Rozwiązanie głównych problemów konkursowych w matematyce zbioru pod redakcją M. I. Skanaviego”

Pracował na lekcji:

Samylina M.V.

S.A. Poturnak

Władimir Łagowskyj

Zadaj pytanie na temat nowoczesna edukacja, wyrazić pomysł lub rozwiązać pilny problem, możesz Forum Edukacyjne gdzie rada wychowawcza świeżej myśli i działania spotyka się na arenie międzynarodowej. Tworząc blog, Nie tylko zwiększysz swój status kompetentnego nauczyciela, ale także wniesiesz znaczący wkład w rozwój szkoły przyszłości. Gildia Liderów Oświaty otwiera drzwi dla najwyższej klasy specjalistów i zaprasza do współpracy w kierunku tworzenia najlepszych szkół na świecie.

Miejsce punktów. Mediana prostopadła. Dwusieczna kąta.

Koło. Koło . Środek koła. Promień. Łuk. Sieczna. Akord.

Średnica. Tangens i jego własności. Człon. Sektor. Narożniki w kole.

Długość łuku . Radian. Relacje między elementami koła.

Miejsce geometryczne – ta mnogość ze wszystkich punkty, satysfakcjonujące które mają pewne dane warunki.

PRZYKŁAD 1. Mediana prostopadła dowolnego odcinka linii jest geometryczną

miejsce punktów (tj. zbiór wszystkich punktów), równoodległe z

końce tego segmentu. Niech PO AB i AO = OB:

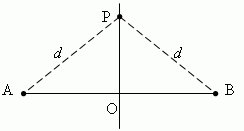
Następnie odległości od dowolnego punktu P leżący na środkowym prostopadłym PO, do końców A i B odcinka AB są takie same i równeD.

Zatem, każdy punkt środkowej prostopadłej człon ma następującą właściwość: jest w równej odległości od końców segmentu.

Przykład 2. Dwusieczna kąt jest rozmieszczenie punktów równoodległych od jego boków .

PRZYKŁAD 3 . Okrąg to miejsce punktów (tj. zbiór stan

wszystkie punkty), równoodległy od jego centrum ( na ryc. podczas Sama Zana

z tych punktów - A).

Koło - to jest umiejscowienie punktów (tj. zbiór wszystkich punktów) na płaszczyźnie ,równoodległy z jednego punktu,zwany środkiem koła. Odcinek łączący środek okręgu z dowolnym z jego punktów nazywa się promień i oznaczoner lub r. Część płaszczyzny ograniczona kołem nazywa się na około. Część koła (

A m B, (Patrz Rysunek 39) nazywa łuk. Proste PQ,przechodząc przez punkty m oraz n koła (ryc. 39 ) nazywa się sieczna, i jego segment MN leżąc wewnątrz kręgu - akord.

Akord przechodzący przez środek koła (na przykład pne , rys. 39) nosi nazwęśrednica i oznaczone D lub D.Średnica to największa cięciwa równa dwóm promieniom (D= 2 r).

Tangens. Załóżmy, że secans PQ (rys. 40) przechodzi przez punkty K i M kręgi. Załóżmy również, że punkt m porusza się po okręgu, zbliżając się do punktu K. Następnie sieczna linia PQ zmieni swoją pozycję, obracając się wokół punktu K ... W miarę zbliżania się do punktu M do punktu K secans PQ będzie dążył do pewnej ograniczającej pozycji AB. Proste AB nazywa tangens do okręgu w punkcie K. Punkt K nazywa punkt kontaktu. Linia styczna i okrąg mają tylko jeden wspólny punkt - punkt styczności.

Właściwości styczne.

1) DOWznoszenie się do okręgu jest prostopadłe do narysowanego promienia do punktu kontaktowego(AB OK, rys. 40) .

2) Z punktu znajdującego się poza okręgiem możesz narysować dwie styczne do ten sam okrąg; ich segmenty są równe (rys. 41).

Człon Jest częścią koła łuk ograniczony ACB i odpowiedni akord AB (rys. 42). Długość prostopadła Płyta CD od środka akordu AB przed przekroczeniem łuku ACB nazywa się wzrost człon.

Sektor – to jest część koła ograniczona łukiem A m b i dwa promienie OA i OB, narysowany na końcach tego łuku (ryc. 43).

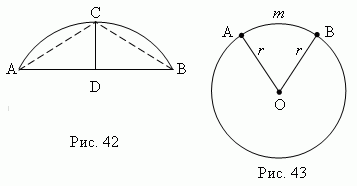
Narożniki w kole. Środkowy róg – kąt utworzony przez dwa promienie ( AOB, rys. 43). Wpisany narożnik- kąt utworzony przez dwa cięciwy AB i AC zaczerpnięte z ich wspólnego punktu ( BA C, rys. 44). Opisany kąt- kąt utworzony przez dwie styczne AB i AC zaczerpnięty z jednego wspólnego punktu ( BAC, rys. 41).

Długość łuku okrąg jest proporcjonalny do jego promieniar i odpowiedni róg środkowy :

l = r

Tak więc, jeśli znamy długość łukuja i promień r, to wartość odpowiedniego kąta środkowego

można zdefiniować na podstawie ich relacji: = l / r.

Ten wzór jest podstawą do określenia wymiar w radianach rogi. Więc jeślija = r, następnie = 1 i mówimy, że kąt równa się 1 radianowi (jest to oznaczane przez: = 1 zadowolony). Więc mamy po definicji radiany jako jednostki kątowe: radian to kąt środkowy ( AOB, rys. 43), w którym długość łuku jest równa jego promieniowi (A m B = AO, rys. 43). Więc, miarą radiacyjną dowolnego kąta jest stosunek długości łuku narysowanego przez dowolny promień i zawartego między bokami tego kąta do jego promienia. W szczególności, zgodnie ze wzorem długości łuku, obwódCmożna wyrazić w następujący sposób:

gdzie jest zdefiniowany jako relacjaCdo średnicy koła 2r :

= C / 2 r.

Liczba niewymierna; jego przybliżona wartość 3.1415926…

Z drugiej strony, 2- to jest kąt kołowy koło, które w układzie stopni miar wynosi 360º. W praktyce często zdarza się, że zarówno promień łuku, jak i kąt są nieznane. W takim przypadku długość łuku można obliczyć za pomocą przybliżonego wzoru Huygensa:

P 2ja + (2NS) / 3 ,

gdzie (patrz rys. 42): P- długość łuku ACB; ja- długość cięciwy AC; L- długość cięciwy AB... Jeśli łuk zawiera nie więcej niż 60º błąd względny tego wzoru nie przekracza 0,5%.

Relacje między elementami koła. Wpisany narożnik (ABC, rys. 45) równy połowie kąta środkowego , opierając się na tym samym łuku A mC (AOC, rys. 45) . Dlatego, wszystkie wpisane kąty(rys. 45), na podstawie jednego i to ten sam łuk(A m C , rys. 45), są równe. A ponieważ kąt środkowy zawiera taką samą liczbę stopni jak jego łuk ( A m C , rys. 45), następnie każdy wpisany kąt jest mierzony przez połowę łuku, na którym się opiera(w naszym przypadku A m C).

Wszystkie wpisane rogi spoczywają na półokręgu (APB, AQB,…, rys. 46), prosty (Udowodnij to, proszę!).

Zastrzyk(AOD, rys. 47 )utworzone przez dwa akordy( AB i CD), środki Xia jako pół sumy łuków zamkniętych między jego bokami: (A n D + C m B) / 2.

Zastrzyk(AOD, rys. 48) , utworzone przez dwie sieczki (AO i OD ), mierzona połową różnicy łuków, więźniowie między jej stronami: (A n D– B m C ) / 2. sieczna(CO i BO ), mierzone o połowę różnicy łuki między jego bokami: (B m C – C n D ) / 2 .

Opisany kąt(AOC, rys. 50 )utworzone przez dwie styczne( CO i AO ), jest mierzona przez połowę różnicy łuków zawartych między jego imprezy:(ABC – CDA) / 2 .

Produkty segmentów akordów (AB i CD , rys. 51 lub rys. 52), przez które są dzielone przez punkt przecięcia, są równe: AO BO = CO DO.

Kwadrat stycznej jest równy iloczynowi siecznej przez jej część zewnętrzną (rys. 50): OA 2 = OB O D (Udowodnij to!). Tę właściwość można uznać za przypadek szczególny. Rys. 52.

Akord(AB , rys. 53) prostopadle do średnicy( Płyta CD ), jest podzielony w punkcie ich przecięcia O w połowie: AO = OB.

( Spróbuj to udowodnić!).

Posiadanie jakiejś własności.

Kolegium YouTube

1 / 3

✪ Definiowanie paraboli jako GMT

✪ 124. Problemy na powierzchni drugiego rzędu. Miejsce punktów

✪ Odporność materiałów. Wykład 21 (tensor naprężeń, naprężenia główne)

Napisy na filmie obcojęzycznym

Cześć drodzy przyjaciele! Będziemy teraz studiować z tobą geometrię, a potem algebrę, a potem wszystko pomieszamy i nazwiemy matematyką. Bardzo proste pytanie. Wyobraź sobie, że tam, gdzie umieściłem białą kropkę, gra muzyka (jeden głośnik). A potem pojawił się technik i umieścił głośnik w miejscu różowej kropki. Co więcej, odległość między nimi jest dość duża. Jeśli staniesz w zielonym krzyżu, to dla Ciebie muzyka zostanie dostarczona z dwóch miejsc z opóźnieniem. Jeden z większym opóźnieniem niż drugi. Jak byś stanął, aby móc słyszeć muzykę lewym i prawym uchem dokładnie w ten sam sposób, zsynchronizowany? Oznacza to, że stań w równych odległościach od dwóch głośników. Odpowiedź jest bardzo prosta, oczywiście wiesz, czy poszedłeś do co najmniej 7 klasy. A jeśli nie, możesz zgadywać intuicyjnie. Konieczne jest zbudowanie odcinka łączącego różowy i biały punkt i narysowanie prostopadłego w jego środku (w jego środku). Wtedy dowolny punkt pionu prostopadłego na tej planszy jest jednakowo oddalony od różu i od bieli. Dlaczego? Bardzo prosta. Są tu dwa identyczne trójkąty. Dlaczego są takie same? Ponieważ mają wspólną stronę, dwie kolejne strony są oznaczone równymi pociągnięciami. A kąty proste są oczywiście sobie równe. W konsekwencji mamy prawo stawiać równe znaki na takich stronach. Tak więc narysowaliśmy z tobą miejsce punktów równo odległych od dwóch podanych punktów. A co z dwiema liniami prostymi? Narysujmy kilka linii. Na początek narysuję dwie równoległe linie. To są dwa brzegi i chcesz płynąć (z jakiegokolwiek powodu) w równej odległości od obu brzegów. Jak zbudować tę trajektorię? Narysujmy ponownie prostopadłą do dwóch równoległych linii. Znajdźmy jego środek. A potem, uzbrojeni w oko, próbujemy narysować zieloną linię równoległą do tych dwóch brzegów. Oczywiście, jeśli weźmiemy dowolny punkt na tej zielonej linii i sprowadzimy prostopadłą do jakiegoś brzegu, to zobaczymy prostokąt. Oznacza to, że te strony będą równe. Linie proste mogą i przecinają się. I ty też możesz łatwo rozwiązać taki problem: zbiór punktów równie odległych od tych dwóch prostych to para dwusiecznych. Wszystkie te rozwiązania są zbudowane za pomocą cyrkla i linijki i są dość łatwe do przekazania geometrii. A teraz zaproponuję inny zbiór, którego nie dają dwa identyczne obiekty, ale z pierwszego zadania weźmiemy jeden obiekt: gdzieś jest punkt, a drugi obiekt z drugiego: jest prosta. Co więcej, ten punkt jest nam potrzebny od dawna, więc wpiszemy dla niego osobistą nazwę: powiemy, że jest to punkt F. Linia prosta jest również spersonalizowana i nazywana literą d. Wyobraź sobie przez chwilę, że jest to granica plaży: powyżej jest plaża, a poniżej morze. A punkt F to np. stoisko z lodami. A chcesz siedzieć tak, aby odległość do stoiska z lodami i do brzegu była równa. Wtedy przykład takiego miejsca jest dość oczywisty: tak jak tu i tutaj budujemy prostopadłą od punktu F do linii d, znajdujemy jej środek i to jest najkorzystniejsze miejsce: do kiosku masz bardzo mało i bardzo mało do morza ... Jak inaczej można usiąść, żeby była też taka sama odległość do kiosku i do brzegu morza? Oto kolejny przykład. Jeśli zbudujemy kwadrat o takim boku, to równość tych boków i prostopadłej tutaj również gwarantuje nam, że ten punkt jest dobry. Co więcej, jasne jest, że skoro przędza rozciąga się w obu kierunkach, to tutaj możemy narysować ten sam kwadrat. Rozwiązanie będzie symetryczne. Napiszmy rozwiązanie takiego problemu. Czego szukamy to: potrzebujemy zbioru liter M (punkty wyznaczone przez literę M), a warunkiem dla nich jest to: (ta może być litera M) odległość od dowolnego punktu od tego zbioru do F to... Zamiast słowa „odległość” napiszę teraz literę „ro”, bo chcę odległość od punktu M do linii d. Skoro szukamy kompletu, to są tutaj szelki. I szukamy wszystkich takich punktów, oznaczonych literą M, aby ta równość została zachowana. Znaleźliśmy już dwa. Mam prawo zakreślić ten punkt zielonym kółkiem i ten też. Czy jest między nimi przynajmniej jeden punkt, który należy do tego zestawu? Równie odległe od F i d. Tak jest. Wypróbujmy następujące. Przesuńmy się o pewną wartość na lewo od znanego punktu ze zbioru. Pytanie: wtedy dostajemy punkt z tego samego seta? Spójrzmy na tę figurę, na ten czworokąt. To jest prostokąt, więc tutaj dozwolone jest również jedno pociągnięcie. Jak odległość od otrzymanego punktu do F ma się do tego odcinka? Oczywiście jest większy, nie można tu wstawić jednego pociągnięcia, bo takim ukośnym segmentem jest hipotinus w trójkącie, gdzie noga zaznaczona jest jednym pociągnięciem. Ten punkt jest za nisko, za blisko prostej d. Więc musisz go trochę podnieść. Podnieś go tak, aby był wystarczająco daleko od d i trochę bliżej F. Jak dokładnie - jeszcze się nie dowiemy, ale jest to możliwe. Pomysł jest taki: poruszając się w lewo i idąc w górę, możemy uzyskać punkty należące do zbioru M. A jeśli przyjmiemy też, że krok może być dowolnie mały, to zrozumiemy, że zbiór jest ciągły: jest to prosta które można narysować ruchem ręki bez zatrzymywania się i nigdzie nie skacząc. Wiemy też, że linia jest symetryczna. Ta zielona linia jest reprezentacją tego zestawu, na co wskazują nawiasy klamrowe. Okazuje się, że to parabola. To jest geometryczna definicja paraboli. I tu zaczynają się problemy.

Przykłady

Rola różnic w wprowadzaniu różnic gatunkowych do figury. Liczba różnic może być dowolna; różnice mogą w ogóle nie istnieć.